Методика обучения геометрии в основной школе с использованием фузионистского подхода 13. 00. 02 Теория и методика обучения и воспитания (математика)

Вид материала

Автореферат

Содержание Актуальность проблемы Цель исследования Объект исследования Гипотеза исследования Ведущая идея исследования Теоретико-методологическим обоснованием Источники исследования Научная новизна и теоретическая значимость Практическая значимость На защиту выносятся Апробация и внедрение результатов исследования. Основная часть Подготовительный этап Констатирующий этап Критерии оценивания. Выше среднего Формирующий этап Макет урока по теме «Первый и второй признаки равенства треугольников». Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника Домашнее задание. ... Полное содержание

Подобный материал:

• Методика обучения решению математических задач учащихся основной школы в условиях дифференциации, 489.79kb.
• Методика дифференцированного обучения решению математических задач с использованием, 253.93kb.
• Вестник Калужского университета 200, 154.13kb.
• Программа-минимум кандидатского экзамена по специальности 13. 00. 02 «Теория и методика, 223.63kb.
• Программа-минимум кандидатского экзамена по специальности 13. 00. 02 «Теория и методика, 223.55kb.
• Программа вступительного экзамена в аспирантуру по курсу теория и методика обучения, 45.44kb.
• Взаимосвязанное обогащение синонимической лексикой родной и русской речи учащихся VI-VII, 389.12kb.
• Методика обучения студентов педагогических вузов будущих учителей математики интегральному, 295.38kb.
• Методика обучения профессионально ориентированному устному общению студентов бакалавриата, 955.93kb.
• Программа-минимум кандидатского экзамена по специальности 13. 00. 08 «Теория и методика, 336.94kb.

УДК 373.5.016.026:514.1(574) На правах рукописи


Рабинович Борис Владимирович


МЕТОДИКА ОБУЧЕНИЯ ГЕОМЕТРИИ В ОСНОВНОЙ ШКОЛЕ

С ИСПОЛЬЗОВАНИЕМ ФУЗИОНИСТСКОГО ПОДХОДА


13.00.02 – Теория и методика обучения и воспитания (математика)


Автореферат

диссертации на соискание учёной степени

кандидата педагогических наук


Республика Казахстан

Алматы, 2010


Работа выполнена в Казахском Национальном педагогическом

университете имени Абая


Научные руководители: доктор педагогических наук

Абылкасымова А.Е.

кандидат педагогических наук

Пустовалова Н.И.


Официальные оппоненты: доктор педагогических наук

Мубараков А. М.


кандидат педагогических наук

Балыбердина Е. Г.


Ведущая организация: Павлодарский государственный университет им. С. Торайгырова


Защита диссертации состоится « » __________2010г. в ______ часов на заседании диссертационного совета Д 14.08.05. по защите диссертаций на соискание степени доктора педагогических наук в Казахском Национальном педагогическом университете имени Абая по адресу: 050012, г. Алматы, ул. Толе-би, 86, ауд.415.


С диссертацией можно ознакомиться в библиотеке Казахского Национального педагогического университета имени Абая по адресу: 050010, ул. Казыбек-би, 30.


Автореферат разослан «___» ____________ 2010г.


Ученый секретарь

диссертационного совета Ж.А. Шокыбаев

Введение


Одним из аспектов развития личности является развитие мыслительной деятельности, в частности, пространственного мышления. Важным подспорьем в этом вопросе выступает процесс обучения геометрии в средней школе.

Проблеме повышения эффективности обучения математике в школе, а также их методическим аспектам посвящены работы А.Е.Абылкасымовой, И.Б.Бекбоева, Н.Я. Виленкина, Г.Д. Глейзера, А.К.Кагазбаевой, А.М.Мубаракова, Е. Ж. Смагулова и др.

Проблемой формирования пространственного мышления занимались многие ученые психологи: Б.Г. Ананьев, О.И. Галкина, Л.Л. Гурова, В.П.. Кабанова-Меллер, A.M. Леонтьев, Б.Ф. Ломов, С.Л. Рубинштейн Е.Ф., Н.Ф. Талызина, И.С. Якиманская и другие. В их исследованиях раскрывается природа восприятия пространства, в частности, процессы ощущений, восприятий и представлений рассматриваются в неразрывном единстве.

Проблемой развития пространственного мышления занимались многие математики - методисты: Александров А.Д., Вернер А.А., Глейзер,Г.Д., Гусев В.А., Маслова Г.Г., Пышкало А.М., Семушин А.Д., Ходот Т.Г., Шарыгин И.Ф. и другие.

Особый интерес представляют исследования Г.Д. Глейзера, который описывает уровни развития пространственных представлений, дающие возможность представить этапы этого процесса. «Так, «элементарный» уровень должен быть достигнут учащимися в начальной школе, «фрагментарный» - в 5-6 классах, «статически-динамический»- в 7-8, «динамический»- в 9-10, «творческий»- в 11 классе. Отдельные учащиеся, однако, могут продвигаться значительно быстрее».

Анализ программы курса геометрии основной школы показал, что в нем содержатся богатые возможности для формирования и развития не только пространственных представлений, но и пространственного воображения учащихся. Это объясняется тем, что геометрия, как учебный предмет, имеет в своем распоряжении огромный потенциал, содержащийся в задачном материале, имеющем решающее значение для развития пространственного и логического мышления учащихся. Задачи в геометрии не только объект, реализующий теорию на практике, но и средство, раскрывающее содержание этого курса. Поэтому возникает естественная потребность в специальных задачах стереометрического характера, которые, с одной стороны, способствуют развитию пространственного мышления, с другой стороны, направлены на формирование понятий и усвоение теорем планиметрии.

Анализ психолого-педагогической и учебно-методической литературы показывает, что недостаточный уровень пространственных представлений восьмиклассников объясняется тем, что пространственные объекты изучаются только в 5-6 классах и при этом им уделяется незначительное внимание, а в 7-9 классах изучаются только плоские фигуры. Последнее связано с тем, что в современной школе сложилась практика изучения геометрии в следующей последовательности: вначале изучается планиметрия
(7-9 класс) и лишь затем – стереометрия (10-11 класс). Между тем, как отмечают психологи, уже школьники 6 класса готовы к восприятию и оперированию мысленными пространственными объектами, поэтому изучение только двумерных фигур тормозит развитие пространственного мышления

Таким образом, сложилось противоречие между необходимостью использования фузионистского подхода в процессе обучения учащихся при изучении курса планиметрии и недостаточной научно-методической разработанностью и освещенностью в психолого-педагогической и методической литературе методики внедрения данного подхода с помощью специальных средств, направленных на развитие пространственного мышления. Это определило проблему диссертационного исследования, которая состоит в выявлении и раскрытии возможных путей реализации фузионистского подхода в процессе обучения геометрии в основной школе.

Актуальность проблемы и необходимость её решения позволили определить тему исследования: «Методика обучения геометрии в основной школе с использованием фузионистского подхода»

Цель исследования: разработать научно-обоснованную методику обучения геометрии в основной школе с использованием фузионистского подхода, содержательным компонентом которой является специально разработанный комплекс задач, направленный на развитие пространственного мышления и экспериментально проверить её эффективность.

Объект исследования: процесс обучения геометрии в основной школе.

Предмет исследования: методика обучения геометрии в основной школе с использованием фузионистского подхода.

Гипотеза исследования: процесс обучения геометрии в основной школе будет более эффективен, если будет осуществляться на основе фузионистского подхода, посредством внедрения в учебный процесс специально разработанного комплекса задач, направленного на развитие пространственного мышления, так как при решении данных задач у учащихся формируются образы пространственных фигур и начальные умения оперирования этими образами, позволяя осознать связь свойств реальных, окружающих нас объектов со свойствами фигур планиметрии.

Для достижения поставленной цели и проверки выдвинутой гипотезы исследования потребовалось решение следующих задач:

1. Изучить различные подходы к обучению геометрии в школе и выявить их особенности.

2. Раскрыть роль фузионистского подхода в курсе геометрии основной школы.

3. Разработать комплекс задач, направленный на развитие пространственного мышления для внедрения в учебный процесс на уроках геометрии в 7 – 9 классах.

4. Разработать методику реализации фузионистского подхода в процессе обучения геометрии в основной школе, содержательным компонентом которой является разработанный комплекс задач.

5. Экспериментально проверить и оценить педагогическую эффективность разработанной методики реализации фузионистского подхода при изучении курса геометрии основной школы.

Ведущая идея исследования: целенаправленное и систематическое использование специального комплекса задач на уроках геометрии в 7 – 9 классах будет способствовать развитию пространственного мышления учащихся и как следствие, повышению качества знаний, так как при решении данных задач у учащихся формируются образы пространственных фигур, позволяя осознать связь свойств реальных, окружающих нас объектов со свойствами фигур планиметрии.

Теоретико-методологическим обоснованием работы явились: исследования по теории: познания, поэтапного формирования умственных действий, учебных задач, а также по проблеме развития пространственного мышления и фузионистского подхода в процессе изучения школьной геометрии, теории и методики обучения математике в школе (Абылкасымова А. Е., Баймуханов Б.Б., Бекбоев И. Б., Болтянский В. Г., Глейзер Г.Д., Гусев В.А., Добрица В. П., Кагазбаева А. К., Смирнов С.Д., Шарыгин И.Ф. и др.)

Источники исследования: труды философов, психологов, педагогов и ученых по проблеме исследования, официальные и нормативные документы Республики Казахстан в области образования и науки.

В ходе решения поставленных задач применялись различные методы исследования: теоретические, социопедагогические, эмпирические, диагностические, экспериментальные, методы математической статистики.

Научная новизна и теоретическая значимость исследования заключается в том, что впервые была решена проблема обучения геометрии учащихся 7-9 классов на основе фузионистского подхода посредством внедрения в учебный процесс специального комплекса задач, направленного на развитие пространственного мышления и удовлетворяющего возрастным особенностям подростков и разработана методика включения его в учебный процесс.

Практическая значимость исследования заключается в том, что в учебный процесс внедрен специально разработанный комплекс задач планиметрии в стереометрической среде, направленный на развитие пространственного мышления, обеспечивающий связь теоретических знаний и практических умений учащихся.

Базой опытно-экспериментальной работы явились: Первая гимназия, школа-лицей «Дарын», СШ №2 города Петропавловска. Экспериментальная работа по теме исследования велась в период с 1999г. по 2008 г.

На защиту выносятся:

1. Теоретическое обоснование роли и места фузионистского подхода в обучении геометрии и необходимости его внедрения в учебный процесс основной школы при изучении курса планиметрии с целью решения проблемы развития пространственного мышления школьников.

2. Методическое обеспечение процесса обучения геометрии учащихся 7-9 классов при изучении планиметрии на фузионистской основе, включающее комплекс задач, в которых плоские геометрические фигуры, рассматриваются как элементы пространственных объектов.

3. Результаты экспериментальной проверки эффективности реализации методики обучения геометрии в основной школе с использованием фузионистского подхода, за счет включения в содержательный компонент разработанного комплекса задач.

Апробация и внедрение результатов исследования. Основные положения диссертации докладывались на научно-практических конференциях разного уровня (международных, региональных), на методических семинарах учителей и методистов г. Алматы (2000г., 2010г.), Петропавловска (1993г., 2001г.), Омска (1995г.), Тулы (2008); На научно-методическом семинаре факультета информационных технологий, кафедры математики СКГУ им. М. Козыбаева; лекциях, семинарских и практических занятиях по геометрии, истории математики и методике преподавания геометрии. Кроме того, апробация и использование результатов исследования осуществлялась в ходе педагогического эксперимента в 7 – 9 классах, затем в 10 – 11 классах Первой гимназии г. Петропавловска, в 7- 11х классах средней школы № 2 и в 7- 11х классах школы-лицея «Дарын», г. Петропавловска.

Структура диссертации. Диссертация состоит из введения, двух разделов, заключения, списка использованных источников и приложения.

ОСНОВНАЯ ЧАСТЬ


В первом разделе «Теоретические основы обучения геометрии в основной школе с использованием фузионистского подхода» на основе анализа психолого-педагогической и научно-методической литературы, практического изучения педагогических и методических аспектов проблемы формирования пространственного мышления школьников обосновывается целесообразность реализации фузионистского подхода, выделяются направления разработки методики его реализации в процессе обучения геометрии основной школы.

Анализируются различные подходы обучения геометрии в их историческом развитии – от догматически-эмпирических методов древних цивилизаций Египта, Вавилона, Китая до систематического, аксиоматического построения курса геометрии Евклидом и его последователями вплоть до наших дней. На основе анализа различных подходов обучения геометрии и возникших в связи с этим противоречий определяются направления путей совершенствования обучения геометрии.

Особенностью обучения геометрии на современном этапе является деление курса на две части - пропедевтическую и систематическую. В первой учащиеся знакомятся с видами геометрических фигур, причём как плоских, так и пространственных, и с их основными свойствами, учатся измерять длины, находят по формулам площади и объёмы некоторых фигур. Основной метод обучения на этом этапе – эмпирический. Во второй части – «систематическом курсе» – учащиеся приступают к собственно математической деятельности – учатся проводить строгие доказательства теорем, изучают новые, более тонкие, свойства геометрических фигур, применяют аксиоматический метод.

В казахстанской школе к систематическому развитию логического мышления учащихся приобщают на достаточно раннем этапе развития, что является несомненным плюсом и одним из компонентов геометрического образования.

Не менее важным компонентом является пространственное мышление. Оно также является одной из важнейших составляющих формирования интеллектуально развитой личности.

Процесс формирования пространственного мышления может активно протекать лишь в тесной связи с развитием логического мышления и речи учащихся. Проблема восприятия пространства и формирования пространственного мышления тесно смыкается с проблемой мыслительных задач и формирования геометрических понятий.

При обучении геометрии в 7-9 классах учащиеся не рассматривают пространственных фигур, в результате чего развитие их пространственных представлений затормаживается. Так как этот процесс связан с развитием логического мышления и речи учащихся, то происходит нарушение гармоничности функционирования их мышления.

Наше исследование показало, что уже младшие школьники вполне готовы к усвоению понятия трёхмерного пространства, широкому его использованию в процессе решения учебных задач. Хотя ознакомление с теоретическим содержанием этого понятия осуществляется лишь в старших классах.

Попытки применения фузионистского подхода в обучении геометрии повторялись неоднократно на протяжении двух столетий. Термин «фузионизм»  происходит от латинс­кого слова fusio - слияние. Фузионизмом называли слитное преподава­ние нескольких разделов математики: алгебры и геометрии; геометрии и арифметики; наконец, планиметрии и стереометрии.

Методические особенности фузионистского подхода в организации содержательного и процессуального компонентов обучения геометрии в основной школе определяются внедрением в учебный процесс системы специально подобранных задач стереометрического характера, удовлетворяющих разработанным критериям.

В нашем исследовании задачей применения фузионистского подхода было обеспечить продолжение развития пространственного мышления в период обучения в 7 – 9-х классах. При этом основная часть должна приходится все же на развитие пространственных представлений. Поэтому стереометрическая составляющая в курсе геометрии 7 – 9 должна содержать по возможности меньше теоретического материала, а ее элементы целесообразно вводить через задачи. Эти задачи, с одной стороны, направлены на изучение планиметрии, с другой стороны, они способствуют развитию пространственных представлений, подготавливают учащихся к успешному усвоению систематического курса стереометрии.

Проведенный анализ результатов научных исследований позволил нам выделить требования к комплексу задач, способствующих развитию пространственного мышления учащихся, формированию логического мышления с учетом их индивидуальных особенностей и возможностей.

Преемственность стереометрических знаний является одним из условий реализации фузионистского подхода. Реализация преемственности с точки зрения стереометрии, соотносится с внутрипредметными связями, прежде всего с планиметрией и с межпредметными связями с черчением, трудовым обучением, физикой и т.п. Находясь в органической взаимосвязи, все эти части являются неотъемлемыми для реализации фузионистского подхода.

Учитывая психолого-педагогические условия развития пространственных представлений и пространственного воображения, требования к содержанию планиметрической и стереометрической составляющей курса геометрии 7 – 9, нами определены критерии отбора задач стереометрического характера. При этом нами выделены два подхода к осуществлению изучения элементов стереометрии - непосредственное включение элементов стереометрии в курс планиметрии; косвенное изучение стереометрических объектов через включение в систему упражнений действующих учебных пособий стереометрического материала.

Первый подход называют «чистым фузионизмом», а второй - «частично-фузионистическим». Именно второго подхода мы придерживались в процессе нашего исследования.

Во втором разделе «Методика реализации идеи фузионизма в обучении геометрии учащихся в 7- 9 классах» дается характеристика разработанного комплекса задач как содержательного компонента методики реализации фузионистского подхода в обучении геометрии в основной школе, разработанного на основе выработанных критериев. С учетом принципов дидактики, задачный материал внутри каждой темы подобран таким образом, чтобы его решение способствовало уяснению учащимися данной темы и новых математических идей, заложенных в ней. Правильная постановка задач и подбор упражнений в обучении математике во многом определяет современную методику преподавания. так как решение задач служит различным конкретным целям обучения.

Таким образом, в учебном процессе необходимо тесно переплетать элементы стереометрии с материалом планиметрии, являющимся основным. Определим основные темы планиметрии, изучающиеся в основной школе Казахстана, в которые целесообразно включать стереометрический материал, не нарушая сформулированные выше принципы и критерии.

Анализ школьных программ и учебников по геометрии в 7 – 9 классах позволил выявить темы, при изучении которых применим фузионистский подход и объекты стереометрии, которые следует при этом использовать. Так, треугольники, четырехугольники и другие многоугольники могут служить гранями многогранников. Наиболее простыми из них является треугольная пирамида. Поэтому целесообразно ставить задачи на треугольники именно на этом многограннике.

Учащиеся уже знакомы с такими четырехугольниками как квадрат и прямоугольник, поэтому, в некоторых задачах используется и четырехугольная пирамида, основанием которой служит квадрат или прямоугольник. Окружность и круг являются элементами фигур вращения: цилиндра, конуса и шара (сферы). Изучение темы параллельные прямые можно сопровождать рассмотрением призмы, поскольку боковые ребра призмы являются параллельными отрезками. При этом в 7-м классе достаточно ограничиться прямой призмой, поскольку ее грани являются прямоугольниками. Наклонная призма появляется уже после изучения свойств параллелограмма и трапеции. Правильные пирамиды и призмы используются уже в 9-м классе.

С целью проверки сформулированной гипотезы был проведен педагогический эксперимент, состоящий из четырех этапов: подготовительного, констатирующего, формирующего и контрольного. Основной базой для проведения эксперимента являлись: Первая гимназия, школа-лицей «Дарын» и СШ № 2 города Петропавловска. Эксперимент продолжался с 1999 г по 2008 г. Кроме того, в последующие годы и по настоящее время учителя продолжают использовать разработанный в процессе эксперимента комплекс задач для реализации фузионистского подхода при обучении геометрии.

С целью подтверждения актуальности выбранной темы научного исследования и определения возможных путей решения исследуемой проблемы был проведено анкетирование учителей математики города Петропавловска. Результаты анкетирования подтвердили, что наибольшие трудности при обучении школьников геометрии учителя связывают со стереометрией и отмечают в ряду основных причин трудностей у учащихся недостаточно развитые пространственные представления геометрических фигур, умение применять теоретический материал при решении задач и недостаточное владение приемами решения геометрических задач.

Подготовительный этап проводился в 1999 – 2003 годах. На этом этапе изучалась и анализировалась научная, психолого-педагогическая и учебно-методическая литературы по проблеме исследования и проведен анализ состояния проблемы в современных условиях. Разрабатывались критерии отбора задач, на основе которых подбирались, составлялись и классифицировались задачи «планиметрии в стереометрической среде» для будущего комплекса задач, направленного на развитие пространственного мышления. Разрабатывалась методика включения данного комплекса задач в учебный процесс.

Констатирующий этап эксперимента проводился в 2003 году. Для его проведения были выбраны 4 класса: 2 экспериментальных класса – 7-й класс «А» в Первой гимназии и 7-й класс «А» в СШ № 2. А в качестве контрольных классов – 7-й класс школы-лицея «Дарын», где обучаются не только городские дети, но и дети из сельской местности по рекомендации районного отдела образования и 7 «В» класс Первой гимназии. Количество участников эксперимента составило – 104 человека.

На данном этапе важно было решить следующие задачи:

– установить, какими учебными действиями владеют учащиеся 7-х классов;

– изучить возможности развития пространственного мышления учащихся основной школы;

– разработать критерии и показатели уровней развития пространственного мышления школьников;

- выявить уровни развития пространственного мышления учащихся на начало эксперимента;

- сравнить уровни развития пространственного мышления учащихся контрольной и экспериментальной групп;

Для выявления уровня развития пространственного мышления на начало эксперимента в контрольных и экспериментальных классах мы провели самостоятельную работу №1, в качестве которой учащимся был предложен тест, состоящий из 15 заданий. Задания теста направлены на проверку не только способности учащихся к деятельности по созданию пространственного образа, но и на элементы оперирования пространственными образами, что позволяет говорить о проверке уровня развития пространственного мышления. В связи с тем, что учащиеся до начала эксперимента в контрольных и экспериментальных классах обучались по традиционной методике, то задания в этом тесте подобраны таким образом, чтобы они опирались на знания, полученные учащимися на предыдущем этапе обучения, то есть в 1-х – 6-х классах.

Критерии оценивания. Правильность выполнения задания определялась числом верных ответов на каждый из вопросов, поставленных в задании. Всего 39 вопросов.

Задания оценивали по баллам (правильно выполненное задание - 1 балл, неправильно выполненное задание - 0 баллов). При верных ответах во всех 15 заданиях учащиеся могли получить 39 баллов, при всех неверно выполненных заданиях - 0. Таким образом, результаты выполнения работы учащимися, выраженные в числе баллов, распределились от 0 до 39 баллов.

В соответствии с принятой в школе четырех балльной системой отметок, было выделено четыре уровня:

- Высокий (ставилась отметка «5») - набравшим не менее 90% (бралась целая часть числа, составляющего данный процент от 39 – 35 баллов);

- Выше среднего (ставилась отметка «4») - набравшим от 75% , но меньше 90% (от 29 до 34 баллов);

- Средний (ставилась отметка «3») - набравшим от 50%, но меньше 75% (от 19 до 28);

- Низкий (ставилась отметка «2») - набравшим меньше 50% (от 0 до 18 баллов).

Ряды распределения учащихся контрольных и экспериментальных классов по уровням развития пространственного мышления и отметкам, полученным за выполнение работы, использовались в качестве показателей уровня развития пространственного мышления учащихся. Результаты учащихся обеих выборок показаны в таблице 1.


Таблица 1 - Распределение учащихся контрольных и экспериментальных классов по уровням развития пространственного мышления на начало эксперимента

Группа	число учащихся	уровни развития пространственного мышления
		высокий	выше среднего	средний	низкий
Контрольные классы	51	5	15	18	13
Экспериментальные классы	53	6	12	25	10

Для того чтобы показать, что различия в распределениях оценок носят случайный характер применим критерий ², который для этого и предназначен. Все ограничения для применения данного критерия выполнены. Сформулируем гипотезы, которые будем проверять при помощи данного критерия.

Гипотеза H₀: Различия в распределении учащихся по уровням развития пространственного мышления в контрольных и экспериментальных классах носят случайный характер.

Гипотеза H₁: Различия в распределении учащихся по уровням развития пространственного мышления в контрольных и экспериментальных классах существенны, то есть не являются случайными.

Расчет наблюдаемого значения критерия производится по формуле:

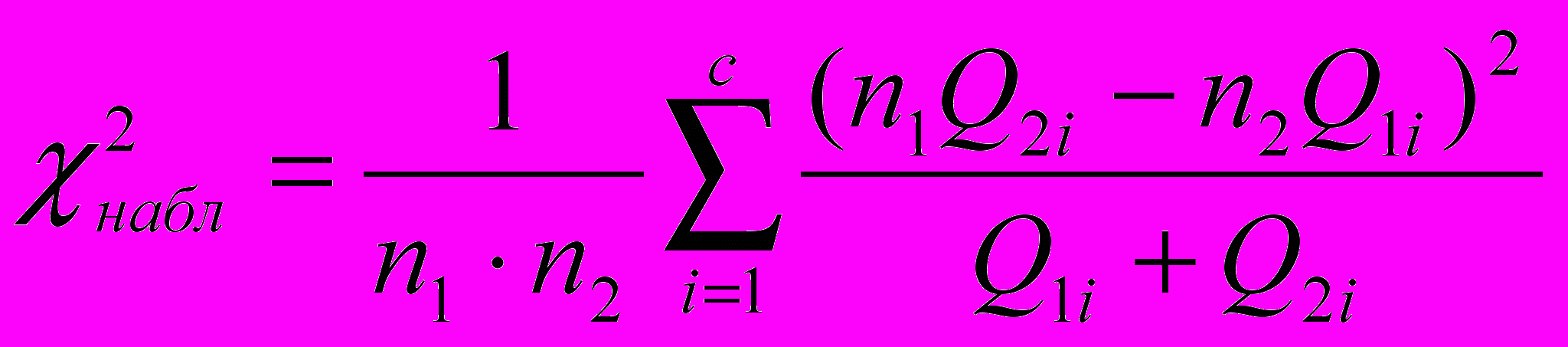(1).

Где n₁, n₂ – объемы независимых выборок экспериментальных и контрольных классов; Q_1i, Q_2i – число учащихся экспериментальных и контрольных классов, уровень развития пространственного мышления которых находится на i-том уровне; c – число уровней.

Критическое значение критерия 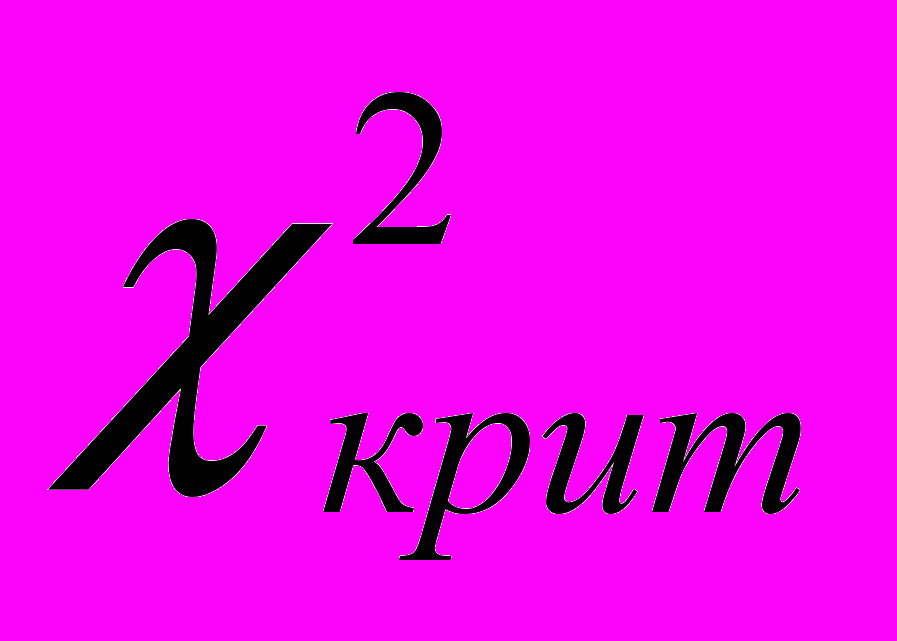на начало эксперимента, находим по таблице значений статистик ² с числом степеней свободы  = c – 1, для уровней значимости  = 0,05. В нашем случае c=4, следовательно,  = 3 и 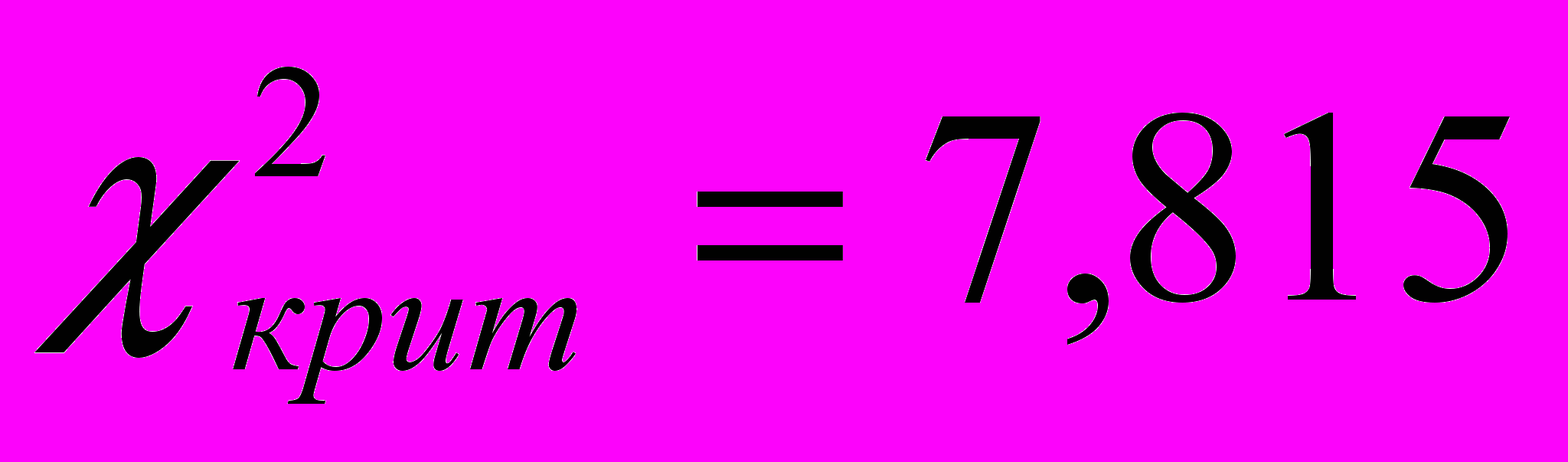. Значение критерия, вычисленное по формуле (1) .

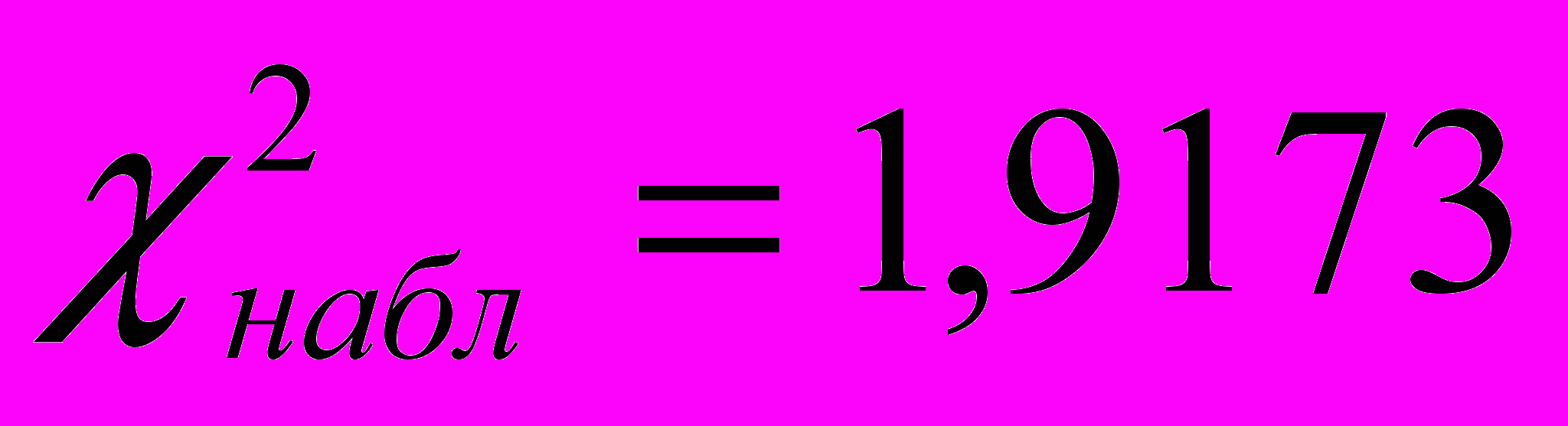Поскольку , то принимается гипотеза H₀, смысл которой в данном случае состоит в том, что различия в уровне развития пространственного мышления в экспериментальных и контрольных классах носят случайный характер, с уровнем статистической значимости 0,05. Как видим на начало эксперимента распределения учащихся по уровням развития пространственного мышления в обеих группах были примерно одинаковыми. Распределение учащихся по уровням пространственного мышления в процентном соотношении показано в Таблице 2.


Таблица 2 - Распределение учащихся по уровням пространственного мышления в процентном отношении на начало эксперимента

группа	уровни развития пространственного мышления (в %)
	высокий	выше среднего	средний	низкий
Контрольные классы	9,8	29,4	35,3	25,5
Экспериментальные классы	11,3	22,6	47,2	18,9

Таблица 2 позволяет сравнить данные по качеству знаний. Результаты сравнения качества знаний на момент начала эксперимента приведены в таблице 3.


Таблица 3 - Качественные показатели уровня развития пространственного мышления учащихся на начало эксперимента (в %)

группа	качество знаний
Контрольные классы	39, 2
Экспериментальные классы	33,9

Как видно из таблицы 3, качество знаний в контрольных классах на момент начала эксперимента было на 5,3% выше, чем в экспериментальных классах.

Формирующий этап эксперимента проводился с 2003 по 2008 годы.

В ходе формирующего этапа эксперимента в процессе обучения геометрии в экспериментальных классах использовались:

- разработанный комплекс задач стереометрического характера, расположенных в соответствующих темах планиметрии, на основе выработанных критериев отбора задач,

- разработанная методика включения задач стереометрического содержания в учебный процесс,

- различные наглядные средства (модели, развертки, рисунки и т. п.). Комплекс задач, наглядных средств и соответствующая методика изучения геометрии на основе фузионистского подхода были предназначены, с одной стороны, для оптимального усвоения школьниками курса планиметрии, а с другой стороны, для формирования и развития пространственных представлений и пространственного воображения учащихся 7 – 9 классов.

На данном этапе обучение геометрии в контрольных классах велось традиционно, в экспериментальных классах – на основе фузионистского подхода по разработанной нами методике. Следует подчеркнуть, что и в контрольных и в экспериментальных классах обучение велось в соответствии с Государственным общеобразовательным стандартом и учебной Программой по геометрии.

Приведём пример применения разработанной методики в экспериментальных классах.

Одной из основных тем курса геометрии 7-го класса является тема: «Первый и второй признаки равенства треугольников».


Макет урока по теме «Первый и второй признаки равенства треугольников».

Основная цель: Изучить формулировки и доказательства первого и второго признаков равенства треугольников. Рассмотреть примеры решения задач на применение первого и второго признаков равенства треугольников.

1. Формулируем и доказываем первый признак равенства треугольников.

Первый признак равенства треугольников. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то эти треугольники равны.

2. После доказательства теоремы рассматриваем пример решения задачи на применение этого признака.

Задача 1. Доказать равенство треугольников, изображенных на рисунке 1. Какие стороны и углы этих треугольников будут соответственно равными?

3
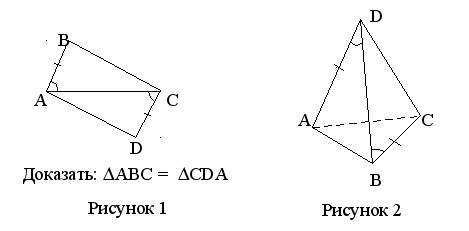
. После обсуждения решения задачи 1 предложить решить самостоятельно задачу 2, которую тоже следует сформулировать по готовому чертежу.

Задача 2. В треугольной пирамиде DABC (рисунок 2) ADB = DBC, AD = BC. Какие ещё рёбра и углы граней пирамиды будут равными?

4. Формулируем и доказываем второй признак равенства треугольников.

Второй признак равенства треугольников. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Для лучшего усвоения и закрепления изученной теоремы полезно устно решить задачи по готовым чертежам (рисунки 3 и 4).





6. Домашнее задание тоже следует дать комбинированное, состоящие из «плоских» и «пространственных» задач.

Домашнее задание. Выучите формулировки и доказательства первого и второго признаков равенства треугольников. Решите следующие задачи.

З
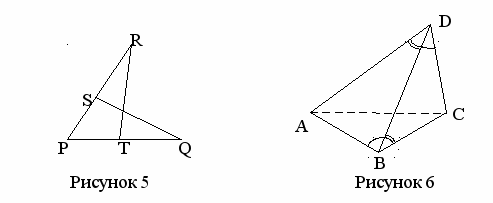
адача 1. В треугольниках PRT и PQS PR = PQ и PT = PS (рисунок 5). Докажите, что а) PRT = PQS; б) RSQ = QTR.

Задача 2. В треугольной пирамиде DABC (рисунок 6) DBC = BDA и ABD = BDC. Докажите, что AD = BC и AB = DC.

При проведении данного урока в экспериментальном классе задачи стереометрического содержания не только не вызвали затруднений, но решались с интересом, а при выполнении домашнего задания с задачей 2 справились больше учащихся, чем с задачей 1б.

Контрольный этап проводился в конце первой четверти 10-го класса, так как к этому времени учащиеся контрольного класса, участвующие в эксперименте изучили достаточное количество стереометрического материала для написания контрольной работы. Ими изучены аксиомы и основные положения геометрии, тема «Параллельность прямых и плоскостей» и они познакомились с основными видами многогранников, таких как призма и пирамида и с их изображениями. Чтобы оценить, повысился ли уровень развития пространственного мышления учащихся в экспериментальных классах, благодаря включению разработанного комплекса задач, необходимо было сравнить его с уровнем развития пространственного мышления учащихся, занимавшихся по традиционной методике в контрольных классах.

Для этого учащимся была предложена контрольная работа. Для решения задач контрольной работы учащимся потребовались как навыки деятельности по созданию пространственного образа (задачи 1, 2), так и деятельности по простейшим преобразованиям образа (задача 3). Поэтому выполнение данной контрольной работы учащимися позволяет оценить уровни развития у них пространственного мышления.

Критерии оценивания. Оценки уровня развития пространственного мышления учащихся производились по следующему принципу:

Высокий уровень - (ставилась отметка «5») – решены все задачи, но в одной имеются несущественные неточности;

Выше среднего уровень - (ставилась отметка «4») – решены две задачи, а в третьей правильно выполнен чертеж;

Средний уровень - (ставилась отметка «3») – решение одной задачи полностью отсутствует, одна задача решена полностью, а в решении другой задачи содержатся неточности, но чертеж выполнен верно, а также в том случае, если выполнены правильно чертежи всех трех задач и имеются верные попытки их решения, не доведенные до конца;

Низкий уровень - (ставилась отметка «2») - решена только одна задача, а решение других отсутствует или видны попытки неправильного решения задач и нет ни одной решенной.

Распределение учащихся контрольных и экспериментальных классов по уровням развития пространственного мышления после окончания эксперимента показаны в таблице 4.


Таблица 4 - Распределение учащихся контрольных и экспериментальных классов по уровням развития пространственного мышления после окончания эксперимента

Группа	всего	уровни развития пространственного мышления
		высокий	выше среднего	средний	низкий
Контрольные классы	51	6	12	23	10
Экспериментальные классы	53	14	20	13	6

Проверим, используя статистический критерий ², являются ли различия в распределении уровней развития пространственного мышления случайными (H₀) или появились в результате применения в экспериментальных классах разработанной методики обучения геометрии (H₁).

Расчет наблюдаемого значения критерия снова производим по формуле (1). Поскольку число уровней c = 4 ( = 3), как и на начало эксперимента, то и критическое значения критерия ² соответствующее уровню значимости  = 0,05 будет таким же: 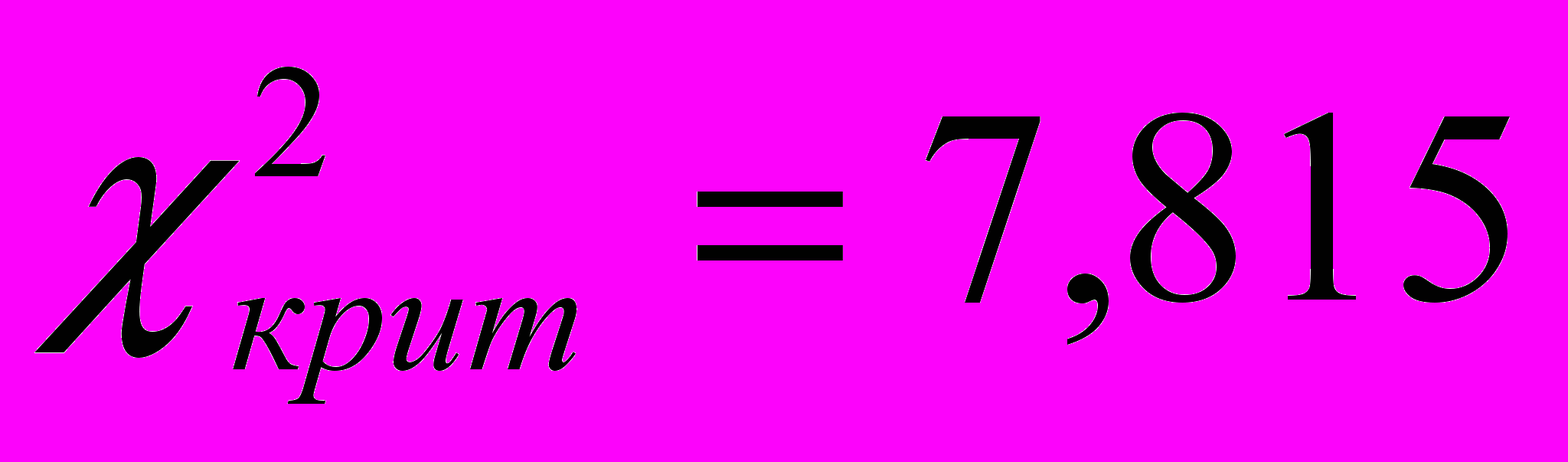. Наблюдаемое значение критерия вычисленное по формуле (1) по данным таблицы 4: .

Поскольку 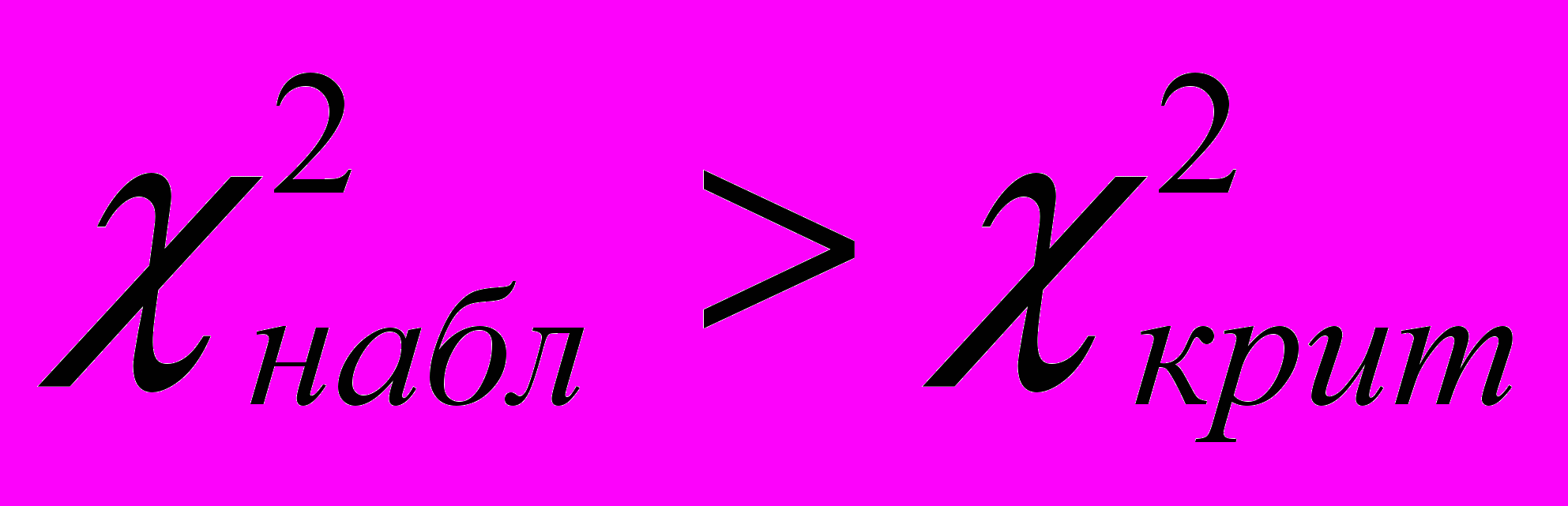, то гипотеза H₀ отклоняется, а принимается гипотеза H₁, смысл которой в данном случае состоит в том, что различия в уровне развития пространственного мышления в экспериментальных и контрольных классах носят статистически значимый характер, с уровнем статистической значимости 0,05.

Это означает, что применение методики обучения геометрии на основе фузионистского подхода в экспериментальных классах повлияло на уровень развития пространственного мышления. Поскольку обучение в контрольных и экспериментальных классах проводилось по единым стандартным программам и никаких других воздействий, кроме изменения подхода в обучении геометрии на учащихся не производилось, то можно сделать вывод, что статистически значимые различия в распределениях обусловлены именно применением элементов стереометрии в курсе планиметрии.

Для того чтобы оценить направление этого влияния сравним качественные изменения в уровне развития пространственного мышления контрольной и экспериментальной групп на начало и после окончания эксперимента.

Распределение учащихся по уровням пространственного мышления в процентном соотношении показано в таблице 5.


Таблица 5 - Распределение учащихся по уровням пространственного мышления в процентном отношении после окончания эксперимента

группа	уровни развития пространственного мышления (в%)
	высокий	выше среднего	средний	низкий
контрольные классы	11,8	23,5	45,1	19,6
экспериментальные классы	26,4	37,7	24,5	11,3

Результаты сравнения качественных показателей уровней развития пространственного мышления учащихся на момент окончания эксперимента приведены в таблице 6.


Таблица 6 - Качественные показатели уровня развития пространственного мышления учащихся на момент окончания эксперимента (в %)

группа	качество знаний
Контрольные классы	35, 3
Экспериментальные классы	64,1

Динамика качественных изменений уровней развития пространственного мышления на начало и конец эксперимента показана в таблице 7.


Таблица 7 - Изменение качественного уровня развития пространственного мышления в контрольных и экспериментальных классах до начала и после окончания эксперимента (в %)

группа	на начало эксперимента	после окончания эксперимента	Направление изменений
контрольные классы	39,2	35,3	- 3,9
экспериментальные классы	33,9	64,1	+30,2

Как видно из таблицы 7 качественный уровень в контрольных классах немного уменьшился (на 3,9%). Это произошло потому, что в течение трех лет (с 7-го по 9-й класс) учащиеся контрольных классов не изучали свойств пространственных объектов и встречались с пространственными фигурами лишь постольку, поскольку это требовалось при изучении других дисциплин. Учащиеся же экспериментальных классов систематически работали с пространственными фигурами на уроках геометрии, так как обучение геометрии велось на основе фузионистского подхода с применением разработанной нами методики. Поэтому качественный уровень значительно вырос (на 30,2%). Результаты представлены на рисунке 7.






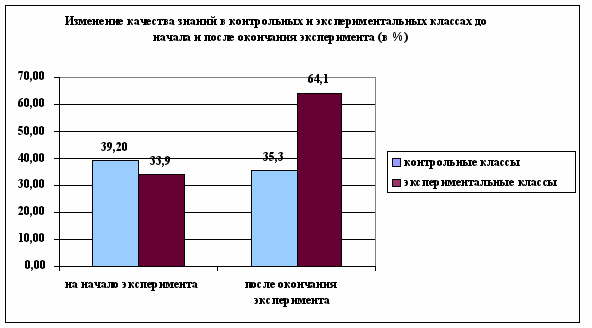
Рисунок 7 - Гистограмма изменения качественного уровня развития пространственного мышления до начала и после окончания эксперимента


Результаты, полученные на основе анализа качественных различий в уровнях пространственного мышления, подтверждаются и проверкой медиан выборок по данным рассчитанным по таблицам 1 и 4. Для этого надо приписать каждому уровню числовое значение. В нашем случае в качестве числовых рангов выберем отметки учащихся, полученные в начале и в конце эксперимента:

- Высокому уровню – «5».

- уровню выше среднего – «4».

- среднему уровню – «3».

- низкому уровню – «2».

Значения медиан выборок, полученные по данным таблиц 1 и 4 даны в таблице 8.


Таблица 8 - Медианы распределений значений выборок уровней развития пространственного мышления в контрольных и экспериментальных классах

	Контрольные классы до начала эксперимента	Контрольные классы после окончания эксперимента	Экспериментальные классы до начала эксперимента	Экспериментальные классы после окончания эксперимента
Медиана	3	3	3	4

Увеличение значения медианы, также как и качественный рост уровней развития пространственного мышления учащихся экспериментальных классов по сравнению с учащимися контрольных классов позволяют сделать вывод об эффективности предложенной нами методики обучения геометрии в основной школе на основе фузионистского подхода.

Таким образом, на момент окончания эксперимента уровень развития пространственного мышления учащихся экспериментальных классов стал выше, чем у учащихся контрольных классов.

Для полного подтверждения всех полученных результатов исследования, было принято решение проверить: не произошло ли выравнивание знаний стереометрии учащихся контрольных и экспериментальных классов к концу обучения в 11 классе. С этой целью в конце 11класса (апрель 2008) учащимся контрольных и экспериментальных классов был предложен тест, составленный из стереометрических задач ЕНТ прошлых лет. Тест состоял из 15 заданий по стереометрии. За каждое правильно решенное задание учащиеся получали 1 балл, за неправильно решенное – 0 баллов. Максимальное число баллов, которое мог набрать каждый учащийся – 15 баллов, минимальное – 0 баллов.

Критерий оценки. Были выделены четыре уровня стереометрических знаний: высокий, выше среднего, средний, ниже среднего.

- Высокий – набрано на менее 14 баллов (округленное до целых 90% от максимального числа баллов), ставилась отметка «5».

- Выше среднего – набрано от 11 до 13 баллов (75%), ставилась отметка «4».

- Средний – набрано от 7 до 10 баллов (50%), ставилась отметка «3».

- Низкий – набрано менее 7-ми баллов (менее 50%), ставилась отметка «2».

Распределение учащихся по уровням стереометрических знаний приведено в таблице 9.


Таблица 9 - Распределение учащихся контрольных и экспериментальных классов по уровням стереометрических знаний в конце 11-го класса

Группа	всего	уровни знания стереометрии
		высокий	выше среднего	средний	низкий
Контрольные классы	51	10	14	20	7
Экспериментальные классы	53	15	24	9	5

Для проверки статистической значимости различий распределения учащихся контрольных и экспериментальных классов по уровням стереометрических знаний применим критерий ².

Поскольку количество учащихся и количество уровней в данном случае то же самое, что и в предыдущих, то и критическое значение критерия будет тем же: 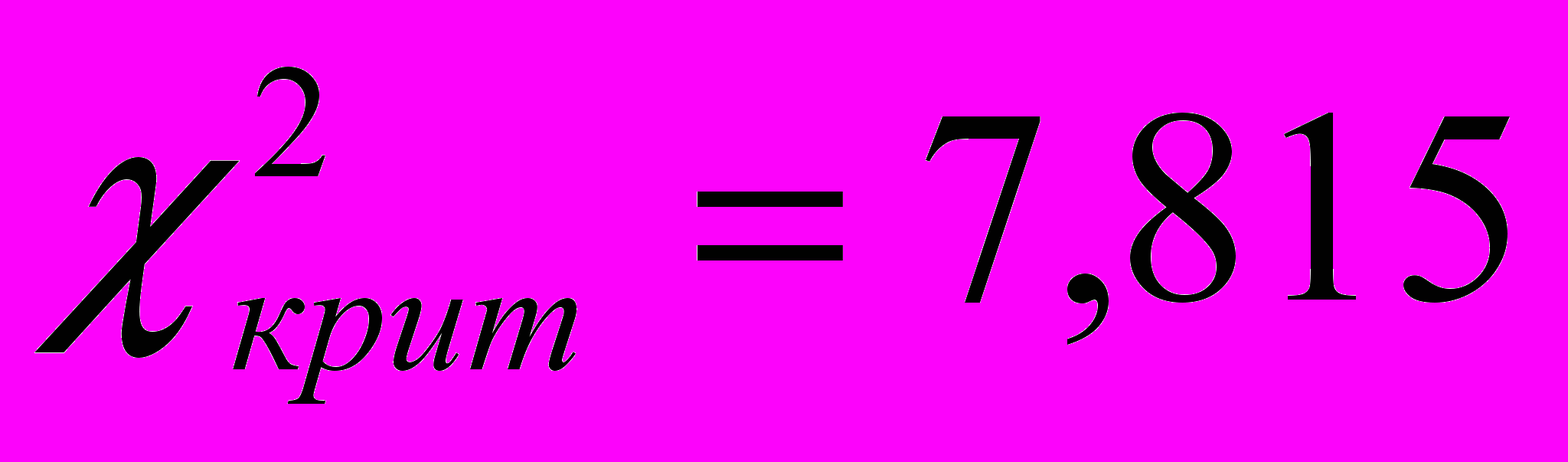. Наблюдаемое значение критерия, вычисленное по формуле (1) получается таким: .

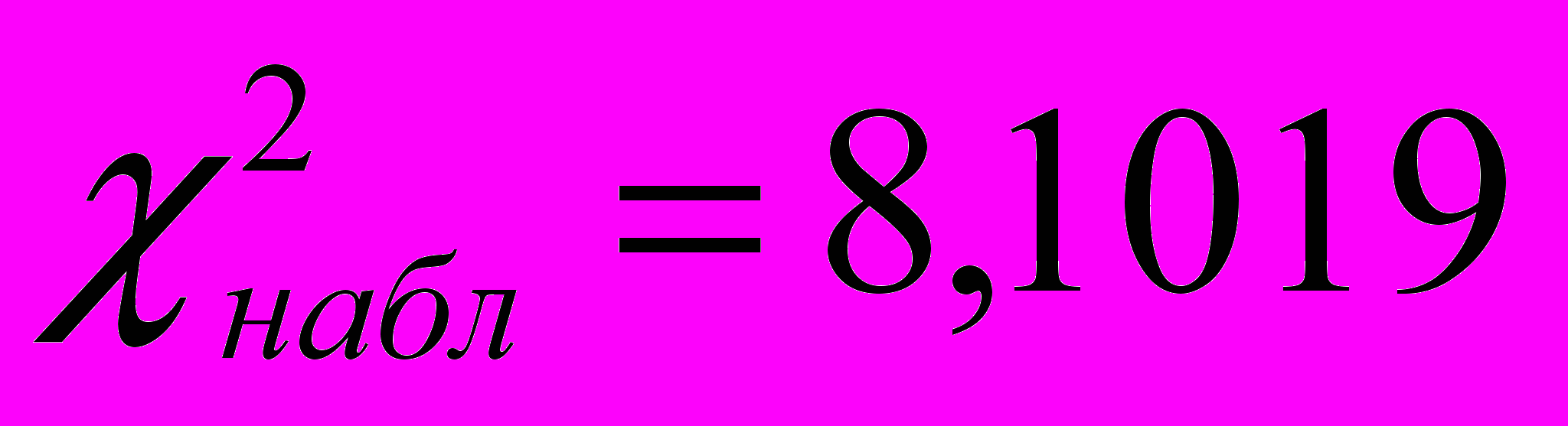Поскольку 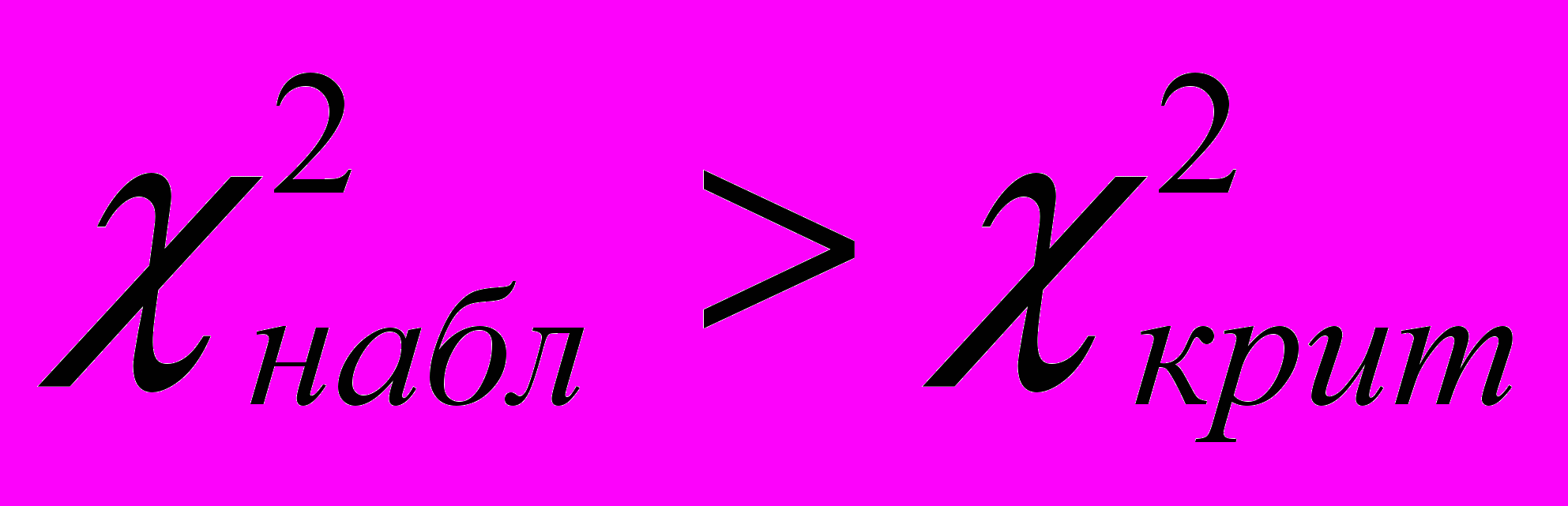, то принимается гипотеза H₁, смысл которой в данном случае состоит в том, что различия в уровнях знаний стереометрии в экспериментальных и контрольных классах не исчезают к концу 11-го, а носят статистически значимый характер, с уровнем статистической значимости 0,05.

Распределение учащихся контрольных и экспериментальных классов по уровням стереометрических знаний в конце 11-го класса (в%) показаны в таблице 10 и на рисунке 8.


Таблица 10 - Распределение учащихся контрольных и экспериментальных классов по уровням стереометрических знаний в конце 11-го класса (в %)

группа	уровни знания стереометрии (в%)
	высокий	выше среднего	средний	ниже среднего
контрольные классы	19,6	27,5	39,2	13,7
экспериментальные классы	28,3	45,3	17	9,3

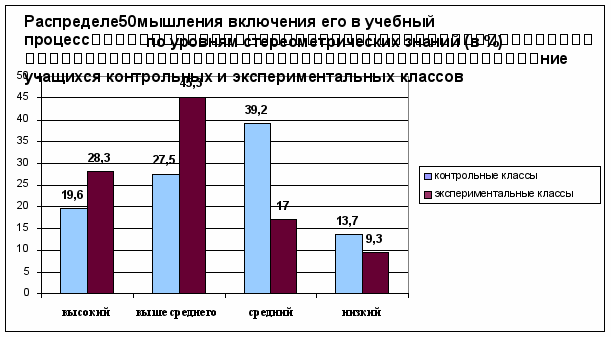
Рисунок 8 - Распределение учащихся контрольных и экспериментальных классов по уровням стереометрических знаний в конце 11-го класса (в %)


В таблице 11 показаны качественные показатели уровня знаний стереометрии учащихся на момент окончания эксперимента (в %).


Таблица 11 - Качественные показатели уровня знаний стереометрии учащихся на момент окончания эксперимента (в %)

группа	качество знаний
Контрольные классы	47,1
Экспериментальные классы	73,6

Как видно из этой таблицы качественный уровень знаний учащихся экспериментальных классов остался значительно выше, чем у учащихся контрольных классов.

Поставим в соответствие каждому уровню стереометрических знаний числовое значение, соответствующее данному уровню:

Высокий – 5; Выше среднего – 4; Средний – 3; Низкий – 2.

Тогда значение медианы для контрольных классов остается равным 3, а экспериментальных – 4.

Сравнение медиан в пользу экспериментальных классов говорит о том, что различия в распределениях по уровням знаний стереометрии не просто имеют место, а средний статистический уровень этих знаний в экспериментальных классах остался существенно выше.

Проведенное тестирование и анализ его результатов говорит о том, что преимущество, полученное учащимися экспериментальных классов при обучении геометрии на основе фузионистского подхода с использованием «задач планиметрии в стереометрической среде», не утрачивается и в конце 11-го класса.

Таким образом, целенаправленная деятельность учителя по развитию пространственного мышления через включение задач стереометрического характера в систематический курс планиметрии создает благоприятные условия для успешного усвоения курса планиметрии, а в дальнейшем и курса стереометрии, а также содействует формированию приемов мыслительной деятельности, позволяет активизировать познавательную деятельность учащихся при обучении, что и подтверждает справедливость выдвинутой гипотезы.