Федорова Людмила Федоровна 26. 09. 2008 Сценарии урок

Вид материала

Содержание

Подобный материал:

Модульная технология

Фамилия, имя, отчество автора (полностью) Колупаева Галина Геннадьевна
Год, месяц, день рождения 1970 июль 29
Место работы МОУ «Чойская СОШ» полный адрес Республика Алтай Чойский район с. Чоя ул. Советская,14 индекс 649180 тел. Код (8 388 40) телефон 22 – 3 – 59
Должность учитель математики
Педагогический стаж работы 15 лет
Преподаваемый предмет математика
Название работы, подаваемой на конкурс Сценарии уроков по алгебре и началам анализа Модульная технология
Домашний адрес автора с. Чоя, ул. Садовая,10 , Чойский район, Республика Алтай, 649180, (838840) 22530, kolugalina@yandex.ru
ФИО руководителя образовательного учреждения Колупаев Сергей Митрофанович, (838840) 22359
Адрес, телефон, факс, телефонный код, районного отдела образования 649180 Республика Алтай с. Чоя ул. Ленина (838840) 22146
ФИО руководителя органа управления образования района Федорова Людмила Федоровна

26.09.2008

Сценарии уроков по алгебре и началам анализа 10 класс (автор учебника Мордкович А.Г.)

Модульная технология

Автор Колупаева Галина Геннадьевна

Предмет преподавания математика

Должность учитель математики

Название учреждения образования МОУ «Чойская СОШ»

Адрес учреждения: Республика Алтай, Чойский район,

с. Чоя. Ул. Советская ,14

Телефон учреждения образование: 22 – 1 - 59, 22 – 3 – 59

Адрес автора: Республика Алтай, Чойский район, с. Чоя. Ул. Садовая,10

Домашний телефон 22 – 5 – 30

ЧДЦ (частная дидактическая цель)

	Единицы усвоения	знать	уметь
			Репродуктивный уровень	Конструктивный уровень	Творческий уровень
		1 2 3 группы	1 2 3 группы	1 2 3 группы	1 2 3 группы
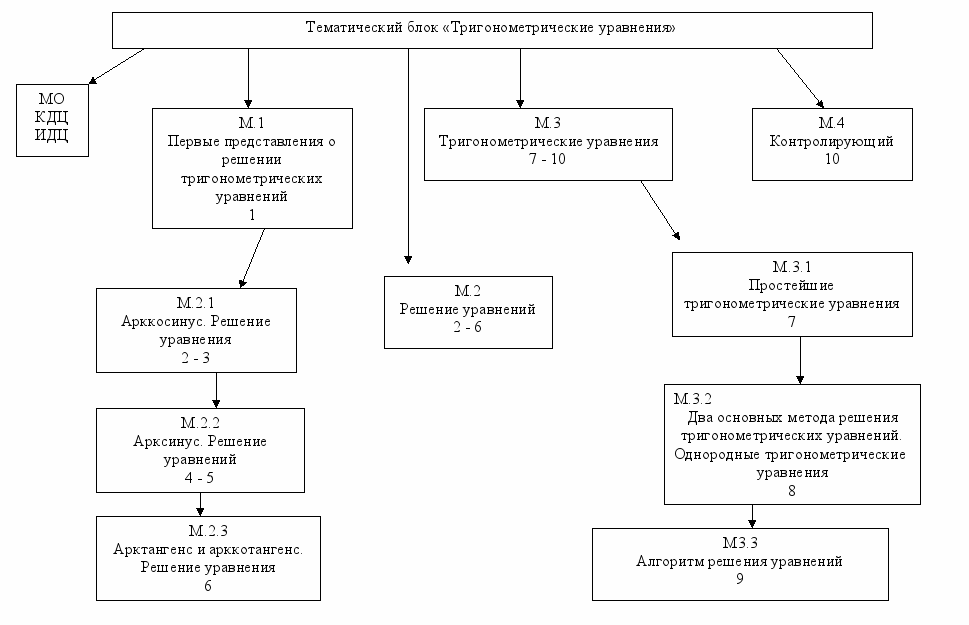
М.1	Первые представления о решении тригонометрических уравнений	+ + +	Напомнить учащимся решение уравнений с помощью числовой окружности; показать приёмы применения метода введения новых переменных при решении тригонометрических уравнений.
М.2.1	Арккосинус. Решение уравнения	+ + +	Ввести понятие арккосинуса; изучить общие формулы решения, выработать алгоритм.
М.2.2	Арксинус. Решение уравнения	+ + +	Ввести понятие арксинуса; изучить общие формулы решения, выработать алгоритм.
М.2.3	Арктангенс и арккотангенс. Решение уравнения	+ + +	Ввести понятие арктангенса и арккотангенса; изучить общие формулы решения, выработать алгоритм.
М.3.1	Простейшие тригонометрические уравнения	+ + +	Повторить общие формулы для решения простейших тригонометрических уравнений.
М.3.2	Два основных метода решения тригонометрических уравнений.	+ +	Выработать у учащихся навыки решения более сложных тригонометрических уравнений, выделив общую идею решения: приведение уравнения к виду, содержащему лишь одну тригонометрическую функцию одного аргумента с последующей заменой переменной, или разложение на множители.
М.3.3	Однородные уравнения	+ +	Выработать у учащихся навыки решения более сложных тригонометрических уравнений, выделив общую идею решения: приведение уравнения к виду, содержащему лишь одну тригонометрическую функцию одного аргумента с последующей заменой переменной, или разложение на множители.

ЧДЦ (частная дидактическая цель)

	Единицы усвоения	знать	уметь
			Репродуктивный уровень	Конструктивный уровень	Творческий уровень
		1 2 3 группы	1 2 3 группы	1 2 3 группы	1 2 3 группы
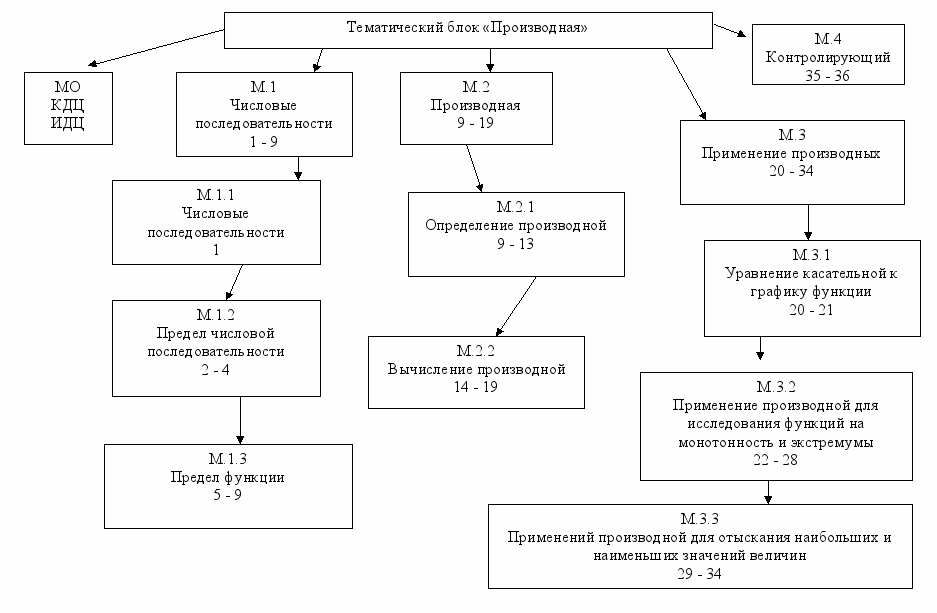
М.1	Числовые последовательности	+ + +	Повторить определение последовательности, основные способы её задания, изучить свойства числовых последовательностей.
		+ +		Выработать у учащихся умения приводить примеры последовательностей, заданных различными способами и обладающих различными свойствами
М.1.2	Предел числовой последовательности.	+ + +	Ввести определение предела числовой последовательности, изучить свойства сходящихся последовательностей; выработать у учащихся умения вычислять пределы последовательностей и суммы бесконечных геометрических прогрессий.
М.1.3	Предел функции	+ + +	Познакомить учащихся с понятиями: предел функции на бесконечности, предел функции в точке, приращение аргумента и приращение функции.
		+ +		Выработать у учащихся умения определять по графикам, имеет ли функция предел и чему он равен.
		+			Строить эскизы графиков функции
М.2.1	Определение производной	+ + +	Изучить физический и механический смысл производной; выработать у учащихся прочные навыки пользованием алгоритмом отыскания производной.

		+ +		Сформировать у учащихся умения по графику определять дифференцируема ли функция.
М.2.2	Вычисление производной	+ + +	Изучить формулы и правила дифференцирования для конкретных функции; выработать у учащихся умение использовать двухшаговый алгоритм
		+ +		Изучить правило дифференцирования сложной функции
М.3.1	Уравнение касательной к графику функции	+ + +	Выработать умение пользоваться алгоритмом составления уравнения касательной к графику функции в точке.
		+ +		Умение проводить касательную параллельно заданной прямой; умение находить угол, который касательная образует с положительным направлением оси абсцисс.
М.3.2	Применение производной для исследования функции на монотонность и экстремумы.	+ +		Уметь применять методы дифференциального исчисления для нахождения промежутков возрастания, убывания и экстремумов функции: выработать умение строить график функции
М3.3	Применение производной для отыскания наибольших и наименьших значений величин	+ +		Умение находить наибольшие и наименьшие значения величин.

ЧДЦ (частная дидактическая цель)

	Единицы усвоения	знать	уметь
			Репродуктивный уровень	Конструктивный уровень	Творческий уровень
		1 2 3 группы	1 2 3 группы	1 2 3 группы	1 2 3 группы
М.1.1	Синус и косинус суммы аргументов	+ + +	Показать учащимся важность формул синуса суммы и косинуса суммы, многообразие их применения.
		+ +		Отработать навыки применения этих формул
М.1.2	Синус и косинус разности аргументов	+ + +	Изучить формулы синуса разности и косинуса разности: показать многообразие их применения
		+ +		Выработать навыки применения изученных формул при тождественных преобразованиях тригонометрических выражений
М.1.3	Тангенс суммы и разности аргументов	+ + +	Изучить формулы, показать варианты их применения
		+ +		Выработать прочные навыки применения изученных формул
М.2.1	Формулы двойного аргумента	+ + +	Вывести формулы тригонометрии, позволяющие выразить одну функцию через другую: показать многообразие их применения.
		+ +		Выработать у учащихся прочные навыки в умении использовать полученные формулы в тригонометрических преобразованиях
М.2.2	Формулы понижения степени	+ + +	Вывести формулы для понижения степени
		+ +		Выработать прочные навыки применения изученных формул
М.3.1	Преобразование сумм тригонометрических функций в произведении	+ + +	Выработать умение применять изученные формулы при преобразованиях тригонометрических выражений и при решении тригонометрических уравнений.
М.3.2	Преобразование произведений тригонометрических функций в суммы	+ + +	Показать учащимся примеры и варианты использования формул, позволяющих преобразовывать произведение тригонометрических функций в сумму.
		+ +		Предложить учащимся алгоритм, который может помочь при решении достаточно сложных примеров.
М.3.3	Преобразование выражения к виду	+ + +	Проверить умение учащихся самостоятельно работать с учебником: обобщить и систематизировать знания учащихся по теме «Преобразование тригонометрических выражений»; подготовиться к контрольной работе.

Технологическая карта по теме «Числовые последовательности» 1 час

№	Содержание задания	Советы учителя
1.	Цель: Повторить определение последовательности, основные способы ее задания, изучить свойства числовых последовательностей: уметь приводить примеры последовательностей, заданных различными способами и обладающих различными свойствами.
2.	Цель: Изучение нового материала. 1. Повторите определение числовой последовательности. 2. Вспомните способы задания последовательностей (приведите примеры): а) словесный б) аналитический. в) рекуррентный 3. Изучить свойства числовых последовательностей как частного случая числовых функций: а) ограниченность сверху б) ограниченность снизу в) возрастание г) убывание. 4. Ввести термин монотонные последовательности (привести примеры)
3.	Цель: Закрепление изученного материала. 1. Решить устно: №581, №584, № 585. 2. Решить с последующей проверкой № 582, №583, № 586, № 587. 3. Решить устно № 590, №592, №595, №597. 4. Решить с последующей проверкой № 598, 599. 5. Решить устно № 602, 603, 604, 605, 606. 6. Выполнить совместно № 614, 616, 617, 626, 627, 610	Правильные ответы на доске
4.	Задание на дом:§ 29, № 608, №611, № 618(а,г), № 628. Заполните лист качественного контроля.

Технологическая карта по теме «Предел числовой последовательности» 3 часа

№	Содержание задания	Советы учителя
1	Цель: Ввести определение последовательности, изучить свойство сходящих последовательностей.
2.	Цель: Изучить новый материал. 1. Ввести определение «окрестности точки а» и «радиуса окружности». 2. Ввести определение предела последовательности, показать символическую запись предела. 3. Рассмотреть примеры нахождения пределов последовательностей: 4. Изучить геометрический смысл полученных результатов. 5. Познакомить учащихся с понятием горизонтальная асимптота для графиков функции: 6. Ввести понятие сходящейся последовательности. 7. Изучить свойства сходящихся последовательностей.	Новый материал, в виде лекции выдает учитель.
3	Цель: Закрепить изученный материал. Выполнить устно № 633, 634, 635. Выполнить № 638. 652, 653.	Выполняем вместе. Записи оформить в тетради.
4	Запишите задание на дом: § 30, п. 1,2; № 636, 637, 655.
1	Цель: Выработать у учащихся умения вычислять пределы последовательностей.
2	Цель: Изучить новый материал. 1. Ввести понятие предела стационарной последовательности. 2. Изучить правила нахождения пределов последовательностей: а) «предел суммы», б) «предел произведения», в) «предел частного». 3. Разобрать примеры, показывающие приемы применения правил нахождения пределов последовательностей.	Лекция учителя.
3	Цель: Закрепить изученный материал. Устно выполнить № 639, 640 Выполнить № 656. 657	Работа выполняется на доске
4	Цель: Проверка усвоения темы. Проверочная самостоятельная работа. Вариант 1. № 641(а,б), 642(в,г), Вариант 2. № 641(в.г), 642(а,б).	Тетради сдать на проверку.
5	Запишите задание на дом: §30 п.З, № 643, 657(в,г), 654(в).
1	Цель: Выработать умения вычислять сумму бесконечных геометрических прогрессий.
2	Цель: Изучение нового материала. 1. Разобрать способ нахождения суммы бесконечной геометрической прогрессии через понятие предела. 2. Разобрать примеры 7 и 8 из учебного пособия.	Работа с учебником. Записи делать в тетрадях.
3	Цель: Закрепить изученный материал. № 648(устно), Письменно выполнить № 651, 658, 659,660	Правильные ответы на доске
4	Запишите задание на дом: §30, п.4,№ 649, 650, 658(в,г). 660(6). Заполните лист качественного контроля.

Технологическая карта по теме «Предел функции на бесконечность» 2 часа

№	Содержание заданий	Советы учителя
1.	Цель: Познакомить учащихся с понятием «предел функции
	на бесконечности». Выработать у учащихся умения
	определять по графикам, имеет ли функция предел и чему
	он равен.
2.	Цель: Актуализации опорных знаний учащихся.
	1. Повторить условия существования у графика функции
	горизонтальной асимптоты. (у= в является горизонтальной
	асимптотой графика функции у=f(х), если lim f(x)=в)
	2. Вспомнить: какие прямые являются горизонтальными
	асимптотами для графиков функций

3.	Цель: Изучить новый материал.
		Лекция учителя.
	1. Ввести понятие предела функции на бесконечности.
	2. Изучить правила вычисления предела функции на
	бесконечности: а) для любого натурального
	показателя m и любого коэффициента k справедливо
	соотношение
	б) о пределе суммы,
	в) о пределе произведения,
	г) о пределе частного,
	д) о вынесении за знак предела постоянного множителя.
		Подробная запись в тетрадях
	3 . Разобрать пример 1 из п. l, § 31 учебного пособия.
4	Цель: Закрепление изученного материала.	№ 675,676 самостоятельно, ответы на доске
	Устно: № 667, 668. 671, 672, 673.
		№ 677, 697 разобрать подробно сучителем
	Письменно № 675(а,б), 676(а,б), 677(а,г), 697(а,б)
5.	Задание на дом: § 31 п.1, № 669, 674, 677(б,в), 676(в,г).
1.	Цель: Закрепление материала.	№ 698,699 разобрать на доске
		№ 702 самостоятельно,
	Письменно: № 698(в,г), 699(в,г), 702	правильные ответы на доске
2.	Цель: Проверка знаний	Тетради сдать учителю.
	Проверочная работа:
	Вариант 1: № 696(а,б), 700(в,г)
	Вариант 2: № 696(в,г ), 700(а,б)
3.	Задание на дом: §31 п.1, № 698(а,б), 699(а,б), 701.
	Заполните лист рефлексии.

Технологическая карта по теме «Приращение аргумента. Приращение функции» 2 часа

№	Содержание задания	Советы учителя
1.	Цель: Познакомиться с понятиями «приращение аргумента»
	и «приращение функции». Выработать умения находить
	приращение аргумента и приращение функции.
2.	Цель: Изучить новый материал.
		конспект теории
	1. Изучить определение приращения аргумента и	вместе с учителем.
	приращения функции.
	2. Познакомится с устной и письменной символикой	Составьте конспект теории вместе с учителем
	введенных понятий.
	3. Разобрать примеры 5,6,7 из учебного понятия.
	4. Рассмотреть новое истолкование понятия
	непрерывности функции в точке.
	5. Познакомиться с геометрическим смыслом
	отношения приращения функции к приращению
	аргумента.
3	Цель: Закрепить изученный материал.	№ 708 (а) разобрать на доске
	Решение №708, 709, 710,711.	(б.в) самостоятельно.
		№ 709,710 - правильные отв.
		на доске. № 711 совместно
4.	Задание на дом: §31 .п.3, № 688, 689, 690.
	Заполните лист рефлексии.

Технологическая карта по теме «Задачи, приводящие к понятию производной» 1час.

№	Содержание заданий	Советы учителя
1.	Цель: Разобрать решения физической и геометрической задач, в процессе решения приходим к новой математической модели.
2.	Цель: Изучить новый материал. 1. Решить две классические задачи: а) задача о скорости, б) задача о касательной. 2. Сделайте вывод, что процесс решения этих задач приводит к новой математической модели.	Лекция учителя.
3.	Цель: Закрепить изученный материал. Выполнить № 715(а) 722(а,б), 723(а,в),	Все решения разбираются на доске.
4.	Задание на дом: §32.п.1,№714, 722(в,г), 723(б,г). Заполните лист рефлексии.

Технологическая карта по теме «предел Функции в точке» 2часа.

№	Содержание задания	Советы учителя
1.	Цель: Познакомить учащихся с понятием «предел функции в точке». Выработать умение строить эскизы графиков функций, вычислять пределы функции в точке.
2.	Цель: Изучение нового материала. 1. Подробно изучить особенности, сходство и различие функций, графики которых изображены на рис. 109 -111 учебного пособия. 2. Познакомиться с понятием предела функции в точке. 3. Ввести понятие функции непрерывной в точке. 4. Дать определение функции непрерывной на промежутке. 5. Вспомнить функции, изученные в курсе алгебры 7-9 классов, и проследить непрерывность этих функций, опираясь на определение непрерывности функции. 6. Разобрать примеры 2,3,4 из учебного пособия.	Совместная работа учитель - ученик.
3.	Цель: Закрепить изученный материал. Устно № 678 Письменно № 679,683, 684.	№ 679 проверяем по правильным ответам №683, 684 выполняем на доске.
4.	Задание на дом: § 31, п.2, № 680, 681, 682.
1.	Цель: Закрепляем изученный материал. Выполняем № 685. 704, 706, 707(а,б).	№ 685, 706 выполняем самостоятельно, взаимопроверка №704, 707 выполняем на доске.
2.	Задание на дом: §31, п.2, № 686,703, 705, 707(в,г) Заполните лист качественного контроля.

Технологическая карта по теме «Определение производной, её геометрический и физический смысл» 1час.

№	Содержание заданий		Советы учителя
1.	Цель: Ввести определение производной. Изучить ее геометрический и механический смысл.
2	Цель: Изучение нового материала. 1. Ввести определение производной. 2. Ввести обозначение для производной. 3. Используя результаты примеров 6,7 из § 31, вычислить производные для функций: y=kx, y=x . 4. Изучить механический смысл производной. 5. Изучить геометрический смысл производной. 6. Разобрать содержательный смысл приближенного равенства		Лекция учителя.
3.	Цель: Закрепление изученного материала. Устно №716, 725, 726 Письменно №718(а,б)		№ 718 разбирается на доске.
4.	Задание на дом: § 32. п.2, №717,718(в,г),724.
Технологическая карта по теме «Алгоритм отыскания производной (для функции у=f(х))» 1 час.
№	Содержание заданий	Советы учителя
1.	Цель: Выработать прочные навыки пользования алгоритмом отыскания производной для функции у=f(х). Формировать умения по графику определять, дифференцируема ли функция.
2.	Цель: Изучить новый материал. 1. Подробно изучить пятишаговый алгоритм отыскания производной функции.(обратите внимание на важность и значимость первого шага) 2. Отработать навыки применения изученного алгоритма на примерах нахождения производной для функций: а) у = с, б) у = (примеры 1,2 из учебного пособия). 3. Изучить условие дифференцируемости функции в точке. 4. Выяснить, что называют дифференцированием функции. 5. Изучить вопрос: как связаны между собой свойства непрерывности и дифференцируемости функции в точке. 6. Научиться снимать с графика информацию о дифференцируемости функции.	Совместная работа учитель - ученик
3	Цель: Закрепить изученный материал. Найдите производную функций: Найти среднюю скорость изменения функции у= при изменении х от х=3 до х=3,5 Прямолинейное движение точки задано уравнением: где t дано и секундах, a S - в метрах. Найти скорость движения точки в момент t=5с. 4. Определить знак углового коэффициента касательной к графику функции через точки с абсциссами х1,х2,х3,х4 (если касательная существует) Какой угол (острый или тупой) образует эта касательная с осью абсцисс? В окрестности каких точек графика функция 5. Используя формулы дифференцирования, полученные при решении предыдущих заданий, найдите производную функции в точке х, если: Задание на дом: §32: 1) №727 2) Пользуясь определением производной и алгоритмом отыскания производной, найдите значения производной функции, если:	Работа ведётся в тетрадях с подробным разбором на доске Заполните лист рефлексии

Технологическая карта по теме «Формулы дифференцирования» 2 часа

№	Содержание заданий	Советы учителя
1	Цель: Изучить формулы дифференцирования для конкретных функций. Выработать умения использовать при вычислениях алгоритм.
2	Цель: Изучить новый материал. 1. Выписать формулы дифференцирования конкретных функций, полученных в § 32 2. Новые формулы: 3. разобрать примеры 1,2 из учебника 4. №728, №729 (устно)	Все записи подробно выполняются в тетрадях
3	Домашнее задание: теория §33,п.1
1	Цель: Вывести новые формулы, используя алгоритм. Отработать навык работы с алгоритмом отыскания производной.
2	Цель: вывести новые формулы:	Практическая работа учителя. Запись в тетрадях.
3	Цель: 3aкрепить изученный материал № 732(б), 733(а,б,в), 734(в,г), 735(в_?г)	Частично самостоятельна работа.
4	Домашнее задание: № 730, 731, 734(а,б), 735(в,г)
5	Заполните лист самоконтроля.

Технологическая карта по теме: «Правила дифференцирования» - 3 часа

№	Содержание заданий	Советы учителя
1	Цель: выработать умение использовать при вычислениях производных двухшаговый алгоритм: сначала применять правило дифференцирования, а затем использовать нужные формулы. Изучить правило дифференцирования функции вида:
2	Цель:Изучить новый материал. 1. Изучить правила дифференцирования для нахождения производных суммы, произведения, частного функций (каждое правило сопроводить примером) 2. Вывести правило дифференцирования суммы функции: 3. Вывести правило дифференцирования функции. 4. Закрепить правила решением примеров 3,4 из учебного пособия. 5.Вывести формулы для нахождения производных функций: 6. Разобрать решение примера 5 из учебника.	Лекция учителя.
3	Цель: Закрепление материала. № 739(а,в) № 740 - 744	Выполнить самостоятельно Сдать тетради.
4	Домашнее задание:§33, п.2 , самостоятельно проработать по учебнику правило дифференцирования произведения. №737, 738, 741, 745, 746.

1.	Цель: Контроль знаний, умений и навыков. Самостоятельная работа. 1 2 3 4 1.№756 а б в г 2.№757 б в г а 3.№758 в г а б 4.№759 г а б в 5.№760 а б в г	Работы сдать.
2.	Цель: Закрепить материал. № 748(а). 749(в), 750(6), 754(в), 761(а,г), 763(в,г), 765(в,), 766(г)	Самопроверка по эталону.
3.	Домашнее задание: п.2, №747, 752, 753, 762.
1	Цель: Проанализировать типичные ошибки и устранить пробелы в знаниях. 1. Подвести итог самостоятельной работы. 2. Анализ ошибок. 3. Вопросы по работе.
2.	Цель: Закрепить изученный материал. № 784(в), 785(а,г), 786, 790(а,б), 793(а), 794, 797.	№ 786 самостоятельно.
3.	Задание на дом: № 783, 791, 792.
4.	Заполните лист рефлексии.

Колупаева Галина Геннадьевна МОУ «Чойская СОШ»

Blog

Федорова Людмила Федоровна 26. 09. 2008 Сценарии урок

Содержание