Geum.ru

Межпредметные связи на уроках физики недведская Людмила Фёдоровна

Вид материалаУрок
Подобный материал:
МЕЖПРЕДМЕТНЫЕ СВЯЗИ НА УРОКАХ ФИЗИКИ


Недведская Людмила Фёдоровна




cредняя общеобразовательная школа № 4 г. Могилёва, учитель физики, руководитель методического объединения учителей естественного цикла


Межпредметные связи в школьном обучении - это дидактический эквивалент междунаучных связей.

Обучение физике будет более успешным, если школьники почувствуют необходимость учебных занятий, с интересом воспримут изучаемые явления и законы, если ощутят себя участниками процесса познания. Все это облегчается при учете знаний, полученных на занятиях по другим учебным дисциплинам.

Науки дифференцированы, но ученых в их служении истине объединяют общие принципы познания природы. Многие крупнейшие достижения человеческого разума последнего времени обусловлены переносом результатов теоретических и экспериментальных исследований из одной области науки в другую. Поэтому в учебном процессе и важна роль межпредметных связей. При их использовании исключается формализм при изучении материала. Учащиеся с удовольствием иллюстрируют примеры физических закономерностей, используя знания из биологии, географии, истории, математики и т.д. Использование информации, полученной при изучении других учебных предметов, способствует развитию не только познавательного интереса, но и кругозора, более глубокому пониманию материала.

Математический аппарат необходим физике как язык для описания физических процессов и явлений, один из методов физического исследования.

Одна из наиболее важных характерных черт современной физики состоит в том, что выводы, сделанные из исходных идей, имеют не только качественный характер, но и количественный характер; чтобы сделать количественные выводы, мы должны использовать математический язык. И если мы хотим сделать выводы, которые можно сравнивать с результатами эксперимента, нам необходима математика как орудие исследования. Английский физик П.Дирак писал: «Физический закон должен быть математически красивым».

Математика многое дает физике. Так, язык дифференциального и интегрального исчислений открывает большие возможности для более строгого определения ряда физических величин, записи физических законов (второго закона Ньютона, закона электромагнитной индукции и др.), формул, выражающих суть отдельных физических понятий (ЭДС индукции; силы тока, возникающего в рамке, вращающейся в магнитном поле, и др.).

Перед изучением графической интерпретации равномерного прямолинейного движения прошу учеников записать на доске уравнение y=4+6x и вспомнить из курса алгебры следующее:

Какую зависимость представляет данное уравнение?

Как линейная зависимость y=f(x) выглядит графически?

После этого можно попросить сравнить «математическое» уравнение y = 4 + 6x и «физическое» x = x0 + vхt, выражающее закономерность изменения координаты при равномерном движении. Вспомнив алгебру, ученики легко сами приходят к выводу, что выражение: x = x0 + vхt - линейная функция, что время t служит аргументом, а координата x - функцией.

Далее ученики записывают на доске частные случаи равномерного прямолинейного движения при а) x0 = 0, б) x0 > 0, в) x0 < 0? г) v < 0, а затем строят графики и характеризуют каждую разновидность движения.

В начале решения физических задач с использованием тригонометрических функций на доске вычерчиваем прямоугольный треугольник, обозначаем его стороны и углы и вместе с учениками, повторяем, что такое sinα, cosα, tgα, ctgα, записываем на доске формулы нахождения катетов и гипотенузы. Эта запись в течение всего урока помогает ученикам.

При решении задач по геометрической оптике очень полезно вспоминать геометрические теоремы о подобии треугольников, равенстве углов.

Аналогичная работа целесообразна и при изучении уравнений и графиков равноускоренного движения υ = f(t), x = f(t).

На уроках математики учащиеся рассматривают свойства функции y = κsinx. Отмечают, что функция y периодична, ее наименьший положительный период равен 2π, значения функции равны 0 при x = 0, π, 2π…,в точках x = 0, π, 2π… функция меняет знак на противоположный, наибольшее абсолютное значение функция принимает при x = , , 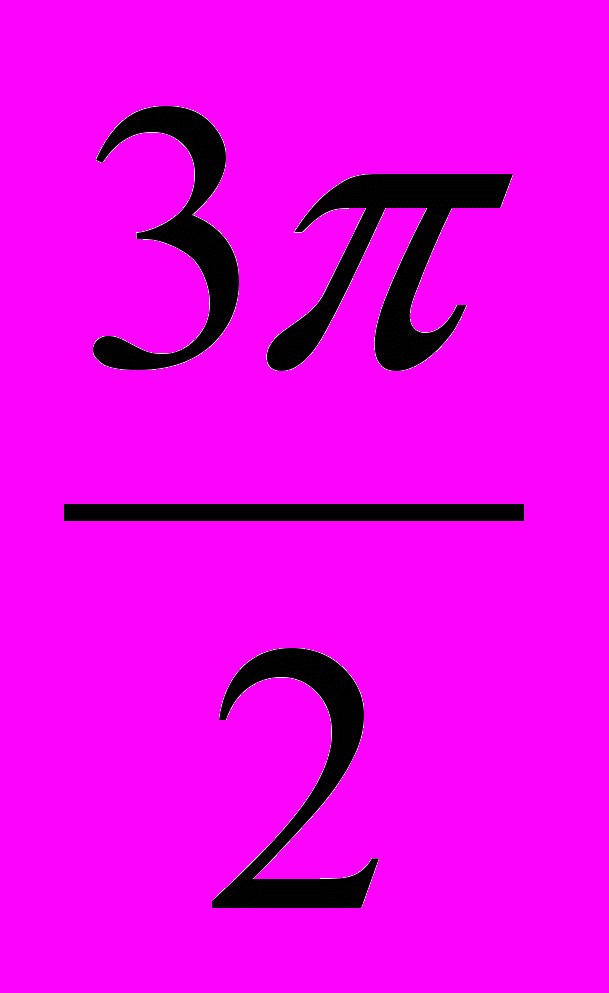… (2n+1).

На уроках физики изучают зависимость электродвижущей силы индукции εi, возникающий в витке, вращающемся в магнитном поле, от угла α.Эта зависимость выражается формулой: εi = ε0sinα.

Полезно предложить учащимся сопоставить эту формулу с функцией y=κsinx и на этом сравнении сделать вывод о свойствах электродвижущейся силы индукции.

В курсе математики учеников учат читать графики и составлять по ним задачи.

Поэтому можно предложить учащимся VIII класса в теме «Тепловые явления» такое задание: «Составьте задачу на определение количества теплоты по графику, изображенному на рисунке, и решите ее».



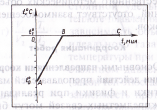
Может быть составлена такая задача: «Определить количество теплоты, необходимое для осуществления процесса, показанного на рисунке, со льдом массой m = 0,5 кг, взятого при температуре t0 = -70C».

Анализ учебных программ по математике и физике позволяет выделить две группы межпредметных знаний и умений, связанных с изучением функций:

1) работа с формулой, задающей функцию:

а) распознавание вида функции по формуле,

б) вычисление значения функции по заданному значению аргумента,

в) расчет по формуле значения аргумента, при котором функция принимает заданное значение,

г) выражение из формулы одной величины через другую,

д) нахождение области определения функции;

2) работа с графиком функции:

а) строить график,

б) по абсциссе точки графика находить ее ординату,

в) по ординате точки графика находить е абсциссу,

г) по нескольким графикам, вычерченным в одной общей системе координат, находить координаты точек пересечения графиков,

д) определять интервалы, где функция возрастает и убывает,

е) указывать области «знакопостоянства» функции,

ж) находить наибольшее и наименьшее значения функции и абсциссы точек, в которых эти значения достигнуты,

з) определять по формуле, принадлежит ли точка с заданными координатами графику представленной функции.

Анализ курса физики показывает, что перечисленные умения преимущественно применяются к трем видам функций:

прямой пропорциональности y = kx, k > 0,

обратной пропорциональности y = , где k > 0,

линейной функции y = ax + b.

Учителю физики есть смысл подсказать своему коллеге-математику, что при изучении различных функций в курсе математики полезно иллюстрировать их соответствующими физическими формулами.

Так, при рассмотрении прямой пропорциональности можно привести в качестве примеров ряд формул, попросить привести их к стандартному математическому виду и указать k:

а) m = ρV – зависимость массы тела от объема при постоянной плотности,

б) Q = λm-зависимость количества теплоты, поглощенной при плавлении или выделяющейся при кристаллизации, от массы тела при данной удельной теплоте плавления,

в) 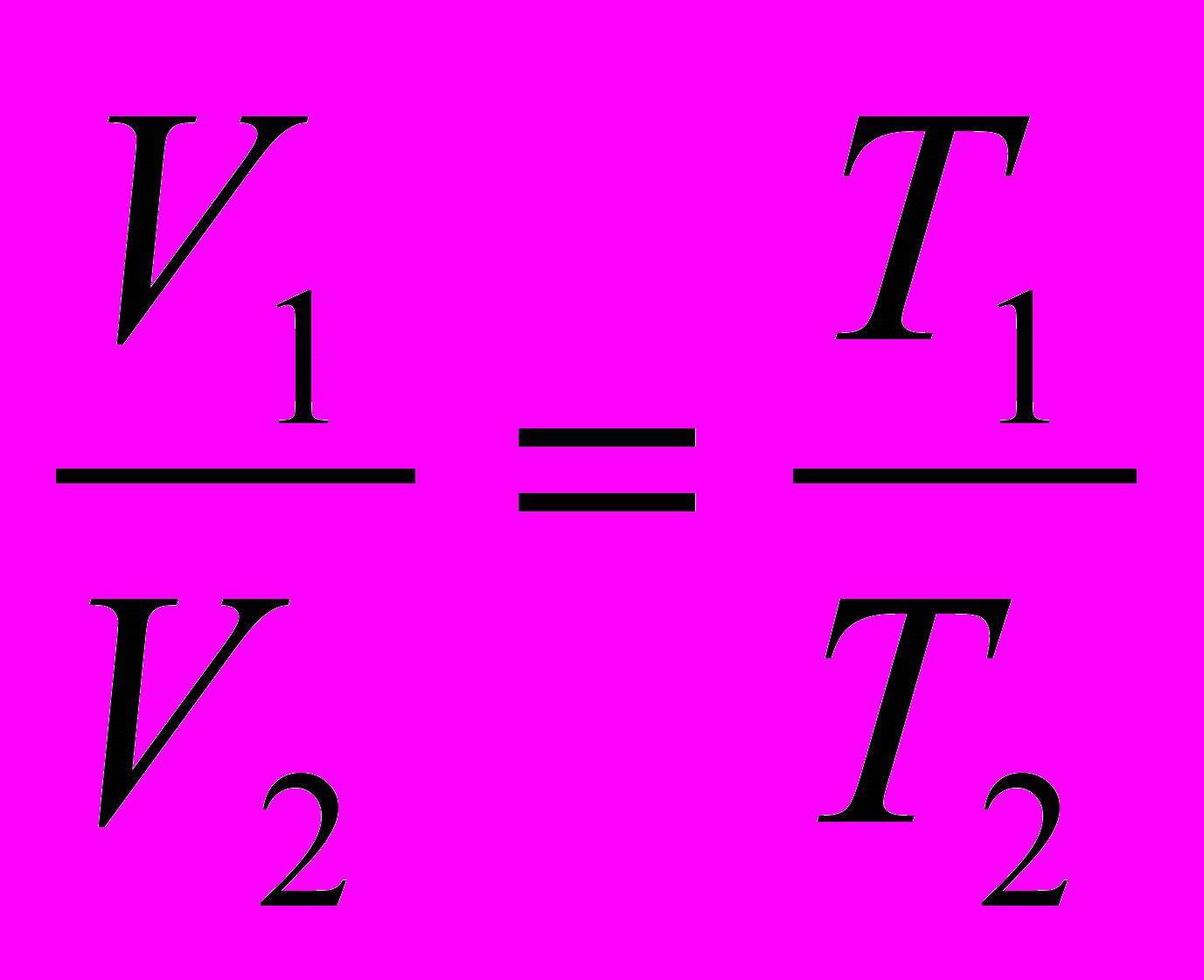– зависимость объема идеального газа от температуры при постоянном давлении,

г) q = It – зависимость прошедшего по проводнику заряда от времени при постоянной силе тока.

При рассмотрении или повторении на уроках математики обратно пропорциональной зависимости можно обратиться в качестве примера к указанным ниже формулам д) - ж), изученным в курсе физики:

д) 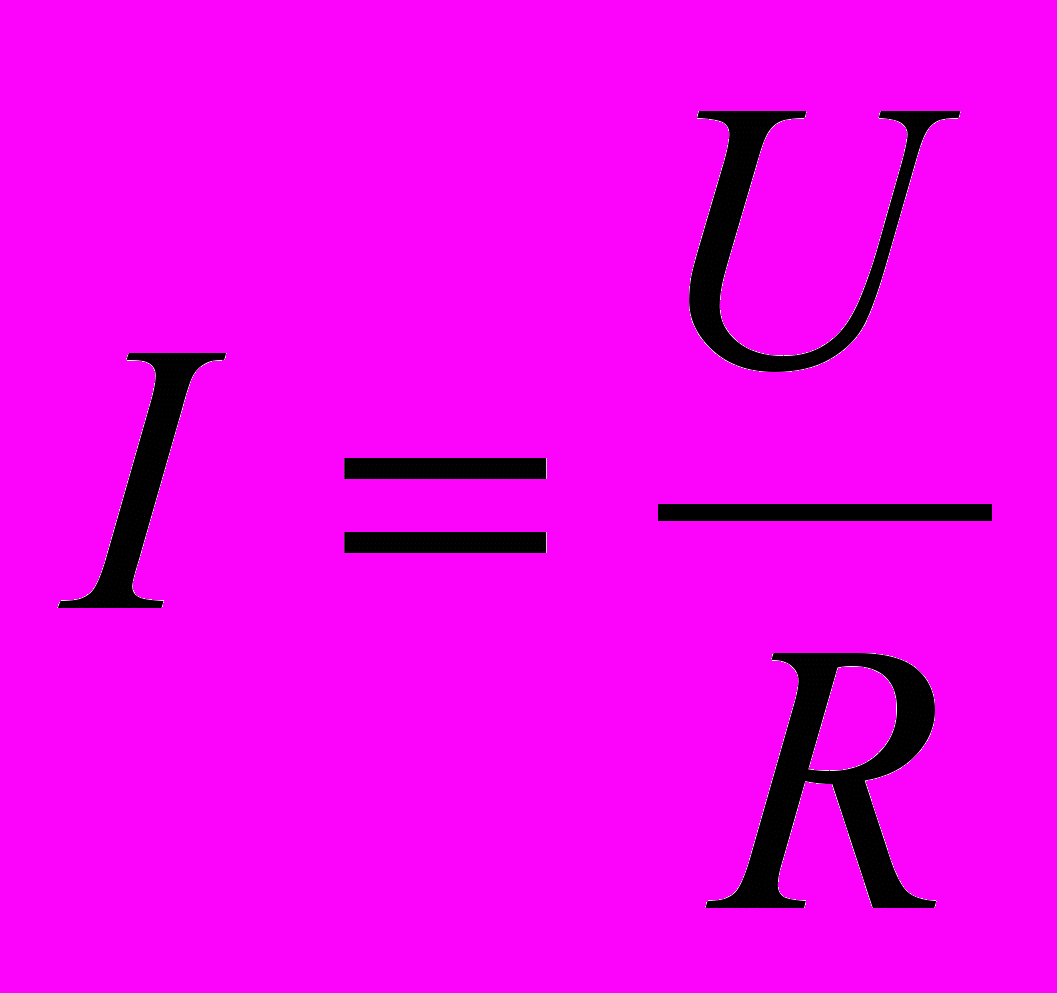- зависимость силы тока на участке электрической цепи от сопротивления при постоянном напряжении,

е) 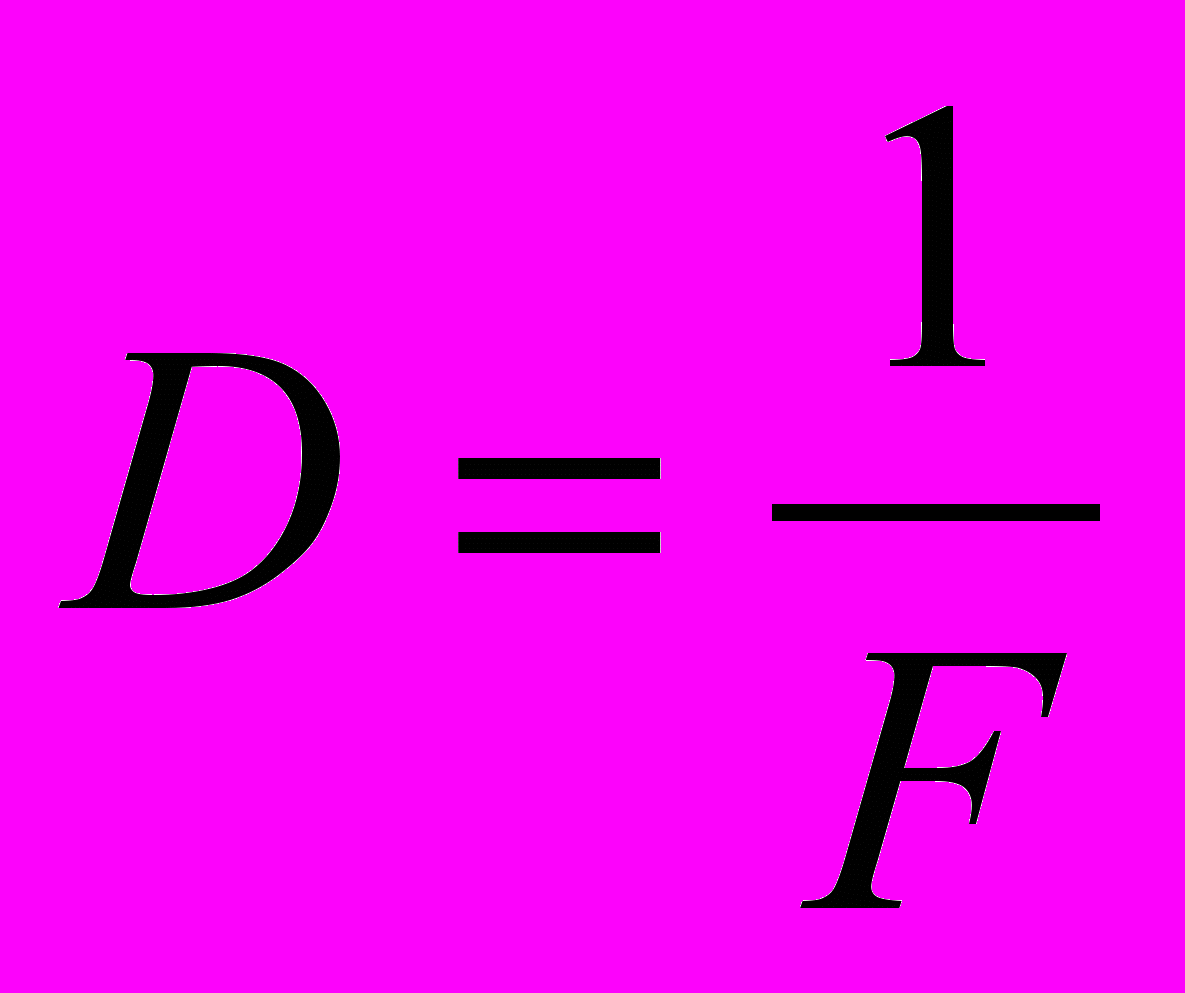- зависимость оптической силы тонкой линзы от главного фокусного расстояния,

ж) 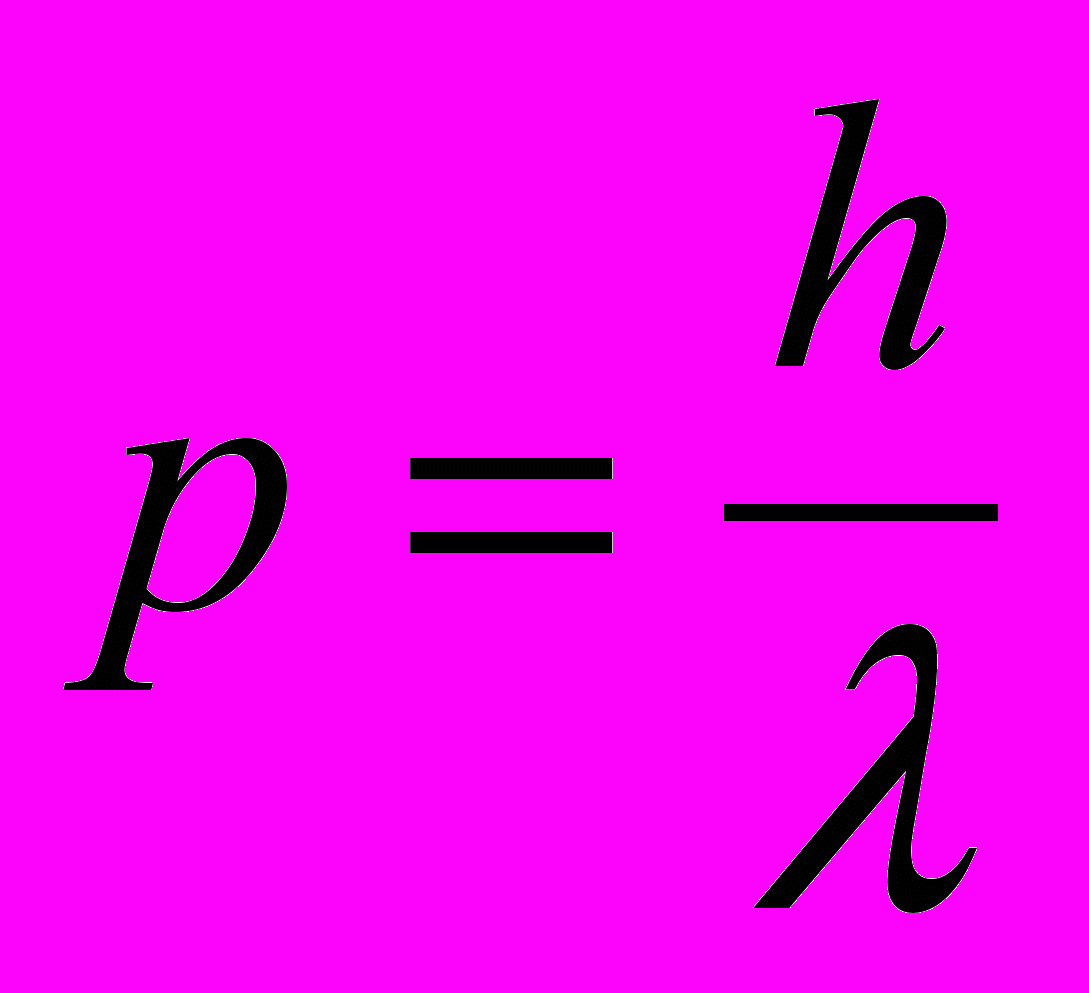- зависимость импульса фотона от длины волны излучения.

Формулы з) - к) могут быть использованы при изучении квадратичной функции:

з) Eкин = 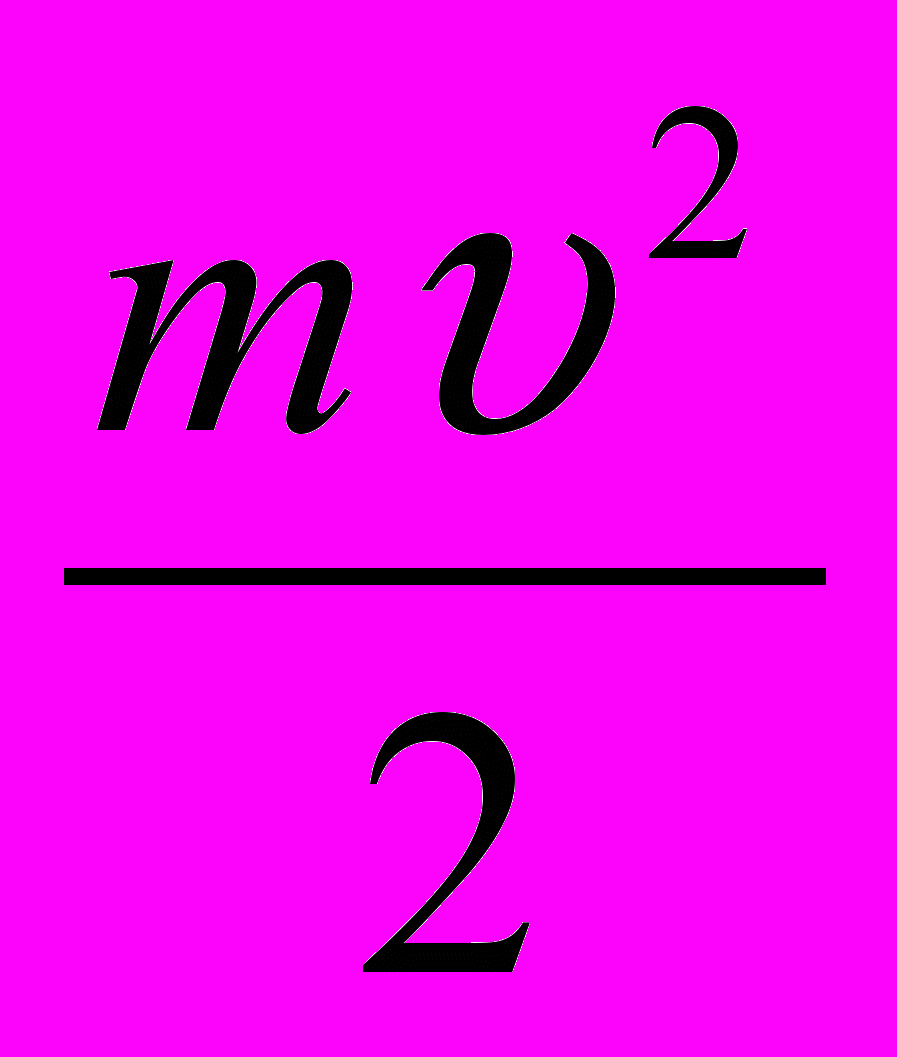- кинетическая энергия физического тела,

и) 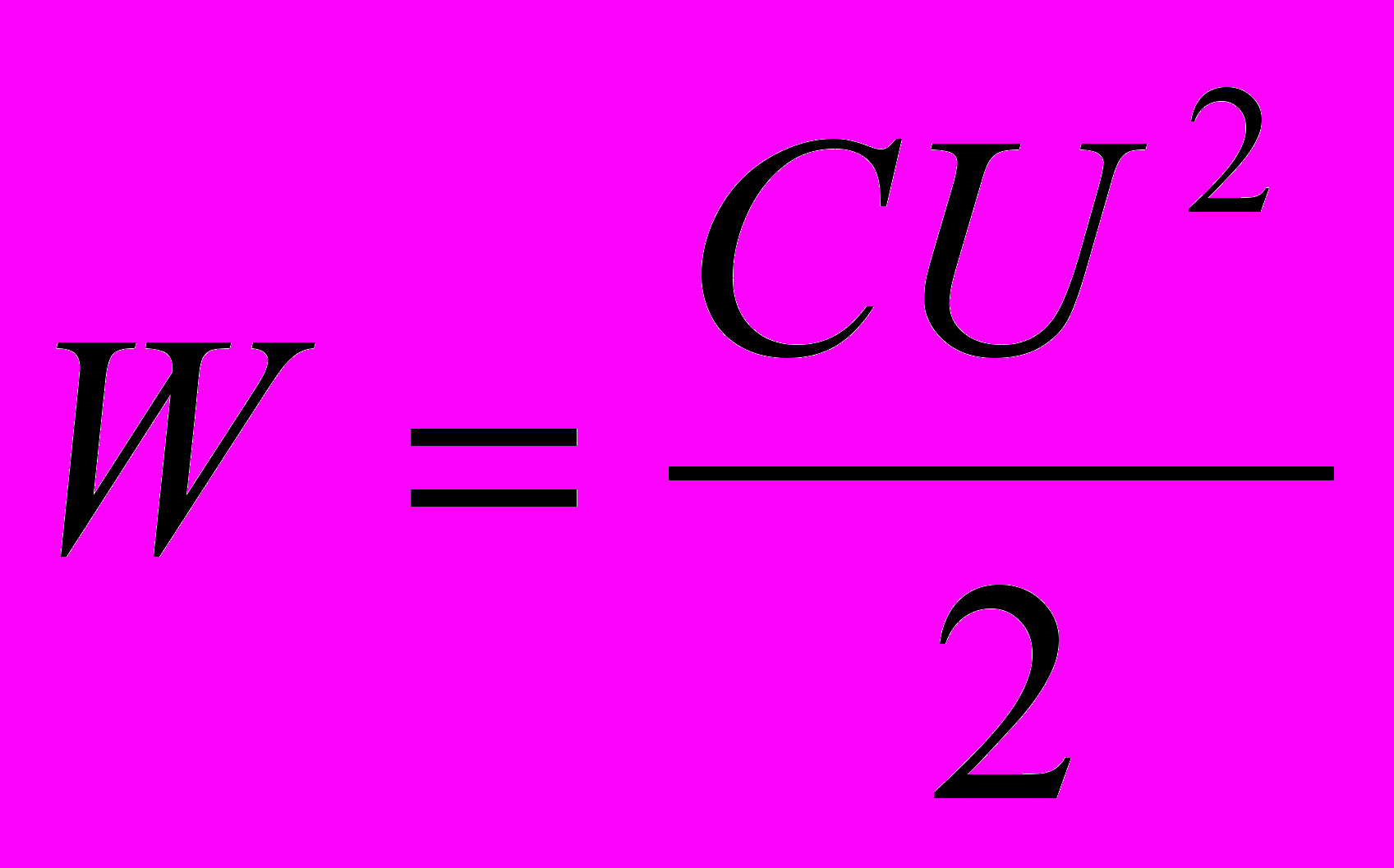- энергия заряженного конденсатора,

к) P = I2R - мощность электрического тока.

При повторении тригонометрических функций полезно обратиться к формулам л) - о):

л) x = Asin(ωt + φ0) - уравнение гармонического колебания,

м) F = IBlsinα - закон Ампера,

н) Fл = qBυsinα - сила Лоренца,

о) Ф = ВScosα - магнитный поток.

В процессе реализации межпредметных связей курсов математики и физики возникают трудности:

1. Физические понятия, используемые на уроках математики, не всегда своевременно сформированы в курсе физики, и наоборот: математики не всегда своевременно знакомят с понятиями и действиями, необходимыми для курса физики.

2. В курсе физики применяют такие математические понятия, которые в рамках учебной математической программы вообще не вводятся.

3. Несогласованность терминологии и обозначений в курсах математики и физики.

Рассмотренные приемы - всего лишь несколько способов реализации межпредметных связей курсов физики и математики.

При изучении простых механизмов и машин показываю плакат по истории с египетскими пирамидами и предлагаю ученикам рассказать об их строительстве. Учащиеся называют использованные при строительстве приспособления (рычаг, блок, ворот и др.), собирают их модели из имеющихся деталей, приводят в действие и поясняют принципы работы. Говорю, что следует различать полезную и затраченную работу, и прошу сравнить эти работы в каждом конкретном случае. Рассмотренный пример иллюстрирует межпредметные связи курсов физики и истории.

При изучении механизмов проводимости электрического тока в различных средах полезно использовать знания учащихся из курса химии для объяснения разной электропроводности металлов.

Взаимосвязь с биологией я реализую так:

при изучении диффузии использую пример из ботаники, а при прохождении звуковых и световых явлений - материал из зоологии и анатомии (в частности, о строении уха, глаза, световом восприятии, особенностях зрения рыб и человека).

При изучении темы «Тепловые явления» можно предложить заслушать отрывок из стихотворения А.С.Пушкина «Руслан и Людмила».

«На месте славного побега

Весной растопленного снега

Потоки мутные текли

И рыли влажну грудь земли…»

Потом задать вопросы:

О каком тепловом процессе идет речь в данном отрывке?

При какой температуре тает снег?

Как называется эта температура?

Так осуществляется межпредметная связь физики и литературы.

Мы рассмотрели различные способы реализации межпредметных связей. Хотелось подчеркнуть, что эта работа важна, и поэтому заслуживает внимания педагога.