9 6 Контрольные вопросы
| Вид материала | Контрольные вопросы |
- Александр Леонидович Симанов Содержание История философии. Онтология и гносеология., 225.58kb.
- Рабочая программа. Тематический план. Темы семинарских занятий. Контрольные вопросы, 127.79kb.
- Контрольные вопросы какую роль в жизни общества играет познание?, 291.58kb.
- Далакишвили Татьяна Васильевна контрольные вопросы, 16.39kb.
- Контрольные задания по дисциплине «Налогообложение», 237.01kb.
- Контрольные вопросы по дисциплине Деньги, кредит, банки в целом (вопросы к экзамену), 25.31kb.
- Контрольные вопросы по дисциплине Финансы, денежное обращение и кредит в целом (вопросы, 17.05kb.
- Контрольные вопросы по курсу в целом Вопросы к зачету, 87.71kb.
- Методическое пособие по курсу педагогики имеет цель оказать помощь студентам в овладении, 724.88kb.
- Психология личности контрольные вопросы по разделам дисциплины Примерный перечень вопросов, 51.04kb.
4.6 Контрольные вопросы
1. Охарактеризуйте методику экспертного анализа инвестиционных рисков.
2. В каких случаях применяется экспертный анализ инвестиционных рисков.
3. Каким требованиям должен отвечать эксперт.
4. Дайте характеристику основным этапам экспертного анализа.
- ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №5
АНАЛИЗ ЧУВСТВИТЕЛЬНОСТИ ИНВЕСТИЦИОННОГО ПРОЕКТА
5.1 Цель занятия
Овладеть методикой анализа чувствительности инвестиционного проекта.
5.2 Задачи занятия
Изучить алгоритм и последовательность анализа чувствительности инвестиционного проекта.
5.3 Краткие теоретические сведения
Цель анализа чувствительности состоит в сравнительном анализе влияния различных факторов инвестиционного проекта на ключевой показатель эффективности проекта, например, внутреннюю норму прибыльности или чистую текущую стоимость проекта.
Приведем наиболее рациональную последовательность проведение анализа чувствительности.
1. Выбор ключевого показателя эффективности инвестиций, в качестве которого может служить внутренняя норма прибыльности (IRR) или чистое современное значение (NPV).
2. Выбор факторов, относительно которых разработчик инвестиционного проекта не имеет однозначного суждения (т. е. находится в состоянии неопределенности). Типичными являются следующие факторы:
- капитальные затраты и вложения в оборотные средства,
- рыночные факторы - цена товара и объем продажи,
- компоненты себестоимости продукции,
- время строительства и ввода в действие основных средств.
3. Установление номинальных и предельных (нижних и верхних) значений неопределенных факторов, выбранных на втором шаге процедуры. Предельных факторов может быть несколько, например
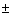5% и 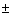10% от номинального значения (всего четыре в данном случае) 4. Расчет ключевого показателя для всех выбранных предельных значений неопределенных факторов.
5. Построение графика чувствительности для всех неопределенных факторов. В западном инвестиционном менеджменте этот график носит название “Spider Graph”. Ниже приводится пример такого графика для трех факторов.
График, представленный на рисунке 2 позволяет сделать вывод о критических факторах инвестиционного проекта. В ходе реализации проекта на эти факторы необходимо обратить особое внимание с целью сокращения риска, связанного с реализацией инвестиционного решения.
Рисунок 2 - Чувствительность проекта к изменению неопределенных факторов
Так, например, если цена продукции оказалась критическим фактором, то в ходе реализации проекта необходимо улучшить программу маркетинга и (или) повысить качество товаров. Если проект окажется чувствительным к изменению объема производства, то следует уделить больше внимания совершенствованию внутреннего менеджмента предприятия и ввести специальные меры по повышению производительности. Наконец, если критическим оказался фактор материальных издержек, то целесообразно улучшить отношение с поставщиками, заключив долгосрочные контракты, позволяющие, возможно, снизить закупочную цену сырья.
5.4 Решение типовых заданий
Задание 1
Фирма рассматривает инвестиционный проект, связанный с выпуском продукта «А». Полученные в результате опроса экспертов данные по проекту приведены в таблице 20. Требуется провести анализ чувствительности NPV к изменениям ключевых исходных показателей.
Таблица 20 - Исходные данные по проекту производства продукта «А», в условных денежных единицах
| Показатели | Диапазон изменений | Наиболее вероятные значения |
| Объем выпуска, Q | 150 – 300 | 200 |
| Цена за штуку, P | 35 – 55 | 50 |
| Переменные затраты, V | 25 – 40 | 30 |
| Постоянные затраты, F | 500 | 500 |
| Амортизация, A | 100 | 100 |
| Налог на прибыль, T | 30% | 30% |
| Норма дисконта, r | 8 – 15% | 10% |
| Срок проекта, n | 5 – 7 | 5 |
| Остаточная стоимость, Sn | 200 | 200 |
| Начальные инвестиции, Io | 2000 | 2000 |
Первым этапом решения является определение зависимости результирующего показателя от исходных. Подобная зависимость может быть выражена соотношением:
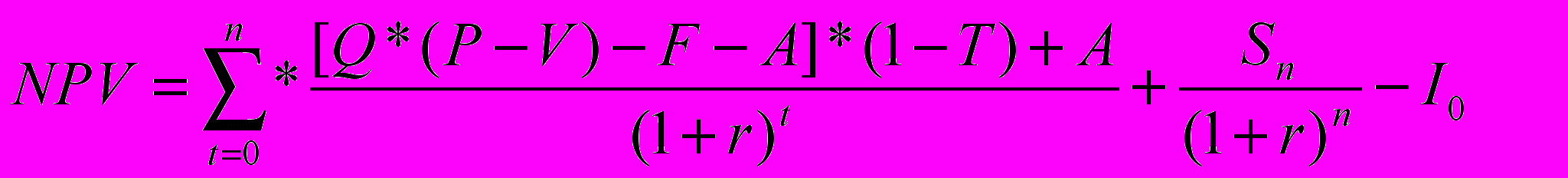, (5.1) Диапазоны возможных изменений исходных показателей или их пограничные значения определены ранее (в условии задачи), поэтому можно приступать расчету результирующего показателя NPV.
Таблица 21 - Анализ чувствительности NPV к изменению цены
| Значения показателя Р | 50 | 45 | 40 | 35 | 30 | 25 |
| Значения NPV | 7525,3 | 4871,72 | 2218,13 | -435,46 | -3089,05 | -5742,64 |
Таблица 22 - Анализ чувствительности NPV к изменению объема
| Значения показателя Q | 300 | 250 | 200 | 150 | 100 | 50 |
| Значения NPV | 12766,26 | 10178,9 | 7591,54 | 5004,18 | 2416,82 | -170,54 |
Из результатов сравнительного анализа чувствительности NPV к изменению объема и к изменению цены следует вывод, что для данного проекта выбранный результирующий показатель более эластичен к изменению цены.
При неизменных значениях остальных показателей падение цены менее чем на 20 % приведет к отрицательной величине NPV, тогда как снижение объема выпуска с 300 до 100 единиц при прочих равных условиях все еще обеспечивают положительную величину NPV. Таким образом, разработчикам проекта особое внимание необходимо уделить контролю качества продукции, поиску возможностей его повышения, а, также комплексу маркетинга, связанного с продуктом.
Задание 2
Рассчитать точку безубыточности для предприятия с тремя видами продукции. Исходные данные и алгоритм расчета точки безубыточности представлены в таблице 23.
Таблица 23 – Расчет точки безубыточности для предприятия, выпускающего три вида продукции
| Наименование позиции | «А» | «В» | «С» | Итого |
| Объем продаж, млн. руб. | 100 | 200 | 700 | 1000 |
| Доля в объеме продаж, % | 10 | 20 | 70 | 100 |
| Цена за единицу, тыс. руб. | 2 | 5 | 10 | - |
| Переменные издержки, млн. руб. | 40 | 120 | 380 | 540 |
| Доход, млн. руб. | 60 | 80 | 320 | 460 |
| Уровень дохода от объема продаж, % | - | - | - | 46 |
| Постоянные издержки, млн. руб. | - | - | - | 200 |
| Точка безубыточности для производства в целом, млн. руб. (с.7 / с.6) | - | - | - | 434 |
| Точка безубыточности по видам продукции, млн. руб. (с.2с.8) | 43,4 | 86,8 | 303,8 | 434 |
| Точка безубыточности по видам продукции, шт. (с.9 1000/ с.3) | 21 700 | 17 360 | 30 380 | - |
5.5 Задания для самостоятельного решения
Задание 1
Предприятие рассматривает проект по выпуску продукции «А». Исходные данные представлены в таблице 24
Таблица 24 – Исходные данные
| Показатели | Сценарии реализации проекта | ||
| Пессимистический | Оптимистический | Вероятный | |
| Объем выпуска, шт. | 15 000 | 25 000 | 20 000 |
| Цена единицы продукции, у.е. | 1 500 | 2 500 | 2 000 |
| Переменные затраты, у.е. | 1 400 | 1 000 | 1 200 |
| Норма дисконта, % | 16 | 8 | 12 |
| Постоянные затраты, у.е. | 5 000 | 5 000 | 5 000 |
| Амортизация, у.е. | 2 000 | 2 000 | 2 000 |
| Налог на прибыль, % | 40 | 30 | 35 |
| Срок проекта, лет | 4 | 4 | 4 |
| Остаточная стоимость, у.е. | 7 200 | 7 200 | 7 200 |
| Начальные инвестиции, у.е. | 26 000 | 26 000 | 26 000 |
Требуется определить:
1) критерии NPV, IRR, PI, PBP при наиболее благоприятных, наименее благоприятных и вероятных значениях ключевых параметров;
2) проведите анализ чувствительности NPV к изменениям ключевых переменных с шагом 10 %;
3) проведите анализ чувствительности IRR к изменениям ключевых переменных с шагом 5 %.
Задание 2
Используя исходные данные проведите абсолютный анализ чувствительности:
1) рассчитайте показатели предельного уровня ключевых параметров проекта, используя в качестве результирующего критерия NPV;
2) проведите анализ (в том числе графический) безубыточного объема производства продукции «А».
Таблица 25 - Исходные данные
| Показатели | Сценарии реализации проекта | ||
| Пессимистический | Оптимистический | Вероятный | |
| Объем выпуска, шт. | 15 000 | 25 000 | 20 000 |
| Цена единицы продукции, у.е. | 1 500 | 2 500 | 2 000 |
| Переменные затраты, у.е. | 1 400 | 1 000 | 1 200 |
| Норма дисконта, % | 16 | 8 | 12 |
| Постоянные затраты, у.е. | 5 000 | 5 000 | 5 000 |
| Амортизация, у.е. | 2 000 | 2 000 | 2 000 |
| Налог на прибыль, % | 40 | 30 | 35 |
| Срок проекта, лет | 4 | 4 | 4 |
| Остаточная стоимость, у.е. | 7 200 | 7 200 | 7 200 |
| Начальные инвестиции, у.е. | 26 000 | 26 000 | 26 000 |
5.5 Задания для самостоятельного решения
1. Охарактеризуйте методику анализа чувствительности инвестиционного проекта.
2. Определите цель проведения анализа чувствительности инвестиционного проекта.
3. Дайте характеристику этапов проведения анализа чувствительности.
- ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №6
АНАЛИЗ СЦЕНАРИЕВ РЕАЛИЗАЦИИ ИНВЕСТИЦИОННЫХ РЕШЕНИЙ
6.1 Цель занятия
Освоить навыки анализа сценариев реализации инвестиционных решений.
6.2 Задачи занятия
Изучить этапы процедуры анализа сценариев реализации инвестиционных решений. Изучить методику нахождения критериев колебания признаков. Изучит принципы имитационного моделирования.
6.3 Краткие теоретические сведения
Анализ сценариев - это прием анализа риска, который на ряду с базовым набором исходных данных проекта рассматривает ряд других комбинаций исходных показателей, которые по мнению разработчиков проекта могут иметь место в процессе реализации. Данный метод предусматривает подбор показателей при неблагоприятном (малый объем продаж, низкая цена продажи, высокая себестоимость единицы товара, и т. д.), при наиболее вероятном и при “успешном” стечении обстоятельств. После этого рассчитываются NPV или иные выбранные результирующие показатели для каждого из выбранных вариантов.
Данный метод позволяет совместить исследование чувствительности исходного показателя с анализом вероятностных оценок его отклонений. В общем случае процедура использования данного метода в процессе анализа инвестиционных рисков включает выполнение следующих шагов:
- определяют несколько вариантов изменений ключевых исходных показателей, например пессимистический, наиболее вероятный и оптимистический.
- каждому варианту изменений приписывают его вероятностную оценку (сумма вероятностей наступления каждого из вариантов должна составлять 1).
- для каждого варианта рассчитывают вероятное значение результирующего критерия, а также оценки его отклонений от среднего значения.
- проводится анализ вероятностных распределений полученных результатов.
Среднее ожидаемое значение является средневзвешенным значением всех возможных результатов, где вероятность наступления каждого из результатов используется в качестве веса соответствующего значения.
Оно рассчитывается по следующей формуле:
=
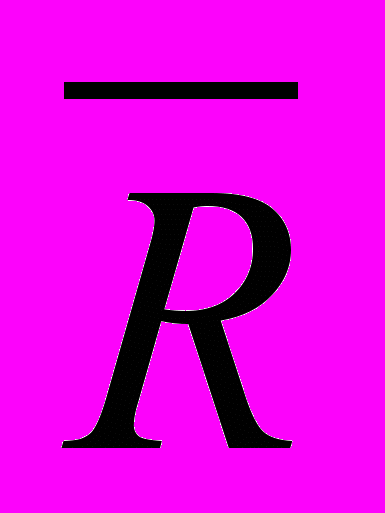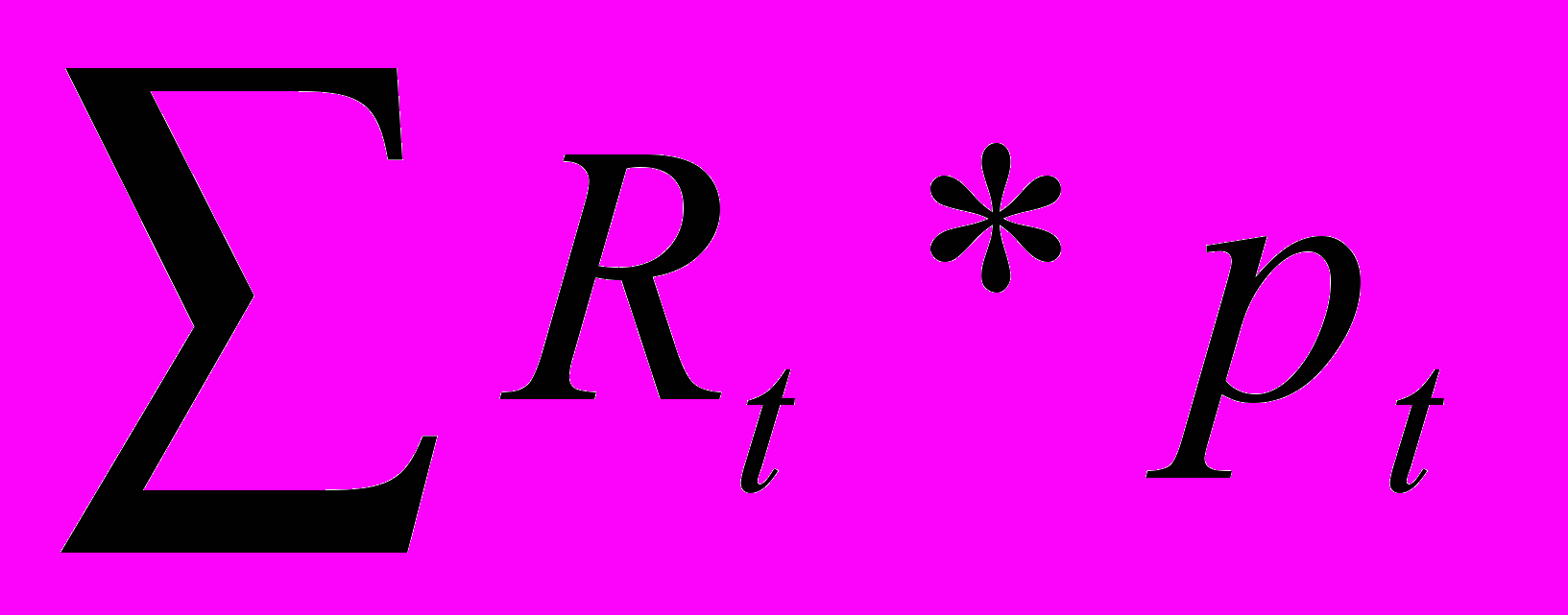, (6.1)где R – среднее ожидаемое значение;
Ri – значение показателя, которое может наступить с вероятностью pi.
Уровень колебания возможного результата представляет собой степень отклонения возможного значения от среднего ожидаемого значения результирующего показателя.
Для оценки уровня колебания используют два критерия:
- дисперсию и стандартное (среднеквадратичное) отклонение;
- коэффициент вариации.
Дисперсия и стандартное отклонение служат мерами абсолютной колеблемости, поэтому на эти величины влияют абсолютные значения измеряемых показателей.
Они рассчитываются следующим образом:
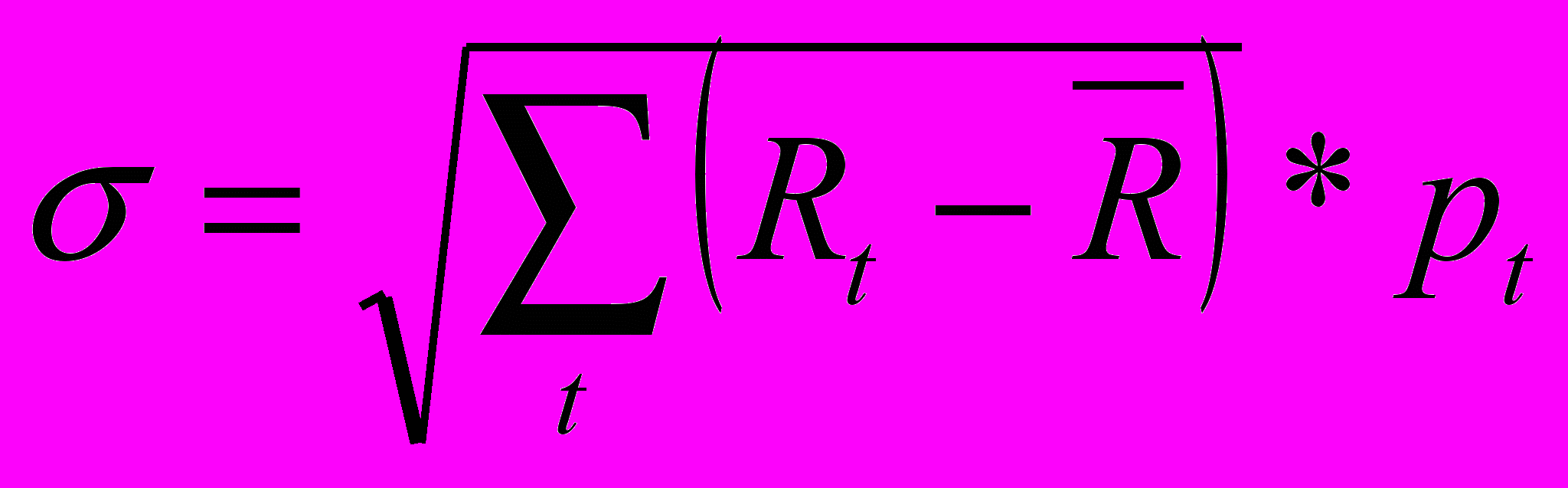, (6.2) 
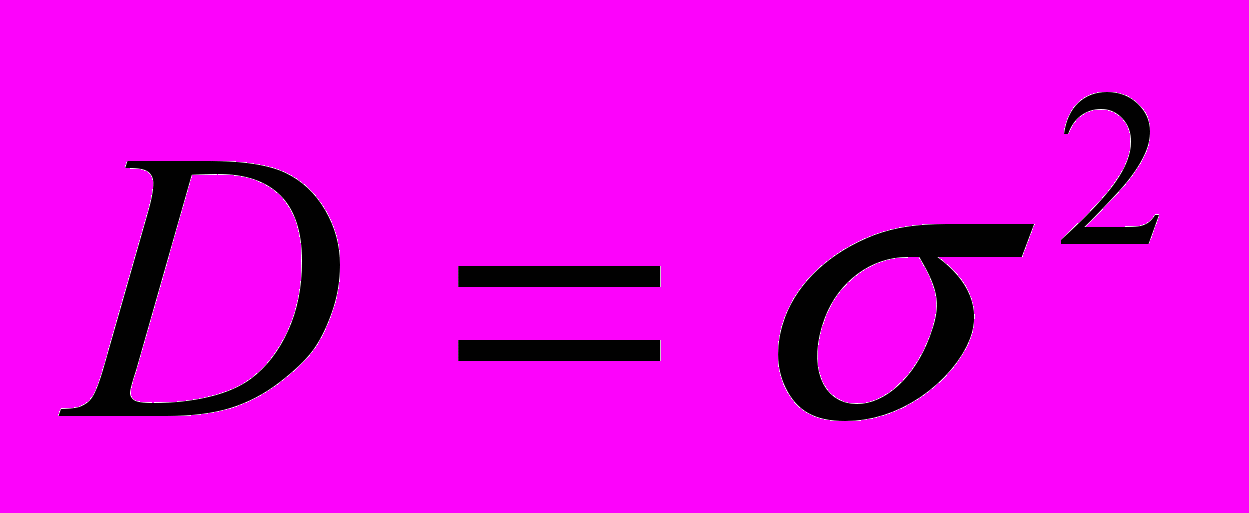, (6.3)где - стандартное отклонение, а D – дисперсия.
Чтобы исключить влияние абсолютных значений используют коэффициент вариации.
Данный показатель является относительной величиной. Он рассчитывается по следующей формуле:
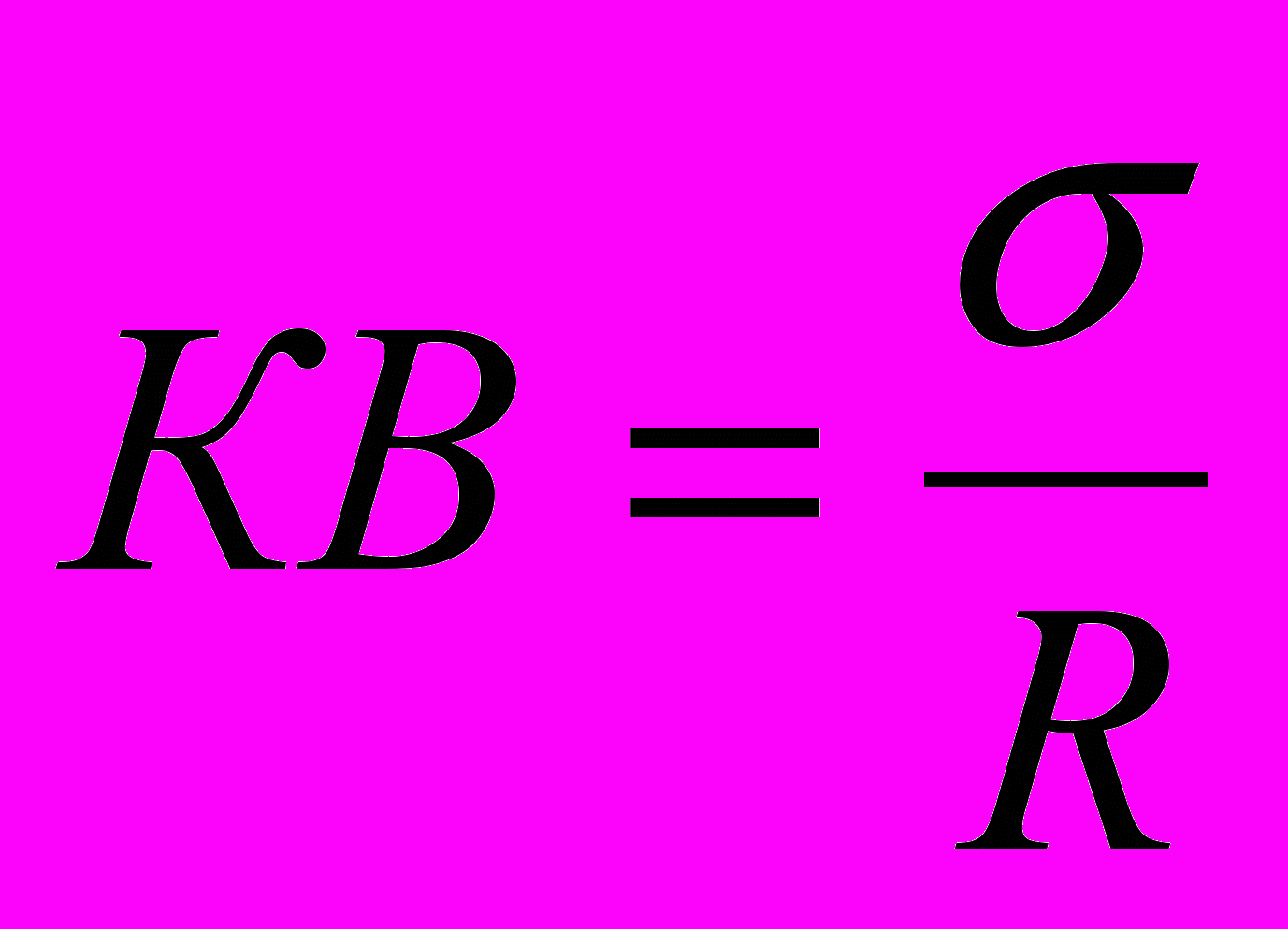, (6.4) С помощью коэффициента вариации можно сравнивать даже колеблемость признаков, выраженных в разных единицах измерения. В экономических расчетах принята следующая оценка значения коэффициента вариации:
- до 10% - слабая колеблемость;
- от 10 до 25% - умеренная колеблемость;
- более 25% - высокая колеблемость.
Как правило, в экономических и иных расчетах значение коэффициента вариации изменяется от 0 до 1. Поскольку в инвестиционном анализе результирующий показатель, например NPV, может быть выражен отрицательной величиной значение коэффициента вариации может превышать значения единицы.
Проект с наименьшим стандартным отклонением и коэффициентом вариации считается менее рисковым.
Недостатком данного метода является то, что его использование направлено на исследование только результирующих показателей (NPV, IRR, PI). Метод сценариев не обеспечивает пользователей информацией о возможных отклонениях потоков платежей и других ключевых показателей, определяющих в конечном итоге ход реализации проекта. Несмотря на присущие ему ограничения данный метод успешно применяется в инвестиционном анализе.
Метод имитационного моделирования Монте-Карло создает дополнительную возможность при оценке риска за счет того, что позволяет создать случайные сценарии.
Применение анализа риска использует богатство информации, будь она в форме объективных данных или оценок экспертов, для количественного описания неопределенности, существующей в отношении основных переменных проекта и для обоснованных расчетов возможного воздействия неопределенности на эффективность инвестиционного проекта. Результат анализа риска выражается не каким-либо единственным значением NPV, а в виде вероятностного распределения всех возможных значений этого показателя. Следовательно, потенциальный инвестор, с помощью метода Монте-Карло будет обеспечен полным набором данных, характеризующих риск проекта. На этой основе он сможет принять взвешенное решение о предоставлении средств.
При формировании сценариев с использованием методов имитационного моделирования применяется следующая последовательность действий:
- определяются интервалы возможного изменения исходных переменных, внутри которых эти переменные являются случайными величинами;
- определяются виды распределений вероятностей внутри заданных интервалов;
- устанавливаются коэффициенты корреляции между зависимыми переменными;
- многократно (не менее 200 раз) рассчитываются результирующие показатели;
- полученные результирующие показатели рассматриваются как случайные величины, которым соответствуют такие характеристики, как математическое ожидание, дисперсия, функция распределения, плотность распределения вероятностей;
- определяется вероятность попадания результирующих показателей в тот или иной интервал, вероятность превышения минимально допустимого значения и др.
В общем случае имитационное моделирование Монте-Карло - это процедура, с помощью которой математическая модель определения какого-либо финансового показателя (в нашем случае NPV) подвергается ряду имитационных экспериментов с помощью компьютера. В ходе процесса имитации строятся последовательные сценарии с использованием исходных данных, которые по смыслу проекта являются неопределенными, и потому в процессе анализа полагаются случайными величинами.
Процесс имитации осуществляется таким образом, чтобы случайный выбор значений из определенных вероятностных распределений не нарушал существования известных или предполагаемых отношений корреляции среди переменных. Результаты имитации собираются и анализируются статистически, с тем, чтобы оценить меру риска. Процесс анализа риска может быть разбит на следующие стадии.
Первая стадия в процессе анализа риска - это создание прогнозной модели. Такая модель определяет математические отношения между числовыми переменными, которые относятся к прогнозу выбранного финансового показателя. В качестве базовой модели для анализа инвестиционного риска обычно используется модель расчета показателя NPV.
Использование этой формулы в анализе риска сопряжено с некоторыми трудностями. Они заключаются в том, что при генерировании случайных чисел, годовой денежный поток выступает как некое случайное число, подчиняющееся определенному закону распределения. В действительности же это совокупный показатель, включающий множество компонент рассмотренных в предыдущих публикациях. Этот совокупный показатель изменяется не сам по себе, а с учетом изменения объема продаж. Поэтому необходимо тщательно изучить эту корреляцию для максимального приближения к реальности.
| Прогнозная модель Подготовка модели, способной прогнозировать расчет эффективности проекта | | Распределение вероятности (шаг 1) Определение вероятностного закона распределения случайных переменных | | Распределение вероятности (шаг 2) Установление границ диапазона значений переменных | |
| | Условия корреляции Установление отношений коррелированных переменных | | Имитационные прогоны Генерирование случайных сценариев, основанных на наборе допущений | | Анализ результатов Статистический анализ результатов имитации |
Рисунок 3 - Процесс анализа риска
Общая прогнозная модель имитируется следующим образом. Генерируется достаточно большой объем случайных сценариев, каждый из которых соответствует определенным значениям денежных потоков. Сценарии собираются и производится их статистическая обработка для установления доли сценариев, которые соответствуют отрицательному значению NPV. Отношение таких сценариев к общему количеству вариантов дает оценку риска инвестиций.
Распределения вероятностей переменных модели (денежных потоков) диктуют возможность выбора величин из определенных диапазонов. Такие распределения представляют собой математические инструменты, с помощью которых придается вес всем возможным результатам. Этим контролируется случайный выбор значений для каждой переменной в ходе моделирования сценариев инвестиционного проекта.
При традиционном подходе к анализу риска, связанного с реализацией инвестиций, используется один тип распределения вероятности для всех переменных, включенных в модель анализа. Такой тип называют детерминированным распределением вероятности. При оценке имеющихся данных аналитик ограничен выбором единственного варианта из множества возможных результатов или расчетом сводного показателя. Затем аналитик должен принять, что выбранное значение обязательно реализуется, то есть он придает выбранному наиболее обоснованным образом показателю с единственным значением вероятность, равную 1. Поскольку такое распределение вероятности имеет единственный результат, итог аналитической модели можно определить на основании всего одного расчета (или одного эксперимента модели).
В анализе рисков используется информация, содержащаяся в распределении вероятности с множественными значениями. Именно использование множественных значений вместо детерминированных распределений вероятности и отличает имитационное моделирование от традиционного подхода.
Определение случайных переменных и придание им соответствующего распределения вероятности является необходимым условием проведения анализа рисков. Успешно завершив эти этапы, можно перейти к стадии моделирования. Однако непосредственный переход к моделированию будет возможен только в том случае, если будет установлена корреляция в системе случайных переменных, включенных в модель. Под корреляцией понимается случайная зависимость между переменными, которая не носит строго определенного характера, например, зависимость между ценой реализации товара и объемом продаж.
Наличие в модели анализа зависимых переменных может привести к серьёзным искажениям результатов анализа риска, если эта корреляция не учитывается. Фактически наличие корреляции ограничивает случайный выбор отдельных значений для зависимых переменных. Достаточно сложно объективно определить точные характеристики корреляции случайных переменных в модели анализа, на практике имеется возможность установить направление таких связей и предполагаемую силу корреляции. Для этого применяют методы регрессионного анализа. В результате этого анализа рассчитывается коэффициент корреляции, который может принимать значения от -1 до 1.
После того, как все допущения тщательно обоснованы, остается только последовательно просчитывать модель (каждый пересчет является одним экспериментом) до тех пор, пока не будет получено достаточно значений для принятия решения. В ходе моделирования значения переменных выбираются случайно в границах заданных диапазонов и в соответствии с распределениями вероятностей и условиями корреляций. Для каждого набора таких переменных вычисляется значение показателя эффективности проекта. Все полученные значения сохраняются для последующей статистической обработки.
Окончательной стадией анализа рисков является обработка и интерпретация результатов, полученных после проведения экспериментов. Каждый эксперимент представляет вероятность события, равную
p = 100 / n, где p - вероятность единичного прогона, %; n - размер выборки.
Например, если количество случайных прогонов равно 5000, то вероятность одного прогона составляет p = 100 / 5000 = 0,02 %.
В качестве меры риска в инвестиционном проектировании целесообразно использовать вероятность получения отрицательного значения NPV. Эта вероятность оценивается на основе статистических результатов имитационного моделирования как произведение количества результатов с отрицательным значением и вероятности единичного эксперимента.
Например, если из 5000 прогонов отрицательные значения NPV окажутся в 3454 случаях, то мера риска составит 69.1%.