Методические материалы для учителей по итогам организации и проведения единого государственного экзамена в Саратовской области в 2011 году
| Вид материала | Методическое пособие |
- Методические материалы для учителей по итогам организации и проведения единого государственного, 2976.24kb.
- Пензенской области, 33.85kb.
- Методические материалы по подготовке и проведению гиа-9 в пунктах проведения экзамена, 688.23kb.
- Методические материалы по подготовке и проведению егэ в пунктах проведения экзамена, 879.12kb.
- Приказ 23. 09. 2010 №2447 г. Саратов, 2042.38kb.
- План подготовки и проведения единого государственного экзамена, государственного выпускного, 201.13kb.
- План подготовки и проведения единого государственного экзамена, государственного выпускного, 198.55kb.
- О преподавании учебного предмета «химия» в общеобразовательных учреждениях кемеровской, 213.56kb.
- Рабочая программа по литературе в 5 а и в 6 Бклассах учитель Черновол Татьяна Геннадьевна, 205.64kb.
- Рабочая программа по русскому языку в 5 а и в 6 Бклассах учитель Черновол Татьяна Геннадьевна, 304.04kb.
Выполнение заданий С1 не требовало обоснований, многошаговых преобразований и вычислений, применения каких-либо особых, необычных приемов, но проверяло владение известными алгоритмами действий и методами решений.
Фактически баллы за выполнение этих задач выставлялись в том случае, когда участник ЕГЭ явно демонстрировал владение выбранным им методом решения: правильно проводил требуемые операции, исследовал все возможные случаи, выполнял отбор соответствующих решений согласно условию задания. При этом ему давалось право только на описку и/или несущественную вычислительную ошибку. Чаще всего выпускники не могли правильно сформулировать ответ, учесть множество, на котором задача имеет смысл, имело место много вычислительных ошибок. Типичными ошибками были:
- неумение решать квадратные уравнения;
- незнание свойств тригонометрических функций;
- неумение решать простейшие тригонометрические уравнения.
Задание С2 проверяло умение работать с простейшими геометрическими объектами в трехмерном пространстве, уметь применять метод сечений. Большинство экзаменующихся не смогли даже верно записать условие задачи и сделать чертеж. При выполнении задания было проявлено отсутствие навыков: переходить от трех мерной пространственной задачи к плоской; оперировать с определениями двугранного угла, расстояния от точки до прямой и плоскости, умение обосновать выполненные действия..
В зависимости от полноты и правильности приведенного решения за выполнение заданий С1 и С2 обучающиеся получали от 0 до 2 баллов
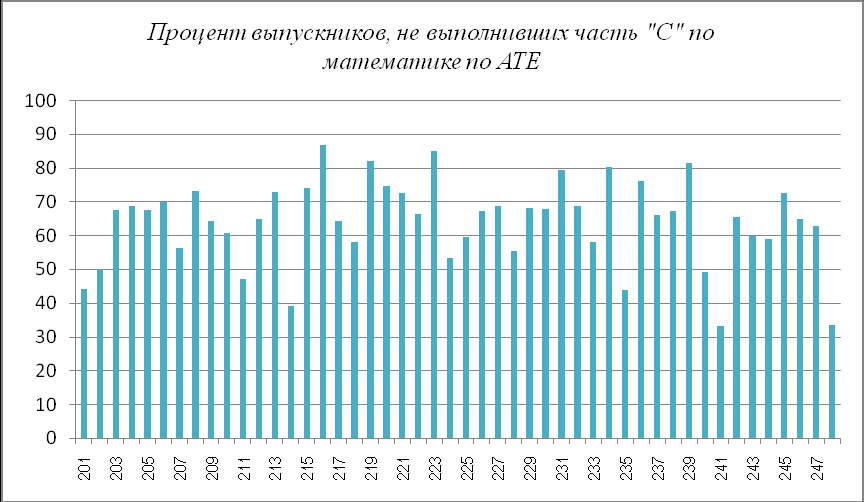
Сложность заданий СЗ- С6 состояла в том, что при их решении необходимо было применить знание материала, относящегося к различным разделам школьного курса математики. Основная цель этих заданий - проверка умения анализировать задачу, разрабатывать математическую модель, выбирать рациональный метод решения, интегрировать и применять теоретические знания к решению задач
В зависимости от типа задачи, полноты и правильности приведенного решения за выполнение заданий обучающиеся получали до 3-4 баллов.
Выполнение заданий С3 требовало обоснований, многошаговых преобразований и вычислений, применения каких-либо особых, нетрадиционных приемов. Это, в основном, были логарифмические и показательные неравенства. Традиционные способы решения требовали больших аналитических выкладок и вычислений.
Менее 1% выпускников выполнили это задание на 2-3балла. Основными ошибками были: - неверное определение границ множества, на котором решалась задача; неумение различать эквивалентные преобразования и следствие; вычислительные ошибки; слабое владение методом интервалов, незнание свойств логарифмов и степеней, не верное понимание операций пересечения и объединения множеств..
Задание С4 проверяло умение работать с геометрическими объектами на плоскости. В основном это были задачи, требующие использовать свойства многоугольников, вписанных и описанных окружностей. Здесь нужны были не только вспомогательные построения, но и объяснения использованных конфигураций. Большинство экзаменующихся не смогли продвинуться дальше исходного чертежа и записи основных формул. Типичные ошибки: неумение строить вписанные и описанные окружности, незнание свойств правильных многоугольников и прямоугольных треугольников, вычислительные ошибки, неумение рационально описать ход решения задачи При решении этих заданий выпускники неправильно применяли правила подобия треугольников, определяли тип искомого четырехугольника.
Задание С5 относится к наиболее сложным, здесь представлены задачи с параметрами. традиционно, очень мало выпускников приступает к решению этих задач. Причем, большинство из начавших решение, так же как при решении задач с модулями, делают это аналитически, с использованием систем уравнений и неравенств, при решении которых используют не эквивалентные преобразования, запутываются в вычислениях. Решение задач такого типа, как правило, требует не только хорошего знания свойств функций, но и умение применять графические методы в решении задач, умение обоснованно отобрать значения параметра.
Задание С6 решили полностью меньше 30 человек. Здесь не только требовалось построить уравнения и неравенства по условиям задачи, но и доказать единственность решения. Много ошибок было вызвано незнанием свойств натуральных и целых чисел. Большинство выпускников к решению задачи не приступали.
Таблица 38
Распределение доли учащихся, имеющих ненулевую отметку при выполнении
Части « С» ЕГЭ по математике
| № зада-ния | Проверяемые элементы содержания | Процент ненулевых ответов выпускников | |
| 2010 г. | 2011г. | ||
| С1 | Решение уравнений и неравенств | 22,71 | 33,64 |
| С2 | Выполнение действий с геометрическими фигурами, координатами и векторами | 5,072 | 6,87 |
| С3 | Решение уравнений и неравенств | 5,332 | 12,76 |
| С4 | Выполнение действий с геометрическими фигурами, координатами и векторами | 0,977 | 1,89 |
| С5 | Решение уравнений и неравенств | 1,208 | 2,76 |
| С6 | Построение и исследование простейших математических моделей с использованием уравнений и неравенств | 1,324 | 0,75 |
При подготовке к экзамену по математике, который является обязательным для всех выпускников, необходимо обратить особое внимание на аккуратность вычислений, умение решать простейшие уравнения и неравенства, извлекать квадратные корни.
Школьники показали крайне низкий уровень знания геометрии, отсутствует культура выполнения чертежей, как плоских, так и трехмерных. Возможно, это связано с тем, что теперь нет отдельного курса геометрии в школе.
Вызывают трудности текстовые задачи, в которых необходимо составлять уравнения или системы уравнений, такие задачи решаются в 5-6 классах школы, и, видимо в старших классах не повторяются.
Анализ результатов экзамена по физике.
В экзаменационной работе контролируются знания и умения из следующих разделов (тем) курса физики:
1. Механика (кинематика, динамика, статика, законы сохранения в механике, механические колебания и волны).
2. Молекулярная физика (молекулярно-кинетическая теория, термодинамика).
3. Электродинамика (электрическое поле, постоянный ток, магнитное поле, электромагнитная индукция, электромагнитные колебания и волны, оптика, основы СТО).
4. Квантовая физика (корпускулярно-волновой дуализм, физика атома, физика атомного ядра).
Задания части 3 (задания С2–С6) проверяют, как правило, комплексное использование знаний и умений из различных разделов курса физики.
В экзаменационной работе представлены задания разного уровня сложности: базового, повышенного и высокого.
Задания базового уровня включены в первую часть работы (20 заданий с выбором ответа) и во вторую часть (2 задания с кратким ответом). Это простые задания, проверяющие усвоение наиболее важных физических понятий, моделей, явлений и законов.
Задания повышенного уровня распределены между всеми тремя частями работы: 5 заданий с выбором ответа, 2 задания с кратким ответом и 1 задание с развернутым ответом. Эти задания направлены на проверку умения использовать понятия и законы физики для анализа различных процессов и явлений, а также умение решать задачи на применение одного-двух законов (формул) по какой-либо из тем школьного курса физики.
Пять заданий части 3 являются заданиями высокого уровня сложности и проверяют умение использовать физические теории и законы в измененной или новой ситуации. Выполнение таких заданий требует применения знаний сразу из двух-трех разделов физики, т.е. высокого уровня подготовки.
В 2011 году в г. Саратове и Саратовской области ЕГЭ по физике сдавало 3227 человек. Минимальный балл – 33, средний балл по области – 49,4. Имеет место устойчивая положительная динамика результатов за последние три года. , однако не увеличивается процент выпускников, выбирающих предмет для сдачи в форме ЕГЭ. Самые высокие средние баллы показали учащиеся лицеев (55,7) и гимназий (54,8). Лучшие результаты по среднему баллу в ОУ г. Саратова (65,3), Романовского района (56,8), Волжского района (55,8). Минимальные значения среднего балла в Федоровском (40,9), Красноармейском (41,4), Калининском (42,1) районах.
Таблица 39
Анализ результатов экзамена по физике.
Распределение правильных ответов по заданиям части А по физике
( приведено к спецификации 2010 года)
| № зада- ния | Проверяемые элементы содержания | Процент правильных ответов выпускников | |
| 2010 г. | 2011 г. | ||
| А1 | Кинематика | 55,90 | 74,60 |
| А2 | Кинематика, законы Ньютона | 67,59 | 61,64 |
| А3 | Силы в природе | 43,26 | 67,65 |
| А4 | Силы в природе, импульс, закон сохранения импульса | 51,89 | 71,96 |
| А5 | Механическая энергия, работа, закон сохранения энергии | 51,68 | 85,06 |
| А6 | Статика, механические колебания и волны | 66,27 | 49,96 |
| А7 | Механика | 39,42 | 46,41 |
| А8 | МКТ | 59,71 | 61,78 |
| А9 | МКТ | 59,59 | 62,05 |
| А10 | МКТ, термодинамика | 39,01 | 49,14 |
| А11 | Термодинамика | 53,77 | 64,05 |
| А12 | Молекулярная физика, термодинамика | 37,84 | 55,48 |
| А13 | Электростатика | 56,53 | 58,06 |
| А14 | Постоянный ток | 50,09 | 66,96 |
| А15 | Магнитное поле, электромагнитная индукция | 58,09 | 36,21 |
| А16 | Электромагнитные колебания и волны | 44,10 | |
| А16* | Электромагнитная индукция, электромагнитные колебания и волны | | 49,14 |
| А17 | Оптика | 59,62 | 53,79 |
| А18 | Элементы СТО, оптика | 54,43 | 57,72 |
| А19 | Электродинамика | 41,07 | 40,83 |
| А20 | Корпускулярно-волновой дуа-лизм, физика атома | 57,43 | 69,72 |
| А21 | Физика атома, физика атомного ядра | 46,64 | 60,71 |
| А22 | Физика атомного ядра | 62,58 | 65,62 |
| А23 | Квантовая физика | 24,30 | 59,02 |
| А24 | Физика и методы научного по-знания. Механика – квантовая физика | 65,13 | |
| Механика – квантовая физика (методы научного познания) | | 59,84 | |
| А25 | Физика и методы научного по-знания. Механика – квантовая физика | 27,74 | |
| Механика – квантовая физика (методы научного познания) | | 51,61 | |
100 баллов имеет один выпускник МАОУ «Физико-технический лицей №1» г. Саратова Слонов Алексей Дмитриевич, 6 выпускников имеют результат 98 баллов.
Наибольший процент выпускников, не выполнивших часть С экзаменационной работы, в ОУ Татищевского – 86,1%, Питерского- 77,1%, Красноармейского – 75% районов.
В период проведения ЕГЭ на этапе государственной (итоговой) аттестации по физике было подано 26 апелляций о несогласии с выставленными баллами, из них – 17 апелляций было подано выпускниками г. Саратова. Поданные апелляции рассмотрены в надлежащем порядке, по результатам рассмотрения приняты решения об увеличении баллов – 4 апелляции, уменьшения баллов не было.
Таблица 40
Распределение доли учащихся, имеющих ненулевую отметку при выполнению заданий части В по физике
| № зада- ния | Проверяемые элементы содержания | Процент правильных ответов выпускников | |
| 2010 г. | 2011г. | ||
| В1 | Механика – квантовая физика. | 57,23 | 61,03 |
| В2 | Механика – квантовая физика. | 60,26 | 51,32 |
| В3 | Механика (Расчетная задача) | 15,87 | |
| Механика – квантовая физика. | | 61,06 | |
| В4 | МКТ, электродинамика (Расчетная задача) | 32,40 | |
| Механика – квантовая физика. | | 56,67 | |
| В5 | Электродинамика, квантовая физика (Расчетная задача) | 28,24 | |
Представленные в 2011 г. в Саратовской области КИМ ЕГЭ по физике, имели следующее распределение заданий части С по разделам:
| С1: |
|
| С2: |
|
| С3: |
|
| С4: |
|
| С5: |
|
| С6: |
|
В части «С» встречается ряд задач, при решении которых обязательно наличие рисунка. (Например, по геометрической оптике, где рисунок поясняет ход лучей и введенные обозначения величин). В этом случае наличие рисунка оговаривается в условии задачи, а в критерии полного правильного решения вводится условие наличие рисунка. Отсутствие рисунка в работе учащегося приводит к снижению оценки на 1 балл.
Оценивание задач, в условиях которых приводятся фотографии реальных экспериментов, учитывает необходимость правильной записи показаний приборов. В этом случае в критерии полного правильного решения вводится условие верной записи показаний измерительных приборов. Если же показания приборов в работе экзаменующегося записаны неверно и отклонение в записи превышает цену деления прибора, то оценка снижается на один балл.
Решение учащегося может иметь логику, отличную от авторской логики решения (альтернативное решение). В этом случае эксперт оценивает возможность решения конкретной задачи тем способом, который выбрал учащийся.
Если в решении задачи записаны утверждения, законы или формулы, которые затем не использовались в ходе решения, то ошибки в этих записях не влияют на оценивание и не являются основанием для снижения оценки.
При решении заданий с развернутым ответом не требуется записи каких-либо комментариев об используемых законах или формулах, перевода всех заданных в условии задачи физических величин в СИ и проверки полученного ответа «в общем виде» по единицам измерения входящих в неё величин.
Отсутствие промежуточных этапов между первоначальной системой уравнений и окончательным ответом (т.е. математических преобразований) служит основанием для снижения оценки на 1 балл. Однако допускается вербальное указание на проведение преобразований без их алгебраической записи с предоставлением исходных уравнений и результата этого преобразования.
Таблица 41
Распределение доли учащихся, имеющих ненулевую отметку при выполнению заданий части С ЕГЭ по физике
| № зада- ния | Проверяемые элементы содержания | Процент правильных ответов выпускников | |
| 2010 г. | 2011г. | ||
| С1 | Механика – квантовая физика. (Качественная задача) | 22,32 | 26,79 |
| С2 | Механика (Расчетная задача) | 17,77 | 27,70 |
| С3 | Молекулярная физика (Расчетная задача) | 14,14 | 30,17 |
| С4 | Электродинамика (Расчетная задача) | 8,84 | 15,14 |
| С5 | Электродинамика (Расчетная задача) | 14,05 | 17,09 |
| С6 | Квантовая физика (Расчетная задача) | 15,88 | 12,50 |
При решении задач С1 наиболее типичные ошибки:
- Для объяснения конечного эффекта необходимо правильно выстроить логическую цепочку последовательности физических явлений: электромагнитная индукция–правило Ленца–закон взаимодействия параллельных токов. В большинстве представленных решений отсутствовало даже упоминание о взаимодействии токов.
- Основная проблема объяснения закона изменения индукционного тока во времени – правильное определение характера изменения магнитного потока через рамку (кольцо) во времени (первоначальное увеличение и последующее уменьшение) и использование правила Ленца для определения направления индукционного тока.
- Задание относится к типу задач, для решения которых важны численные значения параметров – в данном случае начальной и конечной температуры. Типичная ошибка – отсутствие ссылок на график зависимости плотности воды от температуры.
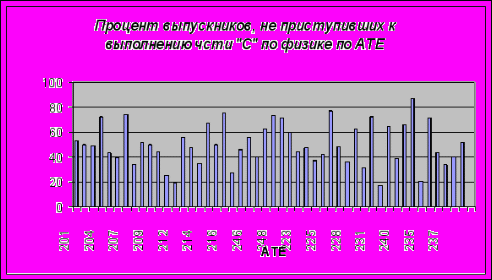
При решении задач С2 наиболее типичные ошибки:
- Типичная ошибка при решении этих задач заключалась в неправильной записи условия отрыва шайбы от кольца. В точке отрыва скорость шайбы отлична от нуля, а нулю равна сила реакции опоры, т.е. в этой точке на шайбу действует только сила тяжести.
- Стандартная задача на совместное использование законов сохранения импульса и закона изменения механической энергии под действием внешних сил. Однако задача требует введения в рассмотрение ряда вспомогательных величин, которых не было в условиях задачи (масса бруска или пули, скорость бруска после вылета из него пули).
- Сложная задача, которая разделяется на две: скатывание с горки до ее конца (точка А и движение тела, брошенного под углом к горизонту. Основная проблема при решении этой задачи связана с нестандартным заданием условий движения в свободном полете: известны начальная скорость и максимальная высота подъема.
- Эта задача, как и предыдущая, разбивается на две части. Основная проблема решения второй части задачи – использование двойного неравенства.
- Достаточно простая задача, требующая только внимания при разложении сил на оси системы координат.
- Стандартная задача, однако требующая внимания при выборе направления силы трения покоя: в первом и втором вариантах направления этой силы противоположны.
При решении задач С3 наиболее типичные ошибки:
- Стандартные задачи на уравнение теплового баланса. Основная проблема, возникающая при их решении – необходимость введения не заданной в условиях задачи массы m льда, а затем ее исключение.
- Основная проблема, возникающая при решении этой задачи, заключается в том, что в процессах сжатия и охлаждения уменьшается масса газа, так что эти процессы не являются изопроцессами. Поэтому выражение для внутренней энергии надо преобразовать так, чтобы в него явно не входило количество молей газа.
- Стандартные задачи на первое начало термодинамики и изопроцессы. Однако задачи усложнены тем, что графическое изображение процессов представлено не в привычных координатах р–V, а в координатах Т–V, р–Т или V–Т.
- Задача на изопроцессы, усложненная тем, что надо учитывать массу поршня и внешнее атмосферное давление.
При решении задач С4 наиболее типичные ошибки:
- Самым сложным в этих простых задачах оказалось построение двух схем соединения резисторов при двух разных полярностях подключения батареи к точкам А и В с учетом сопротивлений диодов в прямом и обратном направлениях.
- Стандартная задача на использование закона сохранения энергии с учетом выделяющегося тепла. Наибольшие сложности вызвал учет работы источника тока.
При решении задач С5 наиболее типичные ошибки:
- Нестандартная задача на явление электромагнитной индукции. Ее нестандартность заключается в том, что проводник в магнитном поле движется неравномерно, так что ЭДС индукции будет меняться в процессе движения и определяться в каждый момент мгновенной скоростью движения проводника.
- Стандартная задача на закон электромагнитной индукции, когда среднее значение ЭДС индукции определяется изменением магнитного потока за конечный промежуток времени.
- Не совсем стандартные для школьников задача преломления луча на одной цилиндрической поверхности. Если все построения хода луча выполнены правильно, то дальнейшее решение задачи не вызывает затруднений.
- Комбинированная оптическая задача. Если взаимное расположение источника света, линзы, его изображения и зеркала выполнены хотя бы с качественным соблюдением всех расстояний, то дальнейшее построение хода лучей и расчеты не вызывают затруднений.
При решении задач С6 наиболее типичные ошибки:
- Комбинированная задача по квантовой физике и специальной теории относительности. Сложность задачи заключается в том, что в законах сохранения энергии и импульса следует учитывать не только энергию и импульс фотонов, но и начальные энергию и импульс пиона. Так как по условию задачи скорость пиона много меньше скорости света в вакууме (в 100 раз), то энергию и массу движущегося пиона можно считать равной энергии и массе покоящегося фотона, а его импульс р = т0V.
- Простая задача. Однако после получения численного ответа следует убедиться, что скорость вылетевшего электрона υ << c, и тем самым оправдано применение классической формулы
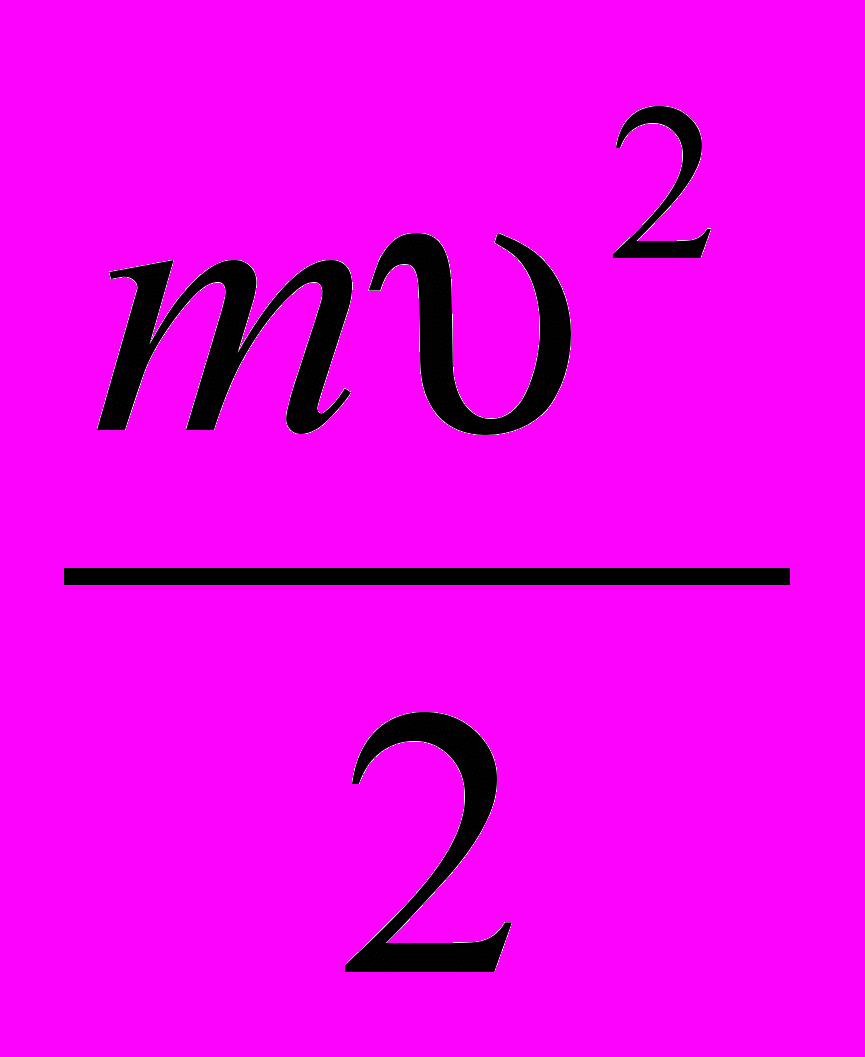для расчета кинетической энергии электрона.