Ответы к билетам по курсу «Информатика и икт» для проведения экзамена в 9 классе (2010-2011 учебный год) Билет №1
| Вид материала | Документы |
- Рабочая программа курса информатики и икт 10 класс Составитель: учителя физики и информатики, 502.33kb.
- Тематическое планирование курса «Информатика и икт» в 10 классе на 2011-2012 уч год., 579.08kb.
- Анализ работы районного методического объединения учителей информатики Аткарского муниципального, 62.76kb.
- Рабочая программа по информатике и икт на 2011/2012 учебный год, 463.81kb.
- Программа вступительного экзамена для поступающих в профильную и научно-педагогическую, 68.1kb.
- Шпаргалки к билетам, 1203.69kb.
- Рабочая программа (фио) учителя информатики и икт по учебному курсу «Информатика, 317.58kb.
- Рабочая программа «Основы микроэлектроники» для специальностей «Информатика и английский, 501.86kb.
- Анализ пробного экзамена по русскому языку в 9 классе моу малощербединская сош 2010-2011, 39.97kb.
- Публичный доклад за 2010-2011 учебный год, 179.62kb.
Логическое сложение (дизъюнкция) от латинского disjunctio - разобщение, различие.
Если два высказывания соединены союзом "ИЛИ", то полученное сложное высказывание обычно считается истинным, когда истинно хотя бы одно из составляющих высказываний. Например, возьмем два высказывания: "Мел черный." (А), "Доска черная." (В). Высказывание "Мел черный или доска черная" будет истинным, т.к. одно из исходных высказываний (В) истинно.
Таким образом, дизъюнкцией двух высказываний называется такое новое высказывание, которое истинно тогда и только тогда, когда истинно хотя бы одно из этих высказываний.
Дизъюнкцию высказываний А и В мы обозначим символом А V В и будем читать: А или В. Определение дизъюнкции может быть записано в виде таблицы истинности:
| А | В | АVB |
| И И Л Л | И Л И Л | И И И Л |
Определение дизъюнкции двух высказываний естественным образом распространяется на любое конечное число составляющих: дизъюнкция А1 V А2 V А3 V...V АN истинна тогда и только тогда, когда истинно хотя бы одно из высказываний А1, А2, А3, ..., АN (а следовательно, ложна, когда ложны все эти высказывания).
Логическое следование (импликация) от латинского implico - тесно связываю.
В наших рассуждениях, особенно в математических доказательствах, мы часто пользуемся сложными высказываниями, образованными с помощью слов "если..., то...". Здесь высказывание, расположенное после слова "если", называется основанием или посылкой, а высказывание, расположенное после слова "то", называется следствием или заключением.
Высказывание "Если А, то В" с логической точки зрения имеет тот же смысл, что и высказывание "неверно, что А истинно и В ложно". Это означает, что функцию импликации можно заменить комбинацией двух функций (отрицания и конъюнкции). Обычно, когда мы хотим установить ложность высказывания "Если А, то В", мы стараемся показать, что возможен случай, когда А истинно, а В ложно (доказательство "от противного"). Обозначим импликацию символом => и запись "А => В" будем читать: "Из А следует В".
Таким образом, импликацией А => В называется высказывание, которое ложно тогда и только тогда, когда А истинно и В ложно.
Запишем это определение в виде таблицы истинности:
| А | В | А=>В |
| И И Л Л | И Л И Л | И Л И И |
Логическое тождество (эквиваленция).
Интуитивно можно догадаться, что высказывания эквивалентны (равносильными), когда их значения истинности одинаковы. Например, эквивалентны высказывания: "железо тяжелое" и "пух легкий", так же как и высказывания: "железо легкое" и "пух тяжелый". Обозначим эквиваленцию символом <=> и запись "А <=> В" будем читать "А эквивалентно В", или "А равносильно В", или "А, если и только если В".
Таким образом, эквиваленцией двух высказываний А и В называется такое высказывание, которое истинно тогда и только тогда, когда оба эти высказывания А и В истинны или оба ложны.
Отметим, что высказывание типа " А, если и только если В" можно заменить высказыванием "Если А, то В и, если В, то А" (обдумайте это на досуге и обратите внимание на символ <=>). Следовательно, функцию эквиваленции можно заменить комбинацией функций импликации и конъюнкции. Запишем таблицу истинности для эквиваленции:
| А | В | А<=>В |
| И И Л Л | И Л И Л | И Л Л И |
Приведем примеры записи сложных высказываний с помощью обозначения логических связок:
"Быть иль не быть - вот в чем вопрос." (В. Шекспир) А V ¬ A <=> В
"Если хочешь быть красивым, поступи в гусары." (К. Прутков) А => В
Построение таблиц истинности для логических функций
Логическая функция - это функция, в которой переменные принимают только два значения: логическая единица или логический ноль. Истинность или ложность сложных суждений представляет собой функцию истинности или ложности простых. Эту функцию называют булевой функцией суждений f (a, b).
Любая логическая функция может быть задана с помощью таблицы истинности, в левой части которой записывается набор аргументов, а в правой части - соответствующие значения логической функции.
При построении таблицы истинности необходимо учитывать порядок выполнения логических операций. Операции в логическом выражении выполняются слева направо с учетом скобок в следующем порядке:
1. инверсия;
2. конъюнкция;
3. дизъюнкция;
4. импликация и эквивалентность.
Для изменения указанного порядка выполнения логических операций используются круглые скобки.
Предлагается следующий алгоритм построения таблицы истинности.
1. Определить количество наборов входных переменных - всевозможных сочетаний значений переменных, входящих в выражения, по формуле: Q=2n , где n - количество входных переменных. Оно определяет количество строк таблицы.
2. Внести в таблицу все наборы входных переменных.
3. Определить количество логических операций и последовательность их выполнения.
4. Заполнить столбцы результатами выполнения логических операций в обозначенной последовательности.
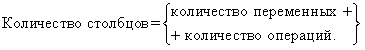
Чтобы не повторить или не пропустить ни одного возможного сочетания значений входных переменных, следует пользоваться одним из предлагаемых ниже способов заполнения таблицы.
Например, построим таблицу истинности для логической функции:
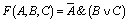
Количество входных переменных в заданном выражении равно трем (A,B,C). Значит, количество входных наборов Q=23=8.
Столбцы таблицы истинности соответствуют значениям исходных выражений A,B,C, промежуточных результатов
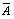и (B V C), а также искомого окончательного значения сложного арифметического выражения 
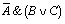:| A | B | C | 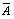| B V C | |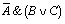
| 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 | 0 |
- Запишите вычислительный алгоритм с ограниченным набором команд. (Задание выполняется без использования компьютера).
У исполнителя Утроитель две команды, которым присвоены номера:
- вычти 1
- умножь на 3
Первая из них уменьшает число на экране на 1, вторая увеличивает его в три раза.
Запишите порядок команд в про грамме получения из числа 3 числа 22, содержащей не более 5 команд.
Билет N18.
- Программные средства и технологии обработки (электронные калькуляторы и электронные таблицы).
Электронные калькуляторы
Электронные калькуляторы являются специализированными программными приложениями, предназначенными для произведения вычислений. Электронные калькуляторы по своим функциональным возможностям соответствуют аппаратным микрокалькуляторам.
Аппаратные микрокалькуляторы могут существенно различаться по своим возможностям и областям применения. Простые микрокалькуляторы позволяют осуществлять только арифметические операции над числами и используются в быту. Инженерные микрокалькуляторы позволяют также вычислять значения различных функций (sin, cos и др.) и используются в процессе обучения и для инженерных расчетов; программистские микрокалькуляторы позволяют проводить вычисления в различных системах счисления и другие операции.
Электронные калькуляторы гораздо удобнее, так как могут обладать возможностями всех вышеперечисленных типов аппаратных микрокалькуляторов. Электронный Калькулятор является стандартным приложением операционной системы Windows. Также кроме стандартной программы Калькулятор существует не мало других удобных калькуляторов.
Электронные таблицы
Электронная таблица — это программа обработки числовых данных, хранящая и обрабатывающая данные в прямоугольных таблицах.
Электронная таблица состоит из столбцов и строк. Заголовки столбцов обозначаются буквами или сочетаниями букв (A, G, АВ и т. п.), заголовки строк — числами (1, 16, 278 и т. п.). Ячейка — место пересечения столбца и строки.
Каждая ячейка таблицы имеет свой собственный адрес. Адрес ячейки электронной таблицы составляется из заголовка столбца и заголовка строки, например: Al, B5, E7. Ячейка, с которой производятся какие-то действия, выделяется рамкой и называется активной.
Электронные таблицы, с которыми работает пользователь в приложении, называются рабочими листами. Можно вводить и изменять данные одновременно на нескольких рабочих листах, а также выполнять вычисления на основе данных из нескольких листов. Документы электронных таблиц могут включать несколько рабочих листов и называются рабочими книгами.
Типы данных.
Электронные таблицы позволяют работать с тремя основными типами данных: число, текст и формула.
Числа в электронных таблицах Excel могут быть записаны в обычном числовом или экспоненциальном формате, например: 195,2 или 1.952Ё + 02. По умолчанию числа выравниваются в ячейке по правому краю. Это объясняется тем, что при размещении чисел друг под другом (в столбце таблицы) удобно иметь выравнивание по разрядам (единицы под единицами, десятки под десятками и т. д.).
Текстом в электронных таблицах Excel является последовательность символов, состоящая из букв, цифр и пробелов, например запись «32 Мбайт» является текстовой. По умолчанию текст выравнивается в ячейке по левому краю. Это объясняется традиционным способом письма (слева направо).
Формула должна начинаться со знака равенства и может включать в себя числа, Имена ячеек, функции (Математические, Статистические, Финансовые, Дата и время и т.д.) и знаки математических операций. Например, формула «=А1+В2» обеспечивает сложение чисел, хранящихся в ячейках А1 и В2, а формула «=А1*5» — умножение числа, хранящегося в ячейке А1, на 5. При вводе формулы в ячейке отображается не сама формула, а результат вычислений по этой формуле. При изменении исходных значений, входящих в формулу, результат пересчитывается немедленно.
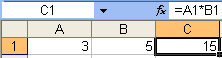
Абсолютные и относительные ссылки.
В формулах используются ссылки на адреса ячеек. Существуют два основных типа ссылок: относительные и абсолютные. Различия между ними проявляются при копировании формулы из активной ячейки в другую ячейку.
Относительная ссылка в формуле используется для указания адреса ячейки, вычисляемого относительно ячейки, в которой находится формула. При перемещении или копировании формулы из активной ячейки относительные ссылки автоматически обновляются в зависимости от нового положения формулы. Относительные ссылки имеют следующий вид: А1, ВЗ.
Абсолютная ссылка в формуле используется для указания фиксированного адреса ячейки. При перемещении или копировании формулы абсолютные ссылки не изменяются. В абсолютных ссылках перед неизменяемым значением адреса ячейки ставится знак доллара (например, $А$1).
Если символ доллара стоит перед буквой (например: $А1), то координата столбца абсолютная, а строки — относительная. Если символ доллара стоит перед числом (например, А$1), то, наоборот, координата столбца относительная, а строки — абсолютная. Такие ссылки называются смешанными.
Пусть, например, в ячейке С1 записана формула =А$1+$В1, которая при копировании в ячейку D2 приобретает вид =В$1+$В2.
Относительные ссылки при копировании изменились, а абсолютные — нет.
Сортировка и поиск данных.
Электронные таблицы позволяют осуществлять сортировку данных. Данные в электронных таблицах сортируются по возрастанию или убыванию. При сортировке данные выстраиваются в определенном порядке. Можно проводить вложенные сортировки, т. е. сортировать данные по нескольким столбцам, при этом назначается последовательность сортировки столбцов.
В электронных таблицах возможен поиск данных в соответствии с указанными условиями — фильтрами. Фильтры определяются с помощью условий поиска (больше, меньше, равно и т. д.) и значений (100, 10 и т. д.). Например, больше 100. В результате поиска будут найдены те ячейки, в которых содержатся данные, удовлетворяющие заданному фильтру.
Построение диаграмм и графиков.
Электронные таблицы позволяют представлять числовые данные в виде диаграмм или графиков. Диаграммы бывают различных типов (столбчатые, круговые и т. д.); выбор типа диаграммы зависит от характера данных.
- Различные типы компьютерных вирусов: методы распространения, профилактика заражения.
Различные типы компьютерных вирусов: методы распространения, профилактика заражения.
Первая массовая эпидемия компьютерного вируса произошла в 1986 году, когда вирус Brain «заражал» дискеты для первых массовых персональных компьютеров. В настоящее время известно несколько десятков тысяч вирусов, заражающих компьютеры с различными операционными системами и распространяющихся по компьютерным сетям.
Обязательным свойством компьютерного вируса является способность к размножению (самокопированию) и незаметному для пользователя внедрению в файлы, загрузочные
секторы дисков и документы. Название «вирус» по отношению к компьютерным программам пришло из биологии именно по признаку способности к саморазмножению.
После заражения компьютера вирус может активизироваться и заставить компьютер выполнять какие-либо действия. Активизация вируса может быть связана с различными событиями (наступлением определенной даты или дня недели, запуском программы, открытием документа и так далее).
Компьютерные вирусы являются программами, которые могут «размножаться» и скрытно внедрять свои копии в файлы, загрузочные секторы дисков и документы. Активизация компьютерного вируса может вызывать уничтожение программ и данных.
Разнообразны последствия действия вирусов; по величине вредных воздействий вирусы можно разделить на:
• неопасные, влияние которых ограничивается уменьшением свободной памяти на диске, графическими, звуковыми и другими внешними эффектами;
• опасные, которые могут привести к сбоям и зависаниям при работе компьютера;
• очень опасные, активизация которых может привести к потере программ и данных (изменению или удалению файлов и каталогов), форматированию винчестера и так далее.
По «среде обитания» вирусы можно разделить на файловые, загрузочные, макровирусы и сетевые.
Файловые вирусы. Файловые вирусы различными способами внедряются в исполнимые файлы (программы) и обычно активизируются при их запуске. После запуска зараженной программы вирус находится в оперативной памяти компьютера и является активным (то есть может заражать другие файлы) вплоть до момента выключения компьютера или перезагрузки операционной системы.
При этом файловые вирусы не могут заразить файлы данных (например, файлы, содержащие изображение или звук).
Профилактическая защита от файловых вирусов состоит в том, что не рекомендуется запускать на выполнение файлы, полученные из сомнительного источника и предварительно не проверенные антивирусными программами.
Загрузочные вирусы. Загрузочные вирусы записывают себя в загрузочный сектор диска. При загрузке операционной системы с зараженного диска вирусы внедряются в оперативную память компьютера. В дальнейшем загрузочный вирус ведет себя так же, как файловый, то есть может заражать файлы при обращении к ним компьютера.
Профилактическая защита от таких вирусов состоит в отказе от загрузки операционной системы с гибких дисков и установке в BIOS вашего компьютера защиты загрузочного сектора от изменений.
Макровирусы. Макровирусы заражают файлы документов Word и электронных таблиц Excel. Макровирусы являются фактически макрокомандами (макросами), которые встраиваются в документ.
После загрузки зараженного документа в приложение макровирусы постоянно присутствуют в памяти компьютера и могут заражать другие документы. Угроза заражения прекращается только после закрытия приложения.
Профилактическая защита от макровирусов состоит в предотвращении запуска вируса. При открытии документа в приложениях Word и Excel сообщается о присутствии в них макросов (потенциальных вирусов) и предлагается запретить их загрузку. Выбор запрета на загрузку макросов надежно защитит ваш компьютер от заражения макровирусами, однако отключит и полезные макросы, содержащиеся в документе.
Сетевые вирусы. По компьютерной сети могут распространяться и заражать компьютеры любые обычные вирусы. Это может происходить, например, при получении зараженных файлов с серверов файловых архивов. Однако существуют и специфические сетевые вирусы, которые используют для своего распространения электронную почту и Всемирную паутину.
Интернет-черви (worm) — это вирусы, которые распространяются в компьютерной сети во вложенных в почтовое сообщение файлах. Автоматическая активизация червя и заражение компьютера могут произойти при обычном просмотре сообщения. Опасность таких вирусов состоит в том, что они по определенным датам активизируются и уничтожают файлы на дисках зараженного компьютера.
Кроме того, интернет-черви часто являются троянами, выполняя роль «троянского коня», внедренного в операционную систему. Такие вирусы «похищают» идентификатор и пароль пользователя для доступа в Интернет и передают их на определенный почтовый адрес. В результате злоумышленники получают возможность доступа в Интернет за деньги ничего не подозревающих пользователей.
Лавинообразная цепная реакция распространения вируса базируется на том, что вирус после заражения компьютера начинает рассылать себя по всем адресам электронной почты, которые имеются в адресной книге пользователя. Кроме того, может происходить заражение и по локальной сети, так как червь перебирает все локальные диски и сетевые диски с правом доступа и копируется туда под случайным именем.
Профилактическая защита от интернет-червей состоит в том, что не рекомендуется открывать вложенные в почтовые сообщения файлы, полученные из сомнительных источников.
Особой разновидностью вирусов являются активные элементы (программы) на языках " onclick="return false">скрипт-вирусами). Такие программы передаются по Всемирной паутине в процессе загрузки Web-страниц с серверов Интернета в браузер локального компьютера.
Профилактическая защита от скрипт-вирусов состоит в том, что в браузере можно запретить получение активных элементов на локальный компьютер.
Наиболее эффективны в борьбе с компьютерными вирусами антивирусные программы. Антивирусные программы могут использовать различные принципы для поиска и лечения зараженных файлов.
Полифаги. Самыми популярными и эффективными антивирусными программами являются антивирусные программы полифаги (например, Kaspersky Anti-Virus, Dr.Web). Принцип работы полифагов основан на проверке файлов, загрузочных секторов дисков и оперативной памяти и поиске в них известных и новых (неизвестных полифагу) вирусов.
Для поиска известных вирусов используются так называемые маски. Маской вируса является некоторая постоянная последовательность программного кода, специфичная для этого конкретного вируса. Если антивирусная программа обнаруживает такую последовательность в каком-либо файле, то файл считается зараженным вирусом и подлежит лечению.
Для поиска новых вирусов используются алгоритмы «эвристического сканирования», то есть анализ последовательности команд в проверяемом объекте.
Если «подозрительная» последовательность команд обнаруживается, то полифаг выдает сообщение о возможном заражении объекта.
Полифаги могут обеспечивать проверку файлов в процессе их загрузки в оперативную память. Такие программы называются антивирусными мониторами.
К достоинствам полифагов относится их универсальность. К недостаткам можно отнести большие размеры используемых ими антивирусных баз данных, которые должны содержать информацию о максимально возможном количестве вирусов, что, в свою очередь, приводит к относительно небольшой скорости поиска вирусов.
Ревизоры. Принцип работы ревизоров (например, ADinf) основан на подсчете контрольных сумм для присутствующих на диске файлов. Эти контрольные суммы затем сохраняются в базе данных антивируса, как и некоторая другая информация: длины файлов, даты их последней модификации и пр.
При последующем запуске ревизоры сверяют данные, содержащиеся в базе данных, с реально подсчитанными значениями.
Если информация о файле, записанная в базе данных, не совпадает с реальными значениями, то ревизоры сигнализируют о том, что файл был изменен или заражен вирусом.
Недостаток ревизоров состоит в том, что они не могут обнаружить вирус в новых файлах (на дискетах, при распаковке файлов из архива, в электронной почте), поскольку в их базах данных отсутствует информация об этих файлах.
Блокировщики. Антивирусные блокировщики — это программы, перехватывающие «вирусоопасные» ситуации и сообщающие об этом пользователю. К таким ситуациям относится, например, запись в загрузочный сектор диска. Эта запись происходит при установке на компьютер новой операционной системы или при заражении загрузочным вирусом.
Наибольшее распространение получили антивирусные блокировщики в BIOS компьютера. С помощью программы BIOS Setup можно провести настройку BIOS таким образом, что будет запрещена (заблокирована) любая запись в загрузочный сектор диска и компьютер будет защищен от заражения загрузочными вирусами.
К достоинствам блокировщиков относится их способность обнаруживать и останавливать вирус на самой ранней стадии его размножения.
- Подсчитайте размер текстового файла при заданной кодовой таблице, формате и количестве страниц.
Используется кодовая таблица СР1251 (Windows Cyrillic). Сколько килобайт будет занимать файл в простом текстовом формате (plain text), если в тексте 300 страниц, на странице 25 строк, а в строке в среднем 45 символов?