Домашнее задание. Ход урока: Устная работа На доске записаны уравнения: X
| Вид материала | Урок |
СодержаниеТихий океан |
- Домашнее задание. Подведение итогов урока. Ход урока, 114.86kb.
- Домашнее задание (2 мин.). Подведение итогов урока (2 мин.). Ход урока, 68.93kb.
- Домашнее задание (2 мин) Подготовить уравнения для решения графическим способом Итоги, 30.57kb.
- План урока Опережающее домашнее задание Вводное слово учителя Запись на доске, 40.64kb.
- Домашнее задание 1мин. Итог урока 2 мин. Рефлексия 1мин. Ход урока Оргмомент. И в десять, 54.1kb.
- Самостоятельная работа учащихся по росписи матреш ки / 28 мин/ Подведение итогов., 18.96kb.
- Конспект открытого урока по музыке во 2-ом классе по теме: «Вконцертном зале», 80.83kb.
- Домашнее задание 2 мин Организационное окончание урока 0,5 мин Краткий конспект урока, 103.17kb.
- Домашнее задание Рефлексия Ход урока Организационный момент. Асейчас проверь, дружок,, 138.99kb.
- Домашнее задание Ход урока I. Организационный момент Проверка явки учащихся и их готовности, 65.21kb.
Учитель математики Воробьева И.Н.
решениЕ квадратных уравнений
Цель урока: выработка умений решать квадратные уравнения
Задачи:
а) образовательные: систематизировать знания, выработать умение выбирать рациональный способ решения квадратных уравнений и создать условия контроля (самоконтроля, взаимоконтроля) усвоения знаний и умений;
б) развивающие: формировать учебно–познавательные действия по работе с дополнительным материалом, развивать логическое мышление, внимание, общеучебных умения;
в) воспитательные: содействовать воспитанию интереса к математике, воспитание математической культуры.
План урока
1. Организационный момент.
2. Устная работа.
3.Повторение и закрепление материала.
4. Обобщение и углубление знаний, умений, навыков.
5.Знакомство с приёмом устного решения некоторых квадратных уравнений.
6.Подведение итогов.
7.Домашнее задание.
Ход урока:
1. Устная работа
На доске записаны уравнения:
x2 + 9x – 12 = 0;
- 4x2 + 1 = 0;
- x2 –2x + 5 = 0;
- 2z2 – 5z + 2 = 0;
- 4y2 = 1;
- –2x2 – x + 1 = 0;
- x2 + 8x = 0;
- 2x2=0;
- –x2 – 8x=1
- 2x + x2 – 1=0
Вопросы:
| 1. Дайте определение квадратного уравнения | Уравнение вида ax2+bx+c=0, где a0, называется квадратным |
| 2. Назовите виды квадратных уравнений | - полное; - неполное; - приведенное |
| 3. Запишите номера приведенных квадратных уравнений, записанных на доске | 1,3, 7, 10 |
| 4. Запишите номера неполных квадратных уравнений, записанных на доске | 2, 3, 7, 8 |
| 5. Запишите номера полных квадратных уравнений, записанных на доске | 1, 3, 4, 6, 9, 10 |
| 6. По какому признаку мы можем отнести квадратное уравнение к тому или иному виду? | В зависимости от коэффициентов уравнения. |
| 7. Как называются коэффициенты квадратного уравнения? | a – первый коэффициент, b – второй коэффициент, c – свободный член |
| 8. Запишите квадратное уравнение, у которого свободный член равен 6, первый коэффициент равен 1, а второй, равен –12. Как оно называется? | x2-12x+6=0 |
| 9. От чего зависит количество корней квадратного уравнения? | От знака дискриминанта. |
| 10. Впишите вместо пропуска такой коэффициент, чтобы квадратное уравнение 2х2–8х+....=0 не имело корней | 2х2–8х+…=0 |
| 11. Изменятся ли корни уравнения 2x2 +5x +7=0, если у него изменить знак: - одного коэффициента - трёх коэффициентов | да нет |
Математические знания полезны не только сами по себе. Сегодня мы с их помощью сможем погрузиться в другие науки, пополним свои знания и расширим кругозор.
Презентация
1 задание поможет нам окунуться в историю древнего мира.
Для каждого из заданных уравнений укажите коэффициенты a, b, c.
| Е | x2 + 5x – 2 = 0 | О | –2x2 – x + 1 = 0 |
| Я | 4x2 + 1 = 0 | И | x2 + 8x = 0 |
| П | x2 –2x + 5 = 0 | А | 2x2=0 |
| Т | 2z2 – 5z + 2 = 0 | К | –x2 – 8x=1 |
| С | 4y2 = 1 | Н | 2x + x2 – 1=0 |
Используя найденные выражения, заполните клетки таблицы буквами
 | | 1; 5; 2 | | | |
| | | 1; -12; 8 | | | |
| | | 1; 2; -1 | | | |
| | | 1; 5; 2 | | | |
| | | -2; -1; 1 | | | |
| | | 4; 0; -1 | | | |
| | | 1; 8; 0 | | | |
| | | | -1; -8; -1 | | |
| | | 2; 0; 0 | | | |
| | | | | | |
| | | | | | |
| | | | | | |
| 1; -2; 5 | | 1; 5; 2 | 4; 0; 1 | 2; -5; 2 | |
Используя полученные знания, заполните пропуски в тексте:
В древнегреческой мифологии богиней ПАМЯТИ была МНЕМОСИНА. От ее имени происходит слово МНЕМОНИКА, означающее совокупность приемов для облегчения запоминания. Одни мнемоническим правилом мы уже пользовались для облегчения запоминания числа «». Вспомните его (Это я знаю и помню прекрасно, но многие знаки мне лишни, напрасны».
Хорошо развитая память помогает человеку в жизни. Однако важным качеством является умение забывать. Забывать обиды, боль, переживания. Это понимали и в глубокой древности. Поэтому, в греческой мифологии существовала и богиня забвения, именем которой была названа река в подземном царстве – ЛЕТА.
2 вопрос откроет интересные факты из области географии. Для того, чтобы сделать шаг к их открытию необходимо найти дискриминант квадратного уравнения:
2x2+6x-1=0 D=44 Тихий океан
4x2-5x+2=0 D=-7 Берингов пролив
3x2=0 D=0 Россия
x2-5x+6=0 D=1 США
-4x2+5=0 D=80 остров Крузенштерна
x2+6x=0 D=36 остров Ратманова
Используя найденные ответы, заполните пропуски в тексте:
В -7 есть два острова: 36 , самая восточная точка 0 , и в 12 км к востоку – 80 , территория 1 . На обоих островах часы постоянно показывают одинаковое время, но разница в дате составляет всегда одни сутки. Это объясняется тем, что между этими островами 44 от полюса до полюса проходит международная линия смены даты.
3 вопрос позволит нам прикоснуться к миру птиц.
Птицы издавна привлекали внимание человека. Людей восхищало их яркое оперение, мелодичное пение, их смелые и стремительные полеты. С птицами связаны самые поэтические образы в творчестве народов, в классической музыке, литературе. Пение птиц успокаивает. Давайте послушаем прекрасные звуки природы, представив себе, что находимся в чудесном лесу, полном необычных звуков.
Решив уравнения, используя обратную теорему Виета, и определив названия птиц, мы сможем узнать, что они символизируют.
x2-5x-6=0 – павлин
x2+7x+6=0 – пеликан
x2+5x+6=0 – сова
x2+x-6=0 – аист
x2-7x+6=0 – лебедь
| Множество решений | Название птицы | Является символом |
| -2; -3 | СОВА | мудрости |
| 2; -3 | АИСТ | счастья |
| 6; -1 | ПАВЛИН | бессмертия |
| -6; -1 | ПЕЛИКАН | жертвенности |
| 6; 1 | ЛЕБЕДЬ | верности |
Сегодня мы вспомнили, какое уравнение называется квадратным, виды квадратных уравнений, способы их решения.
В следующем задании необходимо решить как можно больше уравнений, используя различные алгоритмы решения.
| x2=25 | x1=-5; x2=5 |
| (x-3)(x+4)=0 | x1=-4; x2=3 |
| x2-6x+9=0 | x=3 |
| 2x2-7x+6=0 | x1=1,5; x2=2 |
| 2x2-4x–6=0 | x1=-3; x2=1 |
| 4x2 -9=0 | x1=1,5; x2=-1,5 |
| 3x2-5x=0 | x1=0; x2=5/3 |
Проанализируйте высказывания. Зачеркните в таблице буквы, обозначающие ложные высказывания. Из оставшихся букв получите слово.
1. Уравнение x2+9=0 имеет два корня.
2.В уравнении x2-2x+1=0 единственный корень.
3. В уравнении x2-5x+3=0 сумма корней равна 5.
4. В уравнении x2+3x=0 один из корней есть иррациональное число.
5. В уравнении x2=0 дискриминант равен 0.
6. Уравнение x2-8x-3=0 не имеет корней.
7. Корнями уравнения x2-100x+99=0 являются числа 99 и 1.
8. Произведение корней уравнения x2-11x+9=0 равно 9.
10. Уравнение x2-9x+8=0 является неполным.
11. Если дискриминант уравнения – число отрицательное, то уравнение не имеет корней.
12. Уравнение x2-1056=0 корни являются противоположными числами.
| п | н | о | М | к | а | т | ю | с | р | н |
Полученное слово французского происхождения переводится как «ночной» и используется в разных видах искусства. В музыке термин означает сочинение для фортепиано неопределенной формы мечтательного характера. Наиболее известные ноктюрны написаны Шуманом и Шопеном.
Теорема Виета находит широкое применение и в уравнениях вида aх2 + bх + с = 0.
Использование некоторых свойств даёт значительные преимущества для быстрого получения ответа при решении квадратных уравнений.
Рассмотрим эти свойства:
| 1) a + b +с = 0 х1 = 1, х2 = с/а. 5х2 + 4х – 9 = 0; х1 =1, х2 = - 9/2. 2) а - b + с = 0 х1 = - 1, х2 = - с/а. Например: 4х2 + 11х + 7 = 0; х1 = - 1, х2 = - 7/4. 3) ав +с0 Устно решить уравнение: х2 + bх + ас = 0 Его корни разделить на а. а) 2х2 – 11х + 5 = 0. Решаем устно уравнение: х2 – 11х + 10 = 0. Его корни 1 и 10. Делим на 2. Тогда х1 = 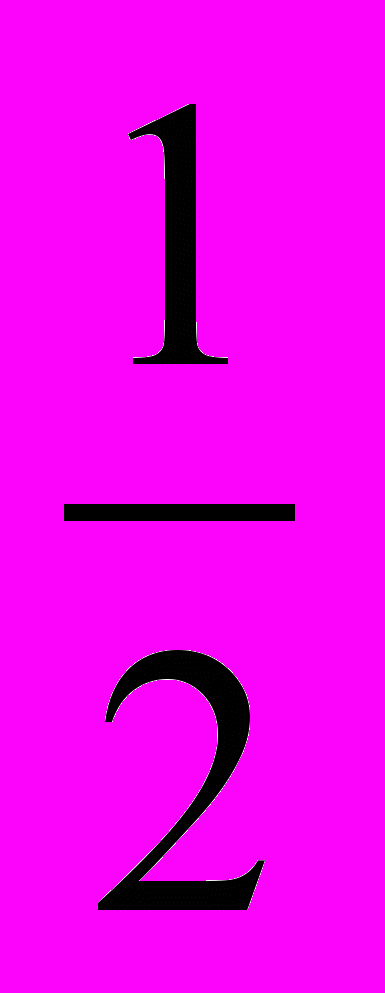 , х2 = 5. , х2 = 5.Ответ: 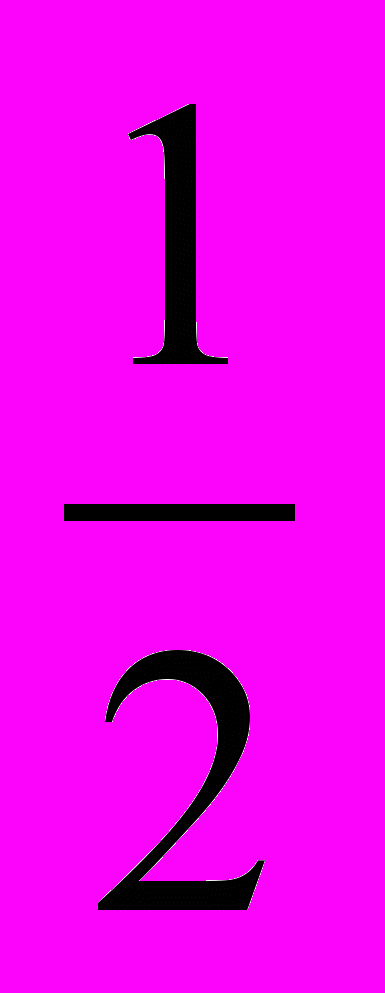 ; 5. ; 5.в) 6х2 –7х – 3 = 0 Решаем устно уравнение: х2 –7х – 18 = 0. Его корни -2 и 9. Делим на 6. Тогда х1 = - 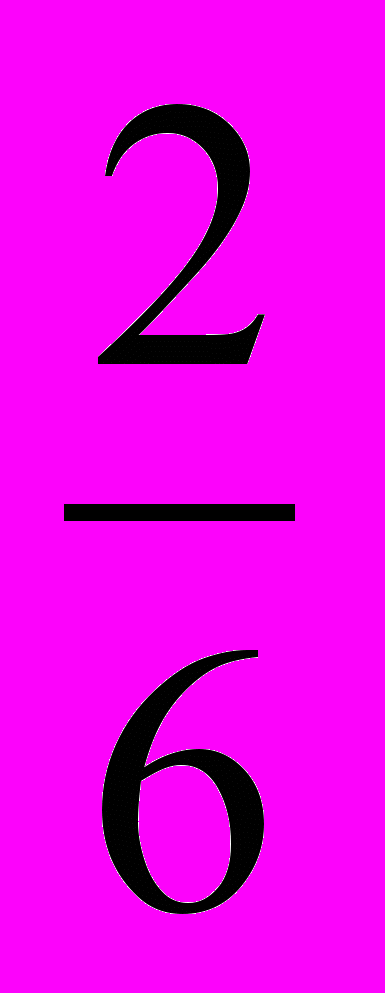 , х2 = , х2 = 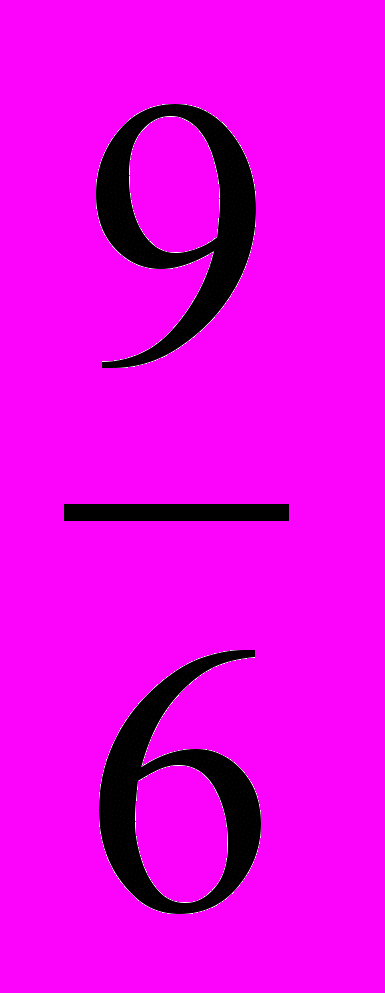 . .Ответ: -  ; ; 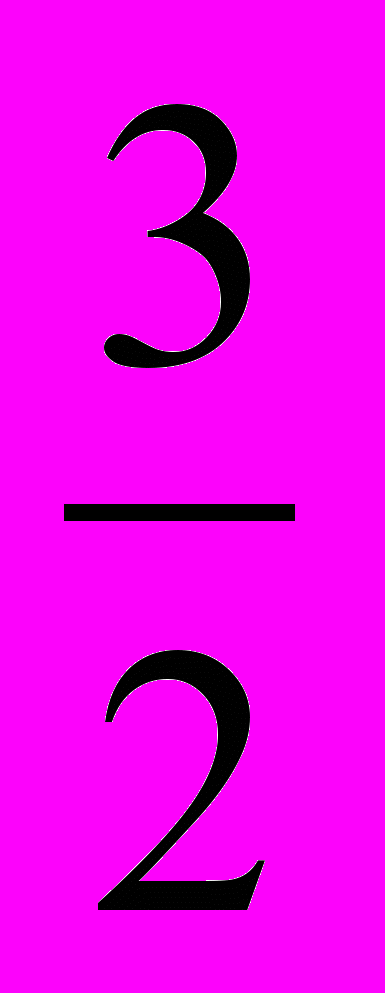 . . | 1) a + b +с = 0 х1 = 1, х2 = с/а. 5х2 + 4х – 9 = 0; х1 =1, х2 = - 9/2. 2) а - b + с = 0 х1 = - 1, х2 = - с/а. Например: 4х2 + 11х + 7 = 0; х1 = - 1, х2 = - 7/4. 3) ав +с0 Устно решить уравнение: х2 + bх + ас = 0 Его корни разделить на а. а) 2х2 – 11х + 5 = 0. Решаем устно уравнение: х2 – 11х + 10 = 0. Его корни 1 и 10. Делим на 2. Тогда х1 = 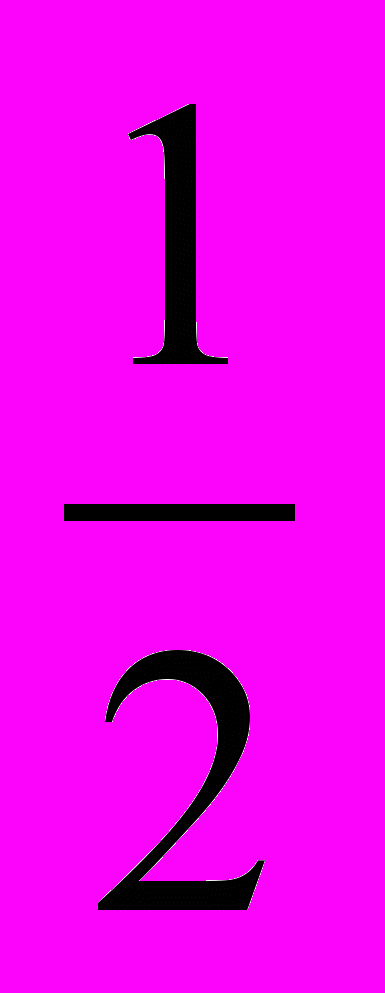 , х2 = 5. , х2 = 5.Ответ: 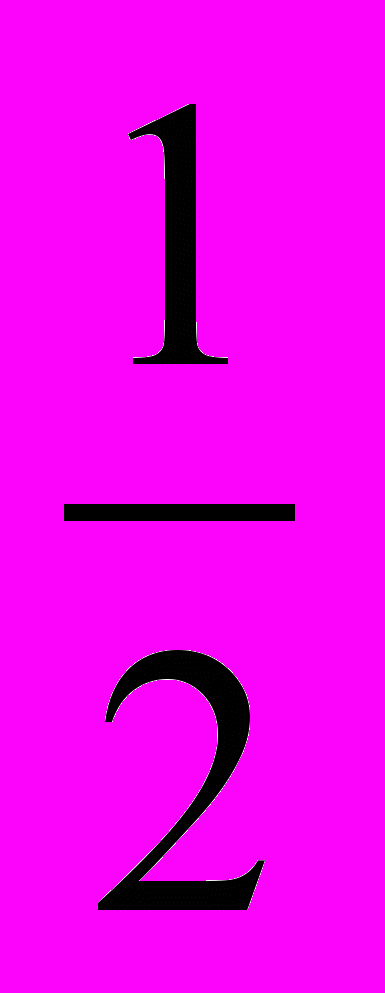 ; 5. ; 5.в) 6х2 –7х – 3 = 0 Решаем устно уравнение: х2 –7х – 18 = 0. Его корни -2 и 9. Делим на 6. Тогда х1 = - 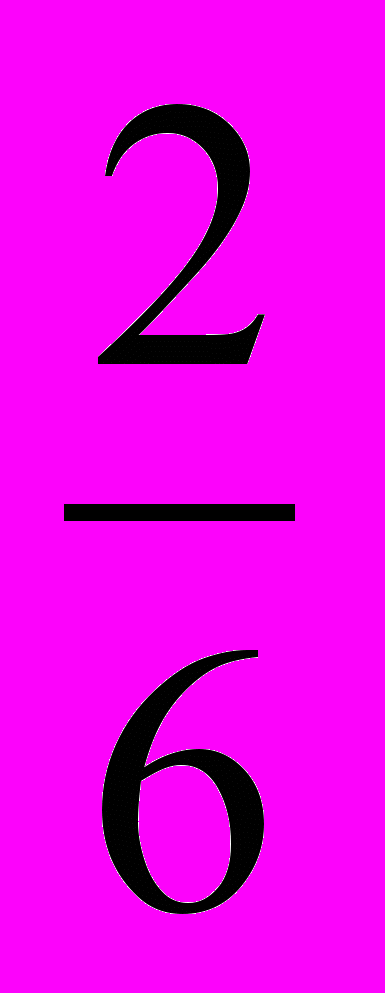 , х2 = , х2 = 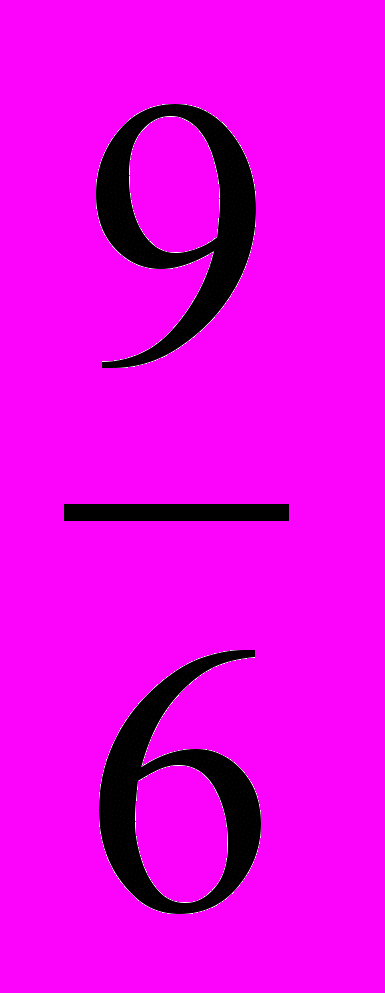 . .Ответ: -  ; ; 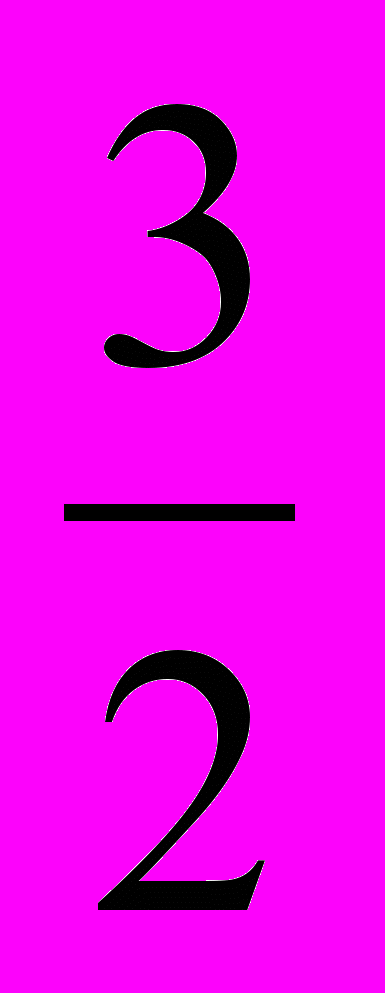 . . |
| Решите двумя способами уравнения: I вариант. 1) 14х2 – 17х + 3 = 0 2) х2 – 39х - 40 = 0 3)100х2 – 83х - 18 3= 0 | Решите двумя способами уравнения: II вариант. 1) 13х2 – 18х + 5 = 0 2)х2 + 23х - 24 = 0 3)100 х2 + 97х - 197 = 0 |
