Тема: «способы решений различных квадратных уравнений»

Вид материала

Документы

Содержание I. введение Задачи доклада Структура доклада Ii. история возникновения квадратных Обезьянок резвых стая Iii. квадратные уравнения 2-е следствие. Решите уравнение Iv. заключение VI. Приложение

Подобный материал:

• Тема: Исследование проблемы решения , 104.57kb.
• Тема: «Решение квадратных уравнений с помощью номограммы», 98.28kb.
• Зюзина Татьяна Ивановна, гимназия №12 г. Липецка Тема: решение, 117.75kb.
• Потешкина Галина Владимировна. Класс: 8 класс. Тема урок, 116.63kb.
• «История возникновения квадратных уравнений», 131.57kb.
• Урока алгебры и информатики «система счисления. Решение задач с помощью квадратных, 98.53kb.
• Цель: Рассмотреть способы решения тригонометрических уравнений, 43.07kb.
• Программа несущую двойную функцию по решению квадратных уравнений, 49.47kb.
• «квадратные уравнения», 46.79kb.
• Герон(1 век н э.), 17.45kb.

I Школьная конференция молодых исследователей


ТЕМА: «СПОСОБЫ РЕШЕНИЙ РАЗЛИЧНЫХ КВАДРАТНЫХ УРАВНЕНИЙ»


ХМАО – Югра

Октябрьский район

Поселок Карымкары




ах ²+вх+с=0

Работу выполнила

Пономаренко Анастасия Александровна

Муниципальное образовательное учреждение

«Карымкарская средняя общеобразовательная школа» 8 «а» класс

Научный руководитель:

Сазонова Наталья Николаевна

учитель математики

План

• I. Введение
  

• II. История возникновения квадратных
  

уравнений

• §1. Квадратные уравнения в Индии
  
• §2. Квадратные уравнения в Древнем Вавилоне
  
• §3. Квадратные уравнения в Европе XIII – XVII вв.
  

• III.Квадратные уравнения
  

• §1. Общий вид квадратного уравнения
  
• §2. Решение неполных квадратных уравнений
  
• §3. Квадратное уравнение всегда имеет два
  

корня

• §4. Частные случаи квадратных уравнений
  

а). Коэффициент, а - очень маленький

в). Коэффициент, с – очень маленький

• §5. Решение квадратных уравнений
  

графическим способом

• §6. Алгоритм устного решение квадратных
  

уравнений

• §7. Теорема Виета
  
• §8. Зависимость между коэффициентами и
  

корнями

• IV. Заключение
  
• V. Литература
  
• VI. Приложение
  

2


I. ВВЕДЕНИЕ


Тема моего доклада – различные решения квадратных уравнений.

Теория уравнений занимает ведущее место в алгебре и математике в целом. Сила теории уравнений в том, что не только имеет теоретическое значение для познания естественных законов, но и служит практическим целям. Большинство жизненных задач сводится к решению различных видов уравнений, и чаще это уравнения квадратного вида.

Квадратное уравнение представляет собой большой и важный класс уравнений, решающих как с помощью формул, так и с помощью элементарных функций.

В учебниках мы знакомимся с несколькими видами квадратных уравнений, и отрабатываем решение по формулам. Вместе с тем, современные научно – методические исследования показывают, что использование разнообразных методов и способов позволяет значительно повысить эффективность и качество изучения решений квадратных уравнений.

Выбор способа должен оставаться за учащимся. Каждый ученик должен уметь верно и рационально решать квадратные уравнения. Так как в некоторых случаях можно их решать устно, только для этого необходимо помнить алгоритм решения квадратных уравнений, который может пригодиться на экзамене ЕГЭ , при поступлении в ВУЗы и различных жизненных ситуациях.

Таким образом возникает необходимость изучения этих дополнительных способов решения. Все сказанное выше определяет актуальность темы выполненной работы.

Проблема исследования заключается в выделении способов решения квадратных уравнений и их структуру алгоритма изучения математики.

Цель работы состоит в изучении теоретических основ и их практическое применение.

Объект исследования. Организация применения различных способов решения изучение математики в школе.

Предмет исследования квадратных уравнений.


ЗАДАЧИ ДОКЛАДА

1. Произвести анализ учебно – методической литературы по решению квадратных уравнений.
   
2. Произвести анализ различных способов решения квадратных уравнений
   
3. Изучить историю развития квадратных уравнений.
   
4. Изучить различные способы решения квадратных уравнений и апробировать материал на практике.
   

СТРУКТУРА ДОКЛАДА


Доклад состоит из введения, основной части, заключения, списка литературы и приложения.

Во введении содержится обоснование актуальности выбранной темы, определенные проблемы и цель работы, объект, гипотеза исследования, выделены задачи доклада.

Во основной части представлена история возникновения квадратных уравнений, в Индии, Древнем Вавилоне, Европе. Виды квадратных уравнений. Некоторые частные случаи, их способы решения, алгоритм устного решения квадратных уравнений.

В заключении делается, вывод из проделанной работы список использованной литературы содержит __8___ наименований.

В приложении содержится некоторые примеры.

-3-


II. ИСТОРИЯ ВОЗНИКНОВЕНИЯ КВАДРАТНЫХ

УРАВНЕНИЙ

§1. Квадратные уравнения в Индии


Задачи на квадратные уравнения встречаются в астрономическом тракторе «Ариабхаттиам», составленном в 499 г. Индийским математиком и астрономом Ариабхатой. Другой индийский ученый – Брахмагупта (VII в.) изложил общее правило решения квадратных уравнений. Правило Брахмагупты по существу совпадает с современным.

В древней Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу другого в народных собраниях, предлагая и решая алгебраические задачи». Задачи часто облекались в стихотворную форму.

Вот одна из задач знаменитого индийского математика XII в Бхаскары.


Обезьянок резвых стая

Власть поевши, развлекалась.

Их в квадрате часть восьмая

На поляне забавлялась,

А двенадцать по лианам

Стали прыгать, повисая..

Сколько ж было обезьянок

Ты скажи мне, в этой стае?


Решение Бхаскары свидетельствует о том, что он знал о двузначности корней квадратного уравнений.




х² – 64 = - 768,

х² – 64х +32² = - 768 + 1024,

(х – 32)² = 256,

х₁ = 16, х₂ = 48

(приложение 1)


§2. Квадратные уравнения в Древнем Вавилоне


Квадратные уравнения умели решать вавилоняне около 2000 лет до н.э. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и таких, например, полные уравнения.




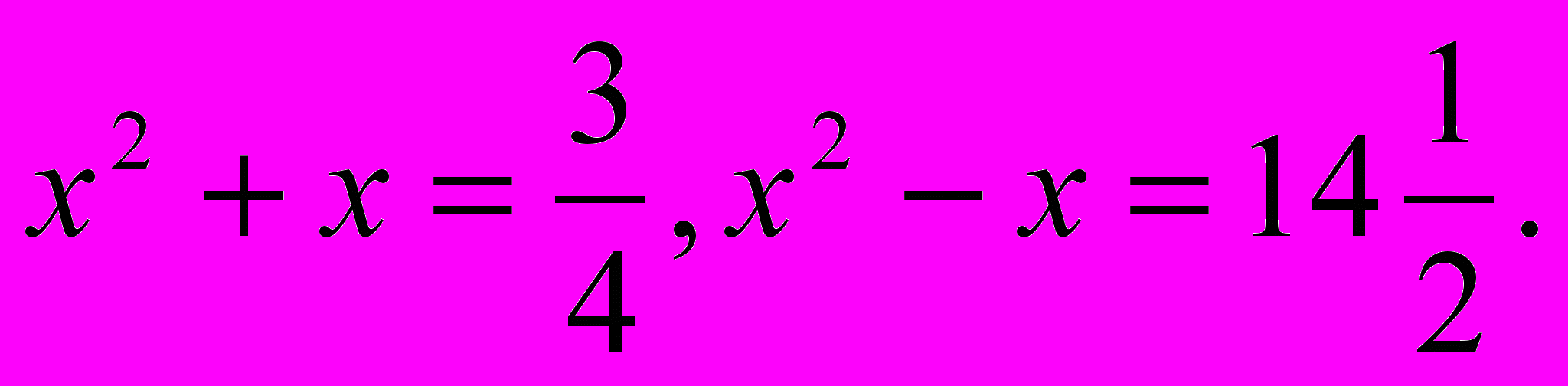
Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденный до сих пор клинописные тексты приводят только задачи с

4

решениями, изложенными в виде рецептов, без указаний относительно того, каким образом

они были найдены. Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.


§3. Квадратные уравнения в Европе в XII – XVII вв.


Формы решения квадратных уравнений по образцу ал - Хорезми в Европе были в первые изложены в «Книге абаха», написанной в 1202 году, итальянским математиком Леонардо Фибоначчи. Автор разработал самостоятельно некоторые новые алгебраические примеры решения задач и первый в Европе подошел к введению отрицательных чисел. Его книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из «Книги абаха» переходили почти во все европейские учебники XVI – XVII вв. и частично XVIII в. Общее правило решения квадратных уравнений, приведенных к единому каноническому виду

х² + bx = с

при всевозможных комбинациях знаков и коэффициентов b, c, было сформулировано в Европе в 1544 г. М. Штифелем. Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни Виет знаменитый француский ученый также по профессии адвокт. Итальянские ученые Тарталья, Кардано, Бомбелли среди первых в XVI в. Учитывают, помимо положительных, и отрицательные корни. Лишь в XVII в. Благодаря трудам Жиррара, Декарта, Ньютона и других ученых, способ решения квадратных уравнений принимает современный вид.¹


III. КВАДРАТНЫЕ УРАВНЕНИЯ

§ 1. Общий вид квадратного уравнения


Предположим, что в данном уравнении мы сделали следующие преобразование: раскрыли скобки, если они есть, уничтожили знаменатели, если в уравнении есть дробные члены, перенесли все члены в левую часть уравнения и сделали приведение подобных членов. Если после этого в левой части уравнения окажется член, содержащий неизвестное в квадрате, и не будет членов, содержащих неизвестное в более высокой степени, то уравнение называется квадратным. Общий вид такого уравнения есть

ах² +bx + c = 0

где а, b, и с суть данные положительные или отрицательные числа, или же алгебраические выражения, составленные из данных количеств; а, b, и с называются коэффициентами квадратного уравнения; из них с называется также свободным членом.

Заметим, что коэффициент а мы всегда можем сделать положительным, переменив в случае надобности перед всеми членами уравнения знаки на обратные.

 Пример 1.



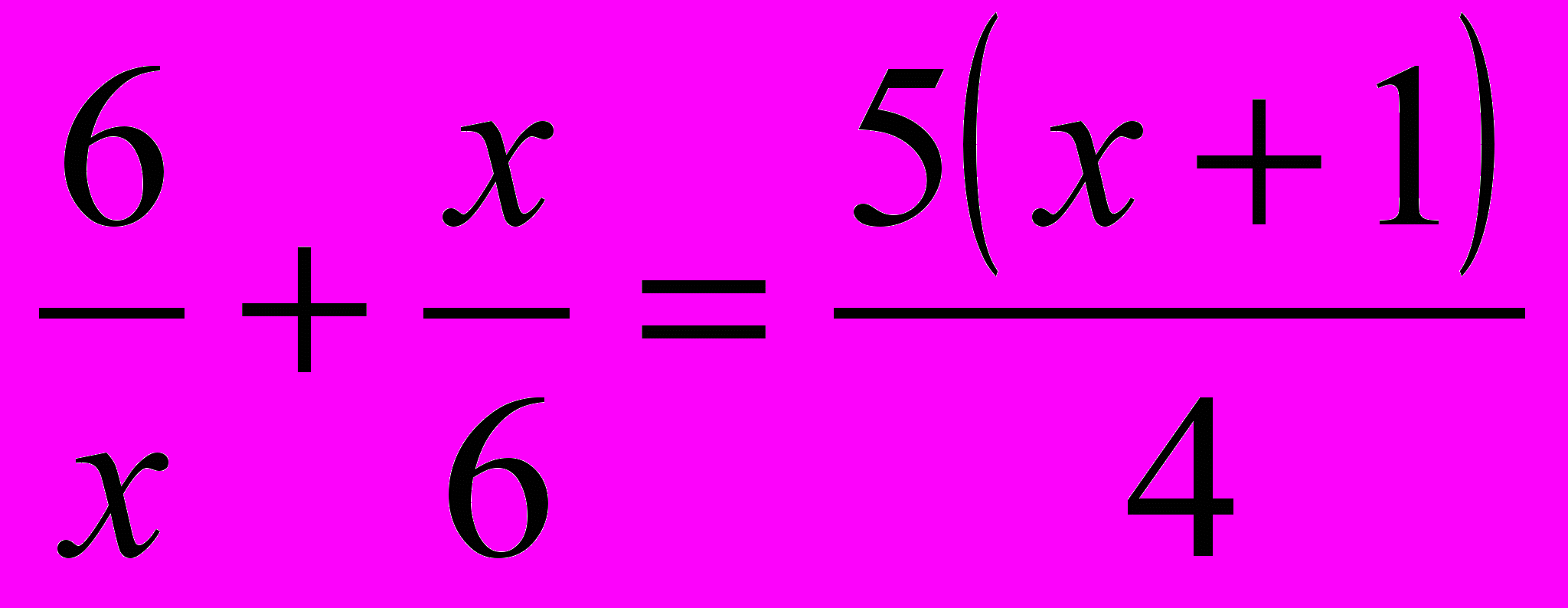
Раскрываем скобки:


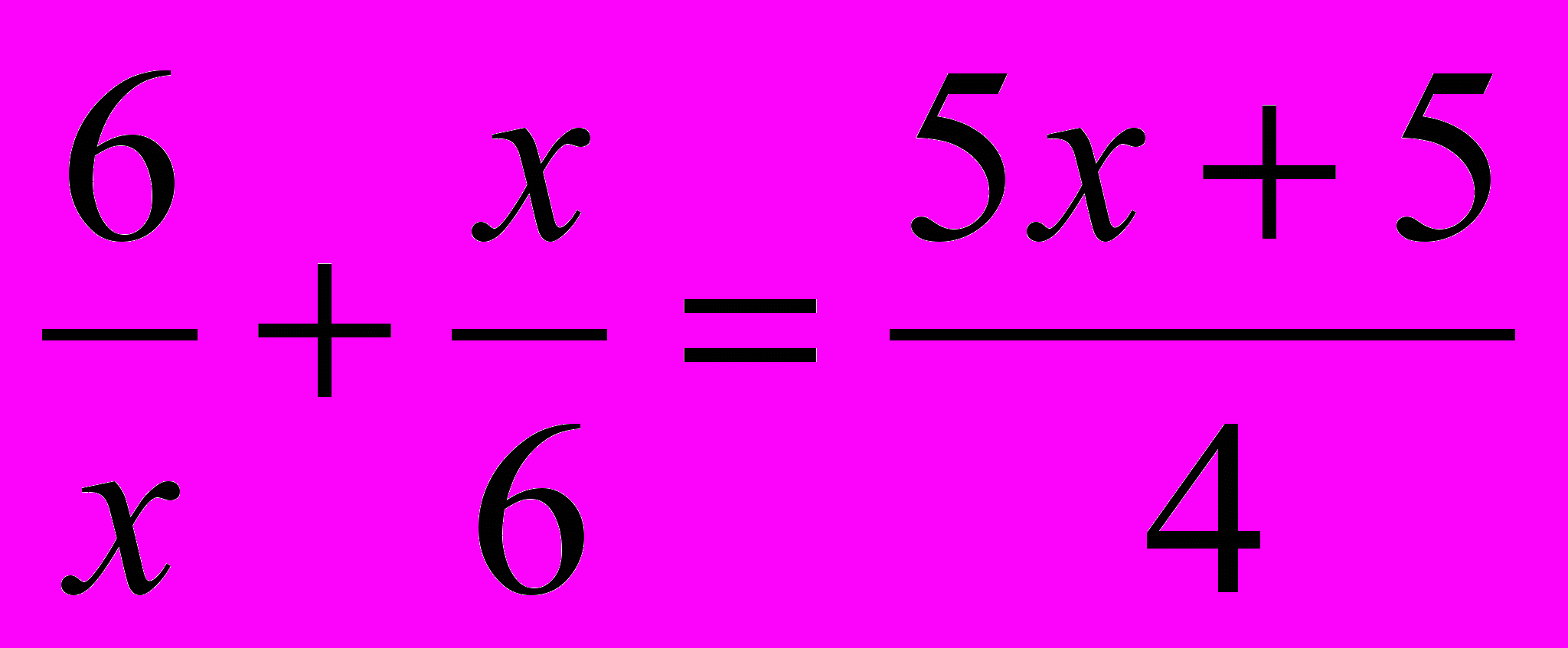
Уничтожаем знаменатель: 72 + 2х² = 15х² + 15х

Переносим все члены в левую часть:

1. газета «Математика» № 42 2001 год стр.2
   

72 + 2х² – 15х² – 15 =0

Делаем приведение: - 13х² – 15х + 72 = 0

Переменяем знаки: 13х² + 15х – 72 = 0

Коэффициенты а, b, b и с общего вида квадратного уравнения приняли в этом примере такие частные значения: а = 13, b = 15 и с = - 72.


 Пример 2.

Решение:

; ;



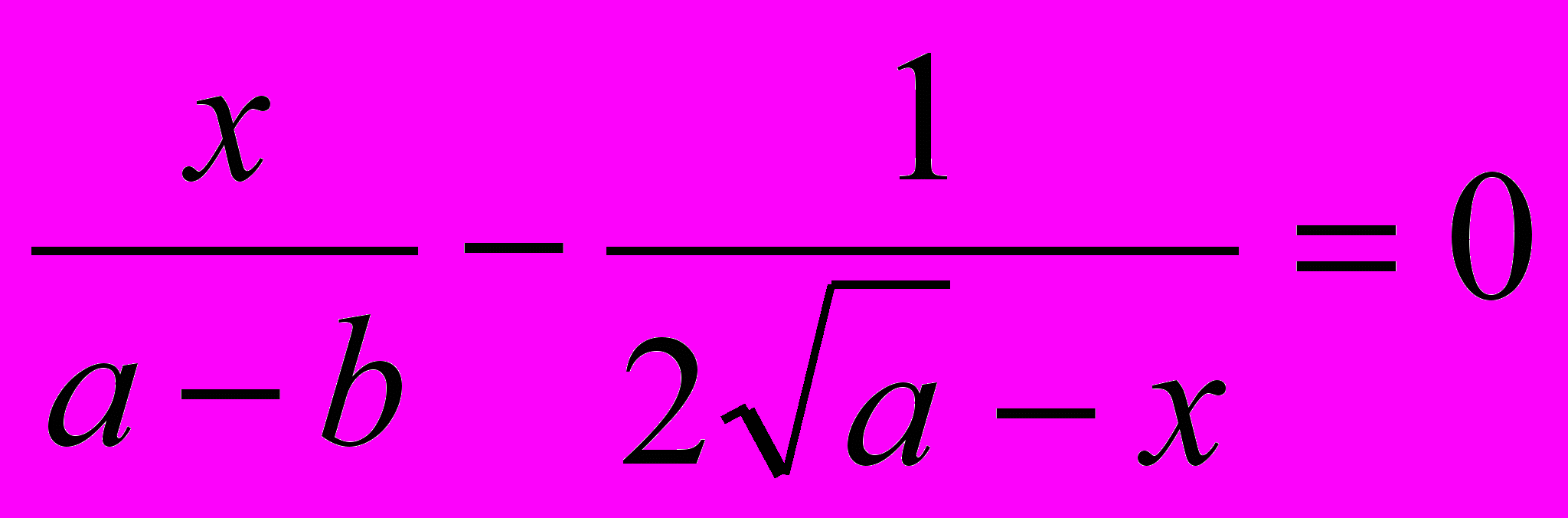
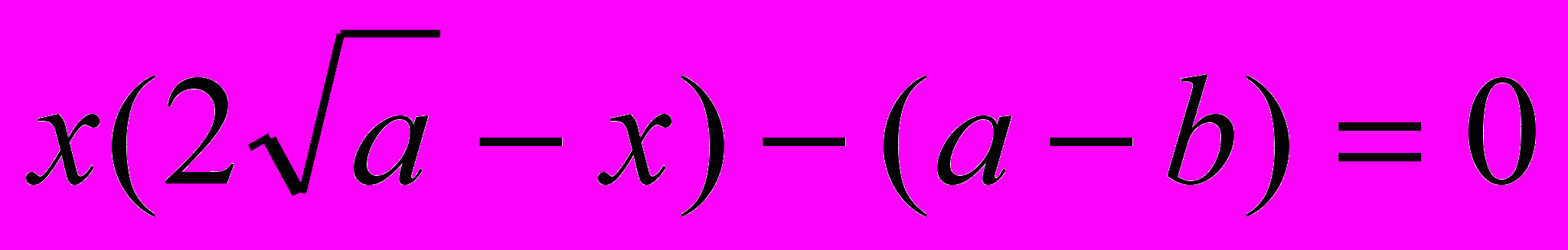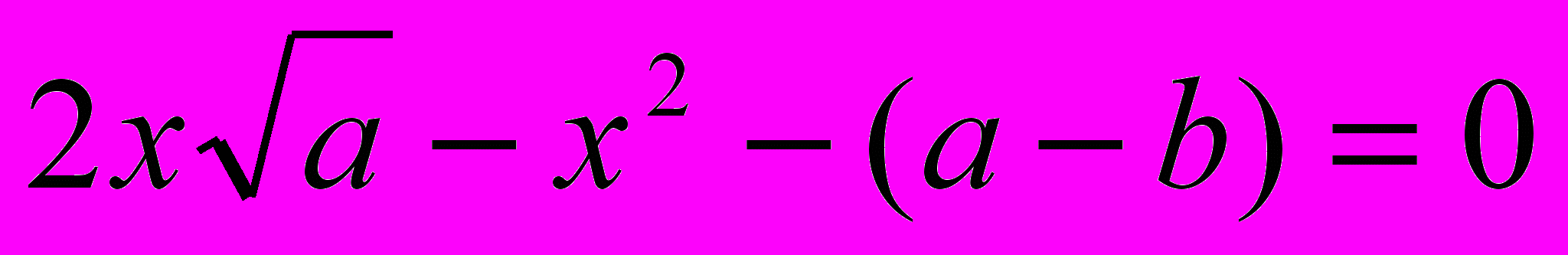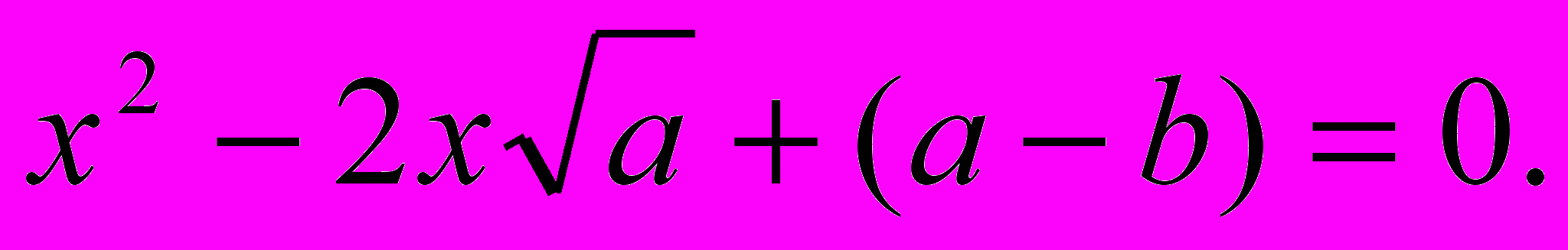
Коэффициенты общего вида квадратного уравнения приняли такие частные значения:

а=1, b= - 2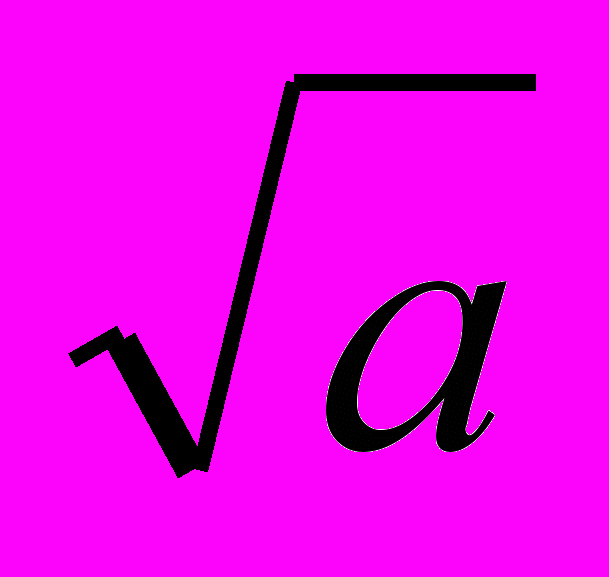, с = а – b.


§2. Решение неполного квадратного уравнения


Квадратное уравнение называется неполным, когда в нем нет члена, содержащего х, или нет свободного члена. Неполные квадратные уравнения могут быть только трех следующих видов:


1. ах² + с = 0; 2. ах² + bx = 0; 3. ax² = 0

Рассмотрим решение каждого из них.


I. Из уравнения х² + с = 0 находит

ах² = - с и х² = .

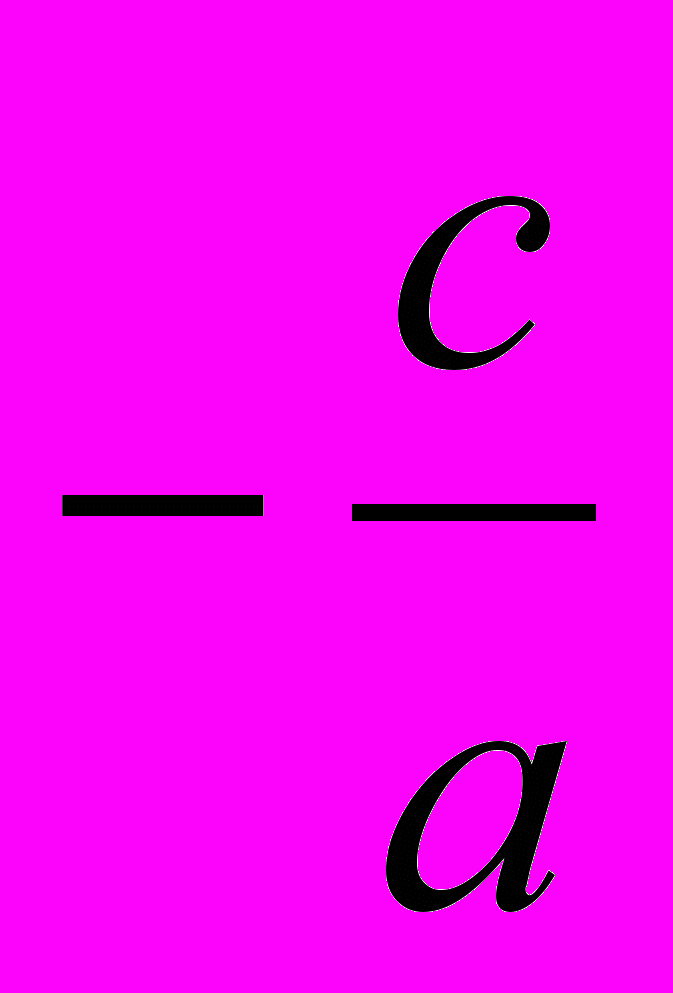Это равенство требует, чтобы квадрат неизвестного равнялся количеству 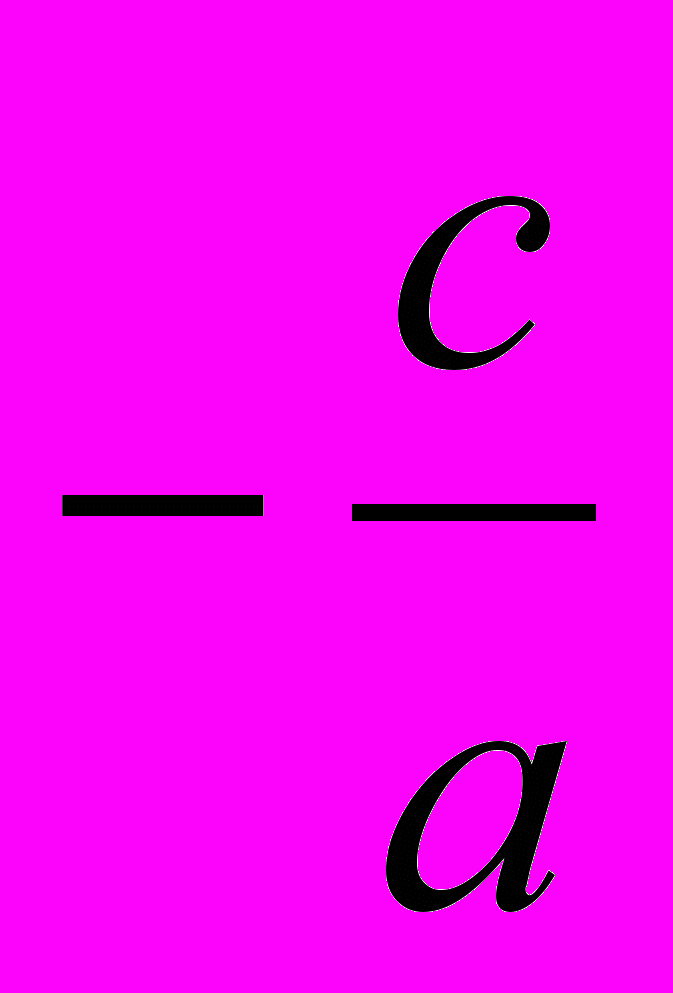; значит, неизвестное должно равняться квадратному корню из этого количества. Это возможно только тогда, когда количество 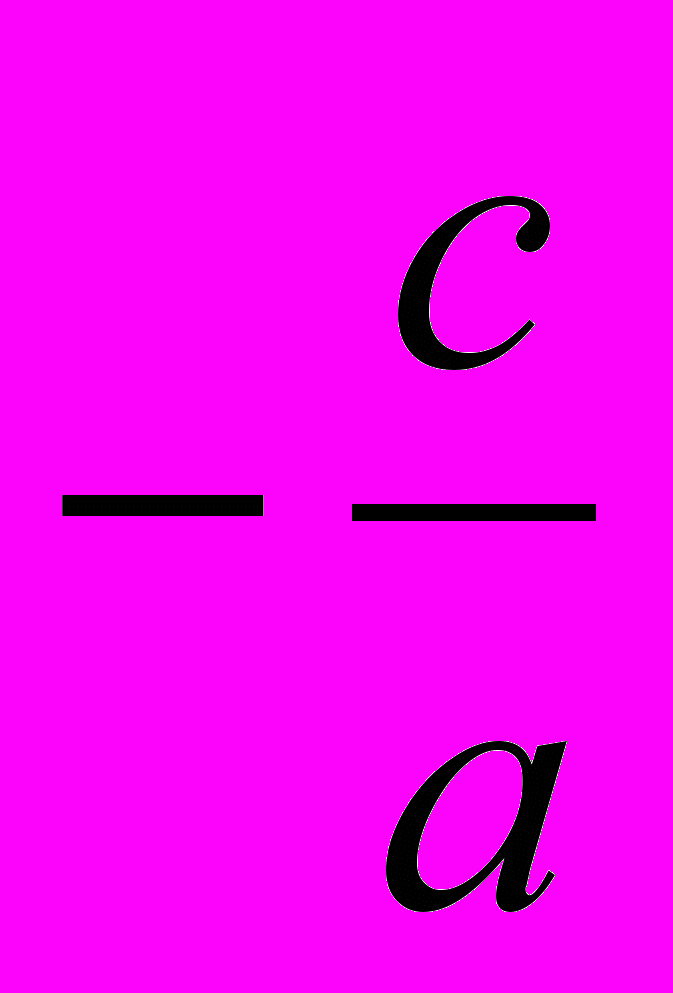есть положительное число, что будет тогда, когда с и а имеют противоположные знаки (если, например, с = - 8, а = + 2, то

Условимся обозначать знаком 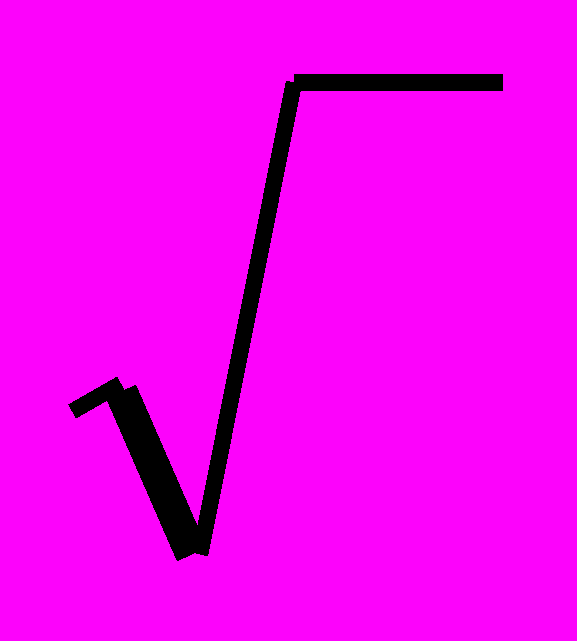только арифметическое значение квадратного корня и примем во внимание, что квадратный корень из положительного числа имеет два значения; тогда, обозначая одно значение через х₁, а другое через х₂, можем написать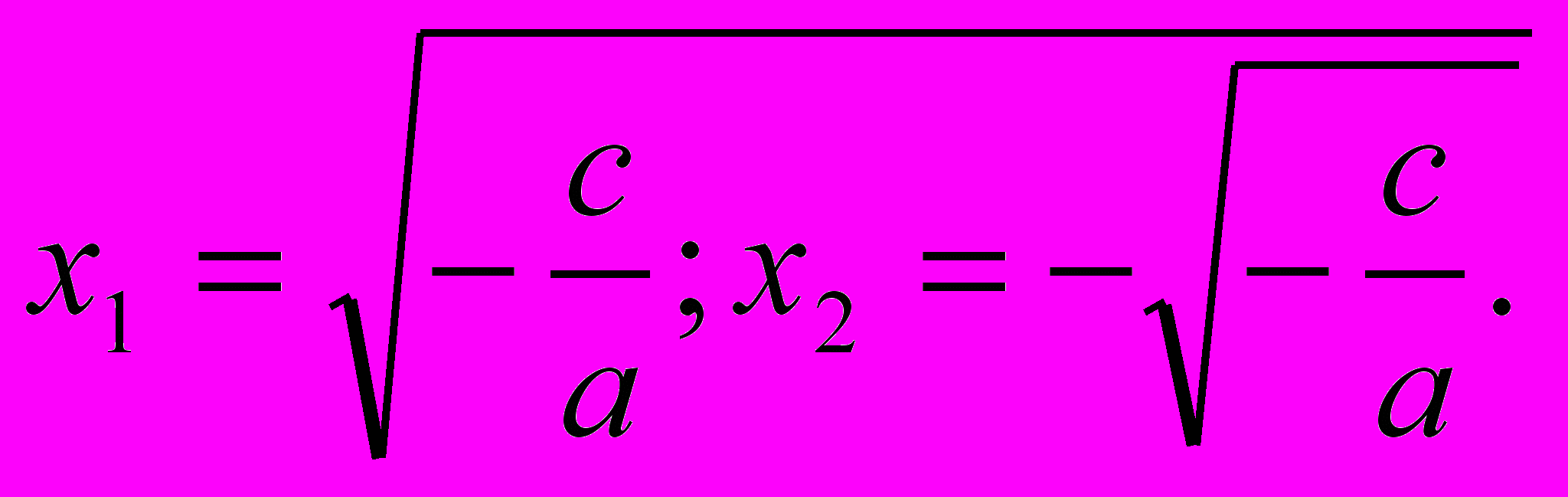




Если числа с и а имеют одинаковые знаки, то количество 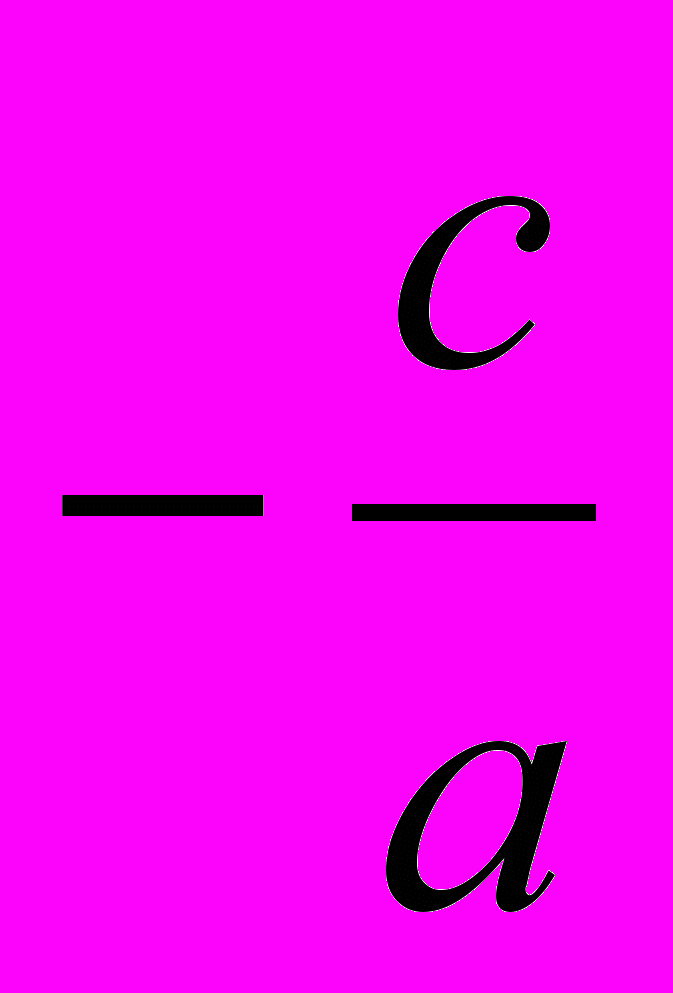представляет собой отрицательное число; тогда уравнение ах² + с = 0 не может быть удовлетворено никаким вещественным числом; в этом случае говорят, что уравнение имеет два мнимых корня.


 Пример 3. Решите уравнение 3х² – 27 = 0.

-6-

Решение: 3х² = 27; х²= 9; х =


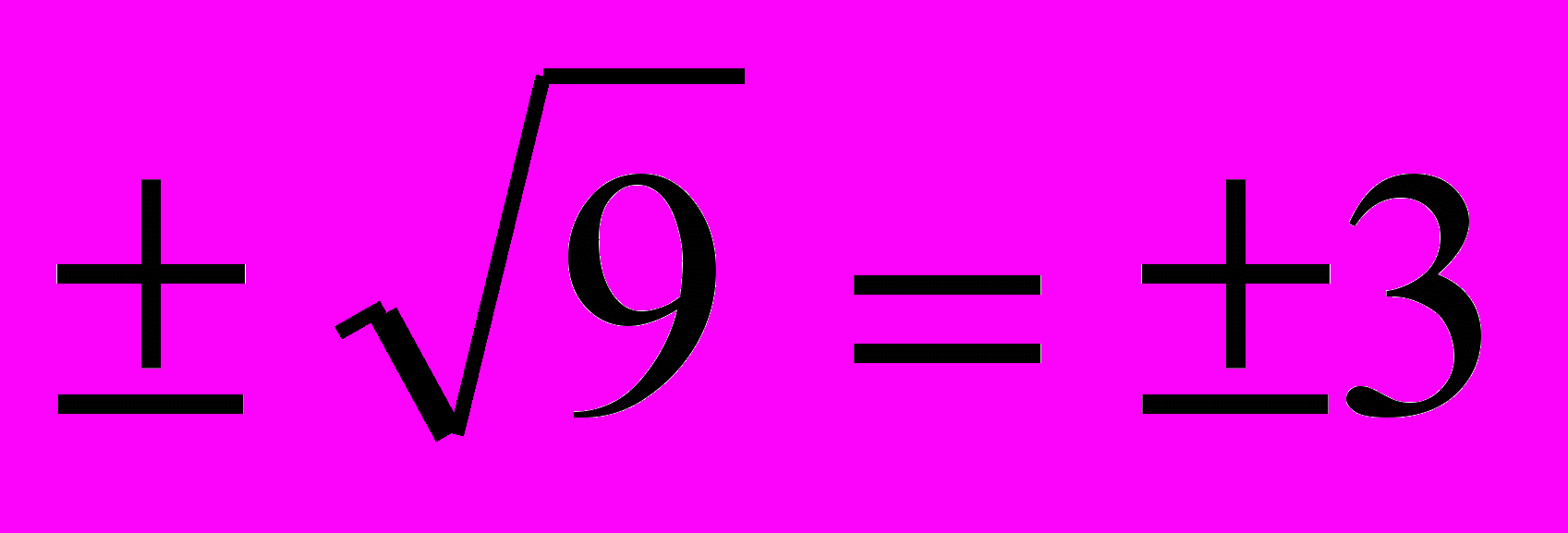
Пример 4. Решите уравнение х²+25 = 0

Решение: х² = - 25; х = ; корни мнимые.


II. Чтобы решить уравнение ах² + bx = 0 , представим его так х(ax +b) = 0. Произведение может равняться нулю только тогда, когда какой – нибудь из сомножителей равен нулю; следовательно, рассматриваемое уравнение удовлетворяется, если положим, что х =0 или ах +b = 0/

Второе равенство дает 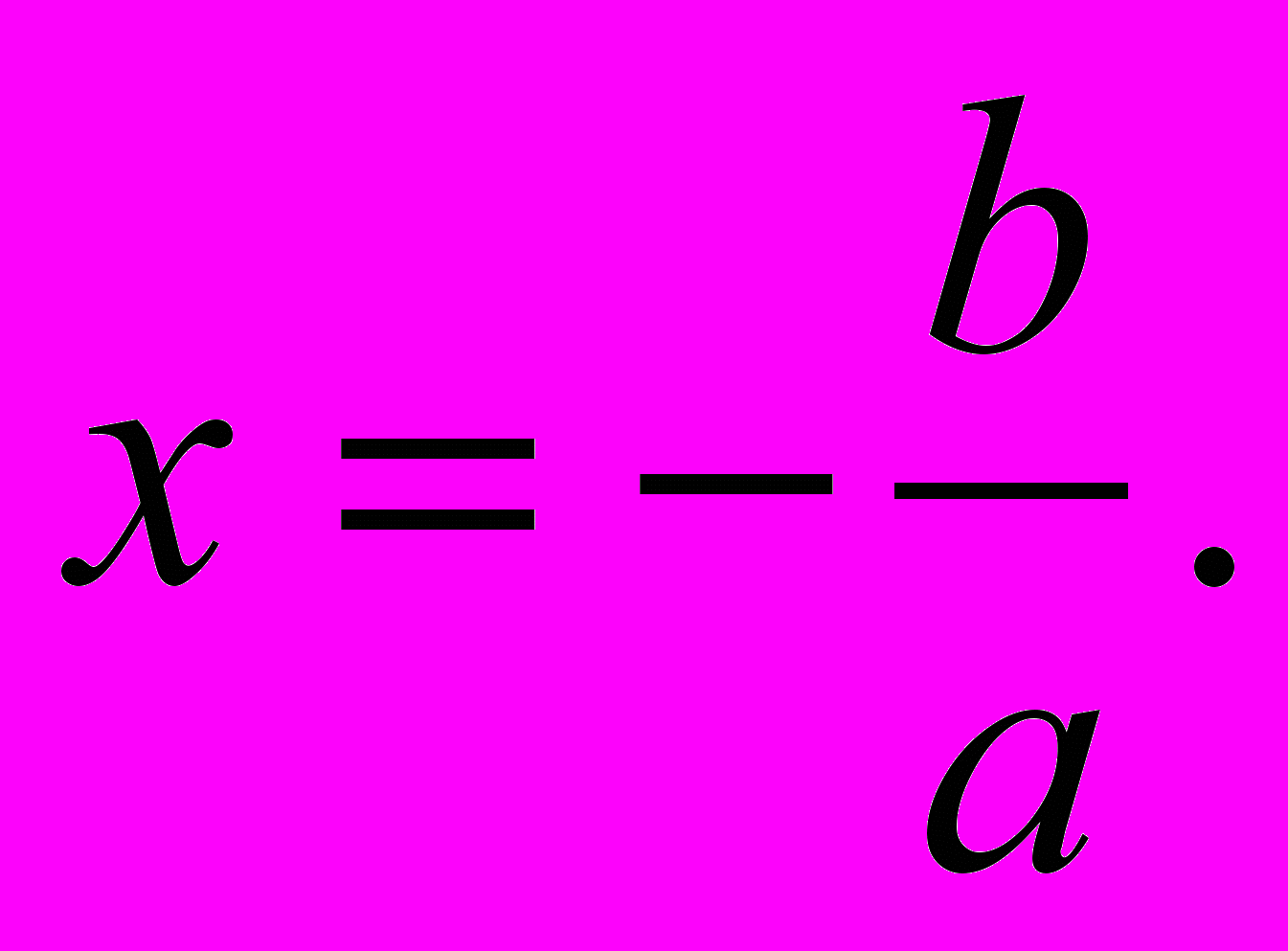Итак, уравнение ах² + bx = 0 имеет два корня

х₁ = 0 и


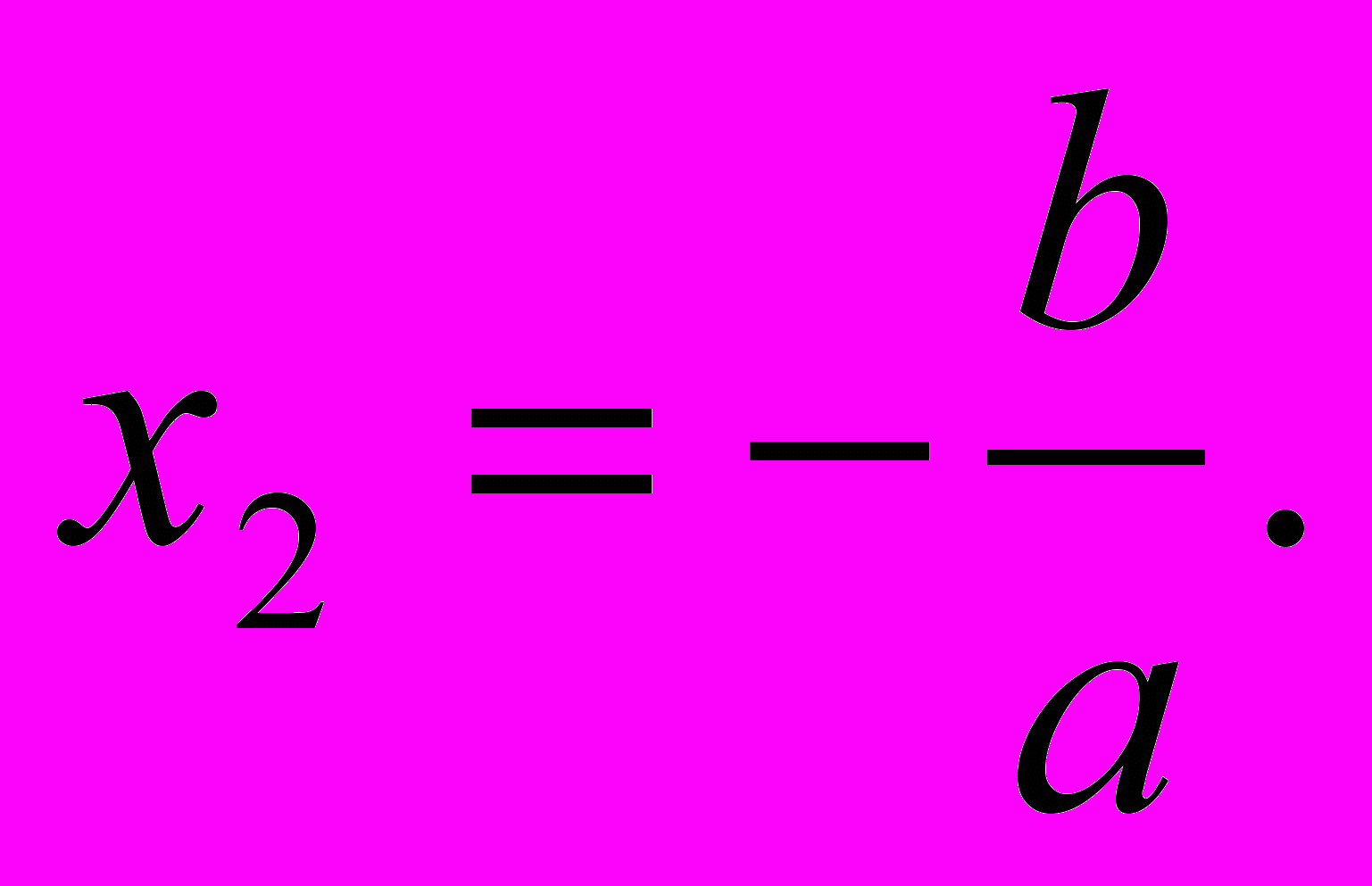
 Пример 5.

Решение: 2х² – 7х = 0, х(2х – 7) = 0; х₁ = 0; х₂ = .


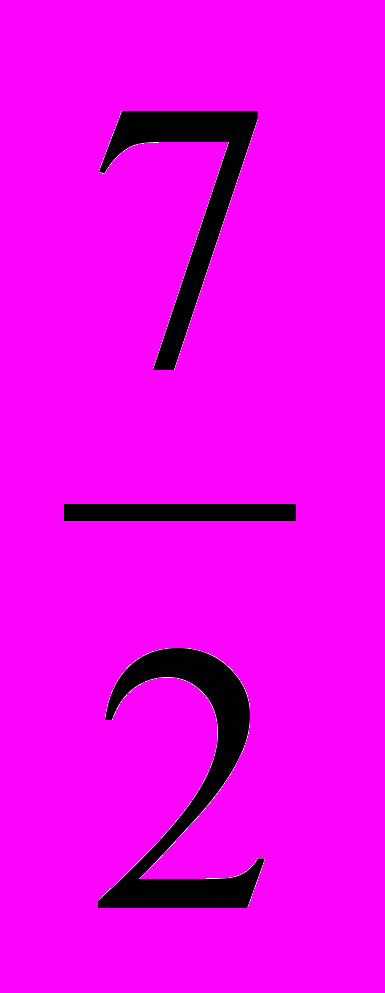III. Наконец, квадратное уравнение ax² = 0 имеет очевидно, только одно решение

х = 0.


§3. Квадратное уравнение имеет всегда два

корня.

Рассматривая решение квадратных уравнений, видим что эти уравнения иногда имеют два корня, иногда один, иногда ни одного. Однако согласились приписывать квадратным уравнениям во всех случаях два корня, разумеется при этом, что корни могут быть иногда равными, иногда мнимыми. Причина такого соглашения состоит в том , что формулы, выражающие мнимые корни уравнения, обладают теми же свойствами , какие принадлежат вещественным корням, состоит только совершая действия над мнимыми количествами, руководиться правилами, выведенными для вещественных количеств, принимая при этом, что (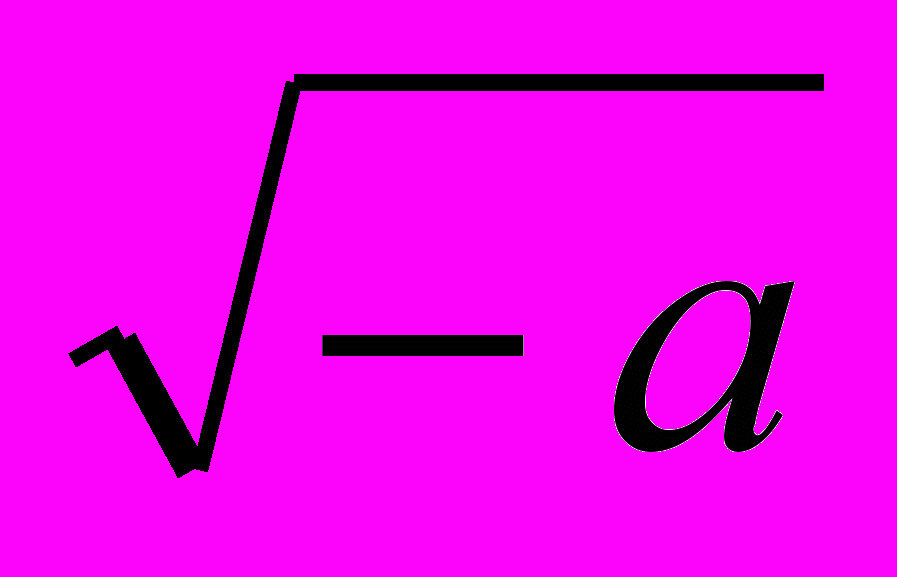)² = - а. Точно так же, когда уравнение имеет один корень, мы можем, рассматривая это корень как два одинаковых, приписать им те же свойства, какие принадлежат разным конам уравнениям. Простейшие из эти свойств выражают в следующей теореме.


ТЕОРЕМА: Сумма корней квадратного уравнения, у которого коэффициент при неизвестном во 2 – й степени есть 1, равна коэффициенту при неизвестном в первой 7 степени, взятому с обратным знаком; произведение корней этого уравнения равна свободному члену.

Доказательство. Обозначив через α и β корни уравнения х² + рх +q = 0, будем иметь ( каковы бы ни были эти корни)




-7-



Это произведение можно найти сокращенным путем, основываясь на равенстве

(a + b)(a – b) = a² – b²:




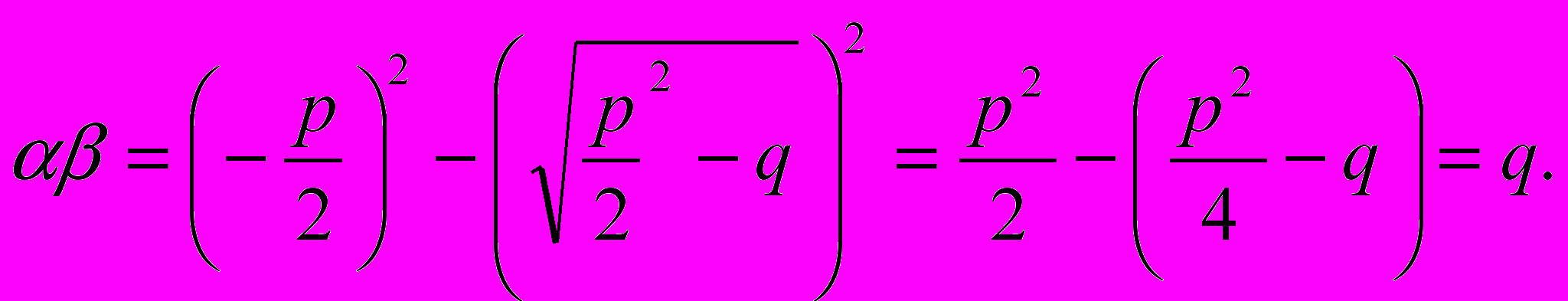
Если α и β есть корни уравнения ах² + bx +c = 0, или что то же уравнения

, то будет иметь .


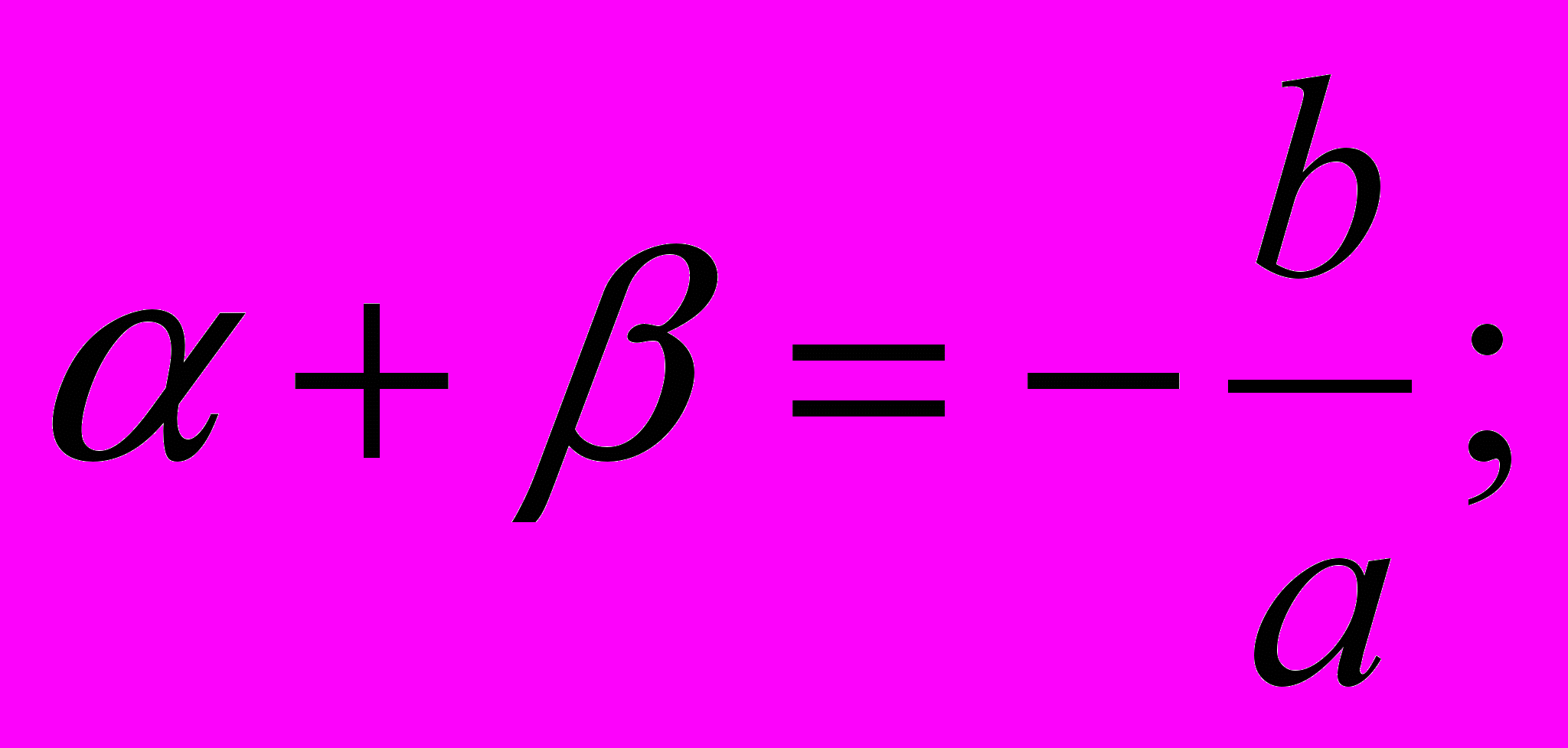
Обратная теорема. Если количества α, β, р и q таковы, что α + β = - р и αβ = q, то

β и α суть корни уравнения х² + рх + q = 0.


Доказательство. Требуется доказать, что каждое из количеств β и α удовлетворяет уравнению х² + рх + q = 0. Из равенства α + β = - р и α = -р – β, после чего равенство αβ = q дает


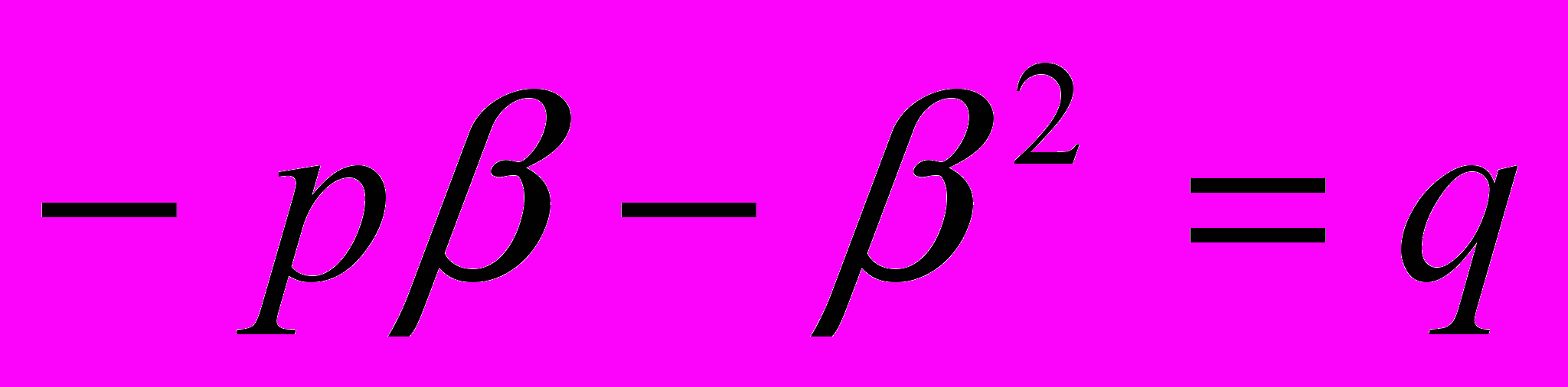или .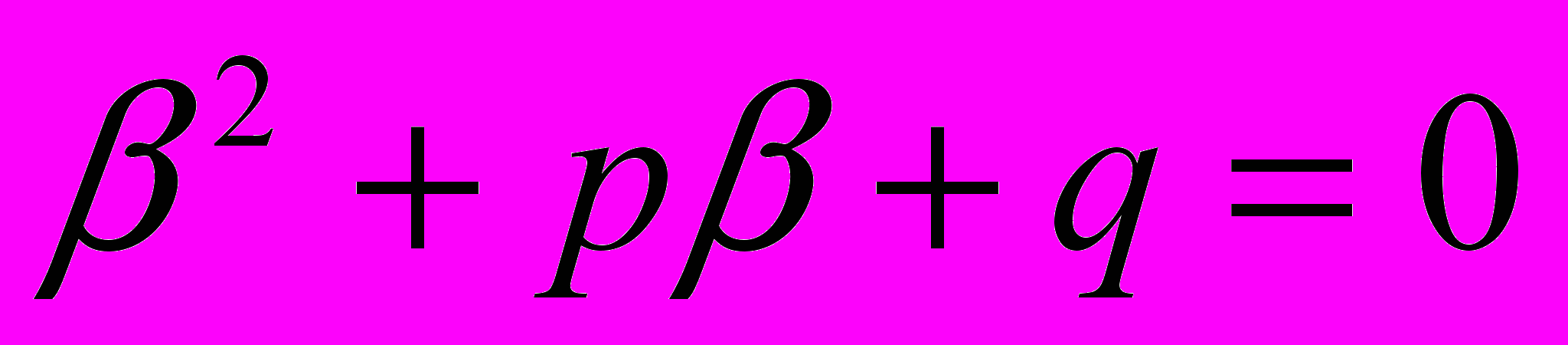

Значит, β есть корень уравнения ах² +bx + c = 0; подобным же образом убедимся, что и α есть корень того же уравнения.

1-е следствие. По данным корням можно составить квадратное уравнение. Пусть требуется составить уравнение, корни которого были бы 2 и – 3. положив, что 2 + (- 3)= - р и 2 · (- 3) = q, находим - р = 1, q = - 6. Значит, искомое уравнение будет

х² + х – 6 = 0

Подобно этому найдем, что – 2 и – 2 являются корнями уравнения х² + 4х + 4 = 0, 3 и 0 являются корнями уравнения х² – 3х = 0 и т. П.


2-е следствие. Не решая квадратного уравнения, можно определить знаки его корней, если эти корни вещественные. Пусть, например, имеем уравнение х² + 8х +10 = 0. Так как


в этом примере количество - q есть положительное число, то оба корня должны быть вещественные. Определим, не решая уравнения, знаки этих корней. Для этого рассуждаем так: обращая внимание сначала на свободный член ( + 10 ), видим, что он имеет знак +; значит, произведение корней должно быть положительное, т. е. оба корня имеют одинаковые знаки. Чтобы определить, какие именно, обратим внимание на коэффициент при х ( т. е. на +8) он имеет знак +; следовательно, сумма коэффициентов отрицательна; потому одинаковые знаки у корней должны быть минус.

-8-

Подобными рассуждениями можно определить знаки у корней и во всяком другом случае. Так, уравнение х² + 8х - 10 = 0 имеет корни с разными знаками ( потому что их произведение отрицательно), причем отрицательный корень имеет большую абсолютную величину (потому что их сумма отрицательна); уравнение х² – 8 – 10 = 0 также имеет корни с разными знаками, но большая абсолютная величина принадлежит положительному корню.


§4.Частные случаи квадратных уравнений


Случай, когда коэффициент а очень мал.


Вычисление корней уравнения ах² +bx + c = 0 по общей формуле, выведенной выше, затруднительно в этом случае, когда коэффициент а очень малое число сравнительно с b и с. В самом деле, вычисляя корни по формуле




Мы в большинстве случаев должны довольствоваться приближенной величиной , а следовательно, и всего числителя. Разделив эту приближенную величину на 2а, мы тем самым разделим на 2а и погрешность, с которой вычислен числитель формулы. Но так как, по предложению,2а очень малая дробь, деление на малую дробь равносильно умножению на большее число, то погрешность значительно возрастает, вследствие чего окончательный результат будет далек от истинного. Если, например, 2а = 0,0001 и мы вычислили до четвертого десятичного знака, то предел погрешности в окончательном результате будет 0,0001 : 0,00001 = 10.

Для вычисления корней уравнения в этом случае употребляется более удобный способ так называемого последовательного приближения.

Заметим, что при очень малой величине а один из корней уравнения немного отличается от 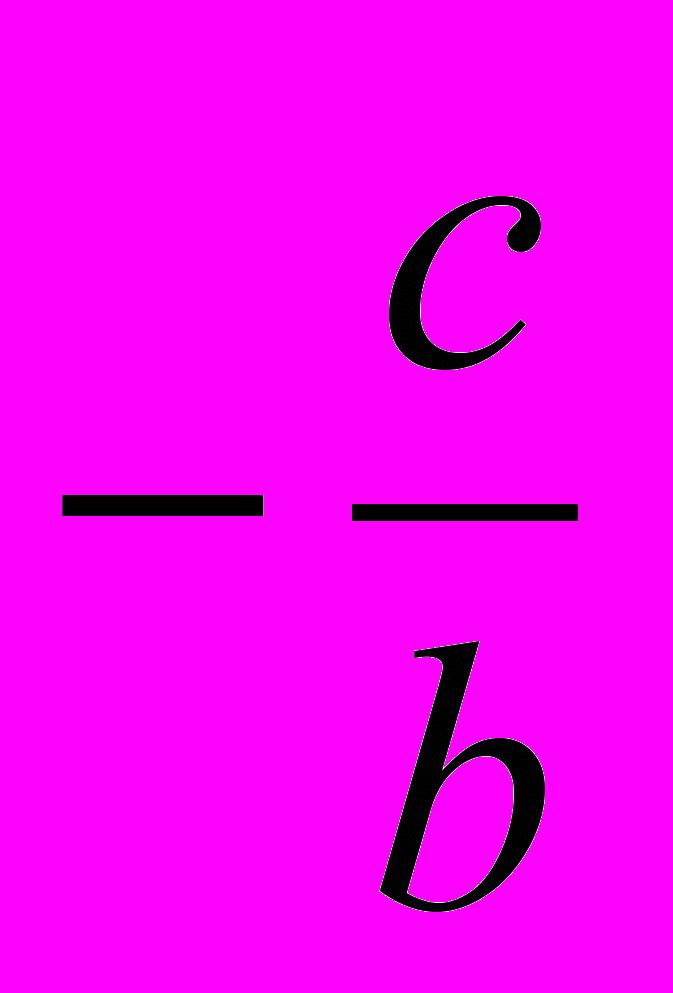, а другой - весьма большое число (по абсолютной величине). Действительно, уравнение ах² +bx + c = 0 равносильно уравнению


,

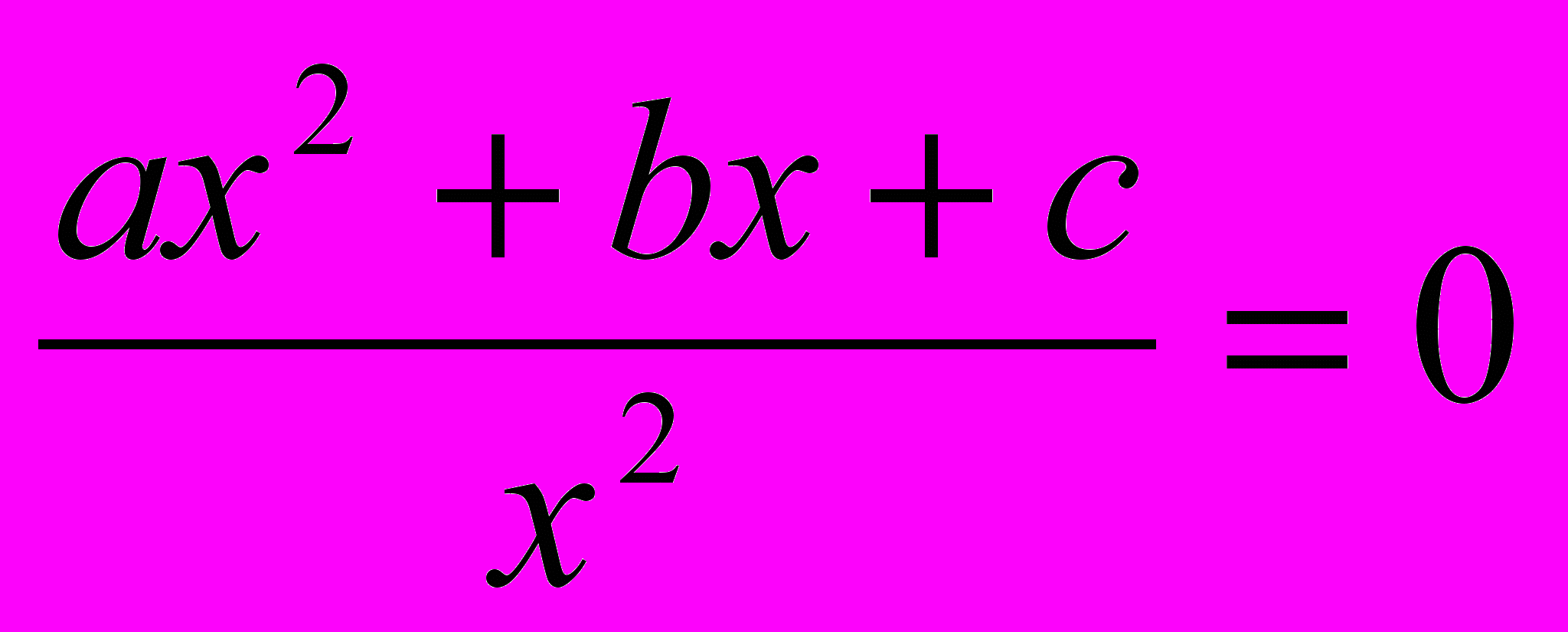которому можно придать вид




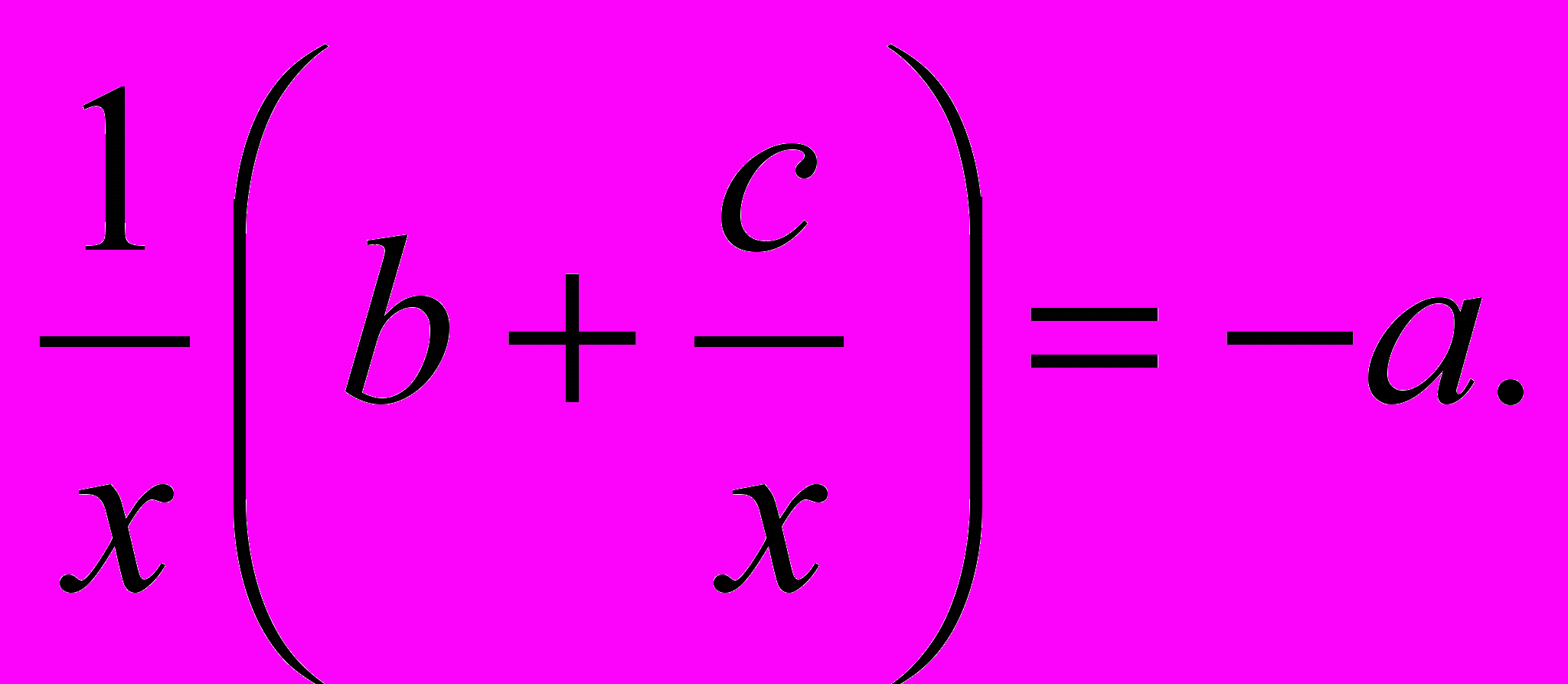
Так как – а близко к нулю, то последние уравнение может быть удовлетворено такими значениями х, при которых один из сомножителей левой части уравнения окажется очень малым числом, а другой – не очень большим; это будет иметь место или тогда, когда придадим х весьма большое абсолютное значение, или же тогда, когда х будет близко к .

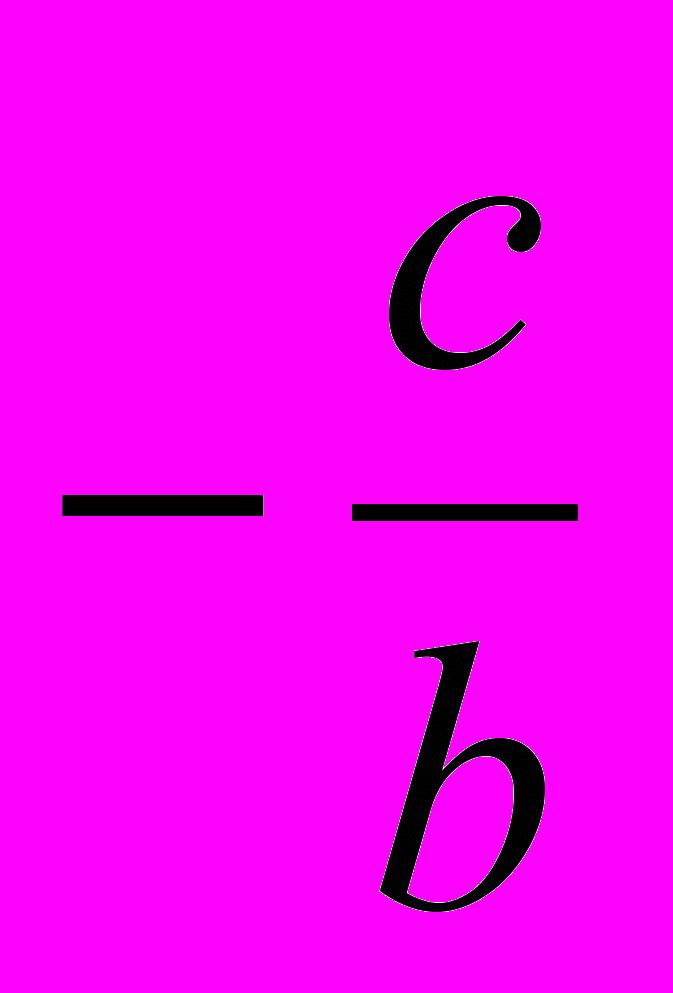Покажем, как вычислить тот из корней, который мало отличается от 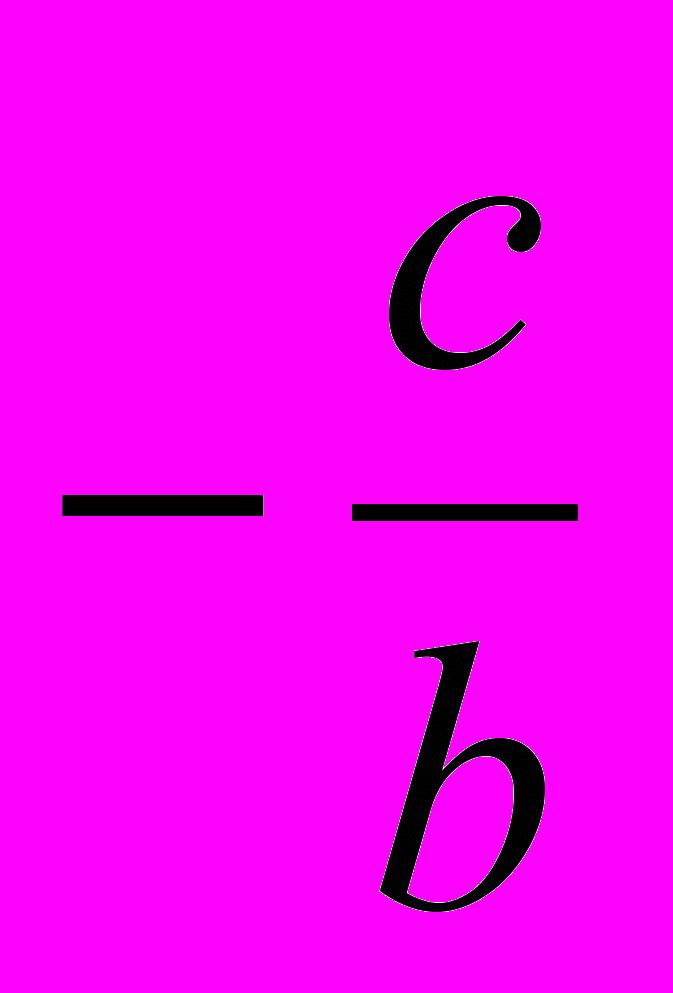( другой корень найдем, вычитая первый из ).

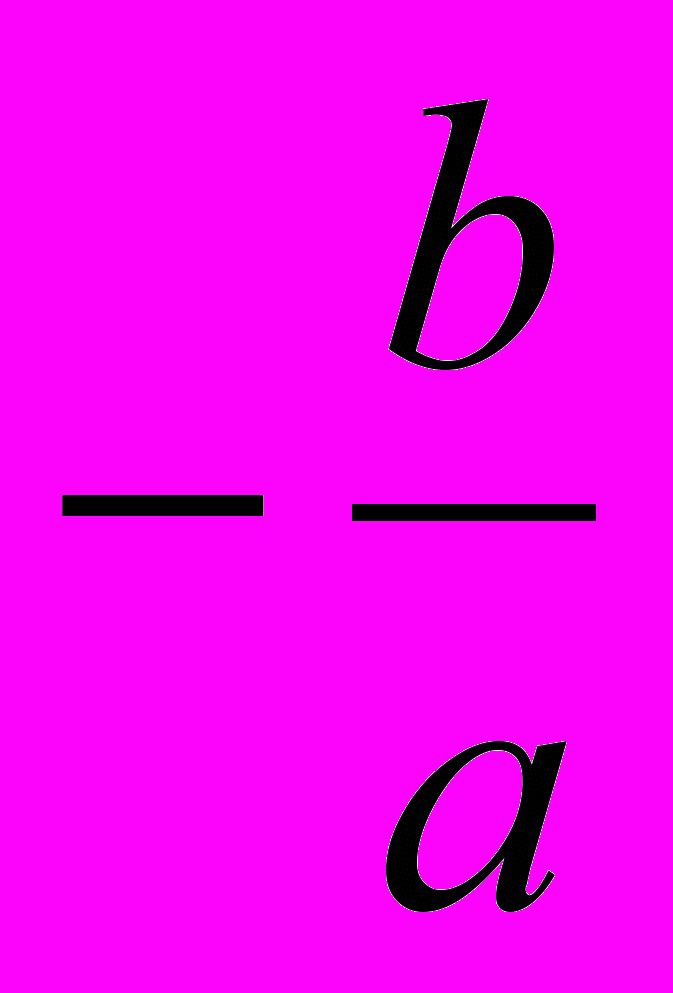-9-

Из уравнения выводим/


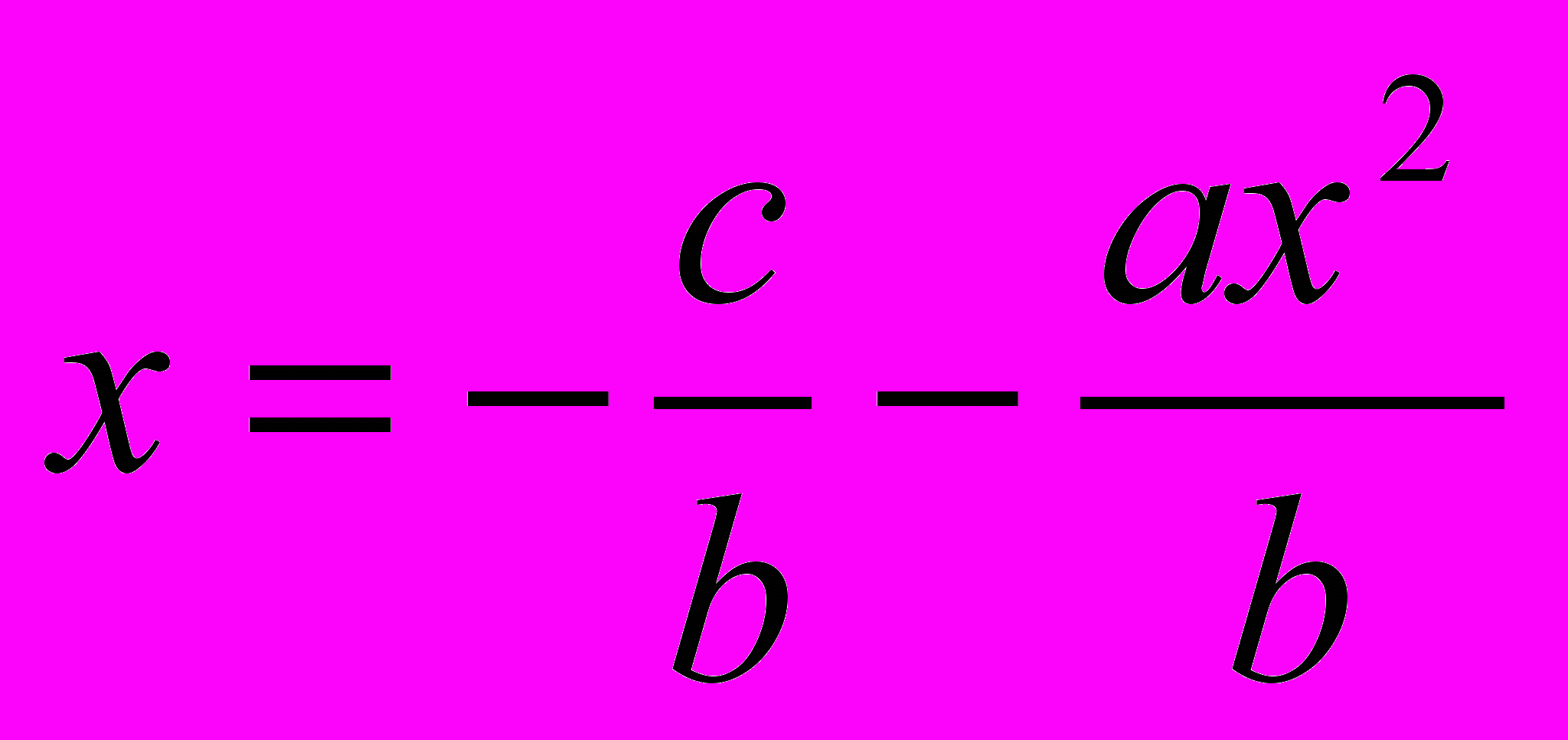Так как а очень малое число, а х и b не очень велики и не очень малы, то абсолютная величина дроби 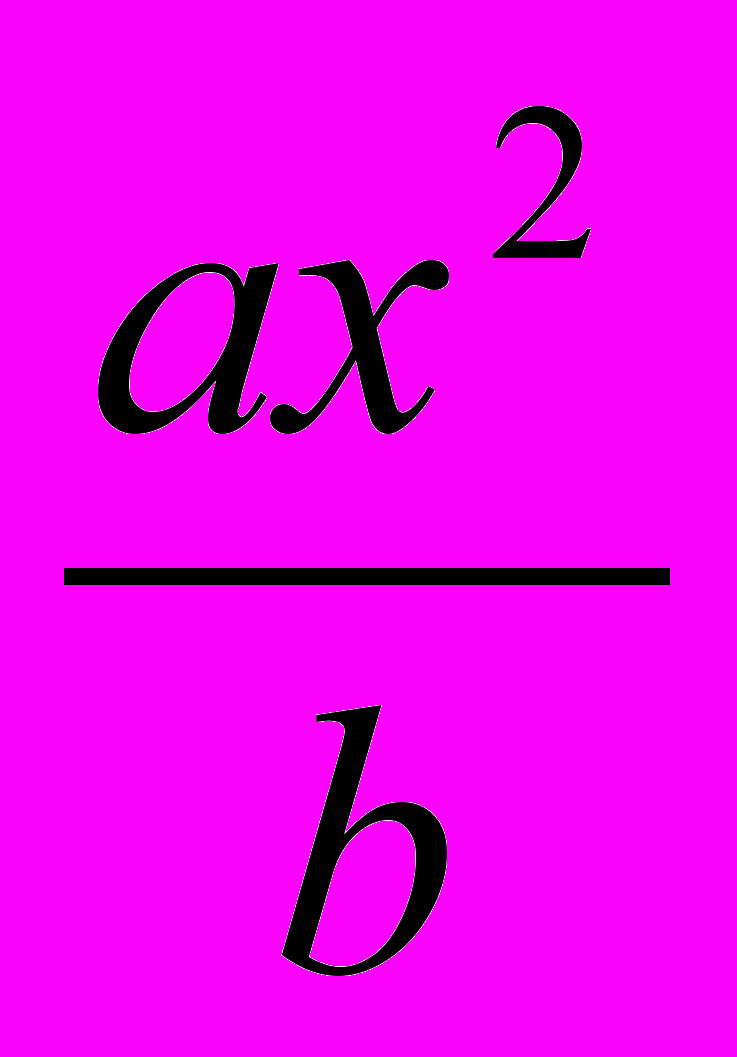очень мала. Пренебрегая этим членом, получим для х первое приближение



Вставив это значение в правую часть уравнения [1] , получим второе приближение, более точное чем первое:



Вставив эту величину в первую часть уравнения [1], получим третье приближение, еще более точное. Подобным же путем можем получить, если нужно, четвертое и следующее приближение.


 Пример 6.

1. Решите уравнение 0,003х² + 5х - 2 = 0
   

.

Первое приближение = 0,4. Это число более истинного значения х², потому что нам пришлось отбросить отрицательный член – 0,0006х².

Второе приближение = 0,4 – 0,0006·(0,4)² = 0,399904. Это число менее истинного значения х² число, большее х² , отчего вычитаемое увеличилось, а разность уменьшилась.

Третье приближение оказалось бы больше истинного значения х, четвертое меньше и т. д.

Так как 0,4 > х >0,399904, то взяв вместо х одно из этих приближений, сделаем ошибку менее 0,4 – 0,399904, т. е. менее 0,0001. Другой корень получится вычитанием найденного корня из 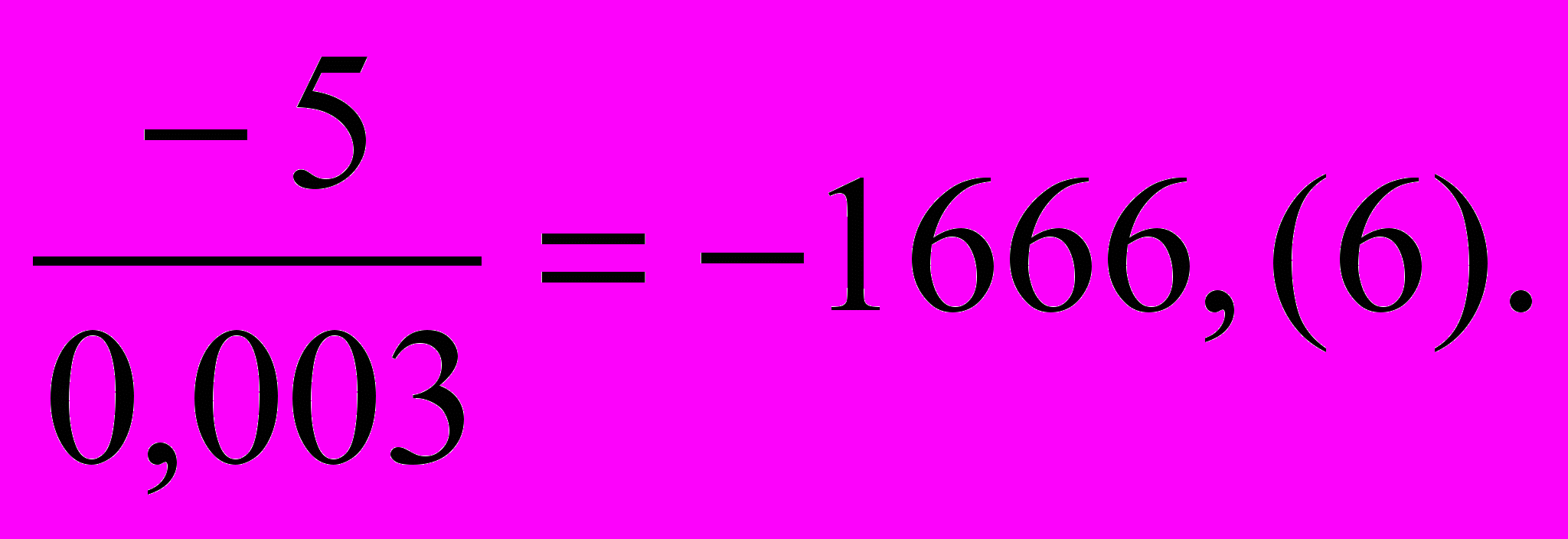Если для первого корня возьмем число 0,4, то другой – 1667,(6).


Случай, когда с очень малое число.

Способ последовательного приближения применим и тогда, когда свободный член уравнения очень малое число сравнительно с а и b. В этом случае один из корней близок к


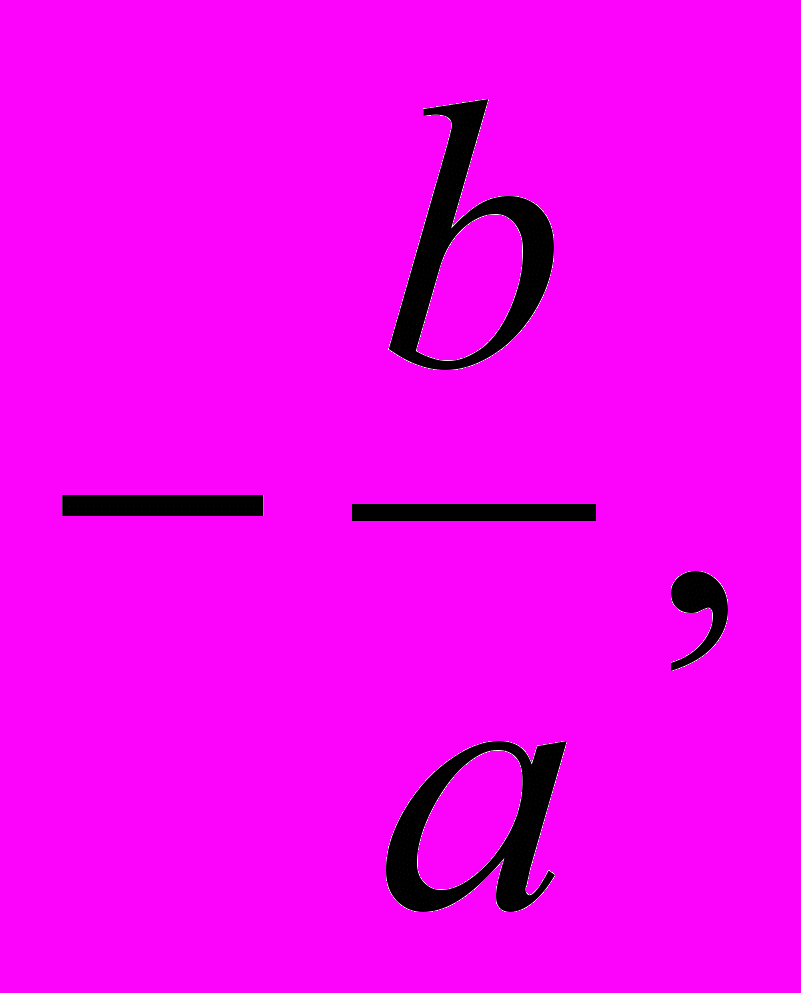а другой – весьма малое количество. В этом нетрудно убедиться, если уравнению придать вид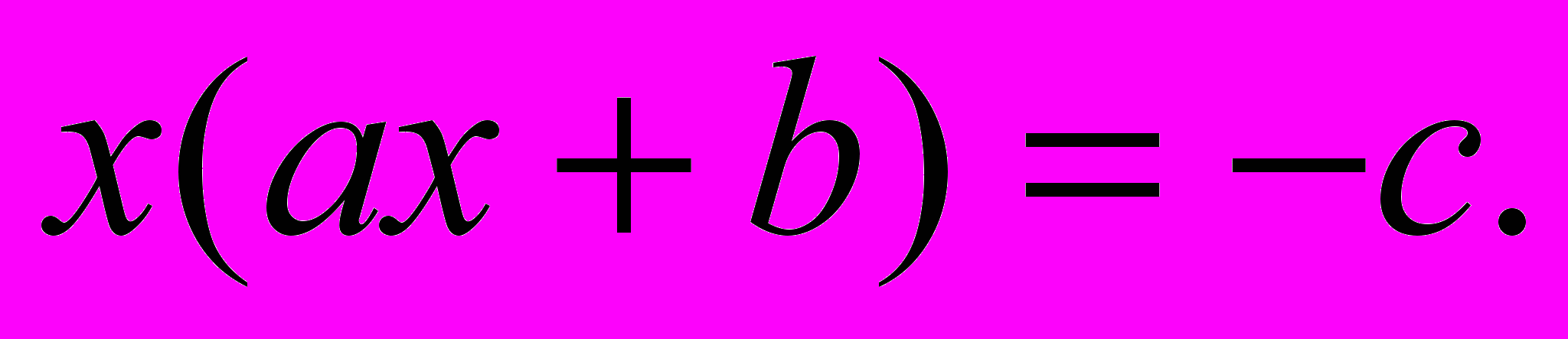

Так как, по предложению, абсолютная величина – с очень мала, то уравнение, очевидно, удовлетворится при х, или очень близком к 0, или мало отличающемся от

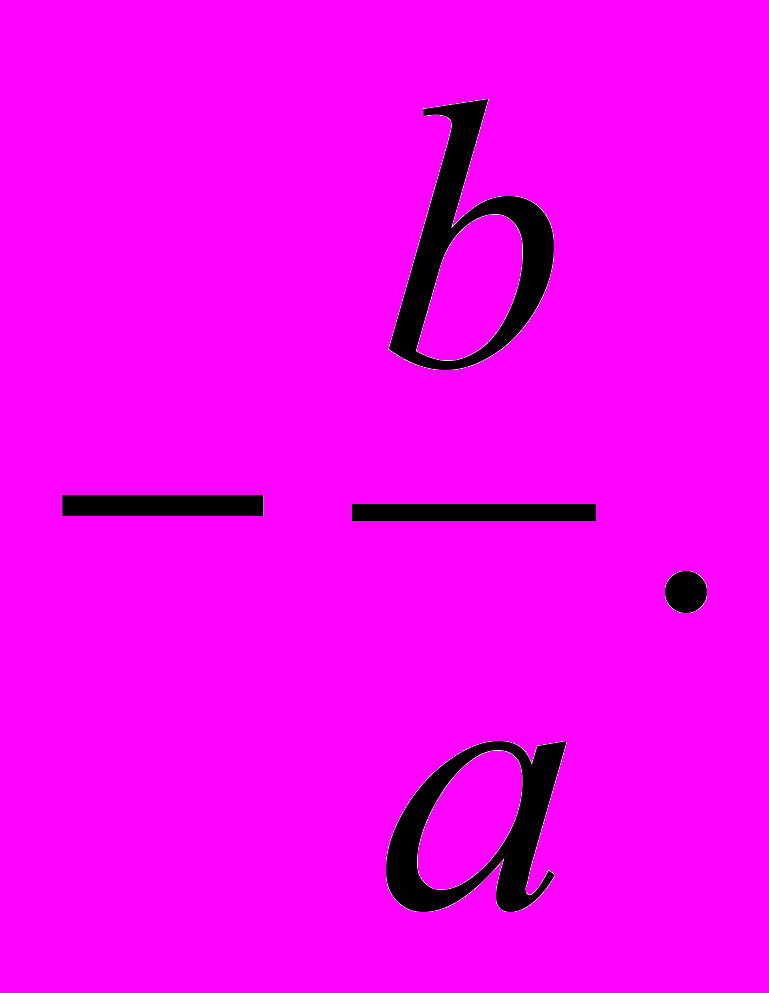
Чтобы найти корень, имеющий очень малую величину, представим уравнение снова в виде




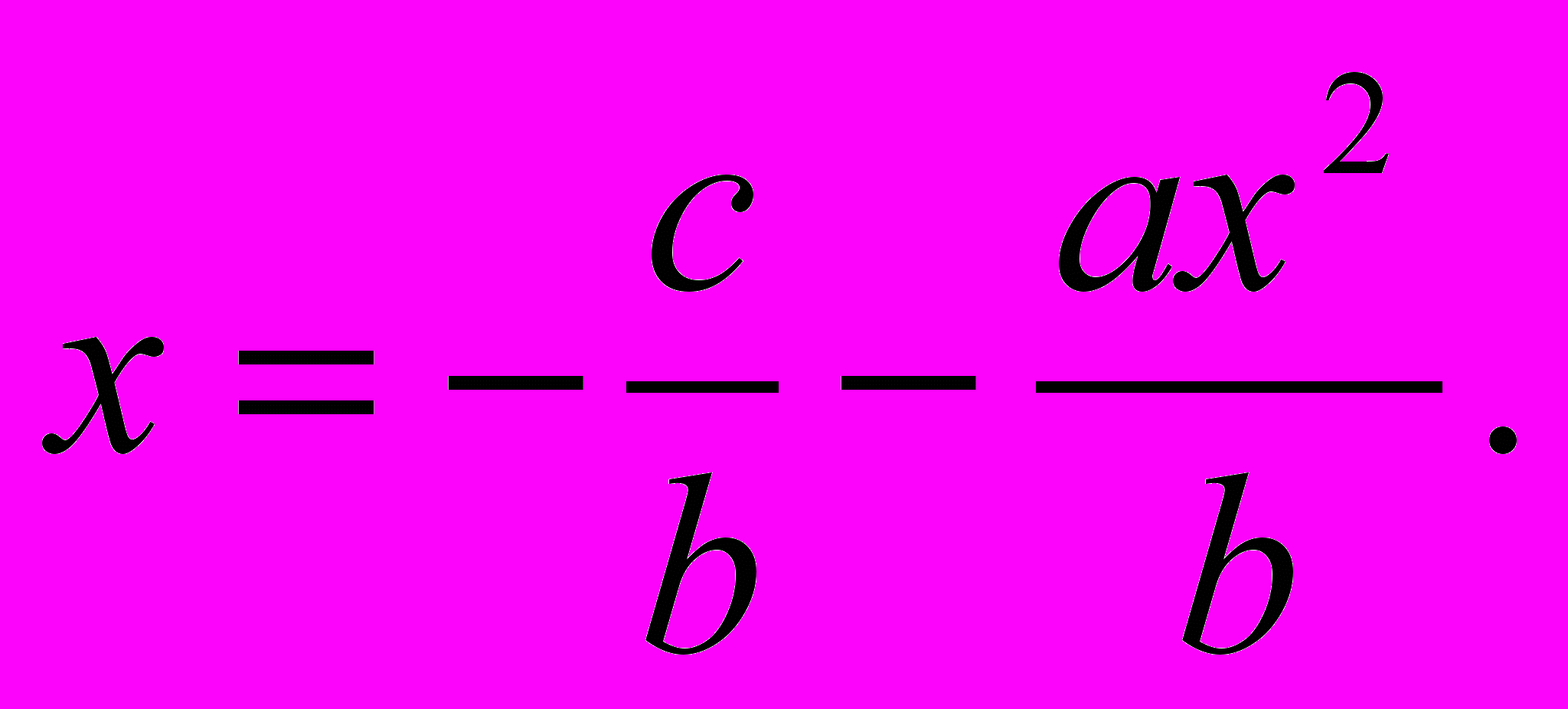
-10-

Так как а и b суть числа не очень большие и не очень малые, а абсолютная величина х² очень мала, то для первого приближения можно пренебречь членом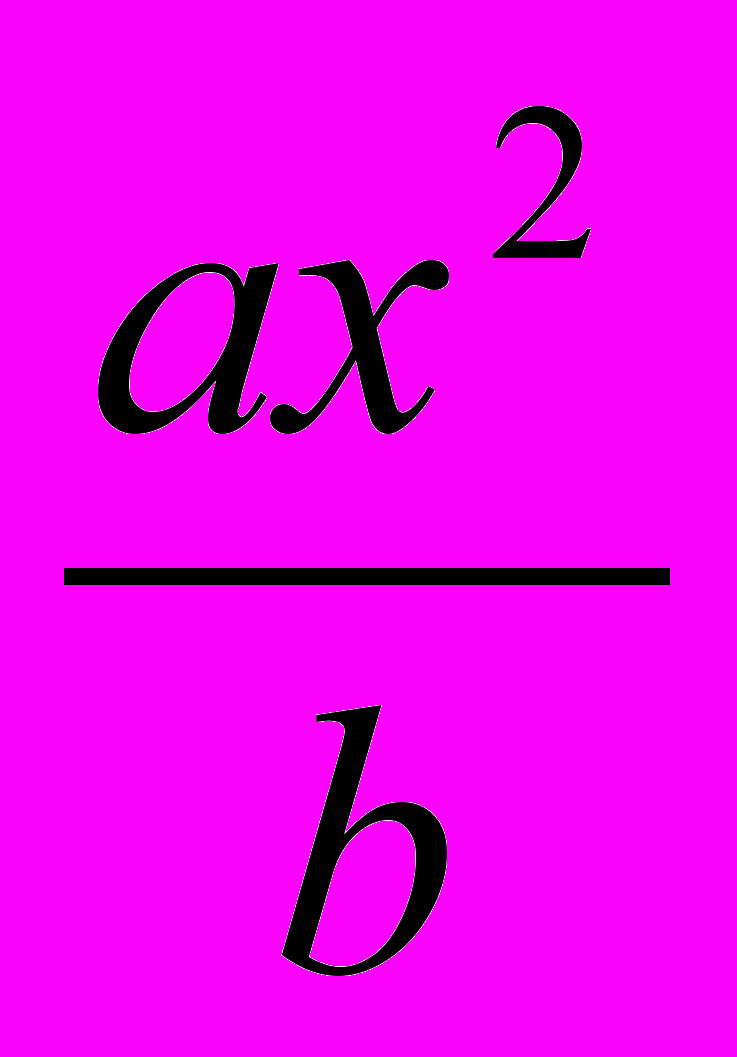; тогда получим .

Вставив это значение на место х в правую часть уравнения [1], получим второе приближение; подобным же образом найдем, если нужно, и следующие приближения.¹


§5. Решение квадратных уравнений

графическим способом

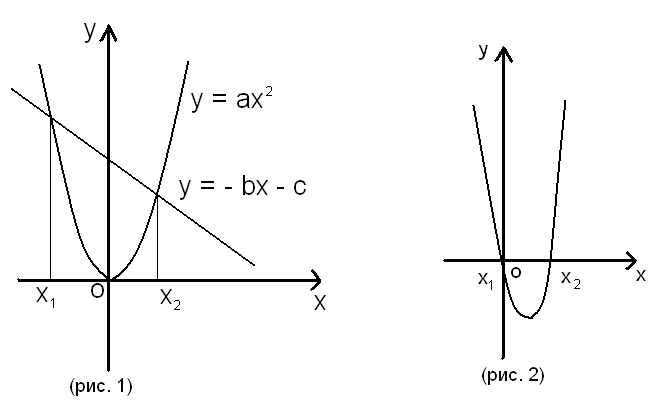
1. Квадратное уравнение можно решать и графическим способом. Решим графически уравнение ах² + bx +с = 0. Оно равносильно уравнению ах² = - (bx + c). Постоим графики функций y = ax² и y = - bx - c в одной системе координат (рис. 1). В точках х₁ и х₂ значения обеих функций равна. Следовательно, х₁ и х₂ являются корнями уравнения ах² = - (bx + c) и равносильного ему уравнения ах² + bx +с = 0
   
2. Если парабола и прямая касаются. То квадратное уравнение имеет два равных корня.
   
3. Если же парабола и прямая не пересекаются и не касаются, то квадратное уравнение не имеет корней.
   
4. Уравнение ах² + bx +с = 0 можно решить иначе, построив параболу y = ах² + bx +с и найдя точки ее пересечения с осью Ох, если D≥0 (рис. 2)² (приложение 12)
   

1. Материал еженедельного учебно – методическогог приложения к газете «Математика» 2.- Материал взят «Повторение и систематизируем школьный курс алгебры и начал анализа». (В. С. Крамор).


-11-

§6. Алгоритм устного решения квадратных

уравнений.


Приведенные квадратные уравнения.


Наиболее распространенно устное решение приведенных квадратных уравнений, но и они у многих учеников вызывает затруднение из – за отсутствия жесткого алгоритма действий, особенно в случаях, когда корни имеют разные знаки.

Приведенное квадратное уравнение имеет вид

x² + рх + q = 0


его корни удовлетворяют теореме Виета, которая при а = 1 имеет вид

х₁ · х₂ = q,

х₁ + х₂ = - p


Отсюда можно сделать следующий вывод:

1. Если в уравнении последним знаком является «минус», то корни имеют разные знаки, причем знак меньше корня совпадает со знаком второго коэффициента в уравнении ( в дальнейшем будет называть его вторым знаком уравнения, а числа з и q будут называться коэффициентами).
   

Зная, что при сложении чисел с разными знаками их модули, вычитаются затем: для нахождения корней приведенного уравнения необходимо выполнить следующие действия:

1. найти такие множители числа q, чтобы их разность была равна числу р;
   
2. поставить пред меньшим из найденных чисел второй знак уравнения, другой корень будет иметь противоположный знак.
   

 Пример 7. Решите уравнение


х² – 2х – 15 = 0


Решение. Из всех множителей числа 15 ( 1 и 15, 3 и 5) выбираем те, разность которых равны 2. Это числа 3 и 5. Перед меньшим числом ставим второй знак уравнения, т. е. «минус. Таким образом, х₁ = - 3, х₂ = 5 – корни уравнения.


Такой алгоритм помогает очень быстро решать уравнения тем учащимся, у которых имеются проблемы с подобным знаком в теореме Виета.


Рассмотрим еще несколько примеров с поэтапной записи рассуждений.


 Пример 8. Решите уравнение


- 12-


Умножим первое уравнение системы на а², а второе уравнение – на а; в результате получим



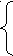
(ах₁) · (ах₂) = ас,

(ах₁) + (ах₂) = - b


Если предложить ах₁ = m, ax₂ = n, то получим корни 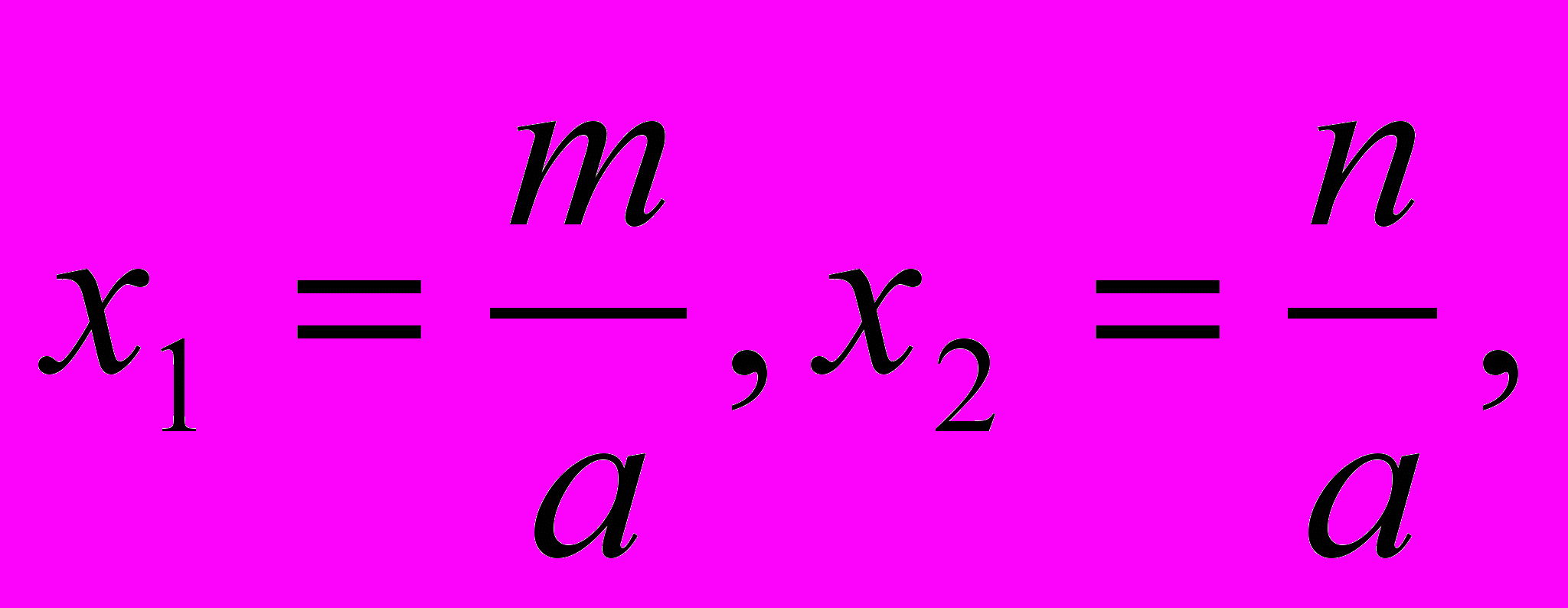о которых говорится в формулировке алгоритма устного решения полного квадратного уравнения.


§7. Теорема Виета

1. Сумма корней приведенного квадратного уравнения х²+ рх + q = 0 равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену, т.е. х₁ + х₂ = - р, а х₁ · х₂ = q.
   
2. Теорема, обратная теореме Виета. Если р, q, x_1, x₂ таковы, что х₁ + х₂ = - р,
   

х₁ · х₂ = q, то х₁ и х₂ – корни уравнения х²+ рх + q = 0

3. Выражение вида ах² +bx + c называется квадратным трехчленом. Корни этой функции являются корнями соответствующего квадратного уравнения ах² +bx + c = 0.

4. Если дискриминант квадратного трехчлена больше нуля, то этот трехчлен можно представить в виде ах² +bx + c = 0 (х – х₁) ×(х - -х₂), где х₁ и х₂ - корни трехчлена.

5. Если дискриминант квадратного трехчлена равен нулю, то этот трехчлен можно представить в виде ах² +bx + c = а(х – х₁)², где х₁ – корень трехчлена. Например,

3х² – 12х + 12 = 3 (х – 2)².


§8. Зависимость между коэффициентами и

корнями

Укажем зависимость, которая существует между коэффициентами и корнями квадратного уравнения.

Решая квадратное уравнение х² – 13х + 40 = 0.

получаем х₁ = 5, х₂ = 8.

Легко заметить, что между корнями данного уравнения и его коэффициентами существует зависимость. Сумма корней равна 13; коэффициент при х в уравнении отличается от суммы корней только знаком; произведение корней, равное 40, и по величине, и по знаку совпадает со свободным членом.

Возьмем квадратное уравнение, у которого коэффициент при квадрате неизвестного равен 1:

х²+ рх + q = 0

Если корни х₁ и х₂ , как известно, определяется следующими формулами:




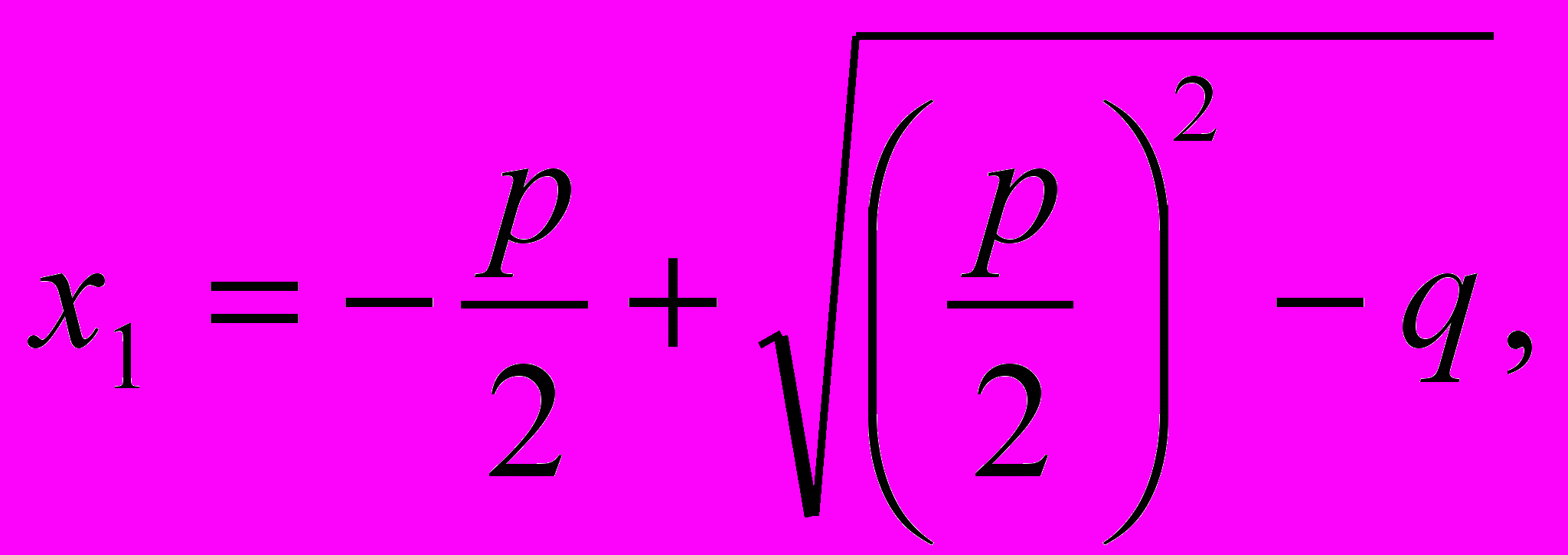
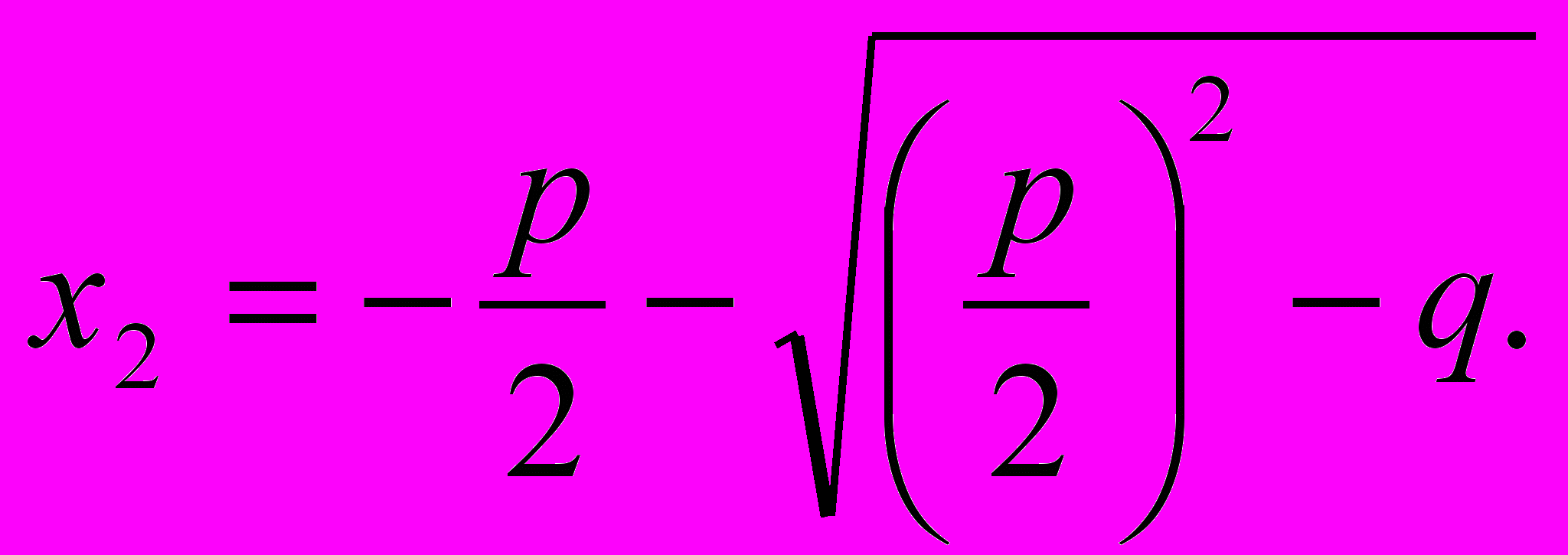
Складывая эти выражения, получаем

х₁ + х₂ = - р


-17-


Таким образом, Сумма корней квадратного уравнения, у которого коэффициент при квадрате неизвестного – единица, равна взятому с обратным знаком коэффициенту при неизвестном первой степени.

Перемножая почтенно формулы для неизвестных квадратного уравнения, получаем




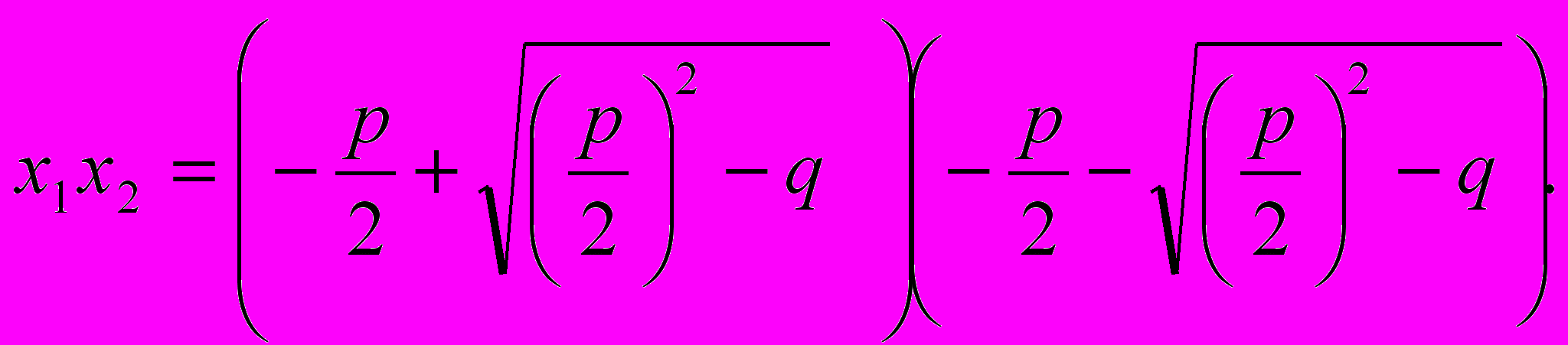
В правой части стоит произведение суммы двух чисел на их же разность; следовательно




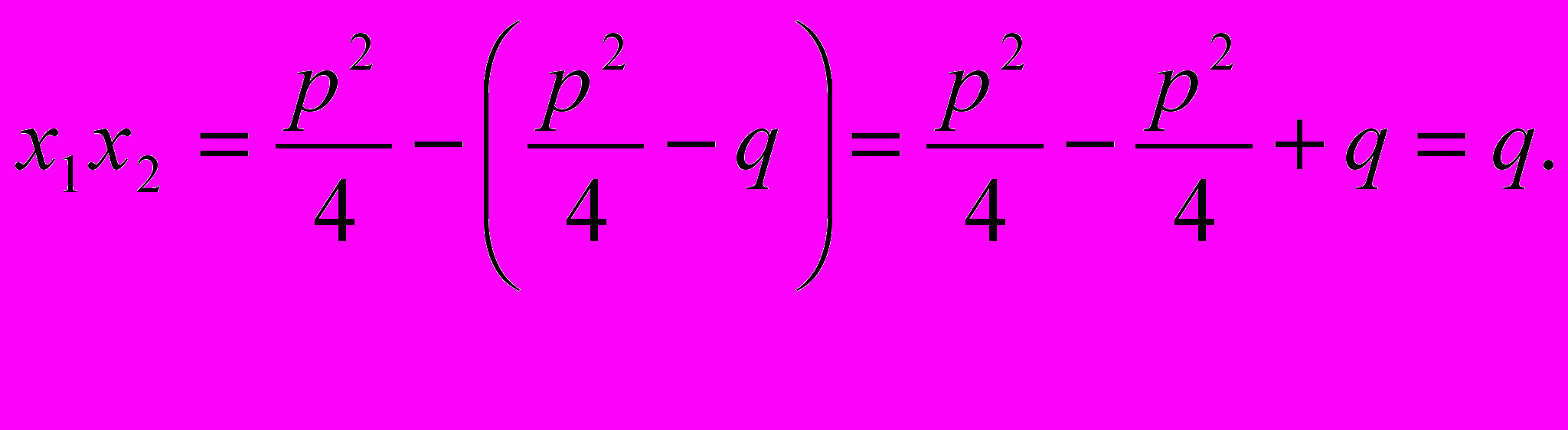
Таким образом,

Произведение корней квадратного уравнения, у которого коэффициент при квадрате неизвестного единица, равна свободному члену.

На основании этих свойств всегда можно указать, не решая самого уравнения, каковы знаки его корней. Например, уравнение

х² + 5х – 7 = 0

имеет два корня с разными знаками, так как произведение их отрицательное, а именно – 7. Так как сумма корней отрицательна, а именно – 5, то мы можем сказать, что корень, больший по абсолютной величине, отрицателен.

Уравнение

3х² + 5х – 10 = 0

Может быть преобразовано в такое




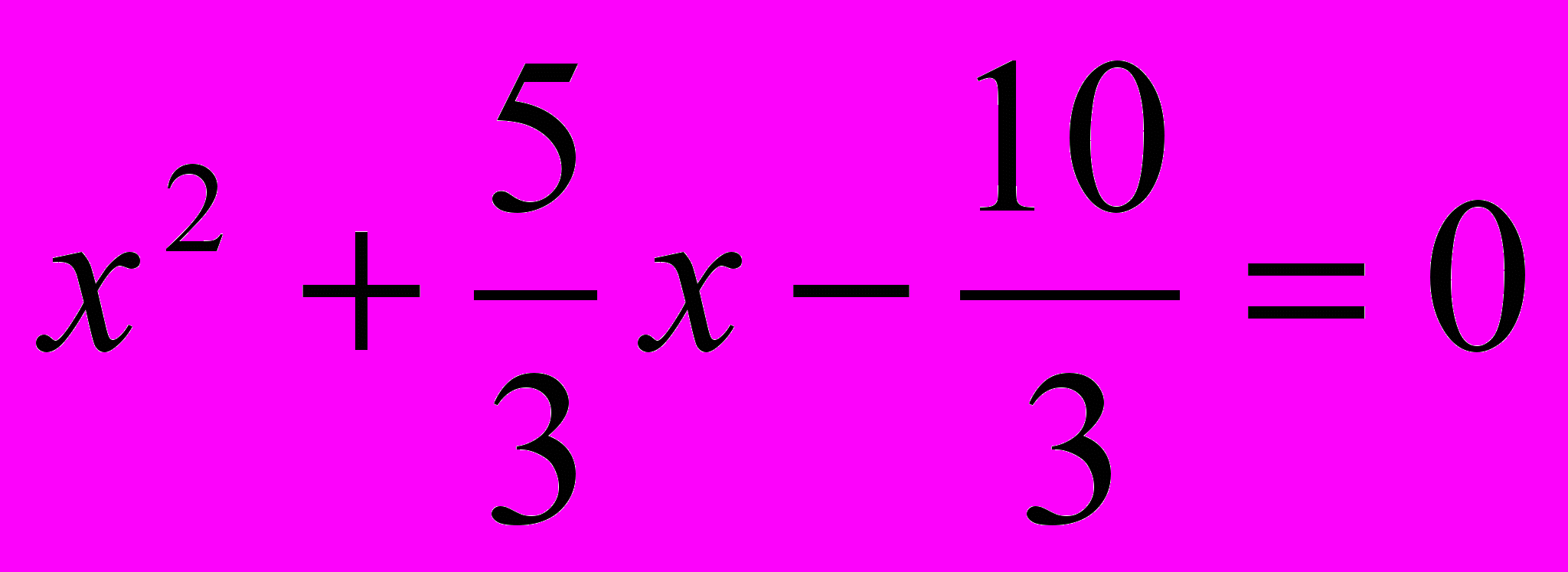
Так как свободный член отрицателен, то произведение корней отрицательно, следовательно, корни разных знаков. Сумма их равна 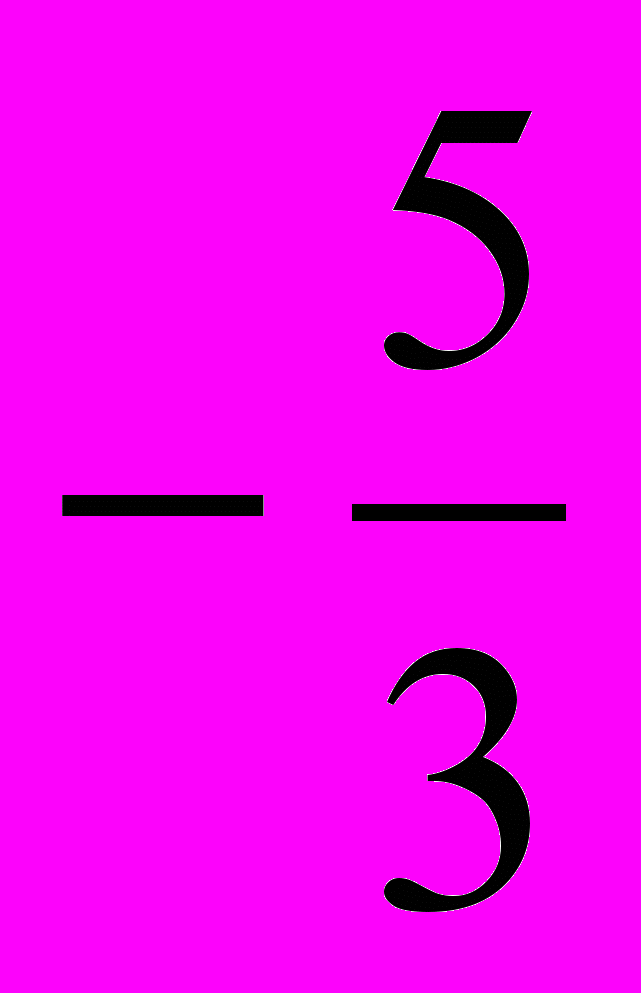; следовательно, больший по абсолютной величине корень отрицателен.

Как видим, даже нет надобности делить на коэффициент при неизвестном для суждения о знаках корней; нужно только следить, чтобы при применении этого приема коэффициент при квадрате неизвестного был положительным.

Приведем следующую табличку дл распознания знаков корней.

Знаки коэффициентов			Знаки корней
a > 0	b>0	c<0	Разные: больший по абсолютной величине отрицателен
a > 0	b> 0	c<0	Разные: больший по абсолютной величине положителен
a > 0	b>0	c > 0	Одинаковые: оба отрицательные
a> 0	b < 0	c > 0	Одинаковые: оба положительные

Пользуясь этой зависимостью корней и коэффициентов квадратного уравнения, можно всегда составить такое уравнение, оба корня которого неизвестны.

Пусть имеем корни

х₁ = 2, х₂ = - 5

Согласно правилу

p = x ₁ + x₂ = 2 + (-5) = - 3

откуда р = 3

Из произведения корней получаем

q = x₁ х₂ = 2(- 5) = - 19.

Таким образом, уравнение, имеющее корнями данные числа, будет следующим:

х² + 3х – 10 = 0.


-19-

IV. ЗАКЛЮЧЕНИЕ


В результате выполнения доклада можно сделать следующие выводы:

1. Изучение научно – методической литературы по теме выполненной работы показали, что использование различных способов решения квадратных уравнений является важным звеном изучении математики, повышает интерес, развивает внимание и сообразительность.
   
2. Система использования различных способов решений уравнений на разных этапах урока является эффективным средством активизации учащихся, положительно влияет на повышение качества знаний, умений и навыков учащихся, развивает умственную деятельность.
   
3. Основным в решении квадратных уравнений является правильно выбрать рациональный способ решения и применить алгоритм решения
   
4. Работа над докладом способствует дальнейшему изучению решений уравнений.
   

-20-

V. Литературы:


1). Газета «Математика» № 18 2004 г. Стр. 28

2). Газета «Математика» №4 2004 г. Стр.28

3). Газета «Математика» № 11 2004 г. Стр. 10

4). Газета «Математика» № 42 2001 г. Стр.2

5). Газета «Математика» №48 2001 г. Стр. 17

6).Епишева О. Б. Специальная методика обучения арифметики, алгебре и началом анализа в средней школе. Курс лекций: Учебное пособие для студентов физ. – мат. Специальностей педагогических институтов. – Тобольск: Изд. ТГПИ им Д. И. Менделеева, 1997г. – стр. 17

7). Зайцев В. В., Рыжков В. В., Сканави М. И. «Элементарная математика» Москва 1976 г. Стр. 152

8). Крамор В. С. Повторяем и систематизируем школьный курс алгебры и начал анализа. «Просвещение» 1990 г. Стр. 109 и стр. 107


-21-

VI. Приложение


Приведем примеры решения квадратных уравнений графическим способом.

 Пример 7.

Решение: 2x² + 6x – 5 = 0

Разделим уравнение на две части: y = 2x² и y = 6x – 5

Построим вспомогательную таблицу:

х	- 3	- 2	- 1	0	1	2	3
у	18	8	2	0	2	8	18

y = 2x²

х	0	2
у	-5	7

y = 6x – 5


Построим график функций y = 2x² и y = 6x – 5




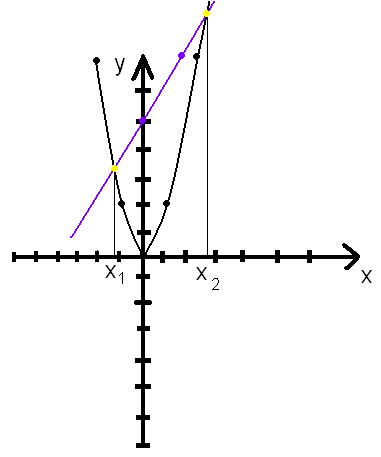
Из графика видно, что два уравнения пересекаются в двух точках х₁ и х₂ следовательно уравнение будет иметь два корня х₁ ≈ - 1,1 и х₂ ≈ 2,7


Ответ: х₁ ≈ - 1,1 и х₂ ≈ 2,7


-22-