Робоча навчальна програма з дисципліни "Теорія ймовірностей І математична статистика" для професійного спрямування спеціальності
| Вид материала | Документы |
- Робоча навчальна програма з дисципліни "Інформаційні технології у перекладі" для професійного, 164.4kb.
- Робоча навчальна програма для студентів спеціальності 030. 302 "Реклама та зв'язки, 208.25kb.
- За переліком дисциплін програми підготовки бакалаврів з економіки підприємства дисципліна, 92.49kb.
- Робоча навчальна програма з дисципліни " ділова українська мова " для професійного, 410.96kb.
- Робоча навчальна програма з дисципліни " Інформаційні технологі ї в перекладі " для, 58.49kb.
- Робоча навчальна програма з дисципліни " Інформатика та комп’ютерна техніка" для професійного, 660.32kb.
- Навчальна програма дисципліни " теорія алгоритмів І математична логіка" (для бакалаврів,, 481.02kb.
- Робоча навчальна програма з дисципліни "Основи інформатики та обчислювальної техніки", 370.15kb.
- Робоча навчальна програма для студентів спеціальності 030. 302 "Реклама та зв'язки, 310.69kb.
- Робоча навчальна програма дисципліни для студентів спеціальності 030304 Археологія, 408.61kb.
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
Київський національний лінгвістичний університет
“ЗАТВЕРДЖУЮ”
Проректор
з навчально-виховної роботи
_________ Соловей М.І.
(підпис) (прізвище, ініціали)
“ _______ “ _______________ 2007 р.
Декан факультету заочного та вечірнього навчання
_________ Фатєєв С.П
(підпис) (прізвище, ініціали)
“ _______ “ _______________ 2007 р.
РОБОЧА НАВЧАЛЬНА ПРОГРАМА
з дисципліни
“Теорія ймовірностей і математична статистика“
для професійного спрямування
спеціальності 6.050200 “Менеджмент організацій”
(шифр, назва)
кафедра інформатики та комп’ютерних технологій
факультет заочного та вечірнього навчання
курс 1 -й семестр II
Всього годин/кредитів за навчальним планом: 72 (2 кр.)
У тому числі: аудиторна робота – 8 годин
позааудиторна самостійна робота студента – 64 години
Залік II семестр
Київ –2007
Робоча програма складена на основі типової програми з дисципліни “ Теорія ймовірностей та математична статистика”
Укладач програми: доцент Бесклінська О.П.
(посада, науковий ступінь, прізвище, ініціали)
Робоча програма затверджена на засіданні кафедри інформатики та комп’ютерних технологій
Протокол № 10 від 24 травня 2007 року
Завідувач кафедри: _________________ Коваль Т.І.
(підпис) (прізвище, ініціали)
Програму узгоджено з кафедрою/ами:
(назва кафедри) (прізвище, ініціали (підпис)
завідувача кафедри)
ПЕРЕЗАТВЕРДЖЕННЯ РОБОЧОЇ НАВЧАЛЬНОЇ ПРОГРАМИ
-
Навчальний рік
2007/2008
2008/2009
2009/2010
Дата засідання кафедри
Номер протоколу
Підпис завідувача кафедри
ОПИС ДИСЦИПЛІНИ НАВЧАЛЬНОГО КУРСУ
| Загальна характеристика навчальної дисципліни | Напрям, професійне спрямування, освітньо-кваліфікаційний рівень | Тип та структура навчальної дисципліни |
| Кількість кредитів ECTS: 2 Кількість модулів: 2 Кількість змістових модулів: 11 Загальна кількість годин на вивчення дисципліни: 72 | Шифр та назва напряму 0502 Менеджмент Шифр та назва професійного спрямування 6.050200 “Менеджмент організацій Освітньо-кваліфікаційний рівень бакалавр | Назва циклу навчального плану: цикл фундаментальних та професійно-орієнтованих дисциплін. Обов’язкова Курс підготовки: 1 Семестр: II Кількість навчальних годин: 72 з них: лекційних: 4 практичних і лабораторних: 4 позааудиторна самостійна робота студента: 64 Вид контролю: залік |
- Мета та завдання дисципліни, її місце в навчальному процесі
Дисципліна “Теорія ймовірностей та математична статистика” відображає важливий напрямок розвитку сучасної математики, в ній розглядаються питання пов‘язані з дослідженням закономірностей у випадкових явищах.
Мета: формування базових знань з основ застосування ймовірнісно – статистичного апарата для розв’язування теоретичних і практичних економічних задач.
В результаті вивчення дисципліни студент повинен вміти:
- використовувати у своїй практичній діяльності набуті знання щодо застосовування статистичних методів для дослідження економічних явищ;
- проаналізувати та сформулювати постановку економічної задачі з використанням найпростіших статистичних методів;
- використовувати необхідні програмні продукти для аналізу і розв‘язування економічних задач.
Завданнями навчальної дисципліни є формування знань відповідно до освітньо-професійної програми підготовки фахівця.
В результаті вивчення дисципліни студент повинен знати:
- сутність імовірнісного моделювання;
- методи обчислення ймовірностей ;
- методи обчислення числових характеристик випадкових величин;
- основні розподіли випадкових величин;
- методи первинної статистичної обробки ;
- методи оцінювання достовірності моделей та її параметрів;
- методи розрахунків основних статистичних характеристик із застосуванням ПЕОМ.
При вивченні навчальної дисципліни звертається увага на:
- Ознайомлення студентів з основами математичного апарату, необхідного для розв‘язання теоретичних і практичних задач, пов‘язаних з економікою.
- Розвиток логічного мислення та підвищення загального рівня математичної культури.
- Здобуття навичок статистичного дослідження прикладних питань та уміння перевести задачу на математичну мову.
- Формування навичок самостійного вивчення учбової літератури з теорії ймовірностей та математичної статистики.
- Застосуванню отриманих знань для аналізу, моделювання і розв‘язання прикладних задач із застосуванням комп’ютерної техніки
Предмет: кількісні та якісні методи та засоби аналізу закономірностей еволюції систем прикладного напряму, що розвиваються в умовах стохастичної невизначеності.
Змістовні модулі: Теорія ймовірностей, її основні поняття. Залежні та незалежні події. Основні формули обчислення ймовірностей. Моделі повторних випробувань. Випадкові величини та їх числові характеристики. Функції розподілу випадкових величин. Закон великих чисел. Багатомірні випадкові величини. Основи математичної статистики. Статистична оцінка параметрів розподілу. Елементи теорії кореляції.
Місце у структурно-логічній схемі: після вивчення – Вищої математики, передує вивченню – математичне програмування, Дослідження операцій, Статистика, Економетрія.
- РОЗПОДІЛ НАВЧАЛЬНОГО ЧАСУ
Розподіл годин за семестрами і видами навчальних занять здійснюється відповідно до робочих навчальних планів.
ІІ. РОЗПОДІЛ НАВЧАЛЬНОГО ЧАСУ ЗА МОДУЛЯМИ, ТЕМАМИ І ВИДАМИ ЗАНЯТЬ
| Номер і назва модуля, тематика занять | Всього годин | Види занять кількість годин | ||
| Лекції (год) | Практичні і лабораторні заняття (год) | Позааудиторна самостійна робота студента (год.) | ||
| І і ІІ семестри | ||||
| Елементи теорії ймовірностей. | ||||
| | 36 | 2 | 2 | 32 |
| Тема 1.1. Вступ. Основні поняття теорії ймовірностей. | 8 | 2 | | 6 |
| Тема 1.2. Поняття залежності і незалежності випадкових подій. Умовна ймовірність та її властивості. Формула повної ймовірності та формула Байєса. | 6 | | | 6 |
| Тема 1.3. Визначення повторних незалежних спроб. Асимптотичні формули для формул Бернуллі. | 6 | | | 6 |
| Тема 1.4. Випадкова величина. Дискретні та неперервні випадкові величини, закони їх розподілу. | 8 | | 2 | 6 |
| Тема 1.5. Числові характеристики випадкових величин. | 8 | | | 8 |
| Елементи математичної статистики. | ||||
| | 36 | 2 | 2 | 32 |
| Тема 2.1. Математична теорія вибірки. | 10 | 2 | | 8 |
| Тема 2.2. Точкові оцінки параметрів. Інтервальні статистичні оцінки. | 10 | | 2 | 8 |
| Тема 2.3. Статистична перевірка гіпотез. | 8 | | | 8 |
| Тема 2.4. Основи теорії кореляції. | 8 | | | 8 |
| Усього | 72 | 4 | 4 | 64 |
| Залік | 2 | | | |
III.НАВЧАЛЬНО-МЕТОДИЧНА КАРТА ДИСЦИПЛІНИ
| № | Номери і назви модулів, тем, лекцій, їх зміст (мета вивчення, провідна ідея, основні проблеми, ключові поняття), тема, мета, короткий зміст практичних семінарських занять | Кількість навчальних годин | Назва, короткий зміст питань, винесених на позааудиторне самостійне опрацювання | Кількість навчальних годин |
| | Зимова сесія | | ||
| | Лекція 1: Вступ. Основні поняття теорії ймовірностей. Залежні та незалежні випадкові події. Основні формули множення і додавання ймовірностей. Мета: Показати роль і місце теорії ймовірностей у науці і техніці, дати основні поняття. Дати означення залежних і незалежних випадкових подій. Розглянути формули множення і додавання ймовірностей. Зміст: Поняття теорії ймовірностей та ії основні поняття. Залежні і незалежні випадкові події, основні формули множення і додавання ймовірностей.. | 2 | Предмет теорії ймовірностей. Короткі відомості про виникнення і розвиток теорії ймовірностей. Елементи комбінаторики (перестановки, розміщення, сполучення). Випадкові події. Операції над подіями. Класичне означення ймовірності. Геометричні ймовірності. Ймовірність появи події принаймні один раз. Формула повної ймовірності. Теорема гіпотез (формула Байєса). Повторні незалежні випробування. Формула Бернуллі. Локальна і інтегральна теореми Муавра-Лапласа Теорема Пуассона. | 18 |
| | Лекція 2: Математична теорія вибірки. Мета: Дати означення генеральної та вибіркової сукупності, розглянути вибірковий метод. Зміст: Генеральна та вибіркова сукупності. Числові характеристики: вибіркова середня, дисперсія вибірки, середньоквадратичне відхилення, мода і медіана для дискретних і інтервальних статистичних розподілів, емпіричні початкові та центральні моменти, асиметрія та ексцес. | 2 | Предмет і задачі математичної статистики. Первинна обробка статистичних даних. Графічне зображення варіаційних рядів. Емпірична функція розподілу. Точкові оцінки параметрів. Довірчі границі для середніх. Статистичні гіпотези і критерії для їх перевірки. Критерій 2 _ Пірсона. Критерій Колмогорова. | 16 |
| | Літня сесія | | ||
| | Практичне заняття 1:Випадкова величина. Дискретні та неперервні випадкові величини, закони їх розподілу. Числові характеристики випадкових величин. Мета: Дати означення випадкової величини, функції та щільності розподілу випадкової величини. Дати означення числових характеристик випадкових величин. Зміст: Дискретні та неперервні випадкові величини, функція та щільності розподілу випадкової величини. Математичне сподівання, дисперсія та їх властивості, середнє квадратичне відхилення, мода та медіана, початкові і центральні моменти, асиметрія та ексцес. | 2 | Одномірні випадкові величини. Класифікація випадкових величин. Розподіл дискретних випадкових величин. Функція розподілу випадкової величини. Розподіл неперервних випадкових величин. Числові характеристики одновимірних випадкових величин. Математичне сподівання. Властивості математичного сподівання. Математичне сподівання неперервної випадкової величини. Дисперсія. Властивості дисперсії. Середнє квадратичне відхилення. Початкові і центральні моменти, інші числові характеристики. Мода і медіана. | 14 |
| | Практичне заняття 2:Точкові оцінки параметрів генеральної сукупності. Перевірка статистичних гіпотез. Критерії згоди Мета: Розв’язати задачі на знаходження методом моментів точкових оцінок. Розглянути загальну методику побудови правобічної, лівобічної, та двобічної критичних областей. Обчислення критерію Хі-квадрат. Зміст: Точкові оцінки параметрів різних розподілів. Обчислення критерію Хі-квадрат. | 2 | Метод найменших квадратів (загальна постановка задачі). Приклади застосування методу найменших квадратів у випадках, коли функцiя f(x) лiнiйна i коли вона виражається многочленом другого порядку. Основи теорії кореляції. Умовні математичні сподівання. Лінійна кореляція. Найкраще лінійне наближення до функції регресії. Аналіз лінійної кореляції за даними випадкової вибірки. Оцінка значимості коефіцієнта кореляції. | 16 |
| | Залік | | | |
| | Разом | 8 | | 64 |
ІІІ. ЗАВДАННЯ ДЛЯ КОНТРОЛЬНОЇ РОБОТИ
Елементи теорії ймовірностей.
| 1. а).Задано дві множини цілих чисел: 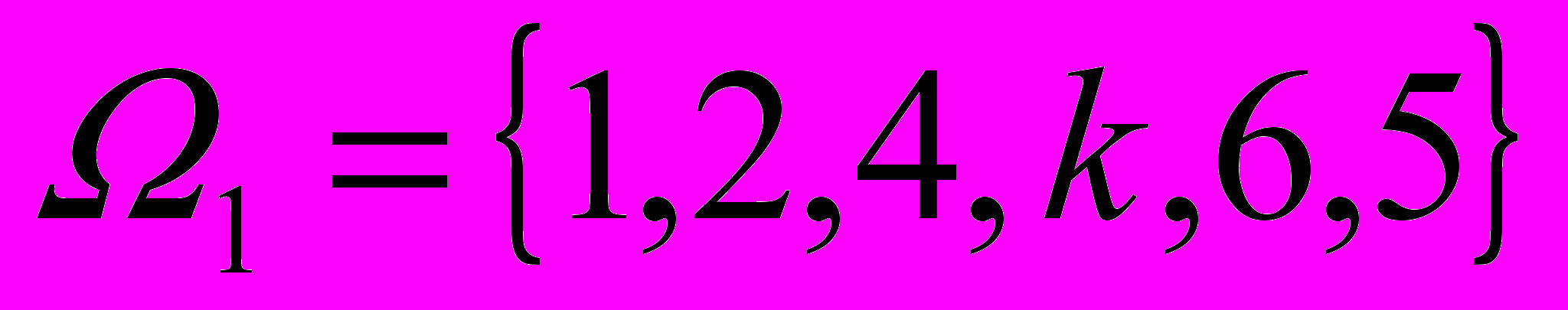 і і 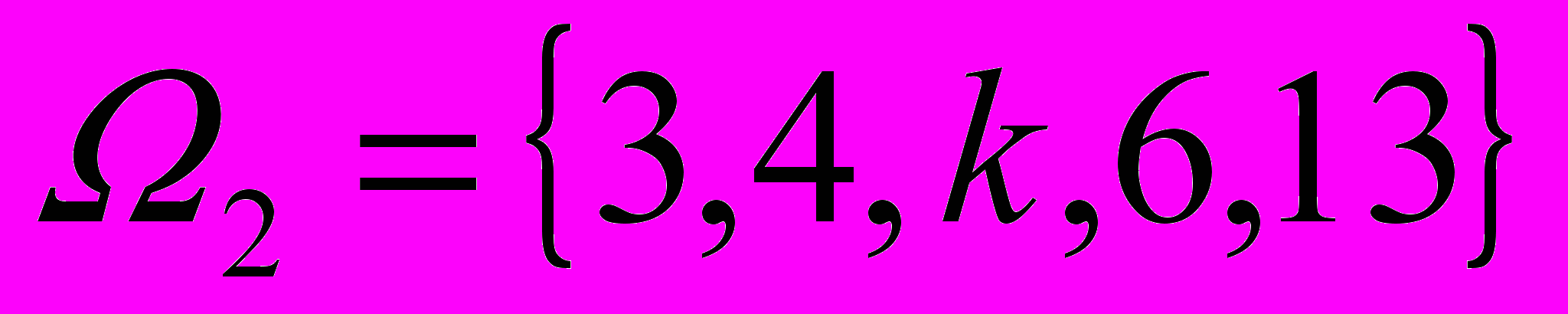 Навздогад із кожної множини береться по одному числу. Побудувати простір елементарних подій для цього експерименту і такі випадкові події: А- сума чисел кратна 7 ; В-сума чисел кратна 2. З’ясувати, чи сумісні випадкові події А і В, і обчислити 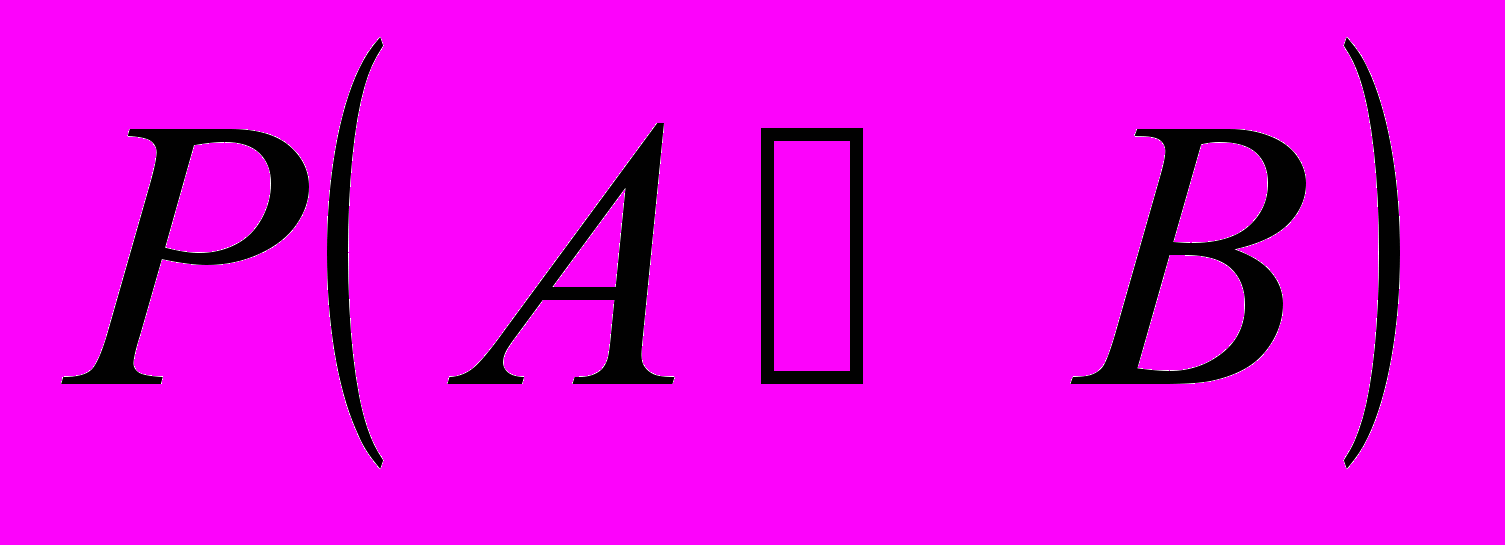 . .б).Скільки різних слів можна скласти з літер вашого: а) імені? б) прізвища? | 2. а).Нехай А, В.С – три випадкові події. Знайти вирази для подій, які полягають в тому, що з подій А,В,С:1) відбулася тільки А; 2) відбулися А і В; 3) відбулися всі три події; 4) відбулася хоча б одна з подій; 5) відбулося не менше 2 подій; 6) відбулася одна і тільки одна подія; 7) відбулися дві і тільки дві події; 8) ні одна з подій не відбулася. б). Оцінити надійність системи: 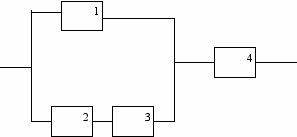 P1=0,к; P2=0,6; P3=0,7; P4=0,8. |
| 3. У урні (к+8) червоних, (к+1) синіх, 8 зелених куль однакового розміру. Навмання беруть 12 куль. Яка імовірність того, що будуть взяті 2 зелених, 2 синіх, 8 червоних кулі? | 4.Продукт виготовляється двома виробниками. Один виробляє 70%, а другий 30% всієї продукції. Перший виробник дає 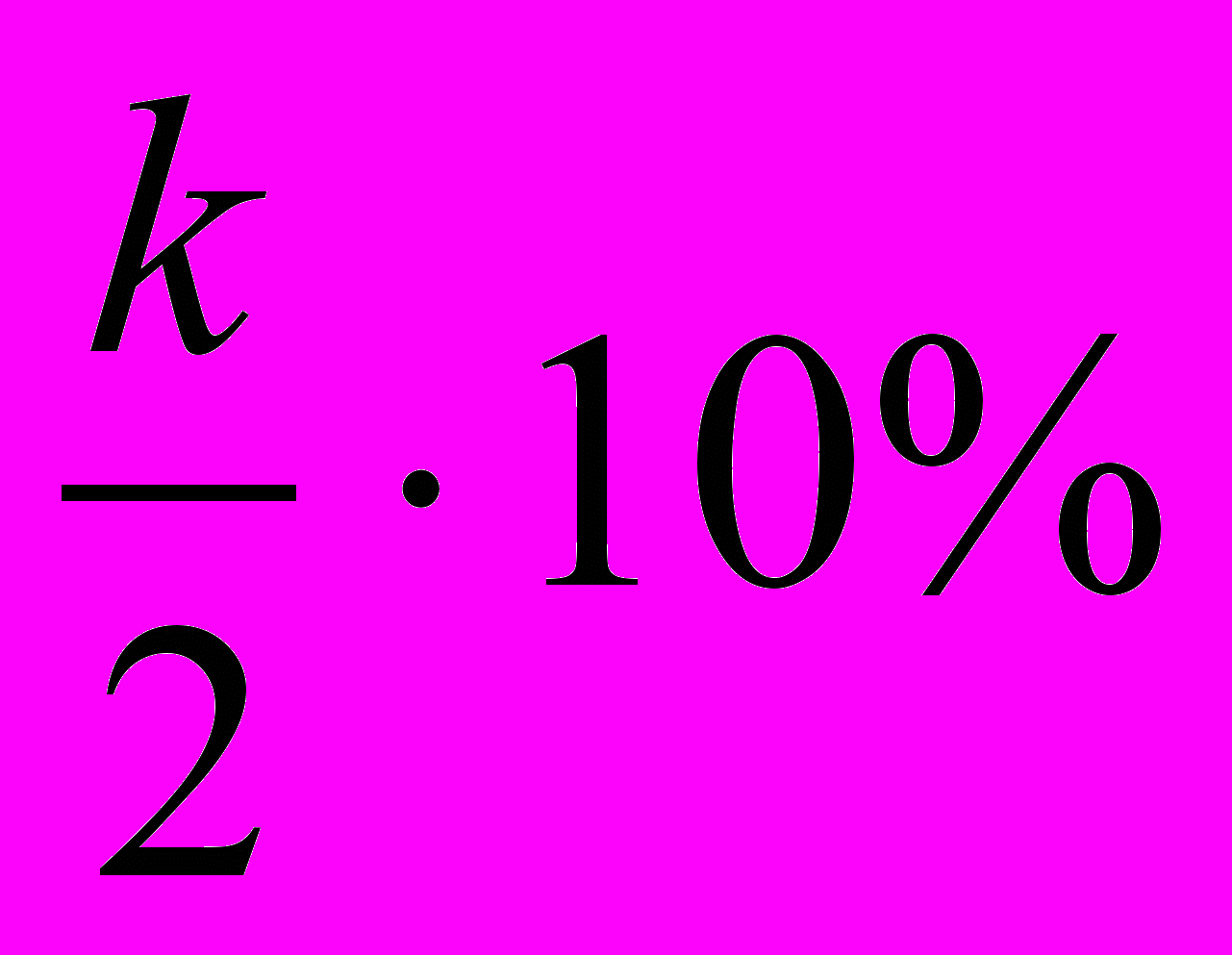 продукту І ґатунку, другий виробник – 80% продукту І ґатунку. Яка ймовірність того, що взята навмання одиниця продукції буде другого ґатунку. продукту І ґатунку, другий виробник – 80% продукту І ґатунку. Яка ймовірність того, що взята навмання одиниця продукції буде другого ґатунку. |
| 5. а). Підручник видано накладом 30000 примірників, Ймовірність того, що примірник випущено з дефектом, дорівнює 0,000к. Знайти ймовірність того, що випущений наклад містить: 1) три бракованих підручника; 2) не більше трьох бракованих підручників. б). Партія однотипних деталей містить 90% стандартних, а решта-браковані. Навмання із неї було взято 400 деталей. Яке значення повинно набути число стандартних деталей mi, щоб імовірність події (350+к | 6. За таблицею розподілу дискретної випадкової величини знайти числові характеристики, побудувати функцію розподілу та многокутник розподілу. 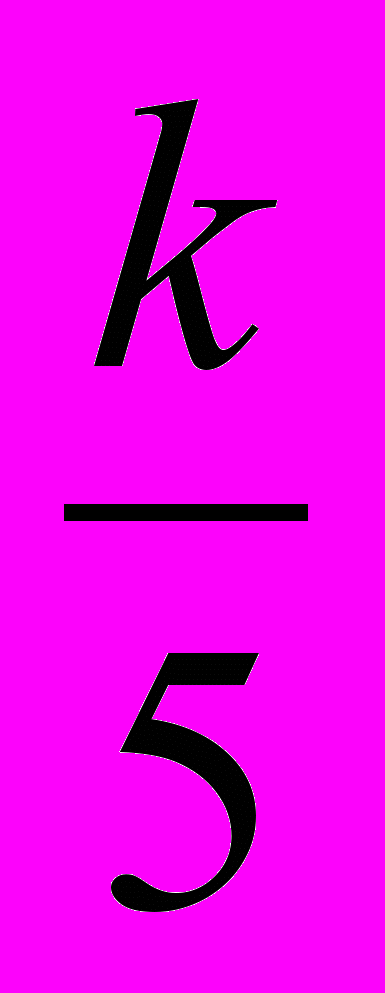 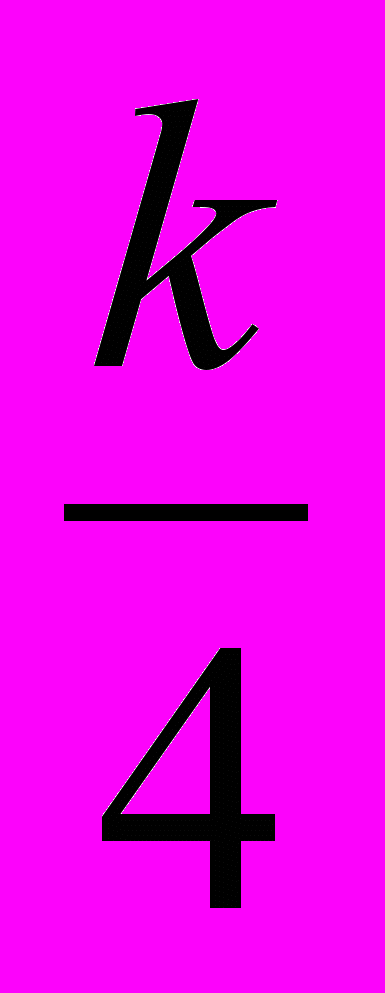 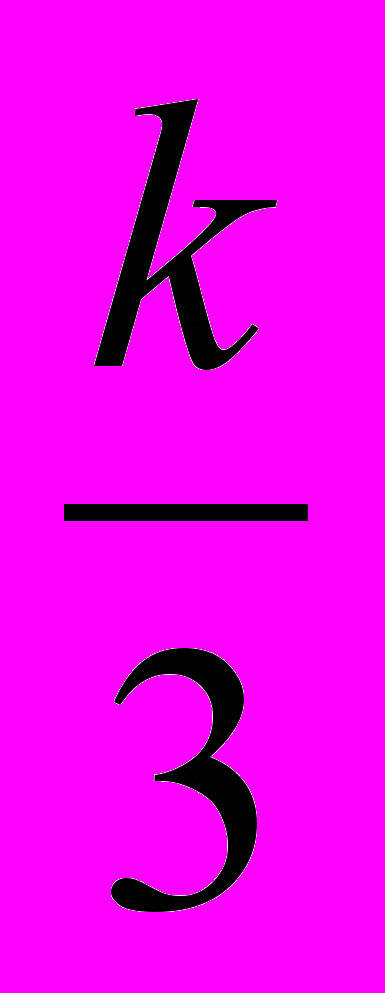 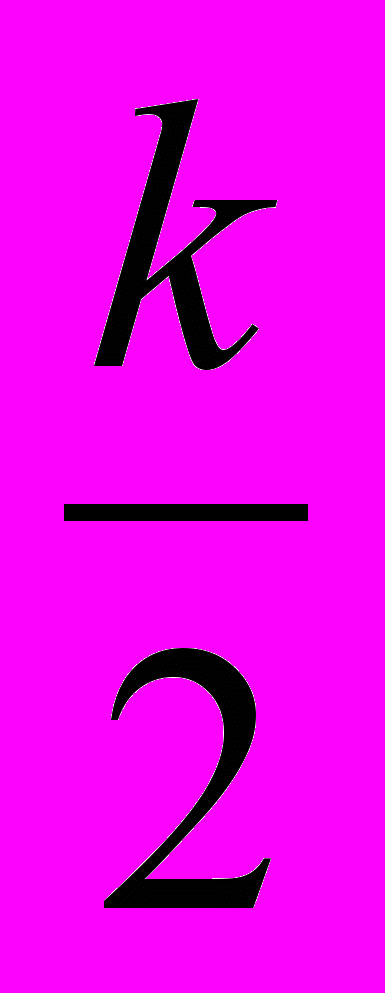 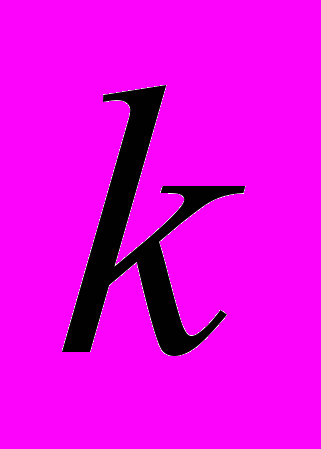 Р 0,13 0,19 0,38 0,20 0,10 |
| 7. За щільністю розподілу неперервної випадкової величини визначити невідомий коефіцієнт, знайти функцію розподілу, числові характеристики та ймовірність попадання в інтервал. Побудувати графік щільності та функції розподілу. 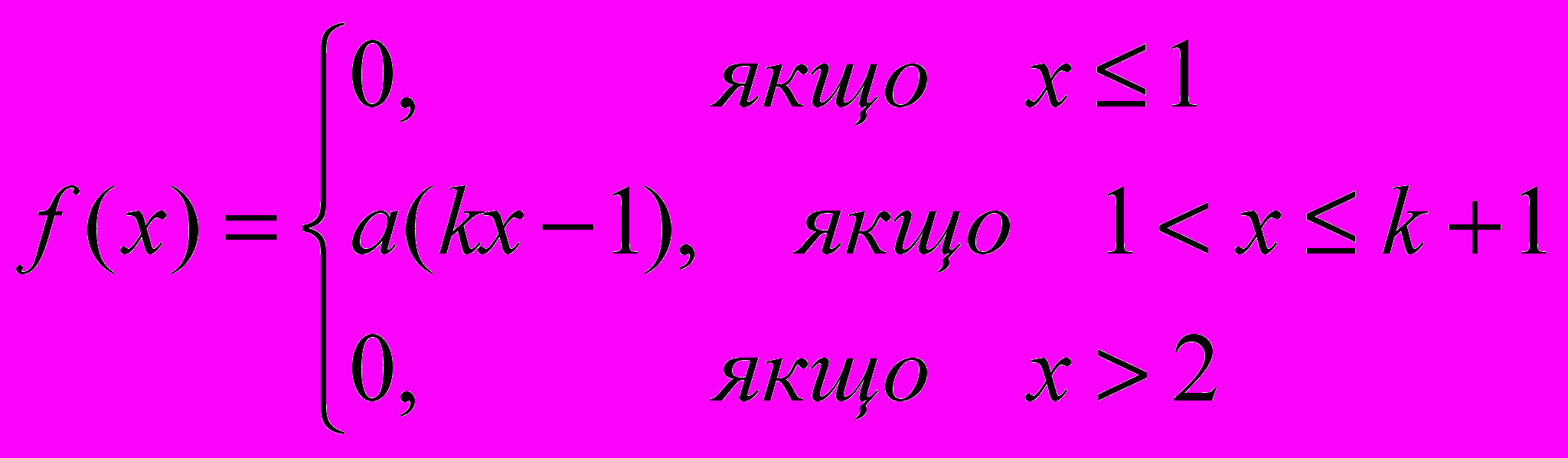 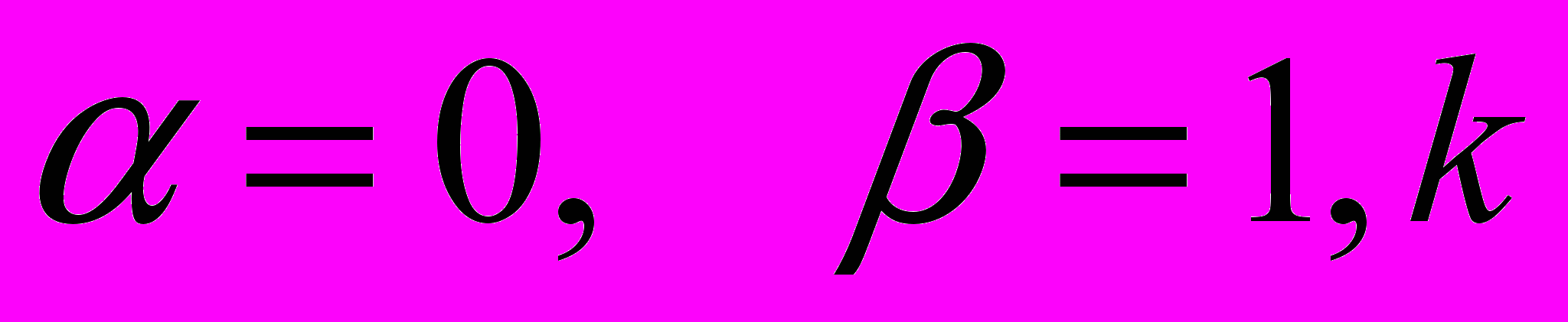 | 8. Імовірність укладання угоди за результатами ділових переговорів дорівнює 0,к. Випадкова величина ξ–число укладених угод після чотирьох ділових зустрічей. Знайти закон розподілу випадкової величини ξ, математичне сподівання Mξ, дисперсію Dξ і середнє квадратичне відхилення σξ. |
Де k-номер студента по списку у журналі групи.
Елементи математичної статистики.
У банку беруть кредит 100 підприємств. Результати вибірки (сума кредиту в тис. грн..):

Побудувати:
- Інтервальний статистичний розподіл
- Гістограму частот
- Гістограму відносних частот
- Полігон відносних частот
- Статистичний розподіл вибірки
- Визначити значення емпіричних показників

- Проаналізувати статистичні характеристики і зробити висновок про близькість розподілу до нормального
- Вирівняти експериментальні дані, використавши нормальний закон розподілу
- Використавши критерій Пірсона, зробити висновок про можливість розподілу
величин Х згідно з нормальним законом
- Побудувати довірчий інтервал для
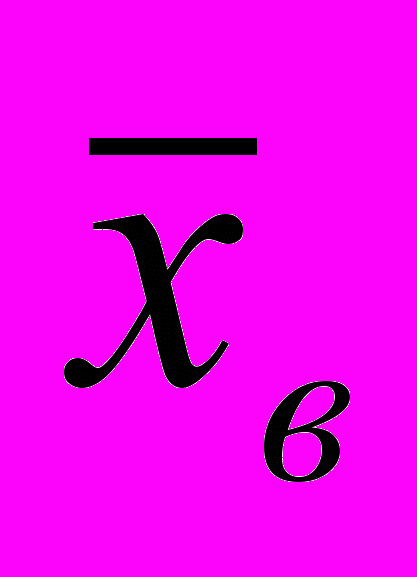 із заданою надійністю =0,95.
із заданою надійністю =0,95.
Де k-номер студента по списку у журналі групи.
ІV. Контроль рівня сформованості математичної компетенції студентів .
Залік з дисципліни “Теорія ймовірностей та математична статистики” для спеціальності 6.050200 “Менеджмент організацій”, проводиться по закінченню другого семестру.
Залік проводиться у відповідності з навчальним планом Економіко–правового інституту та робочою програмою курсу, затвердженою на засіданні кафедри інформатики та комп’ютерних технологій.
Термін часу, протягом якого виконуються письмові завдання – 2 години.
Письмове завдання білету складається з трьох блоків : двох теоретичних питань (репродуктивний і творчий рівень складності, та чотирьох практичних завдань: перші два завдання простіші (творчий рівень складності), наступні два завдання більш складні (інноваційний рівень складності).
- Теоретичні питання, включають 2 теоретичних завдання з переліку орієнтовних питань до заліку.
Об’єктом контролю виконання теоретичного завдання є перевірка засвоєння основ математичного апарату, необхідного для розв‘язання практичних задач, творчого використання знань з теорії.
Під час письмової відповіді на теоретичне питання студент повинен сформулювати основні означення і властивості, навести методи розв’язання, привести доведення основних теорем.
- Задачі репродуктивного і творчого рівня дають можливість виявити ступінь оволодіння студентом необхідним рівнем знань, охоплюють питання всіх ключових проблем предмету.
- Задачі інноваційного рівня орієнтовані на перевірку практичних умінь по використанню різноманітних методів розв’язання задач, та задачі прикладного змісту
Під час розв’язання задач студент повинен використовувати раціональну методику розв’язання та аналізу задачі і обґрунтовано пояснити одержані результати.
Критерії оцінок на письмовому заліку
Перший блок оцінюється таким чином:
“3” бала за правильну, ґрунтовну та повну відповідь, з наведенням доведення необхідних теорем.
“2” бала за правильну повну відповідь, але без доведення.
“1” бал за неповну, але правильну відповідь.
Другий блок оцінюється таким чином:
Правильне вирішення задачі з використанням необхідної методики, що супроводжується поясненням кожної дії – “2”.
Правильне вирішення задачі з використанням необхідної методики, без пояснення алгоритму завдання, або ж використання правильного підходу до вирішення задачі, пояснення кожної дії, але з помилками в розрахунках – “1”.
Третій блок оцінюється так:
Правильне вирішення задачі з використанням необхідної методики, що супроводжується поясненням кожної дії – “3”.
Правильне вирішення задачі з використанням необхідної методики, без пояснення алгоритму завдання – “2”.
Правильний кінцевий результат розв’язку задачі, проте відсутні будь-які коментарі до використаної методики, або правильний опис алгоритму розв’язання задачі, але неправильне використання деяких методів розв’язання, математичні помилки – “1”.
Загальна оцінка за письмовий залік:
- «Зараховано» від “8”-“16” балів;
- «Незараховано» до “8” балів.
Орієнтовні питання до заліку
- Предмет теорії ймовірностей. Короткі відомості про виникнення і розвиток теорії ймовірностей
- Елементи комбінаторики (перестановки, розміщення, сполучення).
- Випадкові події. Операції над подіями.
- Класичне означення ймовірності.
- Геометричні ймовірності. Ймовірність появи події принаймні один раз.
- Формула повної ймовірності. Теорема гіпотез (формула Байєса).
- Повторні незалежні випробування. Формула Бернуллі.
- Локальна і інтегральна теореми Муавра-Лапласа
- Теорема Пуассона.
- Одномірні випадкові величини. Класифікація випадкових величин
- Розподіл дискретних випадкових величин.
- Функція розподілу випадкової величини.
- Розподіл неперервних випадкових величин.
- Числові характеристики одновимірних випадкових величин. Математичне сподівання. Властивості математичного сподівання.
- Математичне сподівання неперервної випадкової величини.
- Дисперсія. Властивості дисперсії. Середнє квадратичне відхилення.
- Початкові і центральні моменти, інші числові характеристики. Мода і медіана.
- Основні дискретні розподіли випадкових величин.
- Біноміальний розподіл. Розподіл Пуассона. Геометричний розподіл.
- Основні неперервні розподіли випадкових величин. Рівномірний розподіл.
- Експоненціальний (показниковий) розподіл.
- Нормальний розподіл.
- Властивості функції Лапласа
- Граничні теореми теорії ймовірностей. Лема Маркова.
- Теорема і нерівність Чебишева
- Теореми Бернуллі і Пуассона
- Поняття про центральну граничну теорему. Теорема Ляпунова
- Предмет і задачі математичної статистики
- Первинна обробка статистичних даних
- Графічне зображення варіаційних рядів
- Емпірична функція розподілу
- Точкові оцінки параметрів
- Довірчі границі для середніх
- Статистичні гіпотези і критерії для їх перевірки
- Критерій 2 _ Пірсона
- Критерій Колмогорова
- Метод найменших квадратів (загальна постановка задачі).
- Приклади застосування методу найменших квадратів у випадках, коли функцiя f(x) лiнiйна i коли вона виражається многочленом другого порядку.
- Основи теорії кореляції. Умовні математичні сподівання
- Лінійна кореляція
- Найкраще лінійне наближення до функції регресії
- Аналіз лінійної кореляції за даними випадкової вибірки. Оцінка значимості коефіцієнта кореляції
Зразок
залікового білету
- Теоретичні питання.
1). Випадкова величина її закони розподілу .
2). Точкові статистичні оцінки: зміщені і незміщені, ефективні і грунтовні.
- Практичні завдання І-го рівня:
1). Скільки різних слів можна скласти з літер вашого: а) імені? б) прізвища?
2). Середнє число викликів, що надходять на АТС за одну хвилину, дорівнює двом. Яка імовірність того, що за дві хвилини на АТС надійде:
- два виклики;
- не більше двох; хоча б один.
- Практичні завдання ІІ-го рівня:
1). Партія однотипних деталей містить 90% стандартних, а решта-браковані. Навмання із неї було взято 400 деталей. Яке значення повинно набути число стандартних деталей mi, щоб імовірність події (4
2).За рівнем значущості =0,01 перевірити гіпотезу про нормальний розподіл генеральної сукупності, якщо відомі емпіричні та теоретичні частоти:
| nk | 8 | 16 | 40 | 72 | 36 | 18 | 10 |
| nk * | 6 | 18 | 36 | 76 | 39 | 18 | 7 |
V. Навчально-методичні матеріали з дисципліни
5.1. Основна література
- Соколенко О.І. Вища математика: Підручник.-К.: Видавничий центр “Академія”,2002.-432с. (Альма-матер)
- Бугір М.К. Посібник з теорії ймовірностей та математичної статистики.-Тернопіль: Підручники і посібники, 1998.-176с.
- Черняк О.І., Обушна О.М., Ставицький А.В. Теорія ймовірностей та математична статистика: Збірник задач: Навч. Посіб.-К.: Т-во “Знання”, КОО,2001.-199с.- (Вища освіта ХХI століття)
5.2. Додаткова література
- Гмурман В.Е. Теория вероятностей и математическая статистика. - М.: Высш. шк., 1998.- 479 с.
- Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. - М.: Высш. шк., 1999.- 400 с.
- Вентцель Е. С., Овчаров Л. А. Прикладные задачи теории вероятностей, 1983.
- Феллер В. Введение в теорию вероятностей и ее приложения. Т. 1, 2. 1984.
5.3. Засоби навчання
Технічною базою для вивчення курсу є локальна мережа ІBM-сумісних ПК з процесорами класу Pentіum ІІІ, дисплеями SVGA, твердими дисками обсягом 10 Гб, дисководом для оптичних дисків.
Програмне забезпечення. Під час виконання контрольної роботи рекомендується використовувати: операційне середовище Wіndows 2000, Пакет Mathcad.
