Лекция №2/2: «Решение тригонометрических уравнений методом приведения к квадратному»
| Вид материала | Лекция |
- Конспект урока. Тема урока. Функционально-графические методы при решении тригонометрических, 66.13kb.
- Методы решения тригонометрических уравнений, 53.9kb.
- "Решение тригонометрических уравнений", 94.47kb.
- Решение алгебраических уравнений высоких степеней. Решение нелинейных уравнений методом, 9.13kb.
- План занятия элективного курса в 10 классе по теме: «Решение тригонометрических уравнений,, 39.39kb.
- Учебного заведения, 120.64kb.
- Основные методы решения тригонометрических уравнений, 22.36kb.
- Неравенств и, если «да», то найдите общее решение и частное решение двумя способами:, 11.47kb.
- Решение систем нелинейных алгебраических уравнений, 20.84kb.
- План конспект па алгебре и началам анализа в 10 классе Тема урока: Тригонометрические, 109.55kb.
Лекция № 2/2: «Решение тригонометрических уравнений методом приведения к квадратному ».
Рассмотрим решение данного вида уравнений на примерах.
1) 2 sin2x – 5 sin x + 2 = 0;
Введем новую переменную sin x = t;
 .
.Запишем уравнение в новом виде.
2 t2 -5 t + 2 =0;
Решаем квадратное уравнение:
D = b2 – 4 ac = (-5)2 – 4
 = 25-16 = 9.
= 25-16 = 9.t 1,2 =
 =
= 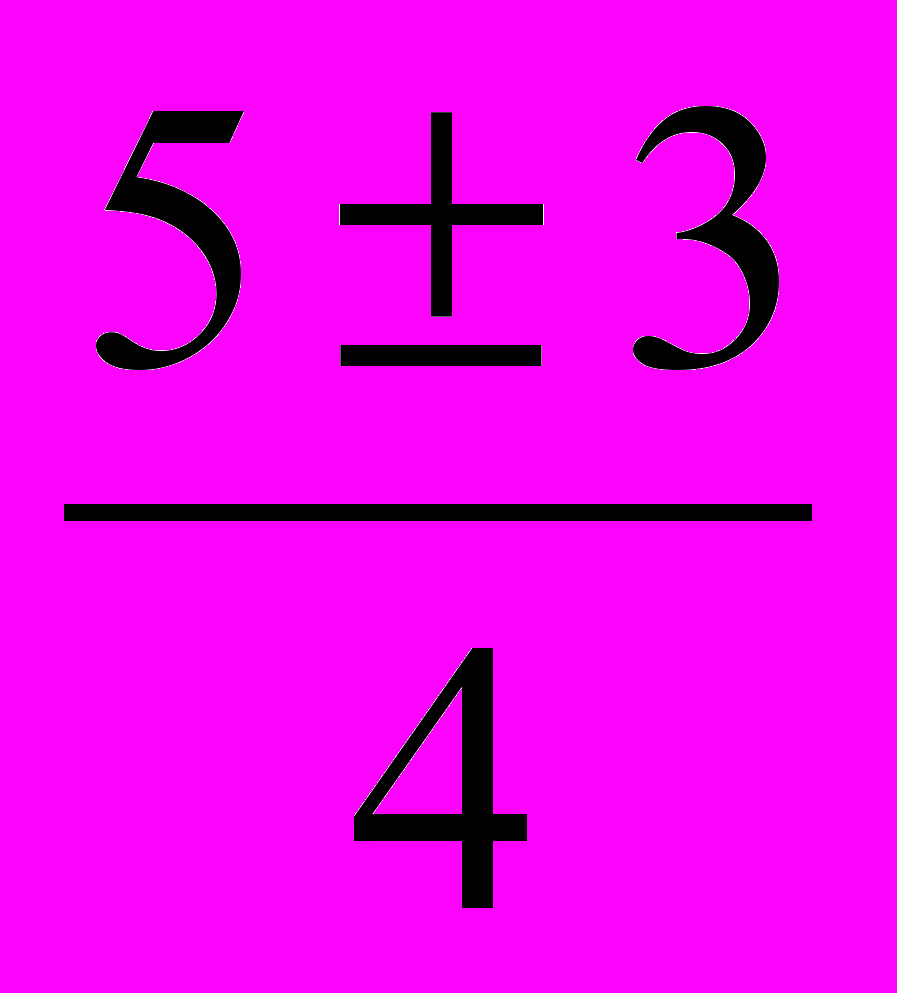 ;
;t1= 2, не удовлетворяет условие;
t2 =
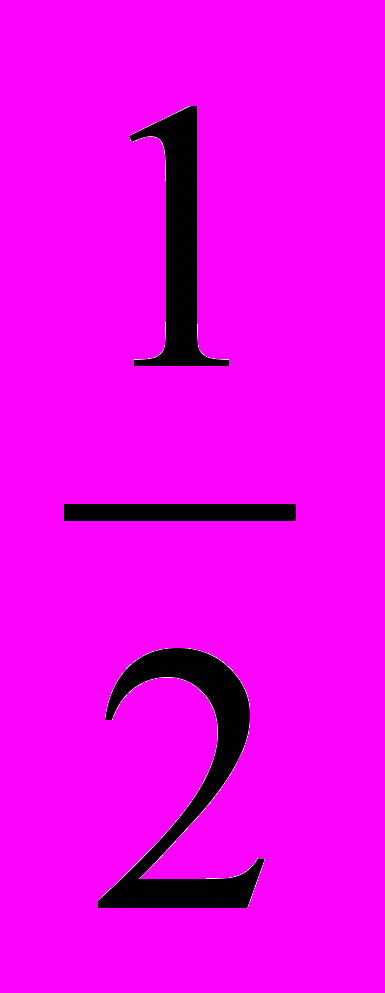 .
.Решаем уравнение замены:
sin x =
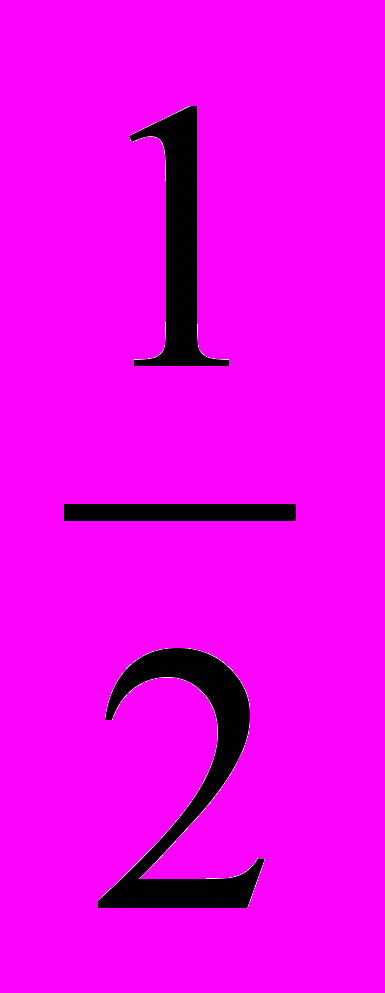 ;
;x = (-1)n arcsin
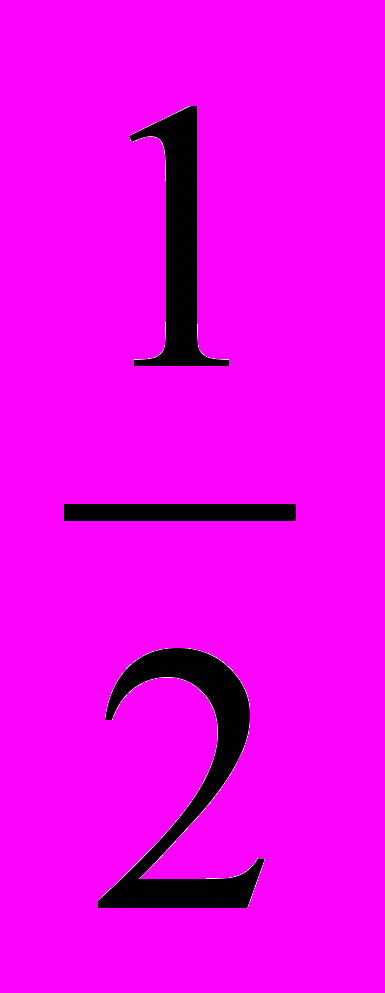 +
+  n,
n,x = (-1)n
 +
+  n, n
n, n 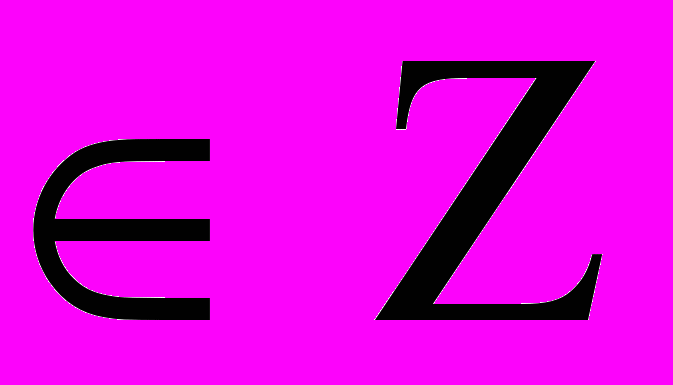 .
.Ответ: x = (-1)n
 +
+  n, n
n, n 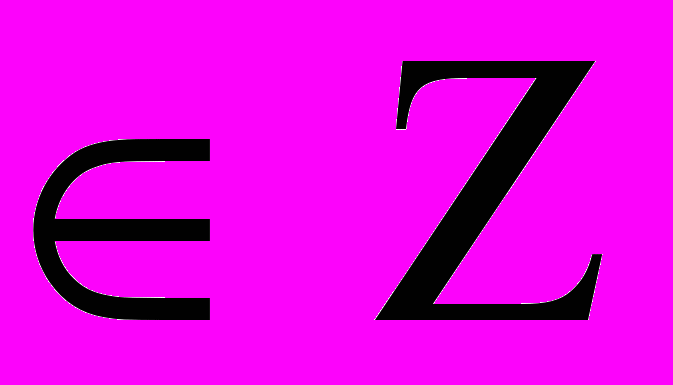 .
.2) 2 cos2 x + 3 sin2 x + 2 cos x = 0;
Произведем замену: из основного тригонометрического тождества следует: sin2 x = 1 – cos2 x.
2 cos2 x + 3 (1 – cos2 x) + 2cos x = 0;
2 cos2 x + 3 - 3 cos2 x + 2 cos x = 0;
- cos2 x + 2 cos x + 3 = 0;
cos x = t;
 .
.D = b2 – 4 ac = 22 – 4
 = 4 + 12 = 16;
= 4 + 12 = 16;t1 =
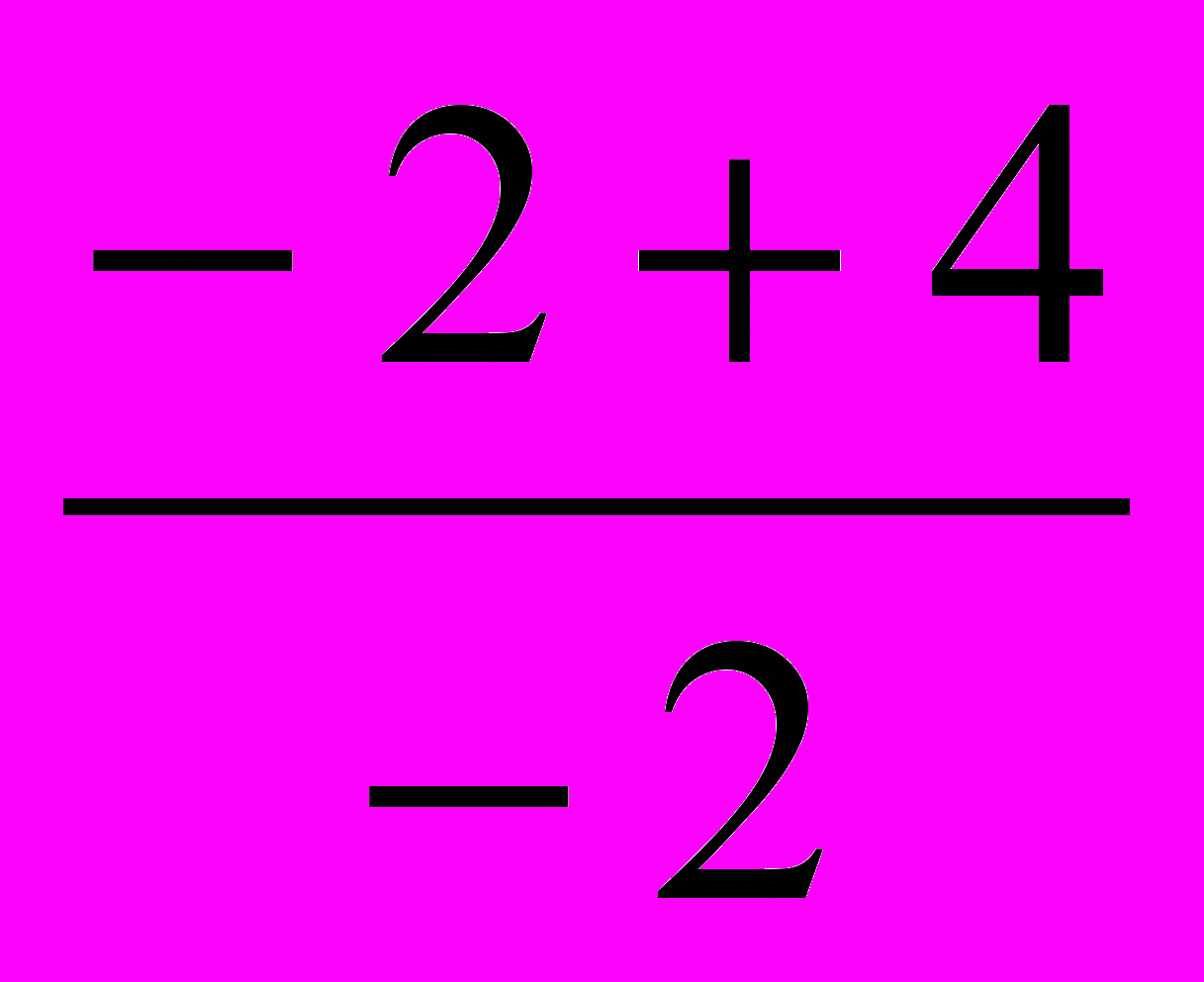 = -1;
= -1;t2 =
 = 3, не удовлетворяет условие.
= 3, не удовлетворяет условие.cos x = -1; ( частный случай)
x =
 , n
, n 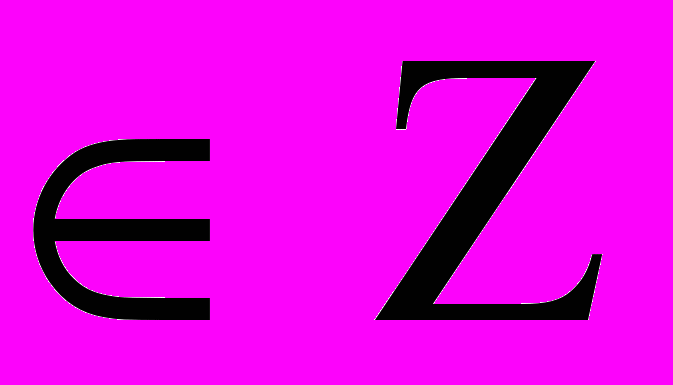 .
.Ответ: x =
 , n
, n 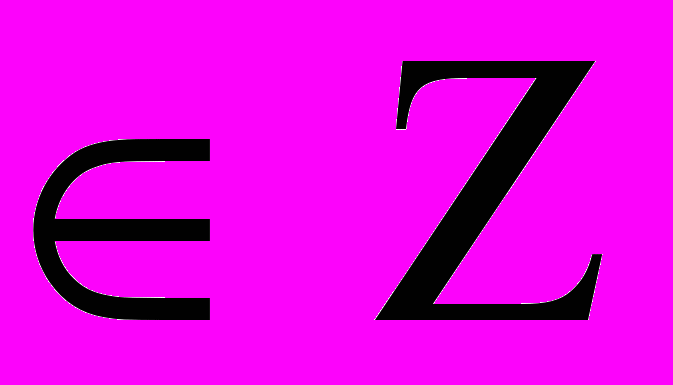 .
.x =
 , n
, n 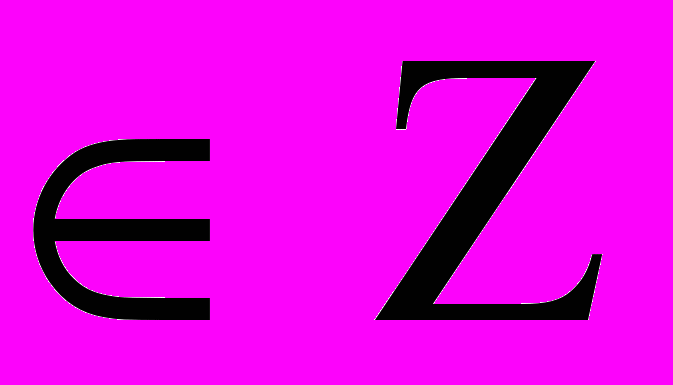 .
.Задания для самостоятельной работы:
- 8 sin2 x – 6 sin x -5 =0;
- 8 cos2 x + 6 sin x – 3 =0;
- sin2 x – 2 sin x -3 =0;
- cos2 x -2 cos x -3 = 0;
- 2 sin2 x +3 cos2 x + 2 sin x =0.
Лекция 2/3 « Решение однородных тригонометрических уравнений уравнений».
Определение: Уравнение называется однородным, если все слагаемые, входящие в его состав одной степени.
ПРИМЕР:
x2y + y3 -4 xy2 =0- это однородное уравнение третьей степени.
Рассмотрим примеры однородных тригонометрических уравнений.
1) 2 sin2 x - 5 sin x cos x + 3 cos2 x =0;
Решаются однородные тригонометрические уравнения путем деления всех слагаемых на косинус в степени уравнения. Т. к. данное однородное уравнение второй степени, то делить его нужно на cos2 x.
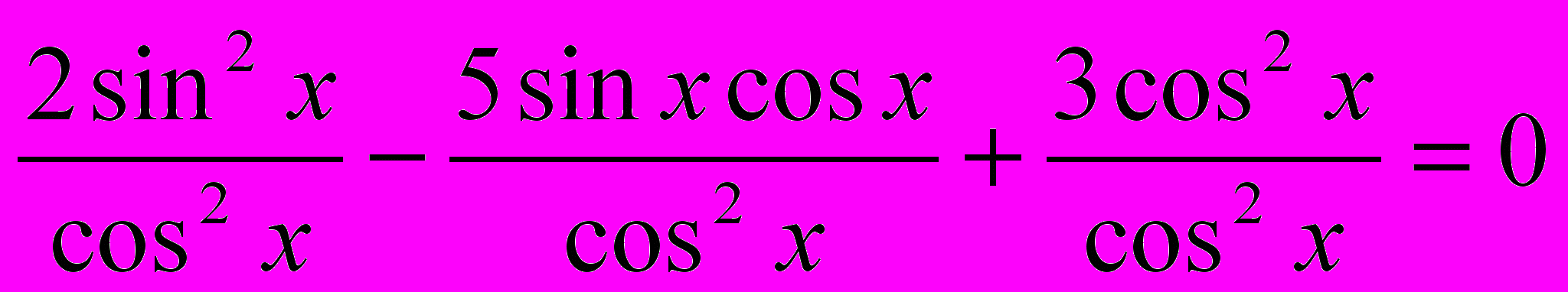 ;
;2 tg2x – 5 tg x + 3 =0;
tg x = t.
2 t2 -5 t + 3 =0;
t1 = 1; t2 = 1,5.
tg x = 1;
x1 = arctg 1+
 n, n
n, n ;
;x1 =
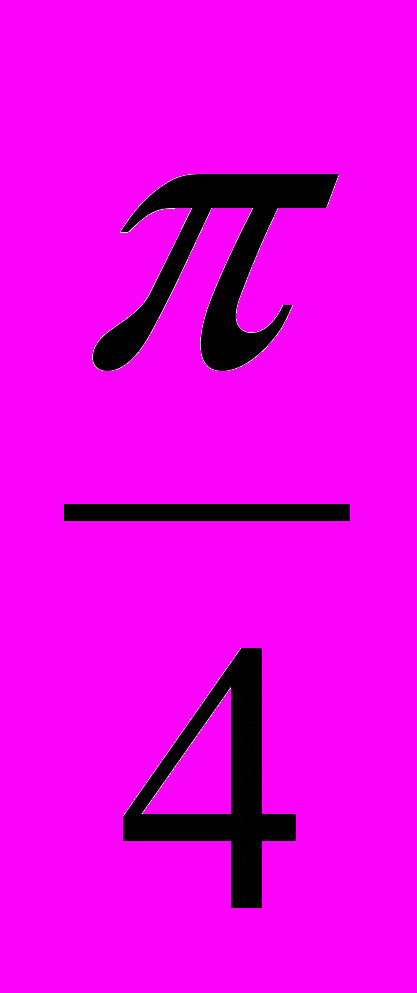 +
+ n, n
n, n .
.tg x = 1,5;
x2 = arctg 1,5 +
 n, n
n, n .
.Ответ: x1 =
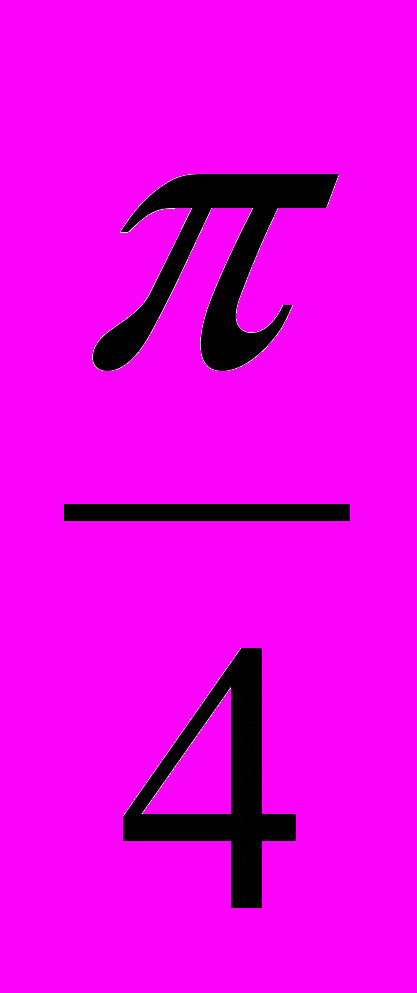 +
+ n, n
n, n . x2 = arctg 1,5 +
. x2 = arctg 1,5 + n, n
n, n .
.- 22 cos2 x + 8 sin x cos x =7.
На первый взгляд это уравнение не является однородным, однако, если мы представим 7= 7
 = 7(cos2 x + sin2 x), это уравнение станет однородным.
= 7(cos2 x + sin2 x), это уравнение станет однородным.22 cos2 x + 8 sin x cos x =7(cos2 x + sin2 x);
22 cos2 x + 8 sin x cos x -7cos2 x -7sin2 x =0;
Приведите подобные слагаемые и доделайте уравнение по предыдущему алгоритму.
Задания для самостоятельной работы:
- sin2 x +2 sin x cos x – 3 cos2 x =0;
- sin2 x – 3 sin x cos x + 1 =0;
- 5sin2 x – 4 cos x sin x + 3 cos2 x = 2.
