Исследование эффективности реализации численных методов на кластерах персональных ЭВМ

Вид материала

Исследование

Содержание 3.4. Общая схема программы 3.5. Генерирование исходных данных 3.6. Последовательный алгоритм Метод штрафов

Подобный материал:

• Рабочей программы дисциплины «Численные методы и программирование» по направлению подготовки, 29.72kb.
• Решение физических задач на эвм" Лекции 20 ч. Практические занятия 96 ч. Учебная, 40.03kb.
• «Исследование и сопоставительный анализ численных методов решения задач не линейного, 321.81kb.
• Автономность эксплуатации без специальных требований к условиям окружающей среды, 258.87kb.
• Тема: «Интеграл» (заключительный урок), 49.41kb.
• Рабочая программа по разделу «Численные методы в строительстве», 71.92kb.
• На первой лекции мы рассмотрим общий смысл понятий бд и субд, 65.83kb.
• Лекция №7. Атрибутивная информация Лекция №7. Атрибутивные данные в гис, 283.92kb.
• Пояснительная записка к курсовой работе по предмету «Языки и технологии программирования», 353.31kb.
• Д. А. Силаев 1/2 года  Физическое явление и математическая модель. Математическое исследование, 20.76kb.

3.4. Общая схема программы

Программа, реализующая алгоритмы вычисления решения транспортной задачи, написана на языке C++ в полном соответствии со спецификацией стандарта MPI. Таким образом, она (программа) является платформенно-независимым приложением, и не должно возникнуть никаких проблем при запуске на каком-либо кластере (при условии, что для платформы существует компилятор языка C++).

Для написания исходных текстов программного комплекса была использована IDE (интегрированная среда разработки, integrated development environment, IDE) Microsoft Visual Studio 6.0.

Программа представляет собой проект, который включает в себя 3-x модуля:

• Модуль генерации начальных данных;
  
• Модуль, реализующий последовательную версию алгоритма решения транспортной задачи (метод минимального элемента, метод северо-западного угла, метод штрафов, метод потенциалов);
  
• Модуль, реализующий параллельную версию алгоритма решения транспортной задачи.
  

Логическая схема программы:



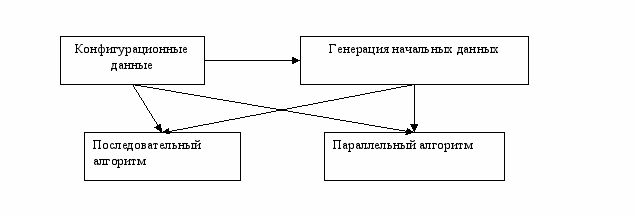
рис. 11


Конфигурационные данные представляют собой текстовый файл. В нем можно определить значения некоторых переменных (минимальный или максимальный размер пакета, передаваемого от корневого процесса рабочему за один раз; имена файлов). Они (конфигурационные данные) являются глобальными и влияют на работу всех модулей.

Для наглядности приведем блок-схемы модулей и поясним суть связей, возникающих между ключевыми функциональными элементами. Под ключевыми функциональными элементами подразумеваются классы, которые подключаются в ходе выполнения программы.

3.5. Генерирование исходных данных

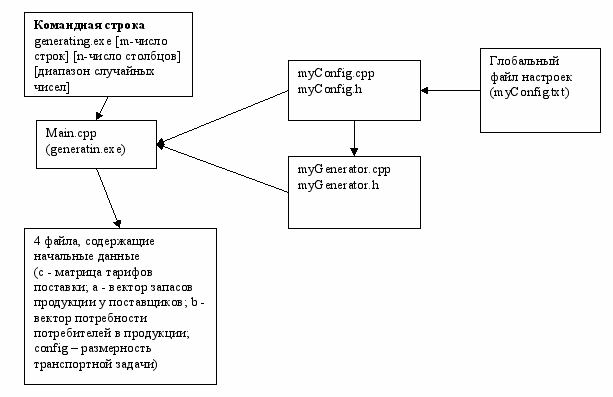
рис. 12


Этот модуль предназначен для создания исходных данных. В контексте транспортной задачи таковыми являются:

• Матрица тарифов поставок;
  
• Вектор запасов продукции у поставщиков;
  
• Вектор потребностей продукции у поставщиков;
  
• Размерность задачи
  

Нужно отметить, что генерируются псевдослучайные числа, так как генератор случайных чисел компьютера работает относительно системного времени операционной системы.

При запуске exe-файла модуля (generating.exe) генерирования из командной строки необходимо задавать следующие параметры:

• Размерность задачи (число строк и столбцов);
  
• Диапазон псевдослучайных чисел;
  

В результате получаем: матрицу тарифов поставок (размерность – m*n), вектор запасов продукции у поставщиков (размерность – m*1), вектор потребностей продукции у поставщиков (размерность – 1*n) и файл содержащий значения m и n.

3.6. Последовательный алгоритм

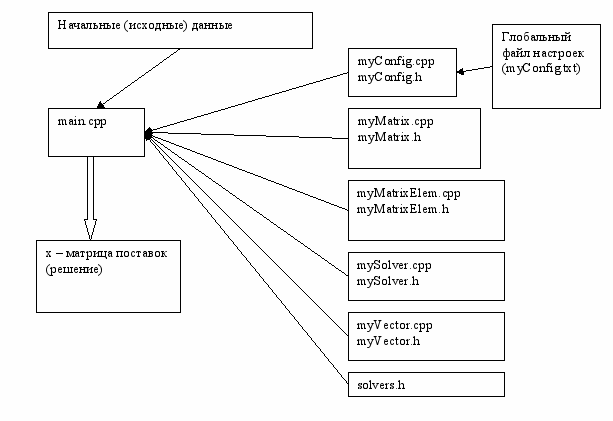
рис. 13


Данный модуль, реализует последовательную версию алгоритма решения транспортной задачи.

В состав модуля входит 5 классов:

• myConfig (осуществляет чтение конфигурационных данных)
  
• myMatrix (класс матрица)
  
• myMatrixElem (класс элемент матрицы)
  
• mySolver (решатель)
  
• myVector (класс вектор)
  

При отладке промежуточные результаты выводились не только на экран. Они также могут сохраняться в файл. Например, класс матрица имеет метод myMatrix::writeMatrix();

Приведем блок-схему последовательного алгоритма решения транспортной задачи методом потенциалов.



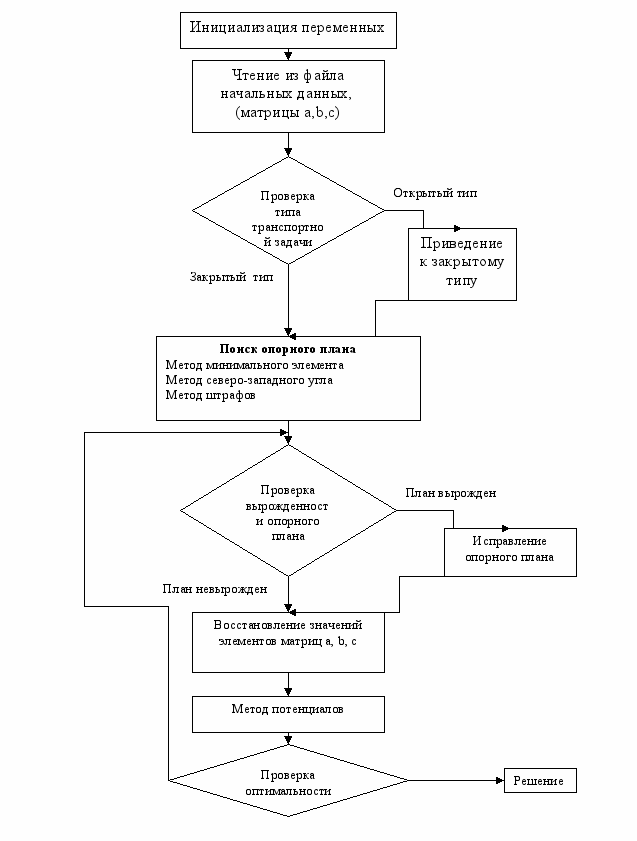
рис. 14


Рассмотрим подробнее методы нахождения опорного плана:

Метод северо-западного угла:

1. Строится нулевая матрица размером n*m.
   
2. Начиная с северо-западного угла в естественном порядке осуществляется заполнение матрицы.
   
3. Заполнение осуществляется по следующему правилу:
   Для каждого элемента выбирается минимальное число из соответствующих ему значений вектора производства и потребления.
   
4. Это минимальное число вычитается из соответствующих данному элементу значений векторов производства и потребления.
   Так как при корректировке один из элементов, либо а, либо b, становится равным нулю, то соответствующая строка или столбец исключаются в дальнейшем из рассмотрения.
   
5. Процесс заполнения продолжается до тех пор, пока все элементы векторов производства и потребления не станут равными нулю.
   
6. Проверяется вырожденность полученного плана.
   

Метод минимальной стоимости:

1. Строится нулевая матрица размером n*m.
   
2. Производится индексирование матрицы стоимости в порядке возрастания.
   
3. Согласно индексам, полученным на предыдущем этапе производится заполнение элементов опорного плана. При этом элементы и правила коррекций вычисляются также как и метод северо-западного угла.
   
4. Процесс заполнения продолжается до тех пор, пока все элементы векторов производства и потребления не станут равными нулю.
   
5. Проверяется вырожденность полученного плана.
   

В ходе тестирования алгоритма было отмечено, что при индексации отсутствует правило в присвоении индекса к матрице стоимости.

К положительным моментам данного метода можно отнести то, что он дает лучший опорный план нежели метод северо-западного угла.


Метод штрафов:

1. Штрафы для строки или столбца представляют положительную разницу между минимальным элементом строки (столбца) и следующим за ним по величине минимальным элементом строки или столбца.
   
2. Рассчитываются штрафы для всех строк и столбцов матрицы.
   
3. Заполнение опорного плана начинается с минимального элемента строки или столбца с максимальным штрафом.
   
4. Выбор элементов плана Х и коррекция векторов потребления и постановок осуществляется, как рассмотрено выше (1-ый и 2-ой метод)
   
5. Строка или столбец матрицы С, которым соответствует нулевое значение потребности или поставки при дальнейшем вычислении не участвуют в формировании штрафов. Процесс продолжается до тех пор, пока не обнулятся все вектора.
   

В ходе тестирования было замечено, что в данном методе отсутствует правило выбора альтернативы при равенстве штрафов.

Рассмотрим подробнее построение оптимального плана транспортной задачи с помощью метода потенциалов.

Опорный план невырожден, если количество ненулевых Х_ij равно (m + n – 1).

Затем для Х_ij > 0 составляется система уравнений:



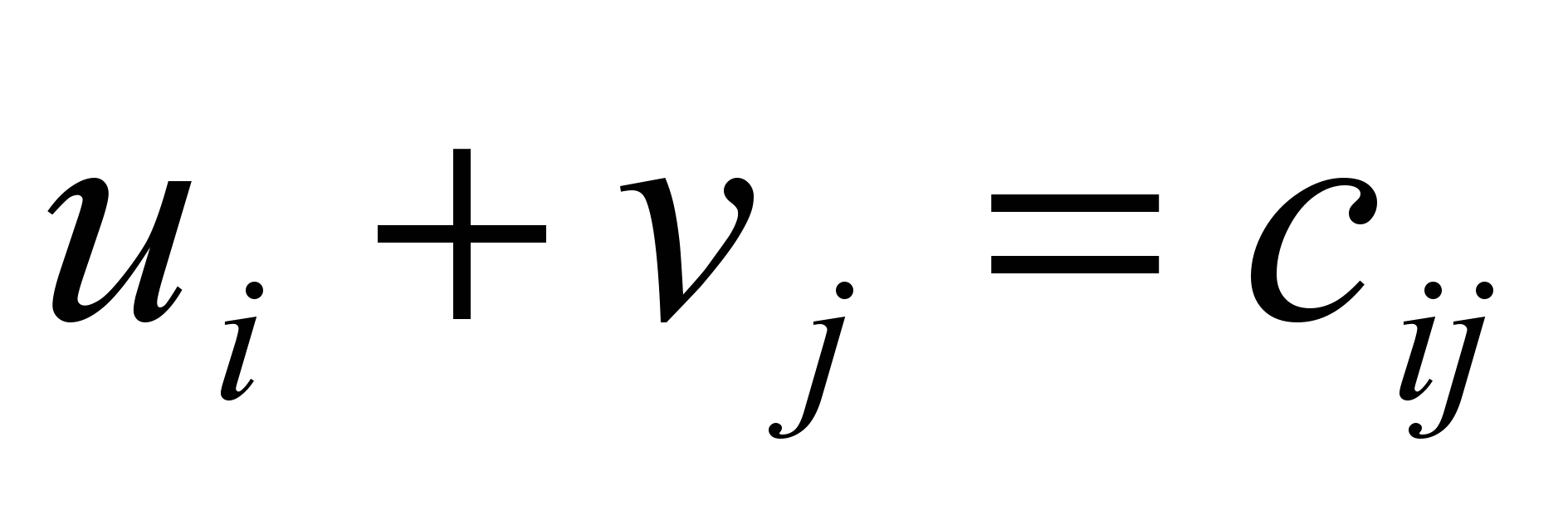
рис. 15


Неизвестные u_i, v_j называются индексами (потенциалами).


Поскольку в системе (рис. 15) количество уравнений на единицу больше числа неизвестных, то одному неизвестному надо присвоить произвольное значение (обычно 0). Система (рис. 15) решается последовательной подстановкой полученных значений в следующие уравнения.

После решения системы (рис. 15) для свободных клеток таблицы определяют потенциалы:



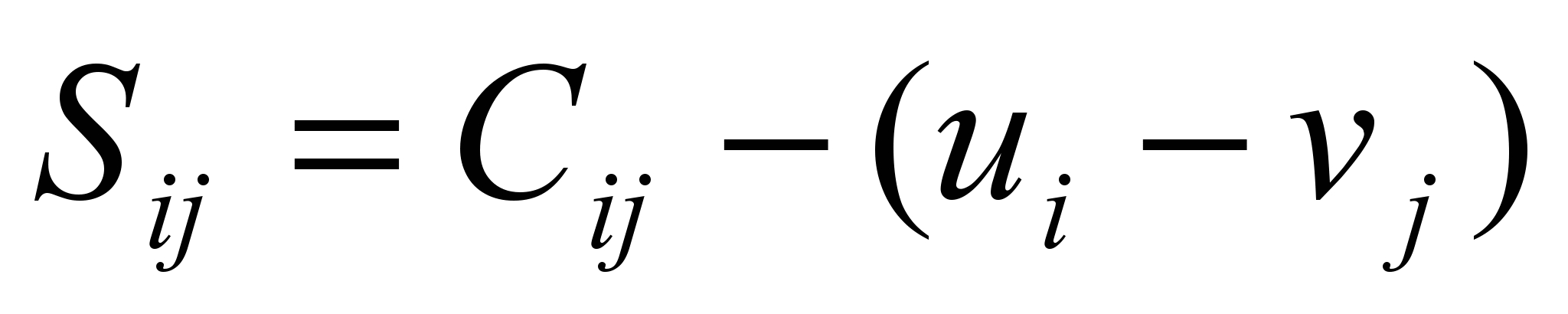
рис. 16


Если все S_ij > 0, то полученный план является оптимальным.

Иначе выбирают клетку с минимальным S_ij < 0.

Hачиная с выбранной клетки матрицы перевозок, стоится замкнутый прямоугольный цикл (цепочка, коммуникация) с вершинами в заполненных клетках (в том числе символом 0 ).

Выбранной клетке присваивается знак «+», следующей вершине цикла по (или против) часовой стрелке – знак «–», далее «+»,«–», и т.д. по циклу. Данная цепочка знаков обязательно заканчивается знаком «–». Цепочка называется вырожденной, если она состоит из одного элемента.

Среди клеток цикла, отмеченных знаком «–», выбирается клетка с наименьшим значением переменной Х_ij, затем из нагрузки клеток, отмеченных знаком «–», вычитают это значение, а клетки, отмеченных знаком «+», прибавляют это значение. Получают новый опорный план, который проверяют на невырожденность и в случае необходимости выполняют переход к невырожденному.

После этого заново строится система уравнений (рис. 15).

При реализации алгоритма построения замкнутой цепочки в способ описанном ранее чувствуется громоздкость. Поэтому было принято решение использовать более подходящий аналог:

Цепочка строится следующим образом. Начиная со строк матрицы Х вычеркиваются те из них, в которых один не нулевой элемент. Подобную операцию повторяют затем по столбцам, следом по строкам и т.д.
В результате проведенной процедуры не вычеркнутыми оказываются элементы, которые составляют цепочку. Цепочка замкнута, содержит четное число элементов и строится, начиная от базового элемента, безразлично в каком направлении, по ходу ладьи в шахматах. При этом элементы, стоящие на нечетных местах помечаются минусом, а на четных - плюсом.