Исследование эффективности реализации численных методов на кластерах персональных ЭВМ

Вид материала

Исследование

Содержание 1.3. Интерфейс параллельного программирования ГЛАВА 2. Эффективность реализации численных методов 2.1 Метод формульного анализа масштабируемости (ФАМ)

Подобный материал:

• Рабочей программы дисциплины «Численные методы и программирование» по направлению подготовки, 29.72kb.
• Решение физических задач на эвм" Лекции 20 ч. Практические занятия 96 ч. Учебная, 40.03kb.
• «Исследование и сопоставительный анализ численных методов решения задач не линейного, 321.81kb.
• Автономность эксплуатации без специальных требований к условиям окружающей среды, 258.87kb.
• Тема: «Интеграл» (заключительный урок), 49.41kb.
• Рабочая программа по разделу «Численные методы в строительстве», 71.92kb.
• На первой лекции мы рассмотрим общий смысл понятий бд и субд, 65.83kb.
• Лекция №7. Атрибутивная информация Лекция №7. Атрибутивные данные в гис, 283.92kb.
• Пояснительная записка к курсовой работе по предмету «Языки и технологии программирования», 353.31kb.
• Д. А. Силаев 1/2 года  Физическое явление и математическая модель. Математическое исследование, 20.76kb.

1.3. Интерфейс параллельного программирования

Наиболее распространенным интерфейсом параллельного программирования в модели передачи сообщений является MPI (Message Passing Interface). Рекомендуемой бесплатной реализацией MPI является пакет MPICH [13] , разработанный в Аргоннской национальной лаборатории США.

Во многих организациях имеются локальные сети компьютеров с соответствующим программным обеспечением. Если такую сеть снабдить бесплатной реализацией MPI, т. е. пакетом MPICH, то без дополнительных затрат получается Beowulf-кластер, сравнимый по мощности с супер-ЭВМ. Это является причиной широкого распространения таких кластеров [1].

Система программирования MPI относится к классу МКМД ЭВМ с индивидуальной памятью, то есть к многопроцессорным системам с обменом сообщениями. MPI имеет следующие особенности:

• MPI − библиотека, а не язык. Она определяет имена, вызовы процедур и результаты их работы. Программы, которые пишутся на FORTRAN, C, и C++ компилируются обычными компиляторами и связаны с MPI–библиотекой.
  
• MPI − описание, а не реализация. Все поставщики параллельных компьютерных систем предлагают реализации MPI для своих машин как бесплатные, и они могут быть получены из Интернета. Правильная MPI-программа должна выполняться на всех реализациях без изменения.
  
• MPI соответствует модели многопроцессорной ЭВМ с передачей сообщений.
  

В модели передачи сообщений процессы, выполняющиеся параллельно, имеют раздельные адресные пространства. Связь происходит, когда часть адресного пространства одного процесса скопирована в адресное пространство другого процесса. Эта операция совместная и возможна только когда первый процесс выполняет операцию передачи сообщения, а второй процесс − операцию его получения.

Процессы в MPI принадлежат группам. Если группа содержит n процессов, то процессы нумеруются внутри группы номерами, которые являются целыми числами от 0 до n-l. Имеется начальная группа, которой принадлежат все процессы в реализации MPI.

Понятия контекста и группы объединены в едином объекте, называемом коммуникатором. Таким образом, отправитель или получатель, определенные в операции посылки или получения, всегда обращается к номеру процесса в группе, идентифицированной данным коммуникатором.

В MPI используются коллективные операции, которые можно разделить на два вида:

• операции перемещения данных между процессами. Самый простой из них – широковещание (broadcasting), MPI имеет много и более сложных коллективных операций передачи и сбора сообщений;
  
• операции коллективного вычисления (минимум, максимум, сумма и другие, в том числе и определяемые пользователем операции).
  

В обоих случаях библиотеки функций коллективных операций строятся с использованием знания о преимуществах структуры машины, чтобы увеличить параллелизм выполнения этих операций.

Часто предпочтительно описывать процессы в проблемно-ориентированной топологии. В MPI используется описание процессов в топологии графовых структур и решеток.

В MPI введены средства, позволяющие определять состояние процесса вычислений, которые позволяют отлаживать программы и улучшать их характеристики.

Программы MPI могут выполняться на сетях машин, которые имеют различные длины и форматы для одного и того же типа datatype, так что каждая коммуникационная операция определяет структуру и все компоненты datatype. Следовательно, реализация всегда имеет достаточную информацию, чтобы делать преобразования формата данных, если они необходимы. MPI не определяет, как эти преобразования должны выполняться, разрешая реализации производить оптимизацию для конкретных условий.

Процесс есть программная единица, у которой имеется собственное адресное пространство и одна или несколько нитей. Процессор − фрагмент аппаратных средств, способный к выполнению программы. Некоторые реализации MPI устанавливают, что в программе MPI всегда одному процессу соответствует один процессор; другие − позволяют размещать много процессов на каждом процессоре.

Если в кластере используются SMP–узлы (симметричная много-процессорная система с множественными процессорами), то для организации вычислений возможны два варианта:

• Для каждого процессора в SMP-узле порождается отдельный MPI-процесс. MPI-процессы внутри этого узла обмениваются сообщениями через разделяемую память (необходимо настроить MPICH соответствующим образом).
  
• На каждой узле запускается только один MPI-процесс. Внутри каждого MPI-процесса производится распараллеливание в модели "общей памяти", например с помощью директив OpenMP.
  

Чем больше функций содержит библиотека MPI, тем больше возможностей представляется пользователю для написания эффективных программ.

ГЛАВА 2. Эффективность реализации численных методов

2.1 Метод формульного анализа масштабируемости (ФАМ)

Масштабируемость – это свойство системы (задача + кластер), сохранять вычислительную эффективность при увеличении размера задачи или размеров кластера. Предельные значения параметров, при которых величина ускорения R все еще остается приемлемой, называются диапазоном масштабируемости [5].

Эффективность вычислений на кластере определяется сетевым законом Амдала:



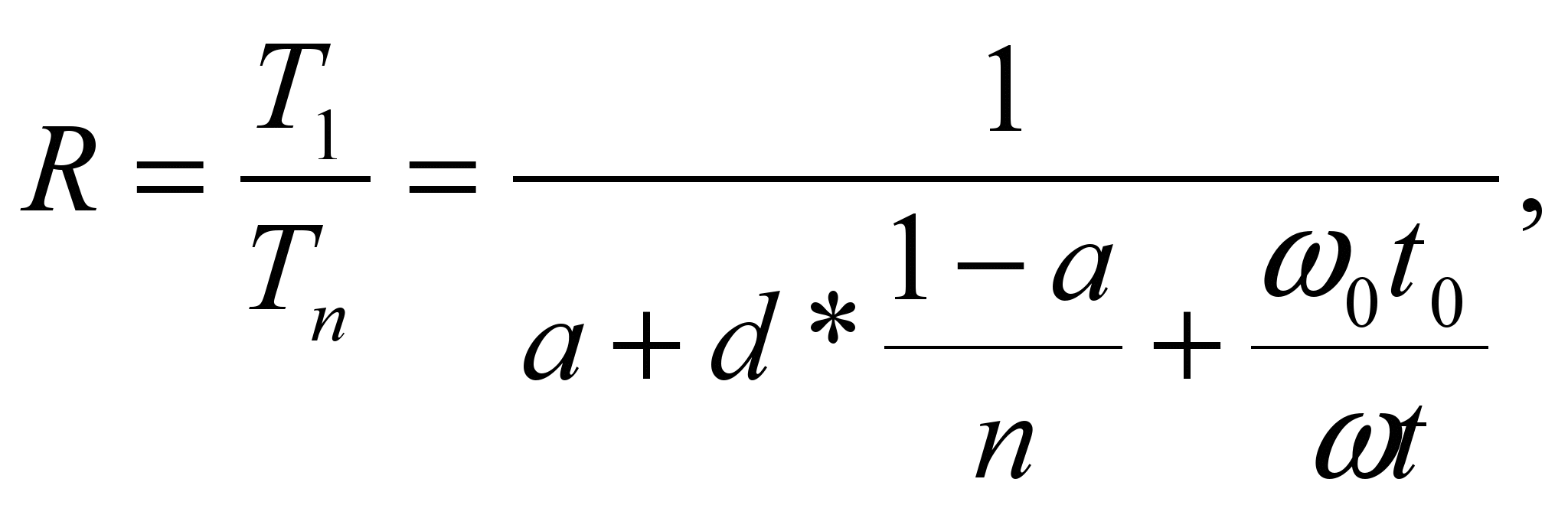
рис. 1


Здесь: R – ускорение вычислений, T₁ и T_n – время выполнения одной и той же задачи на однопроцессорной и n – процессорной системе, a – удельный вес не распараллеливаемых операций, d – коэффициент дисбаланса, и 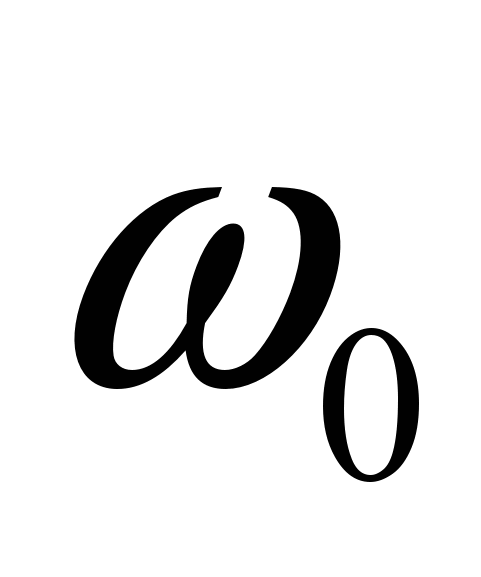– общее количество операций в задаче и количество операций обмена, t и to – время выполнения одной вычислительной операции и одной операции обмена Очевидно, что с увеличением размера задачи и числа процессоров удельный вес операций обмена 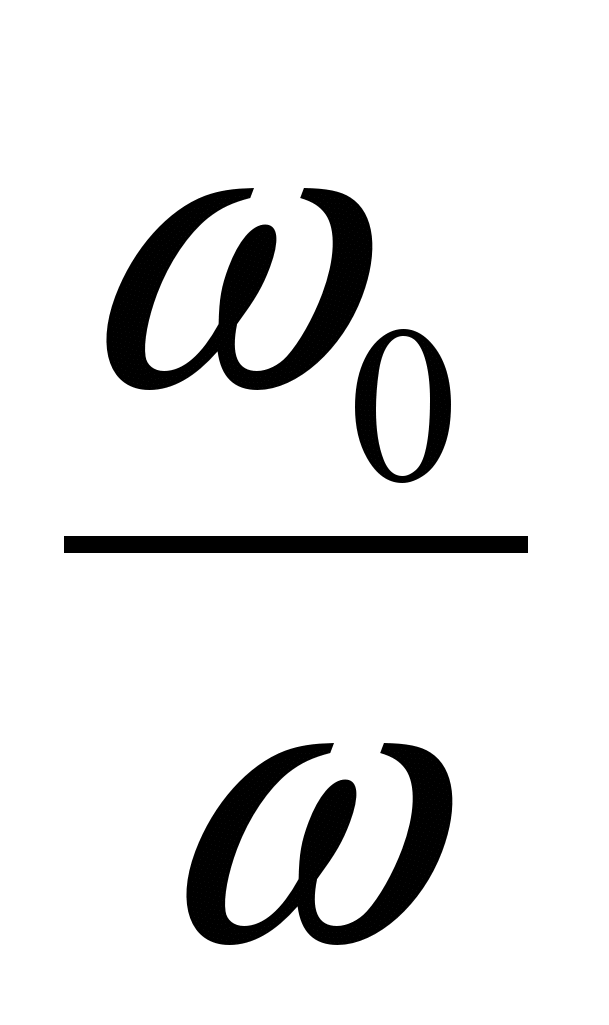и удельный вес одной операции обмена 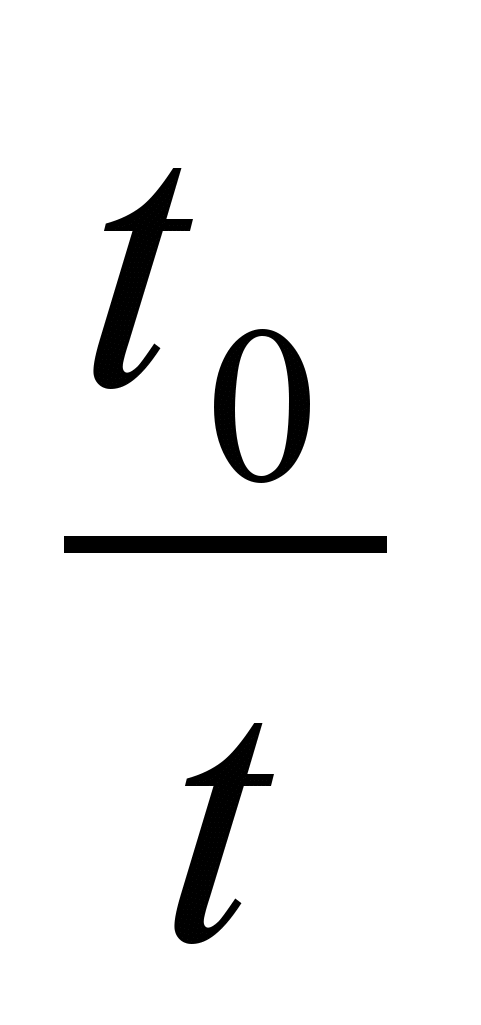возрастают и, соответственно, уменьшается значение R. Величина этого уменьшения характеризует масштабируемость задачи.

Закон Амдала можно представить и в такой форме:



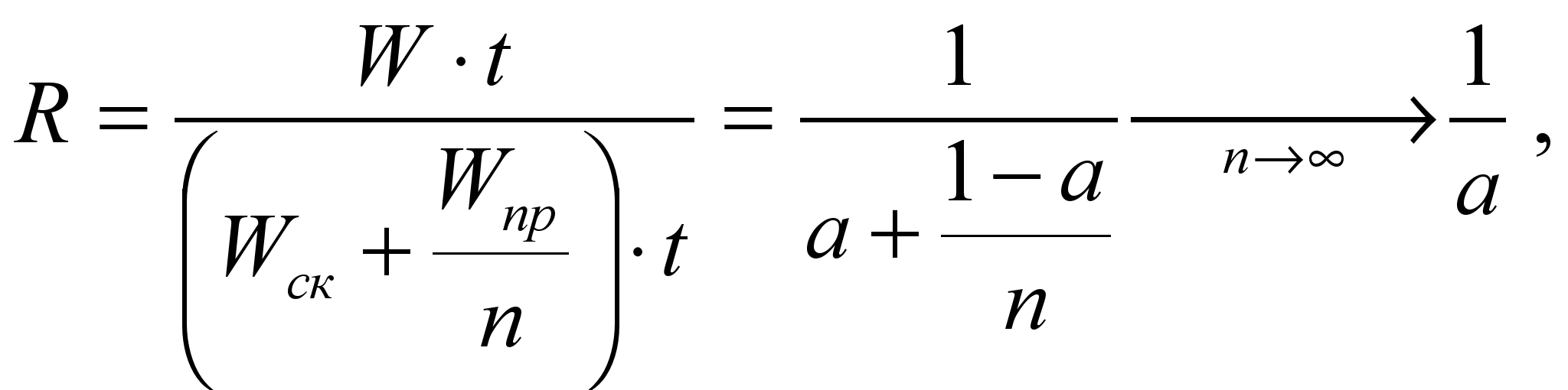
рис. 2

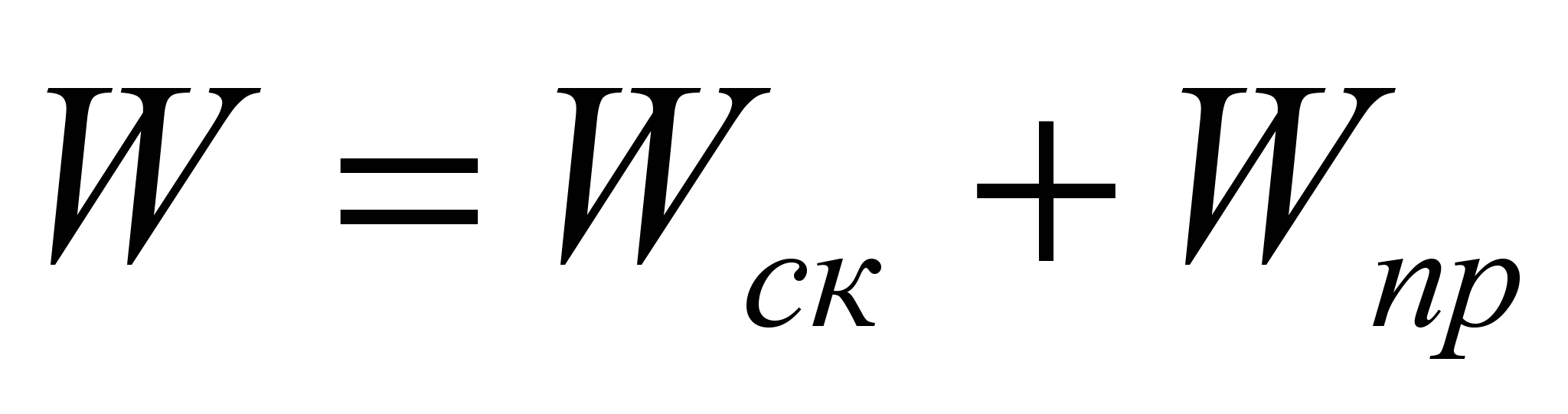где , где 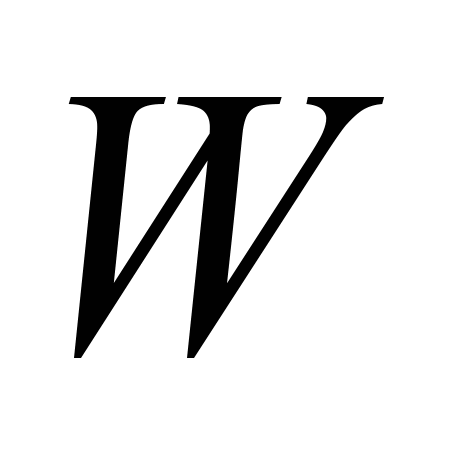- общее число операций в задаче, 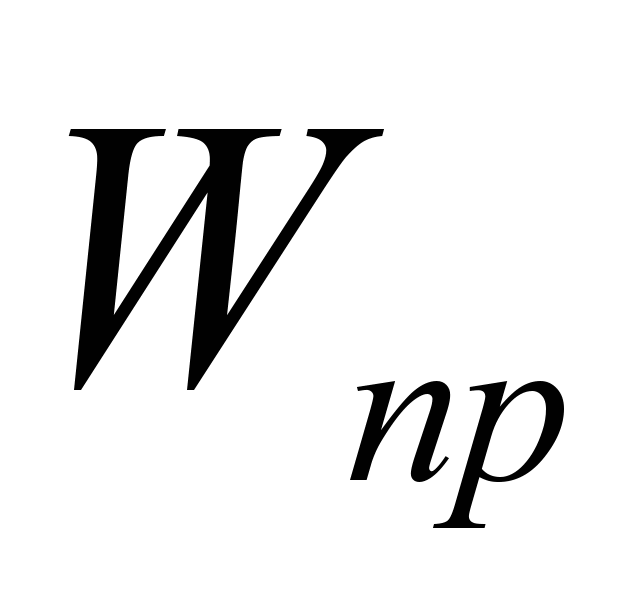- число операций, которые можно выполнить параллельно, 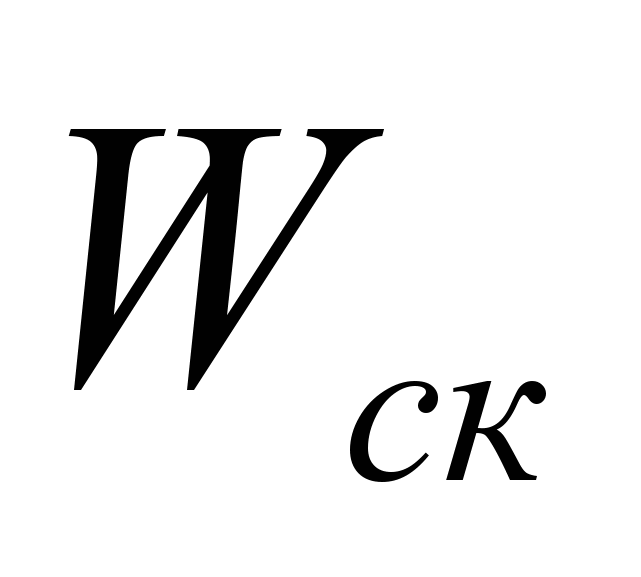- число скалярных (не распараллеливаемых) операций, 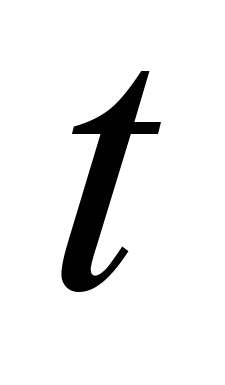− время выполнения одной операции, 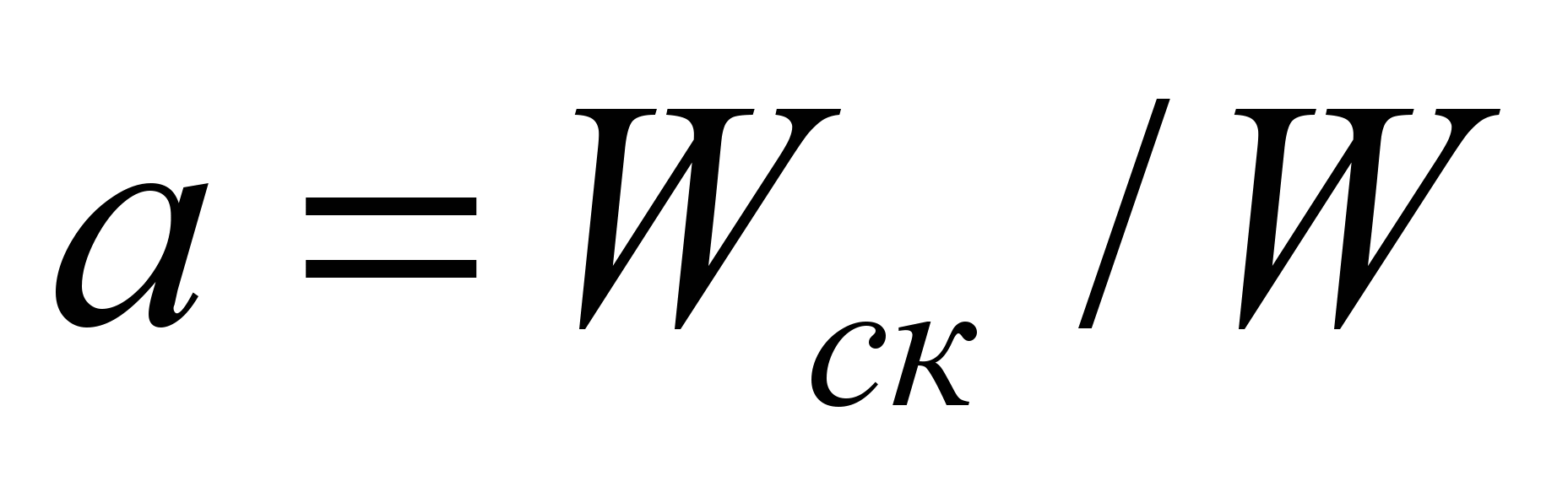- удельный вес скалярных операций.

Закон Амдала определяет принципиально важные для параллельных вычислений положения:

• Ускорение зависит от потенциального параллелизма задачи (величина ) и параметров аппаратуры (число процессоров ).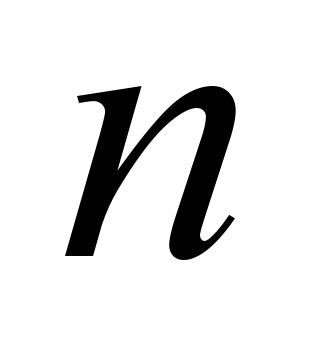
  
• Предельное ускорение определяется свойствами задачи.
  

Сетевой закон Амдала является полноценной моделью для оценки масштабируемости алгоритмов и кластеров. Он расширяем и позволяет учесть неограниченное число дополнительных параметров.

Для измерения масштабируемости можно использовать ряд параметров, основной – коэффициент полезного действия 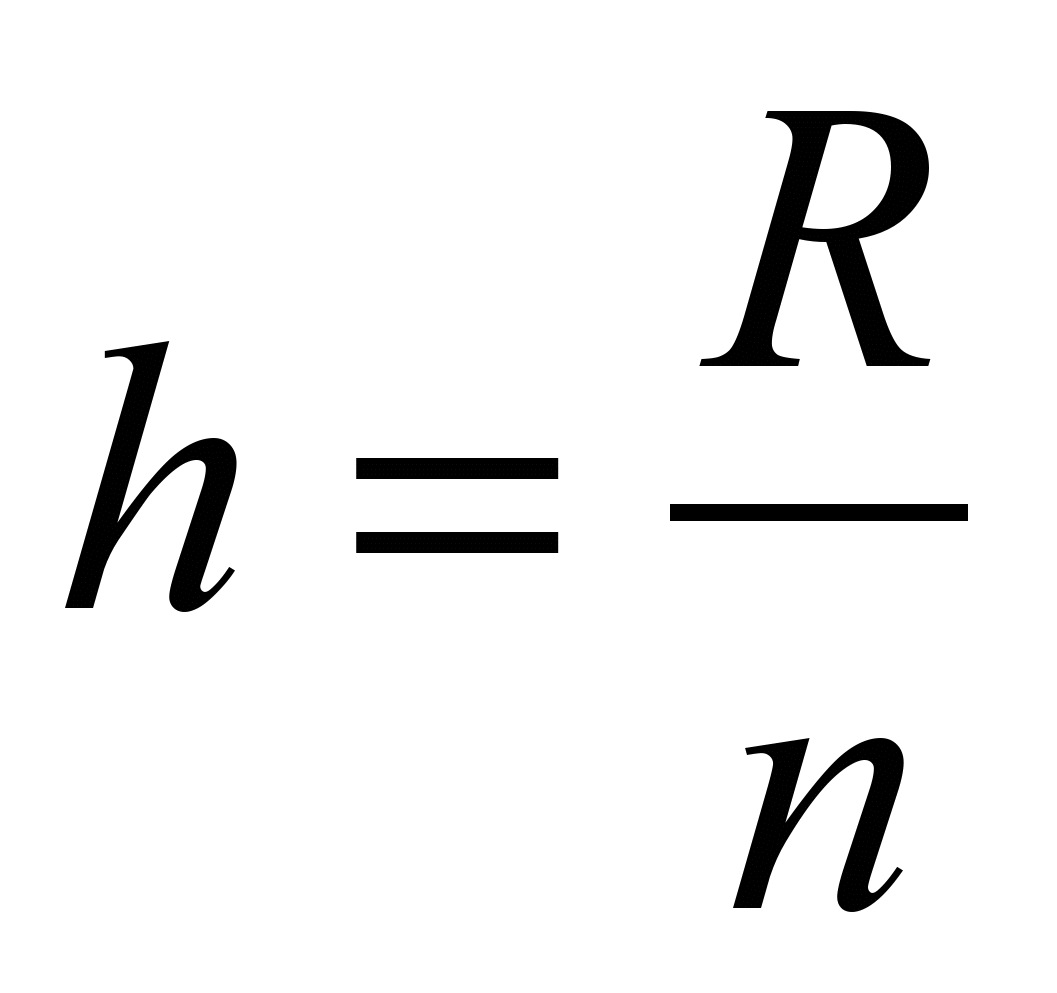. КПД является относительным параметром, но часто необходимо знать абсолютное значение параллельного счета T_n. Например, для кластеров, использующих очень быстрый коммуникатор SCI и медленный коммуникатор Fast Ethernet ускорения на одной и той же задаче при увеличении числа процессоров могут оказаться близкими, а времена вычислений – существенно разным.

Важным свойством базовой модели является возможность во многих случаях отделить параметры алгоритма 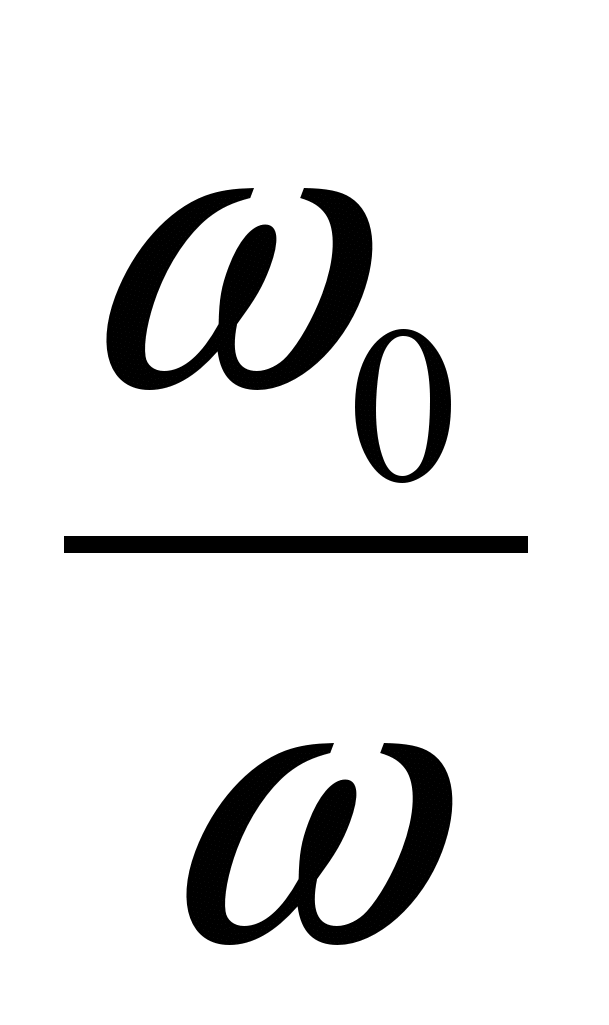от параметров аппаратуры 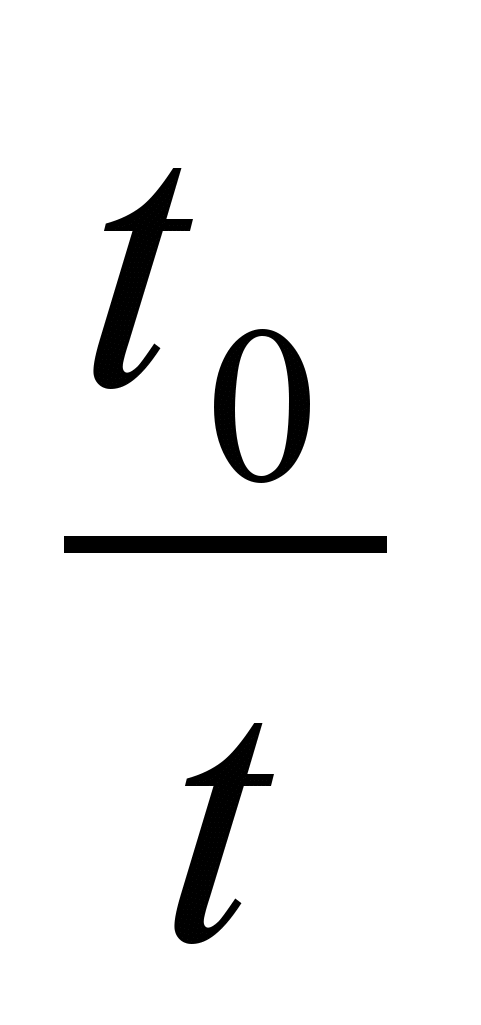. Это позволяет анализировать свойства алгоритмов 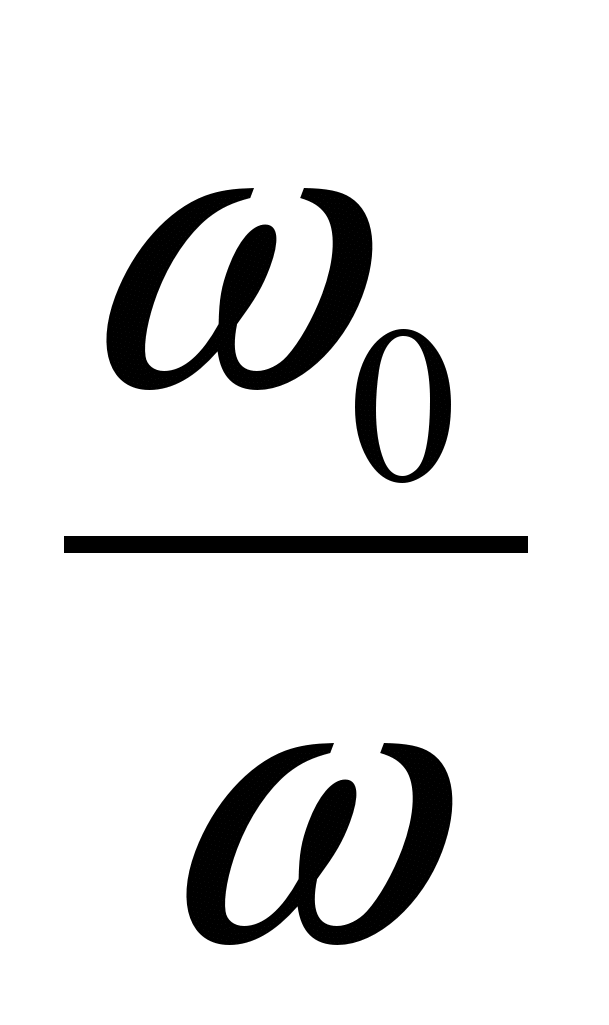независимо от характеристик каких-либо кластеров. Основной задачей в этом случае становится выбор вариантов алгоритмов с наименьшим 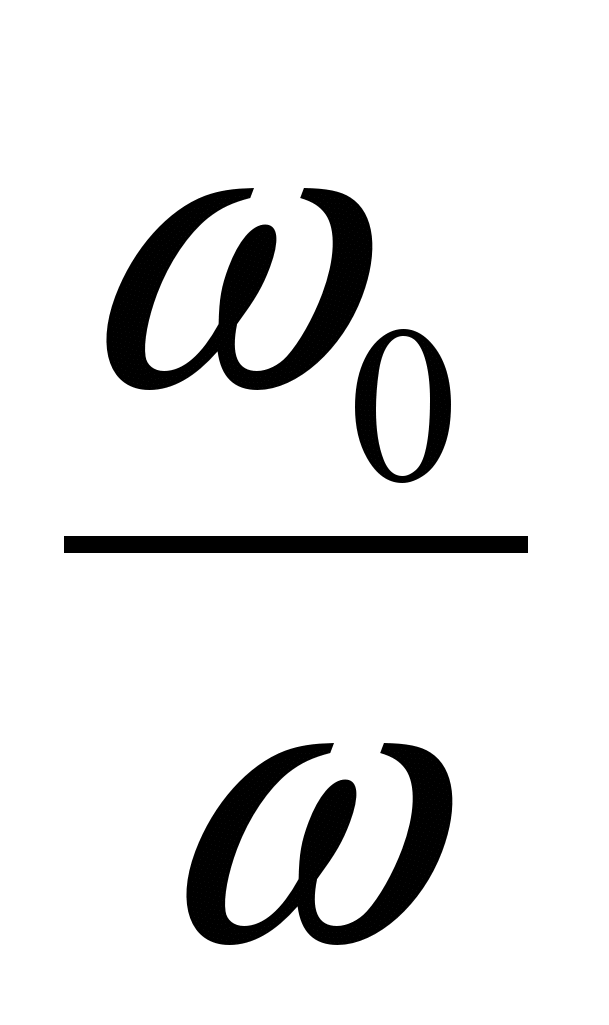и составление списков наилучших параллельных алгоритмов для различных приложений.• Аналогично, можно составить таблицы классов отношений 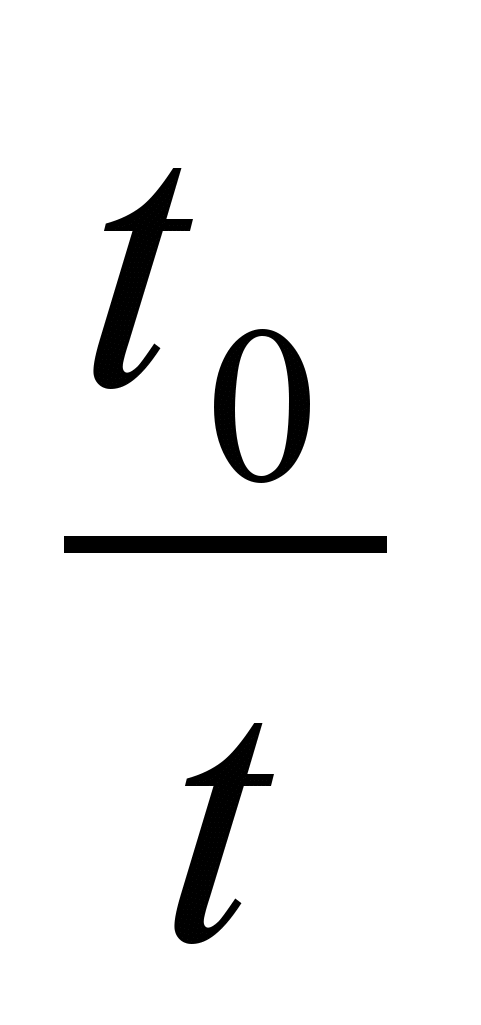для существующей и прогнозируемой аппаратуры кластеров, что позволит оперативно получить характеристики масштабируемости для любого параллельного алгоритма.