Исследование эффективности реализации численных методов на кластерах персональных ЭВМ

Вид материала

Исследование

Содержание 3.2. Двойственность задач линейного программирования 3.3. Постановка транспортной задачи

Подобный материал:

• Рабочей программы дисциплины «Численные методы и программирование» по направлению подготовки, 29.72kb.
• Решение физических задач на эвм" Лекции 20 ч. Практические занятия 96 ч. Учебная, 40.03kb.
• «Исследование и сопоставительный анализ численных методов решения задач не линейного, 321.81kb.
• Автономность эксплуатации без специальных требований к условиям окружающей среды, 258.87kb.
• Тема: «Интеграл» (заключительный урок), 49.41kb.
• Рабочая программа по разделу «Численные методы в строительстве», 71.92kb.
• На первой лекции мы рассмотрим общий смысл понятий бд и субд, 65.83kb.
• Лекция №7. Атрибутивная информация Лекция №7. Атрибутивные данные в гис, 283.92kb.
• Пояснительная записка к курсовой работе по предмету «Языки и технологии программирования», 353.31kb.
• Д. А. Силаев 1/2 года  Физическое явление и математическая модель. Математическое исследование, 20.76kb.

3.2. Двойственность задач линейного программирования

Каждой задаче линейного программирования соответствует двойственная задача. Двойственная задача по отношению к исходной задаче строится по следующим правилам:

Если исходная задача ставится на максимум, то двойственная ставится на минимум и наоборот.

Коэффициенты целевой функции исходной задачи становятся правыми частями ограничений двойственной задачи. Правые части ограничений исходной задачи становятся коэффициентами целевой функции двойственной задачи.

Если A-матрица коэффициентов исходной задачи, то транспонированная матрица A^T будет матрицей коэффициентов двойственной задачи.

В задаче на максимум все ограничения имеют знак ≤ (=), а в задаче на минимум все ограничения имеют знак ≥.

Число переменных в двойственной задаче равно числу ограничений в исходной задаче. Каждому ограничению исходной задачи соответствует переменная двойственной задачи. Если ограничение исходной задач имеет знак (≥), то соответствующая переменная двойственной задачи неотрицательна. Если ограничение имеет знак (=), то соответствующая переменная двойственной задачи может принимать положительные и отрицательные значения и наоборот.

В матричном виде двойственные задачи, заданные в симметричной форме, имеют вид:

Прямая задача	Двойственная задача

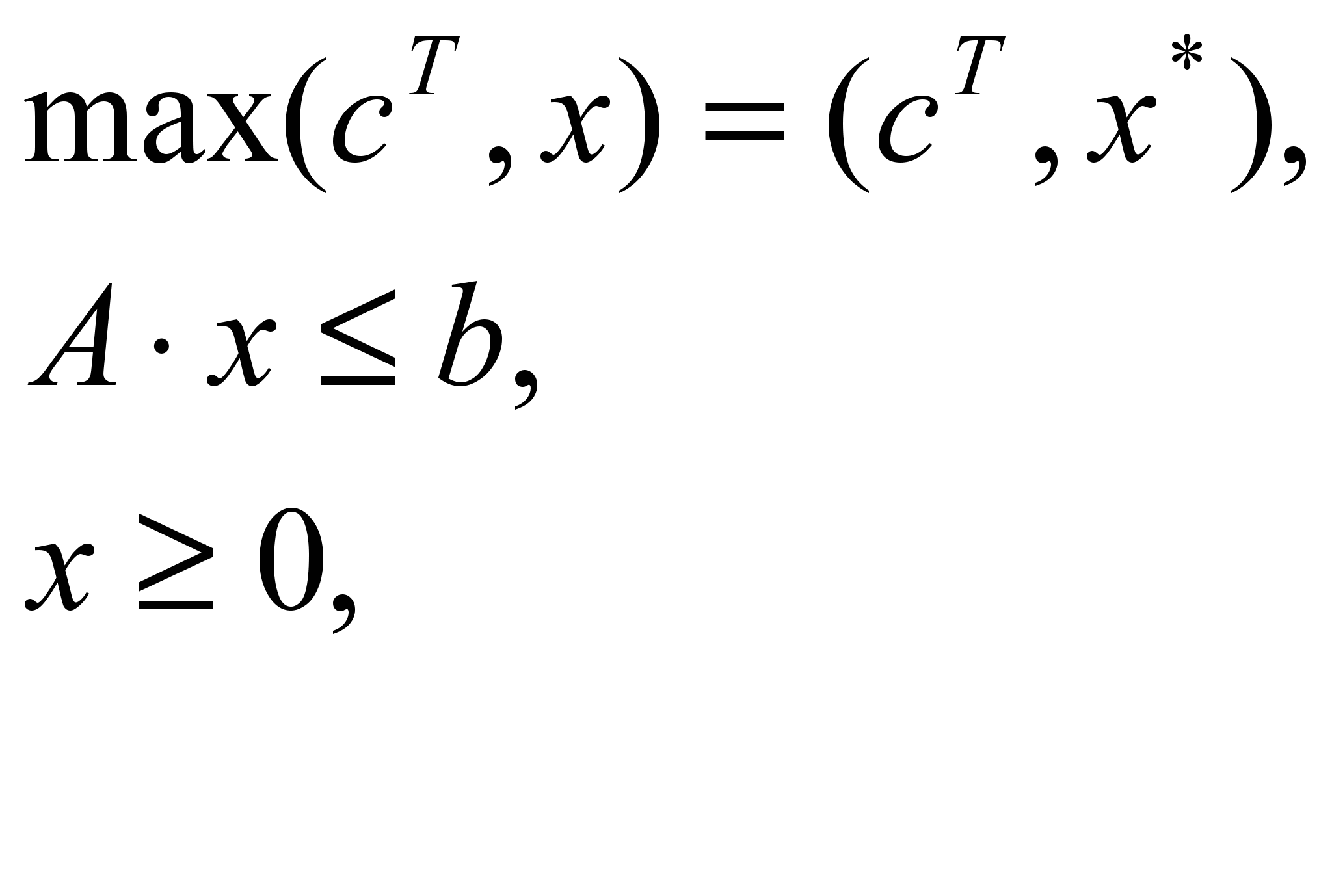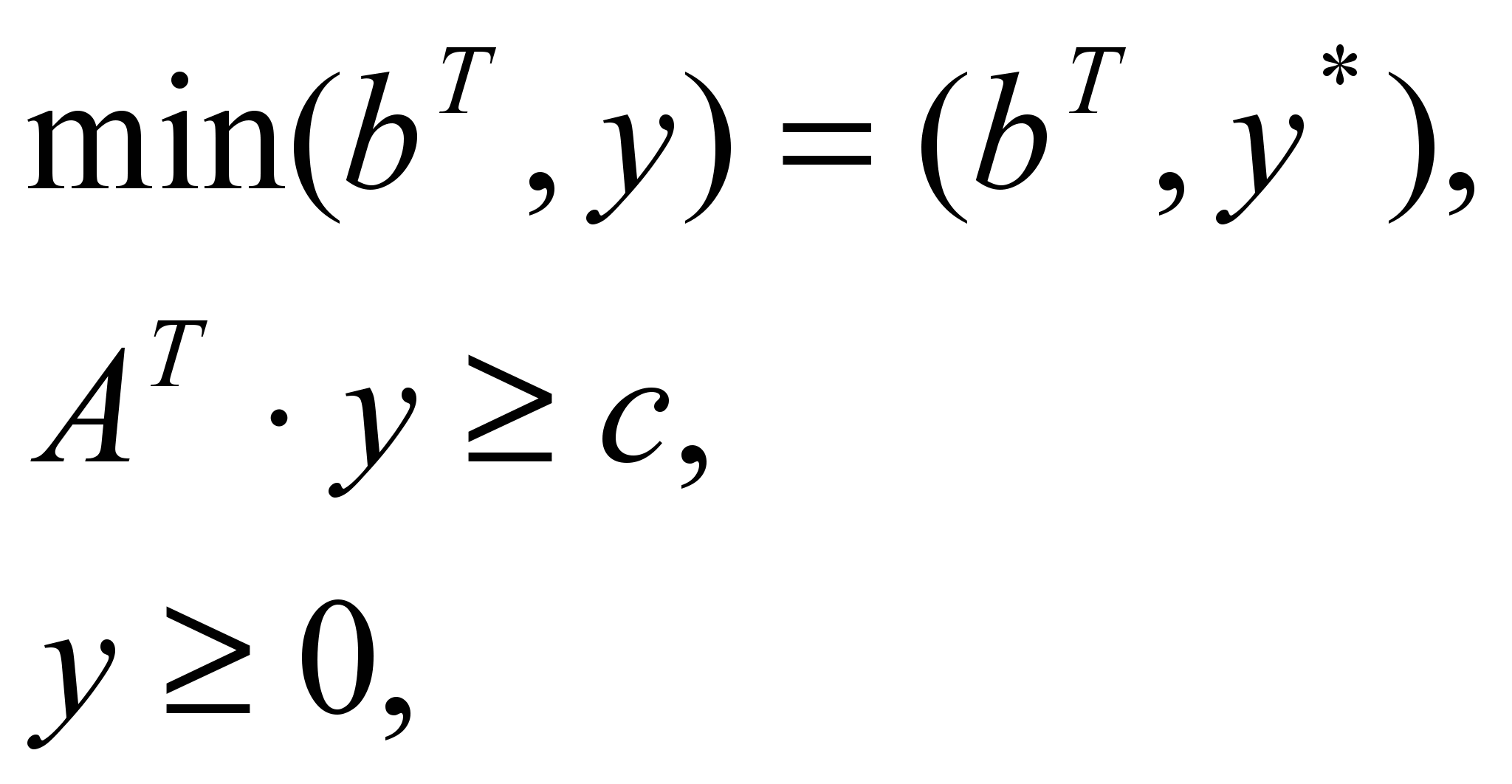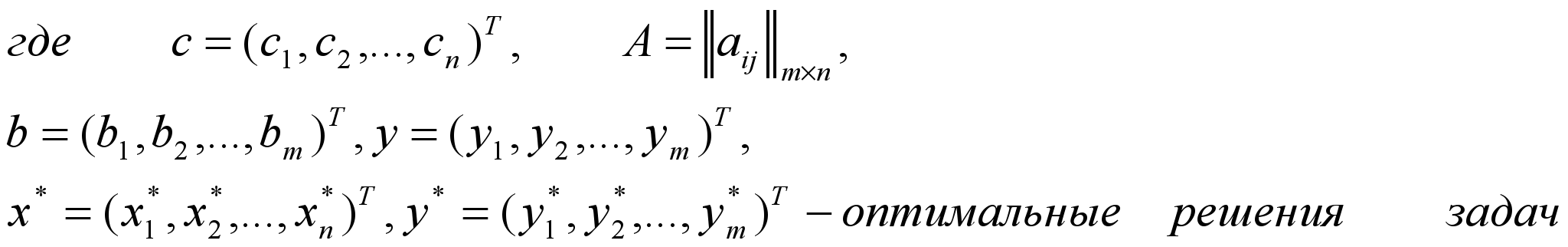рис. 7


Переменные 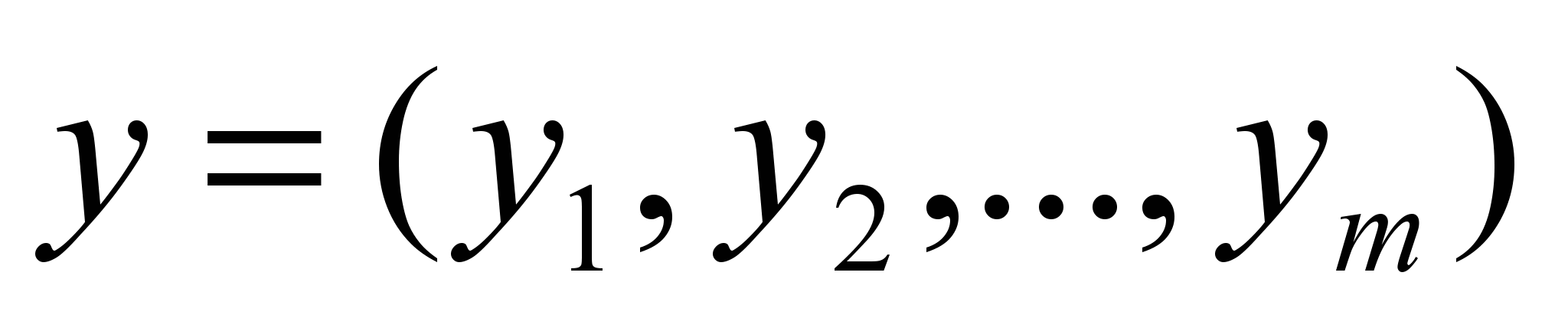называются двойственными (или объективно обусловленными) оценками.

3.3. Постановка транспортной задачи

Транспортная задача является специальным типом задач линейного программирования. Экономическая постановка этой задачи следующая. Имеется m поставщиков и n потребителей некоторой продукции. Заданы тарифы (стоимость) перевозок единицы продукции от поставщиков к потребителям, известны объемы запасов у поставщиков и потребности каждого потребителя в продукции.

Требуется составить план поставок продукции от поставщиков к потребителям так, чтобы суммарная стоимость перевозок была минимальной.

Математическая постановка этой задачи имеет вид:



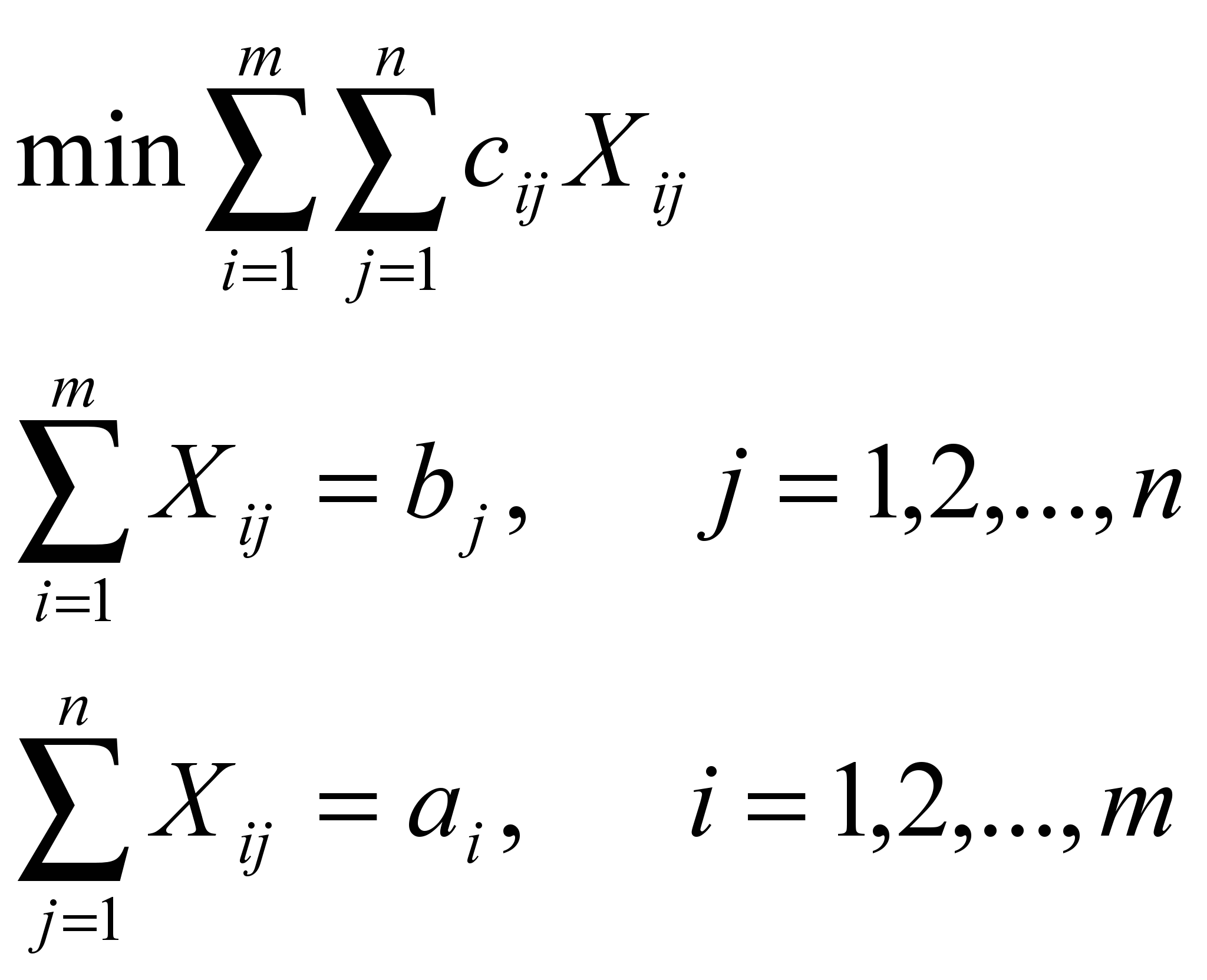
рис. 8


Здесь 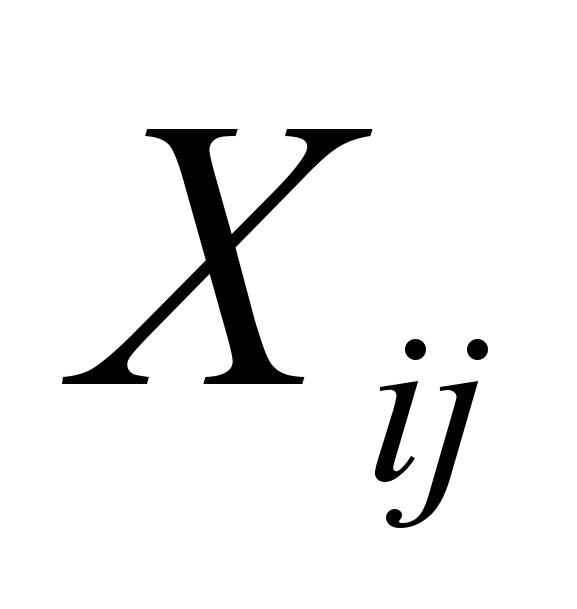- объем, 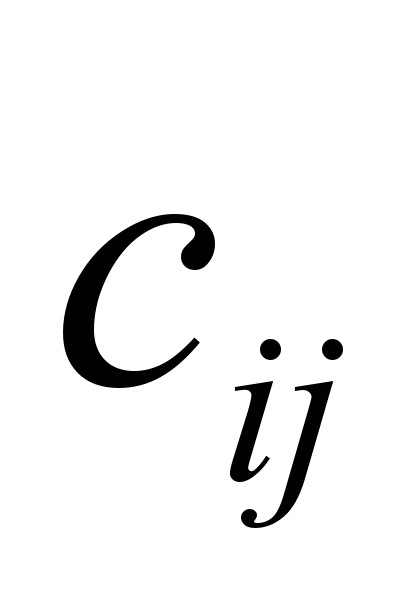- тариф поставки продукции от i-го поставщика к j-му потребителю, 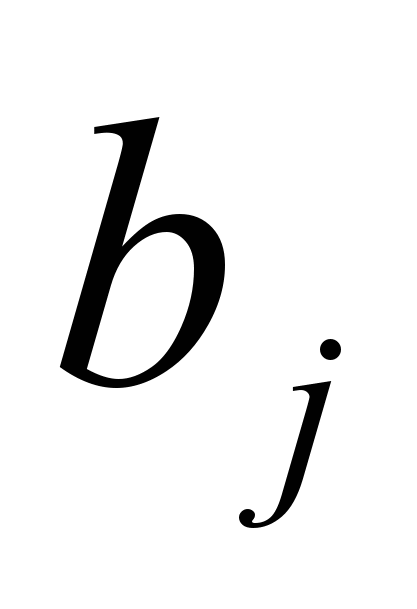- потребности потребителей в продукции, - запасы продукции у поставщиков.

Видно, что (рис. 8) является задачей линейного программирования со специальной матрицей. В задаче (рис. 8) имеется m*n неизвестных X_ij и (m+n) уравнений.

Решение транспортной задачи называется оптимальным планом перевозок (поставок) продукции.

Задача (рис. 8) называется сбалансированной (закрытой), если суммарный объем потребностей равен суммарному объему предложения продукции, т.е.




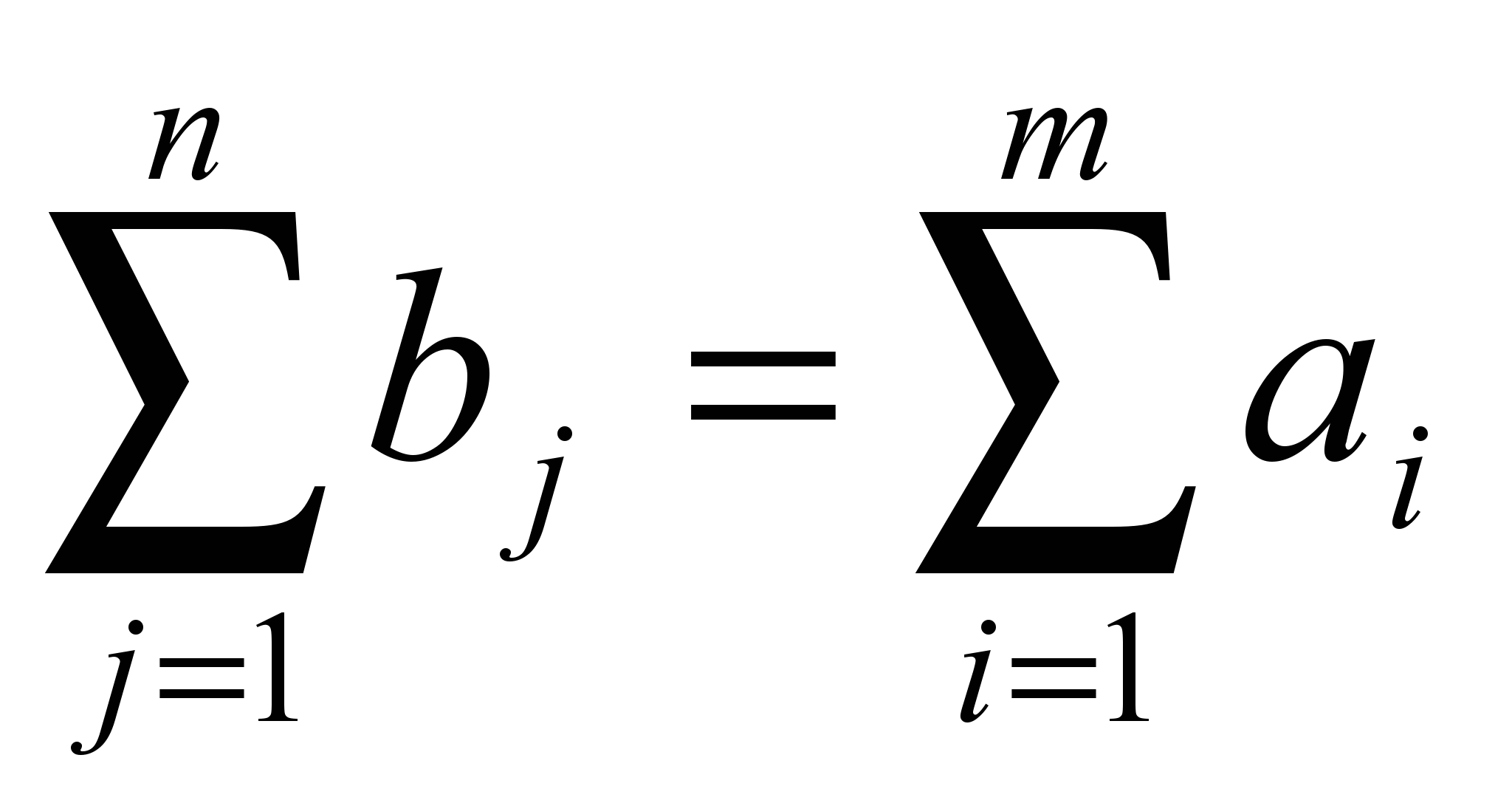
рис. 9


Если условие (рис. 9) не выполняется, то задача называется открытой. Для решения открытую задачу преобразуют в закрытую. Для этого в задачу вводят либо фиктивного поставщика недостающего объема продукции (если потребности больше предложения), либо фиктивного потребителя лишней продукции (если предложение больше потребностей), тарифы которых полагаются равными нулю.

При решении задачи используется свойство, которое состоит в том, что ранг матрицы A задачи (рис. 8) на единицу меньше числа уравнений r(A) = m + n – 1. С учетом этого число ненулевых переменных Xij > 0 в опорном плане будет не больше (m + n – 1).

Если число ненулевых Хij в опорном плане равно (m + n – 1), то план называется невырожденным, иначе – вырожденным.

Для решения задачи (1) составляется таблица ()

Поставщики	Потребители				Запасы продукции	Индексы, U
	1	2	…	n
1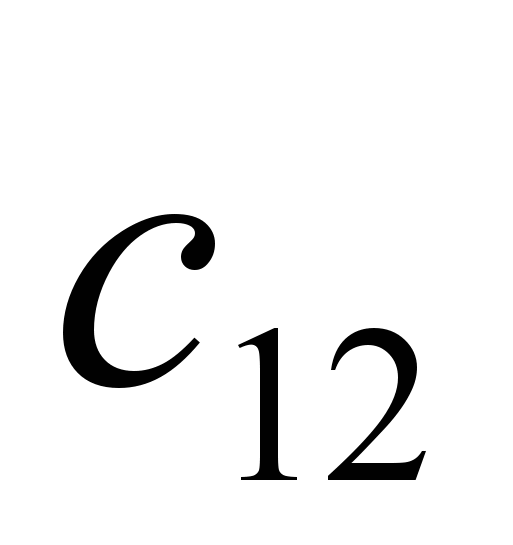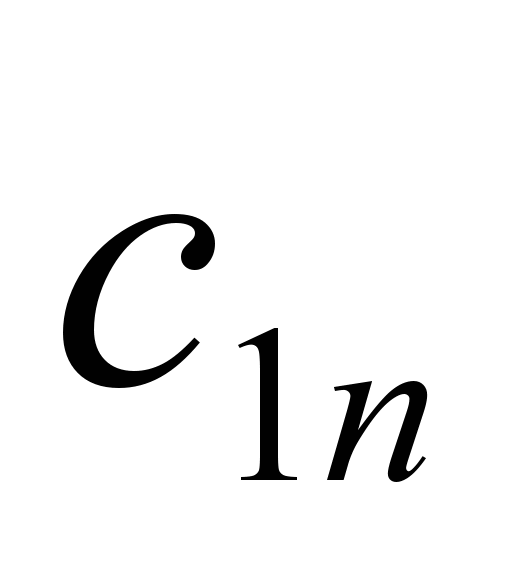
2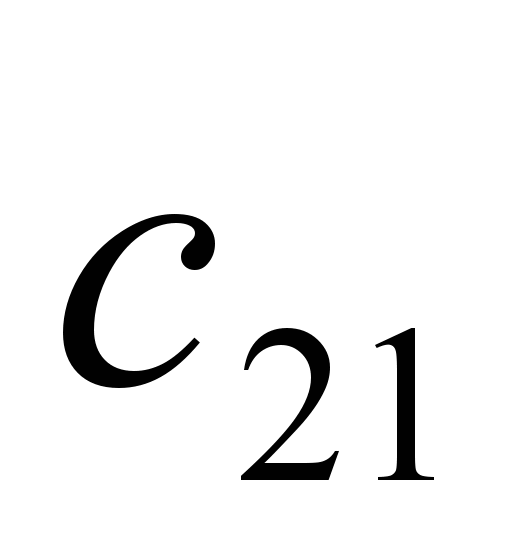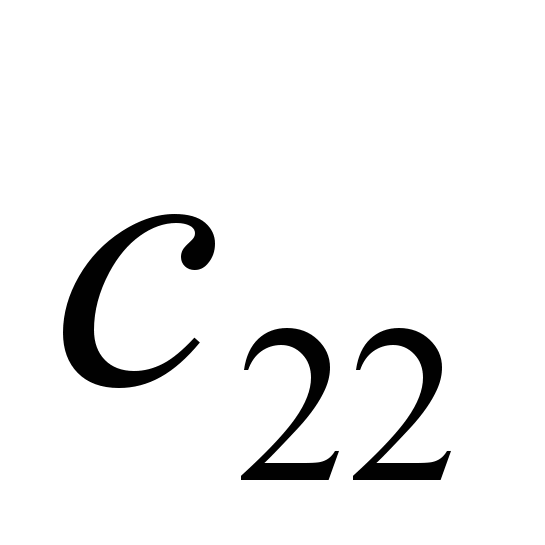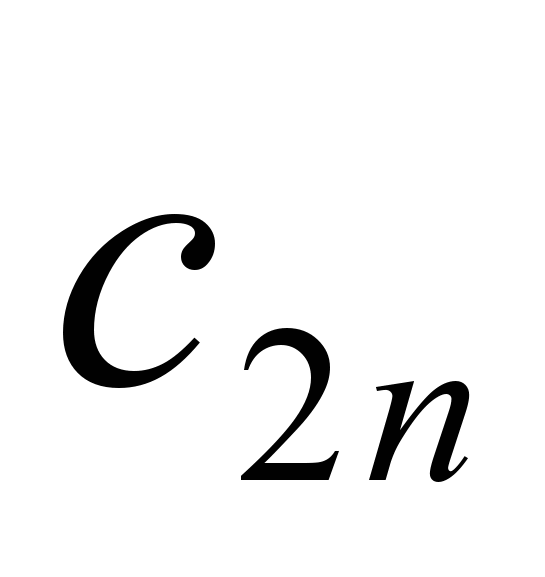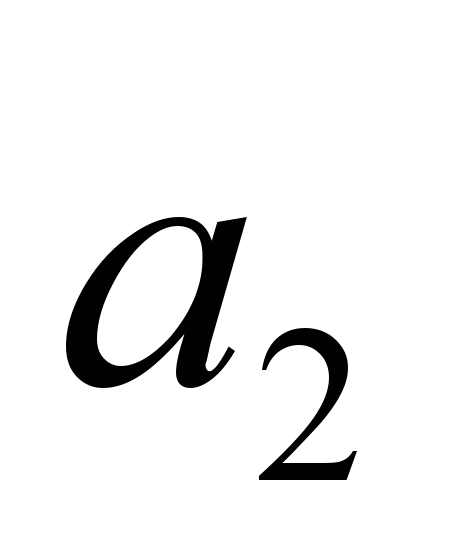
…
M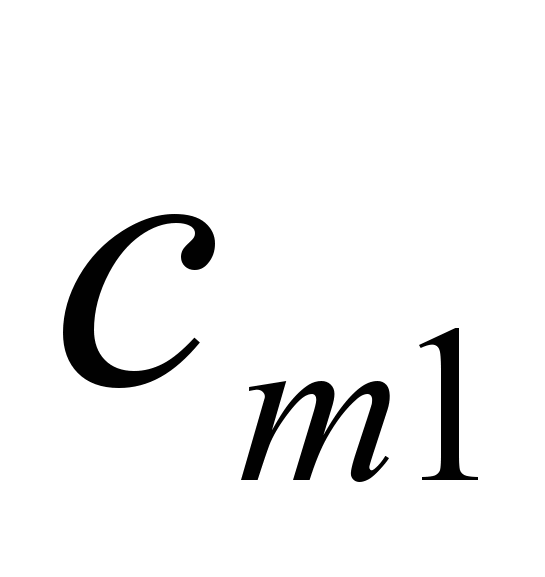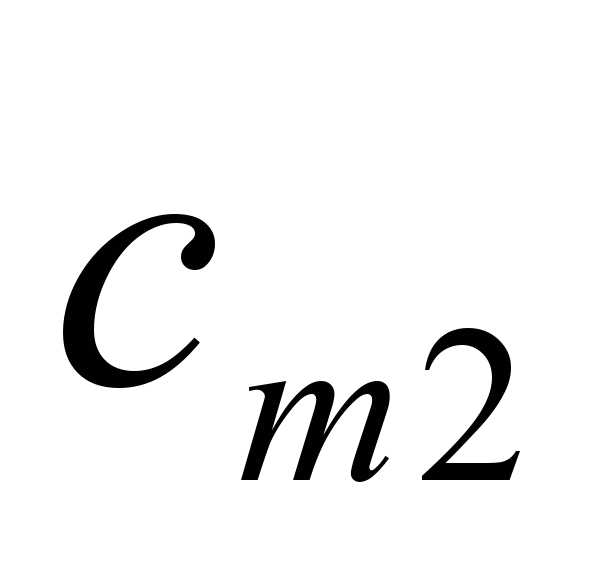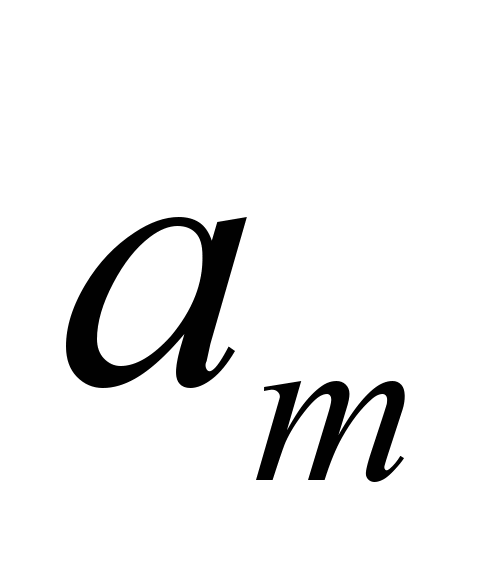
Потребности в продукции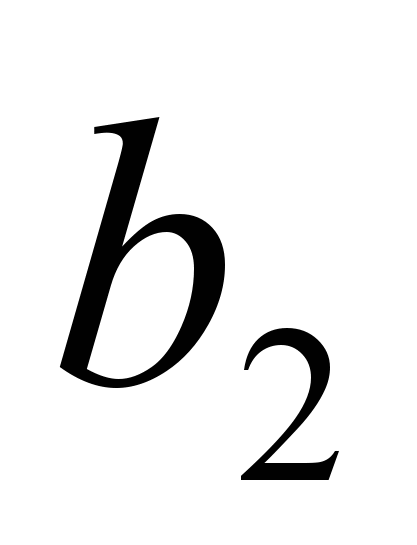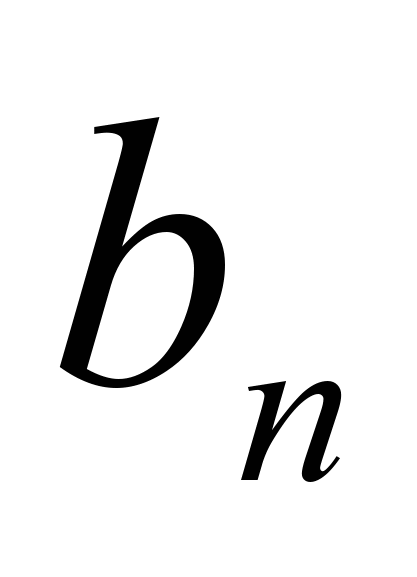
Индексы, V

рис. 10


В случае открытой задачи в таблицу вводят либо фиктивного поставщика, либо фиктивного потребителя, с целью получения равенства (рис. 9), с соответствующим объемом продукции. Поэтому будем считать, что в таблице выполняется соотношение (рис. 9).