Исследование эффективности реализации численных методов на кластерах персональных ЭВМ

Вид материала

Исследование

Содержание ГЛАВА 3. Решение задач линейного программирования 3.1. Постановка задачи линейного программирования

Подобный материал:

• Рабочей программы дисциплины «Численные методы и программирование» по направлению подготовки, 29.72kb.
• Решение физических задач на эвм" Лекции 20 ч. Практические занятия 96 ч. Учебная, 40.03kb.
• «Исследование и сопоставительный анализ численных методов решения задач не линейного, 321.81kb.
• Автономность эксплуатации без специальных требований к условиям окружающей среды, 258.87kb.
• Тема: «Интеграл» (заключительный урок), 49.41kb.
• Рабочая программа по разделу «Численные методы в строительстве», 71.92kb.
• На первой лекции мы рассмотрим общий смысл понятий бд и субд, 65.83kb.
• Лекция №7. Атрибутивная информация Лекция №7. Атрибутивные данные в гис, 283.92kb.
• Пояснительная записка к курсовой работе по предмету «Языки и технологии программирования», 353.31kb.
• Д. А. Силаев 1/2 года  Физическое явление и математическая модель. Математическое исследование, 20.76kb.

Заметим также, что отношение вычислительных затрат к коммуникационным и соответственно ускорение будет выше для вычислительных систем с медленными процессорами (больше время вычислительной работы) и быстрой коммуникационной сетью.

ГЛАВА 3. Решение задач линейного программирования

3.1. Постановка задачи линейного программирования

Произвольная форма задачи линейного программирования (ЗЛП) имеет вид:



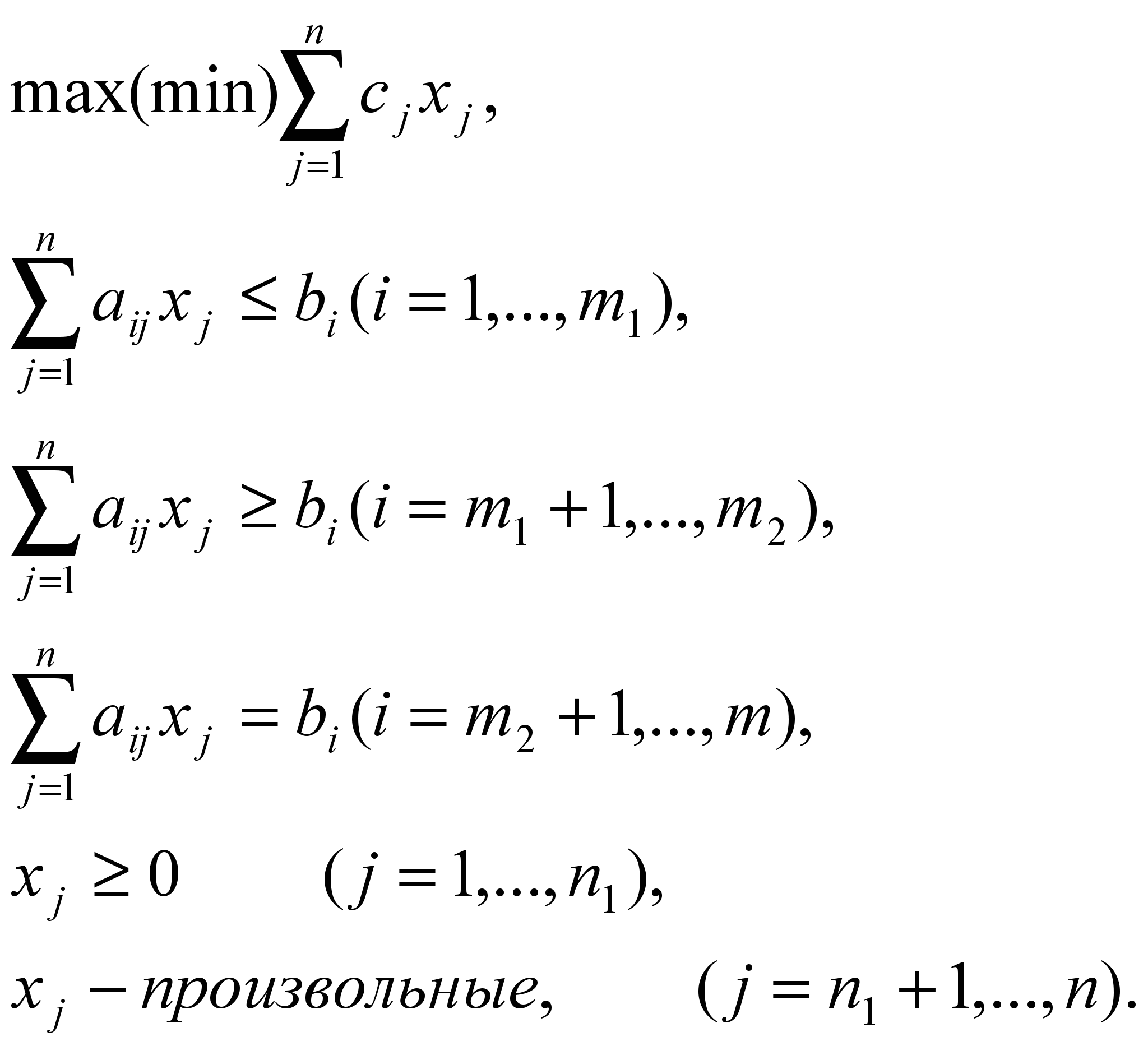
рис. 3



Выражение 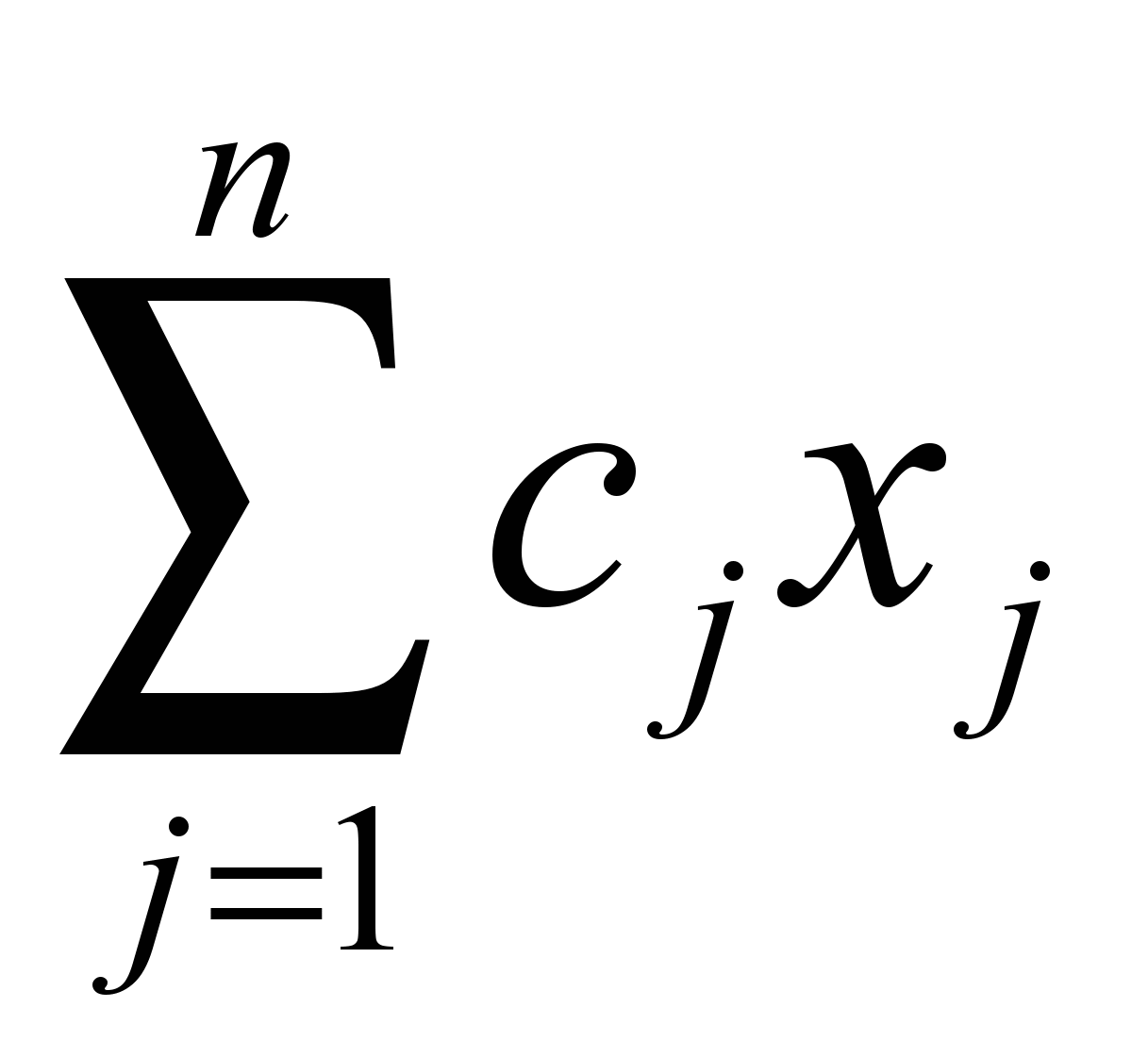называется целевой функцией (или критерием) задачи. Величины 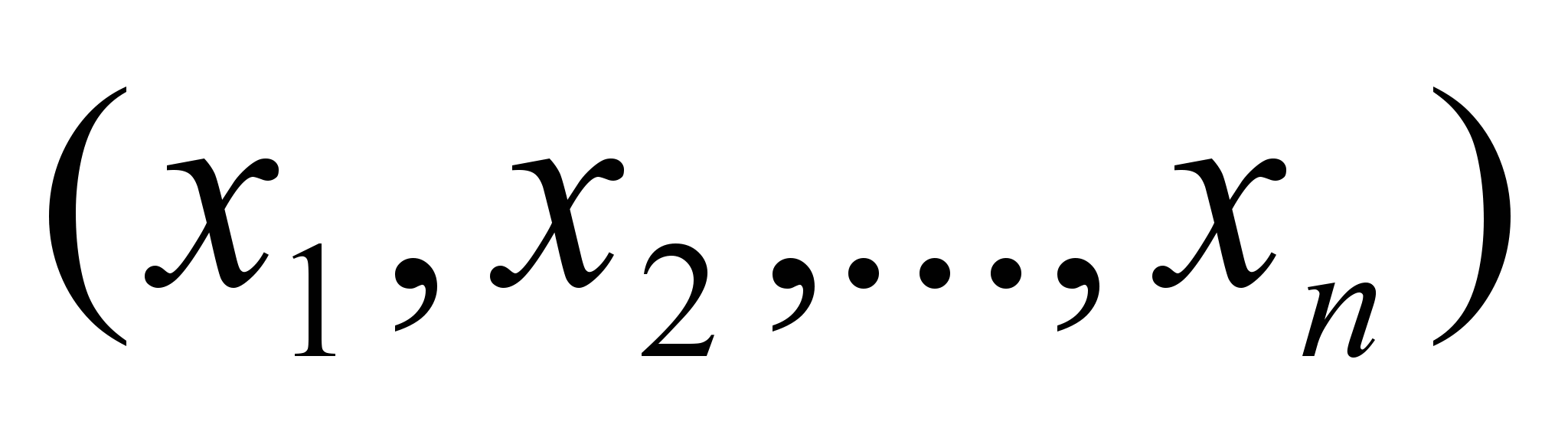– переменные задачи. Система неравенств в задаче (рис. 3) определяет область допустимых значений (планов) задачи D, которая имеет форму выпуклого многогранника.

Неравенства и равенства в задаче (рис. 3) называются ограничениями. Каждое неравенство определяет полупространство, а равенство – плоскость в пространстве переменных.

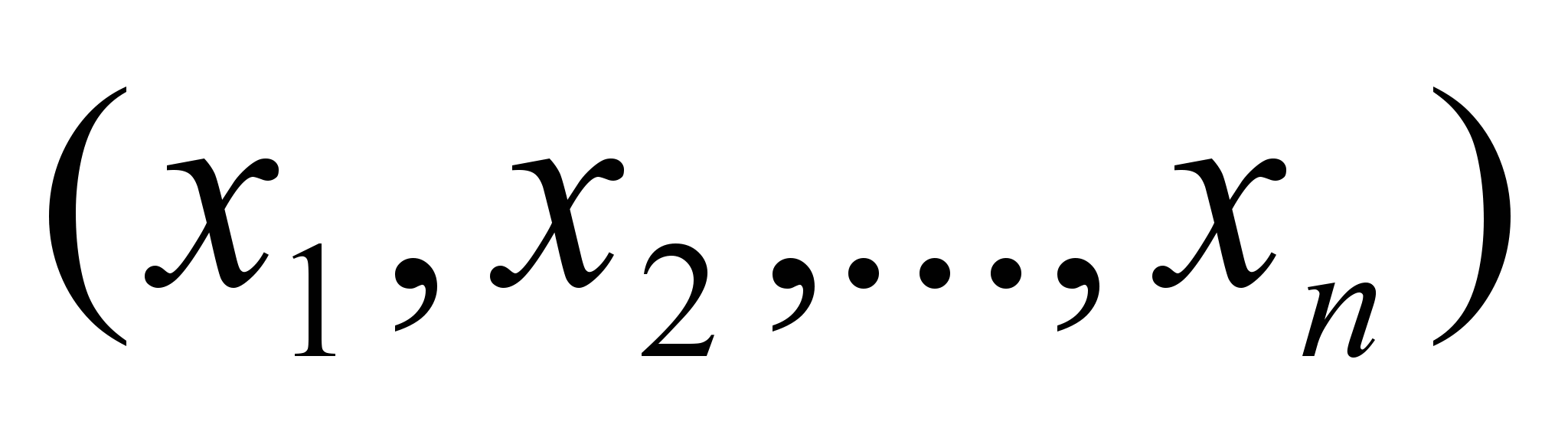Решение задачи (рис. 3) называется оптимальным решением (или оптимальным планом) и обозначается как 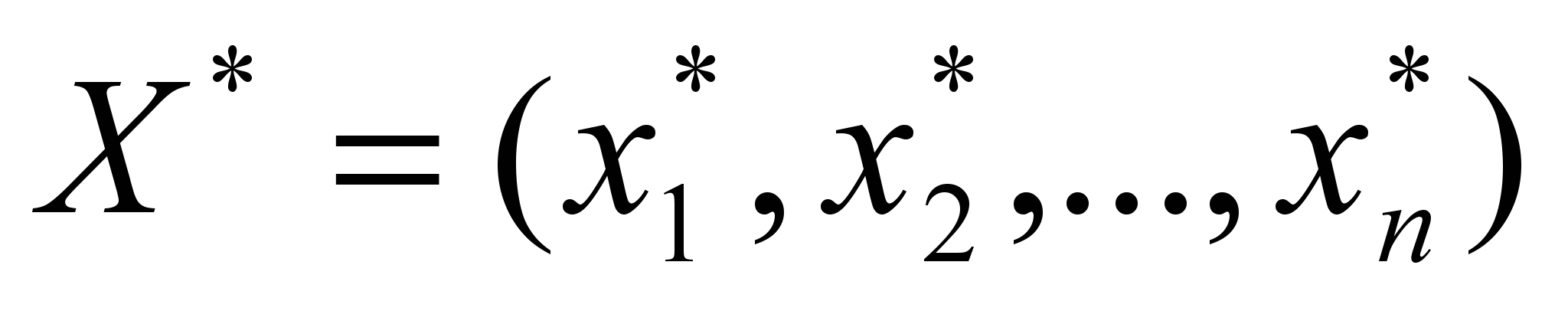. Оптимальные решения лежат на границе области D.

Если область D ограничена, то задача ЛП имеет либо единственное, либо бесконечно много решений. Если решение единственно, то оно совпадает с одной из вершин многогранника D.

Если градиент целевой функции 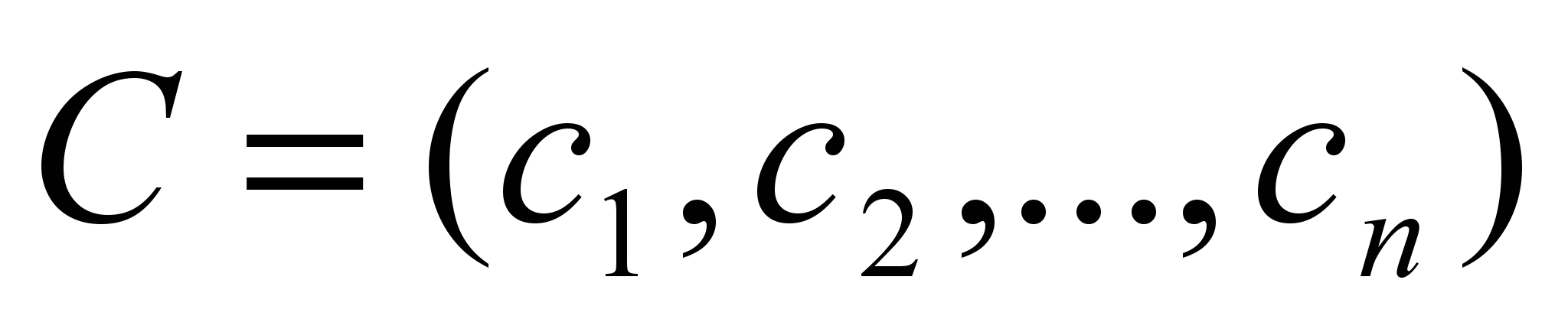коллинеарен градиенту одного из ограничений, то задача имеет бесконечно много решений, лежащих на данном ограничении.

Если ограничения несовместны, или целевая функция неограниченна, то задача (рис. 3) не имеет решения.

Если область области D не ограничена, то решение может существовать либо быть неограниченным.

Всякая задача на минимум может быть сведена к задаче на максимум и наоборот, умножением целевой функции на –1. Оптимальный план задачи при этом не изменится, а значение целевой функции изменит знак. После решения надо снова изменить знак целевой функции.

Симметричная форма ЗЛП на максимум имеет вид:




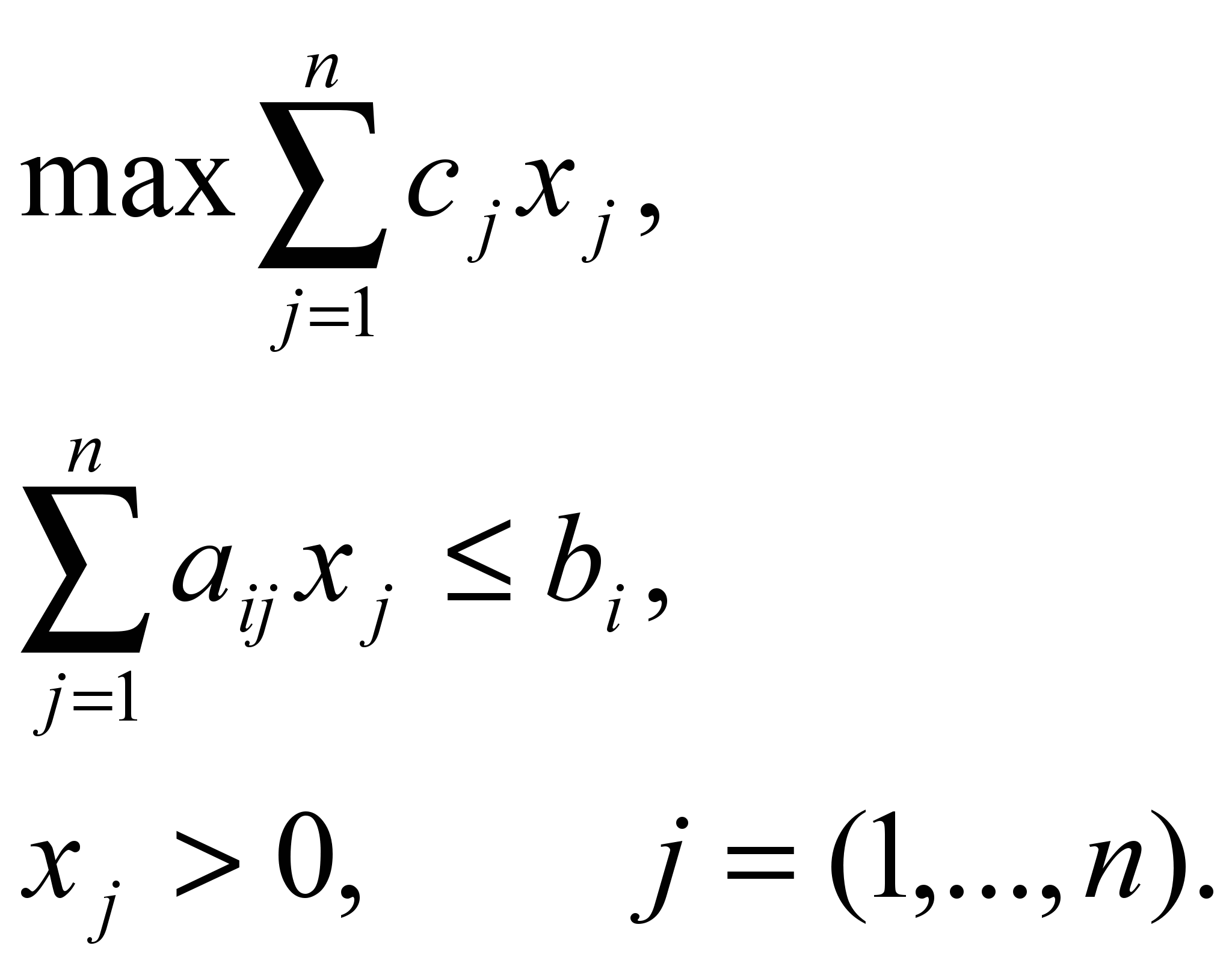
рис. 4


Симметричная форма ЗЛП на минимум имеет вид:




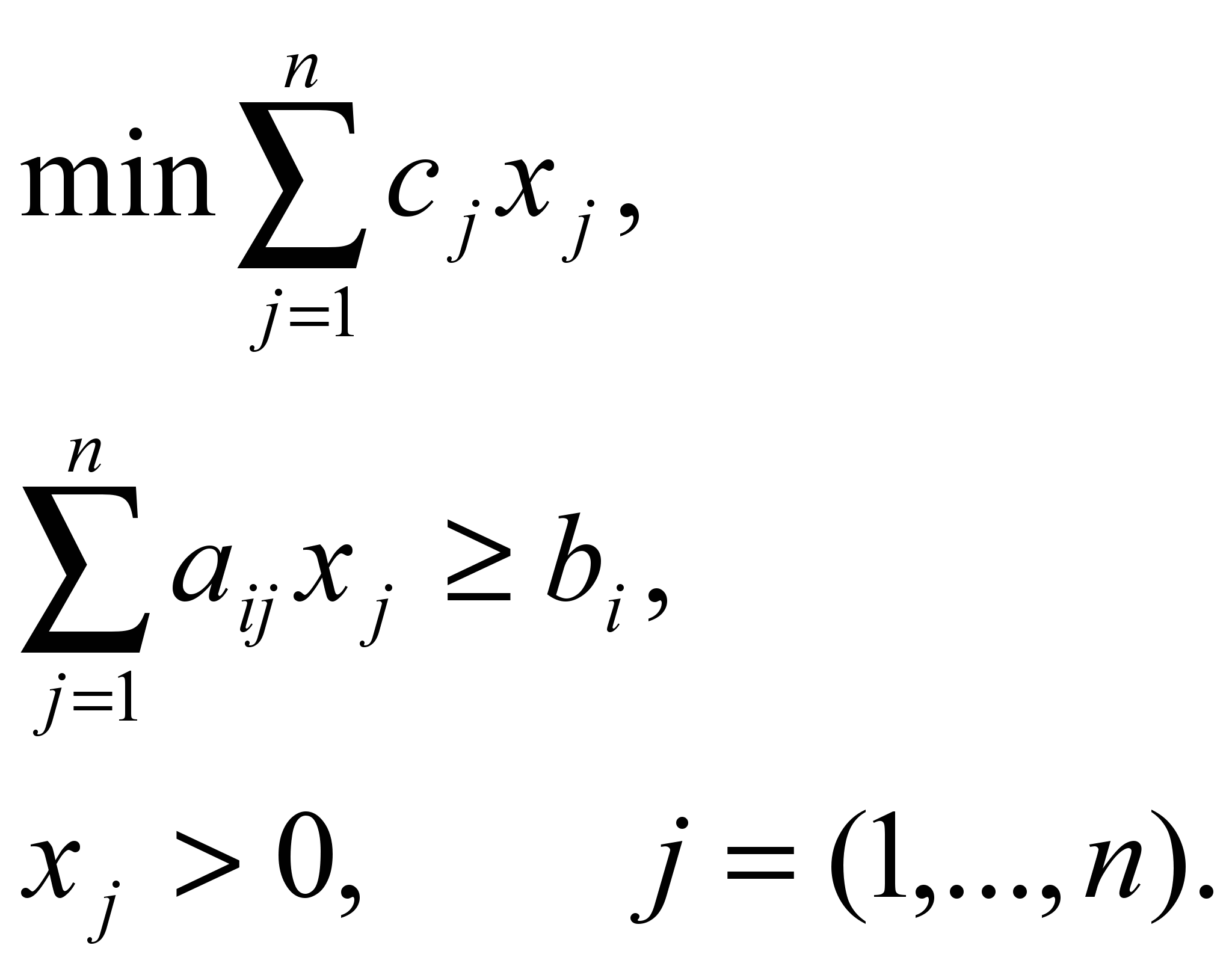
рис. 5

Если все 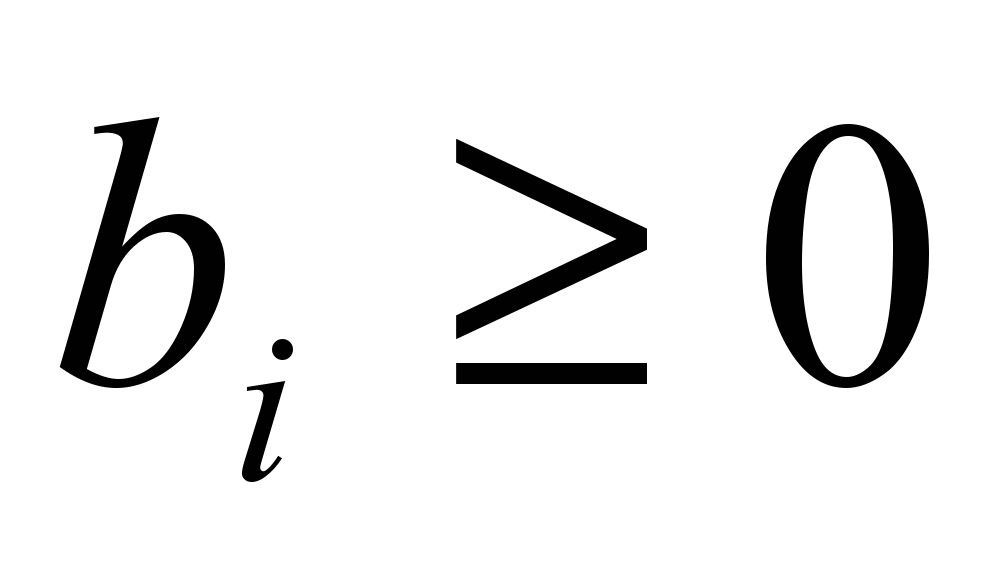, то задача (рис. 4) обычно имеет следующий экономический смысл: 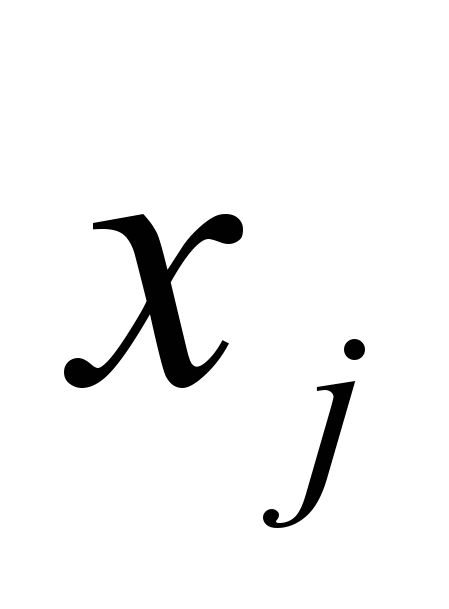− объемы производства j-го вида продукции, 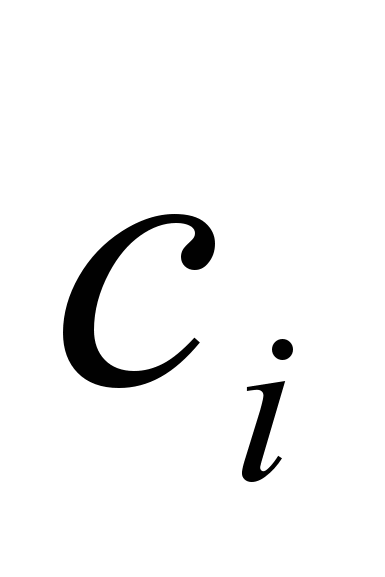− цены или прибыль единицы продукции, − нормативы затрат i-го вида ресурса на производство единицы j-го вида продукции, 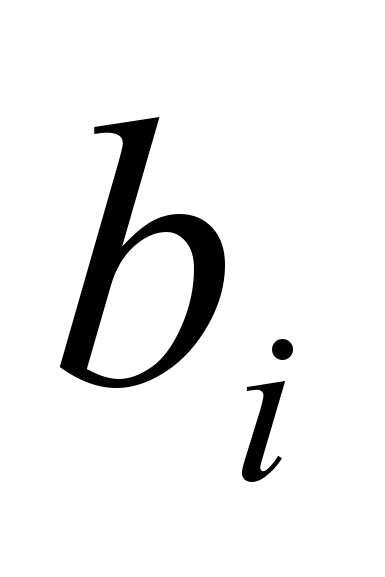− имеющийся запас i-го вида ресурса. Надо определить план производства продукции 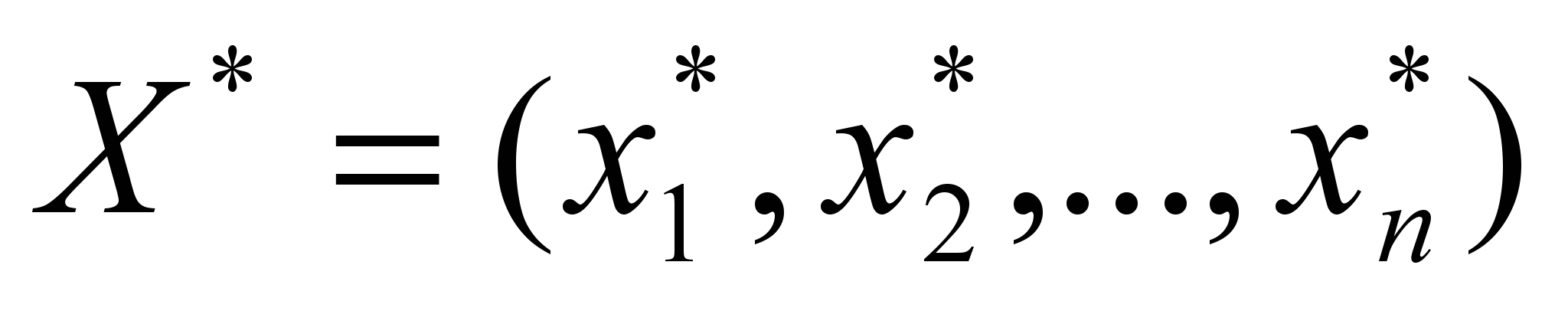, который дает максимальную выручку или прибыль, при заданных ограничениях на имеющиеся ресурсы. Ограничения, на которых в оптимальном плане достигнуто равенство, соответствуют дефицитным ресурсам, остальные ресурсы называются недефицитными.


Каноническая форма ЗЛП представлена ниже:



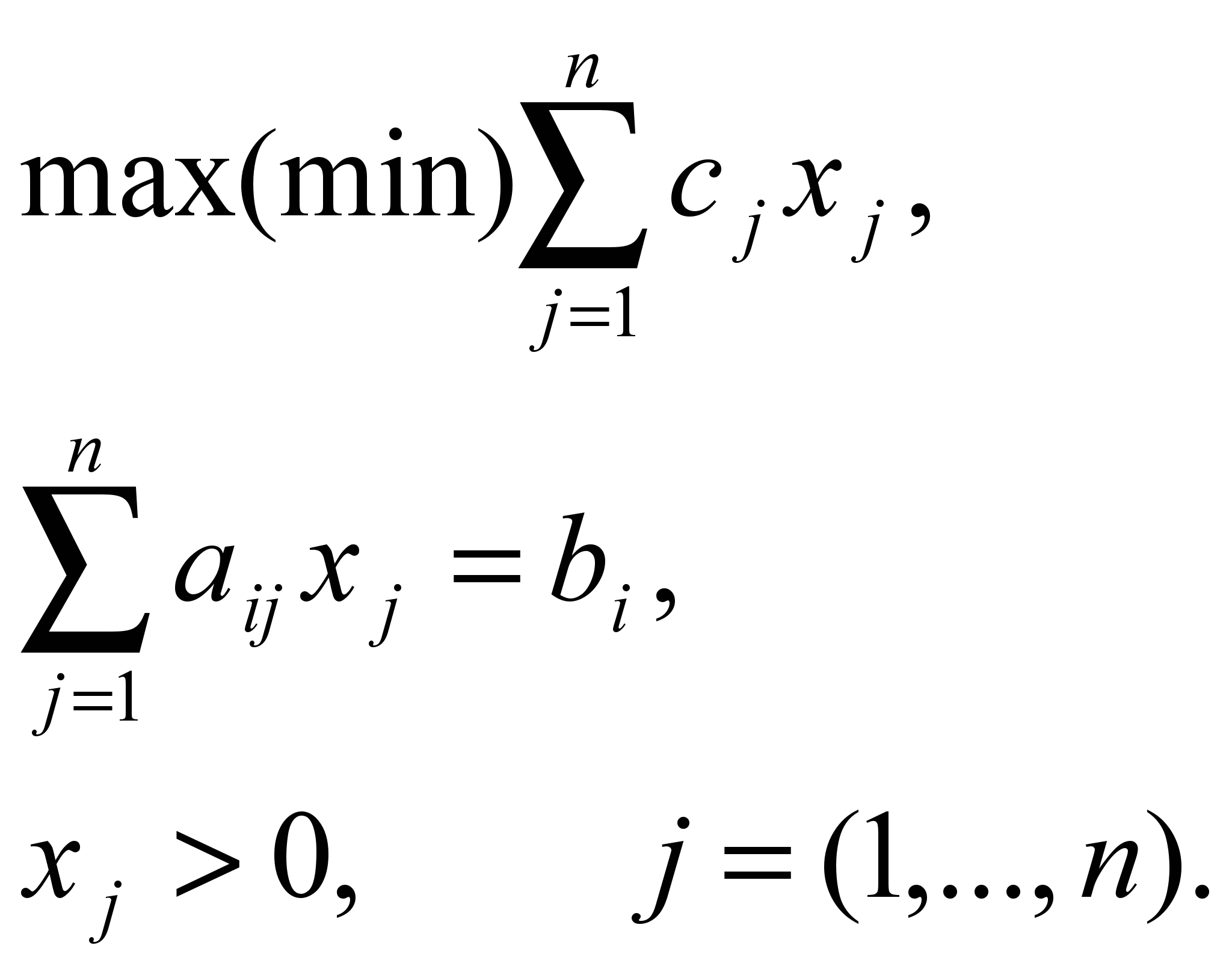
рис. 6

Из линейной алгебры известно, что количество линейно независимых уравнений не может быть больше числа неизвестных. Поэтому в (рис. 6) можно считать, что .

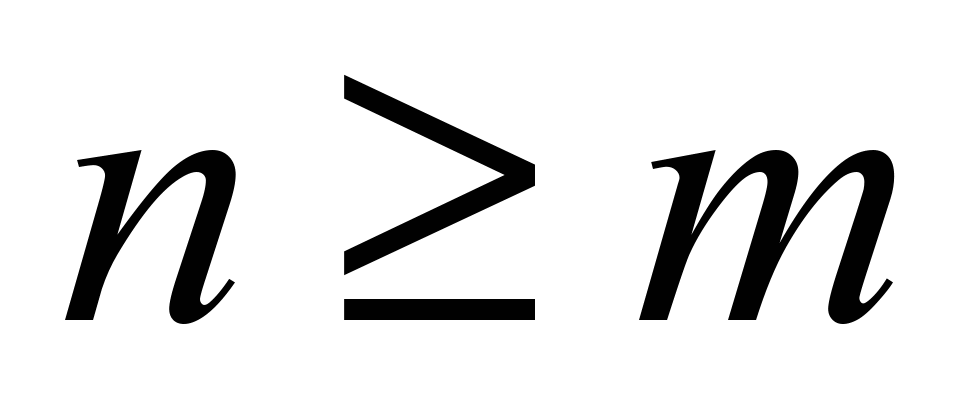Определение. Если в ограничении задачи (рис. 6) есть переменная с коэффициентом, равным единице, отсутствующая в других ограничениях, то она называется базисной, остальные переменные ограничения называются свободными.

Если базисные переменные есть во всех ограничениях, то такая форма ЗЛП называется канонической с базисными переменными. Каноническая форма с базисными переменными является исходной для решения задачи симплексным алгоритмом.


Определение. Опорным планом называется любой вектор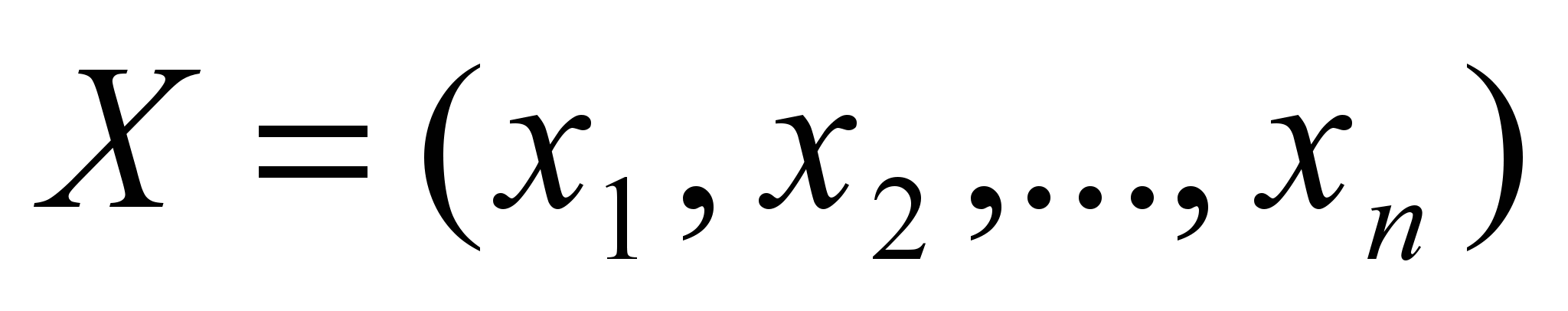, удовлетворяющий условиям (рис. 6) и имеющий не более чем m ненулевых компонент.

Определение. Если в канонической форме все 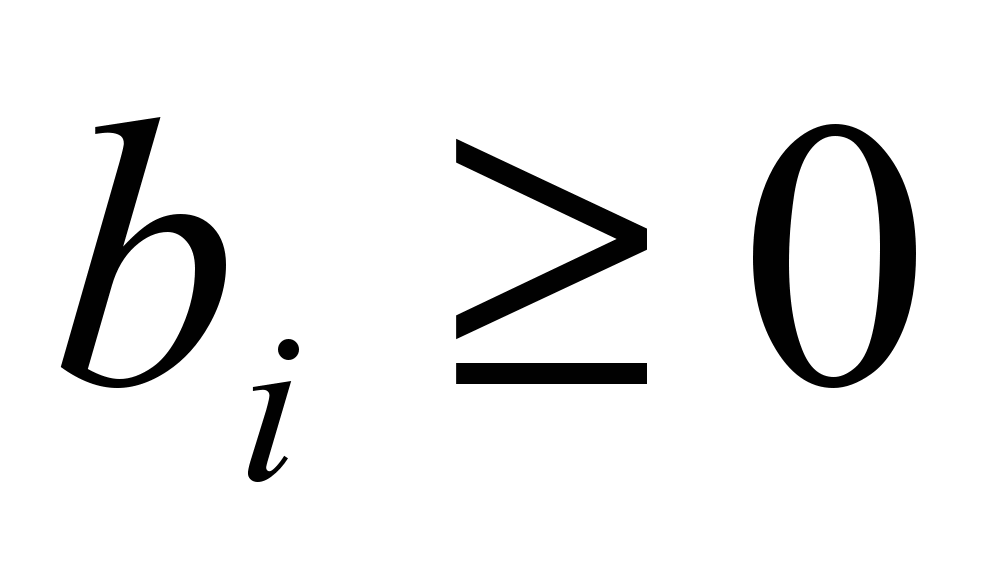, то задача (рис. 6) имеет опорный план, в котором базисные переменные равны 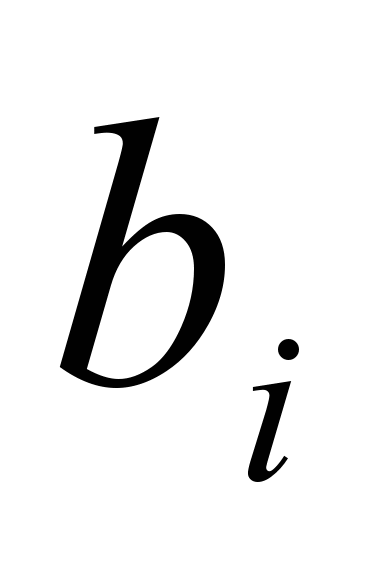, а остальные (свободные) переменные равны 0. Такой план называется начальным опорным планом.

Определение. Балансовой называется переменная, которая добавляется или вычитается из левой части неравенства для получения равенства. В задачах (рис. 4), (рис. 5) балансовые переменные будут базисными.

Любая форма ЗЛП приводится к канонической форме с помощью следующих преобразований:

• замена переменной, которая принимает произвольные значения, на разность двух новых положительных переменных;
  
• введение балансовых переменных.
  

Определение. Искусственная переменная вводится, когда в канонической форме ЗЛП в ограничении нет базисной переменной. В этом случае целевая функция изменяется путем вычитания искусственной переменной с коэффициентом М в задаче на максимум и путем прибавления – в задаче на минимум. Коэффициент М считается большим положительным числом.

Определение. При вводе искусственных переменных и корректировке целевой функции измененная задача называется М-задачей.