Лекция для учеников 8 «А» класса. Учитель математики: Ермеев Валерий Александрович

Вид материала

Содержание

Начало индукции.
Индуктивный шаг.
Применение метода математической индукции в задачах на доказательства равенств.
Задачи для самостоятельного решения.

Подобный материал:

Метод математической индукции.

Лекция для учеников 8 «А» класса.

Учитель математики: Ермеев Валерий Александрович.

Цели лекции: 1) ознакомить учащихся 8 «А» класса методом математической индукции;

2) выработать навыки и умения применять данный метод при решении задач на доказательства равенств, на делимость, на доказательства неравенств, на суммирование.

Одним из самих универсальных методов доказательств математических утверждений, в которых фигурируют слова «для произвольного натурального n» является метод математической индукции.

Доказательство при помощи этого метода состоит из трех этапов:

начало индукции,

индуктивное допущение и

индуктивный шаг.

В простейшем варианте это выглядит следующим образом.

1) Начало индукции. Доказывается (проверяется), что сформулированное утверждение выполняется при n = 1.

2) Индуктивное допущение. Предполагается, что утверждение справедливо при n = k.

3) Индуктивный шаг. Доказывается, что при условии справедливости утверждения при

n = k следует его справедливость при n = k + 1.

Метод математической индукции можно применять только для доказательства утверждений, зависящих от натурального n. В основном он применяется для решения задач двух видов:

1) исходя из частных наблюдений устанавливают некоторую закономерность и затем доказывают её справедливость методом математической индукции;

2) доказывают справедливость некоторой формулы методом математической индукции.

Применение метода математической индукции в задачах на доказательства равенств.

Пример 1. Доказать, что при любом натуральном n верно равенство:

Доказательство. 1) Начало индукции. Проверяем утверждение при n = 1

Неравенство выполняется.

2) Индуктивное допущение. Предположим, что равенство верно при n = k, т. е.

3) Индуктивный шаг. Докажем утверждение при n = k +1:

Таким образом, что доказываемое утверждение справедливо при n = k + 1. По методу математической индукции получаем, что утверждение справедливо при любом

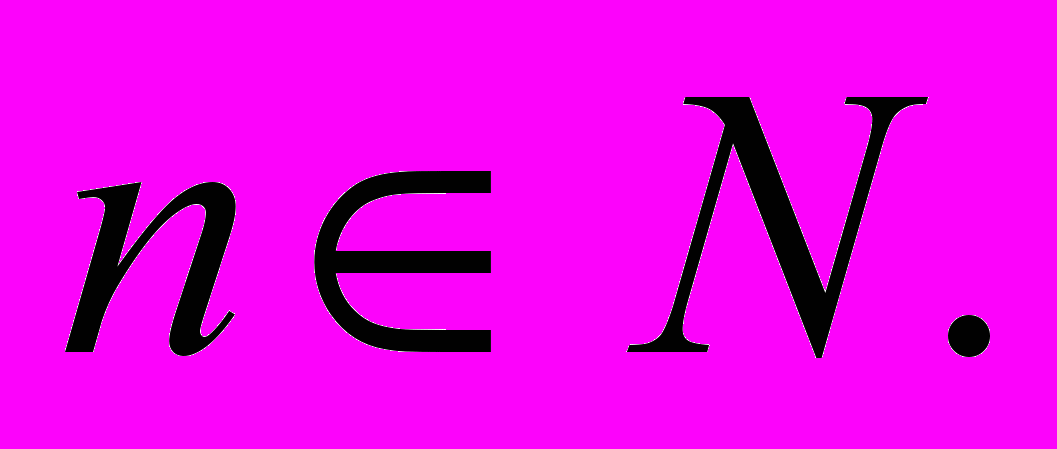
Применение метода математической индукции в задачах на делимость.

Пример 2. Доказать, что при любом натуральном n значение выражения n ³ + 11n делится на 6.

Доказательство. 1) Начало индукции. Проверим утверждение при n = 1.

1³ + 11∙ 1 = 12

Так как 12 : 6 = 2, то утверждение справедливо при n = 1.

2) Индуктивное допущение. Предположим, что утверждение справедливо при n = k, т. е. выражение k ³ + 11k делится на 6.

3) Индуктивный шаг. Докажем, что утверждение выполняется при

n = k +1.

(k+1) ³ + 11(k+1) = k ³ + 3k ² + 3k + 1 + 11k + 11 = (k ³ + 11k) + 3k(k + 1) + 12.

Первое слагаемое делится на 6. При любом натуральном k одно из чисел к ним k + 1 является чётным, поэтому второе слагаемое делится на 6. Третье слагаемое делится на 6.

По методу математической индукции получаем, что утверждение справедливо при любом

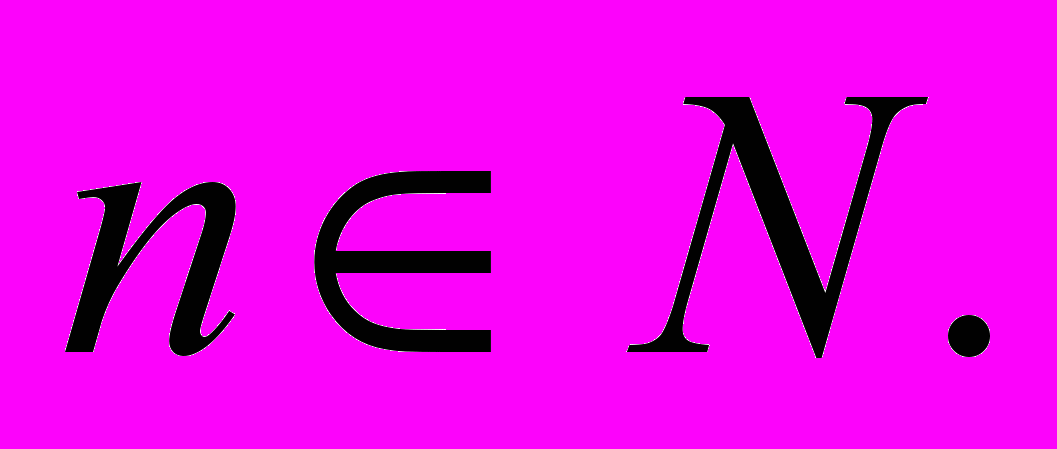
Применение метода математической индукции в задачах на доказательства неравенств.

Пример 3. Доказать, что при любом натуральном n ≥ 3 выполняется неравенства

3 ⁿ> 2ⁿ + 3n.

Доказательство. 1) Начало индукции. Проверим утверждение при n = 3: 3³ > 2³+ 3∙3 – выполняется.

2) Индуктивное допущение. Предположим, что утверждение справедливо при n = k, т. е.3 ^k> 2^k + 3k

. 3) Индуктивный шаг. Докажем, что утверждение выполняется при

n = k +1. Для этого обе части неравенства 3 ^k> 2^k + 3k умножим на 3. Получаем:

3^л^{+ 1} > 3 ∙ 2 ^k + 9k = (2 + 1) 2 ^k+ 3(k + 1) + 6k – 3 = 2 ∙ 2 ^k + 3(k + 1) + 2 ^k + 3(2k – 1) > 2 ^{k + 1}+ + 3(k + 1).

Таким образом, что доказываемое утверждение справедливо при n = k + 1. По методу математической индукции получаем, что утверждение справедливо при любом натуральном n ≥ 3.

Применение метода математической индукции в задачах на суммирование.

Пример 4. Вычислить сумму первых n нечетных чисел натурального ряда.

Решение. S(1) = 1, S(2) = 1 + 3 = 4, S(3) = 1 + 3 + 5 = 9, S(4) = 1 + 3 + 5 + 7 = 16, S(5) = 1 + 3 + 5 + 7 + 9 = 25. Замечаем, что сумма первых n нечетных чисел натурального ряда равна n², т.е. S(n) = n².

Докажем это.

1) Для n = 1 формула верна.

2) Предположим, что она верна для какого-либо натурального n = k, т.е. S(k) =k².

Докажем, что тогда она будет верна и для n = k +1, т.е. S(k+1) = (k + 1)²:S(k + 1) = 1 + 3 + 5 +…+(2k – 1) + (2k + 1) = S(k) + (2k + 1) = k² + 2k + 1 = (k + 1)².

Следовательно, формула верна для всех натуральных значений n, т.е. S(n) = n².

Задачи для самостоятельного решения.

1) Докажите, что для любого натурального n справедливы равенства:

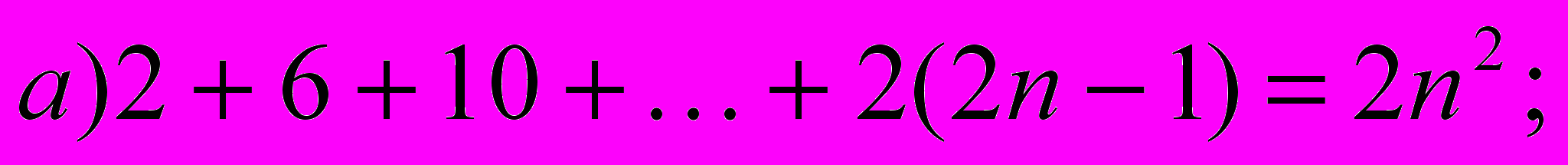
2) Докажите, что при любых натуральных n:

а) n (n²– 1) (n²– 5n + 26) делится на 120;

б) 2 ^{5n+ 1}+ 5 ⁿ^{+ 2} делится на 27;

в) 2 ³ⁿ^{+ 3}– 7n + 41 делится на 49.

3) Докажите, что для любого натурального n справедливы неравенства:

а) 4 ⁿ > n²;

б) 2 ⁿ > n ² – 2n + 2.

4) Найдите сумму:

а) 1 ∙ 1! + 2 ∙ 2! +3 ∙ 3! + … + n ∙ n!;

б)

Используемая литература:

1) Петраков И. С. Математические кружки в 8 – 10 классах: Кн. для учителя.- М.: Просвещение, 1987.-224 с.

2) Галицкий М. Л. и др. Сборник задач по алгебре для 8 – 9 классов: Учебное пособие для учащихся школ и классов с углубленным изучением курса математики. М.: Просвещение, 1992.

3) Шарыгин И. Ф. Факультативный курс по математике: Решение задач: Учеб. пособие для 10 кл. сред. шк.- М.: Просвещение, 1989.-252с.

Blog

Лекция для учеников 8 «А» класса. Учитель математики: Ермеев Валерий Александрович

Содержание