Учебном году

Вид материала

Методическое пособие

Содержание Задание 1: Заполните таблицу. Точка, движимая с бесконечной скоростью, моментально образует линию. (Лейбниц Г.) Олимпиада школьников Задачи окружного этапа Московской городской олимпиады школьников по физике 8.3. В большую кастрюлю с холодной водой бросают десяток ледяных шариков диаметра 1 см (их температура немного ниже 0 10.4. Порция гелия занимает объем 1 л при давлении 0,1 атм. Какую работу может совершить газ, расширяясь без подвода тепла до об

Подобный материал:

• О преподавании учебного предмета «Русский язык» в 2007-2008 учебном году в общеобразовательных, 1500.5kb.
• О преподавании литературы в 2011- 2012 учебном году Нормативно-правовые документы Преподавание, 145.1kb.
• О преподавании курса опк в 2010- 2011 учебном году Нормативно-правовые документы Преподавание, 113.5kb.
• Департамент образования, 978.53kb.
• Учебном году, способствовать развитию партнерских отношений между школой и родителями, 607.52kb.
• Методические рекомендации Опреподавании учебного предмета «География» в общеобразовательных, 141.59kb.
• О преподавании обж в 2010 2011 учебном году Нормативно-правовые документы Преподавание, 112.24kb.
• О преподавании учебного предмета «математика» в общеобразовательных учреждениях кемеровской, 717.16kb.
• Муниципальное общеобразовательное учреждение, 1389.54kb.
• Муниципальное общеобразовательное учреждение, 2175.21kb.

Задание 1: Заполните таблицу.

График	k	b	Функция	v		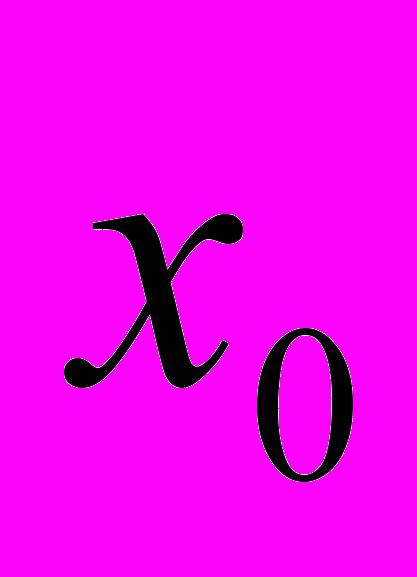Функция
1.	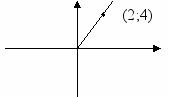2	0	y=2x	2	0	x =2t
2 (0;15) .	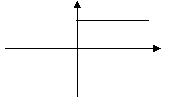0	15	y=15	0	15	x =15
3.	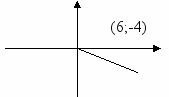	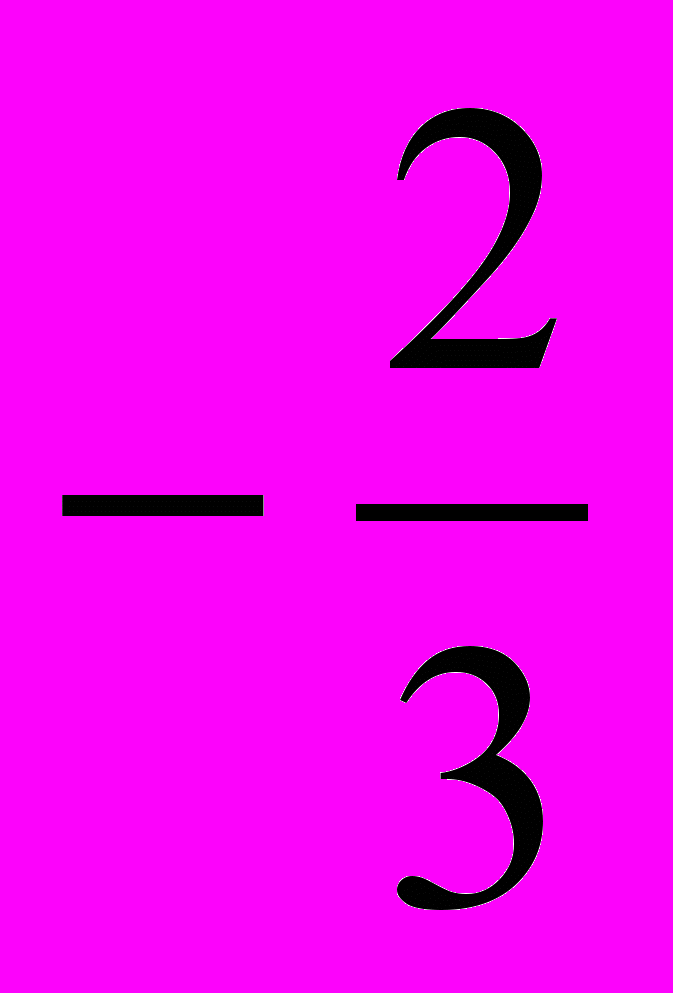0			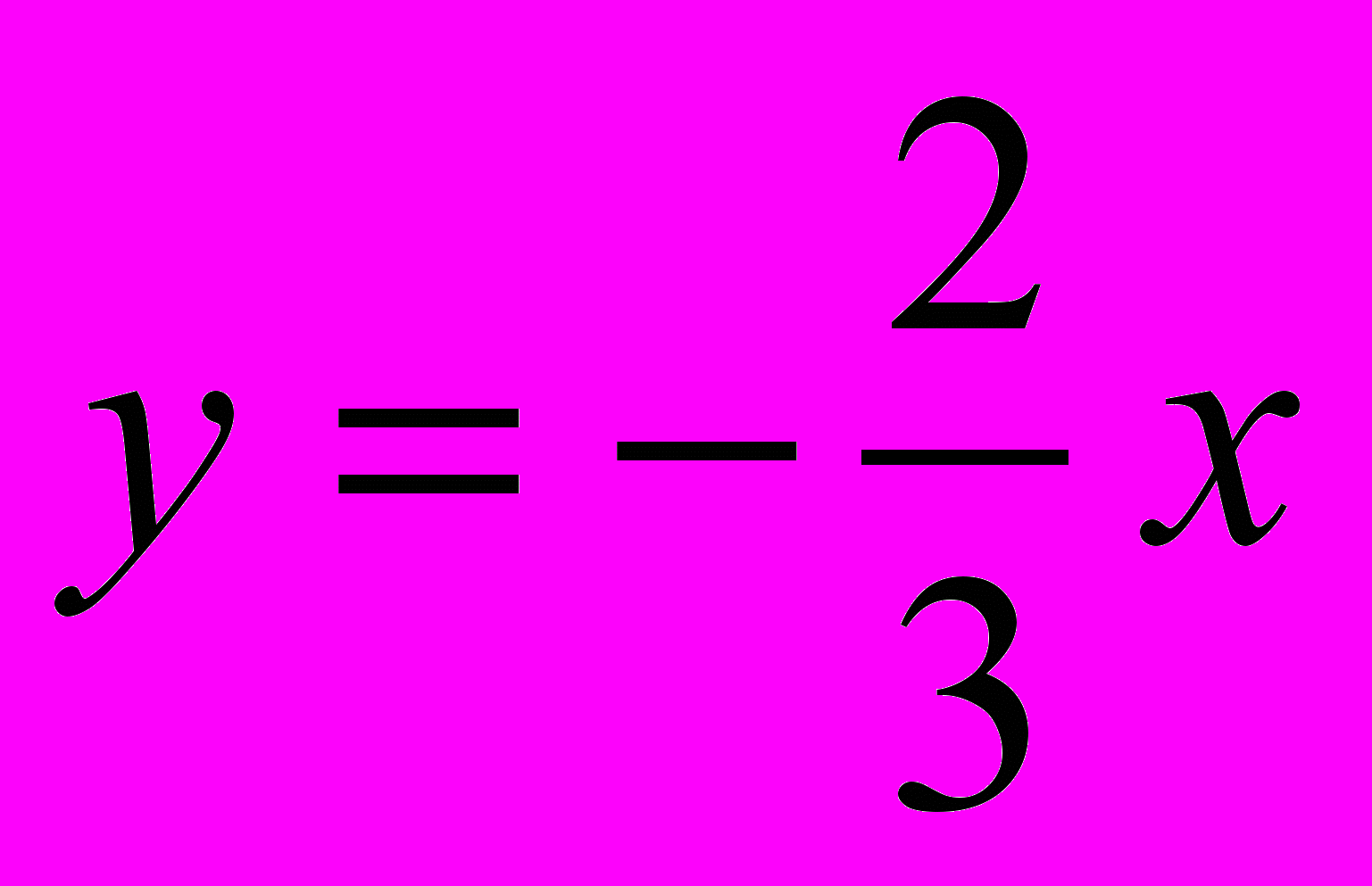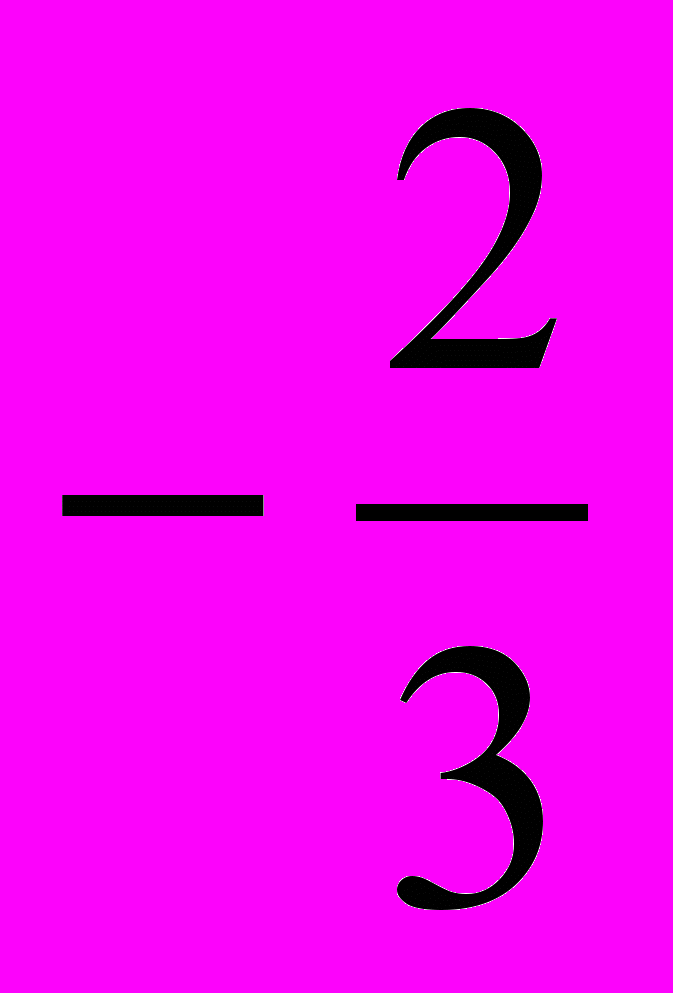0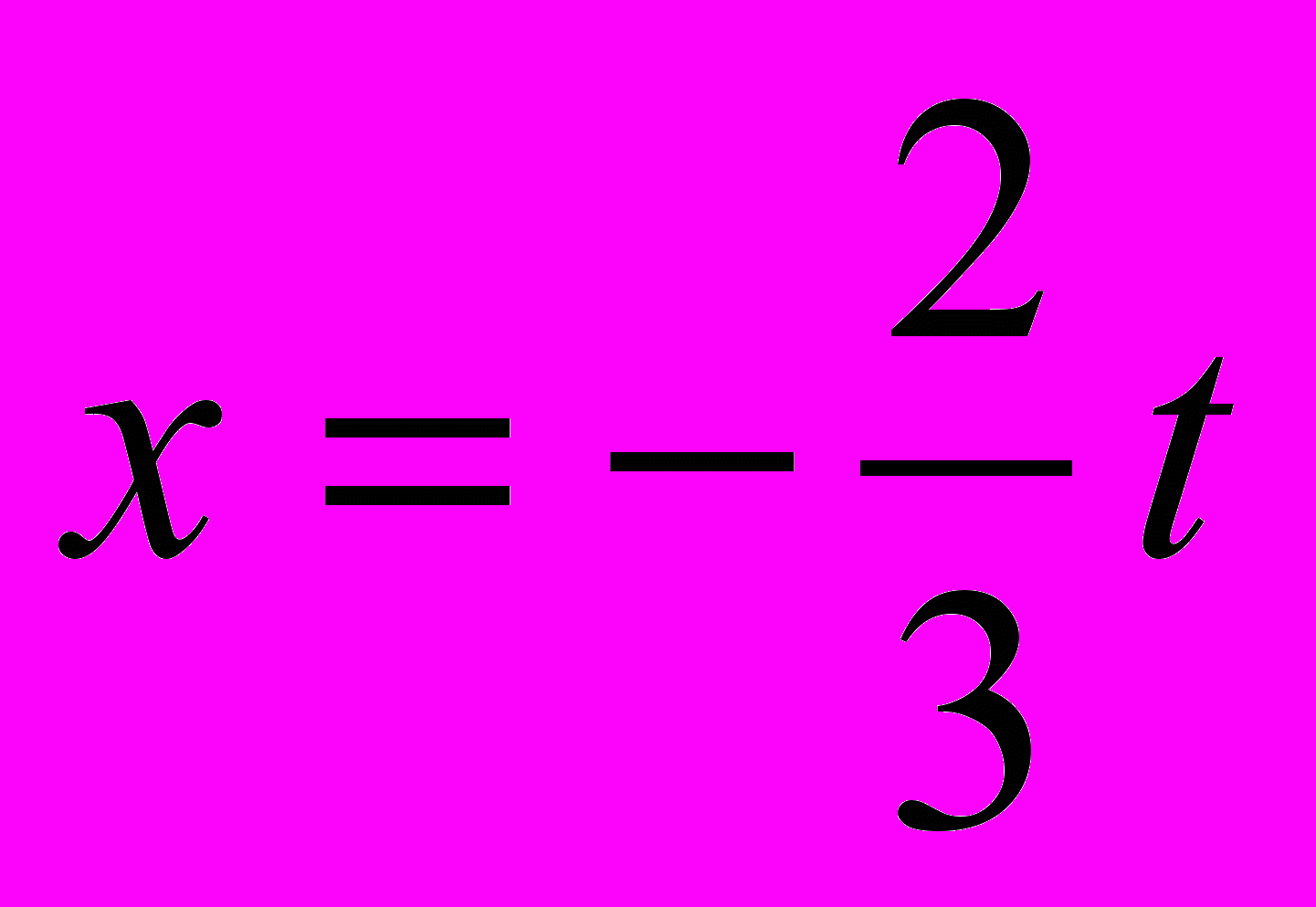
4.	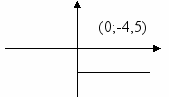0	-4,5	y=-4,5	0	-4,5	x = -4,5
5. 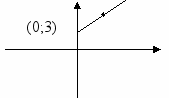(2;7)	2	3	y=2x+3	2	3	x =2t+3
6. 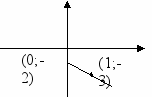(2;7)	-1	-2	y=-x-2	-1	- 2	x =-t-2
7. 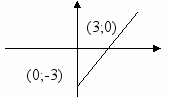(2;7) (2;7)	1	-3	y=x-3	1	-3	x =t-3

Точка, движимая с бесконечной скоростью, моментально образует линию. (Лейбниц Г.)


Задание 2.

Задайте формулой прямую пропорциональность, график которой параллелен графику функций на рис. 5 – 7 из задания 1. (3 примера)

Ответы:

5) у = 2x; y = 2x+5; y = 2x-5

6) y = -x; y = -x+7; y = -x-7

7) у = x; y = x+3; y = x+5


Приведите 3 примера законов движения точечных тел, графики движения которых параллельны графикам движения точечных тел приведенным на рис. 5 – 7 из задания 1.

Ответы:

5. x = 2t; x = 2t+5; x = 2t-5
   
6. x = -t; x = -t+7; x = -t-7
   
7. x = t; x = t+3; x= t+5
   

Задание 3.

Задайте формулой график функции. Напишите закон движения точечного тела,

график движения, которого приведен


Y
на рисунке.


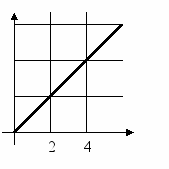
3

6

6

3

X

t

X



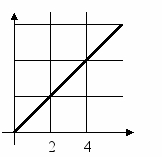
Ответ: y=1,5x x = 1,5t


Вопрос.

Какое взаимное расположение графиков может быть в системе координат?

Ответ.

Графики могут пересекаться или быть параллельными друг другу.

Вопрос.

При каком условии графики параллельны? При каком движении двух тел графики их

движения параллельны?


Ответ.

При условии, что 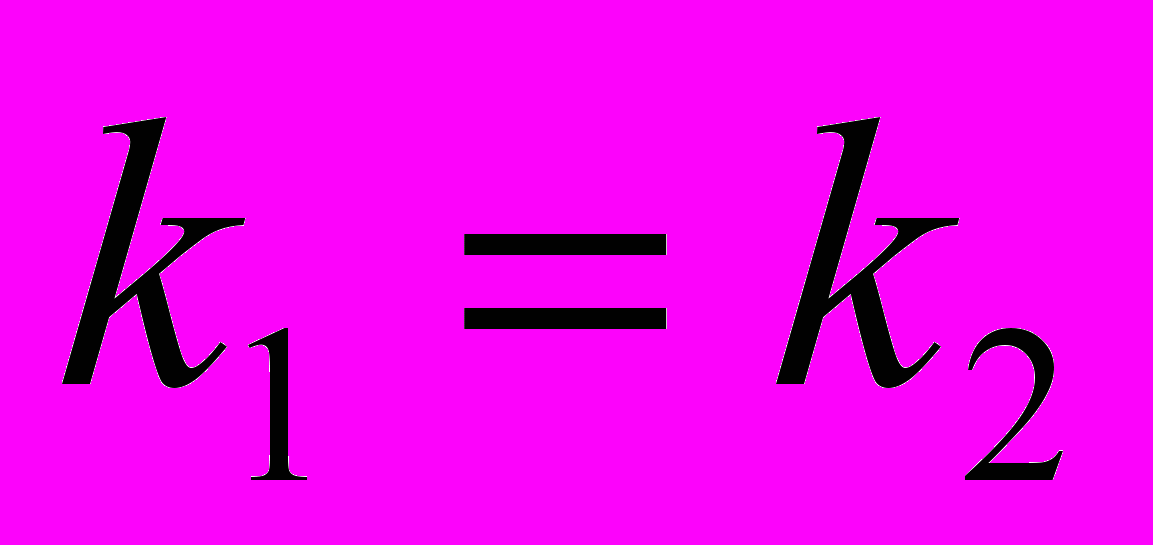. При условии, что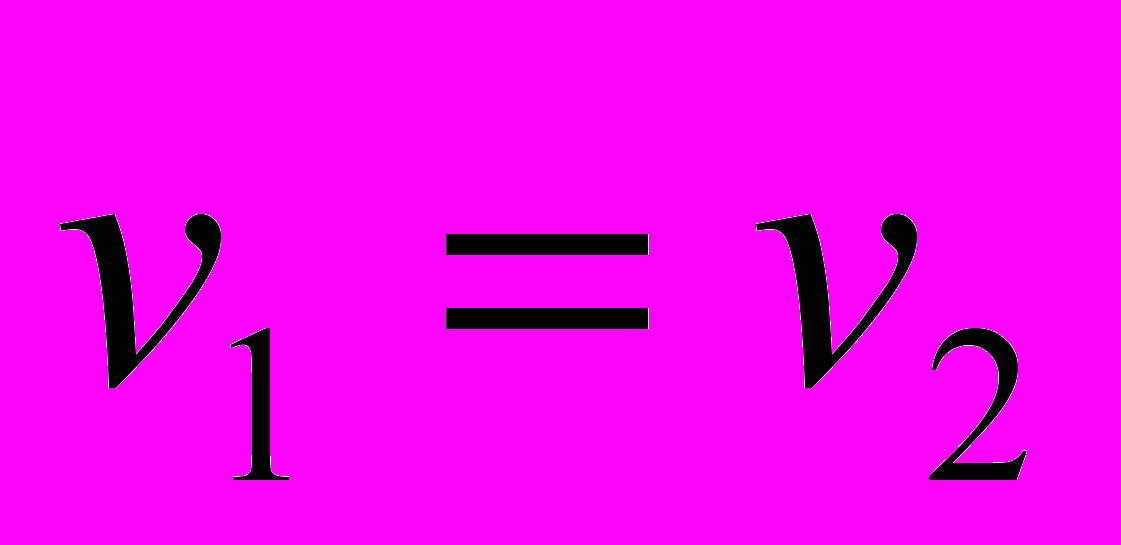 (тела движутся с

одинаковыми скоростями, расстояние

между ними не меняется с течением

времени).


Вопрос.

При каком условии графики пересекаются? При каком движении двух тел графики их

движения пересекаются?


Ответ.

При условии, если 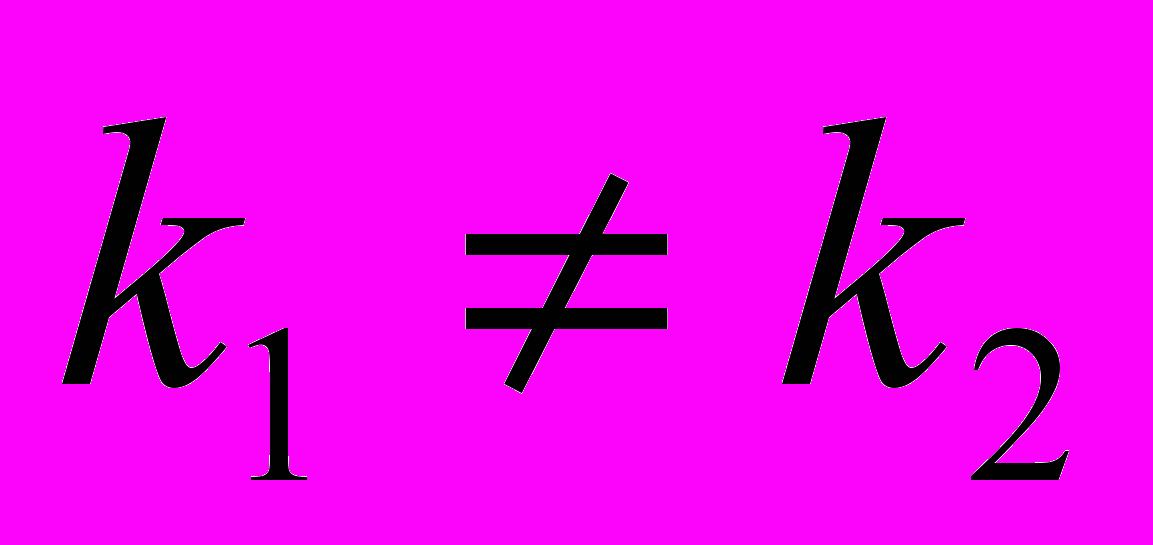При условии, если 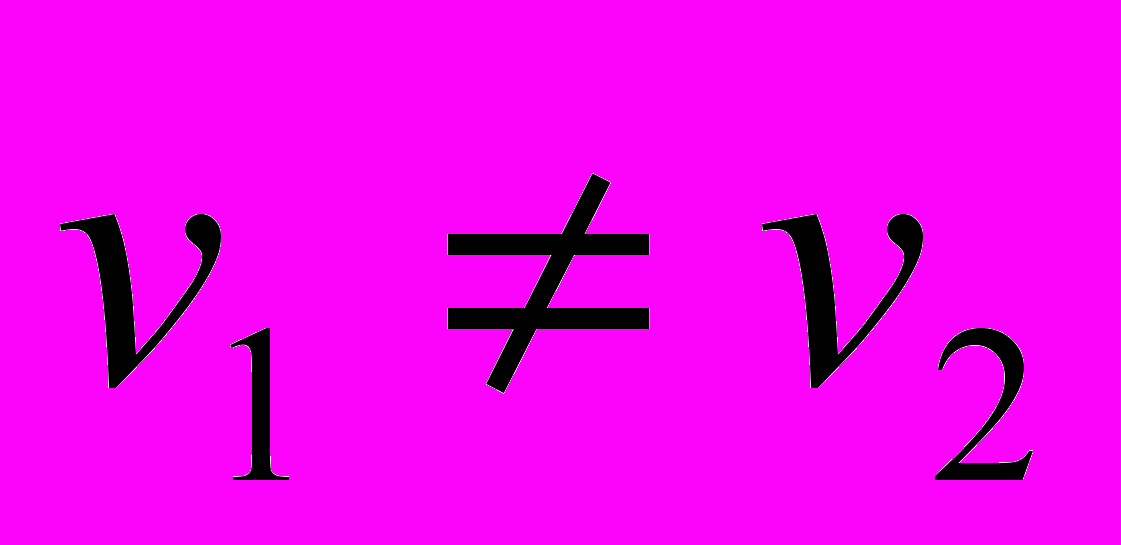(тела движутся

с разными скоростями, они либо

встретятся, либо уже встречались).


Вопрос.

Приведите примеры формул графики Приведите примеры законов движения

функций, которых параллельны. тел, графики движения, которых параллельны.

Ответ.

y = 25x-1 x = 25t-1

y = 25x+17 x = 25t+17


Вопрос.

Приведите примеры формул графики Приведите примеры законов движения

функций, которых пересекаются. тел, графики движения, которых

пересекаются.

Ответ.

y = 17x-3 x = 17t-3

y = 15x+5 x = 15t+5


Вопрос.

Найдите точку пересечения Найдите точку пересечения графиков

графиков двух функций, движения двух тел, законы движения,

формулы,которых которых написаны выше. (Время и

написаны выше. место встречи).

Ответ.

(4; 65) (4; 65)


Задание 5.

Задайте функцию формулой график Напишите закон движения тела,

функции, которой пересекается с которое встретится с телом, закон

графиком функции заданной движения, которого задан

формулой у=2x-3 в т. (1; -1) формулой x = 2t-3 в т. (1; -1)


ОЛИМПИАДА ШКОЛЬНИКОВ

Зильберман А. Р.

доцент кафедры физики МИОО

учитель физики ГОУ «Лицей Вторая школа»

Якута А. А.

методист кафедры физики МИОО

Московская региональная олимпиада школьников по физике


В 2008 году Московская Олимпиада школьников по физике проходила в 69-й раз. Она включала в себя четыре тура: школьный, окружной и два городских теоретических. На Олимпиаду приглашались ученики 7-х – 11-х классов. При этом для семиклассников проводились только три тура (школьный, окружной и первый городской теоретический).

Школьный тур проводился учителями физики школ г. Москвы в декабре 2007 г. Окружной тур проходил 2 февраля 2008 года во всех округах г. Москвы и организовывался УМЛ физики МИОО, окружными методическими центрами административных округов г. Москвы и московскими вузами (физический факультет МГУ им. М.В. Ломоносова, Московский государственный технический университет имени Н.Э. Баумана, Российский университет дружбы народов, Московский институт радиоэлектроники и автоматики, Московский государственный технологический университет СТАНКИН, Московский государственный институт электронной техники, Московский государственный горный университет, Российский государственный технологический университет (МАТИ), Московский педагогический государственный университет, Московский государственный университет природообустройства, Московский государственный университет геодезии и картографии, Московский государственный строительный университет, Московский институт электроники и математики, Московский государственный технический университет гражданской авиации). В окружном туре приняло участие более 12000 человек.

10 февраля 2008 года на физическом факультете МГУ проводился первый теоретический тур городского этапа Олимпиады. Всего в нем приняли участие 1978 человек, в том числе по классам: 7 класс – 239 чел., 8 класс – 323 чел., 9 класс – 310 чел., 10 класс – 496 чел., 11 класс – 610 чел.

Для участия во втором теоретическом туре городского этапа олимпиады, который проходил 29 февраля 2008 года, были приглашены ученики всех классов (кроме 7-го), показавшие лучшие результаты в первом туре, в количестве: 8 класс – 133 чел., 9 класс – 128 чел., 10 класс – 148 чел., 11 класс – 255 чел. (всего – 664 чел.). Затем по итогам второго тура в старших классах (с 9 по 11) были отобраны 58 человек, которые получили приглашение на 3-й (отборочный) экспериментальный тур. Экспериментальный тур прошел 15 марта 2008 года на кафедре физики МИОО. По итогам проведенной Олимпиады с учетом результатов отборочного тура была сформирована команда города Москвы для участия во Всероссийской Олимпиаде школьников по физике 2008 г., которая проходила с 21 по 27 апреля в г. Новосибирске.

В ходе городских туров олимпиады были проведены апелляции. После первого тура на апелляцию имели возможность придти школьники, не прошедшие во второй тур, а после второго – все участники второго тура. Всего было подано более 100 заявлений об апелляции, из них около 30% были полностью или частично удовлетворены.

В состав жюри Олимпиады в этом году входили сотрудники кафедры физики МИОО, физического факультета МГУ им. М.В. Ломоносова и ряда ведущих вузов г. Москвы. Жюри работало с ноября 2007 года по март 2008 года, за это время им было подготовлено свыше 60 задач, большинство из которых являются оригинальными. На окружном туре всем участникам предлагалось решить по 4–5 задач. На городских теоретических турах одиннадцати- и десятиклассники решали по 5 задач, девятиклассники и восьмиклассники – по 4 задачи. Семиклассникам на городском теоретическом туре предлагалось решить 4 задачи.

Анализ работ показал, что на всех турах в каждом классе, кроме девятого, нашелся хотя бы один участник, который решил все задачи. Это свидетельствует о том, что комплект задач был подобран в целом удачно. При этом следует отметить, что наибольшие затруднения у школьников вызвали задачи второго городского теоретического тура для 9 и 10 классов.

Наиболее сложными традиционно были задачи второго городского теоретического тура для 10 и 11 классов. Это объясняется тем, что из числа победителей из этих классов по итогам Всероссийской Олимпиады отбираются кандидаты в команду для участия в Международной олимпиаде по физике нынешнего и следующего годов, что заставляет предъявлять более жесткие требования к уровню знаний учащихся, руководствуясь Программой заключительного этапа Всероссийской олимпиады школьников по физике.

Условия задач городских теоретических туров и экспериментального тура опубликованы в сети Internet по адресу .mccme.ru. Условия избранных задач с решениями ежегодно публикуются в №4 журнала «Квант» за текущий год (ror1.mccme.ru). С материалами, которые могут оказаться полезными при подготовке к олимпиаде, можно ознакомиться по адресам hys.msu.ru/ol и .mccme.ru/mfo .

Ниже приводим варианты окружной олимпиады по физике для 7 – 10 классов

Задачи окружного этапа Московской городской олимпиады школьников по физике

7 класс


7.1. Две сплошные фигурки одинаковых размеров и формы сделаны частью из алюминия, частью – из меди. Первая фигурка: треть массы –алюминий, остальное - медь, вторая: треть объема – медь, остальное - алюминий. Плотность алюминия ровно в три раза меньше, чем меди. Какая из фигурок легче? Во сколько раз?


Пусть ρ – плотность алюминия, V – объем фигурки. Выразим объем фигурки массы М₁: V= (М₁/3)/ρ + (2М₁/3)/3ρ. Отсюда М₁= 9V∙ρ/5. Теперь М₂: М₂= 3ρ∙V/3 + ρ∙2V/3 = 5V∙ρ/3. Видно, что масса в первом случае больше, отношение 27:25 = 1,08.


7.2. Большой аквариум в форме куба имеет объем 1000 м³. Он налит водой до половины. Найти силу, с которой вода давит на дно аквариума. Найти силу, с которой вода давит на одну из боковых стенок. Атмосферное давление 10⁵ Па.


Ребро куба 10 м. Давление на уровне дна 1 атм + 0,5 атм = 1,5 атм. На дно действует сила 1,5∙10⁵∙100 = 1,5∙10⁷ Н. Давление на боковую стенку меняется от 1 атм на уровне воды до 1,5 атм на дне. Возьмем среднюю величину и умножим на площадь «полстенки» (на другую половину давит воздух, но НЕ вода!): 1,25∙10⁵∙50 = 6,25∙10⁶ Н


7.3. Цена пучка петрушки на рынке каждый день меняется, но в среднем за год составляет ровно 1 рубль. Первая старушка приходит на рынок раз в неделю – и покупает ровно 10 пучков петрушки, не глядя на цену. Вторая тоже раз в неделю покупает петрушку – ровно на 10 рублей (если целое число пучков не получается, ей развязывают последний пучок и отмеряют точно необходимое количество). Кто из старушек платит за петрушку больше за целый год? Кому достается за год больше петрушки?


Ясно, что платят за год они одинаково. А вот ДЕШЕВОЙ петрушки вторая покупает больше (при той же сумме), значит она и получит больше. Задача эта вовсе не проста – подойдет и рассуждение «на примере», более туманные соображения (конечно, они должны стоить несколько меньше, чем корректное решение).


8 класс


8.1. Камень бросили вертикально вверх. Известно, что перемещение камня за первые 5 секунд равно по величине перемещению его за последние 3 секунды полета. На какой максимальной высоте побывал камень? Земля в тех местах плоская, воздуха там нет. Камень брошен с уровня земли. Ускорение свободного падения считать 10 м/с².


Ясно, что перемещения имеют РАЗНЫЕ знаки – начальная и конечная точки полета совпадают, получается, что весь полет как раз и занимает 8 секунд. Тогда максимальная высота достигается через 4 секунды после броска, начальная скорость 40 м/с, средняя на пути вверх 20 м/с, максимальная высота 80 м.


8.2. Автомобиль не меняя величины скорости едет по кольцу радиуса 100 км и проезжает его целиком за 12 часов без остановок. Найти среднюю скорость автомобиля за 3 часа, за 6 часов и за 12 часов (приведите три ответа, пожалуйста!).


За 12 часов автомобиль возвращается в начальную точку – средняя скорость (вектор!) за этот интервал получается нулевой. За 6 часов перемещение равно диаметру, т.е. 200 км, средняя скорость 200/6= 33,3 км/час. За 3 часа смещение 100∙√2= 141 км (точнее нет смысла), средняя скорость 141/3= 47 км/час.


8.3. В большую кастрюлю с холодной водой бросают десяток ледяных шариков диаметра 1 см (их температура немного ниже 0⁰С). Они быстро начинают уменьшаться в размерах – таять, через 2 минуты они почти одновременно исчезают. Как изменится время таяния, если шарики с самого начала взять диаметром 2 см?


Количество растаявшего льда определяется поступлением тепла от воды ко льду. Считая температуры воды (большая кастрюля) и кусочков льда (при таянии – 0⁰С) неизменными, получаем постоянный приток тепла на единицу внешней площади льдинки – при этом независимо от размеров льдинки уменьшение размера (радиуса) за секунду окажется постоянным. При увеличении размеров льдинки вдвое, время таяния также вдвое увеличится. Нужно отметить, что это не единственная разумная модель теплообмена, читать решения придется внимательно, не исключая и других (разумных!) вариантов расчета. Но надо иметь в виду, что сильно отличный от «вдвое» ответ разумным не является!


8.4. Две одинаковые батарейки напряжением 1,5 В каждая вначале не соединены друг с другом. Затем между каждым выводом батарейки и каждым из трех оставшихся выводов подключают резистор сопротивлением 1000 Ом. Сколько всего получится резисторов? Какой ток при этом будет течь через каждую из батареек?


Резисторов получается 6. Ясно, что «плюсы» батареек в этой схеме ничем не отличаются друг от друга (это же относится и к «минусам»), токи через соединяющие их резисторы не текут, такие резисторы можно исключить из схемы (это не обязательно делать, перерисовывая схему, рассуждение и без этого проходит!). К «плюсу» первой батарейки оказываются подключенными ровно два резистора, по которым токи будут течь: к «своему» минусу и к «чужому» - эти «минусы» эквивалентны друг другу и токи через них получаются одинаковыми, по 1,5 мА. Тогда ток, «вытекающий» из каждой батарейки, оказывается 3 мА – это и есть ответ задачи.


9 класс


9.1. По гладкому горизонтальному столу едут вдоль одной прямой две одинаковые шайбы, масса каждой шайбы М. Скорости шайб составляют V и 2V, быстрая шайба догоняет медленную. Происходит лобовое столкновение, скорость догонявшей шайбы уменьшается по величине вдвое. Какое количество тепла выделилось при ударе? Могла ли скорость какой-нибудь из шайб изменить при ударе направление движения на противоположное?


Скорости шайб направлены до удара в одну сторону, рассмотрим случай, когда догонявшая шайба не изменила направления скорости: ее скорость после удара составит 2V/2= V. Из закона сохранения импульса мы сразу получим скорость другой шайбы – она получится 2V. Баланс энергий нулевой: суммарная кинетическая энергия шайб до удара такая же, как и после – тепла при ударе не выделится. Теперь с направлениями скоростей: скорость убегавшей шайбы изменить направление явно не может – ее ударяют сзади, а вот скорость налетавшей шайбы в принципе могла бы изменить направление – мешает закон сохранения энергии: если взять скорость ее после удара равной –V, то скорость другой шайбы окажется равной 4V, суммарная кинетическая энергия после удара получается больше, чем до удара, нам это не подходит. Масса шайбы в ответ не попала – проще, все же, задать ее в условии, чем отвечать всем участникам на вопрос: «А чему равна масса шайбы?»


9.2. На гладком горизонтальном столе находится брусок кубической формы массы 2 кг, на его верхней поверхности – второй брусок, его масса 1 кг. Коэффициент трения между поверхностями бруском составляет 0,7. Большой брусок тянут влево горизонтальной силой 6 Н, малый – вправо, горизонтальной силой 3 Н (эти две силы направлены в противоположные стороны!). Найти ускорения брусков.


Нужно разобраться с проскальзыванием: найдем величину силы трения f, при которой тела едут вместе, не проскальзывая. Для этого запишем уравнение для ускорений тел: (F₁-f)/M= (f –F₂)/m , или f= (F₁∙m +F₂ ∙M)/(М+m)= (6∙1+3∙2)/(2+1)= 4 Н. Эта величина меньше максимально возможной величины силы трения μ∙m∙g= 7 Н, тела едут вместе, их ускорения 1 м/с².


9.3. Две одинаковые батарейки напряжением 1,5 В каждая вначале не соединены друг с другом. Затем между каждым выводом батарейки и каждым из трех оставшихся выводов подключают резистор сопротивлением 1000 Ом. Сколько всего получится резисторов? Какой ток при этом будет течь через каждую из батареек?


См решение 8.4.


9.4. В современных цифровых фотоаппаратах объектив часто делается с изменяемым фокусным расстоянием (профессионалы называют такое устройство «трансфокатор», остальные – «зум»). Глаз человека может без напряжения фокусироваться и на очень удаленных предметах, а может «перефокусироваться» на расстояние 8-9 см (близорукий глаз может четко фокусировать и ближе расположенные объекты, но мы говорим о «среднем» зрении). Оцените пределы изменения фокусного расстояния глаза («оптический зум» глаза), считая его шариком диаметра 2 см.


Во всех случаях четкое действительное изображение рассматриваемого предмета нужно получать на глазном дне, сетчатке глаза. Для удаленного на большое расстояние предмета фокусное расстояние получается равным 2 см. Возьмем теперь предмет на минимальном расстоянии от зрачка глаза 8 см. Тогда по формуле линзы: 1/8 + 1/2 = 1/F, F = 8/5 = 1,6 см. Итак, «зум» равен 2/1,6= 1,25.


10 класс

10.1. Автомобиль Жигули самой первой модели едет по огромной горизонтальной асфальтовой площади, описывая круг радиуса 200 м. Его скорость составляет при этом 20 м/с. При каком значении коэффициента трения между асфальтом и шинами автомобиля такое движение возможно? Представим себе, что коэффициент трения ровно вдвое больше этого, минимального значения. За какое время автомобиль сможет увеличить свою скорость до 20,5 м/с, не прекращая движения по кругу? Центр тяжести автомобиля находится на его оси симметрии, на равных расстояниях от передней и задней осей..


Для движения по окружности нужна горизонтальная сила, перпендикулярная направлению вектора скорости – это сила трения, действующая на поворачиваемые вбок передние колеса автомобиля. Максимальная величина силы трения определяется силой реакции в передних колесах (суммарной), при таком положении центра тяжести автомобиля эта сила равна половине силы Mg: μ∙M∙g/2 = M∙V²/R, μ= 2M∙V²/ M∙g∙R = 2∙V²/g∙R= 2∙400/10∙200 = 0,4. Для расчета увеличения скорости автомобиля нужно учесть, что соответствующая сила создается ведущими, задними колесами. Сила трения определяется также половиной силы M∙g и коэффициентом трения 0,8: μ₁∙M∙g/2 = M∙∆V/∆t. Отсюда ∆t =2∙∆V/μ₁∙g = 2∙0,5/0,8∙10 = 0,125 с.


10.2. На гладком горизонтальном столе находится брусок кубической формы массы 2 кг, на его верхней поверхности – второй брусок, его масса 1 кг. Коэффициент трения между поверхностями бруском составляет 0,7. Большой брусок тянут влево горизонтальной силой 6 Н, малый – вправо, горизонтальной силой 3 Н (эти две силы направлены в противоположные стороны!). Найти ускорения брусков.


См. решение 9.2.


10.3. В большом сосуде находится гелий при температуре 100К и давлении 1000 Па. Пылинка в виде кубика объема 1 куб. мм летает по сосуду. Найти число ударов атомов гелия об одну из граней этого кубика за 100 секунд. Все это происходит в состоянии невесомости. Атомная масса гелия 4 г/моль.


Этот маленький кубик по сравнению с размерами частиц огромен, удары частиц о грань этого кубика можно считать по тем же формулам, что и число ударов частиц о стенки сосуда – его скорость можно считать очень малой (нулевой), как и скорости стенок сосуда. Как обычно, N_УД =0,5∙n∙S∙ τ = 0,5∙(N/V)∙S∙V_X∙τ= 0,5∙(N_A∙P/R∙T)∙S∙(k∙T/m)^0,5∙τ. Тут площадь грани кубической пылинки S= 1∙10^-6 м², проекция скорости на направление оси, перпендикулярной грани пылинки V_X= (k∙T/m)^0,5= 4,5∙10² м/с. Число ударов примерно составит N_УД =0,5∙6∙10²³∙10³∙450∙1∙10^-6∙100/8,3∙100= 1,6∙10²² ударов.


10.4. Порция гелия занимает объем 1 л при давлении 0,1 атм. Какую работу может совершить газ, расширяясь без подвода тепла до объема 100 л?


Тут не нужно «интегрировать по адиабате» – достаточно понять, что газ расширяется во много раз, его температура при этом падает до очень малой величины и практически вся начальная внутренняя энергия порции газа переходит в совершенную им работу: A= 1,5ν∙R∙T₁= 1,5P∙V₁= 1,5∙10000∙0,001 = 15 Дж. Конечно, можно решать эту задачу и по точным формулам (хотя, не очень они и точные!), ответ получается практически таким же, нет смысла ставить за такое решение больше баллов.


10.5. Три одинаковые батарейки напряжением 1,5 В каждая вначале не соединены друг с другом. Затем между каждым выводом батарейки и каждым из пяти оставшихся выводов подключают резистор сопротивлением 1000 Ом. Сколько всего получится резисторов? Какой ток при этом будет течь через каждую из батареек?


Резисторов получается 15. Ясно, что «плюсы» батареек в этой схеме ничем не отличаются друг от друга (это же относится и к «минусам»), токи через соединяющие их резисторы не текут, такие резисторы можно исключить из схемы (это не обязательно делать, перерисовывая схему, рассуждение и без этого проходит!). К «плюсу» первой батарейки оказываются подключенными ровно три резистора, по которым токи будут течь: к «своему» минусу и к двум «чужим» - эти «минусы» эквивалентны друг другу и токи через них получаются одинаковыми, по 1,5 мА. Тогда ток, «вытекающий» из каждой батарейки, оказывается равен 4,5 мА – это и есть ответ задачи.