Учебном году
| Вид материала | Методическое пособие |
- О преподавании учебного предмета «Русский язык» в 2007-2008 учебном году в общеобразовательных, 1500.5kb.
- О преподавании литературы в 2011- 2012 учебном году Нормативно-правовые документы Преподавание, 145.1kb.
- О преподавании курса опк в 2010- 2011 учебном году Нормативно-правовые документы Преподавание, 113.5kb.
- Департамент образования, 978.53kb.
- Учебном году, способствовать развитию партнерских отношений между школой и родителями, 607.52kb.
- Методические рекомендации Опреподавании учебного предмета «География» в общеобразовательных, 141.59kb.
- О преподавании обж в 2010 2011 учебном году Нормативно-правовые документы Преподавание, 112.24kb.
- О преподавании учебного предмета «математика» в общеобразовательных учреждениях кемеровской, 717.16kb.
- Муниципальное общеобразовательное учреждение, 1389.54kb.
- Муниципальное общеобразовательное учреждение, 2175.21kb.
Рис.1
ак от чего зависит длина тормозного пути автомобиля, почему она меняется в различных условиях движения? Что мы, как пешеходы, должны учитывать для нашей безопасности при передвижении по улицам и перекресткам?Сообщение «кинематической» группы.
Рассматривается стандартная, достаточно простая, кинематическая задача по определению изменения координаты материальной точки, движущейся с ускорением. Но прежде, давайте определим возможные параметры такого движения, т.е. фактически исходные данные задачи. Для этого вспомним некоторые сведения из кинематики. На рис.1 представлены основные формулы, используемые в кинематике - «Опорный конспект по кинематике». Однако сначала следует определить, можно ли использовать понятие «материальная точка» для рассматриваемого случая. Если начальную скорость автомобиля принять равной 72 км/час, надо сказать весьма обычная величина даже для крупного города, значение удобное и для расчетов, поскольку, как Вы все уже определили, это 20 м/c. Данные экспериментов [
 1], свидетельствуют, что в обычных условиях (горизонтальная дорога, сухой асфальт и др.) длина тормозного пути составит около 30м, что не так уж сильно превышает размеры самого автомобиля (4-5м). В этих условиях, чтобы использовать удобное понятие материальной точки, выберем центр тяжести автомобиля за эту материальную точку и будем спокойно пользоваться формулами кинематики. Однако, прежде всего, следует выбрать удобную систему координат. Будем считать, что движение прямолинейное, поэтому нам понадобится одна ось (Х, декартовой системы координат). Систему координат свяжем с дорогой, а начало поместим в точку, в которой началось торможение автомобиля. Рассмотрим р
1], свидетельствуют, что в обычных условиях (горизонтальная дорога, сухой асфальт и др.) длина тормозного пути составит около 30м, что не так уж сильно превышает размеры самого автомобиля (4-5м). В этих условиях, чтобы использовать удобное понятие материальной точки, выберем центр тяжести автомобиля за эту материальную точку и будем спокойно пользоваться формулами кинематики. Однако, прежде всего, следует выбрать удобную систему координат. Будем считать, что движение прямолинейное, поэтому нам понадобится одна ось (Х, декартовой системы координат). Систему координат свяжем с дорогой, а начало поместим в точку, в которой началось торможение автомобиля. Рассмотрим р
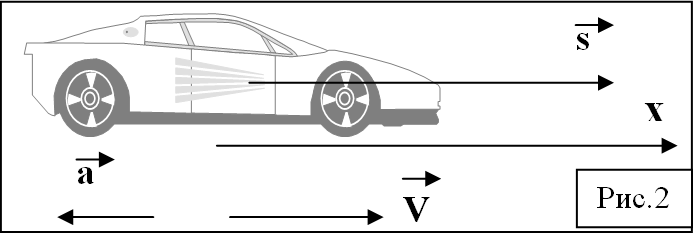
ис.2, поясняющий постановку задачи. Обозначим начальную скорость автомобиля Vo , ускорение a. Если направление вектора скорости вдоль оси Х, то вектор ускорения направлен в противоположную сторону, скорость уменьшается, вплоть до нулевого значения (V=0). Движение будем считать равноускоренным (равнозамедленным) a=сonst. Значения ускорений, соответствующие реальным разнообразным условиям можно взять из [1]. Из уравнения (4) рис.1 легко получить уравнение движения материальной точки S(t)
S = Х - Хо = Vо t + at2/2,
а из уравнения (3) также легко получается уравнение скорости V(t):
V = Vо + at.
Н
 е забудем, что уравнения получены для проекций величин (a0). Из уравнения (5) получается зависимость тормозного пути Sт от начальной скорости и ускорения торможения:
е забудем, что уравнения получены для проекций величин (a0). Из уравнения (5) получается зависимость тормозного пути Sт от начальной скорости и ускорения торможения:Sт = -Vо2 /2a ,
а
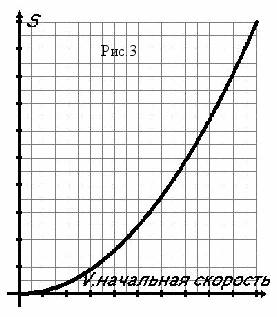
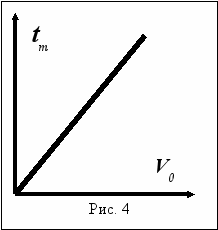 из (3) можно определить время торможения : t = -Vо/a. Из последних двух выражений следует, что тормозной путь квадратично увеличивается от начальной скорости, скажем, при увеличении скорости в 2 раза тормозной путь автомобиля увеличивается уже в 4 раза, время торможения зависит от начальной скорости линейно, т.е. в нашем случае удваивается. Очень удобно анализировать функциональные зависимости, представленные в графическом виде. Вспомним графики линейной и квадратичной функций, недавно изученных нами на уроках математики, и построим зависимость тормозного пути от начальной скорости (квадратичная функция рис.3) и зависимости времени торможения, также от начальной скорости (линейная функция рис.4). Следует обратить внимание, что тангенс угла наклона этой прямой обратно пропорционален ускорению торможения. Интересно также графически рассмотреть, как меняется скорость автомобиля со временем. Это тоже линейная, но «падающая» зависимость рис.5. Несложные вычисления показывают, что прямая пересекает ось абсцисс при t= Vо/a , а это и есть время торможения. Необходимо также добавить, что площадь под графиком равна тормозному пути автомобиля. Вспоминая, что площадь прямоугольного треугольника равна половине произведения его катетов получим: S = Vо2/2a, что согласуется с ранее полученными результатами. Из уравнения (3) , можно получить зависимость координаты (перемещения) автомобиля от времени (рис.6). Максимум квадратичной функции достигается, конечно, при t = Vо/a. Чтобы наше семейство графических зависимостей было полным, необходимо привести график зависимости ускорения автомобиля от времени (рис.7).
из (3) можно определить время торможения : t = -Vо/a. Из последних двух выражений следует, что тормозной путь квадратично увеличивается от начальной скорости, скажем, при увеличении скорости в 2 раза тормозной путь автомобиля увеличивается уже в 4 раза, время торможения зависит от начальной скорости линейно, т.е. в нашем случае удваивается. Очень удобно анализировать функциональные зависимости, представленные в графическом виде. Вспомним графики линейной и квадратичной функций, недавно изученных нами на уроках математики, и построим зависимость тормозного пути от начальной скорости (квадратичная функция рис.3) и зависимости времени торможения, также от начальной скорости (линейная функция рис.4). Следует обратить внимание, что тангенс угла наклона этой прямой обратно пропорционален ускорению торможения. Интересно также графически рассмотреть, как меняется скорость автомобиля со временем. Это тоже линейная, но «падающая» зависимость рис.5. Несложные вычисления показывают, что прямая пересекает ось абсцисс при t= Vо/a , а это и есть время торможения. Необходимо также добавить, что площадь под графиком равна тормозному пути автомобиля. Вспоминая, что площадь прямоугольного треугольника равна половине произведения его катетов получим: S = Vо2/2a, что согласуется с ранее полученными результатами. Из уравнения (3) , можно получить зависимость координаты (перемещения) автомобиля от времени (рис.6). Максимум квадратичной функции достигается, конечно, при t = Vо/a. Чтобы наше семейство графических зависимостей было полным, необходимо привести график зависимости ускорения автомобиля от времени (рис.7). 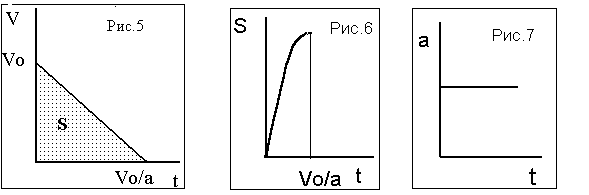
Замечание председателя группы оппонентов:
«

Кинематическая» группа очень полно рассмотрела процесс торможения с этой точки зрения. Однако, в реальности существует один, очень важный фактор, сильно влияющий на параметры торможения автомобиля и который может быть рассмотрен с «кинематической» точки зрения. Я хочу сказать о времени реакции водителя автомобиля. Между моментом, когда водитель заметил препятствие перед автомобилем и началом торможения проходит некоторое время, которое можно назвать временем реакции (tр.). Это время зависит от многих факторов (индивидуума, его состояния, например усталости, внимательности и др.). Для его оценки можно применить очень простой способ. Здесь нам снова поможет кинематика. Для проведения эксперимента, я бы попросил помощи члена группы. Я беру длинную линейку и держу ее вертикально. Мой помощник располагает пальцы руки около начала линейки (нулевого деления), которое расположено снизу, не зажимая ее на расстоянии нескольких см от ее поверхности. Я не буду его предупреждать о моменте, когда я ее отпущу. Поэтому линейка пролетит некоторое расстояние h, как свободно падающее тело. Все хорошо помнят это выражение: h = gt2/2 , отсюда легко определить время реакции моего помощника
tр =
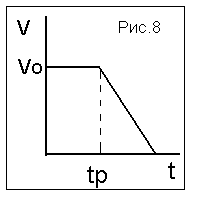
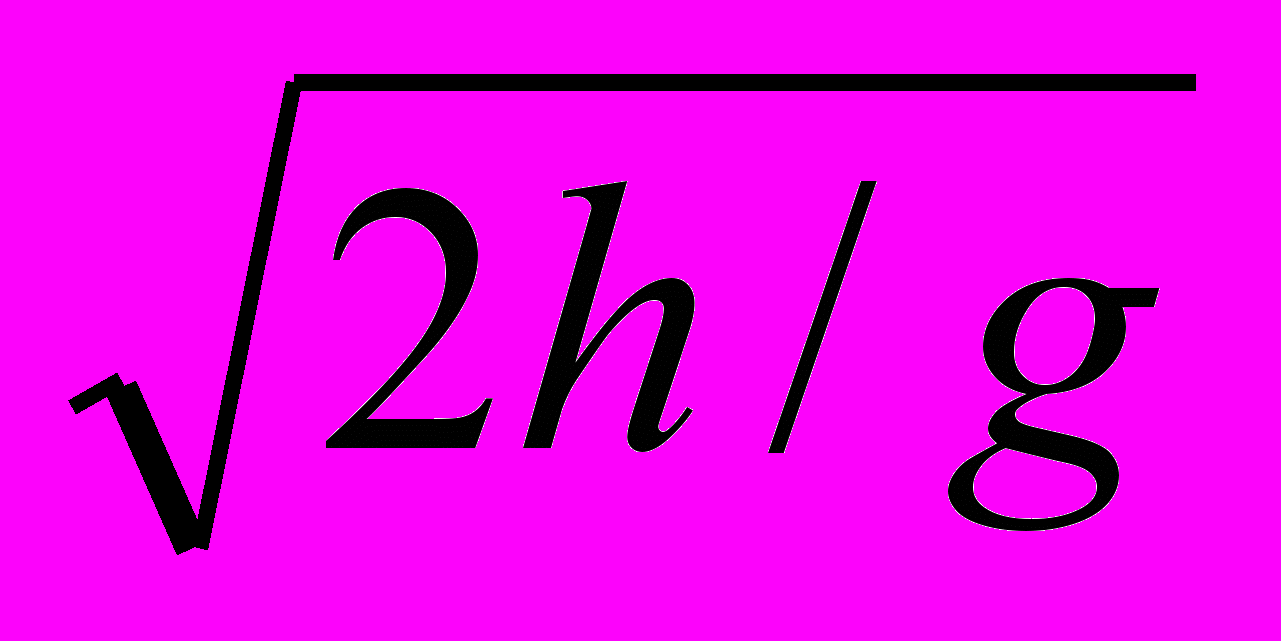 . Итак, попробуем: h =60см, конечно, нужно провести несколько экспериментов, взять среднее значение, но это уже не наша задача. Оценка дает время реакции около 0,35с. Может это покажется небольшой величиной, но автомобиль, движущийся с постоянной скоростью 20 м/c пройдет за это время 7м. Поэтому график на рис. 5 необходимо изменить (см. рис.8). Тормозной путь должен увеличиться на эту величину. Таким образом, движение автомобиля при торможении надо разделить на два этапа: равномерное движение и равнозамедленное движение, вплоть до полной остановки.
. Итак, попробуем: h =60см, конечно, нужно провести несколько экспериментов, взять среднее значение, но это уже не наша задача. Оценка дает время реакции около 0,35с. Может это покажется небольшой величиной, но автомобиль, движущийся с постоянной скоростью 20 м/c пройдет за это время 7м. Поэтому график на рис. 5 необходимо изменить (см. рис.8). Тормозной путь должен увеличиться на эту величину. Таким образом, движение автомобиля при торможении надо разделить на два этапа: равномерное движение и равнозамедленное движение, вплоть до полной остановки.Председатель: если у оппонентов больше замечаний нет, передаю слово «динамической» группе.
С



ообщение «динамической» группы.
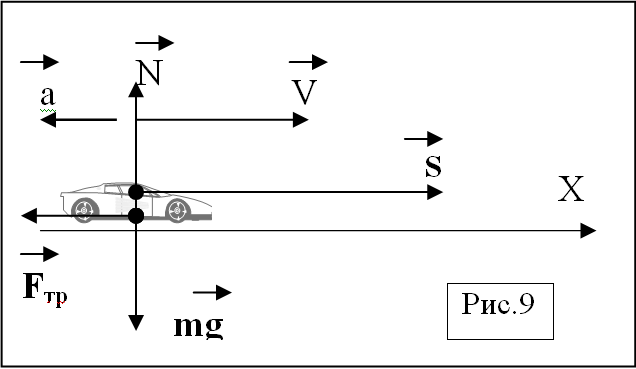
Прежде всего необходимо отметить, что любое движущееся тело стремится сохранить свое состояние равномерного прямолинейного движения. Это следствие I-закона Ньютона-закона инерции. Теперь будем рассматривать задачу с точки зрения II-закона Ньютона. Представляем схематический чертеж (рис.9), поясняющий задачу. Систему координат возьмем ту же, что и кинематическая группа. На рисунке представлены все силы, действующие на тело, а также его ускорение. N-cила реакции опоры, mg- cила тяжести, Fтр.- сила трения. В проекции на ось X II-закон Ньютона можно записать в следующем виде:
 Fтр.= μN = μgm = ma,
Fтр.= μN = μgm = ma, о
 тсюда а = μg., где μ-коэффициент трения скольжения. Будем рассматривать случай экстренного торможения, когда колеса автомобиля заблокированы и скользят по асфальту. Тогда μ-коэффициент трения резины по асфальту. Используя, это значение ускорения и, полученные ранее формулы, можно получить выражение для длины тормозного пути S = V2/2μg и времени торможения t = V/μg , последнее выражение можно получить сразу, если воспользоваться записью II-закона Ньютона в импульсной форме: Ft = Δp= -mVo, отсюда получается уже известное выражение t = Vo/ μg . Проанализируем эти выражения. И тормозной путь, и время торможения обратно пропорциональны коэффициенту трения, поэтому при изменении условий движения (мокрый, грязный асфальт или, тем более обледенелый) величина тормозного пути и времени торможения резко возрастают. Из II закона Ньютона в импульсной форме хорошо видно, что при очень малом времени остановки автомобиля, например при ударе о массивное тело, сила, действующая на автомобиль становится столь большой, что приводит к его разрушению.
тсюда а = μg., где μ-коэффициент трения скольжения. Будем рассматривать случай экстренного торможения, когда колеса автомобиля заблокированы и скользят по асфальту. Тогда μ-коэффициент трения резины по асфальту. Используя, это значение ускорения и, полученные ранее формулы, можно получить выражение для длины тормозного пути S = V2/2μg и времени торможения t = V/μg , последнее выражение можно получить сразу, если воспользоваться записью II-закона Ньютона в импульсной форме: Ft = Δp= -mVo, отсюда получается уже известное выражение t = Vo/ μg . Проанализируем эти выражения. И тормозной путь, и время торможения обратно пропорциональны коэффициенту трения, поэтому при изменении условий движения (мокрый, грязный асфальт или, тем более обледенелый) величина тормозного пути и времени торможения резко возрастают. Из II закона Ньютона в импульсной форме хорошо видно, что при очень малом времени остановки автомобиля, например при ударе о массивное тело, сила, действующая на автомобиль становится столь большой, что приводит к его разрушению.И

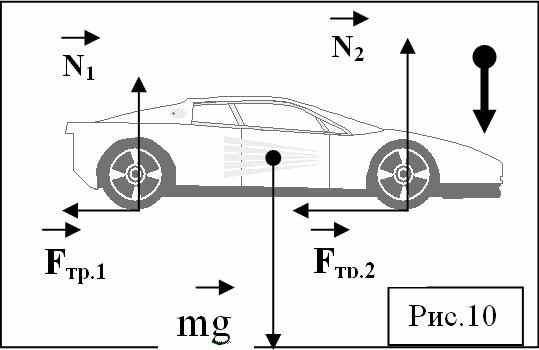
нтересно рассмотреть вопрос: почему при торможении передняя часть автомобиля прижимается к дороге сильнее задней? В этом случае нельзя рассматривать автомобиль как материальную точку. На рис.10 представлены вектора сил, действующих на автомобиль при торможении. Возникает момент сил, приводящий к перераспределению сил реакции опоры, действующих на переднюю и заднюю ось автомобиля. Давление задней оси уменьшается, а передней увеличивается, также меняются и значения сил трения.
Председатель: «динамическая группа расширила задачу и добавила новые результаты в нашу копилку сведений, теперь дадим слово «энергетической» группе.
Сообщение энергетической группы.
Мы будем пользоваться понятиями «работа», «энергия», а основным законом будет закон сохранения энергии. Для рассмотрения нам подойдет рисунок выполненный «динамической» группой (рис.9). Вначале автомобиль обладал кинетической энергией Eк = mVo2/2. Потенциальная энергия автомобиля во время движения не изменялась, т.к. он, как мы полагаем, двигался по горизонтальной дороге. Работа силы трения может быть представлена следующим выражением: Aтр.= Fтр.Scosα, т.к. α =180о то работа силы трения отрицательна, поэтому она фактически “съедает” кинетическую энергию автомобиля, переводя ее во внутреннюю энергию, т.е. в тепло. При этом сильно разогреваются шины автомобиля. Запишем этот процесс в виде уравнения:
Aтр.= Fтр.Scosα= - mVo2/2, (конечное значение кинетической энергии равно 0). Отсюда, используя значение силы трения полученное предыдущей группой, получим выражение для тормознолго пути автомобиля mVo2/2 = μmgS и, наконец, S = Vo2/2μg. Как и следовало ожидать, оно совпадает с полученным ранее динамической группой значением.
Председатель: поблагодарим «энергетическую» группу за интересное сообщение и снова предоставим слово представителю группы оппонентов.
Замечание «математика», представителя группы оппонентов
Мне кажется, что энергетическая группа упустила возможность использования графического подхода для оценки полученных результатов. Представляет интерес исследовать зависимость кинетической энергии автомобиля от его координаты и времени (за ноль принято начало торможения автомобиля). Несложно записать зависимость кинетической энергии от перемещения (координаты), поскольку убыль энергии будет определятся уводом энергии во внутреннюю за счет работы силы трения :
E
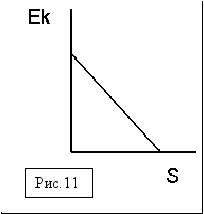 k = Ek0 –Fтр. S = Ek0 - mg S, где Eko = mVo2/2
k = Ek0 –Fтр. S = Ek0 - mg S, где Eko = mVo2/2Теперь несложно построить график (см. рис.11). Это «падающая» линейная зависимость. Прямая пересекает ось абсцисс в точке S = Vo2/2g. Это легко получить из предыдущего уравнения. Разумеется, результат совпадает с длиной тормозного пути.
Н
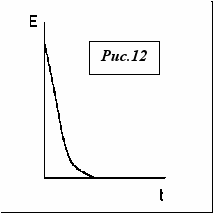 есколько сложнее получить зависимость Ek(t), т.е. зависимость кинетической энергии автомобиля от времени во время торможения. Для этого, воспользовавшись уравнением 4 (рис.1) и выражением для кинетической энергии получим:
есколько сложнее получить зависимость Ek(t), т.е. зависимость кинетической энергии автомобиля от времени во время торможения. Для этого, воспользовавшись уравнением 4 (рис.1) и выражением для кинетической энергии получим: Ek = mV2 /2 = m/2 (V20 + 2atV0 + a2t2)
Напомним, что ускорение отрицательно. Проанализируем эту функциональную зависимость. Это «классическая» парабола. Поскольку корнем выражения в скобках является значение t = Vo/a, то вершина касается оси абсцисс в этой точке, при t = 0 Ek = mV o 2/2. Общий вид графика приведен на рис.12. Из графика хорошо видно, что наиболее интенсивно автомобиль теряет энергию именно в первые моменты торможения.
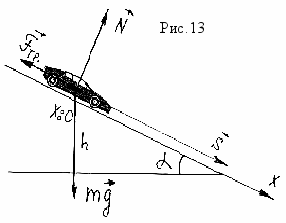
Интересно также разобрать условия торможения автомобиля на наклонной плоскости, ведь не всегда движение происходит на горизонтальной дороге. Для короткого примера снова воспользуемся «энергетическим» подходом. Будем считать, что автомобиль тормозит на спуске (рис.13). Закон сохранения энергии можно записать теперь в таком виде
mVo2/2 = Fтр. S – mgh, где h = S sin , а
Fтр. = mg cos , поэтому: mVo2/2 = mg cos S – mg S sin ,
отсюда нетрудно получить выражение для тормозного пути автомобиля:
S
 = Vo2/2 g (cos – sin )
= Vo2/2 g (cos – sin )Проанализируем его. Мы видим, что в данном случае длина тормозного пути будет больше, чем на горизонтальной дороге. При движении в гору наоборот, т.к. знак (-) заменится на (+). Интересно отметить, что при = tg знаменатель выражения обращается в 0, т.е. автомобиль на наклонной плоскости уже не остановится! Мы предлагаем всем оценить в каких реальных условиях это станет возможным. Очевидно, водители должны учитывать это обстоятельство. Аналогичный подход может быть использован и при «динамическом» рассмотрении задачи.
Заключительное слово председателя.
Мне кажется, что мы провели довольно широкое и многостороннее обсуждение данной проблемы. Различные подходы дали одинаковые конечные результаты, но показали, что в отдельных случаях можно получить более быстро конечный результат пользуясь, например, законом сохранения энергии. Основные выводы:
- Нельзя остановить движущееся транспортное средство мгновенно.
- Длина тормозного пути квадратично возрастает с увеличением скорости.
- На длину тормозного пути оказывает влияние коэффициент трения между шинами и покрытием дороги. На мокрой, грязной, а тем более обледенелой дороге тормозной путь увеличивается.
- Время реакции водителя необходимо учитывать при реальной оценке тормозного пути автомобиля.
- Длина тормозного пути на спусках увеличивается по сравнению с горизонтальной дорогой.
В заключении, следует выразить надежду, что и водители и пешеходы будут учитывать эти обстоятельства, что приведет к снижению трагической статистики на дорогах.
Кулешова Т.Г.,
Учитель физики ГОУ СОШ №1941
Амелькина Г.И.
Учитель математики ГОУ СОШ №1941
Графики линейной функции и их применение при изучении физики в 7 классе по учебнику физики 7 класса Грачева А.В., Погожева В.А., Селиверстова А.В. и алгебры по учебнику алгебры 7 класса Макарычева Ю.Н. и др.
Что касается математики, то она интересует меня лишь постольку, поскольку я могу применить её
в физике
( Эйнштейн А.)
Одним из пунктов целевой ориентации педагогических технологий является интегрирование предметов не формально, а через общие содержательные линии и показ межпредметных связей, что помогает формировать у школьников «целостную картину мира».
Значительная часть учащихся испытывает большие трудности в решении задач, даже несложных, типовых. Это подрывает веру в собственные силы и возможности. При этом наибольшие затруднения учащиеся испытывают при построении и анализе графиков как в курсе математики 7 класса, так и физики. Обучив семиклассников построению графика линейной функции мы приступаем к элементарному исследованию поведения линейной функции. Важно установить как изменение значений коэффициентов К и В отражается на изменении её физического смысла или как физический смысл функции меняется в зависимости от значения коэффициентов К и В.
Легче тем ребятам, которые в начальной школе изучали математику по учебнику Л.Г. Петерсон. Не зная таких сложных для них слов как «функция» и «анализ», они решают много задач, с помощью которых формируется восприятие графика, как наглядного изображения движения. Ребята получают объём знаний, позволяющий по графику движения ответить на ряд очень важных вопросов и решить довольно сложные задачи: определить направление движения тел, место и время встречи – координаты точки пересечения графиков, найти расстояние, пройденное за определённое время, сравнить скорости движущихся тел, записать формулой зависимость расстояния от времени движения, составить рассказ, сказку-событие. Недостаток внимания, который уделяется этим принципиально важным темам в школьном курсе приводит к тому, что проблемы с построением графиков и их анализом сохраняются и в более старших классах.
По учебнику Макарычева Ю.Н. «Алгебра,7», буквально в начале учебного года вводятся и отрабатываются такие новые для ребят понятия как «Функция. График функции». Формирование и развитие функционально-графических представлений и умений учащихся начинается с линейных функций y = kx + b, графиком которых является «Прямая линия – кратчайшая линия между двумя точками» (ал-Каши Д.) Важно обратить внимание ребят на то, что строить графики лучше по двум «хорошим» точкам, достаточно далеко расположенными друг от друга и по возможности имеющими целочисленные координаты. Использование таких точек сыграет в дальнейшем свою положительную роль на уроках физики в уменьшении неточностей при чтении и анализе графиков движений.
Для того чтобы закрепить материал по теме: «Функция. График функции», показать детям область применения, полученных знаний, заинтересовать их изучением этой темы удобно использовать интегрированные уроки математики и физики. Очень хорошо для этого подходит новый учебник физики 7 класса авторов: Грачев А.В., Погожев В.А., Селиверстов А.В.
Интегрированные уроки основаны на идее непрерывного образования, что способствует снятию стрессообразующих факторов учебного процесса и созданию психологической комфортности. Вовлечение учеников в творческий поиск, их активность идет от сознания необходимости приобретения тех знаний и умений, которыми они овладевают. Одним из путей решения этого вопроса на уроках физики является связь изучаемого материала с жизнью через показ использования получаемых ими знаний в науке и создание ситуаций, понятных и близких ученикам в соответствии с их возрастными особенностями.
Изучение в 7 классе кинематики значительно облегчается и упрощается, а также становится наиболее доступным и интересным при использовании межпредметных связей с образовательными областями математики на интегрированных уроках математики и
физики при использовании учебника физики Грачева А.В., Погожева В.А.,
Селиверстова А.В. Особенно это заметно при изучении таких разделов, как прямолинейное равномерное движение и способы описания прямолинейного равномерного движения, в которых рассматриваются графический способ описания движения, закон движения тела в аналитическом виде, графический и аналитический способы решения задач кинематики.
На уроках математики решается целый ряд вопросов тесно переплетающихся с законами, описывающими физические явления. Самостоятельно сопоставить, связать отдельные темы двух таких трудных предметов, как математика и физика, даже для сильных учеников очень сложно. А наша задача помочь им в этом.
Методические рекомендации по итогам диагностики учебных достижений и результатам аттестационного тестирования по физике в 2006 – 2007 учебном году указывают на то, что «следует существенно увеличить удельный вес заданий с использованием графиков. В стандартных задачниках они встречаются достаточно редко, поэтому необходимо для каждой вновь вводимой формулы изучить ее графическую интерпретацию. В заданиях такого типа необходимо предусмотреть возможность проверки умения читать графики функций (находить значения по оси абсцисс или ординат, коэффициент пропорциональности для линейных функций и т.п.), соотносить символическую запись закона (формулы) с соответствующим графиком, преобразовывать графики из одной системы координат в другую и т.д.».
Приведем примеры различных заданий, которые можно использовать при проведении комбинированных уроков математика – физика.
| Повторение и обобщение материала по теме: «Функции и их графики, линейная функция» | Повторение и обобщение материала по теме: «Прямолинейное и равномерное движение» |
| Какую функцию мы сейчас изучаем на уроке математики? (Линейную) | Какое движение мы изучаем на уроке физики? (Прямолинейное равномерное движение) |
| Какой формулой задается линейная функция в общем виде? (y=kx+b) | Какой вид имеет зависимость координаты тела от времени? ( 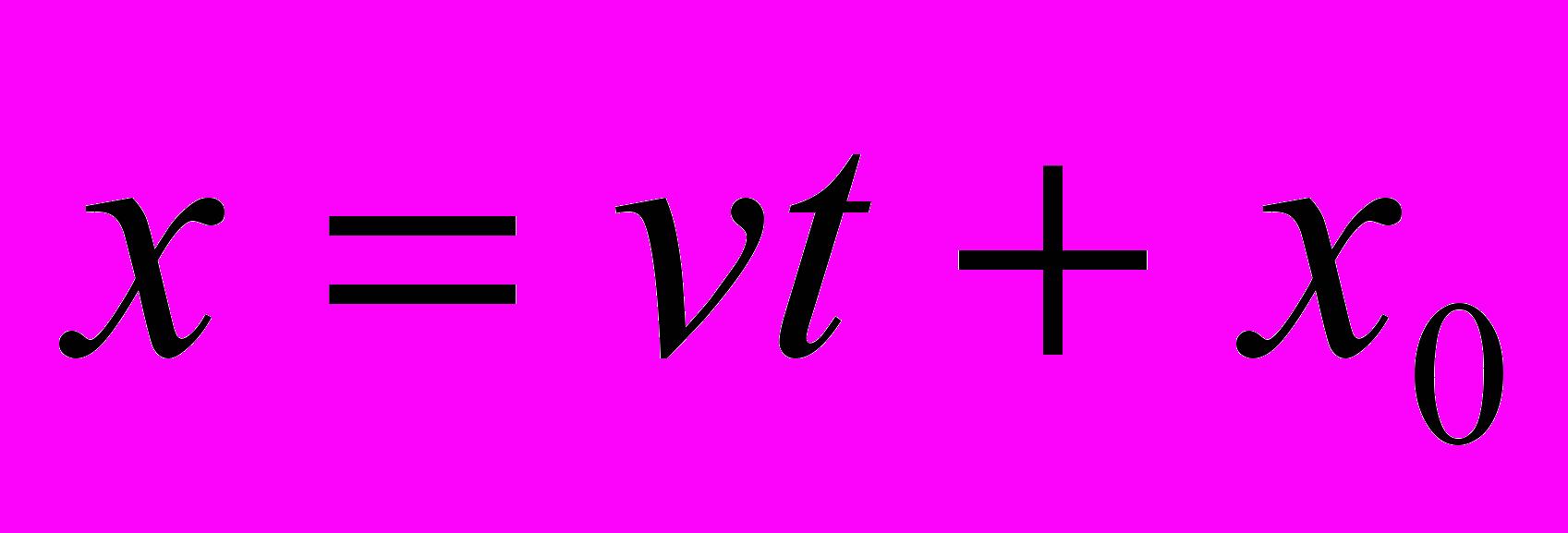 ) ) |
| Что является графиком линейной функции? (Прямая линия) | Что является графиком зависимости координаты от времени при прямолинейном равномерном движении? (Прямая линия) |
| Что обозначают буквами x и y? (Абсциссы и ординаты точек графика) | Что обозначают буквы t и x? (Время и координату положения тела в данный момент времени) |
| Какие значения могут принимать x и y? (Любые) | Какие значения могут принимать t и x? (t>0, т. к. значение времени, x – любое) |
| Как называют число k? (Угловой коэффициент) | Как называют число v? (Скоростью движения тела) |
| Каков смысл знака углового коэффициента k ? (По знаку коэффициента k можно определить вид угла между графиком и положительным направлением оси ox) | Каков смысл знака скорости v движения тела? (по знаку скорости v можно определить вид угла между графиком и положительным направлением оси времени, т. е. определить как меняется координата тела за единицу времени) |
| Что показывает число b? (Ординату точки пересечения графика с осью oy) | Что показывает число 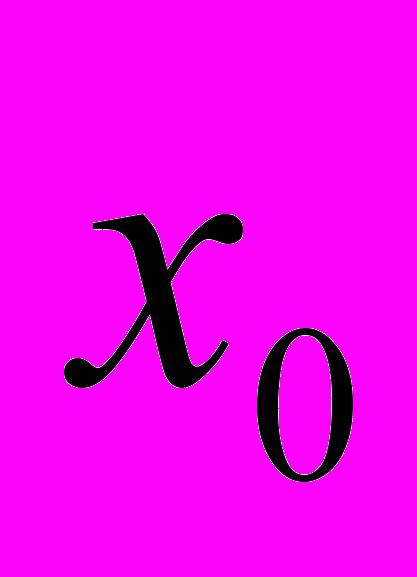 ? (Начальную координату тела, в момент времени t=0) ? (Начальную координату тела, в момент времени t=0) |
| Какие значения могут принимать числа k и b? (Любые) | Какие значения могут принимать числа v и 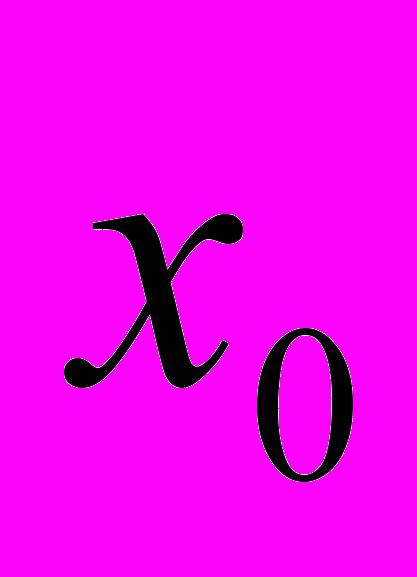 ? (Любые) ? (Любые) |
| Как это отражается на функции и ее графике? (Если b=0, то y=kx – прямая пропорциональность, график проходит через(0;0) Если k=0, то y=b – график параллелен оси ox Если k=0 и b=0, то y=0 – график принадлежит оси ox. | Как это отражается на функции x(t) и ее графике? (Если 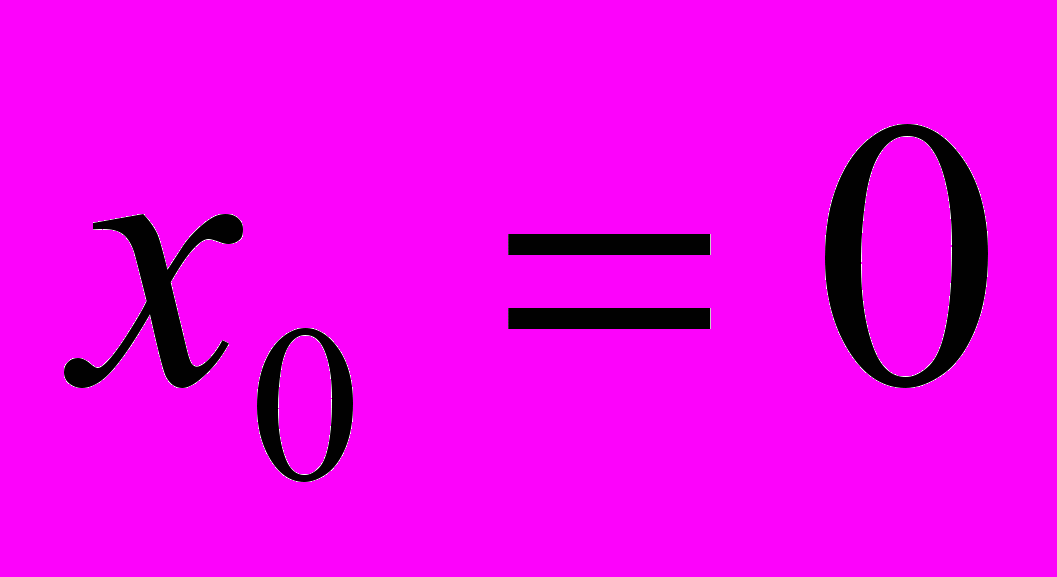 , то x=vt – прямая пропорциональность, график проходит через (0;0) , то x=vt – прямая пропорциональность, график проходит через (0;0) Если v=0, то x= 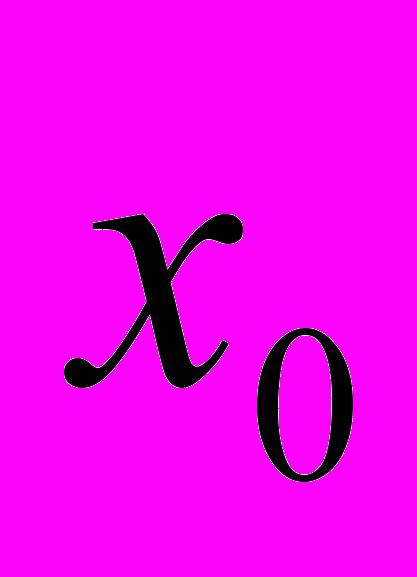 - график параллелен оси ot, т.е тело покоится. Если v=0 и - график параллелен оси ot, т.е тело покоится. Если v=0 и 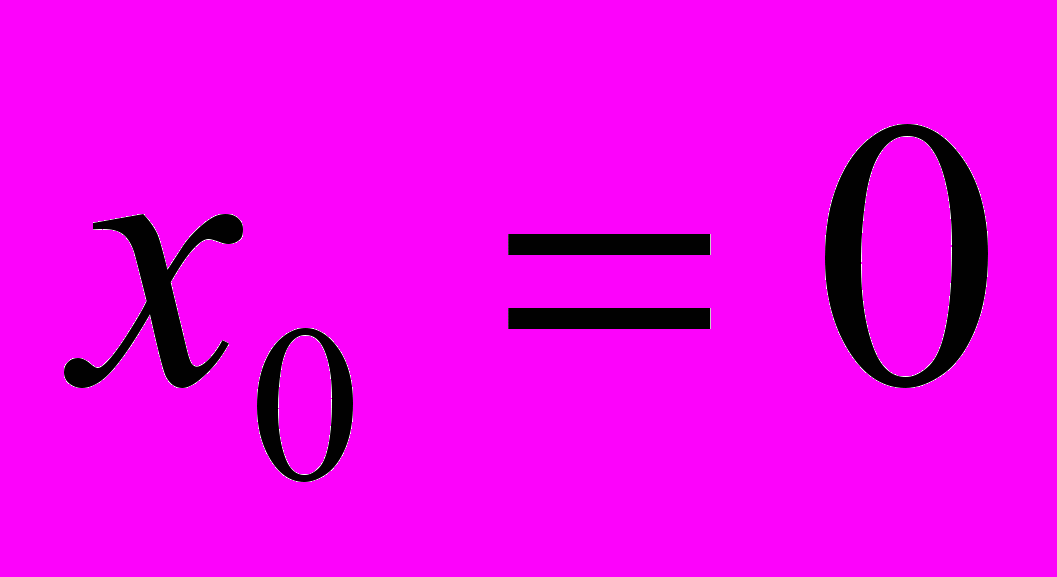 , ,то x=0 – график принадлежит оси 0t, т.е. тело покоится в начале отсчета. |
