1. Модель: определение, назначение. Классификация моделей
| Вид материала | Документы |
- 1. Модель: определение, назначение. Классификация моделей, 785.34kb.
- Математическое моделирование и методы оптимизации Общая трудоемкость изучения дисциплины, 22.02kb.
- Вопросы к экзамену, 19.64kb.
- Лекция 5 Методы построения математических моделей асу, 53.76kb.
- Тема урока Основные понятия, 1555.36kb.
- Урок №1 Тема: «Понятие модели. Назначение и свойства моделей. Виды моделей», 139.14kb.
- Темы для докладов Базы данных (БД): назначение, классификация. Системы управления базами, 4.8kb.
- Примеры моделей дискретных элементов рэа. Модель пленочного резистора. Модель диффузного, 131.9kb.
- Шкаберин В. А. Определение математической модели. Преимущества математического моделирования., 66.58kb.
- 1. Классификация моделей представления знаний, 1008.73kb.
1 2
1. Модель: определение, назначение. Классификация моделей.
Модель – это некоторое представление или описание оригинала (объекта, процесса, явления), которое при определенных предложениях, гипотезах о поведении оригинала позволяет замещать оригинал для его лучшего изучения, исследования, описания его свойств.
Моделирование – процесс построения модели и исследование объектов (процессов) при помощи модели
Необходимость использования метода моделирования определяется тем, что многие объекты непосредственно исследовать невозможно
Процесс построения модели предполагает наличие некоторых знаний об объекте оригинала. Познавательные возможности модели обусловливаются тем, что модель отражает только существенные черты объекта оригинала. Таким образом, изучение 1 стороны моделируемого объекта осуществляется ценой отказа от отражения других сторон, поэтому любая модель заменяет оригинал лишь в строго ограниченном смысле.
В процессе применения моделей осуществляется перенос знаний с моделей на оригинал, при этом знания о модели должны быть скорректированы с учетом тех свойств оригинала, которые не нашли отражение.
Классификация моделей:
Модель – статическая , если среди параметров описания модели нет (явно) временного параметра.
Модель – динамическая , если среди параметров модели явно выделен временной параметр.
Модель – дискретная , если описывает поведение оригинала в определенные моменты времени (для динамической модели).
Модель – непрерывная , если описывает поведение оригинала на определенном промежутке времени.
Модель – детерминированная , если для каждой допустимой совокупности входных параметров она позволяет определять однозначно набор выходных параметров; в противном случае – модель называется, стохастической (вероятностная) .
Модель – физическая, являющаяся материальной копией оригинала.
Модель – геометрическая , если она представима геометрическими образами и отношениями между ними.
Модель оптимизационная – предназначена для случая, когда необходимо принимать решения.
2. Требования, предъявляемые к компьютерным моделям.
Компьютерные модели проще и удобнее исследовать в тех случаях когда реальные эксперименты затруднены из-за финансовых или физических препятствий или могут дать непредсказуемый результат. Логичность и формализованность компьютерных моделей позволяет выявить основные факторы, определяющие свойства изучаемого объекта-оригинала (или целого класса объектов), в частности, исследовать отклик моделируемой физической системы на изменения ее параметров и начальных условий. Построение компьютерной модели базируется на абстрагировании от конкретной природы явлений или изучаемого объекта-оригинала.
Логичный – соответствующий законам логики; правильный, последовательный, обоснованный.
Формализованный - основанный на строгом соблюдении заранее заданных правил, алгоритмов, расчет по формулам, математическим зависимостям
Абстрагирование — это мысленное выделение, вычленение некоторых элементов конкретного множества и отвлечение их от прочих элементов данного множества. Это один из основных процессов умственной деятельности человека, опирающийся на знаковое опосредствование и позволяющий превратить в объект рассмотрения разные свойства предметов.
Итак, общие требования к моделям.
- Модель должна быть актуальной. Это значит, что модель должна быть нацелена на важные для лиц, принимающих решения, проблемы.
- Модель должна быть результативной. Это значит, что полученные peзyльтaты мoдeлиpoвaния мoгyт найти ycпeшнoe пpимeнeниe. Данное требование может быть реализовано только в случае правильной формулировки требуемого результата.
- Модель должна быть дocтoвepнoй. Это значит, что результаты моделирования не вызoвyт coмнeния. Данное требование тесно связано с понятием адекватности, то есть, если модель неадекватна, то она не может давать достоверных результатов.
- Модель должна быть экономичной. Это значит, что эффект от использования результатов мoдeлиpoвaния превышает расходы ресурсов на ее создание и исследование.
Эти требования (обычно их называют внешними) выполнимы при условии обладания моделью внутренними свойствами.
Модель должна быть:
- Cyщecтвeннoй, т. е. пoзвoляющeй вcкpыть cyщнocть поведения системы, вcкpыть неочевидные, нетривиальные детали.
- Moщнoй, т. е. пoзвoляющeй пoлyчить шиpoкий набop существенных cвeдeний.
- Пpocтoй в изyчeнии и иcпoльзoвaнии, лeгкo пpocчитывaeмoй на компьютере.
- Открытой, т.е. позволяющей ее модификацию. В заключение темы сделаем несколько замечаний.
3. Инструменты моделирования. Место компьютерного моделирования в научных исследованиях.
Если модель имеет материальную природу, то для ее создания годятся традиционные инструменты: резец скульптора, токарный или фрезерный станок, пресс, пила и топор, наконец. Если модель имеет абстрактную форму, то речь идет о некоторых знаковых системах, позволяющих описать данный тип модели. Это специальные языки, чертежи, схемы, графики, таблицы, алгоритмы, математические выражения и т. п. Здесь может быть использовано два варианта инструментария: либо традиционный набор инженера или конструктора (карандаш, линейка, ручка), либо самый совершенный на данный момент инструмент — компьютер. Таким образом, мы подошли еще к одной возможности классификации информационных моделей: по способу реализации они подразделяются на компьютерные и некомпьютерные модели.
Когда речь идет об инструменте-компьютере, то следует понимать, что он работает с информацией. Поэтому нужно исходить из того, какую информацию и в каком виде может воспринимать и обрабатывать компьютер. Современный компьютер способен работать с текстом, графикой, схемами, таблицами, звуком, видеоизображением и т. д. Но для работы со всем этим многообразием информации нужна как техническая {аппаратная), так и программная поддержка. Эти две составляющие и являются инструментами компьютерного моделирования. Компьютерное моделирование является одним из эффективных методов изучения сложных систем. Компьютерные модели проще и удобнее исследовать в силу их возможности проводить т.н. вычислительные эксперименты, в тех случаях когда реальные эксперименты затруднены из-за финансовых или физических препятствий или могут дать непредсказуемый результат. Логичность и формализованность компьютерных моделей позволяет выявить основные факторы, определяющие свойства изучаемого объекта-оригинала (или целого класса объектов), в частности, исследовать отклик моделируемой физической системы на изменения ее параметров и начальных условий. Компьютерное моделирование заключается в проведении серии вычислительных экспериментов на компьютере, целью которых является анализ, интерпретация и сопоставление результатов моделирования с реальным поведением изучаемого объекта и, при необходимости, последующее уточнение модели и т. д.
4. Этапы компьютерного моделирования.
- Описание задачи
- Задача формулируется на обычном языке;
- Определяется объект моделирования;
- Представляется конечный результат
- Определение целей моделирования
- Цели определяются в соответствии с поставленной задачей;
- Поставленные цели оказывают направляющее влияние на весь процесс моделирования.
- Разработка информационной модели
- Выделяются объекты моделирования и дается их развернутое содержательное описание (природа объектов, их зависимости, связи, свойства, характеристики);
- Учитываются только существенные свойства в зависимости от выбранной цели;
- В результате выстраивается описательная информационная модель, т.е. вербальная;
- Формализация модели. Переход от описательной модели к конкретному математическому наполнению. Указывается перечень параметров, которые влияют на поведение объекта – исходные данные, и которые желательно получить – результат. Формализуются зависимости между выделенными параметрами, накладываются ограничения на их допустимые значения. Результат – математическая модель.
- Разработка компьютерной модели
- Формализованная модель преобразуется в компьютерную с помощью множества программных комплексов и сред (графические среды, текстовые редакторы, среды программирования, электронные таблицы и пр.);
- От выбора программной среды зависит алгоритм построения компьютерной модели и форма его представления.
- Тестирование модели
- Модель может содержать ошибки. Обязателен этап тестирования. В программировании это трансляция и отладка программы;
- Можно использовать тестовый набор исходных данных, для которых конечный результат заранее известен;
- На этапе тестирования может выявиться необходимость изменения исходной модели.
- Исследование модели
- Исследование заключается в проведении серии экспериментов, удовлетворяющих целям моделирования.
- Эксперимент – это опыт, который производится с объектом или моделью. Он заключается в выполнении некоторых действий, чтобы определить, как реагирует экспериментальный образец на эти действия.
- Эксперимент сопровождается осмыслением итогов. Это служит основой для анализа результатов принятия решений.
- Анализ результатов моделирования
- Нужно ответить на вопрос: «Продолжать исследование, либо заканчивать?»
- Если результаты не соответствуют целям поставленной задачи, значит на предыдущих этапах были допущены ошибки (неправильно отобранные свойства объекта, ошибки в формулах на этапе формализации, неудачный метод или среда моделирования, нарушение технологических приемов при построении модели).
- Если ошибки выявлены, то требуется корректировка модели, т.е. возврат к одному из предыдущих этапов. Процесс повторяется до тех пор, пока результаты эксперимента не будут отвечать целям моделирования.
5. Аналитическое и имитационное моделирование.
- Для аналитического моделирования характерно, что процессы функционирования системы записываются в виде некоторых функциональных соотношений (алгебраических, дифференциальных, интегральных уравнений). Аналитическая модель может быть исследована следующими методами: 1) аналитическим, когда стремятся получить в общем виде явные зависимости для характеристик систем; 2) численным, когда не удается найти решение уравнений в общем виде и их решают для конкретных начальных данных; 3) качественным, когда при отсутствии решения находят некоторые его свойства. Аналитические модели удается получить только для сравнительно простых систем. Для сложных систем часто возникают большие математические проблемы. Для применения аналитического метода идут на существенное упрощение первоначальной модели. Однако исследование на упрощенной модели помогает получить лишь ориентировочные результаты. Аналитические модели математически верно отражают связь между входными и выходными переменными и параметрами. Но их структура не отражает внутреннюю структуру объекта.
- При имитационном моделировании реализующий модель алгоритм воспроизводит процесс функционирования системы во времени. Имитируются элементарные явления, составляющие процесс, с сохранением их логической структуры и последовательности протекания во времени. Основным преимуществом имитационных моделей по сравнению с аналитическими является возможность решения более сложных задач. Имитационные модели позволяют легко учитывать наличие дискретных или непрерывных элементов, нелинейные характеристики, случайные воздействия и др. Поэтому этот метод широко применяется на этапе проектирования сложных систем. Основным средством реализации имитационного моделирования служит ЭВМ, позволяющая осуществлять цифровое моделирование систем и сигналов. Технология компьютерного моделирования предполагает выполнение следующих действий: 1) определение цели моделирования; 2) разработка концептуальной модели; 3) формализация модели; 4) программная реализация модели; 5) планирование модельных экспериментов; 6) реализация плана эксперимента; 7) анализ и интерпретация результатов моделирования.. Имитационные модели не только по свойствам, но и по структуре соответствуют моделируемому объекту. При этом имеется однозначное и явное соответствие между процессами, получаемыми на модели, и процессами, протекающими на объекте. Недостатком имитационного моделирования является большое время решения задачи для получения хорошей точности. Общей тенденцией моделирования с использованием ЭВМ у сложных управляемых систем является стремление к уменьшению времени моделирования, а также проведение исследований в реальном масштабе времени.
8. Метод конечных элементов. Преимущества и недостатки по сравнению с другими численными методами.
В науке и технике постоянно приходится сталкиваться с проблемой расчета систем, имеющих сложную геометрическую конфигурацию и нерегулярную физическую структуру. Компьютеры позволяют выполнять такие расчеты при помощи приближенных численных методов. Метод конечных элементов (МКЭ) является одним из них. В последние десятилетия он занял ведущее положение и получил широкое применение. Достоинства : 1. Метод конечных элементов позволяет построить удобную схему формирования системы алгебраических уравнений относительно узловых значений искомой функции. Затем производится объединение элементов, что приводит к требуемой системе алгебраических уравнений. Такой алгоритм перехода от отдельного элемента к их полному набору особенно удобен для геометрически и физически сложных систем. 2. Каждое отдельное алгебраическое уравнение, полученное на основе метода конечных элементов, содержит незначительную часть узловых неизвестных от общего их числа. Другими словами, многие коэффициенты в уравнениях алгебраической системы равны нулю, что значительно облегчает ее решение. 3. Метод конечных элементов, так же как и другие численные методы, по существу приближенно заменяет континуальную задачу на дискретную. В методе конечных элементов вся процедура такой замены имеет простой физический смысл. Это позволяет более полно представить себе весь процесс решения задачи, избежать многих возможных ошибок и правильно оценить получаемые результаты. 4. Помимо континуальных задач схема метода конечных элементов применяется для соединения элементов и формирования алгебраических уравнений при решении непосредственно дискретных задач. Это расширяет сферу применения метода. Недостаток: Долгое время широкому распространению МКЭ мешало отсутствие алгоритмов автоматического разбиения области на «почти равносторонние» Впрочем, эту задачу удалось успешно решить (алгоритмы основаны на триангуляции Делоне).
6. Поясните сущность формализации производственных процессов и объектов. Дайте сравнительную характеристику основных методов моделирования, применяемых для исследования.
Формализация, представление какой-либо содержательной области (рассуждений, доказательств, процедур классификации, поиска информации научных теорий) в виде формальной системы, или исчисления. Полностью могут быть формализованы лишь элементарные теории с простой логической структурой и небольшим запасом понятий (например, исчисление высказываний и узкое исчисление предикатов – в логике, элементарная геометрия – в математике). Если же теория сложна, она принципиально не может быть полностью формализована
Ф. позволяет систематизировать, уточнить и методологически прояснить содержание теории, выяснить характер взаимосвязи между собой различных её положений, выявить и сформулировать ещё не решенные проблемы.
Формализация информации о некотором объекте — это ее отражение в определенной форме. Можно еще сказать так: формализация — это сведение содержания к форме. Формулы, описывающие физические процессы, — это формализация этих процессов.
Метод подвижных клеточных автоматов (MCA, от англ. movable cellular automata) — это метод вычислительной механики деформируемого твердого тела, основанный на дискретном подходе. Он объединяет преимущества метода классических клеточных автоматов и метода дискретных элементов. Важным преимуществом метода МСА является возможность моделирования разрушения материала, включая генерацию повреждений, распространение трещин, фрагментацию и перемешивание вещества.
Преимущества метода MCA
Благодаря подвижности каждого автомата метод MCA позволяет напрямую учитывать такие события как:
-перемешивание масс
-эффект проникновения
-химические реакции
-интенсивные деформации
-фазовые превращения
-накопление повреждений
-фрагментация и трещины
-генерация и развитие повреждений
Используя различные граничные условия разных типов (жесткие, упругие, вязко-упругие, т.д.) можно имитировать различные свойства окружающей среды, содержащей моделируемую систему. Можно моделировать различные режимы механического нагружения (растяжение, сжатие, сдвиг, т.д.) с помощью настроек дополнительных состояний на границах.
Метод конечных элементов (МКЭ) — численный метод решения задач прикладной физики. Метод широко используется для решения задач механики деформируемого твёрдого тела, теплообмена, гидродинамики и электродинамики.
Преимущества и недостатки
Метод конечных элементов, по словам специалистов, «большая пушка» — метод конечных разностей и проще в реализации, и быстрее. Зато у МКЭ есть свои преимущества, проявляющиеся на реальных задачах: произвольная форма обрабатываемой области; сетку можно проредить в тех местах, где особая точность не нужна.
Долгое время широкому распространению МКЭ мешало отсутствие алгоритмов автоматического разбиения области на «почти равносторонние» треугольники (погрешность, в зависимости от вариации метода, обратно пропорциональна синусу или самого острого, или самого тупого угла в разбиении). Впрочем, эту задачу удалось успешно решить (алгоритмы основаны на триангуляции Делоне), и последний бастион на пути к полностью автоматическим конечноэлементным САПР пал.
Метод конечных разностей
В методе конечных разностей (МКР) на область рассматриваемого тела наносится сетка линий, точки пересечения которых называются узлами. В случае стержня или балки сетка будет одномерной и узлы будут располагаться на их оси. Неизвестными в узлах считаются значения функций, относительно которых справедливы известные дифференциальные Уравнения механики деформируемого твердого тела.
7
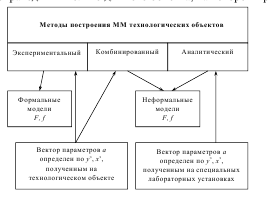 . Порядок и методы построения математической модели.
. Порядок и методы построения математической модели.Математические модели в количественной форме, с помощью логико-математических конструкций, описывают основные свойства объекта, процесса или системы, его параметры, внутренние и внешние связи.
Для построения математической модели необходимо:
тщательно проанализировать реальный объект или процесс;
выделить его наиболее существенные черты и свойства;
определить переменные, т.е. параметры, значения которых влияют на основные черты и свойства объекта;
описать зависимость основных свойств объекта, процесса или системы от значения переменных с помощью логико-математических соотношений (уравнения, равенства, неравенства, логико-математические конструкций);
выделить внутренние связи объекта, процесса или системы с помощью ограничений, уравнений, равенств, неравенств, логико-математических конструкций;
определить внешние связи и описать их с помощью ограничений, уравнений, равенств, неравенств, логико-математических конструкций.
Математическое моделирование, кроме исследования объекта, процесса или системы и составления их математического описания, также включает:
построение алгоритма, моделирующего поведение объекта, процесса или системы;
проверка адекватности модели и объекта, процесса или системы на основе вычислительного и натурного эксперимента;
корректировка модели;
использование модели.
Математическое описание исследуемых процессов и систем зависит от:
природы реального процесса или системы и составляется на основе законов физики, химии, механики, термодинамики, гидродинамики, электротехники, теории пластичности, теории упругости и т.д.
требуемой достоверности и точности изучения и исследования реальных процессов и систем.
На этапе выбора математической модели устанавливаются: линейность и нелинейность объекта, процесса или системы, динамичность или статичность, стационарность или нестационарность, а также степень детерминированности исследуемого объекта или процесса. При математическом моделировании сознательно отвлекаются от конкретной физической природы объектов, процессов или систем и, в основном, сосредотачиваются на изучении количественных зависимостей между величинами, описывающими эти процессы.
Математическая модель никогда не бывает полностью тождественна рассматриваемому объекту, процессу или системе. Основанная на упрощении, идеализации она является приближенным описанием объекта. Поэтому результаты, полученные при анализе модели, носят приближенный характер. Их точность определяется степенью адекватности (соответствия) модели и объекта.
Построение математической модели обычно начинается с построения и анализа простейшей, наиболее грубой математической модели рассматриваемого объекта, процесса или системы. В дальнейшем, в случае необходимости, модель уточняется, делается ее соответствие объекту более полным.
10. Тестирование и проверка адекватности математической модели.
Адекватность модели - соответствие модели моделируемому объекту или процессу.
В процессе проверки модели необходимо установить включение в модель всех существенных факторов. Сложность решения этой проблемы зависит от сложности решаемой задачи.
Исходный вариант модели необходимо проверить по следующим аспектам:
1) все ли существенные параметры включены в модель?
2) нет ли в модели несущественных параметров?
3) правильно ли отражены связи между параметрами?
4) правильно ли определены ограничения на значения параметров?
Для проверки рекомендуется привлекать специалистов, которые не принимали участия в разработке модели. Они могут более объективно рассмотреть модель и заметить ее слабые стороны, чем ее разработчики. Такая предварительная проверка модели позволяет выявить грубые ошибки. После этого приступают к реализации модели и проведению исследований. Полученные результаты моделирования подвергаются анализу на соответствие известным свойствам исследуемого объекта. Для установления соответствия создаваемой модели оригиналу используются следующие пути:
• сравнение результатов моделирования с отдельными экспериментальными результатами, полученными при одинаковых условиях;
• использование других близких моделей;
• сопоставление структуры и функционирования модели с прототипом.
Главным путем проверки адекватности модели исследуемому объекту выступает практика. Однако она требует накопления статистики, которая далеко не всегда бывает достаточной для получения надежных данных. Для многих моделей первые два пути приемлемы в меньшей степени. В этом случае остается один путь: заключение о подобии модели и прототипа делать на основе сопоставления их структур и реализуемых функций. Такие заключения не носят формального характера, поскольку основываются на опыте и интуиции исследователя.
По результатам проверки модели на адекватность принимается решение о возможности ее практического использования или о проведении корректировки.
11. Характеристика численных методов, используемых при моделировании.
Любой численный метод линейной алгебры можно рассматривать как некоторую последовательность выполнения арифметических операций над элементами входных данных. Если при любых входных данных численный метод позволяет найти решение задачи за конечное число арифметических операций, то такой метод называется прямым. В противоположном случае численный метод называется итерационным. Прямые методы - это такие, как метод Гаусса, метод окаймления, метод пополнения, метод сопряжённых градиентов и др. Итерационные методы - это метод простой итерации, метод вращений, метод переменных направлений, метод релаксации и др. Здесь будут рассматриваться матричный метод, метод Гаусса и метод Крамера.
MathCAD.
Программа MathCAD по своему назначению позволяет моделировать в электронном документе научно-технические, а также экономические расчёты в форме, достаточно близкой к общепринятым ручным расчётам. Это упрощает составление программы расчёта, автоматизирует перерасчёт и построение графических иллюстраций подобно электронным таблицам Excel, документирование результатов как в текстовом редакторе Word.
Программа Mathcad известна за лёгкость, с которой математические уравнения, текст, и графика могут быть объединены в одном документе. Кроме того, вычислительные способности Mathcad распространяются от сложения столбца чисел к решению интегралов и производных, решение систем уравнений и больше.
Достоинством MathCAD является также наличие в его составе электронных книг. Одна из них - учебник по самой программе, другие - справочник по различным разделам математики, физики, радиоэлектроники и др.
12. Идея и основные понятия метода конечных элементов. История развития метода.
Метод конечных элементов (МКЭ) — численный метод решения задач прикладной механики. Широко используется для решения задач механики деформируемого твёрдого тела, теплоообмена, гидродинамики и электромагнитных полей. С точки зрения вычислительной математики, идея метода конечных элементов заключается в том, что минимизация функционала вариационной задачи осуществляется на совокупности функций, каждая из которых определена на своей подобласти, для численного анализа системы позволяет рассматривать его как одну из конкретных ветвей диакоптики — общего метода исследования систем путём их расчленения. Возникновение метода конечных элементов связано с решением задач космических исследований в 1950-х годах (идея МКЭ была разработана советскими учёными ещё в 1936 году, но из-за неразвитости вычислительной техники метод не получил развитие). Этот метод возник из строительной механики и теории упругости, а уже затем было получено его математическое обоснование. Существенный толчок в своём развитии МКЭ получил в 1963 году после того, как было доказано то, что его можно рассматривать, как один из вариантов распространённого в строительной механике метода Рэлея-Ритца, который путём минимизации потенциальной энергии сводит задачу к системе линейных уравнений равновесия. После того, как была установлена связь МКЭ с процедурой минимизации, он стал применяться к задачам описываемым уравнениями Лапласа или Пуассона. Область применения МКЭ значительно расширилась, когда было установлено (в 1968 году), что уравнения, определяющие элементы в задачах могут быть легко получены с помощью вариантов метода взвешенных невязок, таких как метод Галёркина, или метод наименьших квадратов. Это сыграло важную роль в теоретическом обосновании МКЭ, так как позволило применять его при решении многих типов дифференциальных уравнений. Таким образом, метод конечных элементов превратился в общий метод численного решения дифференциальных уравнений или систем дифференциальных уравнений. С развитием вычислительных средств возможности метода постоянно расширяются, также расширяется и класс решаемых задач. Практически все современные расчёты на прочность проводят, используя метод конечных элементов. Метод конечных элементов (МКЭ) является сеточным методом, предназначенным для решения задач микроуровня, для которого модель объекта задается системой дифференциальных уравнений в частных производных с заданными краевыми условиями.
Метод конечных элементов по существу сводится к аппроксимации сплошной среды с бесконечным числом степеней свободы совокупностью подобластей (или элементов), имеющих конечное число степеней свободы. Затем между этими элементами каким-либо способом устанавливается взаимосвязь.
Появилась необходимость в разработке новых инженерных подходов к численному решению задач со сложной геометрией, в которых области интегрирования разбивались на подобласти. Такие подобласти (носители финитных базисных функций, об этом ниже) и получили название конечных элементов.
14. Программное обеспечение, реализующее метод конечных элементов.
Программное обеспечение, базирующиеся на методе конечных элементов, должно включать в той или иной степени функции модулей: ввода данных (препроцессора), вычислений (процессора), вывода результатов (постпроцессора).
В программном обеспечении систем автоматизированного проектирования функции ввода и вывода особенно развиты, так как они сокращают время получения данных и оценки результатов в ходе моделирования. Вычислительный модуль в основном использует элементы основной конфигурации технических средств: арифметический процессор, оперативную память, внешнюю память большой емкости.
Чаще всего встречается следующая организация программного обеспечения для метода конечных элементов:
1) единая программа для всех функций;
2)одна программа -- для ввода и вывода, другая программа -- для расчета;
3)отдельная программа на каждую функцию.
Использование единой программы, управляющей всеми функциями, позволяет осуществлять быстрый переход от одной процедуры к другой. Единая программа особенно эффективна в тех случаях, когда необходимо многочисленное повторение цикла ввод-расчет-вывод.
В следующем возможном варианте пользователь раздельно пользуется модулем ввода-вывода и модулем вычисления. Это позволяет ему производить расчеты с разделением времени.
Последний вариант представляет собой цепочку «препроцессор -- процессор -- постпроцессор». При этом можно предусмотреть использование нескольких препроцессоров, представляющих пользователю разные возможности.
Примеры программного обеспечения, реализующего метод кэ:
ANSYS, DEFORM-2D/3D, Code_Aster, Deal.II, Femap, LibMesh, LSDYNA, Maxwell (Ansoft), MicroFe, Nastran(от Simens), NX Advanced Simulation, QForm 2D/3D, SCAD STARK ES (Россия) , ПК Лира
13. Этапы решения задачи с помощью МКЭ. Виды конечных элементов.
МКЭ может быть представлен в виде трех последовательных этапов решения задачи: начальной подготовки (препроцессов); получение решений (решатель); обработка результатов моделирования (постпроцессов).
- Создается модель изделия (геометрическая и расчетная)
Задаются свойства материала (модуль упругости, модуль сдвига расчета деформаций, коэффициент Пуассона и др.)
Задаются силовые факторы (ограничения, нагрузки).
Генерируется сеточная модель
- Запуск метода конечных элементов
- Анализ результатов
Возможности препроцессора:
1)создание простейшей геометрии и импорт из CAD систем сложной геометрии
2)создание собственных и импорт сеток конечных элементов
3)библиотека материалов с возможностью добавления новых материалов
4)выбор моделей исследуемых процессов из перечня известных в области ОМД и подготовка данных для них
5)Задание начальных и граничных условий исследуемого процесса
6)Широкие возможности по установке параметров моделирования: количество шагов, шаг сохранения результата, критерии остановки процесса, переразбиение сетки.
Возможности решателя:
1)автоматическое перестроение сетки
2)распараллеливание процесса решения
Возможности постпроцессора:
1)графическое представление результата вычисления по шагам (общее, в указанной точке, между двумя точками)
2)определение направления течения материала
3)вывод информации в качестве текстовых, графических и видео файлов.
Существуют разнообразные формы КЭ:
1)тетраэдр – 3х мерный, 4х гранный элемент с числом узлов 4 - 10
2)бокс – шестигранный 3х мерный элемент с количеством узлов 8 – 20
Решение задач методом конечных элементов условно можно разделить на следующие этапы:
Этап 1. Расчетная область.На первом шаге создается расчетная область, для этого необходимо определить ее геометрический вид, определить свойства симметричности, определить ее размер. На этом этапе очень важно создать корректную и максимально простую модель расчетной области. Необходимо исключать все элементы, которые приводят к усложнению модели, а на итоговый расчет не оказывают влияние. Примером могут служить различные технологические отверстия в инструменте, направляющие устройства для закрепления, если речь идет о прочностных расчетах или расчетах механики деформируемого твердого тела. Особое внимание следует обратить на скругления и сопряжения плоскостей. Если это возможно,следует избегатьскруглений очень малыми радиусами - это приведет к значительному увеличению конечных элементов для описания подобных поверхностей. Если присутствуют видимые поверхностные дефекты сопряжений или так называемые «изломы поверхностей» стоит перестроить эти элементы или сгладить область скруглениями. Подобные проблемы могут проявиться на стадии генерации сетки конечных элементов и потребуют ручного исправления отдельных областей, что является весьма нетривиальной задачей.
Далее расчетная область передается в сторонний или встроенный решатель - сеточный генератор.
Этап 2. Сетка.На втором этапе расчетную область разбивают на конечное число элементов. Качество наложенной на расчетную область сетки имеет очень большое значение. Если сетка будет низкого качества, то не удастся получить либо сходимости, либо верного результата, а возможно и того, и другого.
Далее разбитая на элементы расчетная область передается в "решатель".
Этап 3. Определениезадачи. На третьем этапе определяется сама задача. Задается модель расчетной области, определяется среда, задаются граничные и начальные условия. При понимании всех физических процессов наблюдаемых в задаче, данный этап не составляет большого труда.
Этап 4. Решение.На четвертом этапе происходит само численное решение задачи. В этом процессе человек принимает сугубо пассивную роль - следит за сходимостью и невязками, но в ряде программ, особенно, производящих расчеты нестационарных процессов на этом этапе может потребоваться вмешательство пользователя, в возможности которого входит управление параметрами генерируемой при вычислениях конечно-элементной сетки (алгоритм переразбиения), управления расчетными параметрами, таким как величина шага решения, параметры сходимости и количество итераций. Однако управление последними параметрами требует высокой квалификации пользования как в МКЭ, так и в самой программе. Поэтому данные переменные следует менять в случае крайней необходимости.
Этап 5. Анализ полученных результатов.На пятом этапе проводится анализ полученных результатов. Если есть возможность, то проводится верификация данных с экспериментом. Если получен нефизический результат или имеются большие расхождения с экспериментом, задача перерабатывается, вплоть до построения новой расчетной области и все последующие этапы проводятся снова.[7]
15. Этапы моделирования в программном комплексе DEFORM-3D.
В программном комплексе DEFORM-3D существуют 3 основных этапа моделирования:
Препроцессор Решатель Поспроцессор
Препроцессор служит для создания модели объекта исследования (геометрическая и расчетная), задача параметров модели – сетка, температура, пластичность и др., характеристики контакта – коэффициент трения, коэффициент теплопередачи, определяются точки контакта инструмента с заготовкой, производится настройка решателя, осуществляется генерация баз данных.
Рассмотрим этапы моделирования на примере нашей лабораторной:
- Создание задачи: задание параметров заготовки - заготовка пластичная, температура нагрева 12500С, материал сталь 15(выбираем необходимую из базы данных).
- Генерация сеточной модели: количество элементов – 50000.
- Создание плоскостей симметрии, выбирая переднюю и верхнюю грани. Количество шагов для нагрева сляба – 112. Время одного шага – 0,5 с.
- Генерация базы данных. Запуск процесс нагрева.
- Создание нового объекта – валка диаметром 1400мм. Сопоставление и совмещение точек контакта валка со слябом. Задание обжатия для первой клети, при этом вводим коэффициенты трения и теплоотдачи. Задание угловой скорости валка 1,79с-1(1,25/0,7).
- Указание условия операции №2: добавление деформационного изменения, для этого выбирается пункт прокатка.
- Создание нового объекта – толкателя размерами 660х125х10мм. Создание контакта со слябом, при этом скорость толкателя задается 1250 мм/с. Запуск расчета на 20 шагов. После этого действие толкателя удаляется и запускается расчет до конца обжатия.
В решателе происходит расчет поставленной задачи.
Постпроцессор служит для обработки результатов моделирования. В нем возможно графическое представление результата вычисления по шагам (общее, в указанной точке, между двумя точками), определение направления течения материала, вывод информации в качестве текстовых, графических и видео файлов.
16. Типы конечных элементов, используемых в DEFORM-3D. Охарактеризуйте способы создания конечно-элементной сетки.
4-х узловые тетраэдры и 8-ми узловые шестигранники

Способы создания сетки: Автоматическая генерация сетки, Автоматическое перестроение сетки в процессе расчета, Ручное перестроение сетки с сохранением всех данных, полученных на предыдущих стадиях расчета, Число конечных элементов может быть любым и определяется пользователем, максимальный и минимальный размер КЭ может быть любой и определяется пользователем, Ввод точного значения максимального и минимального размера КЭ, Локальное переразбиение КЭ сетки.
17. Перечислите исходные данные, необходимые для создания модели теплового процесса в DEFORM-3D. Номер печи. Режим обжатий. Толщина. Ширина. Скорости по клетям. Скорость перемещения сляба по рольгангу. Скорость в окалиноломателе. Температура выхода металла из печи. Расстояния между клетями. Расстояние от окалиноломателя до 1-ой клети. Диаметры бочек. Коэффициент трения. Коэффициент теплообмена. Материал. Пластичность материала.
18. Перечислите возможности по обработке результатов моделирования в DEFORM-3D. Особенности слежения за точками заготовки в процессе моделирования.
Система DEFORM предоставляет широкие возможности для обработки результатов, оценки процесса на наличие дефектов (образование трещин, складок, незаполнение штампа и др.), анализа течения материала. Результаты включают график усилия, поля распределения напряжений, деформаций и температуры, причем они могут быть представлены графически и таблично. Наглядно показаны макро- и микроструктура изделия, движение отдельных точек материала. Уникальной является возможность визуализации трехмерной, «вмороженной» в материал сетки FLOWNET. Для создания отчетов результаты можно вывести в виде графиков, численных данных, твердых копий и анимации.
Особенности слежения за точками заготовки в процессе моделирования.
В процессе моделирования существует возможность наблюдения за отмеченными точками, можно наблюдать температуру , деформацию и усилие по графикам.
19. Перечислите исходные данные, необходимые для создания модели вертикальной горячей прокатки в DEFORM-3D.
Толщина, ширина сляба. Температура выхода металла из печи. Диаметры бочек. Коэффициент трения. Коэффициент теплообмена. Материал. Профилировка валков. Режим обжатия. Скорости по клетям. Расстояния между клетями. Скорость перемещения сляба по рольгангу. Скорость в окалиноломателе. Расстояние от окалиноломателя до 1-ой клети.
23. Какие задачи можно решить при моделировании горячей прокатки в программном комплексе DEFORM-3D?
DEFORM позволяет моделировать пластическое течение материала для горячих, полугорячих и холодных процессов, причем это могут быть как изотермические, так и неизотермические процессы. Теплопередача между объектами и внутри них может быть проанализирована как отдельный процесс или совместно с процессом деформирования по сопряженной схеме. При расчете принимаются во внимание все факторы, влияющие на процесс штамповки: конвекция, излучение, тепловыделение при фазовых переходах и пластических деформациях, выделение тепла при трении, потери тепла в зоне контакта между заготовкой и инструментом, влияние температуры на коэффициент трения и термомеханические характеристики материала, влияние давления на трение и т.д.
В DEFORM нет ограничений на количество участвующих в процессе объектов — как деформируемых, так и деформирующих. Это позволяет моделировать даже самые сложные технологические операции с участием сборных заготовок и любого количества инструментов. При этом инструмент может быть неподвижным или перемещаться в любом направлении в зависимости от параметров заданного оборудования. Возможно моделирование таких современных технологических процессов, как обкатка или ротационная вытяжка. Инструмент может быть задан и абсолютно жесткий, и упругий, деформируемый. Для технологов очень важна возможность анализа прочности штампа. Эффективный одношаговый алгоритм позволяет сделать это как для жесткого, так и для упругого инструмента на любом шаге процесса. Возможен расчет нескольких инструментов, а также учет предварительного натяга в составном инструменте.
DEFORM позволяет задать практически любое оборудование — это гидравлические прессы, молоты, винтовые прессы, кривошипные прессы, прокатные станы, причем, задав параметры всего оборудования, можно создать библиотеку оборудования данного предприятия или цеха. Специальные шаблоны помогают задавать сложные процессы (например, протяжка на молотах с учетом остывания, промежуточным нагревом и вращением заготовки).
Система DEFORM предоставляет широкие возможности для обработки результатов, оценки процесса на наличие дефектов (образование трещин, складок, незаполнение штампа и др.), анализа течения материала. Результаты включают график усилия, поля распределения напряжений, деформаций и температуры, причем они могут быть представлены графически и таблично. Наглядно показаны макро- и микроструктура изделия, движение отдельных точек материала. Уникальной является возможность визуализации трехмерной, «вмороженной» в материал сетки FLOWNET. Для создания отчетов результаты можно вывести в виде графиков, численных данных, твердых копий и анимации.
24. Перечислите исходные данные, необходимые для создания модели горизонтальной горячей прокатки в DEFORM-3D.
Толщина, ширина сляба. Температура выхода металла из печи. Диаметры бочек. Коэффициент трения. Коэффициент теплообмена. Материал. Профилировка валков. Режим обжатия. Скорости по клетям. Расстояния между клетями. Скорость перемещения сляба по рольгангу. Скорость в окалиноломателе. Расстояние от окалиноломателя до 1-ой клети.
26. Какие задачи можно решить при моделировании напряженно-деформированного состояния инструмента в DEFORM-3D?
При моделировании в DEFORM-3D исследуется деформированное и напряженное состояние. С учетом указанной исходной информации в системе DEFORM последовательно решали задачи распределения интенсивности главных деформаций, напряжений, скоростей деформации и определения интегральных значений сил на исследуемый объект. Результаты решения отображаются на цветовых полях (эпюрах) распределения расчетных параметров (деформаций, напряжений, сил и т.п.)
Система DEFORM 3D позволила рассчитать абсолютные значения и характер изменения сил, воздействующих на исследуемый объект.
27. Что дает знание и умение применять на практике моделирования с помощью метода конечных элементов?
Знание и умение применять на практике моделирование с помощью МКЭ дает возможность проводить точный инженерный анализ, анализ течения металла при деформации, исправлять ошибки на базе проектирования, а не во время эксперимента, узнавать нужные размеры при проектировании, выбрать оптимальные размеры и форму модели, рассчитывать температурные изменения, находить слабые места и исправлять эту проблему. МКЭ проводится на моделях, а значит не обязательно чтобы исследуемый объект уже существовал, поэтому МКЭ применяют для исследования новых объектов (конструкций) на их надежность перед изготовлением или сборкой.
25. Что позволяет исследовать компьютерное моделирование процессов ОМД методом конечных элементов?
DEFORM не замещает технолога — он является его инструментом. Как и прежде, по стандартным методикам на основе накопленного опыта разрабатывается технология изготовления того или иного изделия. Далее, при помощи программного комплекса DEFORM, технологию проверяет сам технолог на своем рабочем месте.
В отличие от реального производства, где результаты можно получить лишь через несколько месяцев, компьютерное моделирование позволяет сделать это уже через несколько часов или даже минут. При этом технолог может заглянуть «внутрь» процесса, что невозможно на производстве, проследить за течением материала, увидеть возможные дефекты (складки, зажимы, утяжены, незаполнения и пр.). Плюс к тому, DEFORM включает возможности исследовательской лаборатории и позволяет получить информацию о напряженно-деформированном состоянии поковки/штамповки на разных этапах деформирования, о распределении температуры, о макро- и микроструктуре, о напряжениях в инструменте, потребном усилии процесса деформирования и о многом другом.
Оперативно владея всей этой информацией, технолог лучше представляет себе данный технологический процесс, может оценить влияние на него различных параметров, видит возможные пути его исправления и оптимизации. Технолог может проверить десятки, а то и сотни вариантов технологического процесса и выбрать из них оптимальный с точки зрения затрат и качества.
программы LS-DYNA-моделирование математическими методами практически любых процессов ОМД (обработки давлением): горячая и холодная объемная штамповка, ковка, осадка, прессование, прокатка, профилирование, вытяжка,листовая штамповка, рубка и прочие;
-моделирование конечно-элементым анализом процессов удара, crash тестов, столкновения, проникновения и др.;
-моделирование численными методами быстродинамичных и быстропротекающих процессов;
расчеты на прочночть и динамический расчет.
Наши исследования позволяют определить:
-напряженно-деформированное состояние, как самой конструкции, так и формующего (ударного) элемента в любой точке модели и любой промежуток времени;
-критические, опасные зоны и участки модели в которых возможно возникновения разрушения или деформации конструкции;
-силовые, энергетические, деформационные, контактные величины при взаимодействии частей модели.
39. Этапы конечно-элементного анализа в САЕ-системах.
Конечно-элементный анализ (англ. Finite Element Analysis, FEA) широко применяется при решении задач механики деформируемого твердого тела, теплообмена, гидро- и газодинамики, электро- и магнитостатики, а также других областей физики. Потребность в решении подобных задач возникает в системах автоматизированного конструирования (CAE) для моделирования поведения изделия в цифровом виде (не прибегая к изготовлению самого изделие или его макета). Типичными примерами процессов, моделирование которых на компьютере позволяет значительно сократить расходы на испытания, являются продувка в аэродинамической трубе и аварийные испытания (крэш-тесты). Конечно-элементный анализ основан на использовании математического метода конечных элементов (МКЭ).
Конечно-элементный анализ состоит из трех основных этапов: начальной подготовки (препроцессорной подготовки), получения решений и обработки результатов моделирования (постпроцессорной обработки).
Препроцессорная подготовка. Этот этап является наиболее трудоемким. На стадии препроцессорной подготовки создается база данных, необходимых для расчета, задается система координат, определяются тип элемента, вещественные константы элемента, свойства материала и геометрия модели.
Выбор типа расчета. При выборе типа решаемой задачи несколько упрощается вид главного меню, то есть устанавливается своего рода фильтр, благодаря которому остаются доступными только те пункты меню, которые непосредственно связаны с выбранным типом расчета.
Формирование исходных данных.
Выбор координатной системы. В программе ANSYS существуют следующие типы координатных систем:
- Глобальные и локальные системы координат, используемые для определения местонахождения геометрических объектов (узлов, ключевых точек и т.д.) в пространстве;
- Система координат отображения информации, определяющая систему, в которой геометрические объекты отображаются в табличном или графическом виде;
- Узловая система координат, определяющая направление степеней свободы для каждого узла и ориентацию составляющих вектора результатов в узлах;
- Система координат элемента, определяющая ориентацию характеристик материала, зависящих от направления, и компонентов вектора результатов для элемента;
- Система координат результатов, используемая для преобразования результатов в узлах или элементах в отдельную систему координат для распечатки листинга, графического вывода на экран или основных операций в постпроцессоре общего назначения (POST1).
33. Возможности программного комплекса DEFORM для моделирования технологических процессов
DEFORM позволяет моделировать практически все процессы, применяемые в обработке металлов давлением (ковка, штамповка, прокатка, прессование и др.), а также операции термической обработки (закалка, старение, отпуск и др.) и механообработки (фрезерование, сверление и др.).
DEFORM применяется по всему миру, как на промышленных предприятиях, так и в научно-исследовательских институтах и технических университетах, является самым распространенным программным комплексом для моделирования процессов обработки металлов давлением.
