1. Модель: определение, назначение. Классификация моделей

Вид материала

Документы

Содержание Возможности системы DEFORM 38. Этапы математического моделирования и их взаимосвязь Рис. 2. Варианты степени влияния величины х 42. Система. Основные понятия, характеризующие строение и функционирование систем. 44. Классификация систем. Подходы к исследованию систем. М на базе системного подхода условно представлен на рис. 1.1, б. 45. Этапы расчета методом конечных элементов в системе Autodesk Inventor. 50. Аналитические и эмпирические методы построения математических моделей. Физическое описание объекта моделирования. Составление уравнений статики или динамики объекта моделирования. Определение начальных и граничных условий моделирования. Выбор метода решения уравнений математического описания объекта, разработка алгоритма и составление программы. Проверка соответствия (адекватности) модели объекту.

Подобный материал:

• 1. Модель: определение, назначение. Классификация моделей, 785.34kb.
• Математическое моделирование и методы оптимизации Общая трудоемкость изучения дисциплины, 22.02kb.
• Вопросы к экзамену, 19.64kb.
• Лекция 5 Методы построения математических моделей асу, 53.76kb.
• Тема урока Основные понятия, 1555.36kb.
• Урок №1 Тема: «Понятие модели. Назначение и свойства моделей. Виды моделей», 139.14kb.
• Темы для докладов Базы данных (БД): назначение, классификация. Системы управления базами, 4.8kb.
• Примеры моделей дискретных элементов рэа. Модель пленочного резистора. Модель диффузного, 131.9kb.
• Шкаберин В. А. Определение математической модели. Преимущества математического моделирования., 66.58kb.
• 1. Классификация моделей представления знаний, 1008.73kb.

Возможности системы DEFORM

DEFORM позволяет моделировать пластическое течение материала для горячих, полугорячих и холодных процессов, причем это могут быть как изотермические, так и неизотермические процессы. Теплопередача между объектами и внутри них может быть проанализирована как отдельный процесс или совместно с процессом деформирования по сопряженной схеме. При расчете принимаются во внимание все факторы, влияющие на процесс штамповки: конвекция, излучение, тепловыделение при фазовых переходах и пластических деформациях, выделение тепла при трении, потери тепла в зоне контакта между заготовкой и инструментом, влияние температуры на коэффициент трения и термомеханические характеристики материала, влияние давления на трение и т.д.

В DEFORM нет ограничений на количество участвующих в процессе объектов — как деформируемых, так и деформирующих. Это позволяет моделировать даже самые сложные технологические операции с участием сборных заготовок и любого количества инструментов. При этом инструмент может быть неподвижным или перемещаться в любом направлении в зависимости от параметров заданного оборудования. Возможно моделирование таких современных технологических процессов, как ссылка скрыта или ротационная вытяжка. Инструмент может быть задан и абсолютно жесткий, и упругий, деформируемый. Для технологов очень важна возможность анализа прочности штампа. Эффективный одношаговый алгоритм позволяет сделать это как для жесткого, так и для упругого инструмента на любом шаге процесса. Возможен расчет нескольких инструментов, а также учет предварительного натяга в составном инструменте.

DEFORM позволяет задать практически любое оборудование — это гидравлические прессы, молоты, винтовые прессы, кривошипные прессы, прокатные станы, причем, задав параметры всего оборудования, можно создать библиотеку оборудования данного предприятия или цеха. Специальные шаблоны помогают задавать сложные процессы (например, протяжка на молотах с учетом остывания, промежуточным нагревом и вращением заготовки).

Система DEFORM предоставляет широкие возможности для обработки результатов, оценки процесса на наличие дефектов (образование трещин, складок, незаполнение штампа и др.), анализа течения материала. Результаты включают график усилия, поля распределения напряжений, деформаций и температуры, причем они могут быть представлены графически и таблично. Наглядно показаны макро- и микроструктура изделия, движение отдельных точек материала. Уникальной является возможность визуализации трехмерной, «вмороженной» в материал сетки FLOWNET. Для создания отчетов результаты можно вывести в виде графиков, численных данных, твердых копий и анимации.


41. Исследование напряженно-деформированного состояния деталей методом конечных элементов. Перечислите особенности, которые необходимо учитывать при создании трехмерной расчетной модели детали или узла.

Для исследования напряженно-деформированного состояния (НДС) разработано и используется множество программных продуктов разной степени сложности. В основном такие программы используют метод конечных элементов (МКЭ). Интерес представляет исследование точности получаемых результатов при применении данного метода для линейного анализа статической трехмерной задачи теории упругости.

Ошибки результатов МКЭ складываются из ошибок выбора конечно-элементной модели и ошибок численного решения задачи, связанных с приближенными вычислительными алгоритмами, ошибками округления.

Ошибки выбора конечно-элементной модели связаны с неудачным выбором типа конечных элементов, неудачным построением разбиения. В свою очередь, ошибки разбиения можно разделить на ошибки, связанные с аппроксимацией геометрии поверхностей исследуемых тел, и ошибки, связанные с разбиением на элементы внутри тел.


38. Этапы математического моделирования и их взаимосвязь

Важнейшим этапом моделирования является разделение входных параметров по степени важности влияния их изменений на выходные. Такой процесс называется ранжированием (разделением по рангам). Чаще всего невозможно (да и не нужно) учитывать все факторы, которые могут повлиять на значения интересующих нас величин y_j. От того, насколько умело выделены важнейшие факторы, зависит успех моделирования, быстрота и эффективное гь достижения цели

формулировке, имеющей конкретное математическое наполнение. В этот момент модель предстает перед нами в виде уравнения, системы уравнений, системы неравенств, дифференциального уравнения или системы таких уравнений и т.д.



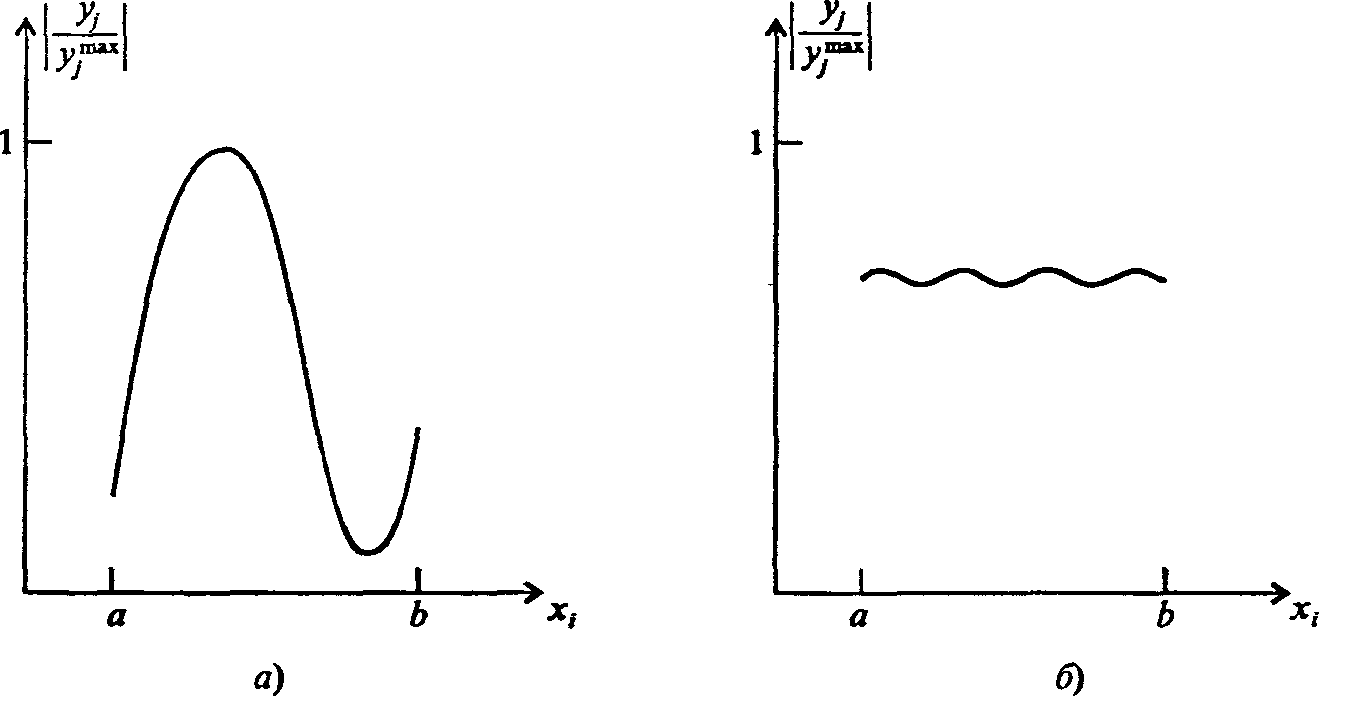
Рис. 2. Варианты степени влияния величины х, на результирующую величину y_i

Когда математическая модель сформулирована, выбираем метод ее исследования. Как правило, для решения одной и той же задачи есть несколько конкретных методов, различающихся эффективностью, устойчивостью и т.д. От верного выбора метода часто зависит успех всего процесса.

Разработка алгоритма и составление программы для ЭВМ - это творческий и трудно формализуемый процесс. В настоящее время при компьютерном математическом моделировании наиболее распространенными являются приемы процедурно-ориентированного (структурного) программирования. Из языков программирования многие профессионалы-физики, например, до сих пор предпочитают FORTRAN как в силу традиций, так и в силу непревзойденной эффективности компиляторов (для расчетных работ) и наличия написанных на нем огромных, тщательно отлаженных и оптимизированных библиотек стандартных программ математической ориентации. В ходу и такие языки, как PASCAL, BASIC, С – в зависимости от характера задачи и склонностей программиста.

После составления программы решаем с ее помощью простейшую тестовую задачу (желательно, с заранее известным ответом) с целью устранения грубых ошибок. Это – лишь начало процедуры тестирования, которую трудно описать формально исчерпывающим образом. По существу, тестирование может продолжаться долго и закончиться тогда, когда пользователь по своим профессиональным признакам сочтет программу верной. Программистский фольклор полон историй об ошибках на этом пути.

Затем следует собственно численный эксперимент, и выясняется, соответствует ли модель реальному объекту (процессу). Модель адекватна реальному процессу, если некоторые характеристики процесса, полученные на ЭВМ, совпадают с экспериментальными с заданной степенью точности. В случае несоответствия модели реальному процессу возвращаемся к одному из предыдущих этапов.

При создании рассматривают следующие основные этапы:

v определение цели моделирования;

Постановка задачи, построение содержательной модели - творческий процесс, основанный на возможностях и знаниях исследователя, базируется на эвристике.

Изучив задание, можно выделить следующие цели создания модели:

1. Определение производительности второго цикла обработки деталей;

2. При каком условии возможно повышение загрузки второго станка и снижение уровня задела на втором цикле обработки;

v идентификация реальных объектов;

На этом этапе осуществляется определение основных элементов реальной системы, и привязка их к образным понятиям модели с дальнейшим конкретизированием и конвертированием в математическое представление на стадии расширения алгоритма программной реализации.

v выбор вида моделей;

Математическое моделирование - замена реального объекта математическим. Делится на аналитическое, имитационное и комбинированное.

Аналитическое моделирование - процессы функционирования элементов системы записываются в виде некоторых функциональных соотношений (алгебраических, интегро-дифференциальных, конечно-разностных и т.п.) или логических условий. Аналитическая модель может быть исследована следующими методами:

v построение моделей и их машинная реализация

v взаимодействие исследователя с моделью в ходе машинного эксперимента

v проверка правильности полученных в ходе моделирования результатов

v определение главных закономерностей, исследуемых при моделировании


42. Система. Основные понятия, характеризующие строение и функционирование систем.

Рассмотрим основные понятия, характеризующие строение и функционирование систем.
Под элементом принято понимать простейшую неделимую часть системы.
Система может быть разделена на элементы не сразу, а последовательным расчленением на подсистемы, которые представляют собой компоненты более крупные, чем элементы, и в то же час более детальные, чем система в целом. Возможность деления системы на подсистемы связана с вычленением совокупностей взаимосвязанных элементов, способных осуществлять относительно независимые функции, подцели, направленные на достижение общей цели системы. Названием "подсистема" подчеркивается, что такая часть должна обладать свойствами системы (в частности, свойством целостности Структура (лат. structure -- строение, расположение, порядок) отражает наиболее существенные отношения между элементами и их группами (компонентами, подсистемами), которые мало меняются при изменениях в системе и обеспечивают существование системы и ее основных свойств. Структура -- это совокупность элементов и связей между ними. Структуру часто представляют в виде иерархии. Иерархия -- это упорядоченность компонентов по степени важности (многоступенчатость, служебная лестница). Между уровнями иерархической структуры могут существовать отношения строгого подчинения компонентов (узлов) нижележащего уровня одному из компонентов вышележащего уровня, т. е. отношения так называемого древовидного порядка.
Понятие "связь" входит в любое определение системы наряду с понятием "элемент" и обеспечивает появление и сохранение структуры и целостных свойств системы. Это понятие характеризует одновременно и строение (статику), и функционирование (динамику) системы.
Связь характеризуется направлением, силой и характером (или видом). По первым двум признакам связи можно разделить на направленные и ненаправленные, сильные и слабые, а по характеру -- на связи подчинения, генетические, равноправные (или безразличные), связи менеджмента. Связи можно разделить также по месту приложения (внутренние и внешние), по направленности процессов в системе в целом или в отдельных ее подсистемах (прямые и обратные). Связи в конкретных системах могут быть одновременно охарактеризованы несколькими из названных признаков.
Важную роль в системах играет понятие "обратной связи". Это понятие, легко иллюстрируемое на примерах технических устройств, не вечно можно применить в организационных системах. Обратная связь является основой саморегулирования и развития систем, приспособления их к изменяющимся условиям существования. Эффективность системы -- способность к достижению поставленных целей за оговоренный срок времени при расходе определенного количества ресурсов и возможном наличии некоторых специфических ограничений. Эмерджентность -- несводимость свойств отдельных элементов к свойствам системы в целом. Только все совместно эти элементы образуют некоторое системное единство - сложную систему.
Со свойством эмерджентности тесно связаны исследовательские процедуры агрегирования и декомпозиции. Агрегирование -- это объединение нескольких параметров системы низшего уровня в параметры системы более высокого уровня (параметры более низкого уровня находят отражение в агрегированных параметрах высшего уровня). Декомпозиция -- это разделение целого на части. По причине сложности не вечно быть может исследовать и провести анализ системы в целом. В этом случае прибегают к декомпозиции и исследуют эти части как самостоятельные объекты. В частности, выделяют подсистемы: субъект (управляющую систему) и объект менеджмента. Выбор принципа декомпозиции является важным этапом исследования. Чаще всего декомпозицию производят путем выделения функций, контуров менеджмента или агрегатов. Многофункциональность -- это способность большой системы к реализации некоторого множества функций (для государства это обеспечение обороноспособности, развитие науки и культуры и т.д.) на заданной структуре. Многофункциональность проявляется в свойствах гибкости, адаптации, живучести. Гибкость -- это свойство системы изменять поставленная проблема и параметры функционирования в зависимости от условий функционирования (адаптация) или состояния подсистем (живучесть). Гибкость обеспечивается избыточностью элементов и менеджментом с обратной связью. Гибкое менеджмент обеспечивает вероятность изменения функций и структуры системы (реконфигурации) и(или) ее параметров. Адаптация -- это способность изменения целей и параметров функционирования при изменении условий функционирования. Живучесть -- это способность изменять цели и параметры функционирования при отказе и(или) повреждении элементов системы. Надежность системы -- это свойство системы реализовывать заданные функции в течение определенного периода времени с заданными параметрами качества. Безопасность системы -- это способность не наносить недопустимые воздействия здоровью нации, персоналу, окружающей среде. Безопасность и опасность составляют полную группу событий. Долговременная (экологическая) безопасность -- характеризуется тем, что недопустимые воздействия не возникают за час, сравнимое с периодом жизни человека. Безопасность чрезвычайных ситуаций обеспечивается возможностью избежать катастрофического поражающего воздействия на самочувствие нации при наступлении природных или техногенных катастроф, конфликтах ветвей власти и т.п.
Стойкость -- это свойство системы осуществлять свои функции при выходе параметров внешних условий системы за определенные ограничения или допуски. В отношении механических систем говорят о запасе прочности.
Уязвимость -- способность получать повреждения при воздействии внешних и(или) внутренних поражающих факторов. Устойчивость -- способность ворочаться в исходное состояние после некоторых возмущающих воздействий, например, острых внешних, экономических или социальных конфликтов.


44. Классификация систем. Подходы к исследованию систем.

Подходы к исследованию систем. Важным для системного под­хода является определение структуры системы — совокупности связей между элементами системы, отражающих их взаимодейст­вие.

При структурном подходе выявляются состав выделенных эле­ментов системы S и связи между ними. Совокупность элементов и связей между ними позволяет судить о структуре системы. После­дняя в зависимости от цели исследования может быть описана на разных уровнях рассмотрения. Наиболее общее описание струк­туры — это топологическое описание, позволяющее определить в самых общих понятиях составные части системы и хорошо фор­мализуемое на базе теории графов.

Менее общим является функциональное описание, когда рас­сматриваются отдельные функции, т. е. алгоритмы поведения систе­мы, и реализуется функциональный подход, оценивающий функции, которые выполняет система, причем под функцией понимается свойство, приводящее к достижению цели.

Простой подход к изучению взаимосвязей между отдельными частями модели предусматривает рассмотрение их как отражение связей между отдельными подсистемами объекта. Такой классичес­кий подход может быть использован при создании достаточно простых моделей. Процесс синтеза модели М на основе классичес­кого (индуктивного) подхода представлен на рис. 1.1, а. Реальный объект, подлежащий моделированию, разбивается на отдель­ные подсистемы, т. е. выбираются исходные данные Д для моделирования и ставятся цели Ц, отображающие отдельные сто­роны процесса моделирования. По отдельной совокупности исход­ных данных Д ставится цель моделирования отдельной стороны функционирования системы, на базе этой цели формируется некото­рая компонента К будущей модели. Совокупность компонент объ­единяется в модель М.



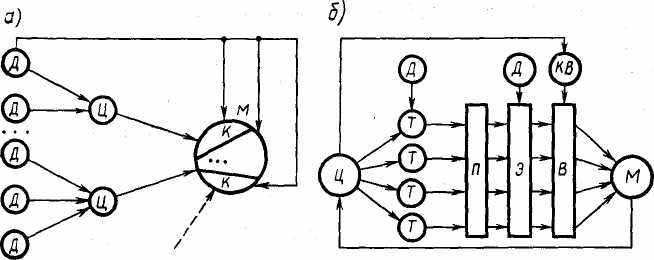
Рис. 1.1. Процесс синтеза модели на основе классического (а) и системного (б) подходов

Таким образом, разработка модели М на базе классического подхода означает суммирование отдельных компонент в единую модель, причем каждая из компонент решает свои собственные задачи и изолирована от других частей модели. Поэтому классичес­кий подход может быть использован для реализации сравнительно простых моделей, в которых возможно разделение и взаимно неза­висимое рассмотрение отдельных сторон функционирования реаль­ного объекта. Для модели сложного объекта такая разобщенность решаемых задач недопустима, так как приводит к значительным затратам ресурсов при реализации модели на базе конкретных программно-технических средств. Можно отметить две отличитель­ные стороны классического подхода: наблюдается движение от частного к общему, создаваемая модель (система) образуется путем суммирования отдельных ее компонент и не учитывается возник­новение нового системного эффекта.

Процесс синтеза модели М на базе системного подхода условно представлен на рис. 1.1, б. На основе исходных данных Д, которые известны из анализа внешней системы, тех ограничений, которые накладываются на систему сверху либо исходя из возможностей ее реализации, и на основе цели функционирования формулируются исходные требования Т к модели системы S. На базе этих требова­ний формируются ориентировочно некоторые подсистемы П, эле­менты Э и осуществляется наиболее сложный этап синтеза — вы­бор В составляющих системы, для чего используются специальные критерии выбора КВ.


45. Этапы расчета методом конечных элементов в системе Autodesk Inventor.

Весь процесс моделирования был реализован с помощью программы Autodesk Inventor. На первом этапе с помощью этой программы создаются модели валков. Сначала необходимо нарисовать эскиз будущей модели. Далее с помощью этого эскиза создается трехмерная модель валка для этого используем инструмент «вращение». Аналогичным способом строятся и модели рабочих валков. На втором этапе производится сборка рабочего и опорного валков для клетей «кварто» и сборка рабочего, промежуточного и опорного валков для шестивалковых клетей. Для этого в программе нужно создать файл сборки, добавить необходимые валки и задать соответствующие зависимости между деталями. В нашем случае достаточно создать 3 зависимости: первая совмещение осей со смещением на расстояние равное половине суммы диаметров валков (для установления линии касания бочек валков); вторая совмещение боковых граней валков со смещением равным половине разности длин бочек (для устранения возможности смещения валков вдоль их оси относительно друг друга), третья совмещения плоскостей, проходящих через оси валков (для запрета возможности перекатывания валков друг относительно друга).

Далее готовая сборка передается в строенный решатель для анализа напряжений. На этом этапе задаются зависимости фиксации опорного валка в соответствии с его закреплением в подушке. В местах посадки под подшипник ограничили перемещение по всем осям, а для рабочего ролика оставили возможность его перемещения вдоль своей оси. Далее задаются нагрузки, действующие на валки. На рабочий валок действует реакция, вызванная прокатываемой полосой, а со стороны опорного валка действует сила, приложенная прижимными подушками. Значения максимальных усилий приведены в таблице 5.1 для каждого из диаметров рабочих валков

50. Аналитические и эмпирические методы построения математических моделей.

Математические модели любых систем могут быть двух типов - эмпирические и теоретические. Эмпирические модели - это математические выражения, аппроксимирующие (с использованием тех или иных критериев приближения) экспериментальные данные о зависимости параметров состояния системы от значений параметров влияющих на них факторов. Для эмпирических математических моделей не требуется получения никаких представлений о строении и внутреннем механизме связей в системе. Вместе с тем задача о нахождении математического выражения эмпирической модели по заданному массиву наблюдений в пределах выбранной точности описания явления не однозначна. Существует бесконечное множество математических выражений, аппроксимирующих в пределах данной точности одни и те же опытные данные о зависимости параметров.
    Теоретические модели систем строятся на основании синтеза обобщенных представлений об отдельных слагающих их процессах и явлениях, основываясь на фундаментальных законах, описывающих поведение вещества, энергии, информации. Теоретическая модель описывает абстрактную систему, и для первоначального вывода ее соотношений не требуется данных о наблюдениях за параметрами конкретной системы. Модель строится на основе обобщения априорных представлений о структуре системы и механизма связей между слагающими ее элементами.
    Наряду с эмпирическими и теоретическими используются и полуэмпирические модели. Для них математические выражения получаются теоретическим путем с точностью до эмпирически получаемых констант, либо в общей системе соотношений моделей наряду с теоретическими выражениями используются и эмпирические.
    Построение эмпирических моделей - единственно возможный способ моделирования тех элементов системы, для которых нельзя построить в настоящее время теоретических моделей из-за отсутствия сведений об их внутреннем механизме. Вопросы, связанные с построением эмпирических моделей, относятся к области обработки наблюдений или, точнее, к математической теории планирования эксперимента.
    Для некоторых систем единственная возможность оценить правильность теоретической модели состоит в проведении численных экспериментов с использованием математических моделей. Поведение модели не должно противоречить общим представлениям о закономерностях поведения процессов.
    Теоретическая модель описывает не конкретную систему, а класс систем. Поэтому проверка теоретической модели возможна при исследовании конкретных частично или полностью наблюдаемых систем. Затем проверенную таким образом теоретическую модель можно применять для описания и изучения конкретных ненаблюдаемых систем, относящихся к тому же либо к более узкому классу.

Методика построения математических моделей объектов аналитическим методом сводится к следующей последовательности действий:

1. Физическое описание объекта моделирования. При этом выделяют «элементарные» процессы, протекающие в объекте моделирования, которые подлежат математическому описанию, и формулируют основные допущения, принимаемые при их описании, а также определяются фундаментальные законы, которые должны быть положены в основу составления математических уравнений исследуемого объекта (системы).
   
2. Составление уравнений статики или динамики объекта моделирования. Данный этап включает составление компонентных и топологических уравнений на базе выделенных на первом этапе физических законов в алгебраической или дифференциальной форме.
   
3. Определение начальных и граничных условий моделирования. Данные условия выбираются исходя из особенностей функционирования моделируемого объекта, обусловленных технологическим процессом, в котором он задействован или для которого он разрабатывается.
   
4. Выбор метода решения уравнений математического описания объекта, разработка алгоритма и составление программы. При выборе метода решения системы уравнений обычно руководствуются требованиями обеспечения максимальной быстроты получения решения.
   
5. Проверка соответствия (адекватности) модели объекту. Математическая модель объекта является лишь его определенным в рамках принятых допущений аналогом. Адекватность модели проверяется путем сравнения значений переменных, получаемых на модели и на реальных объектах, и проверки выполнимости критериев адекватности, которые базируются на методах дисперсионного анализа и анализа остатков, существо которых мы с вами рассматривали на прошлых лекциях.
   
6. Изучение свойств объекта моделирования на математической модели. Данное изучение осуществляется в целях определения оптимальных условий протекания процесса, оптимизации управления процессом, а также выработки решений на создание новых объектов.