Тема Логическое строение школьного курса геометрии

Вид материала

Документы

Содержание Самостоятельное задание 1) -3) с помощью описания процесса нахождения по фигуре F 3 Основной этап изучения геометрических величин 7-11 классов. Самостоятельное задание Основан на идеи исчерпывания (уч. Киселёва, Погорелова (новое издание)). Основан на развёртках (уч. Атанасяна). Формальный подход.

Подобный материал:

• Задачи преподавания геометрии в школе. Различные способы построения школьного курса, 75.88kb.
• И философии математики, 768.66kb.
• Вопросы к зачету по геометрии для 4 курса заочного отделения физико-математического, 22.2kb.
• Учебного курса по геометрии для 9-го класса, 1015.27kb.
• Рабочая программа курса «высшая математика (элементы аналитической геометрии и линейной, 67.54kb.
• Программа курса повышения квалификации учителей математики, 15.17kb.
• Урок биологии в 7 классе. Тема: «Внутреннее строение рыб», 112.94kb.
• Тема: Геометрия на службе архитектуры, 341.17kb.
• Рабочая программа учебного курса по геометрии, 10 класс календарно-тематическое планирование, 281.57kb.
• Проблема учителя, 145.02kb.

Следующий метод задач на построение – метод координат (8 класс) или алгебраический метод. Он сводится к построению фигур на координатной плоскости, исходя из имеющихся уравнений этих фигур. У школьников он особых проблем не вызывает в силу его алгоритмичности, достаточно широкого знакомства с ним как на уроках алгебры, так и геометрии.

Пример: Построить геометрическое место точек плоскости, для которых .

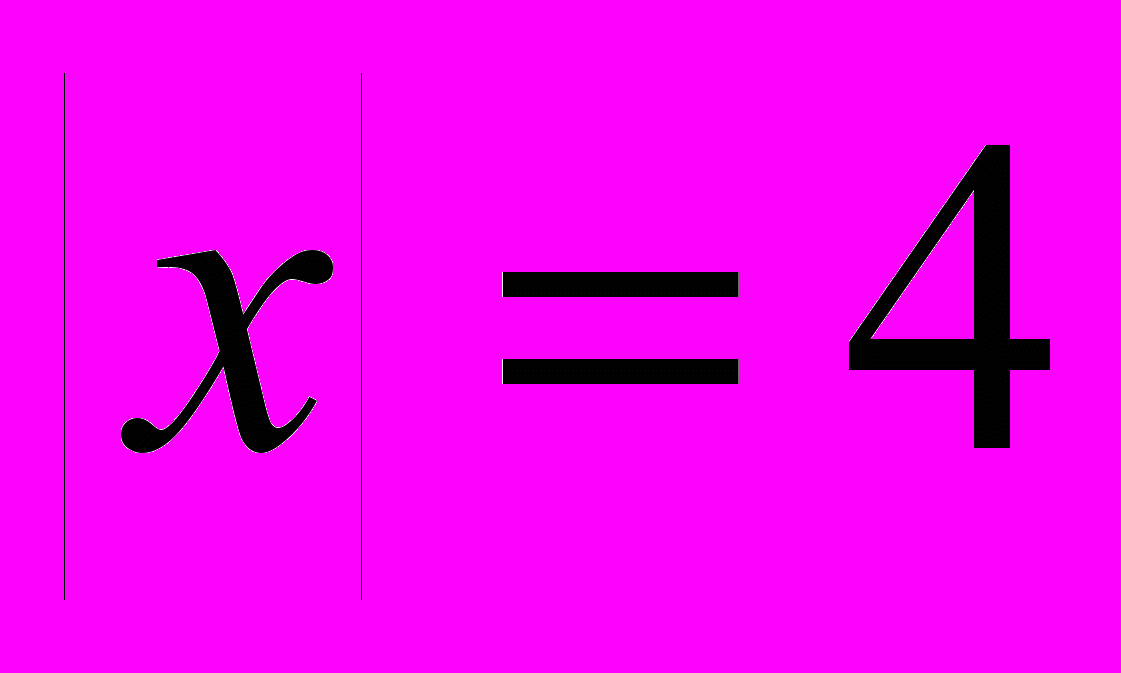Метод движений сводится к подбору такого движения, в результате которого образуется некоторая вспомогательная фигура, удовлетворяющая двум условиям:

1. она может быть построена по данным задачи;
   
2. она связана с искомой так, что ее построение обеспечивает построение искомой фигуры.
   

Наибольшие затруднения у школьников вызывают задачи на построение, решаемые методом подобия (9 кл.) хотя непосредственно таких задач немного, учителю следует в эвристической беседе при решении одной из задач на этапе анализа подвести школьников к выводу, что условие соответствующих задач целесообразно разбить на две части, одна из которых определяет «форму» искомой фигуры (то есть определяет ее с точностью до подобия), а другая – ее размеры. По первой части строят фигуру, подобную искомой, а затем преобразовывают ее в искомую с учетом второй части.


Вопросы для самопроверки:

1. Что такое задача на построение? Когда она считается решенной?
   
2. Какова роль задач на построение в школьном курсе?
   
3. Какие геометрические построения осуществляются в курсе математики: а) начальной школы; б) пропедевтическом курсе 5-6 классов; в) в систематическом курсе геометрии 7-11 классов?
   
4. В чем суть основных этапов решения задач на построение?
   
5. Какие основные методы решения задач на построение Вы знаете? В чем их сущность? Какие из этих методов используются в школьном курсе геометрии?
   

Литература: 4, 6, 7, 14, 16, 17

Дополнительно: Аргунов Б.И., Балк Т.Б. Геометрические построения на плоскости. Учпедгиз, 1955.


Тема 1. Методика изучения многоугольников в школьном курсе планиметрии.

План.

1. Роль материала о многоугольниках в обучении математике.
   
2. Обзор содержания материала о многоугольниках в школьном курсе математики.
   
3. Методические рекомендации по изучению многоугольников.
   

Содержание лекции:

Роль темы «Многоугольники» в обучении обусловлена следующим:

1. Многоугольники и их свойства непосредственно являются основным объектом изучения геометрии, позволяющим развить воображение учащихся.
   
2. Знания, умения и навыки, связанные с данной темой, необходимы для изучения смежных дисциплин (физики, черчения, труда и других) и в реальной жизни.
   
3. Учение о многоугольниках дает основу для использования соответствующего аппарата решения задач и доказательства теорем школьного курса стереометрии и естественным образом способствует развитию логического мышления.
   
4. Многоугольники являются полигоном для раскрытия материала о декартовых координатах, геометрических преобразованиях, векторах и др.
   
5. Материал важен в мировоззренческом аспекте, в историческом и прикладном ракурсах.
   

В систематическом курсе планиметрии материал о многоугольниках можно разбить на 3 основных блока.

1. Учение о треугольниках (7-8 классы) является базовым материалом всей темы, поскольку дальнейшее ее изучение основывается на применении различных свойств треугольников (в частности используются цепочки равных треугольников для доказательства равенства каких либо отрезков, углов при изучении многоугольников. К этому блоку относится следующий материал:
   

1. определение треугольника, сопутствующих понятий,
   
2. равнобедренный треугольник,
   
3. равенство треугольников, аксиома существования треугольника, равного данному,
   
4. зависимость между элементами треугольника,
   
5. подобие треугольников,
   
6. площадь треугольника,
   
7. комбинации треугольника с окружностью.
   

2. Учение о четырехугольниках (8 класс):
   

1. определение четырехугольника и сопутствующих понятий,
   
2. частные виды четырехугольников и их свойства (параллелограмм и его виды: прямоугольник, ромб, квадрат, трапеция),
   
3. площади четырехугольников.
   

3. Учение о многоугольниках (9 класс).
   

1. общее понятие о многоугольниках,
   
2. правильные многоугольники и их построение,
   
3. комбинации правильных многоугольников с окружностью.
   

В учебнике А.В. Погорелов: сначала треугольники (7 класс), четырехугольники (8 класс), многоугольники (9 класс). Происходит постепенное обобщение материала, позволяющее учащимся последовательно установить естественные взаимосвязи между предыдущим и последующими темами.

В учебнике Л.С. Атанасяна смешанный подход: треугольники (7 класс), многоугольники (обзор, 8 класс), четырехугольники, правильные многоугольники (9 класс).

Само определение многоугольника (и его частных видов) производится в основном с двух позиций:

а) как одномерного объекта – простая замкнутая ломанная,

б) как двумерного объекта – плоского многоугольника, включающего в себя кроме простого многоугольника его внутреннюю область.

Оба подхода имеют как достоинства, и так и недостатки. Если мы вводим понятие многоугольника как одномерного объекта, то здесь имеем возможность вывести данное определение из основных понятий – точек и отрезков прямой, то есть четко показать преемственность вводимых понятий. Определяя же многоугольник как плоский, мы имеем возможность в дальнейшем рассмотреть сопутствующие элементы – медиану, высоту и биссектрису треугольника как объекты, принадлежащие треугольнику, а так же ввести понятие площади многоугольника.

Методические особенности изучения многоугольников рассмотрим на примере наиболее характерной темы данного материала «Четырехугольники»

Схема изучения данной темы:

1. Определение четырехугольника и выделение различных их видов.
   
2. Доказательства существования каждого вида.
   
3. Свойства и признаки каждого вида.
   
4. В конце изучения – классификация.
   

Изучение признаков и свойств параллелограмма связано с формулировкой необходимого и достаточного условия того, что четырехугольник является параллелограммом. Данный материал в учебнике А.В. Погорелова изучается вперемежку, по учебнику Л.С. Атанасяна сначала рассматриваются свойства, а затем признаки, как обратные теоремы. Свойства параллелограмма обычно вводятся с помощью практической работы вида: начертить ряд параллелограммов, измерить противолежащие стороны и углы. Сделать вывод.

В конце изучения темы целесообразно провести классификацию выпуклых четырехугольников, изучаемых в школе. Данная классификация зависит от того, как определить трапецию. Возможны два подхода:

1. трапеция, есть четырехугольник, у которого две стороны параллельны, а две другие непараллельны (Киселев, Погорелов, Атанасян). Здесь понятия трапеции и параллелограмма – несовместимы (объемы этих понятий не пересекаются)
   
2. трапеция, есть четырехугольник, у которого две стороны параллельны (Бескин Н.М.). здесь параллелограмм является одним из видов трапеции. Первое определение не позволяет последовательно рассмотреть цепочку частных видов четырехугольников, классификация четырехугольников при этом менее четкая логически.
   

При изучении материала о многоугольниках важное место занимает теорема о сумме углов выпуклого n – угольника.

В действующих школьных учебниках при доказательстве предлагают обычно разбить данный многоугольник на треугольники, соединив диагоналями одну из вершин (фиксированную) со всеми остальными вершинами.

Учитель может предложит другой способ разбиения n – угольника на треугольники , взяв точку О внутри многоугольника и соединив ее со всеми вершинами многоугольника.

Методически оправданы такие подходы при доказательстве теорем, которые отличны от подходов, используемых в действующих школьных учебниках.

Вопросы для самопроверки:

1. Каково значение темы «Многоугольники» в школьном курсе геометрии?
   
2. Какие три содержательных блока можно выделить в данной теме?
   
3. Какие подходы к определению понятия «многоугольник» существуют в учебно-методической литературе?
   
4. Какую методическую схему изучения темы «Четырехугольники» можно составить?
   
5. Каковы методические особенности изучения признаков и свойств параллелограмма?
   
6. Приведите различные доказательства теоремы о сумме углов n – угольника и обоснуйте методическую ценность каждого из доказательств.
   

Литература: 4, 6, 7, 10, 14, 16, 17.


Тема 6. Геометрические преобразования в школьном курсе геометрии.

План.

1. Общая характеристика материала. Различные подходы к изучению геометрических преобразований в школе.
   
2. Методические особенности изложения отдельных вопросов.
   
3. Метод геометрических преобразований и возможности его использования при решении задач.
   

Содержание лекции:

1. Применение преобразований (а частности, движений) к установлению геометрических фактов связывают с именем Фалеса Милетского. Фалес с помощью перегибаний и поворотов чертежа показал справедливость таких фактов, как равенство вертикальных углов, равенство вписанного угла, опирающегося на диаметр окружности, прямому углу и т.д.

Мощный толчок развитию идеи геометрических преобразований, дал немецкий математик Феликс Клейн в своей Эрлангенской программе. По Клейну предмет геометрии составляет теория инвариантов некоторой группы геометрических преобразований каждой из которых соответствует своя ветвь геометрии.

С этих позиций геометрия, определяемая группой преобразований подобия, и является предметом изучения в средней школе.

Впервые значительное внимание этому материалу было уделено известным отечественным математиком и методистом А.Н. Колмогоровым. В его курсе геометрии (1968-1980) преобразования занимали центральное место и служили основой доказательства многих теорем.

В учебниках Погорелова и Атанасяна движения и преобразования подобия стали рассматриваться скорее как объект изучения, чем универсальный аппарат для решения задач.

Роль материала:

1. Введение в школьный курс линии геометрических преобразований позволило дать «аппаратное», «рабочее» истолкование равенства и подобия фигур. Если в учебнике Погорелова первоначально вводятся равные треугольники через равные элементы, то аналогичное определение равенства (подобия) для произвольных фигур ввести затруднительно – нужны геометрические преобразования. По Атанасяну же равенство вводилось через наложение, что не давало эффективного аппарата для решения задач на построение.
   
2. Геометрические преобразования позволили ввести в школьный курс динамику, преодолеть некоторую статичность традиционного синтетического подхода. При этом появилась возможность уделить особое внимание развитию определенных сторон пространственного воображения школьников.
   
3. Геометрические преобразования дают новый эффективный метод решения задач, позволяющий во многих случаях облегчить доказательство теорем и решения задач.
   
4. Геометрические преобразования способствуют реализации внутрипредметных связей с алгеброй (функциональная зависимость, преобразования графиков функций), межпредметных –с физикой (механическое поступательное движение и т.д.). отметим, что в физике исследуется в основном сам процесс движения, в геометрии – фиксированные положения фигуры, подвергшейся движению (исходное, конечное и иногда промежуточное).
   
5. Геометрические преобразования привносят в школьную математику эстетику, изящество. Идея симметрии – орнаменты, снежинки, архитектурные сооружения являются воплощением этой идеи, являясь одним из важнейших средств гуманитаризации обучения математике.
   

Теория геометрических преобразований в школе может быть построена традиционным – синтетическим, а так же аналитическим методами. Наибольшее распространение получил смешенный: аналитико-синтетический подход, использующийся в действующих учебниках. Это позволяет упростить изложение, а так же формировать у школьников представление о возможности использования различных способов задания геометрических преобразований.

В учебнике Погорелова (теоретико-групповой подход) материал представлен в виде двух отдельных тем: «Движения» (8 кл.) и «Преобразования подобия» (9 кл.). Обе темы начинаются с общих вопросов: вводится общее понятие, дается два общих групповых свойства, рассматриваются свойства этих видов преобразований, их виды и специфические свойства каждого вида.

Учебник Атанасяна (реально-практический подход) предусматривает вначале описательное знакомство с симметрией (8 кл.). В конце 9 класса рассматривается общее понятие движения и его свойства, затем отдельно изучаются параллельный перенос и поворот.

2. Рассмотрение частных видов движений осуществляется по следующему примерному плану:

1. Выполняется построение и одновременно проговаривается определение того или иного вида движений (определение – генетическое); вводятся сопутствующие понятия.
   
2. Предлагаются задания на построение фигур, полученных путем, воздействия движением на данные фигуры.
   
3. Неявно вводится тождественное преобразование как преобразование, переводящее фигуру саму в себя.
   
4. Упражнения на распознавание.
   
5. Доказательство того, что данное преобразование является движением (преобразованием подобия) обычно предваряется задачей на построение и последующее измерение или вычисление расстояний.
   
6. Доказательство специфических свойств данного вида преобразований.
   

При изучении преобразований подобия и признаков подобия треугольников можно порекомендовать использование аналогии с движениями. Это можно реализовать на вводной лекции введения понятия преобразования подобия и гомотетии. Одновременно повторяя пройденный материал по теме «Движения» и «Признаки равенства треугольников», учащиеся формулируют соответствующие утверждения, относящиеся к теме «Подобие». Все сведения заносятся в таблицу, и соответствующие факты затем доказываются.

С материалом о геометрических преобразованиях тесно связано рассмотрение признаков подобия треугольников, являющихся основой для решения большого количества задач в синтетической геометрии. Формулировка признаков подобия аналогична формулировке признаков равенства и может быть дана самими учениками в процессе выполнения соответствующих заданий исследовательского характера.

По учебнику Погорелова доказательство признаков подобия треугольников основывается на свойствах гомотетии и допускает использование одного и того же чертежа. Работа по доказательству всех признаков может осуществляться относительно единовременно, крупноблочно, со значительным участием самих учеников. Доказательство признаков подобия треугольников осуществляется последовательно (один признак вытекает из другого).

В частности, выписав соответствующие формулы для всех углов, получим пропорциональность соответствующих сторон.

Еще один подход, в соответствии с которым признаки подобия могут быть доказаны на основе теорем косинусов и синусов.

3. Геометрические преобразования лежат в основе мощного метода, значительно упрощающего решение многих задач планиметрии и стереометрии. Овладение этим методом предполагает сформированность у учащихся умений выполнять ряд специфических действий.

Умения:

1. Строить образы фигур при том или ином геометрическом преобразовании.
   
2. Распознавание точек и фигур, определяющих это преобразование.
   
3. Использование свойств преобразований для обоснования наличия определенного соотношения между рассматриваемыми геометрическими фигурами.
   
4. Выбор вида преобразования, который целесообразно использовать при решении данной конкретной задачи.
   

Овладение методом геометрических преобразований предусматривает несколько этапов:

1. подготовительный, 2) ознакомительный, 3) формирующий; 4) совершенствующий.
   

Задания для самостоятельной работы:

1. Обоснуйте выбор геометрического преобразования для решения следующих задач, и решить задачу выбранным методом.
   
2. Доказать признаки подобия треугольников с использованием теорем синусов и косинусов и продумать возможность использования данного подхода применительно и действующим школьным учебникам.
   

Вопросы для самопроверки:

1. В чем суть Эрлангенской программы Ф. Клейна?
   
2. Что является предметом изучения геометрии в средней школе с точки зрения Эрлангенской программы?
   
3. Какова роль материала о геометрических преобразованиях в школьном курсе?
   
4. Как представлена данная содержательная линия в действующих учебниках по геометрии?
   
5. Какова методическая схема изучения частных видов движений в школьном курсе?
   
6. Каковы методические особенности изучения преобразований подобия?
   
7. Опишите возможную методику изучения всех признаков подобия треугольников на одном уровне.
   
8. Докажите признаки подобия треугольников с использованием подходов, отличных от имеющихся в действующих учебниках.
   
9. Какие этапы овладения методом геометрических преобразований можно выделить? В чем суть каждого из этих этапов?
   

Литература: 4, 6, 7, 10, 14, 16, 17.


Тема 7. Векторы в школьном курсе математики.

План.

1. Место темы в программе. Анализ содержания и подходов к его изложению.
   
2. Методика изучения отдельных вопросов.
   
3. Изучение векторов в курсе стереометрии.
   

Содержание лекции:

1. Понятие вектора является одним из фундаментальных в современной математике. Важность этого понятия для геометрии была показана Германом Вейлем, предложившим в 1918 году векторную аксиоматику евклидовой геометрии.

Материал о векторах стал изучаться в школьном курсе сравнительно недавно. Необходимость его включения в содержание курса геометрии следовала из следующих соображений.

1. Изучение векторной алгебры важно с точки зрения обогащения идейного содержания учебного курса, приближая его к современной геометрической науке.
   
2. Знакомство с векторами необходимо ученикам для изучения смежных курсов: физики, астрономии, химии, географии.
   
3. Векторы дают эффективный и компактный метод решения различных геометрических (аффинных и метрических) задач и доказательства ряда теорем.
   
4. Углубляется представление учащихся о величинах в том плане, что вектор выступает как связывающее звено между метрикой и направлением.
   
5. Происходит обобщение знаний учащихся об арифметических и алгебраических операциях.
   

Рассматриваются 4 варианта введения понятия вектора в школьном курсе:

1. Модернистский Ввести вектор, наряду с точкой и прямой как основное понятие, описываемое соответствующей системой аксиом (по Вейлю). При этом курс геометрии строится на полностью векторной основе.
   
2. Вектор рассматривать как одно из геометрических преобразований, отождествить ею с параллельным переносом (А.Н. Колмогоров).
   
3. Рассмотреть вектор как направленный отрезок (А.В. Погорелов, Л.С. Атанасян).
   
4. Ввести вектор как порядочную пару чисел, то есть на чисто координатной основе (свести геометрию к алгебре), все действия над векторами сводились бы к действиям над числами.
   

Определение вектора как направленного отрезка было значительно более наглядным для школьников и больше подходила к физическим представлениям о векторе, поэтому в некоторых учебниках используется именно такое определение.

При изложении материала о векторах большое значение имеет обеспечение необходимого «равновесия» между наглядно-геометрическим и координатным подходами к данному вопросу. Если наглядно-геометрический подход более характерен для стиля изложения геометрического материала, то координатный метод упрощает многие доказательства, способствует достижению краткости изложения материала.

В учебнике Погорелова изучение векторов относится к концу 8 класса. Перед этим рассматриваются темы «Движения» и «Декартовы координаты на плоскости». изучение векторов идет по следующему плану: понятие вектора, абсолютная величина и направление вектора, равенство векторов, координаты вектора, операции над векторами, разложение вектора на плоскости по двум неколлинеарным векторам.

Основное понятие для векторов в пространстве рассматриваются аналогично.

В учебнике Атанасяна метод координат рассматривается уже позже введения понятия вектора, поэтому большой блок материала дается на чисто геометрической основе. В большой мере используется наглядно-геометрический подход, чем координатный.

2. При введении понятия «вектор» обычно рассматривают физическую ситуацию.

Учащимся предлагается подействовать на вектор различными движениями и выяснить, изменилось ли направление и абсолютная величина вектора при применении того или иного движения. Делается вывод, что в случае параллельного переноса абсолютная величина и направление не меняются. То есть, если векторы совмещаются параллельным переносом, их называют равными, при этом их абсолютная величина и направления совпадают. Отметим, что здесь возникает кажущееся противоречие с определением равных фигур. Это объясняется тем, что век5тор характеризуется не только своим числовым значением, но и направлением, которое сохраняется только при параллельном переносе.

Центральным вопросом является введение координат вектора.

Можно предложить следующую схему:

1. В системе координат с нанесенной координатной сеткой рассмотрим несколько вопросов: Какие из изображенных векторов равны? Как можно показать, не измеряя отрезков и углов? Попробуйте посчитать клеточки при движении от начала к концу этих векторов (3 клеточки вправо и 2 вверх). Таким образом, мы определили координаты векторов.
   
2. Задание: В тетрадях постройте точки А (2, 3) и В (4, 7). Аналогично определите координаты вектора АВ и выясните связь между координатами вектора АВ и соответствующими координатами его начала и конца.
   
3. Итог – определение координат вектора.
   
4. Далее закрепляем определение на примерах.
   
5. Переходим к доказательству этого факта.
   

Скалярное произведение векторов.

Материал, связанный с векторами разделяется на две большие группы вопросов:

1. Вопросы аффинной геометрии. Здесь в основном решаются задачи на установление параллельности, выполнение отношения отрезков, параллельный перенос, гомотетия, принадлежность трех точек одной прямой, принадлежность четырех точек одной плоскости и т.д.
   
2. Описывает метрическую часть темы. Это скалярное произведение векторов и его свойства. Здесь решаются задачи на вычисление расстояний, углов, нахождение множества точек.
   

Таким образом, без изучения скалярного произведения векторов из поля зрения учащихся выпадает большое количество метрических задач и в значительной мере теряется эффективность применения векторного метода..

Однако, скалярное произведение векторов совсем недавно стало изучаться в планиметрии в силу следующих трудностей:

1. Учащиеся привыкли, что умножение –есть операция, ставящая в соответствие двум элементам одного множества элемент того же множества. Скалярное же произведение векторов – есть число, то есть элемент множества, совершенно отличного от множества векторов.
   
2. Свойства скалярного произведения весьма отличны от свойств ранее изученных произведений.
   
3. Само определение скалярного произведения громоздко: либо это сумма произведений двух пар соответствующих координат, либо – произведение длин двух векторов на косинус угла между ними.
   

3. Аксиоматика школьного курса планиметрии не предопределяет строго логическую структуру курса стереометрии, то есть аксиоматика стереометрии может по своему характеру отличаться от планиметрической. Соответственно делались попытки изложить курс стереометрии на основе более современных математических методов, в частности, на векторном. При этом бы появилась возможность объединить курсы геометрии и алгебры на координатно-векторной основе. Однако, данный вариант пока не реализован в силу ряда субъективных трудностей:
   

1. Алгебраизация геометрии не способствует развитию пространственных представление школьников, их геометрической интуиции, не способствует их реальным представлениям.
   
2. В среднем звене трудно воспитать у школьников высокую алгебраическую культуру и дать четкие представления об аксиоматическом методе, которые необходимы для изучения стереометрии на векторной основе.
   
3. Не разработана в должной мере соответствующая методика преподавания.
   

Согласно действующей программе векторы рассматриваются в курсе стереометрии и как объект изучения и как аппарат доказательства теорем и решения задач. Место данной темы в курсе стереометрии может быть различным: 1) изучение векторов идет после параллельности до перпендикулярности в пространстве (Колмогоров, Скопец); 2) векторы рассматриваются после параллельности и перпендикулярности и используются в основном при решении задач на «Многогранник», «Тела вращения» (Погорелов); 3) в конце курса, появляется возможность показать преимущества векторного метода по сравнению с традиционным – геометрическим при решении стандартных задач, однако, теряется возможность использования векторов для первичного доказательства теорем.

Усвоение понятийного аппарата, связанного с векторами, создает предпосылки для овладения учащимися векторным методом решения задач, включающим в себя следующие компоненты:

1. Перевод условия задачи на векторный язык и разложение введенных векторов по базисным (если необходимо).
   
2. Составление векторного равенства и его преобразование.
   
3. Замена векторного равенства алгебраическим уравнением и его решение.
   
4. Объяснение геометрического смысла найденного решения.
   

Задания для самостоятельной работы.

1. Показать реализацию компонентов векторного метода на примере решения задачи: Найти один из углов между диагональю куба и диагональю какой – либо грани куба.
   

Вопросы для самопроверки:

1. Чем вызвана необходимость и целесообразность изучения векторов в школьном курсе?
   
2. Какие возможности введения понятия вектора в школьном курсе можно выделить?
   
3. Каково содержание данной темы в школьных учебниках?
   
4. Методика введения понятий «вектор» и «равные векторы».
   
5. Методика изучения координат вектора и операций над ними.
   
6. Каковы методические особенности изучения скалярного произведения векторов?
   
7. Какие варианты изучения векторов возможны в курсе стереометрии? Положительные и отрицательные стороны этих вариантов.
   
8. Каковы основные компоненты, из которых состоит овладение векторным методом?
   

Литература: 4, 6, 7, 8, 10, 14, 16, 17.


Лекция 8. Методика изучения геометрических величин

в школьном курсе математики.

План.

1. Некоторые методические замечания.
   
2. Место и значение темы в школьном курсе математики. Изучение скалярных геометрических величин в младших классах.
   
3. Методические особенности изучения систем скалярных геометрических величин в средних и старших классах.
   
4. Различные подходы к изучению объёмов многогранников и тел вращения.
   
5. Методические особенности изучения площадей поверхностей тел вращения.
   

Содержание лекции:

1. Предметом изучения данной лекции являются скалярные геометрические величины – длина, площадь, объём, мера угла. Под системой скалярных величин по А.Н. Колмогорову понимается определённое множество
   

S={a, b, c, ….}, удовлетворяющее системе аксиом (10 аксиом).


Самостоятельное задание: Выписать эти аксиомы. Любая скалярная величина по отношению к конкретному объекту обладает свойством быть измеренной, то есть охарактеризованным числом. При этом фактически задаётся соответствие между множеством фигур и множеством положительных действительных чисел так, что выполняются следующие свойства:

1. Равные фигуры имеют равные величины (инвариантность, относительно движения);
   
2. Величина фигуры, являющая объединением нескольких фигур без общих внутренних точек, равные сумме величин этих фигур (аддитивность);
   
3. Существует фигура (единичный отрезок, единичный квадрат, единичный куб), величина которого равна 1 (нормированность).
   

Скалярные геометрические величины могут вводиться либо:

1) аксиоматически, как функции, обладающие указанными выше свойствами:

а) Предполагая существование этой функции, выводят формулы для величин ломаных, многоугольников, многогранников. Показывается возможность вычисления величины произвольных многоугольных и многогранных фигур путём их разбиения на треугольники и тетраэдры и независимость их от способа разбиения, то есть

()

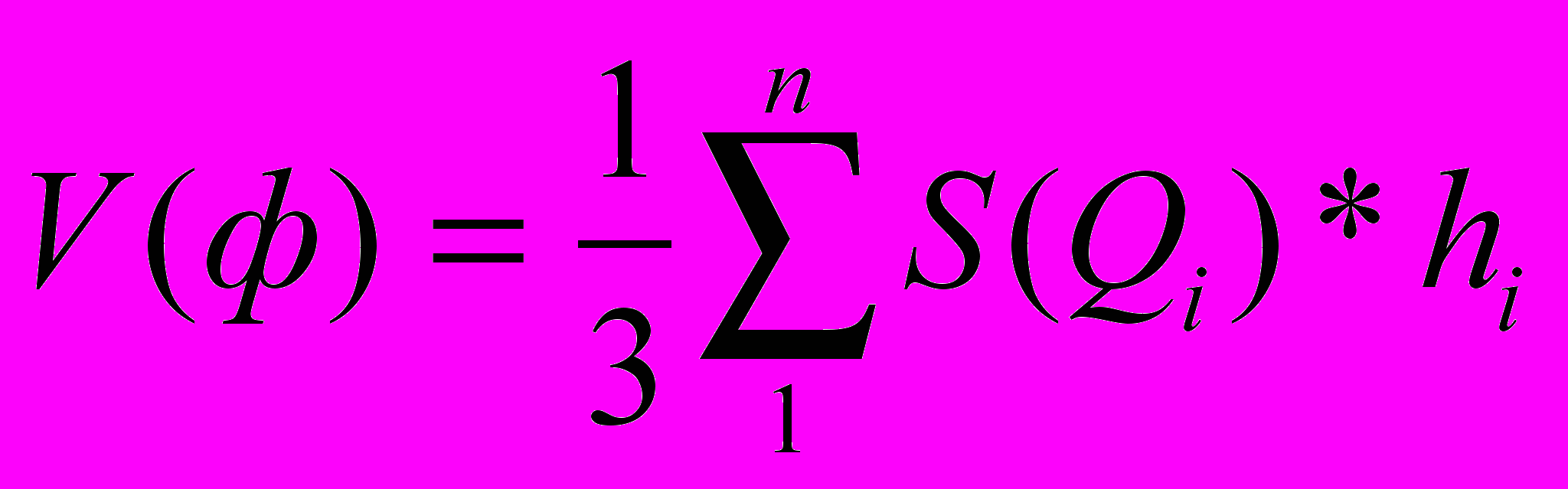теорема о существовании и единственности на классе многоугольных (многогранных) фигур.

б) Вводится множество квадрируемых (кубируемых) фигур, спрямляемых дуг и доказывается существование и единственность рассматриваемой величины на этом множестве.

2. конструктивно (идём в обратном направлении). Строится функция, обладающая свойствами 1) -3) с помощью описания процесса нахождения по фигуре F её величины:
   

1 способ: Рассматривается множество многоугольниках (многогранниках) фигур и показывается возможность их разбиения на треугольники (тетраэдры). Доказывается, что произведение основания на высоту треугольника (тетраэдра) не зависит от высоты основания. Без доказательства принимаются формулы для S треугольника и V тетраэдра. Доказывается, что введение, таким образом, функция обладает свойствами 1)-3). Далее данная функция распространяется на класс квадрируемых (кубируемых) фигур и опять доказываются указанные свойства.

Данный подход редко используется в силу его психологической неубедительности (без доказательства принимаются формулы S треугольника, V тетраэдра), а также довольно сложного доказательства основных свойств площади и объёма.

1. способ: Естественный. Он позволяет ввести систему скалярных геометрических величин сразу для классов многоугольниках, многогранных фигур путём разбиения прямой, плоскости или пространства точками, прямыми или плоскостями. Получаем масштабную сетку, состоящую из квадратов со сторонами 1, 1/10, 1/100, … 1/10ⁿ.
   

Пусть в заданной фигуре F содержится _n квадратов со стороны 1|10ⁿ , а сама фигура F содержится в _n квадратов со стороны 1/10ⁿ. Положим за S_n - число _n/10ⁿ, за S_n – число _n/10ⁿ (число единиц площади, содержащихся в F и содержащих F). Если существует единственное число, заключённое между всеми числами S_n и всеми числами S_n, то фигура F называется квадрируемой (кубируемой). Для отрезков получается что-то типа теории сечений. Дедекинда (теория действительного числа).

В школьных курсах основным путём введения геометрических величин является аксиоматический путь, подкрепляемый особенно на первых этапах изучения материала конструктивными соображениями, связанными с использованием транспортира, линейки, палетки и кубической масштабной сетки, как средствами измерения.

Изложение теории площадей многоугольников и объёмов многогранников существенно опирается на понятие равносоставленности многоугольников и многогранников.

Из свойств скалярных величин вытекает, что равносоставленные фигуры равновелики. Это позволяет ввести простой способ вычисления площадей (использовавшийся ещё Евклидом).

Укажем два важных факта, позволяющие понять логику построения соответствующего школьного материала.

1. Теорема Бойяи – Гервина:
   

Два равновеликих многоугольника равносоставлены. Из этой теоремы вытекает, что достаточно знать формулу для S прямоугольника, чтобы легко вывести площади других многоугольников.

2. Аналогичная теорема для многогранников, сформулированная впервые Д.Гилабертом (1900 г., 3-я проблема) вообще несправедлива. Это следует из результатов Дена (1901 г.), который, в частности, показал, что правильный тетраэдр не равносоставлен с кубом того же объёма.
   

Именно поэтому при изучении объёмов многогранников недостаточно формулы объёма прямоугольного параллелепипеда, а приходится ещё использовать неэлементарные методы для нахождения объёмов тетраэдра. Однако, для некоторых видов многогранников (например призм) рассматриваемый факт справедлив.

2. Важность линии геометрических величин определяется следующими моментами.

1. В реальной действительности мы постоянно сталкиваемся с необходимостью измерения и оценки расстояний, площадей и объёмов фигур. (Примеры подобрать самостоятельно).
   
2. На основе материала данной темы осуществляется знакомство школьников с важными идеями, понятиями и методами метрической геометрии, расширяются возможности применения аналитического метода.
   
3. Реализуются внутрипредметные и межпредметные связи на основе взаимодействия аксиоматического метода, теории действительного числа, инфинитезимальных методов (бесконечно малых), метода координат и т. д.
   
4. Совершенствуются вычислительные навыки, навыки тождественных преобразований и решения уравнений и неравенств.
   
5. На данном материале, как правило, реализуется метод опорного элемента при решении задач
   

В школьном курсе математики изучаются следующие скалярные величины: длина отрезка, мера угла, площади многоугольника и круга, объёмы многогранников и тел вращения, длина окружности, площадь поверхности тел вращения.

Изучение скалярных геометрических величин в школе осуществляется концентрически: 1 концентр – 1 – 6 классы - пропедевтический, 2 концентр – 7-11 классы – основной.

1этап. В курсе 1-4 классов у школьников развивается наглядно-интуитивное представление о величинах и их практическом измерении. Здесь они знакомятся с различными единицами измерения длины и площади, основными соотношениями между ними; измеряют и сравнивают длин отрезков и площади фигур, составленных из единичных отрезков и квадратов, с помощью линейки и палетки вычисляют периметр многоугольника, а также площадь прямоугольника (по формуле). Уже здесь учащиеся начинают производить действия с именованными числами: + и – величин, * и : величин на число, а также сравнение величин.

2 этап. В 5-6 классе представления о геометрических величинах систематизируются и углубляются. В частности, если в начальной школе отрезок и его длина воспринимаются как один и тот же объект, то в 5-ом классе учащиеся получают возможность установить различие между фигурой и её величиной, записываемой в виде числа с наименованием.

Это достигается на основе сопоставления результатов выполнения двух основных задач: построения отрезка заданной длины и измерения длин данного отрезка. Если в первом случае ответ неоднозначен, то во втором результат однозначен.

При изучении площадей и объёмов реализуется тот же план, что и при изучении длин отрезков: а) определение площади и объёма не даётся, а лишь поясняется, что для величин различных поверхностей и вместимостей сосудов надо знать площадь или объём соответствующих фигур; б) на конкретных примерах вводятся свойства площадей и объёмов, единицы их измерения, обращается внимание на то, что в отличие от длины и мер углов равенство площадей или объёмов фигур вовсе не означает равенство этих фигур; в) вводятся и наглядно обосновываются формулы для площади прямоугольника и объёма прямоугольного параллелепипеда. Решаются соответствующие текстовые задачи.

В 6 классе обоснование вводятся важные в практическом отношении формула для длин окружности и площади круга.

3 Основной этап изучения геометрических величин 7-11 классов.

На этом этапе происходит переход от вычислительно-прикладного аспекта к формально-логическому.

В учебнике А.В. Погорелова в §1 в явном виде вводятся аксиомы откладывания и измерения отрезков и углов. Вопрос об измерении отрезков и углов. Вопрос об измерении отрезков и углов в практическом плане не ставится.

В учебнике Л.С. Атанасяна изложение связано с практическими измерениями. Описывается процесс измерения, на наглядном уровне поясняются свойства длины отрезков и градусных мер углов, описываются приборы для измерения расстояний и углов на местности. В аксиоматике (в Приложении 1) есть только аксиомы измерения и откладывания отрезка (аксиом измерения углов нет).

Понятие о площадях и объёмах в учебнике А.В. Погорелова вводится также аксиоматически. Площадь простой фигуры (объём простого тела) – это положительная величина, численное значение которой обладает свойствами: 1)-3).

В учебнике Л.С. Атанасяна и др. площадь определяется как величина части плоскости, занимаемой многоугольником, измерения площадей и объектов с помощью единичных квадратов и кубов и обосновываются основные свойства площадей и объёмов.

В основу изучения площадей плоских фигур и объёмов многогранников в школьных курсах геометрии кладутся формулы S прямоугольника (S квадрата) и V прямоугольного параллелепипеда. (Можно и S треугольника и V тетраэдра и другие).

Можно выделить следующие четыре подхода к изучению площадей:

1. Сравнение площадей (подход Адамара)

В основе подхода - теорема о том, что площади (или объёмы) 2-х прямоугольников (прямоугольных параллелепипедов), имеющих равные основания, относятся между собой как их высоты.

Данный способ обладает достаточной общностью и вместе с тем не согласуется с известными с 5-6 классов способом измерения и имеет чересчур формальный для школы характер. Этот переход использован в учебнике А.В.Погорелова.

2. Традиционный подход (учебники Килелёва, Фетисова 1957 г., Атанасяна). После рассмотрения основных допущений о площадях вводится понятие об измерении площади прямоугольника при помощи сетки квадратов последовательно для случаев, когда обе стороны выражаются через единичный отрезок как:

1. натуральное число;
   
2. конечная десятичная дробь (рациональное число);
   
3. бесконечная десятичная дробь (иррациональное число).
   

3. В 3-ем наиболее сложном случае площадь определяется либо как предел последовательности площадей прямоугольников, длины сторон которого выражаются рациональными числами, либо через введение двух последовательностей приближённых рациональных значений площади по недостатку и по избытку.

4. (на основе равносоставленности) – учебник Глагольева, 1954 г.

В явном виде рассматривается понятие равносоставленности. Определяются условия, при которых параллелограммы и прямоугольники равносоставлены. Рассматривается вывод формулы площади прямоугольника (прямоугольного параллелепипеда) для натуральных и рациональных измерений, а для иррациональных измерений формулы даются без доказательства. Данный подход также громоздок и не обладает достаточной психологической убедительностью в силу последнего допущения.

Наиболее оптимальным в настоящее время учителя считают классический подход (2-й подход) без рассмотрения третьего случая, либо принятие формулы площади квадрата за аксиому.

После доказательства (вывода) формулы площади прямоугольника, пользуясь элементарными методами (теоремой Бойяи-Гервина – 12 равновеликих многоугольника равносоставлены) выводят формулы для площадей остальных прямоугольников, либо разбивая, либо дополняя новый многоугольник.

В основе изложения теории объёмов многогранников лежит формула для объёма прямоугольного параллелепипеда, доказываемая совершенно аналогично формуле для площади прямоугольника.

В силу равносоставленности равновеликих призм вывод формул для объёмов наклонных параллелепипедов и призм можно осуществить элементарными методами. Соответствующие соображения иллюстрируются на наглядных моделях, а выводы аналогичны тем, которые применялись в планиметрии.

Основная методическая проблема при выводе формул для объёмов многогранников является соответствующая формула для тетраэдра (теорема Дена). По этой теореме для вывода этой формулы необходимо использовать неэлементарные методы, связанные с операцией интегрирования (явно или неявно). Подход, при этом используемый, как правило, отражается и на методике изложения теории объёмов тел вращения.

1 подход – метод исчерпывания («чёртова лестница») (учебники Киселёва, Погорелова) осуществляется в двух вариантах:

Первый вариант - косвенный.

1 этап – лемма. Две треугольные пирамиды с равными площадями оснований и равными высотами равновелики.

Разбив высоту на n частей, проводим плоскости, параллельные плоскости основания. Получим разбиение пирамид на слои. Через вершины сечений призмы проводим n прямых, параллельных какому – либо ребру призмы.

Получаем два ступенчатых многогранника, состоящих из входящих в первую пирамиду и содержащих эту пирамиду призм. Их суммарные объёмы отличаются на объём призмы последнего от вершины слоя S 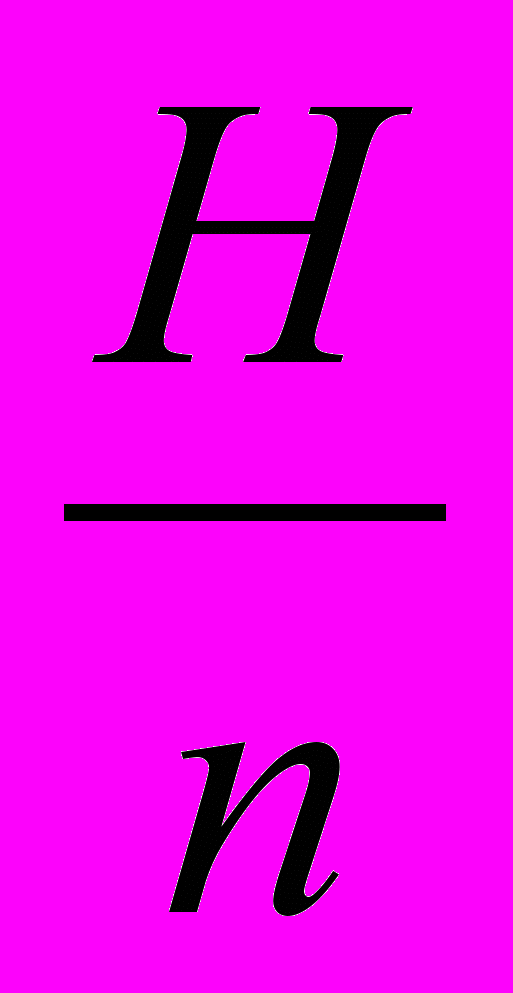(S - площадь основания, H - высота, n - номер слоя).

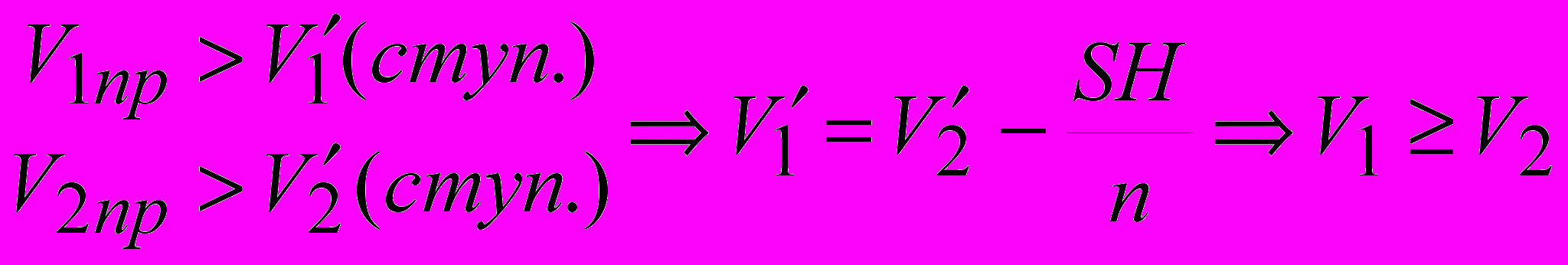, (n – любое )

(см. п. 198 учебник Погорелова)

Аналогично: V₂ V₁ V₂= V₁

2 этап: Треугольная пирамида дополняется до призмы путём присоединения к ней ещё двух пирамид. Все три пирамиды по предыдущей лемме – равновелики V_пир= V_призмы

Второй вариант – прямой. (уч. Глаголева) является модификацией предыдущего варианта.

1 этап: Для пирамиды строится двоякая последовательность призм. Показывается, что V_{пирамиды} является общим пределом последовательности объёмов ступенчатых многогранников при неограниченном увеличении количества составляющих призм:



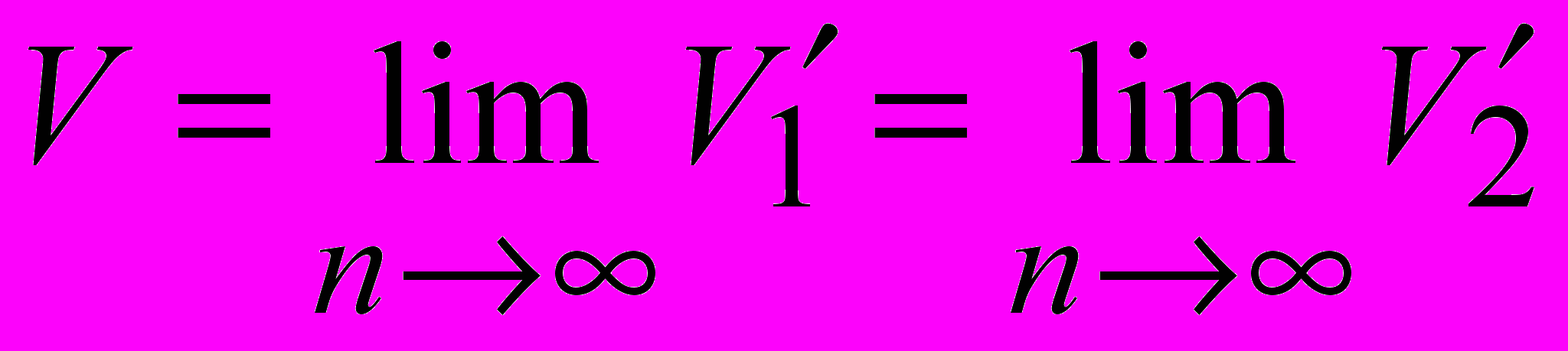
Значит, достаточно вычислить объём ступенчатой фигуры.

2 этап: Объём ступенчатой фигуры вычисляется как сумма объёмов и подобных призм.

2 вариант психологически убедительней, но требует дополнительного времени для формул суммы квадратов натуральных чисел.

Объёмы тел вращения при данном подходе определяются как пределы соответствующих последовательностей объёмов вписанных и описанных многогранников (призм и пирамид). Основную сложность в данном случае составляет вычисленные объёмы шара. Здесь приходится вводить формулу для объёма тела вращения через определённый интеграл.

Третий подход – вычисление объёмов тел с помощью определённого интеграла (уч. Атанасяна и Александрова).

1. Для объёма простого тела рассматривается общий подход:
   

V=S (х) dx,

где S (х) – площадь сечения тела плоскости, перпендикулярной оси абсцисс.

2. Объём наклонной призмы и пирамиды.
   
3. Объёмы тел вращения.
   

Четвертый подход – через принцип Кавальери (итальянский математик 17 века, аббат монастыря). Две фигуры с равными высотами равновелики, если равны любые их сечения, приведённые параллельно основаниям на одинаковой высоте от них. Данный принцип принимается за дополнительную аксиому объёмов (для площадей и объёмов).

==

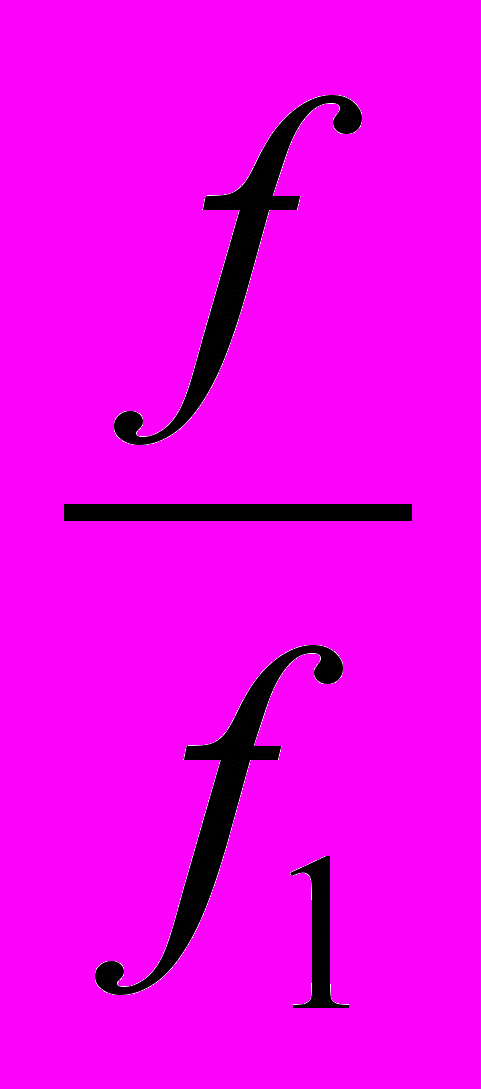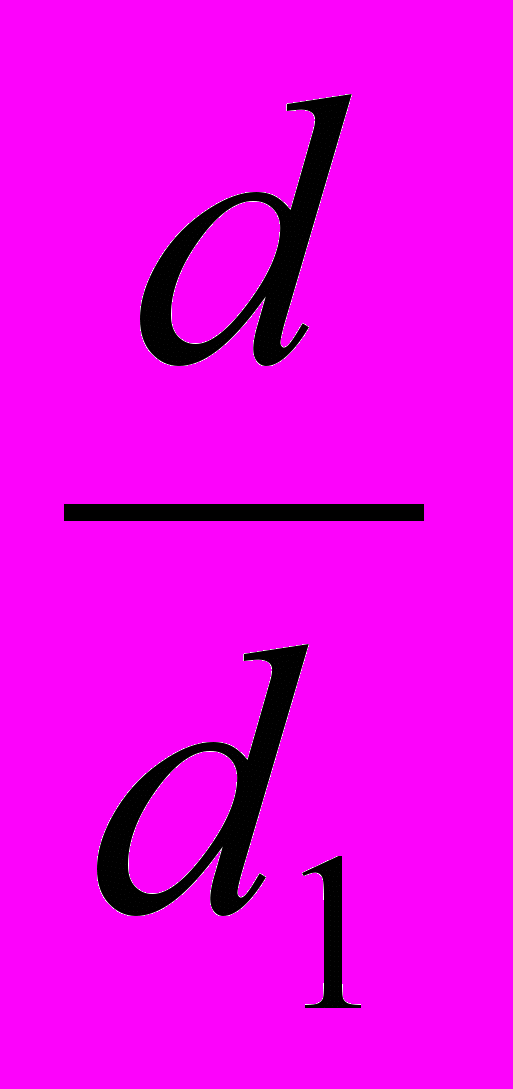Для объёмов – аналогично.

1 вариант. Из принципа Кавальери напрямую следует лемма о равновеликости пирамид, и таким образом, существенно облегчается вывод для объёма пирамиды; можно вычислить и объёмы тел вращения. В частности при выводе формулы V_шара рассматривается полушар и конус, вписанный в центр.

Площади сечений полушара и второй фигуры равны:



2 вариант. Вычисление объёма пирамиды (Виленкин)

а) V_куба = 8 Н³

V_пир = 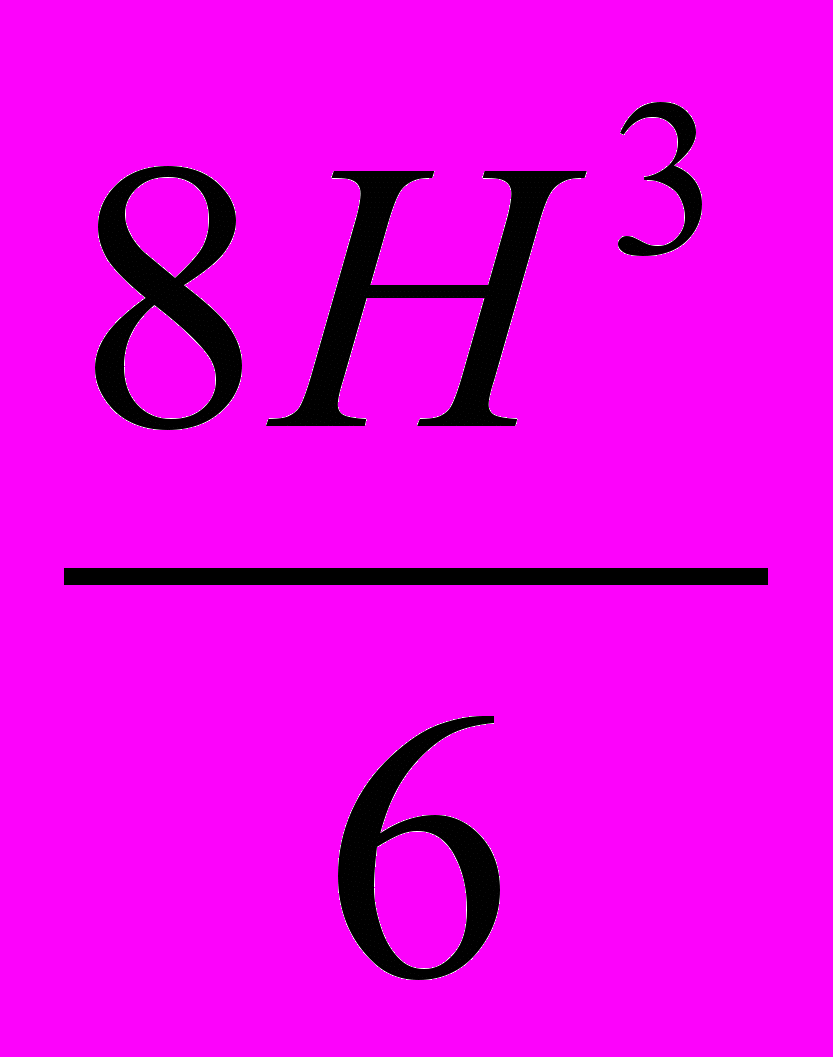= 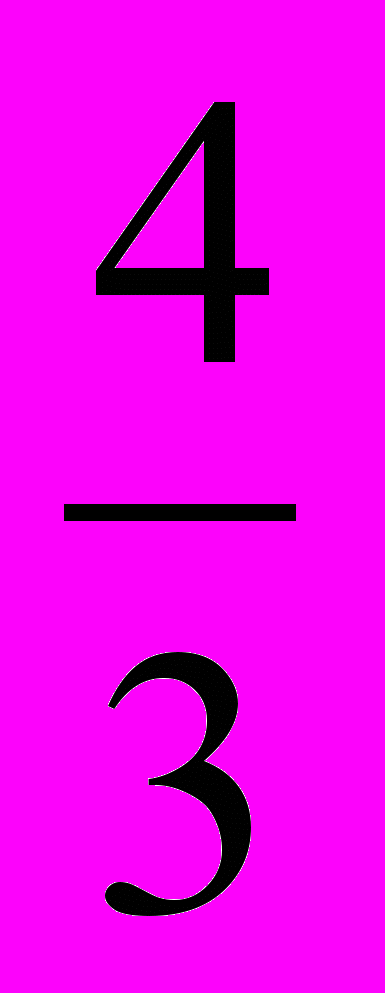Н³ = 4Н² Н = S Н

б) Берём произвольную пирамиду с площадью основания S и выстой Н. По принципу Кавальери объём 4-угольной правильной пирамиды и данной равны. Следовательно, формула верна для любой пирамиды.

Данный подход в настоящее время считается наиболее приемлемым в силу достаточной простоты (предельный переход уходит в доказательство принципа Кавальери).

Четвертый подход – формула Симпсона (Том Симпсон – английский математик 18 века).

Если в пространственной фигуре основания параллельны и площади сечений, параллельны основанию, удовлетворяют условию S(х) = ах² + вх + с, где S (х) – функция от расстояния между сечением и основанием фигуры, то объём фигуры может быть найден по формуле:

V = (Q₀ + 4Q_ср + Q),

где Н – высота, Q₀ и Q – площади оснований, Q_ср – площадь среднего сечения.

Для конуса, пирамиды Q = 0, для шара Q₀ =Q=0, а плоскость оснований считаются параллельными.

Доказательство формулы Симпсона достаточно громоздкое и, как правило, опускают. (На основе интегральной формулы: V = Q (х) dх (кв. ед.) (см. уч. Ю.М. Колягина).

Достоинства метода – его универсальность, недостаток – формальное введения.


Самостоятельное задание: Выписать формулы для сечений конуса, шара, пирамиды и цилиндра как функций от расстояния между сечением и основанием фигуры.

S_{сеч. пир.} = х² , S_{сеч.кон.} = π х² , S_{сеч ш.} = (R² – х²), S_{сеч цил.} = πR².


5. Площадь поверхностей фигур вращения в школе могут рассматриваться на различных уровнях строгости в зависимости от авторских установок и специфики контингента.

1. Общий подход по Минковскому (немецкий математик).
   

Площадь произвольной выпуклой поверхности определяется таким образом:

, где V_h – объём фигуры F_h,

наглядно предоставляемый как двойной слой толщиной 2h, покрывающий с обеих сторон.

Далее на основе соответствующего определения вводились формулы для площади поверхности шара, конуса и цилиндра.

Данный подход был использован в ранних изданиях учебника Погорелова и не оправдал себя в силу формального характера и необходимости применения довольно изощренных оценок. (см. В. Дубровский Площадь поверхности по Минковскому – Квант 1979, № 4.)

2. Основан на идеи исчерпывания (уч. Киселёва, Погорелова (новое издание)).
   

Цилиндры и конусы «исчерпываются» призмами и пирамидами, а поверхность сферы рассматривается через поверхность, полученную при вращении ломаной, вписанной в большую полуось круга.

Тогда площадь этой поверхности будет равна пределу площади поверхности тела при неограниченном увеличении сторон ломаной.

По доказанной ранее лемме S_n = 2π АВ r_n – для конуса, усечённого конуса, цилиндра и шара.

Для шара

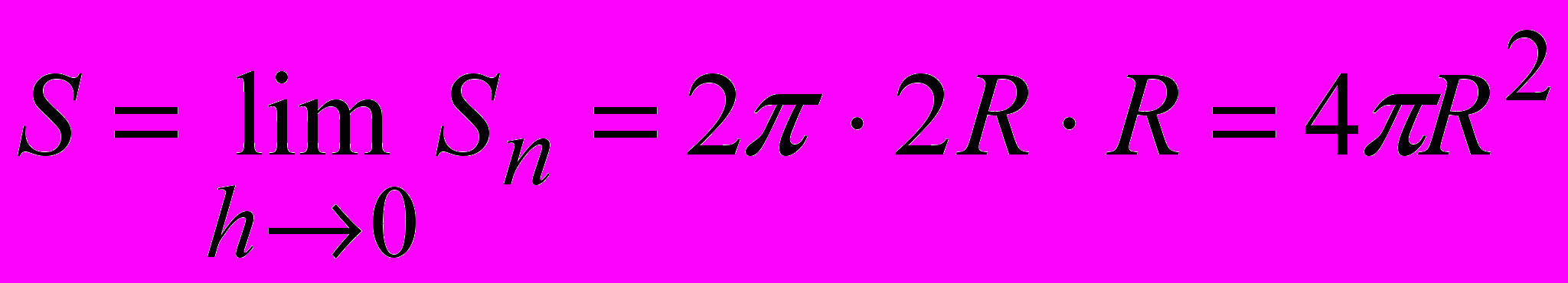
3. Основан на развёртках (уч. Атанасяна).
   

При этом используется допущения о сохранении величин площади при «развёртывании» поверхности вращения. Данный подход неприемлем для площади поверхности сферы, не имеющей плоской развёртки.

Однако, в некоторых учебниках (Погорелов) сделана попытка приближенного представления участков сферы в виде многоугольников, являющихся гранями многогранника, описанного около сферы.

4. Формальный подход.
   

За площадь поверхности фигуры, полученной при вращении вокруг оси ОХ графика функции у = f (х), имеющей на а, b непрерывную произвольную, принимается число:

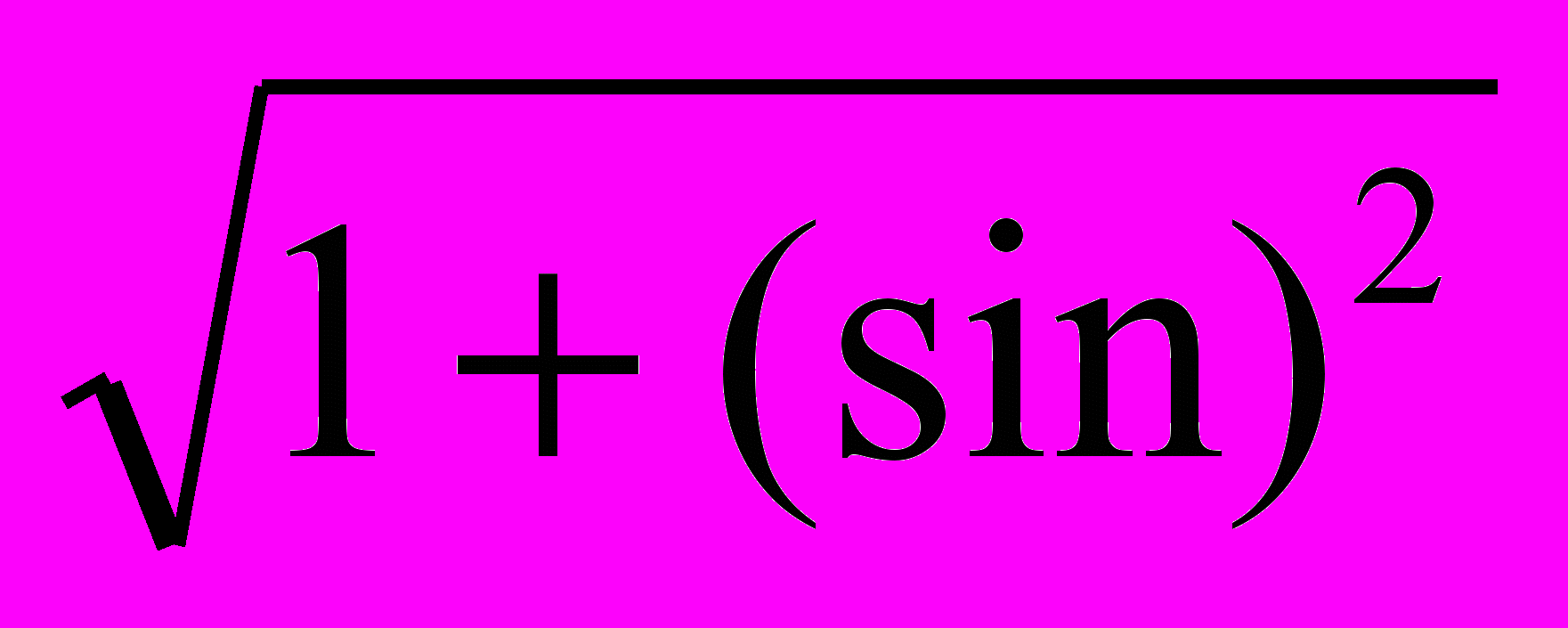S = 2 π f (х) dх

В учебнике А.В. Погорелова используется модификация подходов 2 и 3, взяв за основу идею исчерпывания шара пирамиды с вершиной в центре шара с последующим предельным переходом, соответствующим неограниченному уменьшению размеров граней многогранника, описанного около шара.


V_{впис. ш.} V_{многогр.} V_{опис. ш.}


πR³ _. R 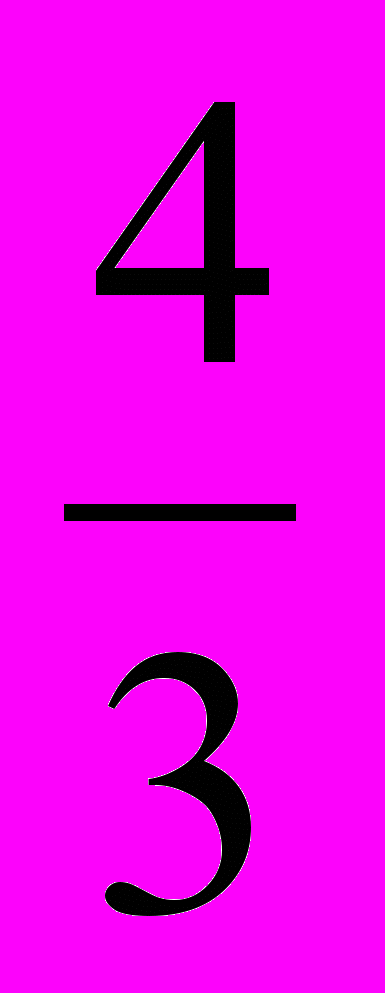П (R+Е)³



площадь поверхности

4π R^{2 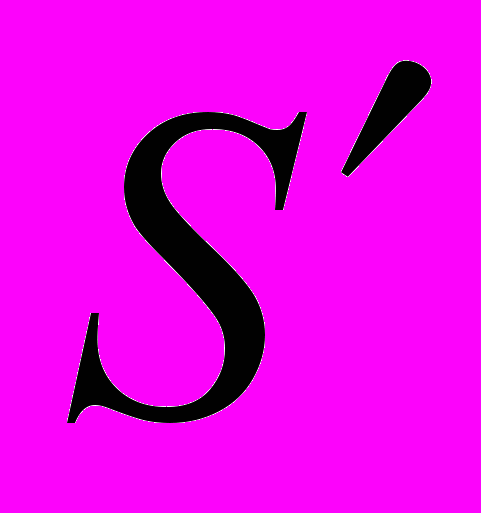`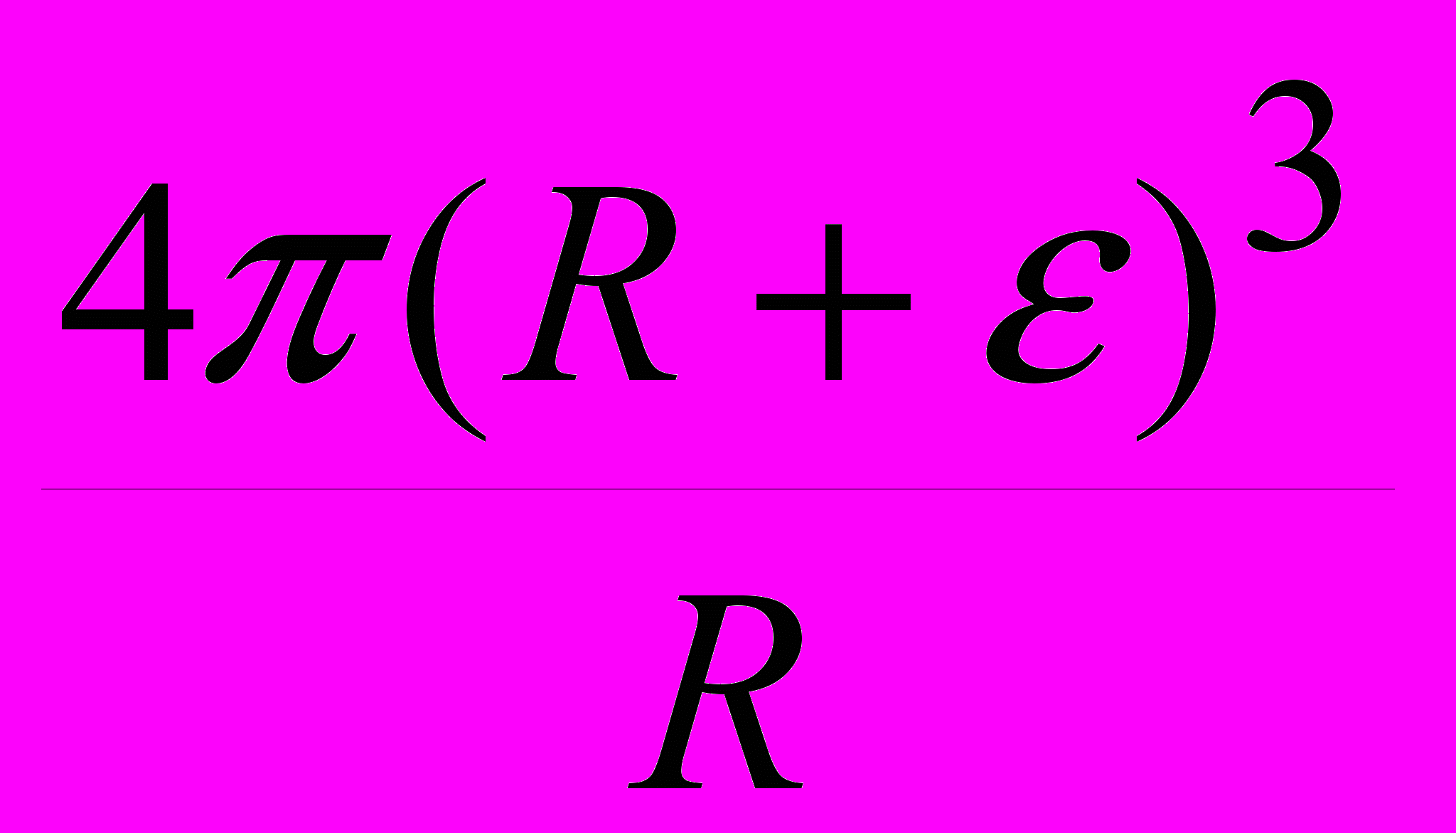}, при ε 0


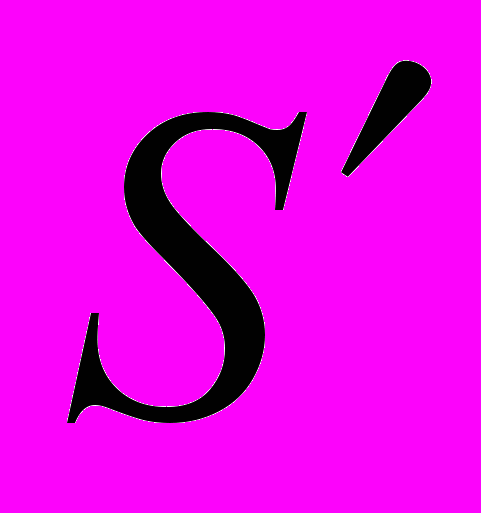
4π R² 4 π R² S_iшара = 4π R²


Задание для самостоятельной работы. Выписать систему аксиом для определения систем скалярных величин по А.Н. Колмагорову их учебного пособия (4).

Вопросы для самопроверки:

1. Перечислите основные скалярные геометрические величины, изучаемые в школьном курсе.
   
2. Что такое величина? Какими свойствами обладает любая скалярная величина?
   
3. В чём суть аксиоматического введения скалярных геометрических величин и конструктивного? И какой путь является основным в школьном курсе?
   
4. Какую роль играет понятие равносоставленности в теории площадей и объектов?
   
5. Каковы основные цели изучения линии геометрических величин в школьном курсе?
   
6. Что известно учащимся о геометрических величинах из пропедевтического курса математики?
   
7. Каковы методические подходы к изучению длин отрезков в школьном курсе?
   
8. Какие 4 основных подхода можно выделить при изучении площадей в школьном курсе геометрии? Суть каждого из этих подходов?
   
9. Какие подходы используются в основной школе при изучении длины окружности и площади круга?
   
10. В чём суть метода исчерпывания при построении теории объёмов многогранников?
    
11. Интегральный подход к нахождению объёмов геометрических тел.
    
12. Нахождение объёмов с помощью принципа Кавальери и формулы Симпсона.
    
13. Каковы возможные подходы к построению теории площадей поверхностей тел вращения в школьном курсе?
    

Литература: 4, 6, 7, 10, 14, 16, 17.


Лекция 9. Особенности изучения стереометрии в средней школе. Методика первых уроков стереометрии.

План.

1. Структура курса стереометрии и его специфические особенности.
   
2. Развитие пространственных представлений школьников на уроках стереометрии.
   

Содержание лекции:

I. Можно выделить следующие основные задачи, решаемые при изучении стереометрии:

1. развитие и закрепление содержательных линий, начатых в неполной средней школе; обобщение основных математических методов на случай пространства;
   
2. изучение основных свойств пространственных фигур;
   
3. овладение навыками изображения пространственных фигур на плоскости на основе свойств параллельного проектирования;
   
4. развитие логического мышления, пространственных представлений учащихся при решении задач и доказательстве теорем курса стереометрии.
   

В изучении стереометрии в школе можно выделить два основных этапа:

1) Формирование первоначальных представлений о пространственных фигурах (1–9 классы);

2) Систематический курс стереометрии (10–11 классы).

Систематический курс стереометрии, на изучение которого отводится приблизительно по 70 часов в десятом и одиннадцатом классах, предусматривает рассмотрение следующих тем:

1. Аксиомы стереометрии и их простейшие следствия.
   
2. Параллельность прямых и плоскостей в пространстве.
   
3. Перпендикулярность прямых и плоскостей в пространстве.
   
4. Координаты, векторы, геометрические преобразования в пространстве.
   
5. Многогранники.
   
6. Тема вращения.
   
7. Площадь поверхностей и объем геометрических тел.
   
8. Изображение пространственных фигур на плоскости.
   

В действующих учебниках ставятся разные содержательные акценты при изучении стереометрии.

Учебник Атанасяна: материал различных по содержанию вопросов часто включается в одну главу (фузионизм). При этом наблюдается частая повторяемость материала, обращение к уже знакомым вопросам. Большое внимание, чем у Погорелова, уделяется векторам, движению к координатам.

Учебник Погорелова: отличается четкой логической структурой, меньше внимания векторам и геометрическим преобразованиям. Это подспудно несет в себе опасность затушевывания естественных связей между темами.

Выделим некоторые методические особенности изучения стереометрии.

1. Курс стереометрии полностью опирается на курс планиметрии.
   

большинство задач курса сводятся к решению планиметрических задач, соответственно все недочеты, имевшие место при изучении планиметрии, ощущаются и при изучении стереометрии.

Следовательно, для успешного изучения стереометрии учитель должен постоянно возвращаться к планиметрическому материалу; перед изучением той или иной теоремы необходимо повторять нужные планиметрические сведения.

2. В стереометрии принципиально другой подход к геометрическим построениям.

Если при изучении планиметрии учащиеся пользуются чертежами, которые дают явные представления об изучаемом объекте, то в стереометрии нет чертежных инструментов, которые позволяют изобразить пространственные фигуры. Здесь мы имеем дело не с самим объектом, а лишь с его изображением.

Каждая стереометрическая задача является одновременно задачей на построение изображения фигуры с помощью свойств параллельной проекции. Это требует от учащихся значительно больших усилий, чем их требуется при решении планиметрических задач.

3. В курсе стереометрии уделяется большое внимание логической стороне проводимых умозаключений; приходится обосновывать каждый свой вывод, четко устанавливая предпосылки.

4. Программа по стереометрии предполагает более быстрый темп прохождения материала, чем в планиметрии. При этом времени на решение задач требуется гораздо больше, соответственно более значительное место занимает самостоятельная работа школьников. Необходим тщательный подбор заданий на уроке – включать только самое необходимое.

5. Курс стереометрии строится аксиоматически. При изучении аксиоматики стереометрии необходимо решить две основные методические задачи:

1) переформулируются аксиомы планиметрии для пространства (некоторые должны быть с уточнениями).

Здесь фактически под видом договоренности между учителем и учащимся вводится, как бы новая аксиома:

В любой плоскости пространства выполняются все аксиомы планиметрии.

2) добавляются новые специфические аксиомы пространства, которые на первых этапах изучения иллюстрируются с помощью моделей, стереометрического ящика, рисунка, геометрии классной комнаты.

При этом появляется возможность более эффективного выявления учащимися сущности аксиоматики и ее роли в построении геометрии.

II. Формирование пространственных представлений идет в несколько этапов и включает в себя:

– умение представить по чертежу целостный образ геометрической фигуры, взаимное расположение ее элементов;

– умение мысленно изменить положение фигуры – посмотреть с другой стороны;

– умение мысленно расчленить фигуру, составить из нее новый объект;

– умение изобразить фигуру на чертеже, адекватно отразив имеющиеся отношения;

– умение представить фигуру на основе ее словесного описания и т.д.

На I этапе на наглядной основе формируются предпосылки для создания целостного образа фигуры с выделением ее существенных признаков. На данном этапе учитель должен широко использовать модели, реальные объекты окружающего мира. После этого строится чертеж, который закрепляет рассмотрение соответствующей геометрической конфигурации.

В конце I этапа и на II у школьников формируются образы фигур и их комбинаций, которые они могут представить себе в почти неизмененных условиях.

Схема формирования пространственных представлений на I и II этапе следующая:

Модель чертеж представление

На II этапе роль моделей несколько уменьшается, т. к. в противном случае у школьников будет тормозиться развитие способностей мысленно представлять себе особенности расположения фигуры и ее элементов.

При построении чертежа на данных этапах учителю не следует сразу демонстрировать готовый чертеж, а стараться его выполнять постепенно вместе с учащимися с целью поэтапного восприятия или пространственных образов.

III этап: – овладение умением оперировать образами в измененных условиях. Школьники сначала работают с основным чертежом, который однако часто не дает возможность увидеть особенности расположения фигуры с разных позиций. Поэтому чертеж, как правило, должен подкрепляться рассмотрением соответствующей модели. Демонстрация сопровождается специально подобранными вопросами.

Например: Какие фигуры могут получиться при пересечении тетраэдра плоскости? Покажите на модели и чертеже различные случаи. Ответ обоснуйте.

Схема формирования пространственных представлений на III этапе:

чертеж модель представление.

IV этап: Учащиеся должны конструировать стереометрические объекты самостоятельно на базе сформулированных ранее представлений. При этом не используется ни чертеж, ни заранее подготовленная модель, а можно лишь учителю задавать вопросы для уточнения расположения фигуры.

Схема на IV этапе: представление чертеж.

Задания для самостоятельной работы:

1. Сравнить последовательность изучения стереометрического материала по учебникам А.В. Погорелова и Л.С. Атанасяна, заполнив таблицу.
   

Учебник А.В. Погорелова Учебник Л.С. Атанасяна и др.

10 класс 10 класс