Выборочный метод решение типовых задач

Вид материала

Решение

Содержание А находятся в пределах 10%  р

Подобный материал:

• Практикум: «Изучение процентов в школьном курсе математики», 90.4kb.
• Решение. Из анализа схемы следует, что резисторы, 80.22kb.
• Решение, 562.63kb.
• Решение типовых задач по теме «Программирование на языке Паскаль», 65.52kb.
• Бухгалтерские программы, обеспечивающие решение типовых учетных задач; учетные системы,, 90.67kb.
• Графический метод при решении задач с параметрами, 32.34kb.
• Линейных алгебраических уравнений ax=B, где, 66.22kb.
• I. Решение логических задач средствами алгебры логики 22 >II. Решение логических задач, 486.64kb.
• Календарно-тематическое планирование элективного курса " методы решения физических, 107.87kb.
• Методика классификации и решения задач с параметрами в курсе средней школы. Уравнения, 18.27kb.

"ВЫБОРОЧНЫЙ МЕТОД"

РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ

Пример 1.

Из партии электроламп взята 20%-ная случайная бесповторная выборка для определения среднего веса спирали.

Результаты выборки следующие:




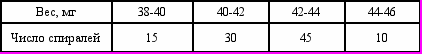
Определите:

• с вероятностью 0,95 доверительные пределы, в которых лежит средний вес спирали, для всей партии электроламп.
  

Решение.

Доверительные интервалы для генеральной средней с вероятностью Р:





Средний уровень признака по выборке 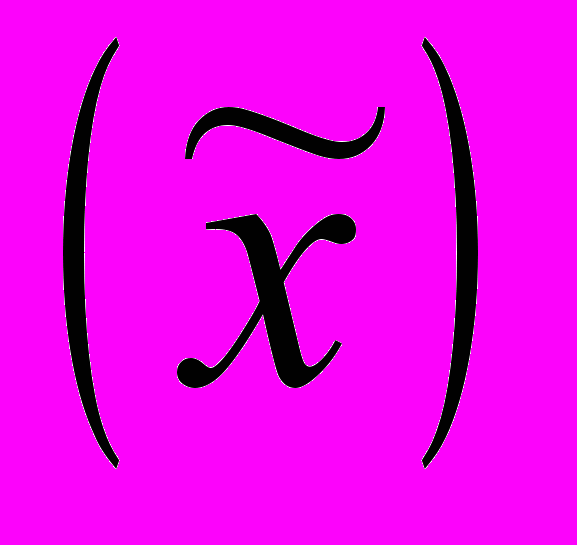найдем по формуле средней арифметической взвешенной:


,


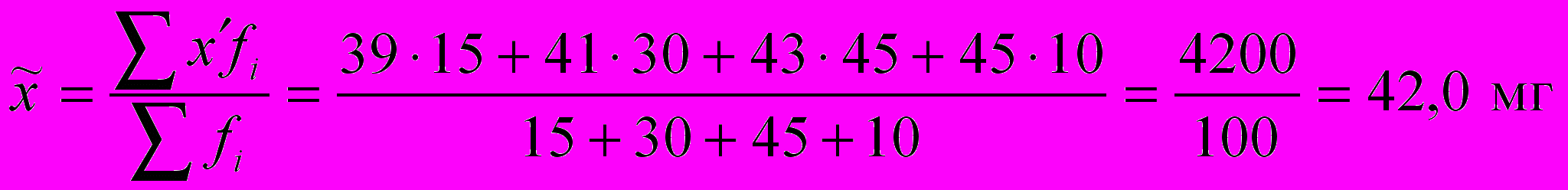Предельную ошибку при случайном бесповторном отборе определим по формуле:





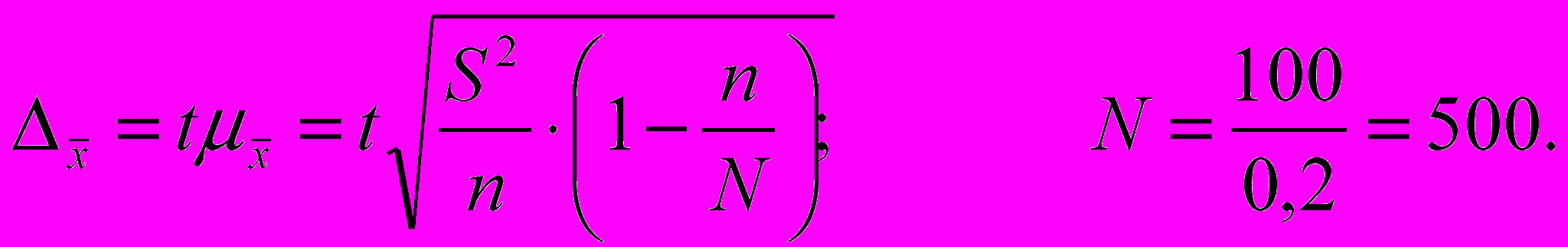
При вероятности Р=0,95 t=1,96 (приложение Ж).


Для определения выборочной дисперсии воспользуемся формулой:


Доверительные интервалы для генеральной средней с вероятностью Р=0,95: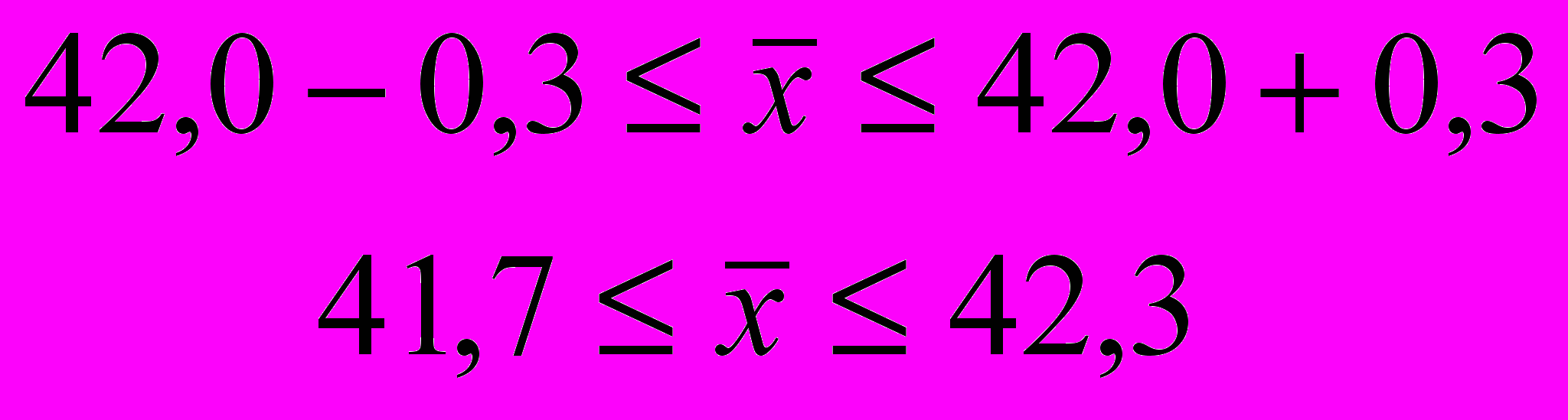




Таким образом, с вероятностью 95% можно утверждать, что средний вес спирали в генеральной совокупности колеблется от 41,7 до 42,3 мг.


Пример 2.

На основе случайного повторного выборочного обследования в отделении связи города предполагается определить долю писем частных лиц в общем объеме отправляемой корреспонденции. Никаких предварительных данных об удельном весе этих писем в общей массе отправляемой корреспонденции не имеется.


Определите:

• численность выборки, если результаты выборки необходимо дать с точностью до 1% и гарантировать это с вероятностью 0,95.
  

Решение.

По условию задачи известны:

размер допустимой (предельной) ошибки - _w=1% или 0,01:

принята вероятность – Р = 0,95;

Необходимая численность выборки при случайном повторном отборе:





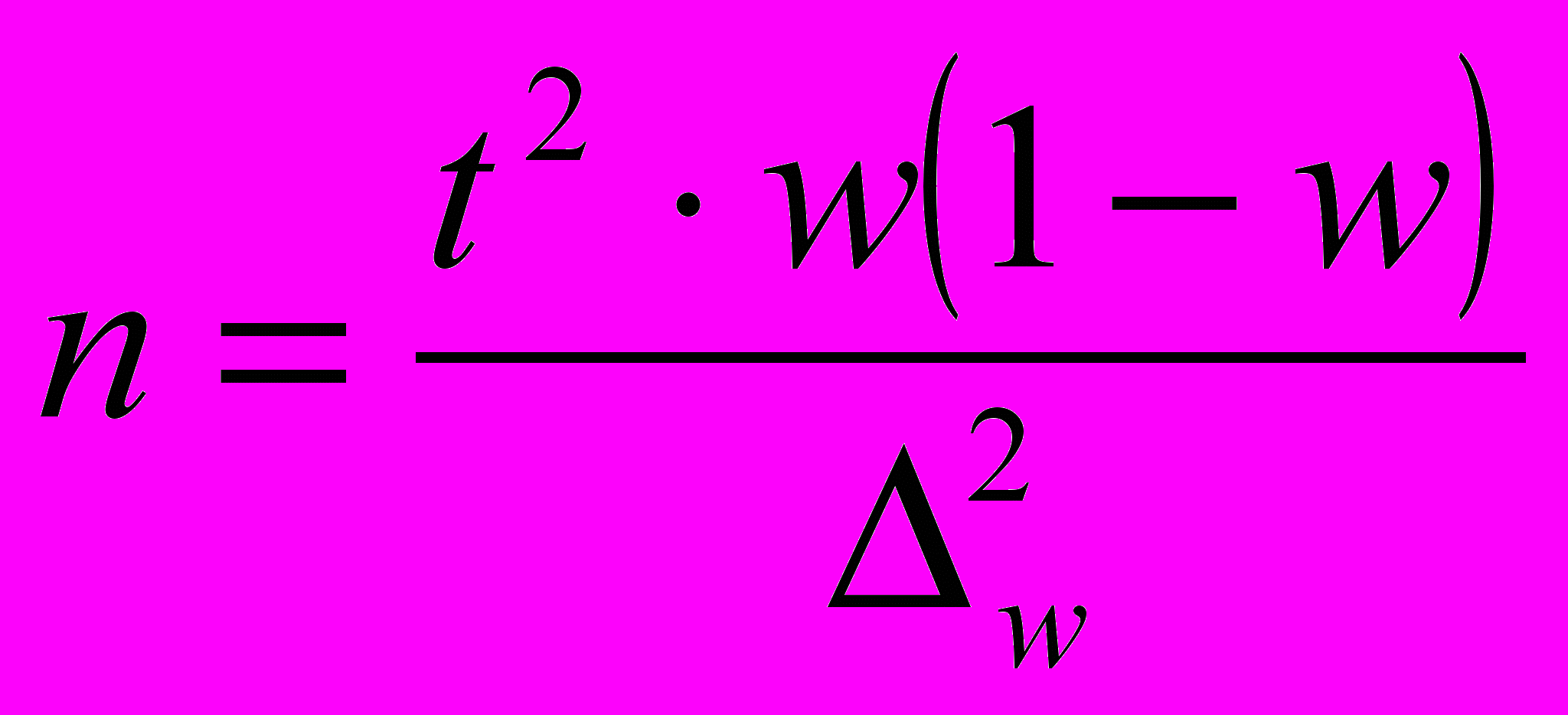
Так как значение w не дано, то следует ориентироваться на наибольшую дисперсию, которой соответствует значение w = 0,5.





Таким образом, чтобы с данной точностью определить долю частных писем в общем объеме отправляемой корреспонденции, необходимо в порядке случайной выборки отобрать 9604 письма.


Пример 3.

В городе 500 тыс. жителей. По материалам учета городского населения было обследовано 50 тыс. жителей методом случайного бесповторного отбора. В результате обследования установлено, что в городе 15% жителей старше 60 лет.


Определите:

• с вероятностью 0,683 пределы, в которых находится доля жителей в городе в возрасте старше 60 лет
  

Решение.

Доверительные интервалы для доли в генеральной совокупности определяются:





По условию задачи, выборочная доля w = 15% (или w = 0,15).

С вероятностью 0,683 определим предельную ошибку выборки для доли альтернативного признака:




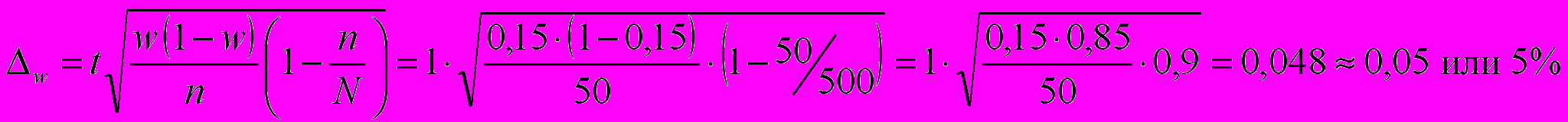
Определяем доверительные интервалы





Таким образом, с вероятностью 0,683 можно утверждать, что доля жителей в возрасте старше 60 лет в городе А находятся в пределах 10%  р  20%.


Пример 4.

В области, состоящей из 20 районов, проводилось выборочное обследование урожайности на основе бесповторного отбора серий (районов). Выборочные средние по районам составили соответственно 14,5 ц/га; 16,0; 15,5; 15,0 и 14,0 ц/га.


Определите:

• с вероятностью 0,954 пределы урожайности во всей области.
  

Решение.

Выборочная средняя 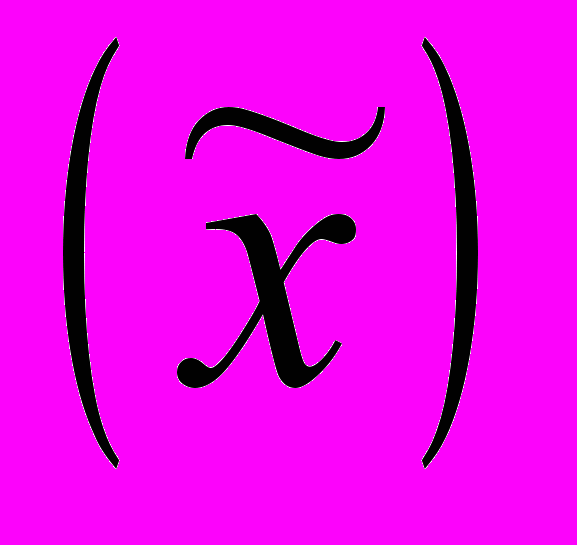определяется по формуле средней арифметической: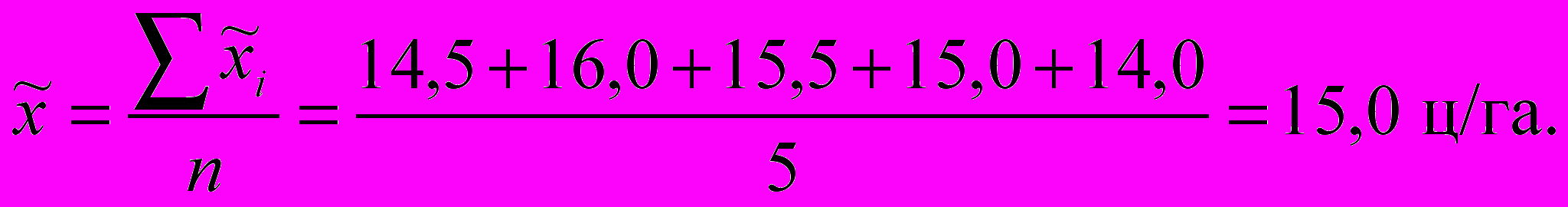





Межгрупповая дисперсия определяется по формуле:





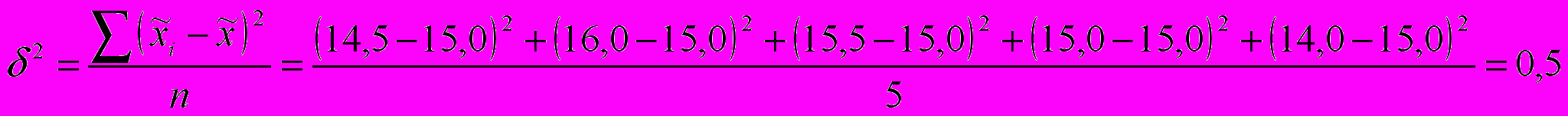
При вероятности 0,954 коэффициент доверия t = 2. Предельная ошибка серийной бесповторной выборки определяется по формуле:





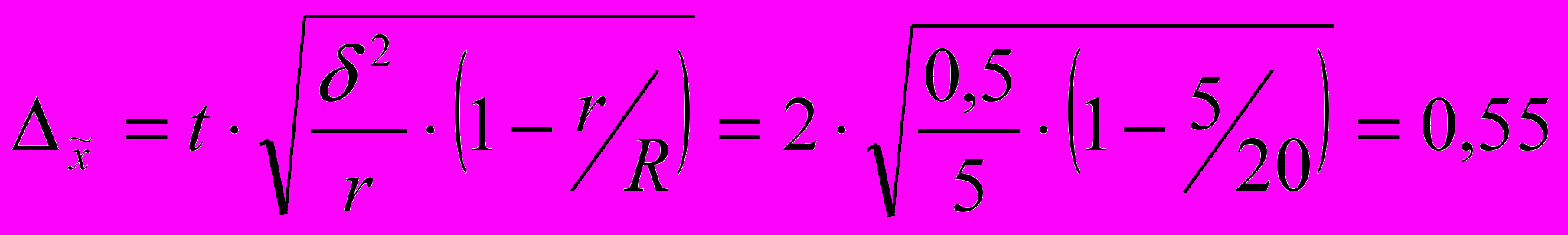
Доверительные интервалы урожайности в области:




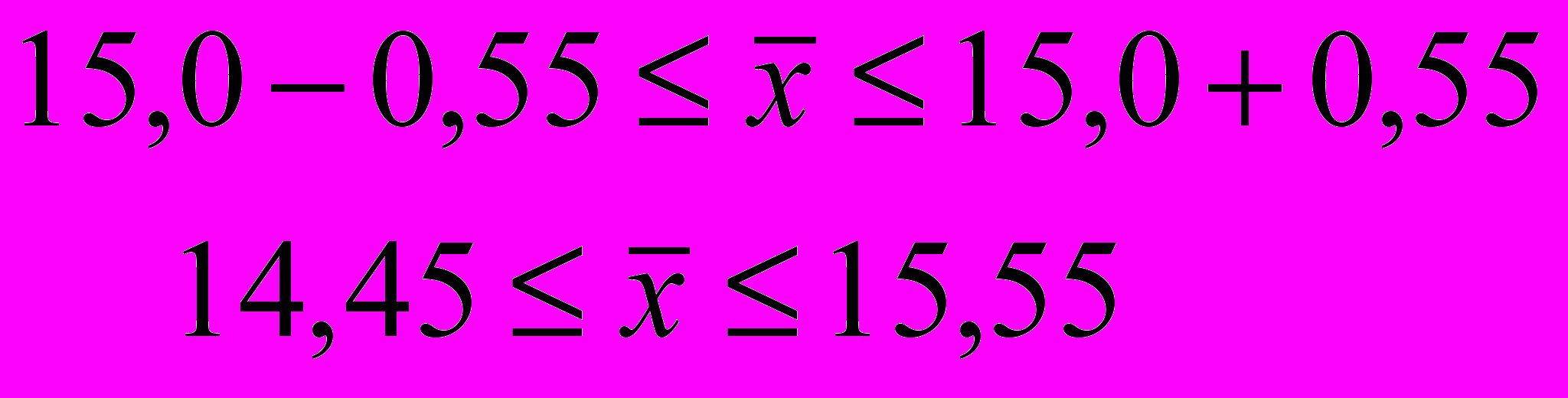
Таким образом, урожайность в области с вероятностью 0,954 будет находиться в пределах от 14,45 до 15,55 ц/га.


Пример 5.

При проверке веса импортируемого груза на таможне методом случайной повторной выборки отобрано 200 изделий. В результате был установлен средний вес изделия 30 г при среднем квадратическом отклонении 4 г.


Определите:

• c вероятностью 0,9973 пределы, в которых находится средний вес изделий в генеральной совокупности.
  

Решение.

Рассчитаем предельную ошибку выборки. Так, при Р=0,9973, t=3.





Определим пределы генеральной средней:




или




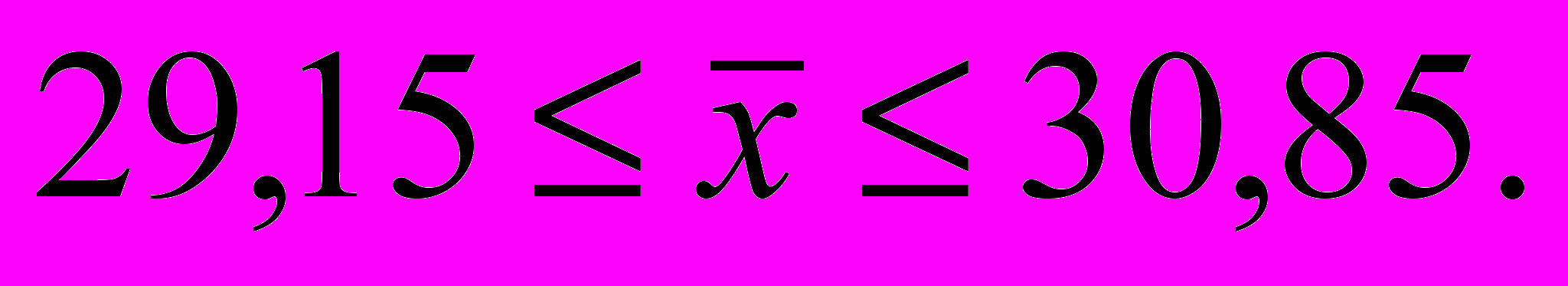
Следовательно, с вероятностью 0,9973 можно утверждать, что средний вес изделий в генеральной совокупности находится в пределах от 29,15 до 30,85 г.


Пример 6.

В 100 туристических агентствах города предполагается провести обследование среднемесячного количества реализованных путевок методом механического отбора. Какова должна быть численность выборки, чтобы с вероятностью 0,683 ошибка не превышала 3 путевок, если по данным пробного обследования дисперсия составляет 225?


Решение.

Так как отбор механический, численность выборки определяется по формуле:




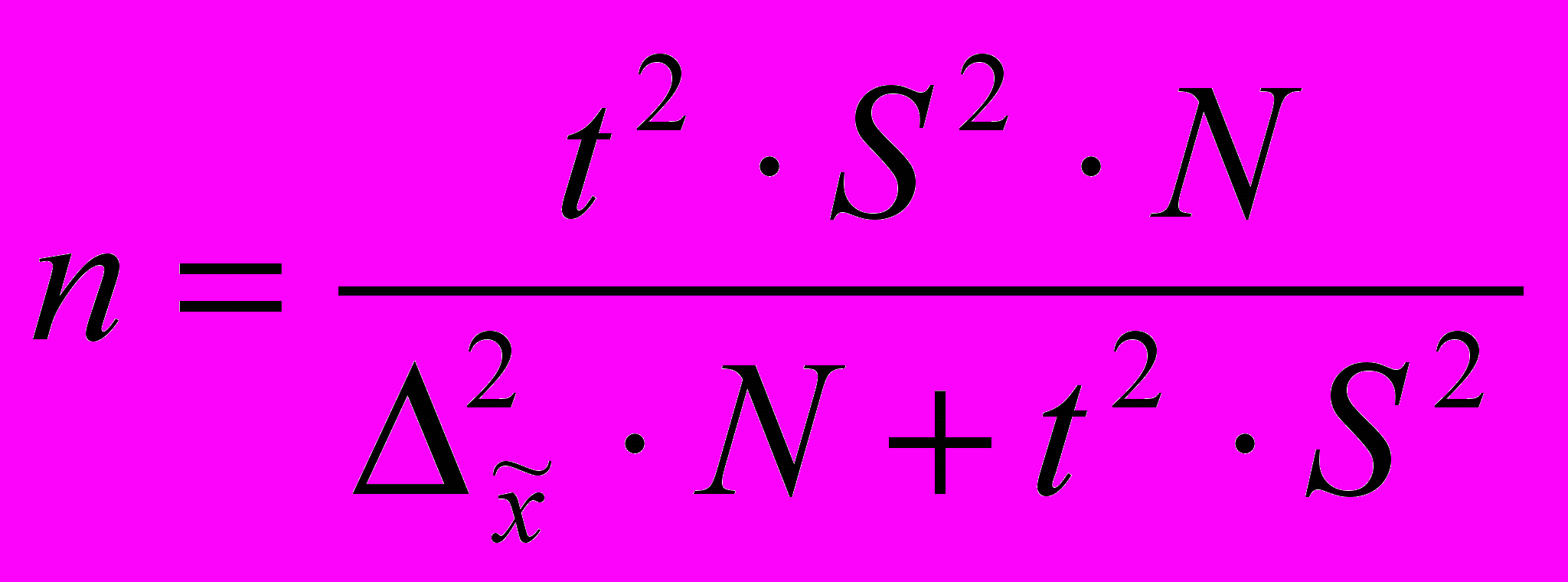
Рассчитаем необходимый объем выборки:





Таким образом, чтобы с данной точностью определить среднемесячное количество реализованных путевок, необходимо отобрать 20 туристических агентств.


Пример 7.

Произведено выборочное наблюдение партии однородной продукции для определения процента изделий высшего сорта.

При механическом способе отбора из партии готовых изделий в 20000 единиц было обследовано 800 единиц, из которых 640 изделий отнесены к высшему сорту.


Определите:

• с вероятностью 0,9973 возможный процент изделий высшего сорта во всей партии.
  

Решение.

В случае механического отбора предельная ошибка определяется по следующей формуле:





Границы генеральной доли изделий высшего сорта:














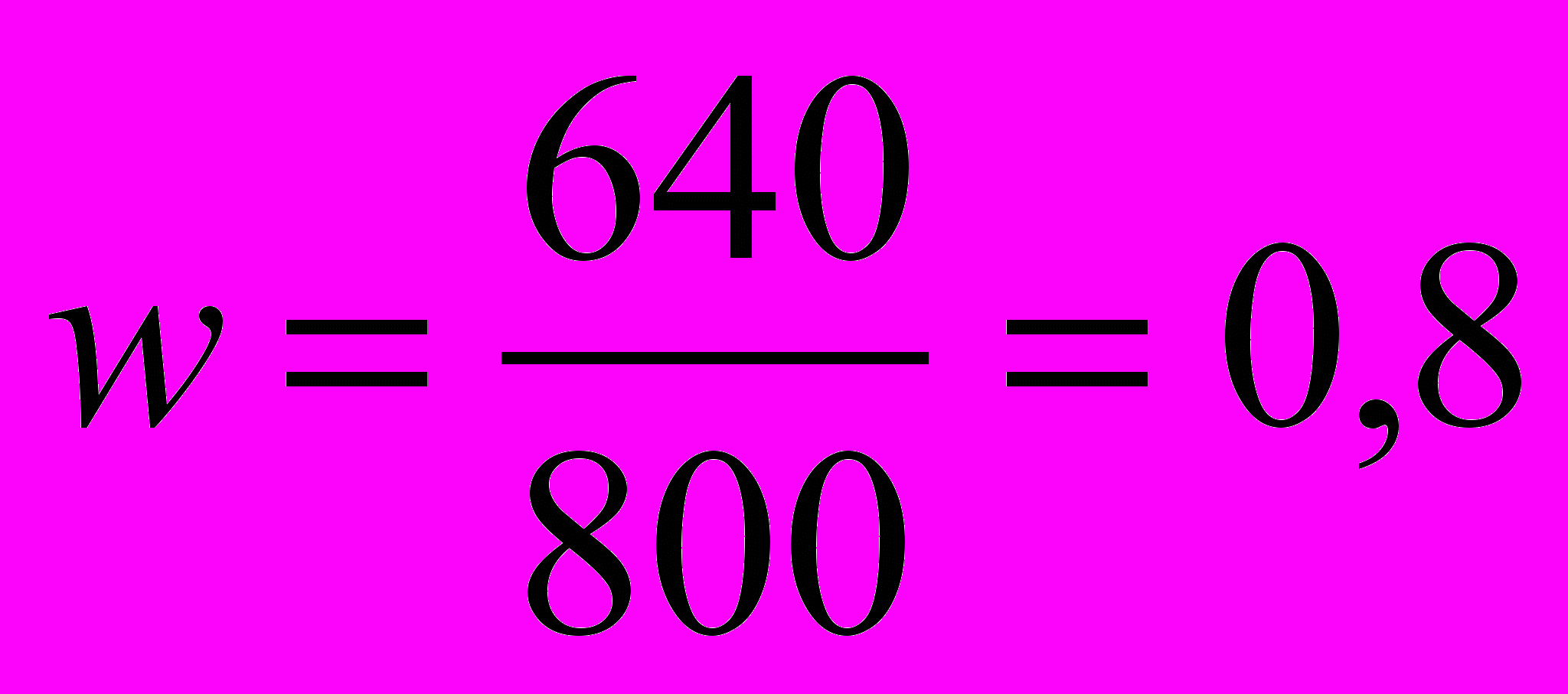
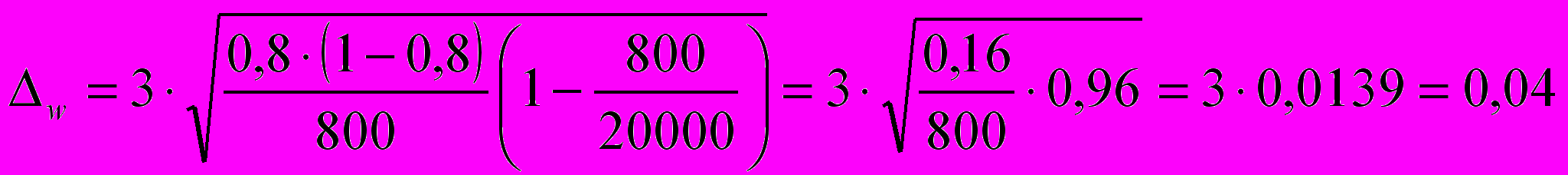
Следовательно, генеральная доля находится в пределах:





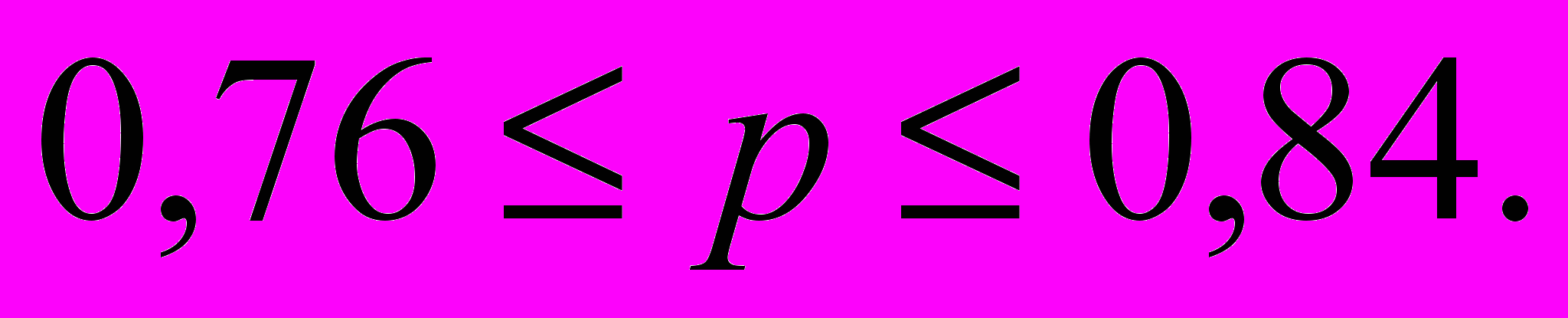
Таким образом, с вероятностью 0,9973 можно утверждать, что во всей партии от 76 до 84 % - продукция высшего сорта.


Пример 8.

При обследовании 100 образцов изделий, отобранных из партии в случайном порядке, оказалось 20 нестандартных.


Определите:

• с вероятностью 0,954 пределы, в которых находится доля нестандартной продукции в партии.
  

Решение.

Чтобы определить границы генеральной доли, необходимо определить выборочную долю и ошибку выборочной доли.

Рассчитаем долю нестандартной продукции в выборочной совокупности:





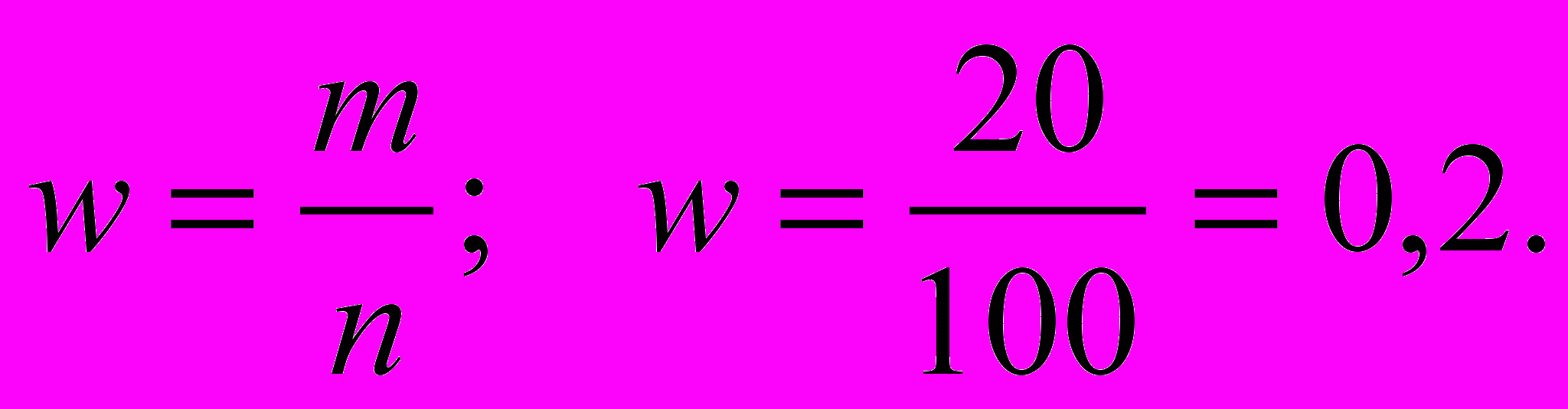
Предельная ошибка выборочной доли с вероятностью 0,954 составит:





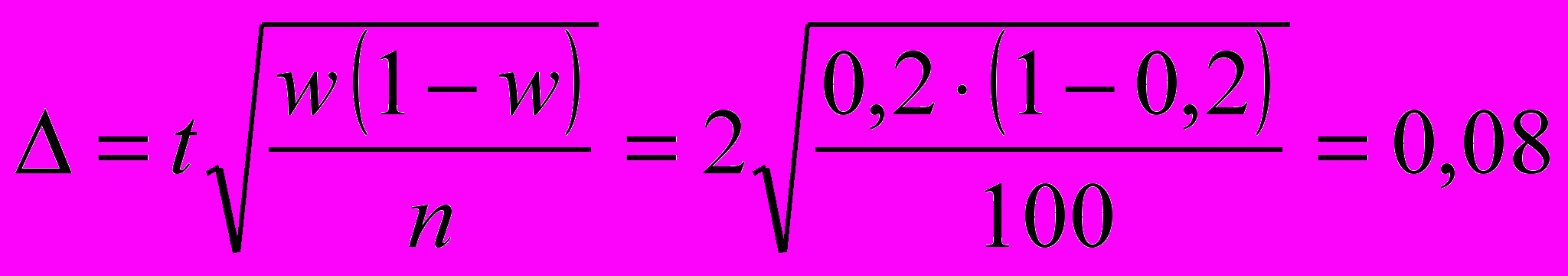
Доля нестандартной продукции в генеральной совокупности определяется по формуле:




Таким образом, с вероятностью 0,954 можно утверждать, что доля нестандартной продукции в партии товара находится в пределах от 12 до 28%.


Пример 9.

200 ящиков деталей упакованы по 40 шт. в каждом. Для проверки качества деталей был проведен сплошной контроль деталей в 20 ящиках (выборка бесповторная). В результате контроля установлено, что доля бракованных деталей составляет 15%. Межсерийная дисперсия равна 49.


Определите:

• с вероятностью 0,9973 пределы, в которых находится доля бракованной продукции в партии ящиков.
  

Решение.

Определим среднюю ошибку выборки:





Предельная ошибка выборки для доли с вероятностью 0,9973 (t=3) равна: _w = 1,48  3 = 4,44%.

Пределы в генеральной совокупности:





Таким образом, с вероятностью 0,9973 можно утверждать, что доля бракованных деталей в партии будет находиться в пределах от 10,59 до 19,41%.


Пример 10.

В районе 10 тыс. семей. Из них 5 тыс. семей рабочих, 4 тыс. семей работников сельского хозяйства, 1 тыс. семей служащих. Для определения числа детей в семье была проведена 10%-ная типическая выборка, с отбором единиц пропорционально численности единиц типических групп. Внутри групп применялся метод механического отбора. Результаты выборки представлены в таблице.





Определите:

• с вероятностью 0,9973 пределы, в которых находится среднее число детей в семье в районе.
  

Решение.

Определим число отобранных семей по типам семей:




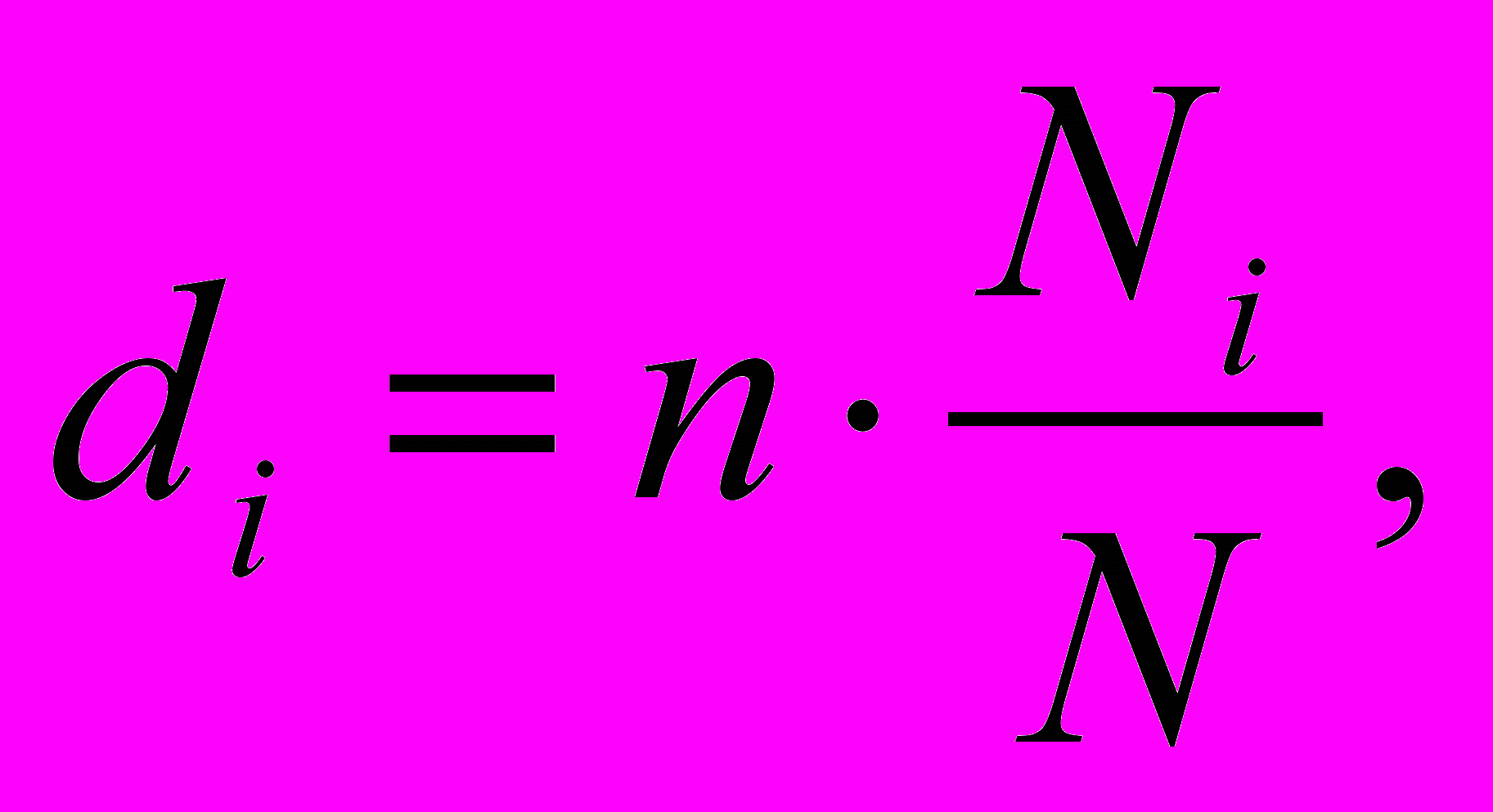
где




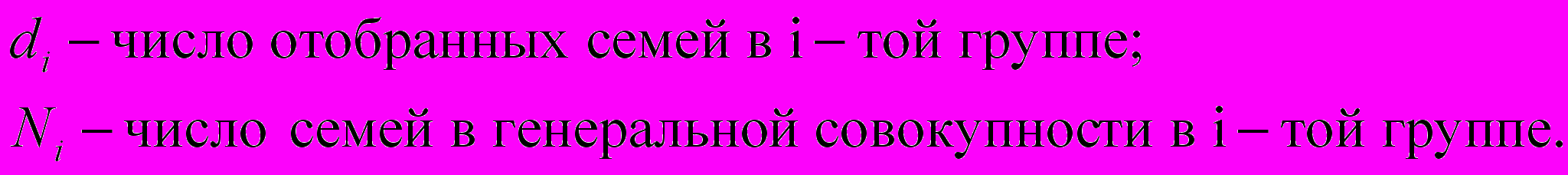
Численность семей в первой группе:




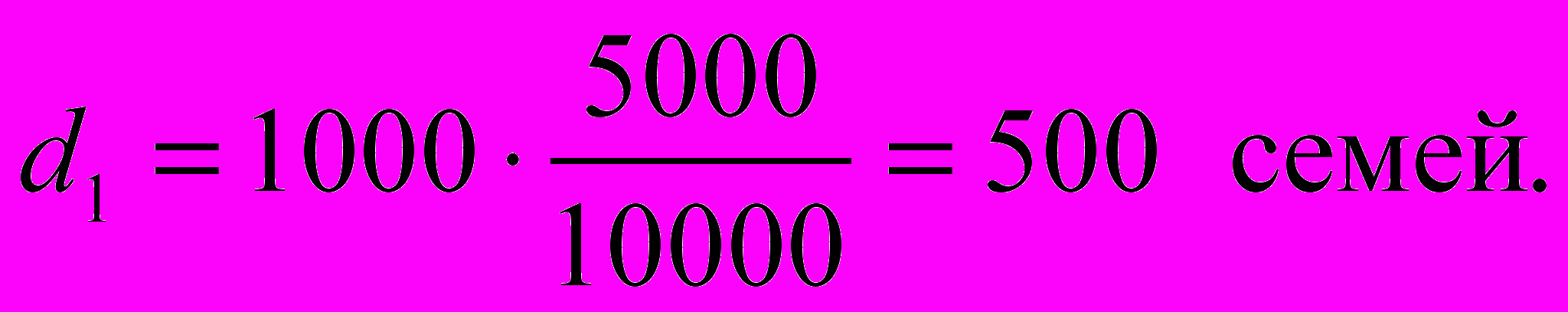
Численность семей во второй группе:




Численность семей в третьей группе:





Выборочная средняя 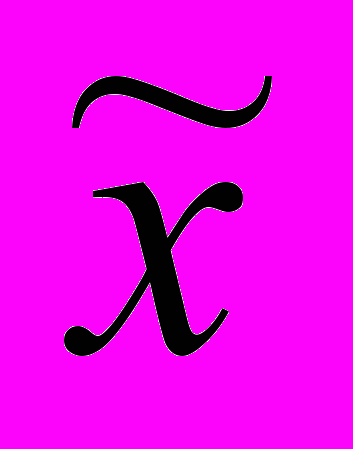определяется по формуле средней арифметической взвешенной: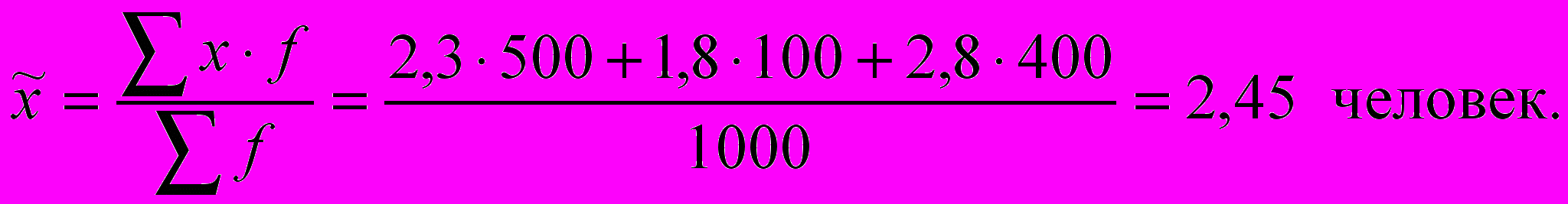





Определим среднюю из внутригрупповых дисперсий:





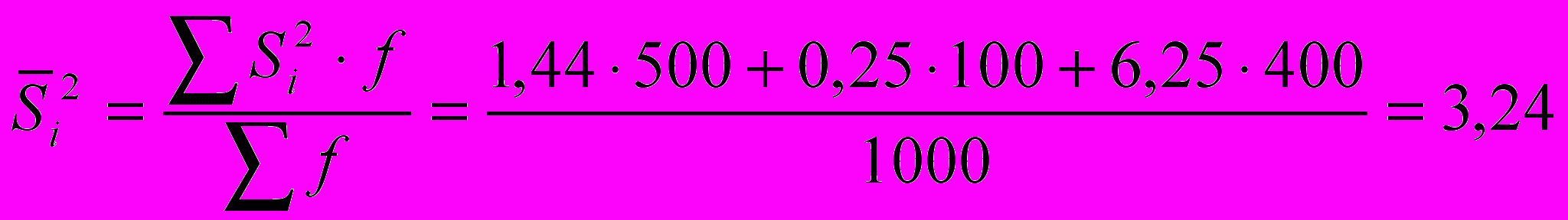
Рассчитаем среднюю ошибку выборочной средней типической выборки:





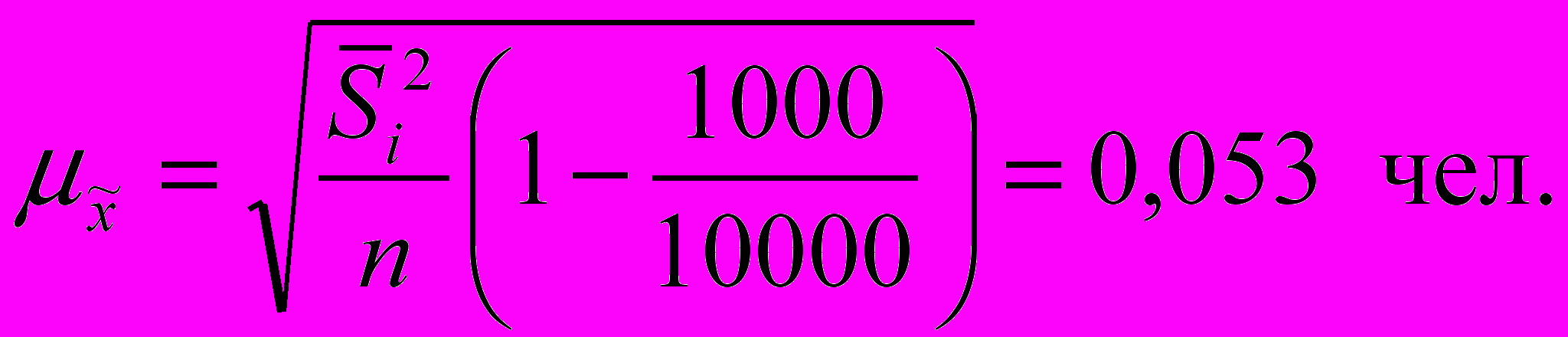
С вероятностью 0,9973 (t = 3) определим предельную ошибку выборочной средней:





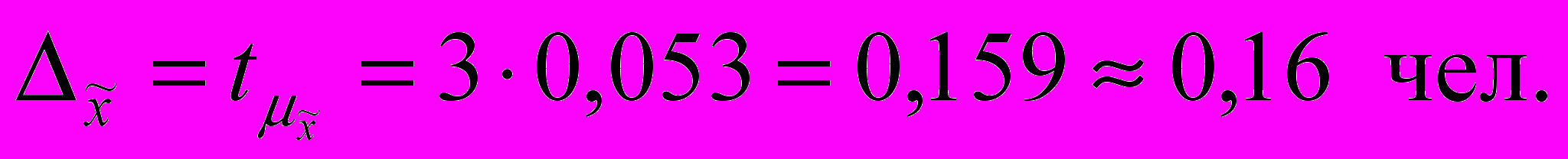
Доверительные пределы определим по формуле:





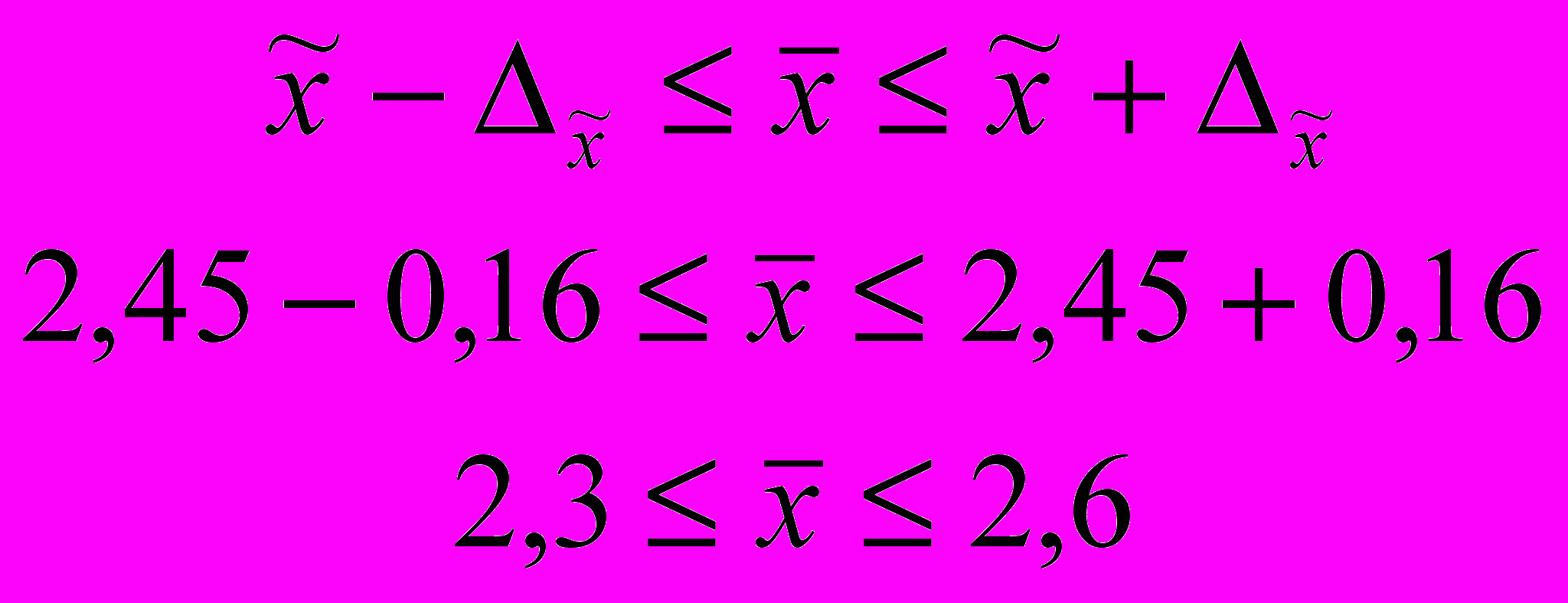
Таким образом, с вероятностью 0,9973 можно утверждать, что в районе среднее число детей в семье находится в пределах


Пример 11.

В акционерном обществе 200 бригад рабочих. Планируется проведение выборочного обследования с целью определения удельного веса рабочих, имеющих профессиональные заболевания. Известно, что межсерийная дисперсия доли равна 225.


Рассчитайте:

• с вероятностью 0,683 необходимое количество бригад для обследования рабочих, если ошибка выборки не должна превышать 5%.
  

Решение.

Рассчитаем необходимое количество бригад на основе формулы объема серийной бесповторной выборки:





Таким образом, чтобы с заданной точностью определить удельный вес рабочих, имеющих профессиональные заболевания, необходимо из 200 бригад обследовать 30 бригад.

Средняя из внутригрупповых дисперсий определяется по формуле:





Определим среднюю ошибку выборочной доли:





Предельная ошибка выборки для доли с вероятностью 0,683 (t = 1)





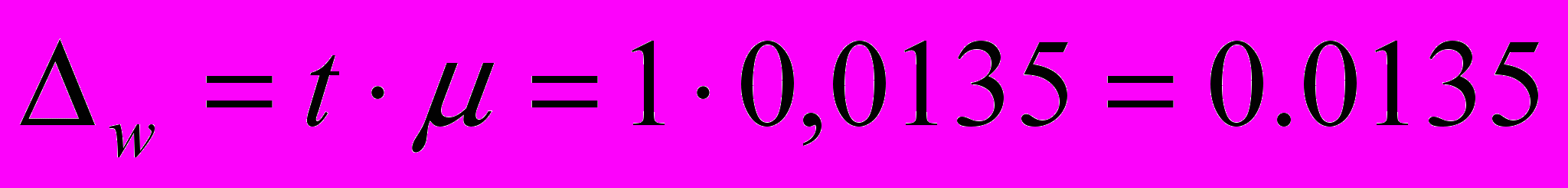
Определим доверительные интервалы:




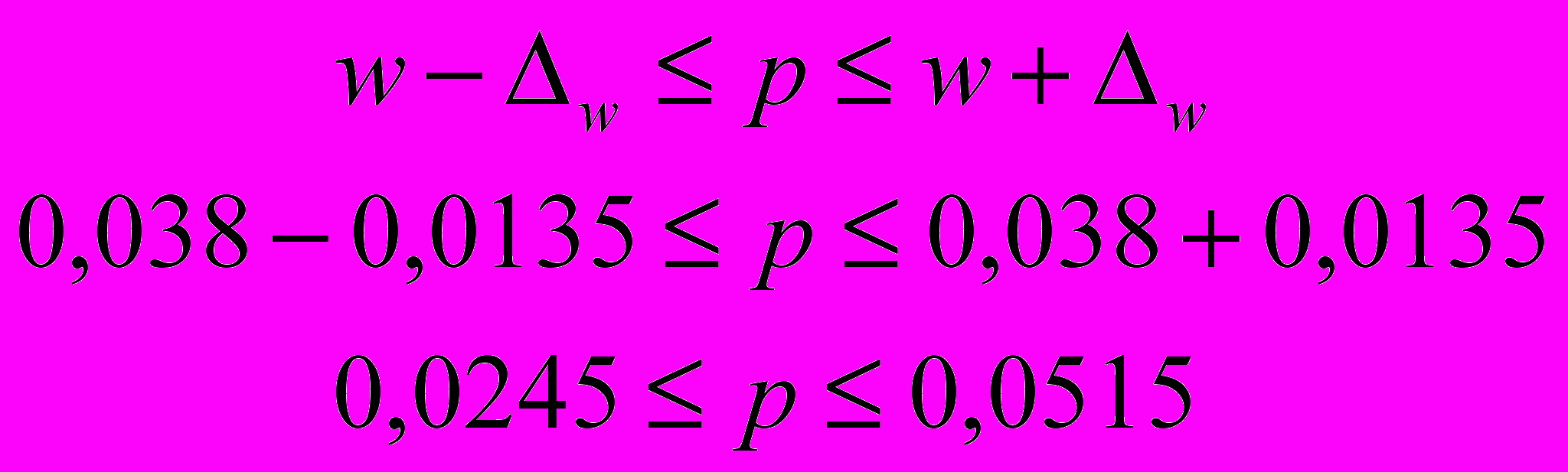
или




Таким образом, с вероятностью 0,683 можно утверждать, что доля рабочих, не выполняющих норму выработки на заводе колеблется от 2,45 до 5,15%.