Графический метод при решении задач с параметрами
| Вид материала | Документы |
- Решение. Из анализа схемы следует, что резисторы, 80.22kb.
- Решение, 562.63kb.
- Дискретная математика Введение, 134.77kb.
- К. Д. Ушинского Обучение младших школьников решению сюжетных математических задач одна, 79.12kb.
- Психотехнический метод исследования и оптимизации мышления при решении творческих задач, 413.87kb.
- Установление связи между параметрами трибоконтакта при приработке зелинский, 57.2kb.
- Процедура восполнения напряжений при решении нелинейных краевых задач механики деформируемого, 69.02kb.
- Методика классификации и решения задач с параметрами в курсе средней школы. Уравнения, 18.27kb.
- Курс является базовым как для изучения других математических дисциплин, так и для более, 39.9kb.
- Программа элективного курса для учащихся 11 классов «Решение задач с параметрами», 107.67kb.
Графический метод при решении задач с параметрами.
Ященко Людмила Анатольевна.
МОУ СОШ № 2 сельского поселения «Село Хурба»
Комсомольского муниципального района
Хабаровского края
Уравнения с параметрами являются традиционно наиболее трудными задачами школьного курса алгебры и математического анализа. Решение этих задач, как правило, представляет собой исследование функций, входящих в уравнение.
При решении задач с параметрами необходимо выяснить, при каких значениях параметра уравнение имеет решение.
Одним из методов решения уравнений с параметрами является графический. Этот метод позволяет учащимся не только исследовать свойства функций, входящих в уравнение, но и наглядно увидеть решение уравнения.
Прежде всего, при решении задач с параметрами необходимо сделать то, что делается при решении любого уравнения: привести заданное уравнение к более простому виду, если это возможно: разложить рациональное выражение на множители, избавиться от модулей, логарифмов и т.д.
При графическом решении уравнения с параметром необходимо:
- Найти область определения уравнения, т.е. область допустимых значений неизвестного и параметра, при которых уравнение может иметь решения.
- Выразить параметр как функцию от x:
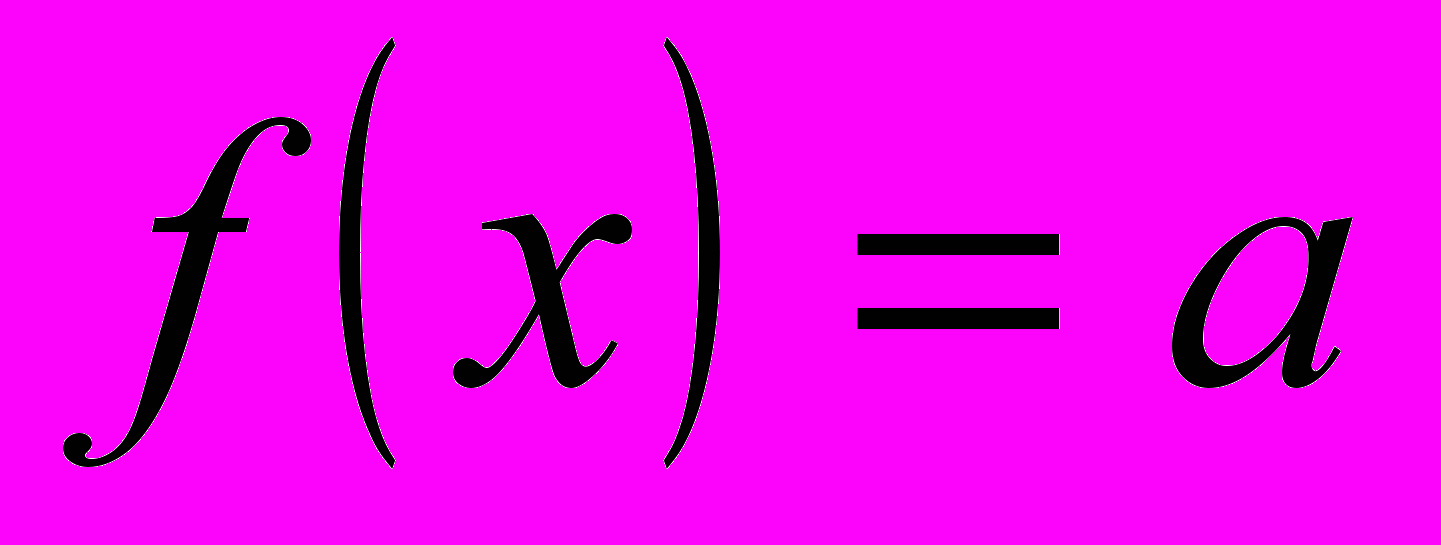
- В системе координат хОa построить графики функций
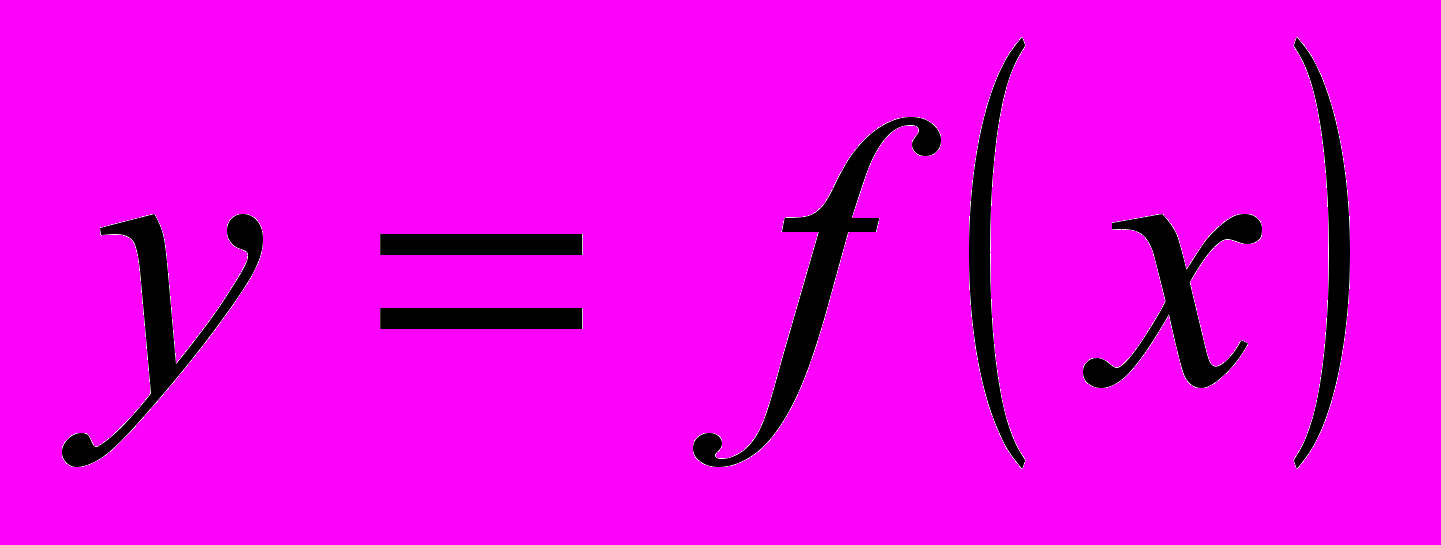 и
и 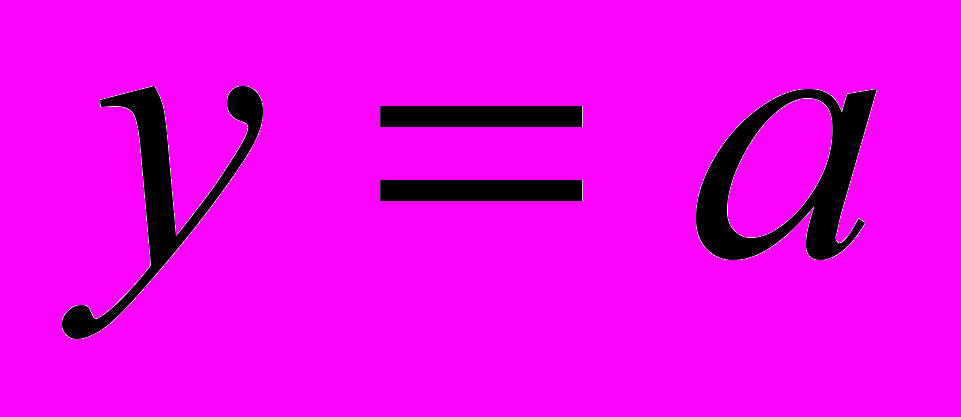 для тех значений х, которые входят в область определения уравнения.
для тех значений х, которые входят в область определения уравнения.
- Определить точки пересечения прямой
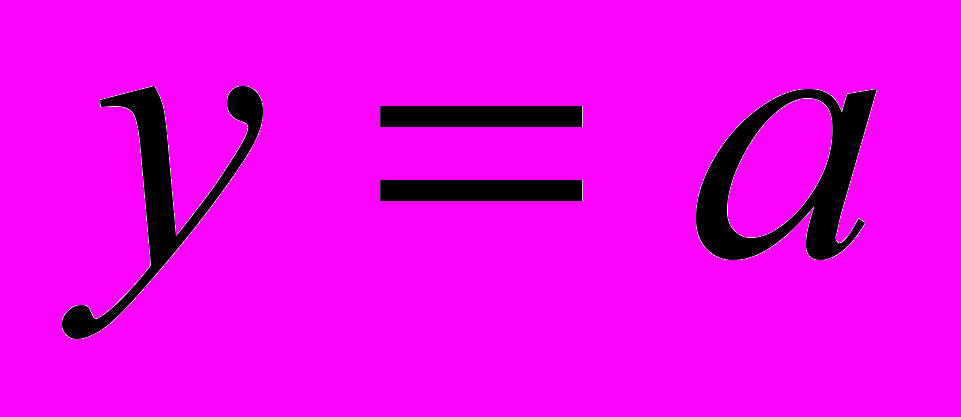
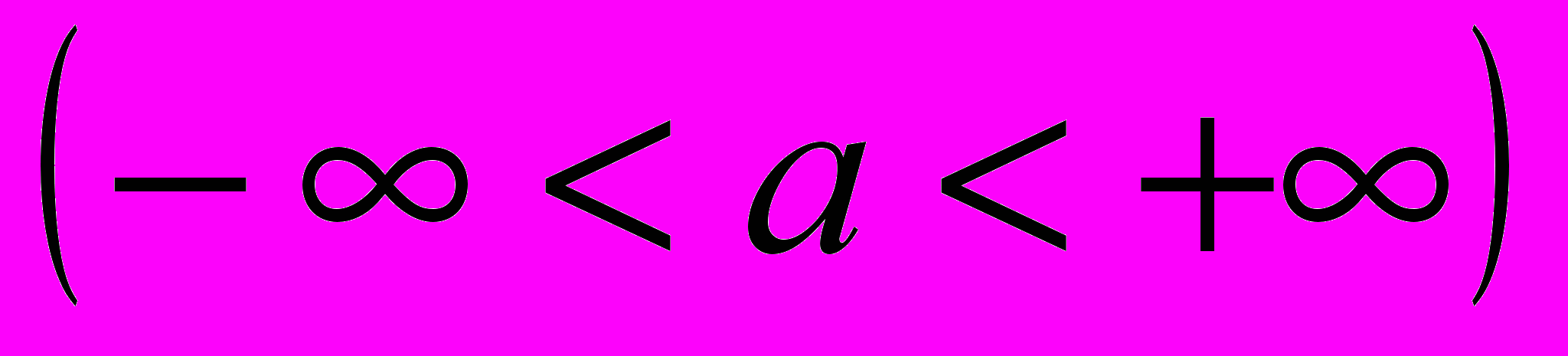 с графиком функции
с графиком функции 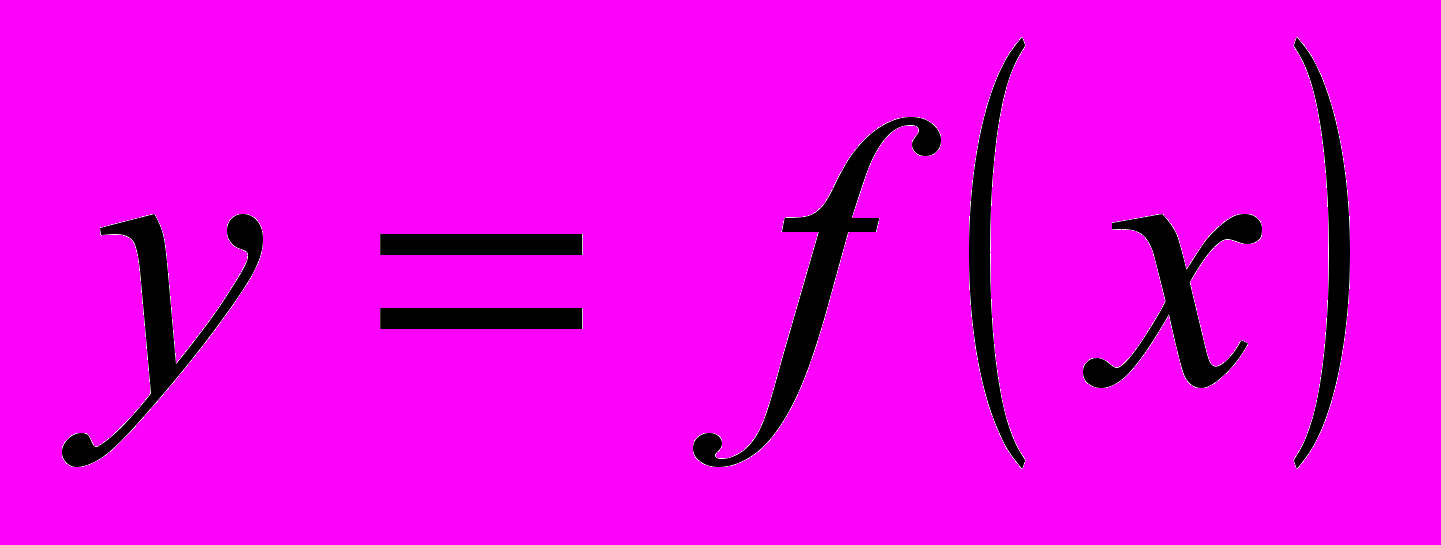 .
.
Возможны ситуации:
- Прямая
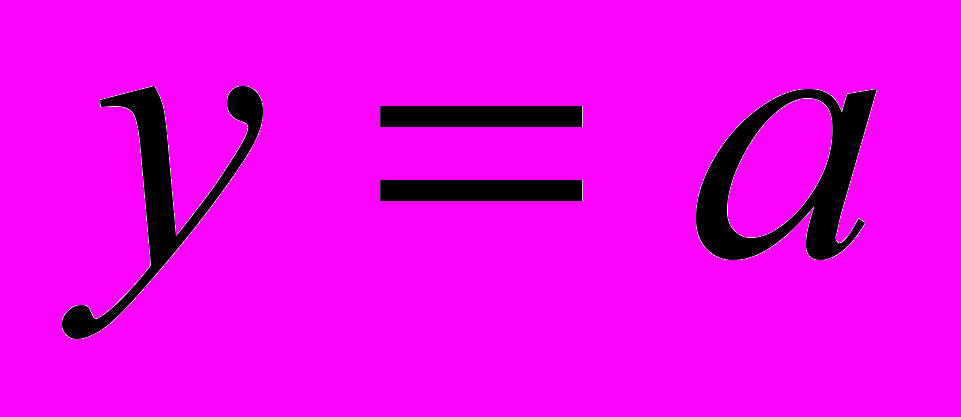 не пересекает график
не пересекает график 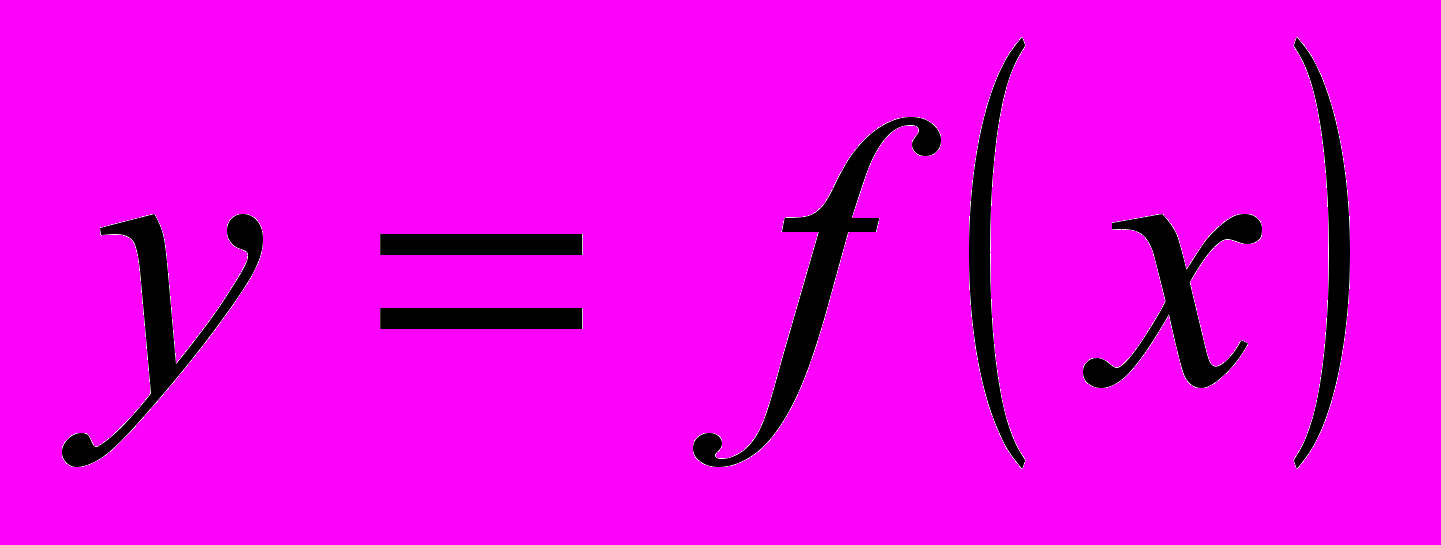 . Следовательно, при данном значении а исходное уравнение решений не имеет.
. Следовательно, при данном значении а исходное уравнение решений не имеет.
- Прямая
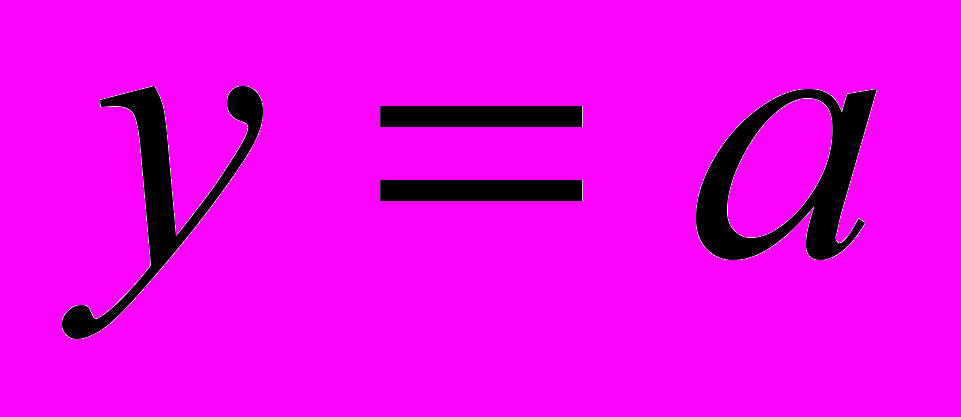 пересекает график
пересекает график 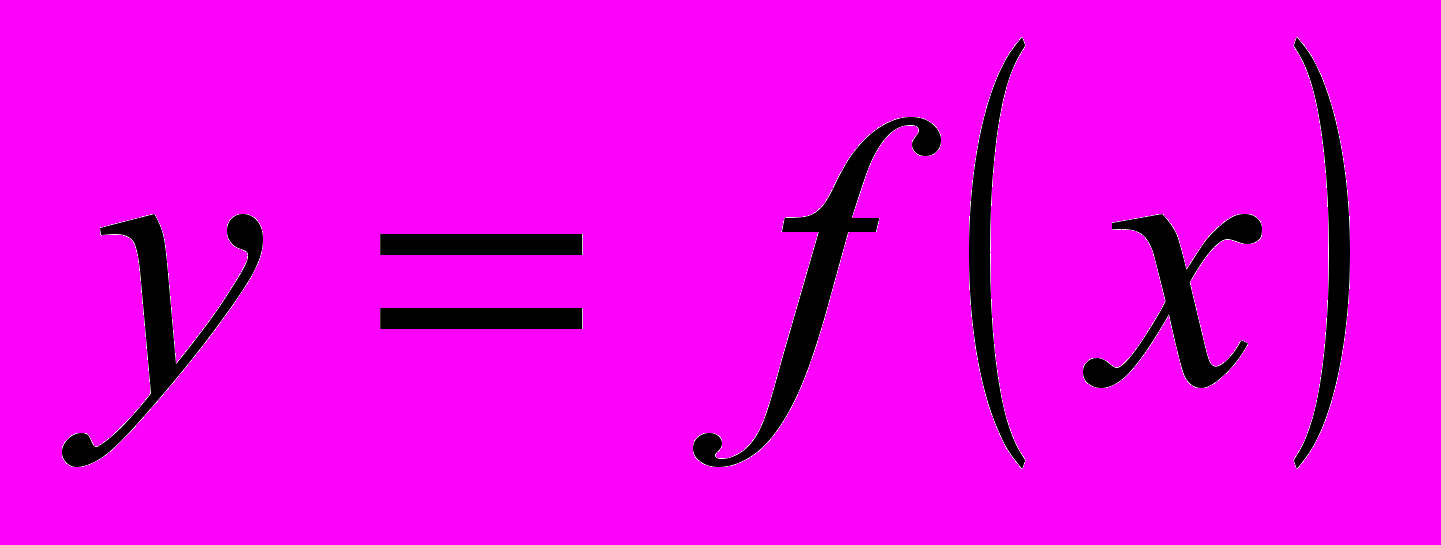 в одной или нескольких точках. Следовательно, при данном значении а можно сделать вывод о числе решений исходного уравнения, найти абсциссы точек пересечения и т.д.
в одной или нескольких точках. Следовательно, при данном значении а можно сделать вывод о числе решений исходного уравнения, найти абсциссы точек пересечения и т.д.
Задача 1. ( С5, ЕГЭ – 2010) Найдите все значения а, при каждом из которых уравнение
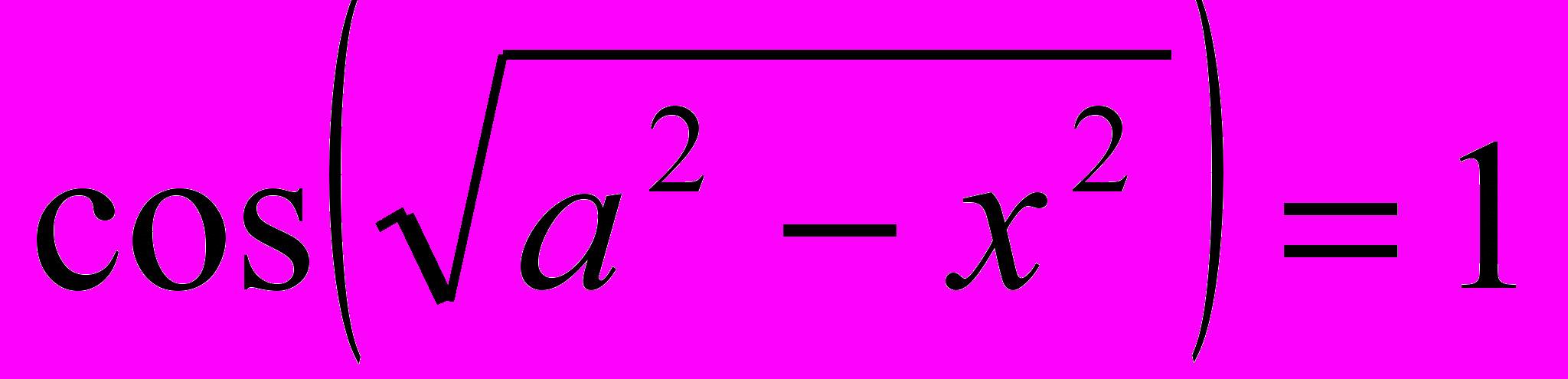 имеет ровно восемь различных решений.
имеет ровно восемь различных решений. Решение: 1 способ.
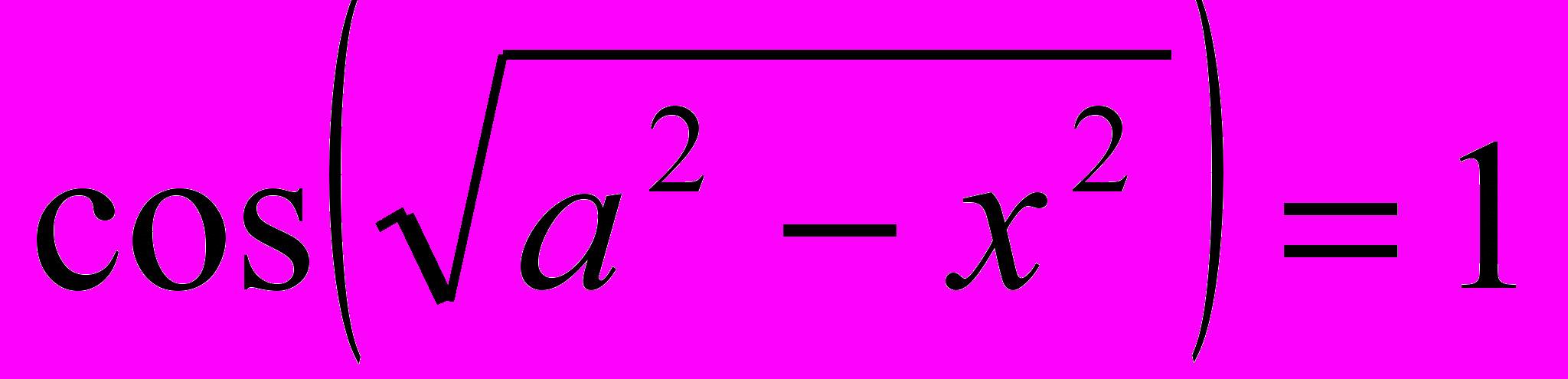 ,
, 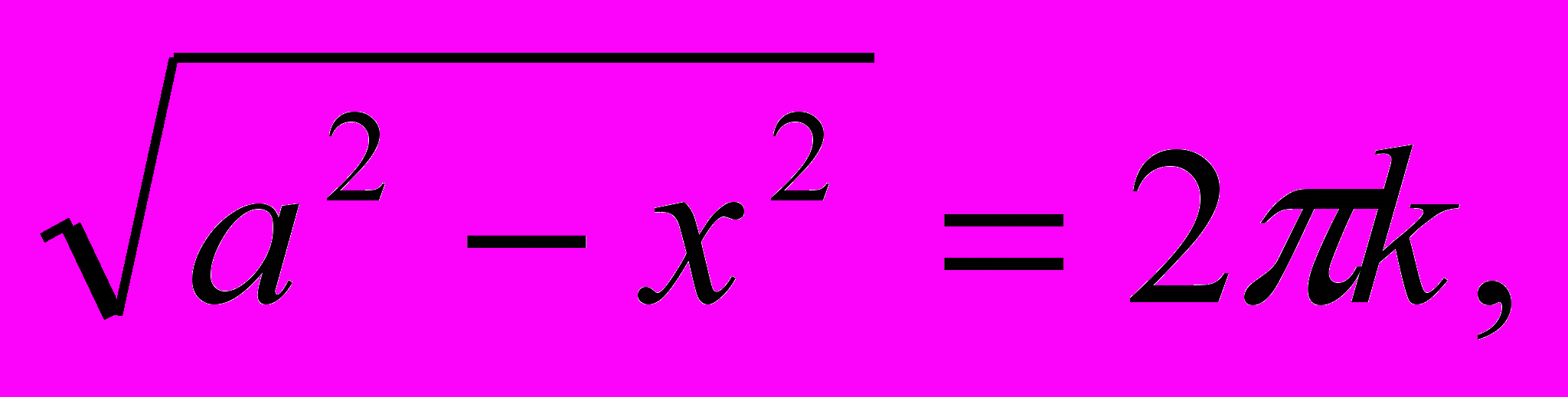
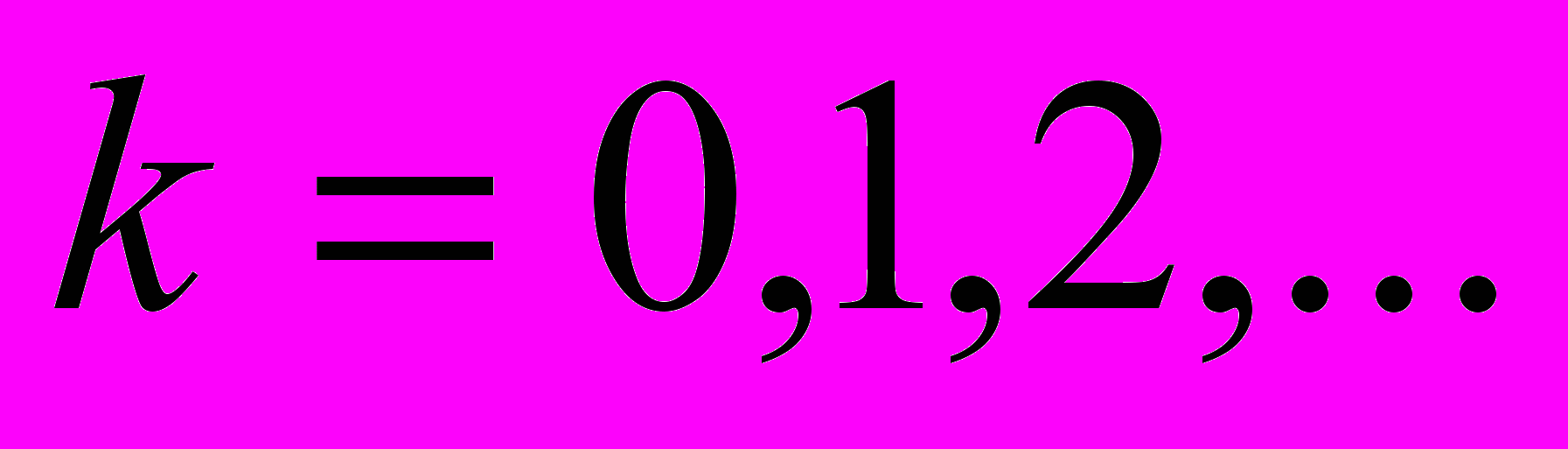
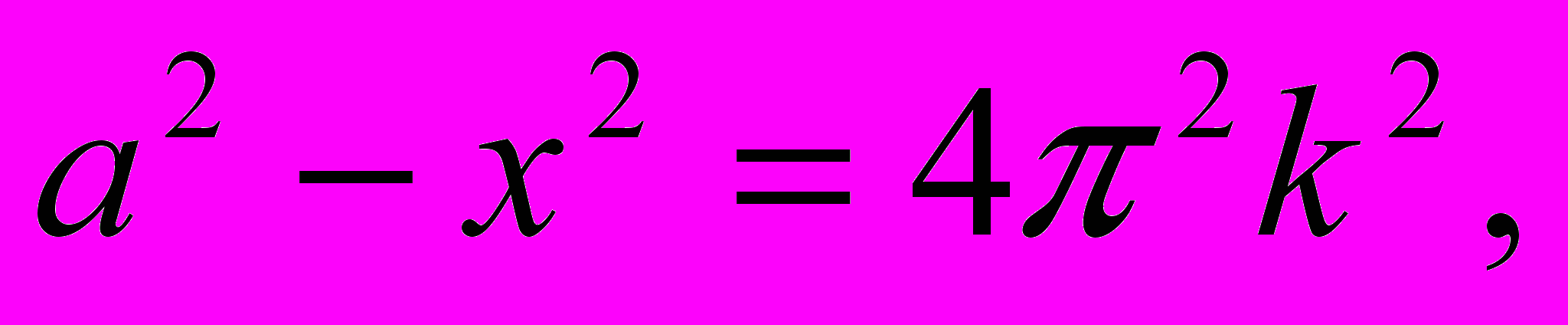
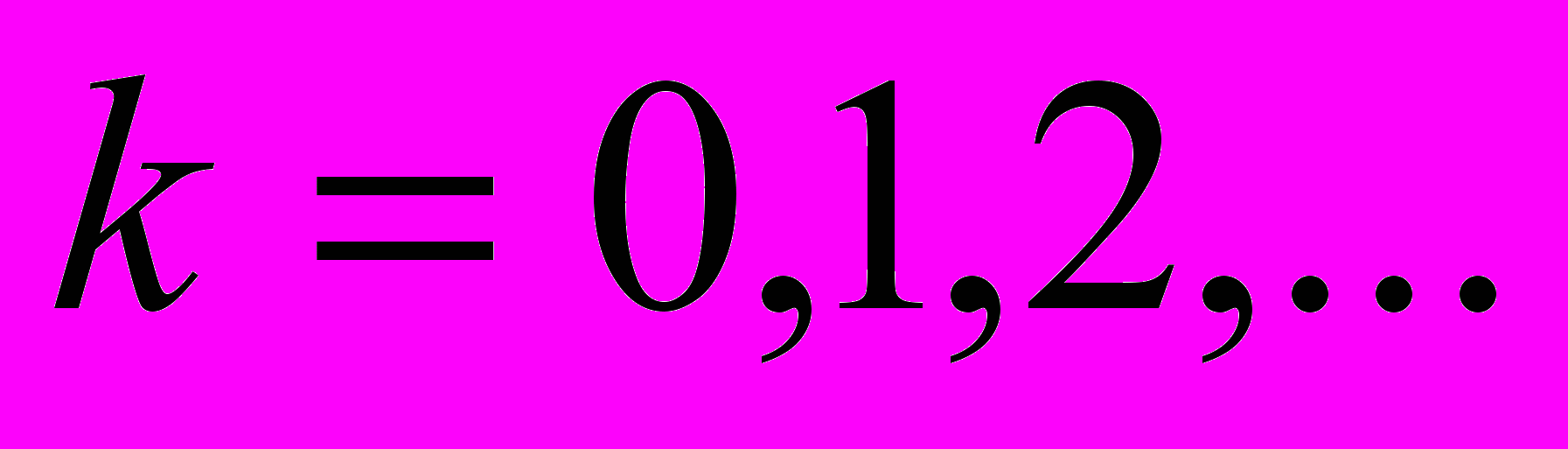
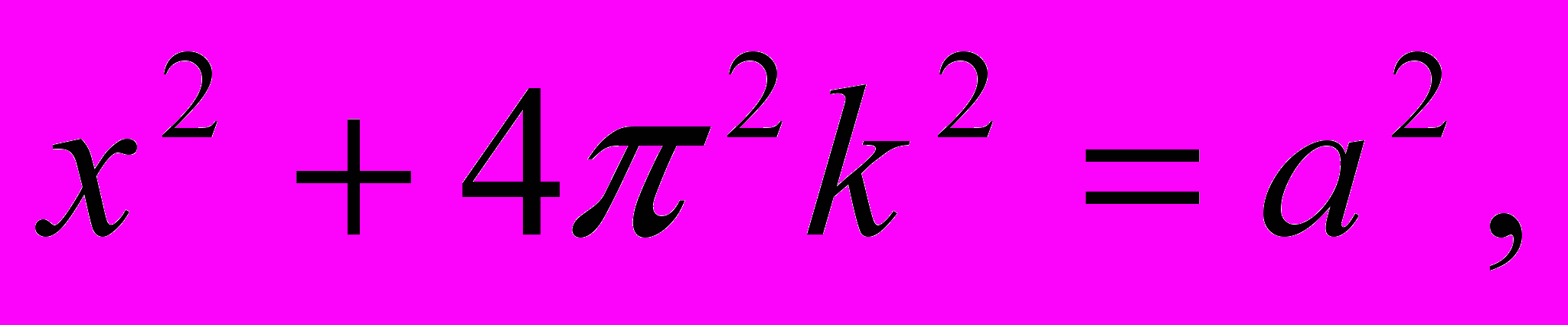
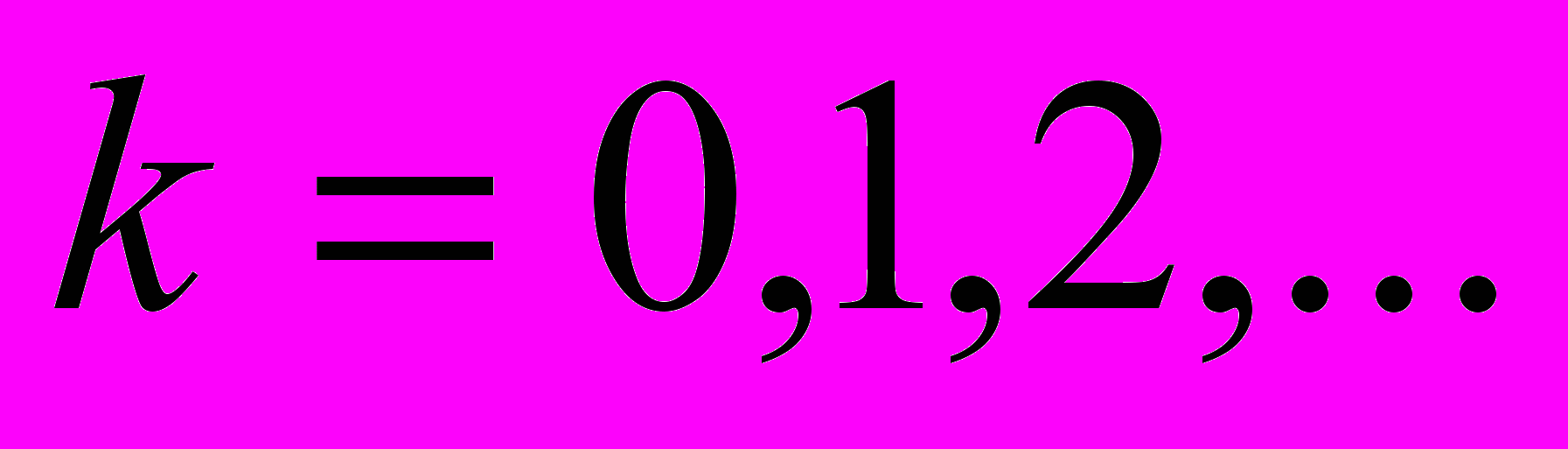
Построим графики функций
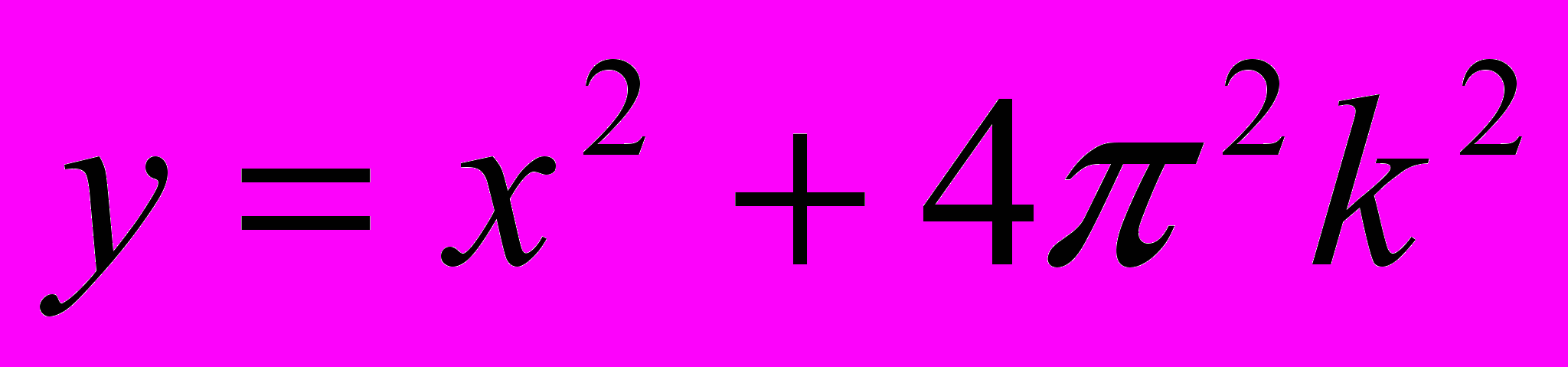 при
при 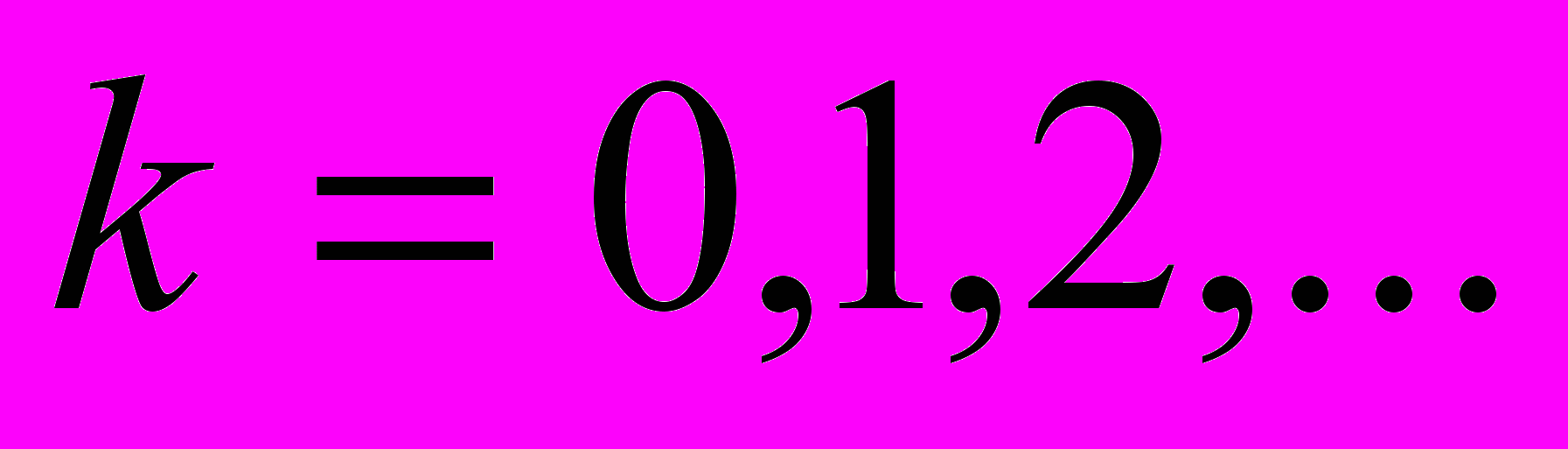 и
и  . Графиком первой функции является семейство парабол с вершинами, расположенных на оси ОУ: у=0,
. Графиком первой функции является семейство парабол с вершинами, расположенных на оси ОУ: у=0, 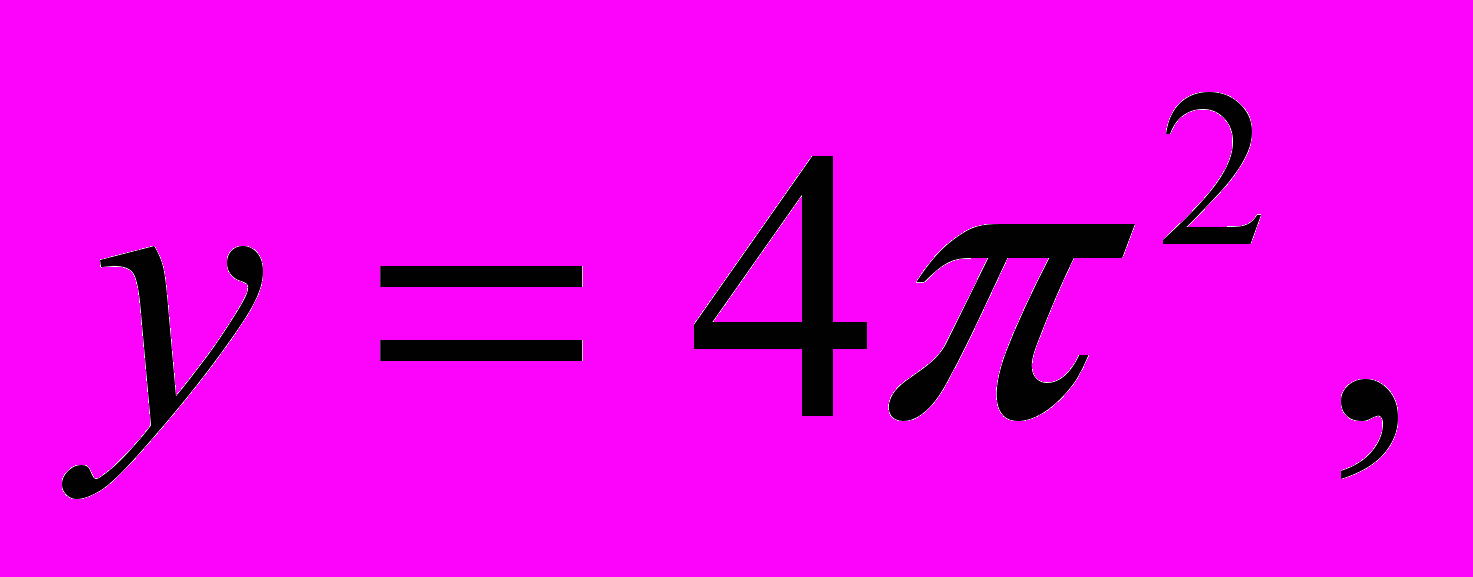
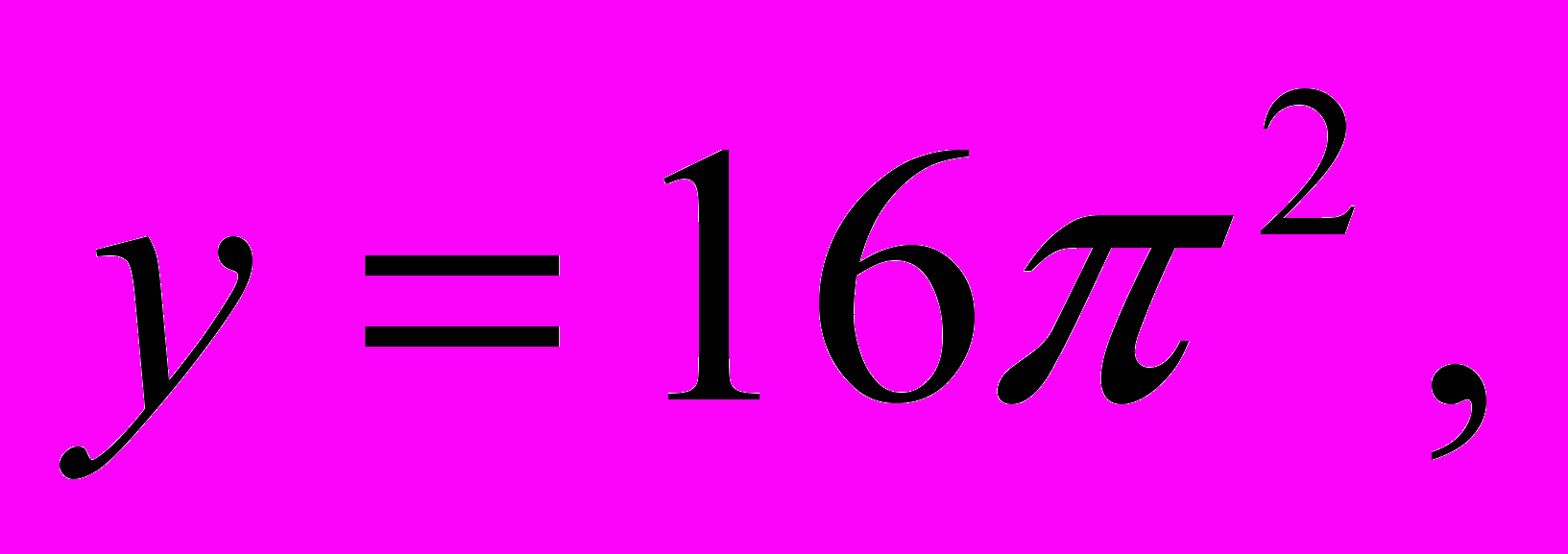
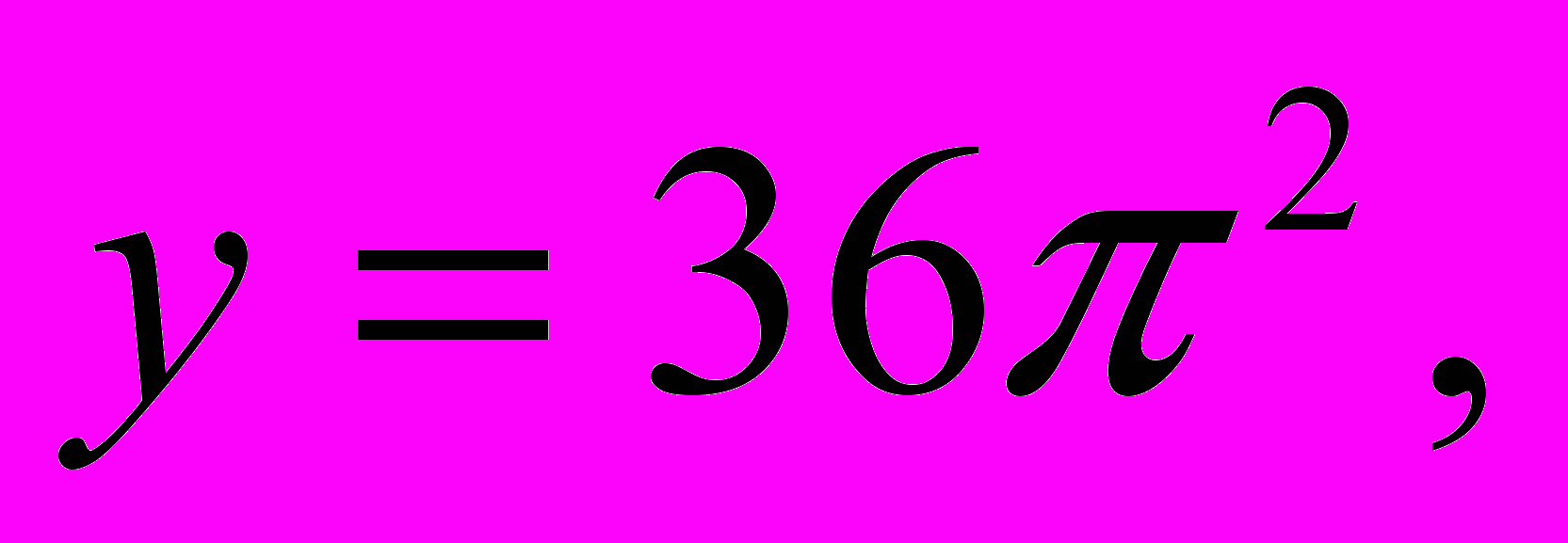
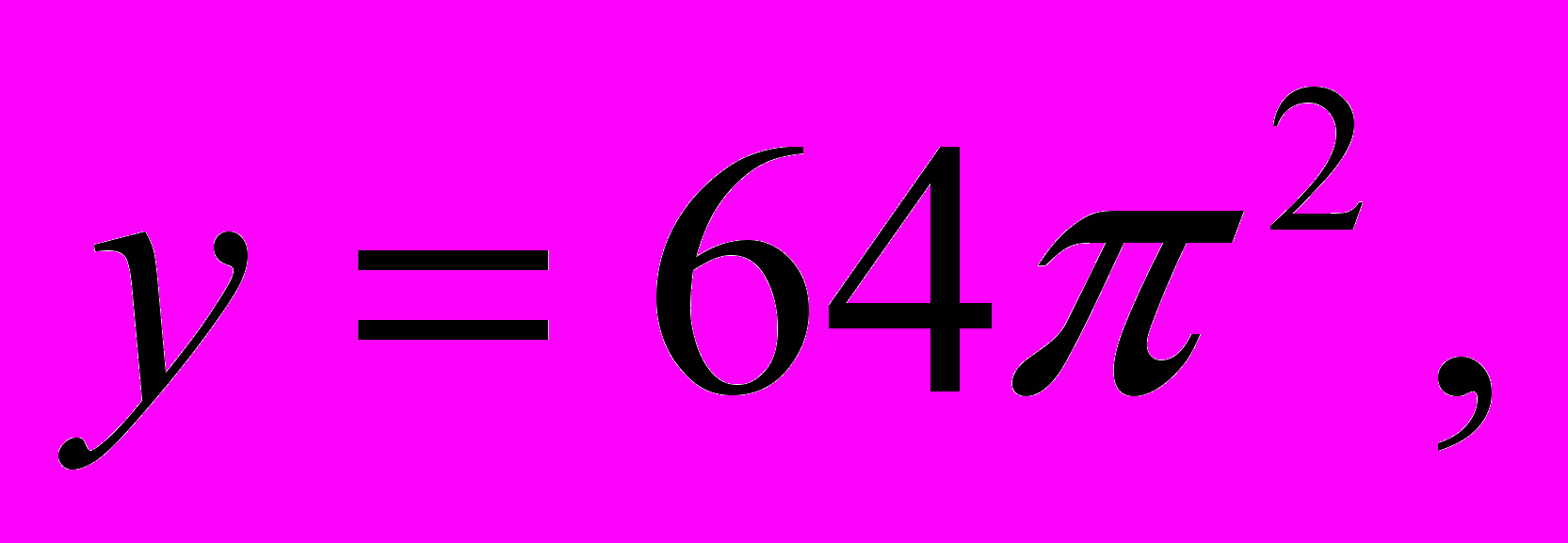
и
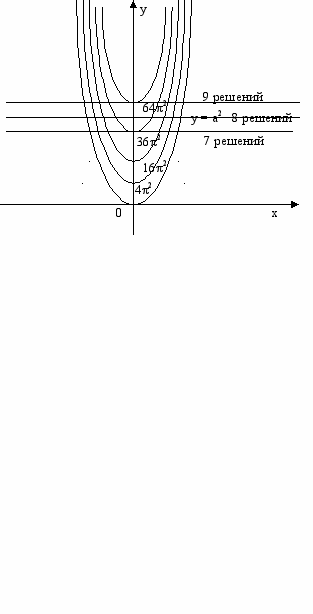 т.д. (в зависимости от k=0,1,2,3,4,…). Графиком второй функции является прямая, параллельная оси ОХ.
т.д. (в зависимости от k=0,1,2,3,4,…). Графиком второй функции является прямая, параллельная оси ОХ.По графику определяем, что
ровно восемь решений (точек пересечения) возможно в том случае, если прямая
 расположена выше прямой
расположена выше прямой 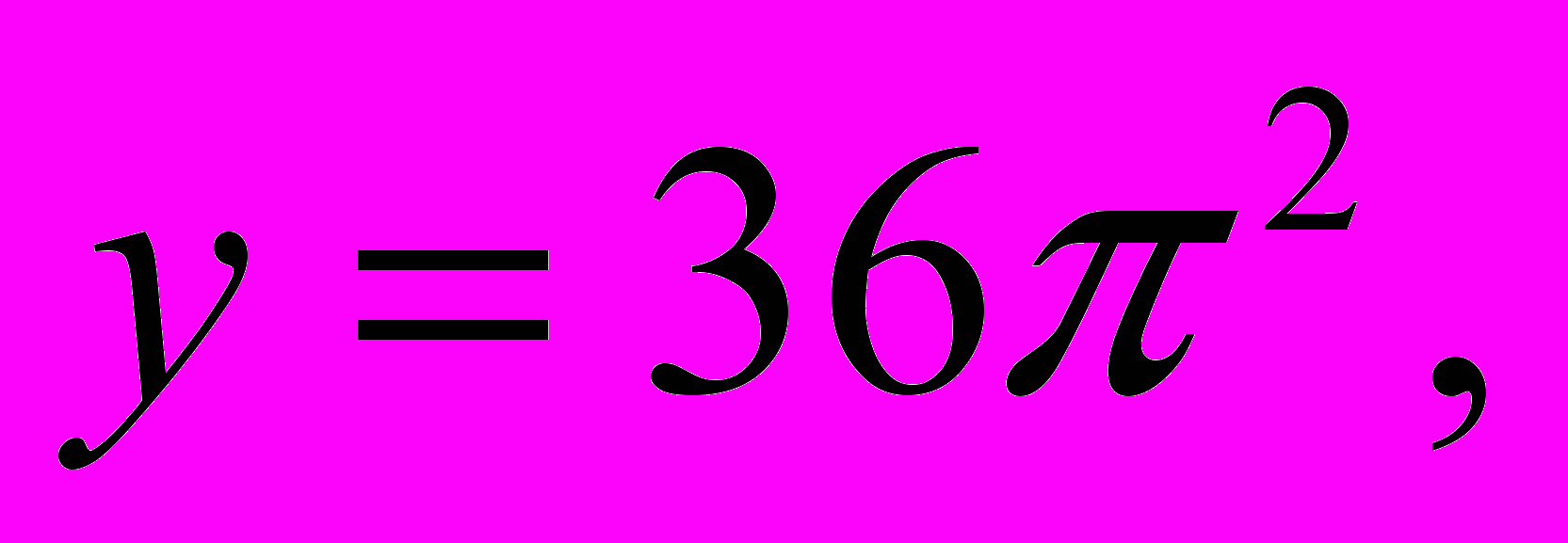 но ниже прямой
но ниже прямой 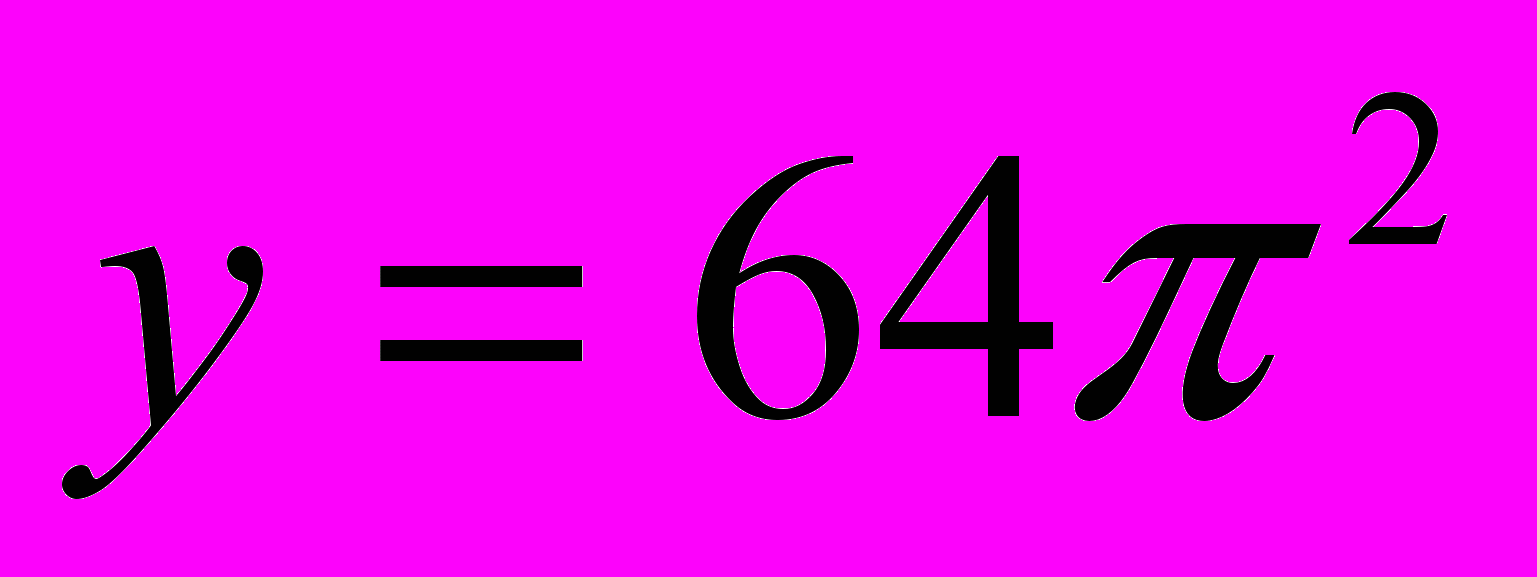 . Следовательно,
. Следовательно, 
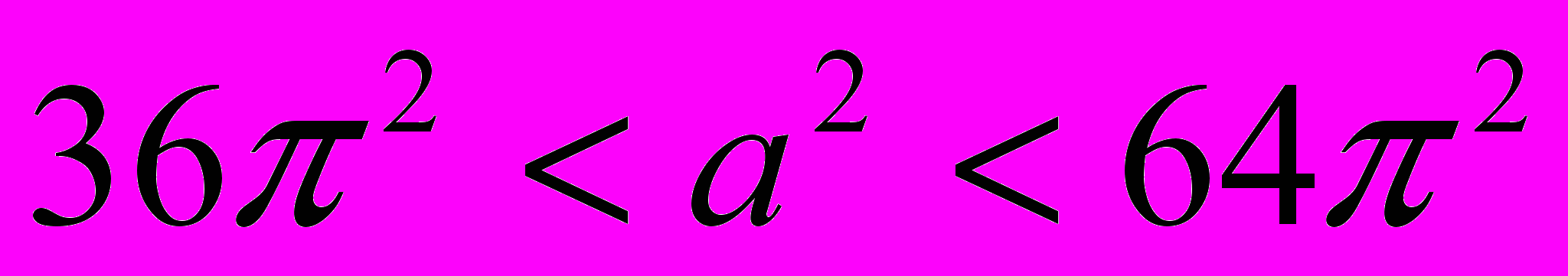 ,
,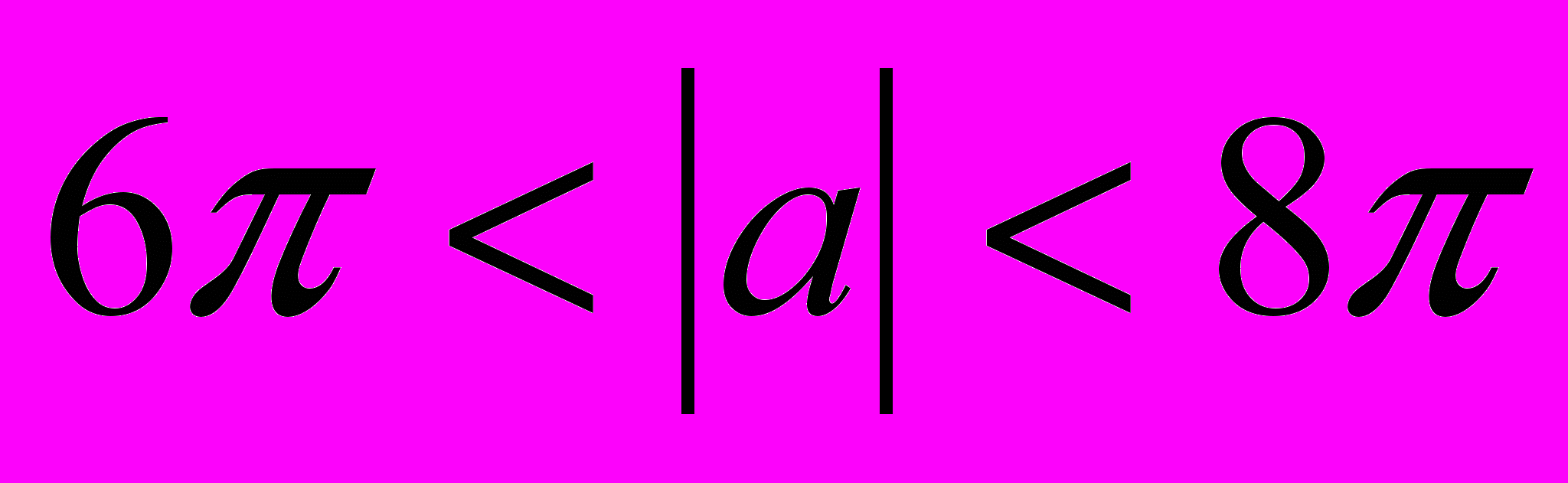 .
. При
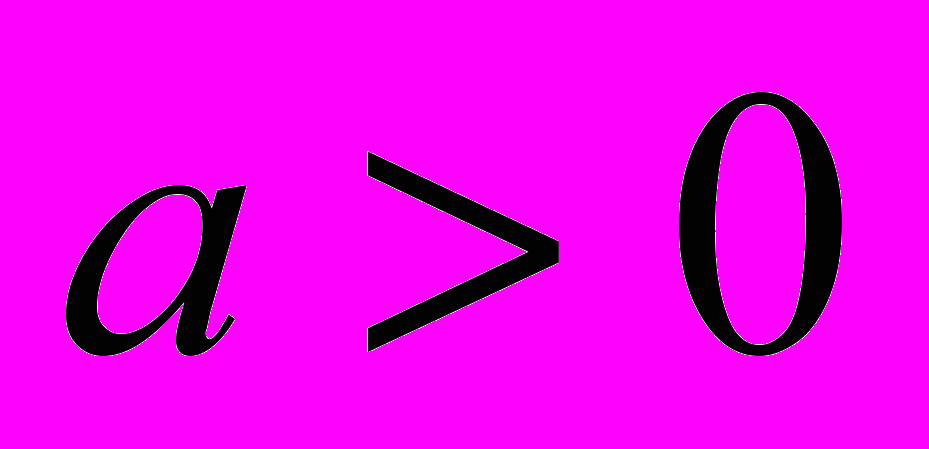
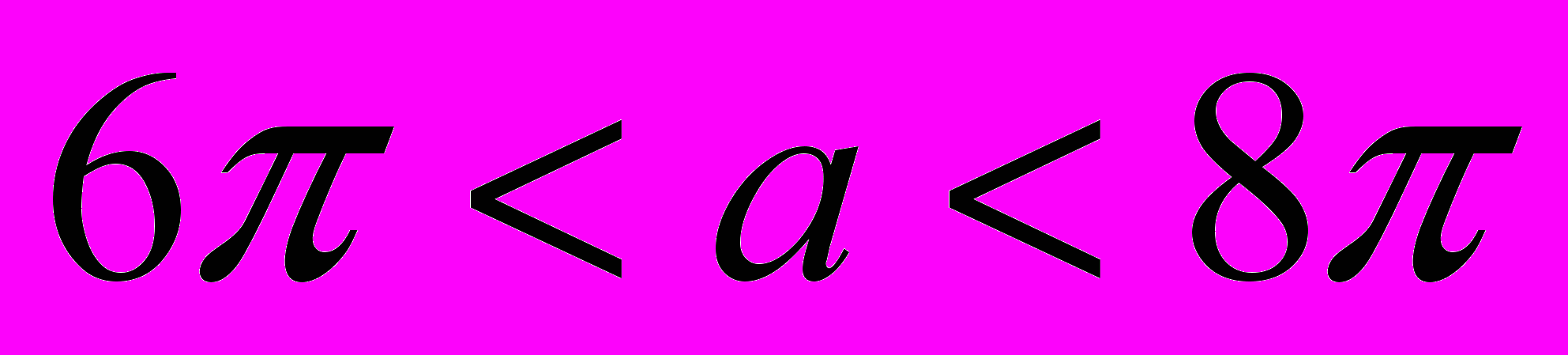 ,
,при
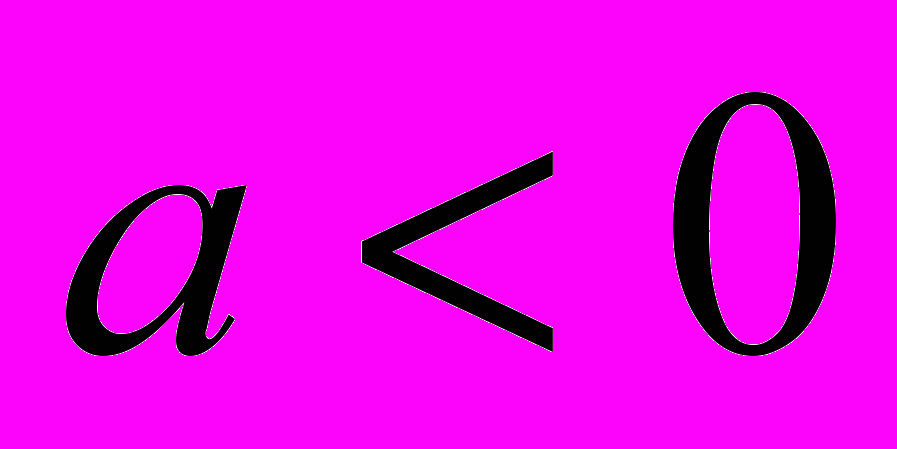
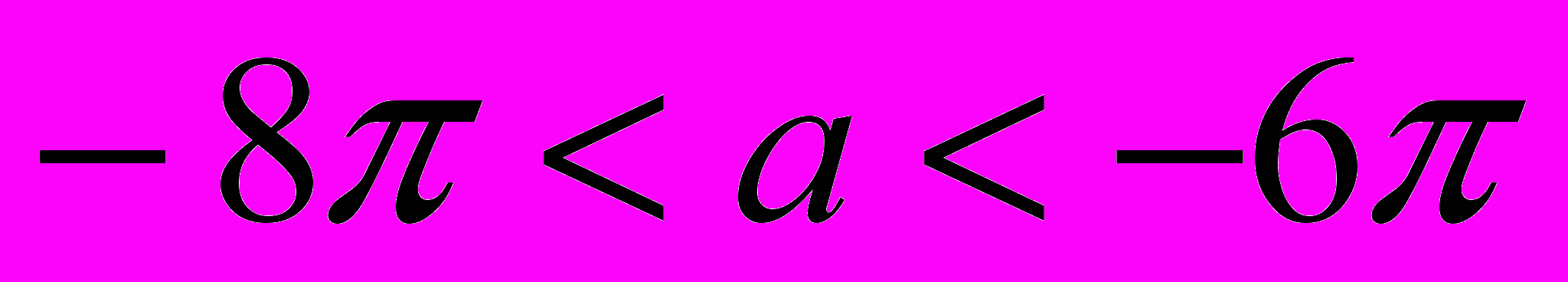 .
.Ответ:
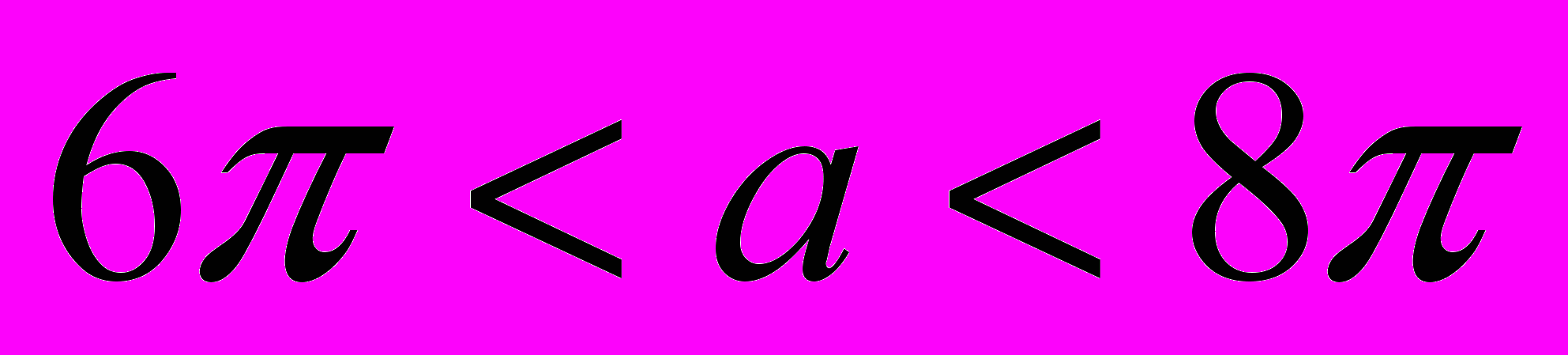 ,
, 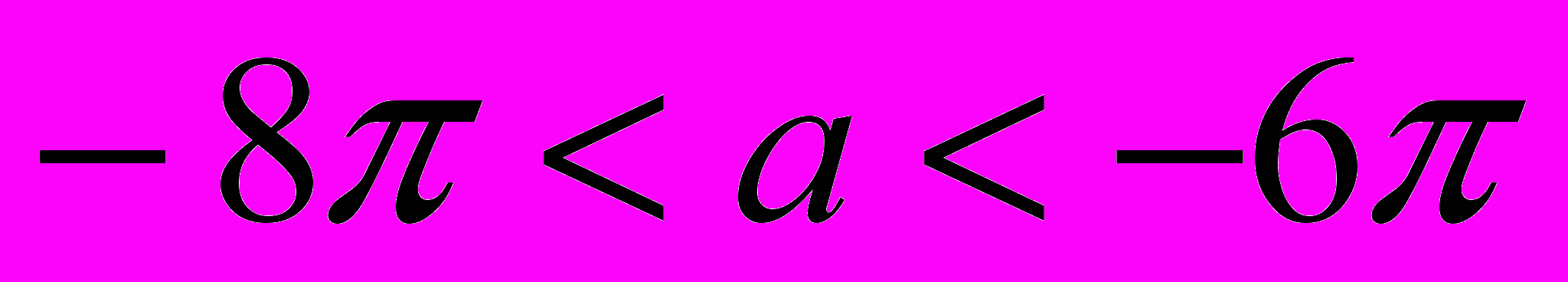
 Решение: 2 способ.
Решение: 2 способ. 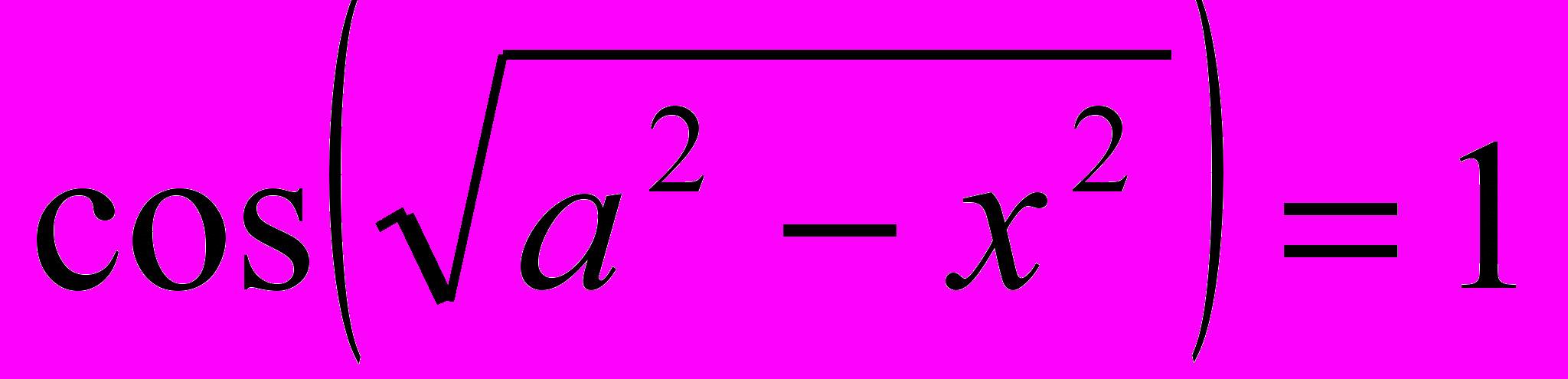 ,
, 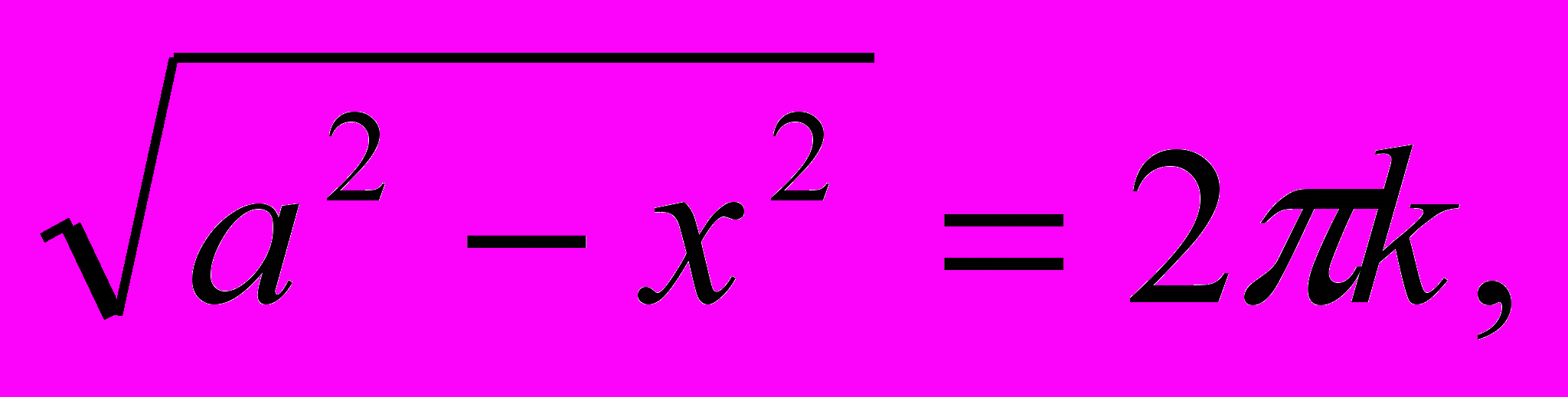
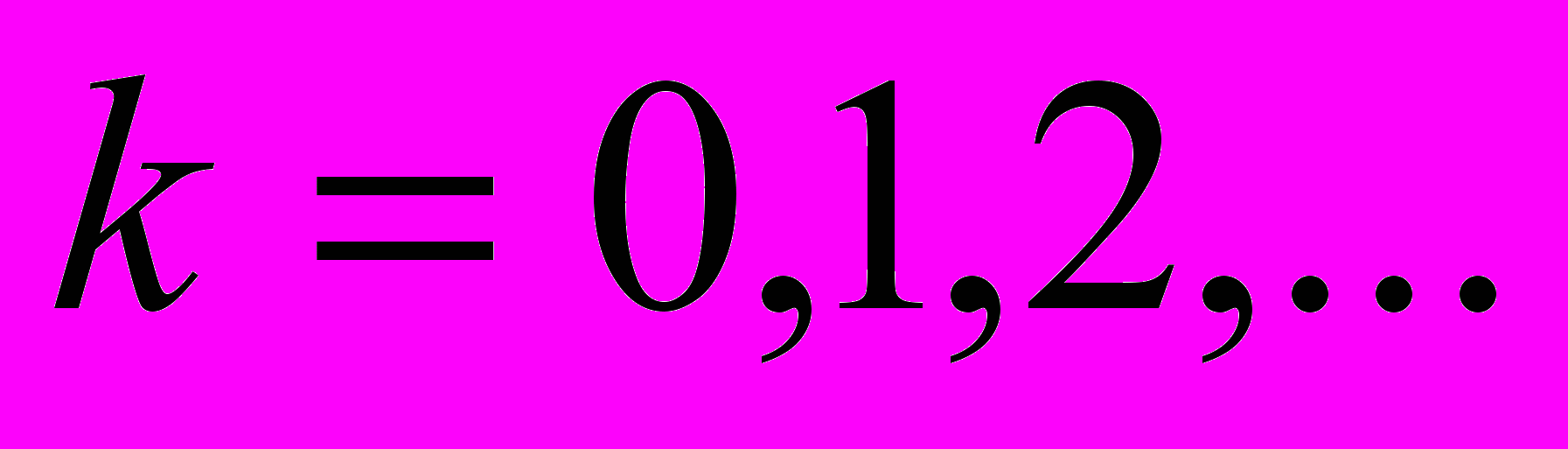 Заметим, что параметр а может принимать как положительные, так и отрицательные значения, но не равен нулю.
Заметим, что параметр а может принимать как положительные, так и отрицательные значения, но не равен нулю.Построим график функции
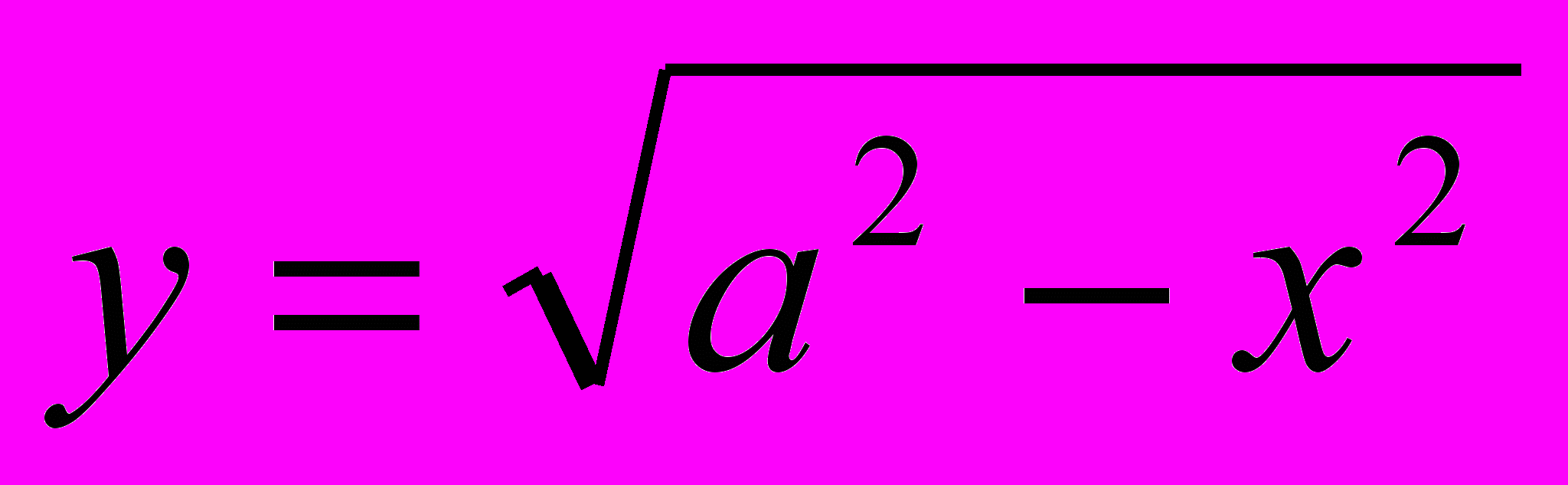 при у>0 , т.е.
при у>0 , т.е. 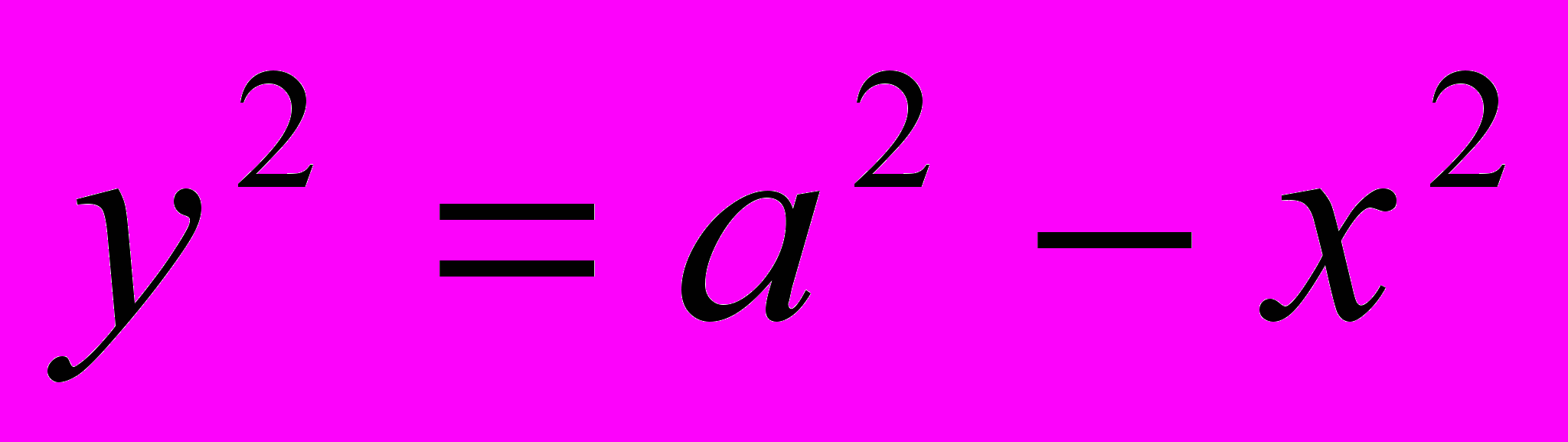 или
или 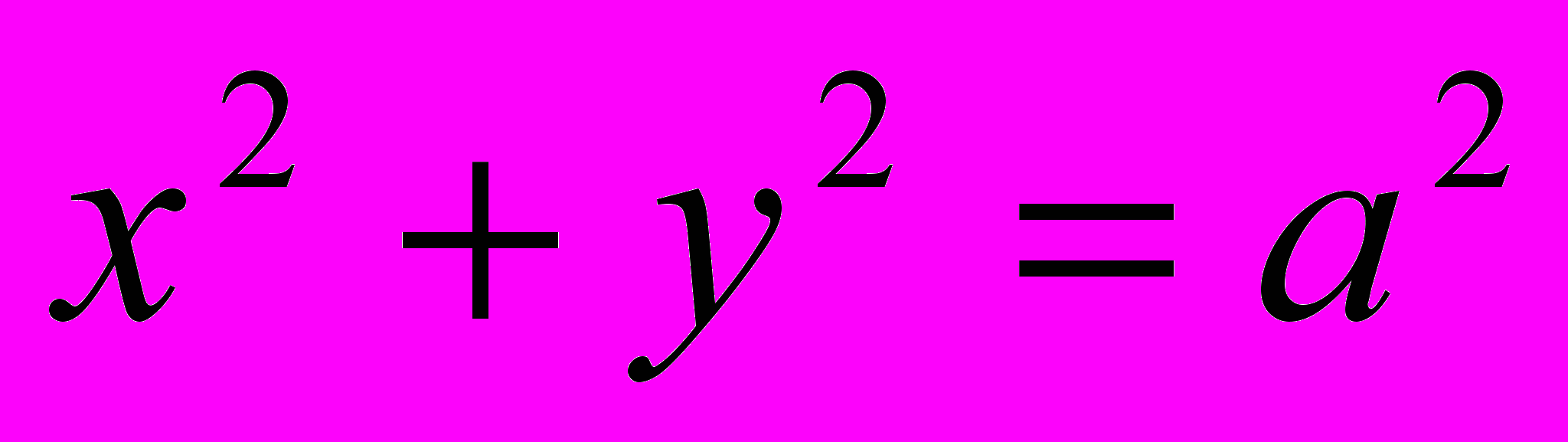 (полуокружность с центром в начале координат) . Графиком второй функции
(полуокружность с центром в начале координат) . Графиком второй функции 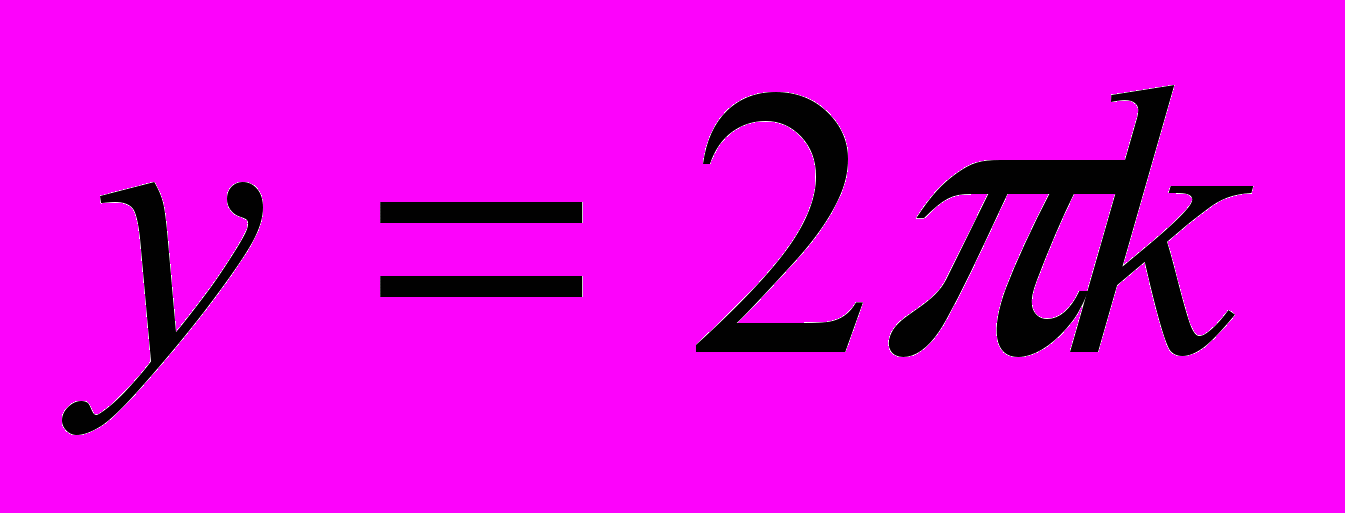 при
при 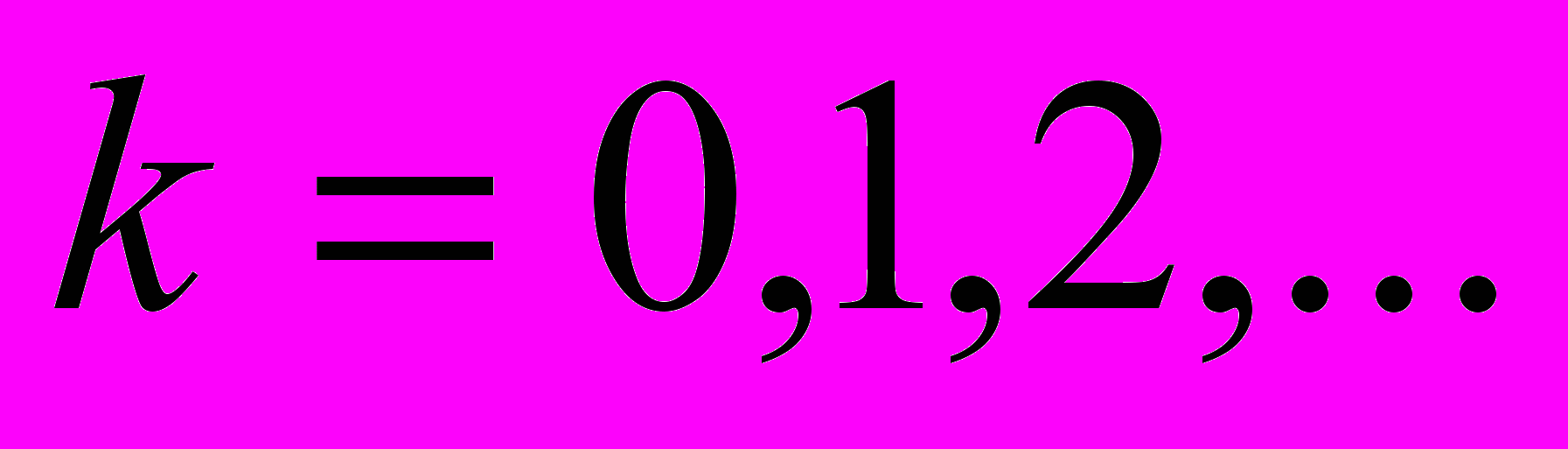 является семейство прямых, параллельных оси ОХ, проходящих через точки с ординатами у=0,
является семейство прямых, параллельных оси ОХ, проходящих через точки с ординатами у=0, 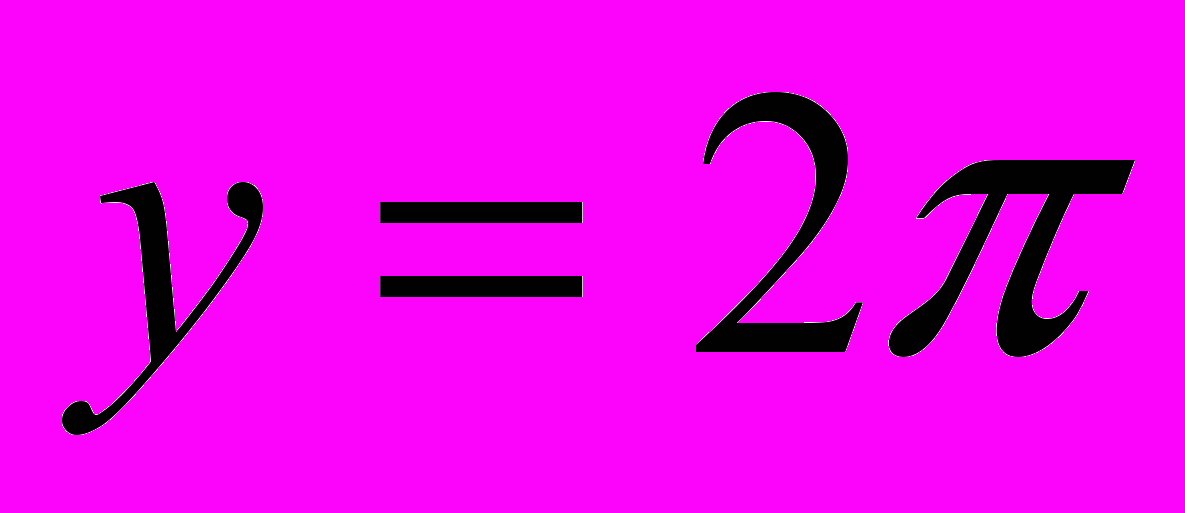 ,
, 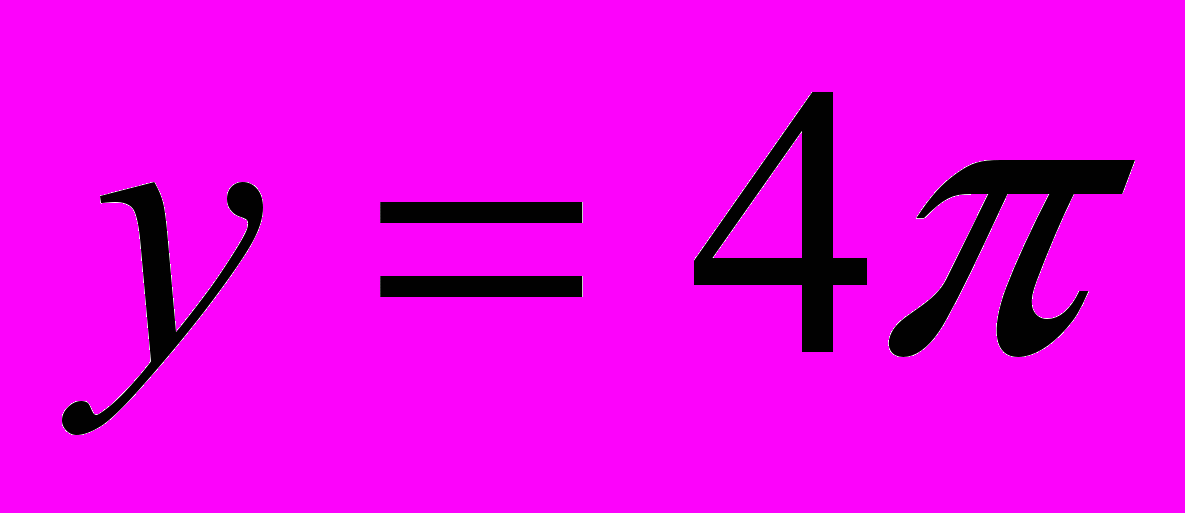 ,
, 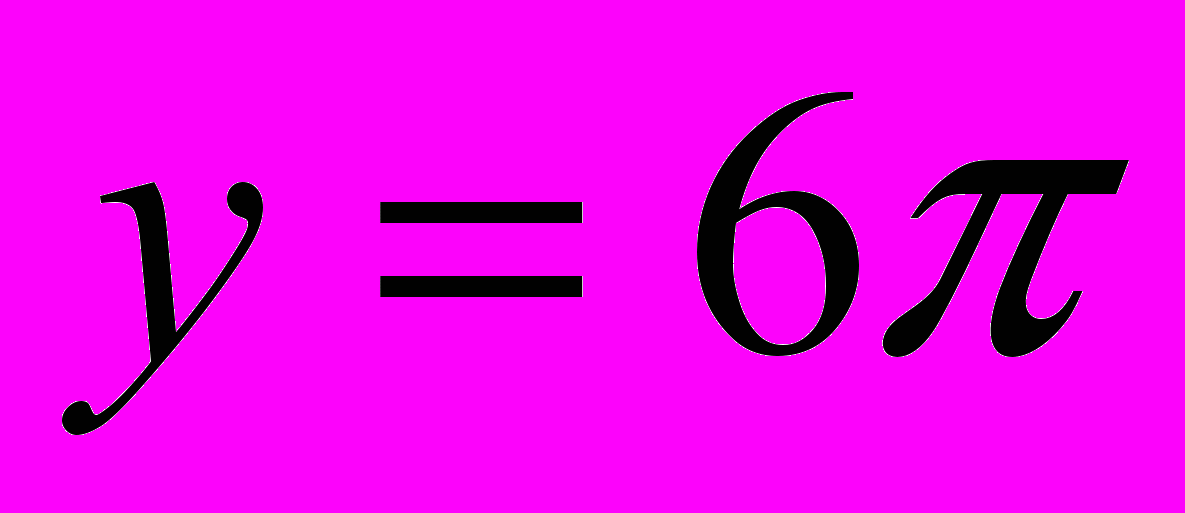 ,
, 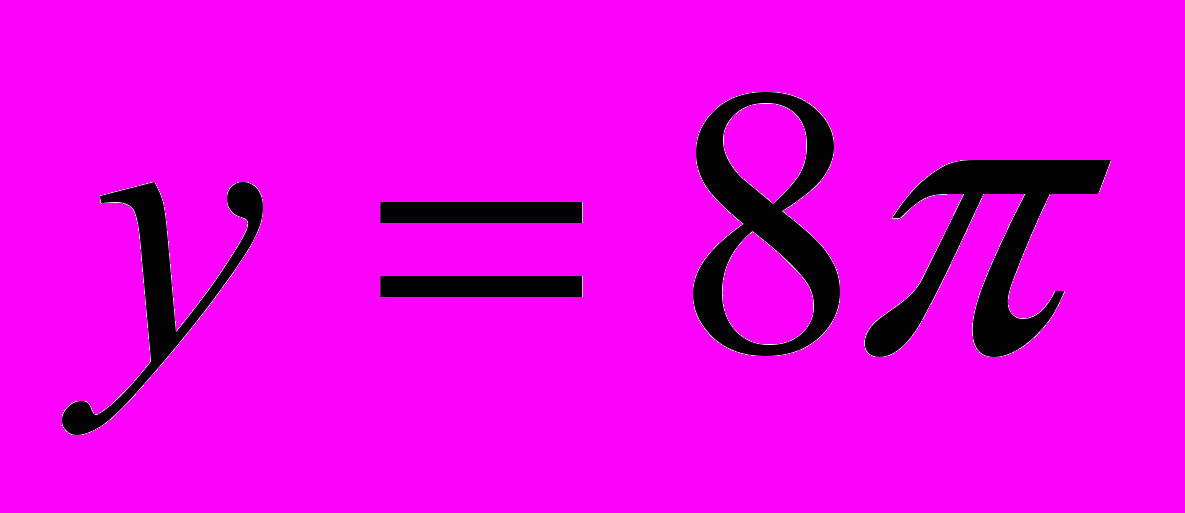 и т.д.
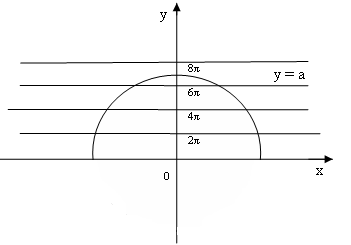
и т.д.Рассмотрим полуокружность радиуса r=a. Если радиус
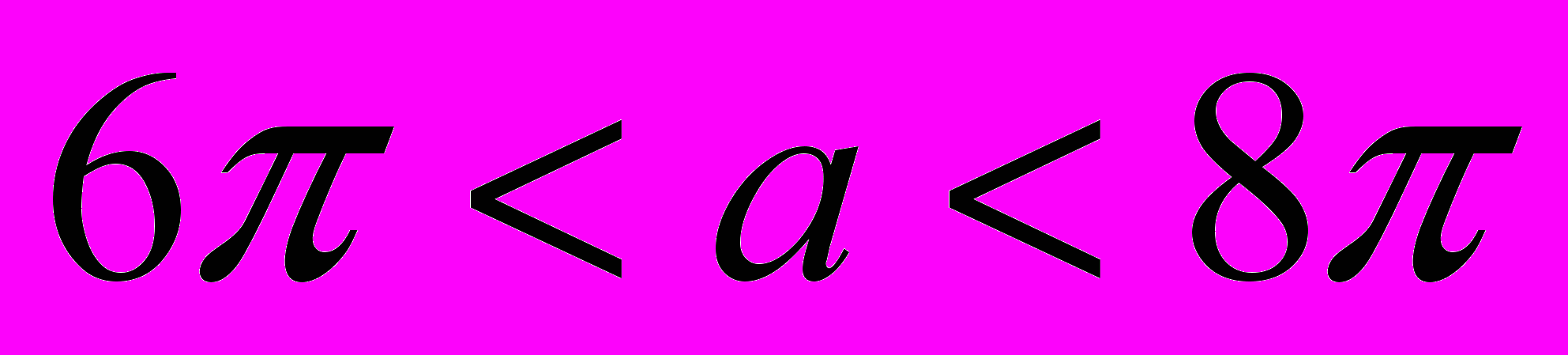 , то полуокружность пересекает серию прямых ровно в восьми точках. Аналогично рассуждаем для случая а<0.
, то полуокружность пересекает серию прямых ровно в восьми точках. Аналогично рассуждаем для случая а<0.Ответ:
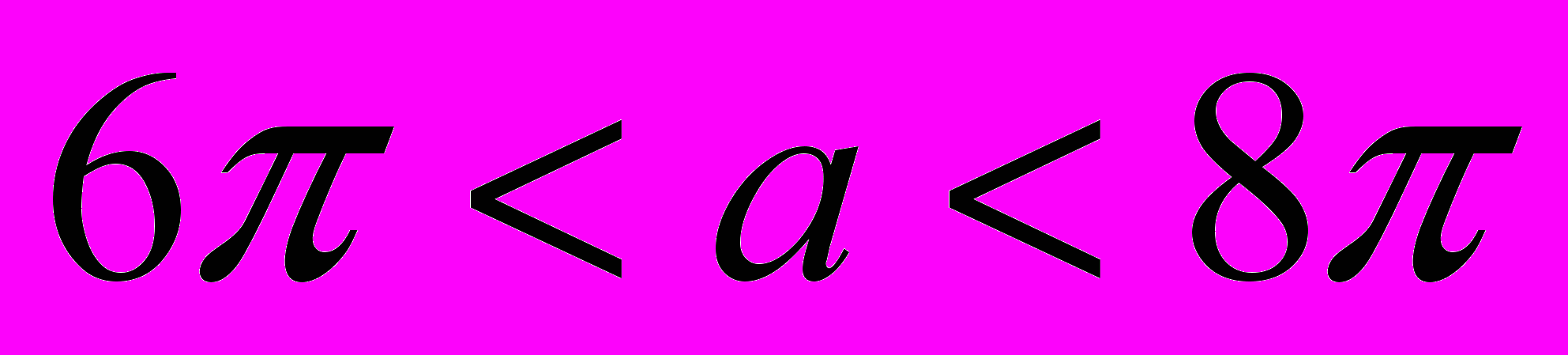 ,
, 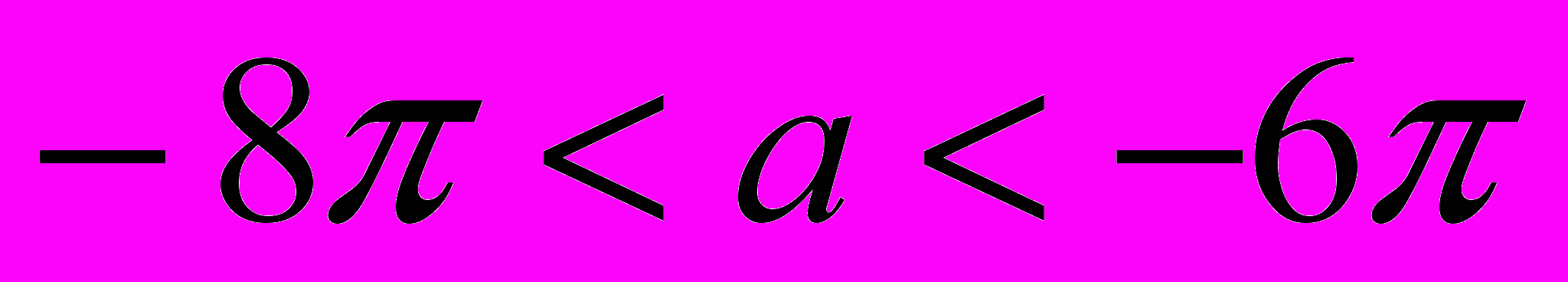
Задача 2. ( С5, ЕГЭ – 2010) Найти число решений уравнения
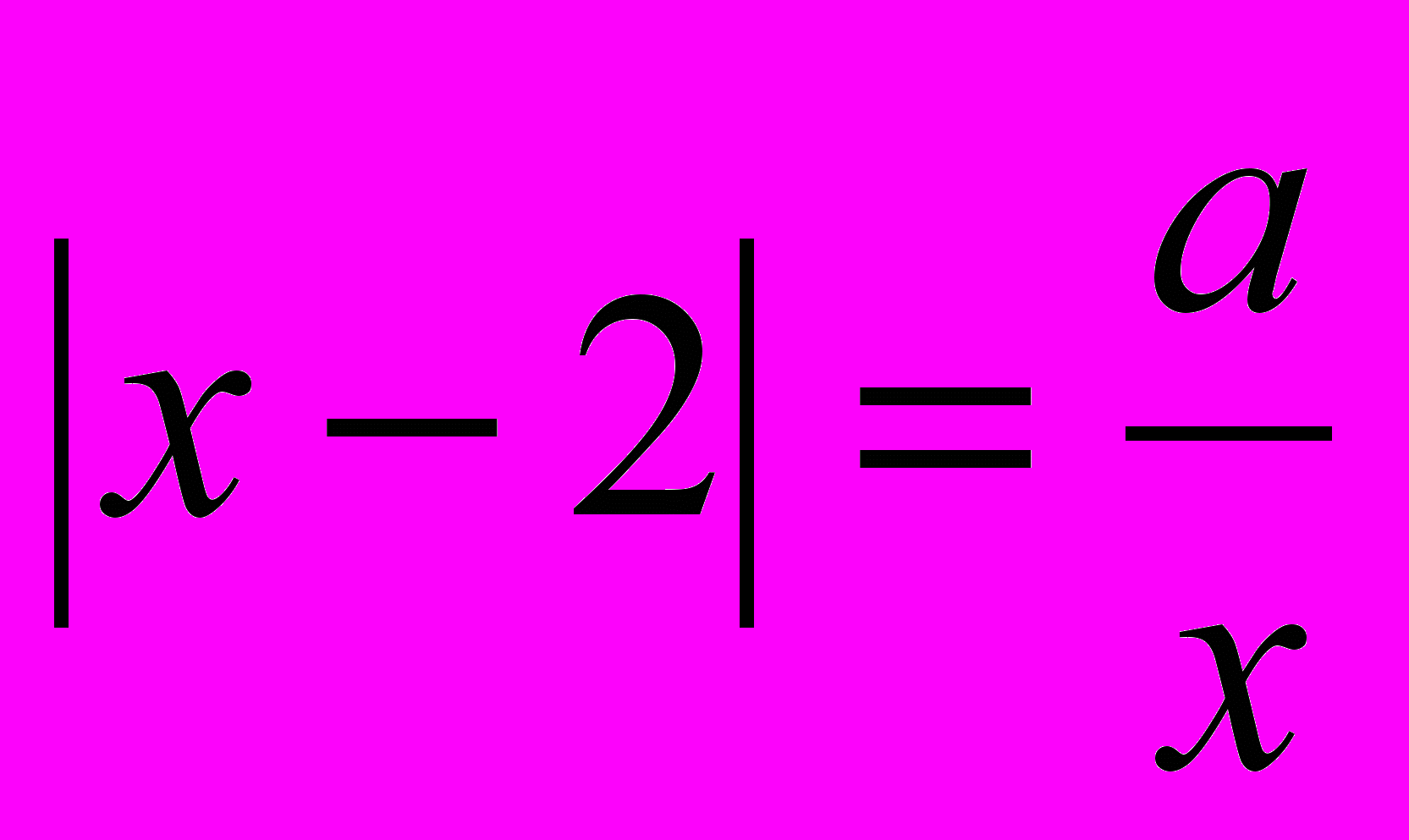 .
.Решение. Заметим, что х не равно нулю. Умножим обе части уравнения на
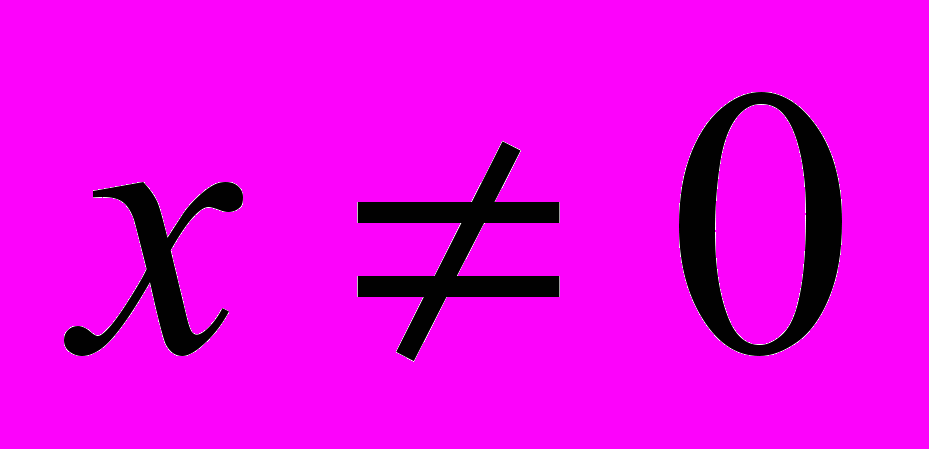 . Получим
. Получим 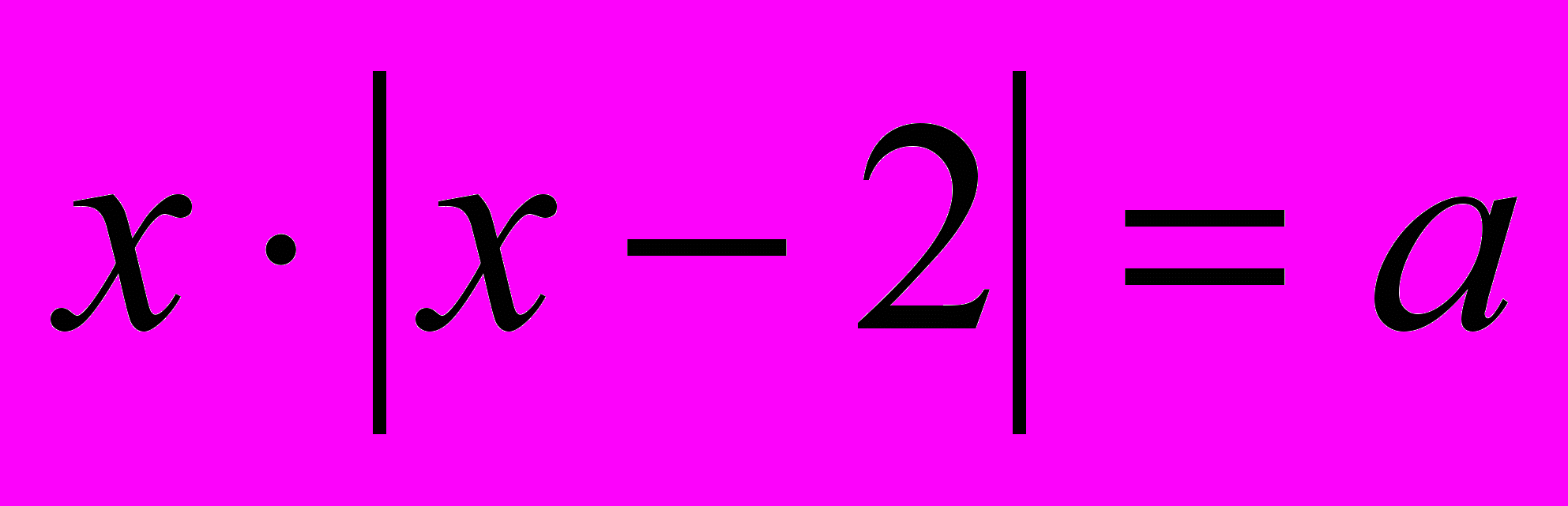
Построим график функции
 .
.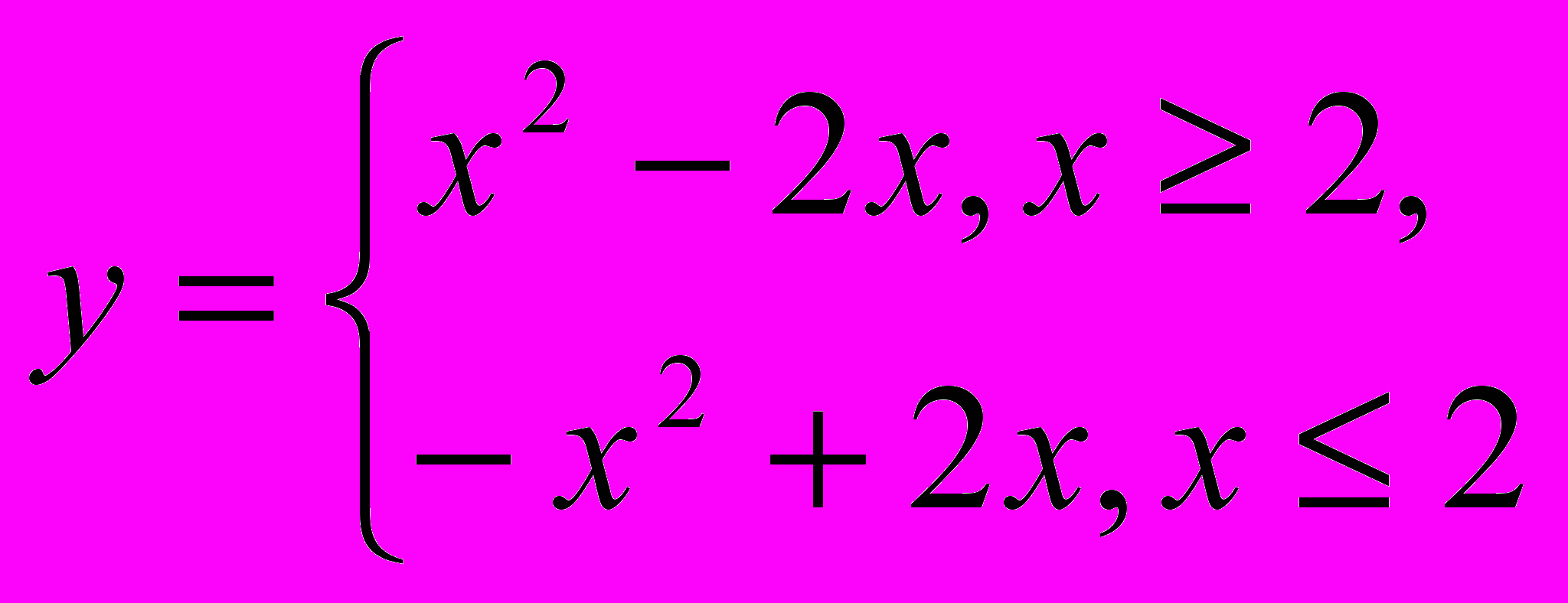
Г
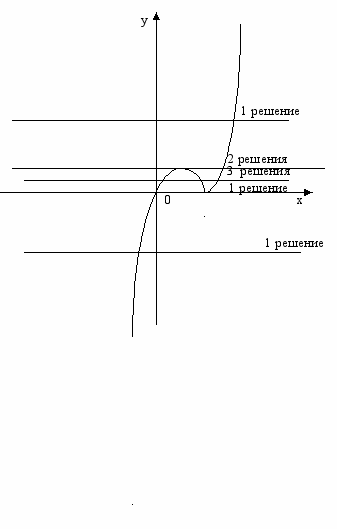 рафиком функции
рафиком функции 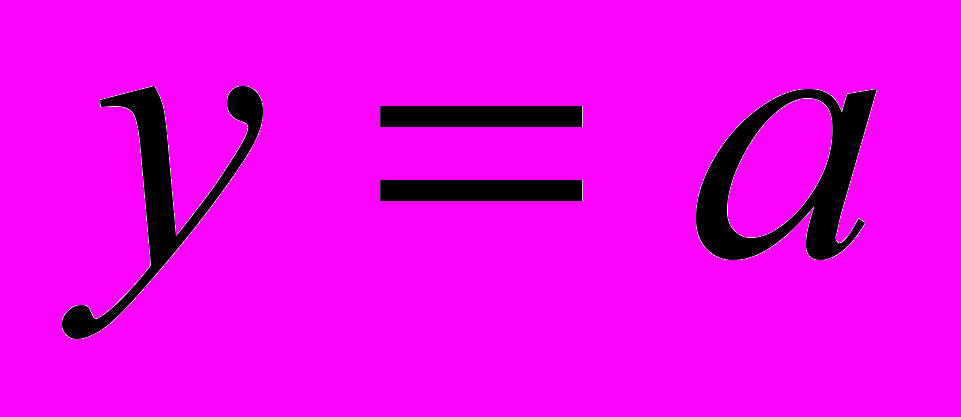 является прямая, параллельная оси ОХ.
является прямая, параллельная оси ОХ. Анализируя графическую иллюстрацию, понятно, что при а=0 одно решение, т.к. одна точка пересечения (не забываем, что х не равен нулю). При а=1 две точки пересечения графика функции и прямой, а значит и два решения. При а<0 получается одна точка пересечения, как и при а>1. Если же
 , то график функции и прямая имеют три точки пересечения.
, то график функции и прямая имеют три точки пересечения.Ответ: при
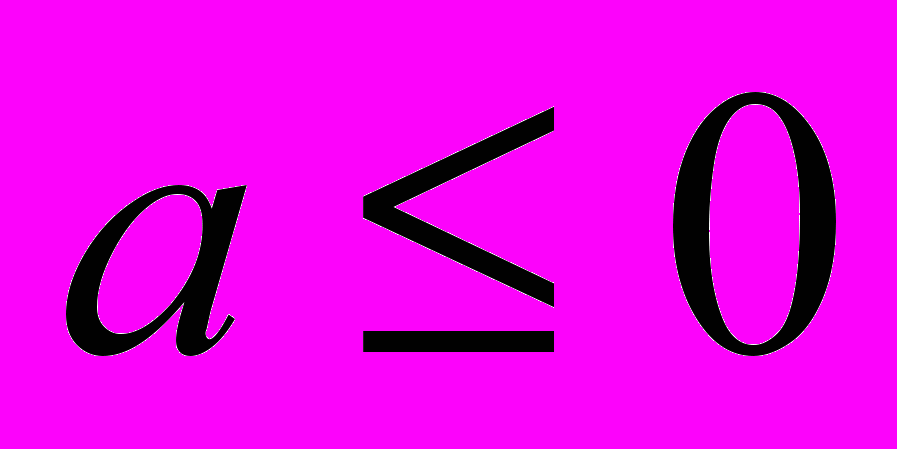 ,
, 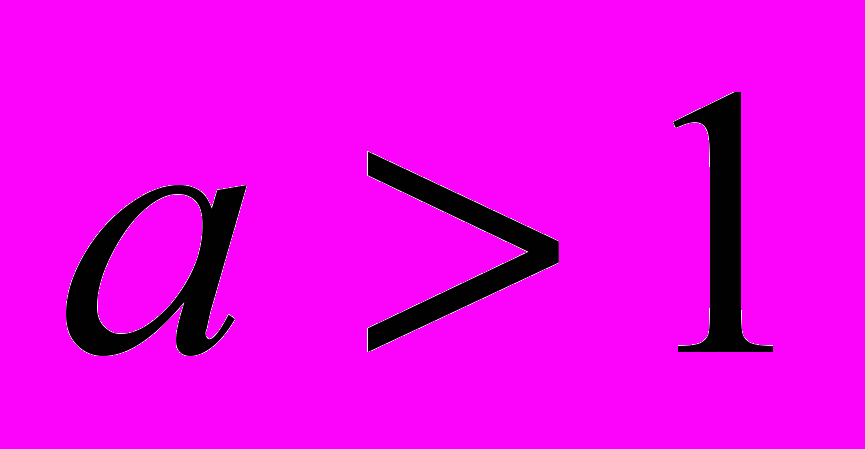 одно решение,
одно решение,при
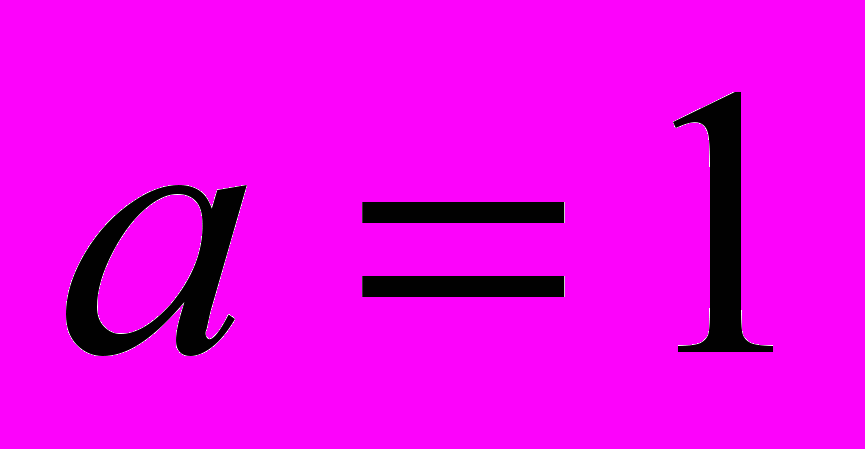 два решения, при
два решения, при  три решения.
три решения.
