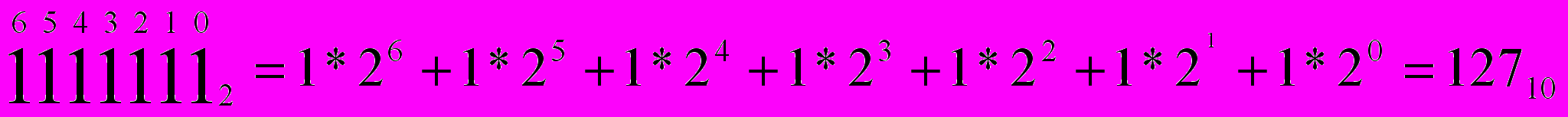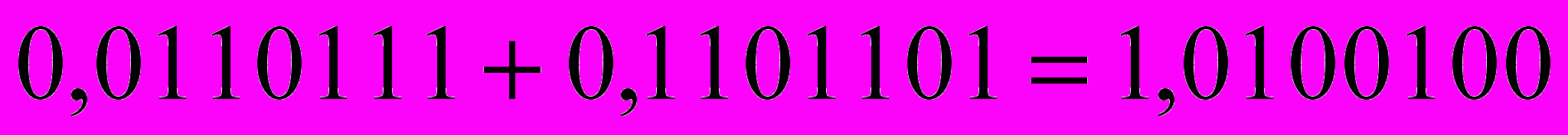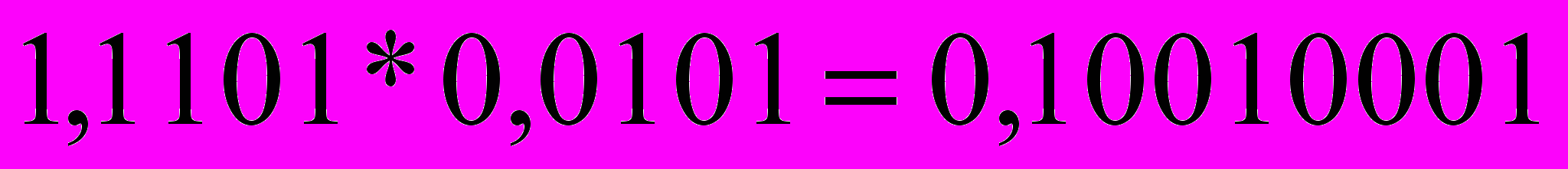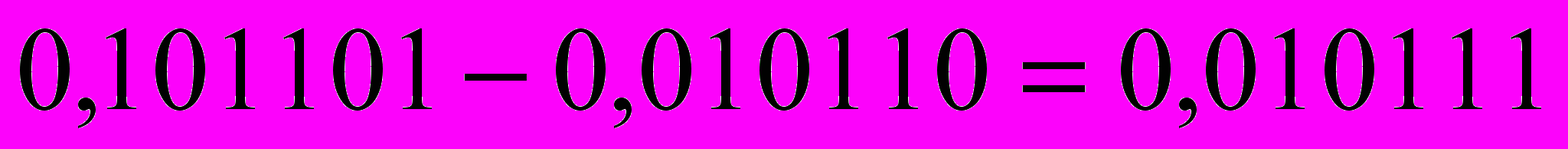Это методическое пособие предназначено для желающих самостоятельно научиться решать задачи по основным разделам предмета на языках Бейсик и Паскаль. Предлагаемая методика включает
| Вид материала | Методическое пособие |
- Учебно-методическое пособие таганрог 2005 ббк 67. 01 Составитель, 578.81kb.
- Курс. 01;Мпк. 01;3 методическое пособие по курсовой работе методика воспитательной, 230.31kb.
- Методика преподавания хореографических дисциплин Учебно-методическое пособие для специальности, 1490.89kb.
- Ниязов Олег Нургалиевич Ниязов О. Н. Н60 методическое пособие, 75.1kb.
- Учебно-методическое пособие Йошкар-Ола, 2009 ббк п 6 удк 636, 3772.57kb.
- Учебно-методическое пособие и ситуационные задачи по урологии для студентов волгоград,, 482.99kb.
- Панасенко Александр Иванович, профессор кафедры органической и биологической химии, 259.01kb.
- Учебное пособие по курсу «управление банковским продуктом» Составитель: к э. н., доцент, 955.86kb.
- Предлагаемая работа представляет собой попытку в краткой форме изложить теоретический, 1296.91kb.
- Российской федерации, 664.65kb.
Введение
Это методическое пособие предназначено для желающих самостоятельно научиться решать задачи по основным разделам предмета на языках Бейсик и Паскаль.
Предлагаемая методика включает:
- теоретический материал;
- задачи к урокам;
- варианты контрольных работ;
- вопросы для самопроверки.
Большое число наглядных, хорошо подобранных примеров облегчает восприятие.
В предложенном пособии предлагаются задачи из различных областей, в частности, обработка текстов, физика, химия, вычислительные задачи, социологические исследования, контроль знаний.
I. Представление информации.
Системы счисления.
I.1.Теоретическое введение.
В компьютерах информация передается в виде последовательности электрических сигналов – импульсов тока или напряжения. Каждой букве и цифре ставится в соответствие цифра «1» или цифра «0». Таким образом, цепочку электрических сигналов можно рассматривать как последовательность. Такая последовательность цифр «0» и «1», называется двоичным кодом или двоичной системой счисления.
Каждая из цифр несет в себе двойную информацию:
- имеет свое собственное значение
- место, которое она занимает в записи числа (т. е. разряд)
Такие системы счисления называются позиционными.
Виды систем счисления:
- десятичная система счисления
- двоичная система счисления
- восьмеричная система счисления
- шестнадцатеричная система счисления
Существует несложный метод перевода чисел из десятичной системы счисления в любую другую систему счисления:
- Разделить исходное число на основание нужной системы. Если частное больше или равно основанию системы, надо снова разделить на основание системы. Эти операции провести до тех пор, пока частное и остатки ни будут соответствовать цифрам нужной системы счисления.
- Зафиксировать остатки и частное.
Чтобы перевести обратно в десятичную систему счисления, надо просуммировать степени основания системы счисления, соответствующие ненулевым разрядам в записи числа.
Чтобы перевести дробную часть числа, записанную Р-ричной системе счисления, умножают в Р-ричной системе на основание системы q. Целая часть произведения будет первой цифрой изображения дроби в q-ричной системе счисления. Дробную часть произведения снова умножают на q. Целая часть произведения будет следующей цифрой записи дроби в q-ричной системе счисления. Процесс продолжается до тех пор, пока дробная часть произведения не будет нулевой или пока не получат требуемое количество знаков записи дроби в q. Целые части, полученные в Р-ричной системе счисления, необходимо записать в q.
Формы представления чисел
| Десятичная система | Двоичная система | Восьмеричная система | Шестнадцатеричная система |
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
Операции с числами двоичной системы счисления
| Сложение | Вычитание | Умножение |
| 0+0=0 | 0-0=0 | 0*0=0 |
| 0+1=1 | 1-0=1 | 0*1=0 |
| 1+0=1 | 1-1=0 | 1*0=0 |
| 1+1=10 | 10-1=1 | 1*1=1 |
Операции с числами восьмеричной системы счисления
-
+
1
2
3
4
5
6
7
10
1
2
3
4
5
6
7
10
11
2
3
4
5
6
7
10
11
12
3
4
5
6
7
10
11
12
13
4
5
6
7
10
11
12
13
14
5
6
7
10
11
12
13
14
15
6
7
10
11
12
13
14
15
16
7
10
11
12
13
14
15
16
17
Операции с числами восьмеричной системы счисления
-
*
1
2
3
4
5
6
7
1
1
2
3
4
5
6
7
2
2
4
6
10
12
14
16
3
3
6
11
14
17
22
25
4
4
10
14
20
24
30
34
5
5
12
17
24
29
36
41
6
6
14
22
30
36
44
52
7
7
13
25
34
43
52
61
П
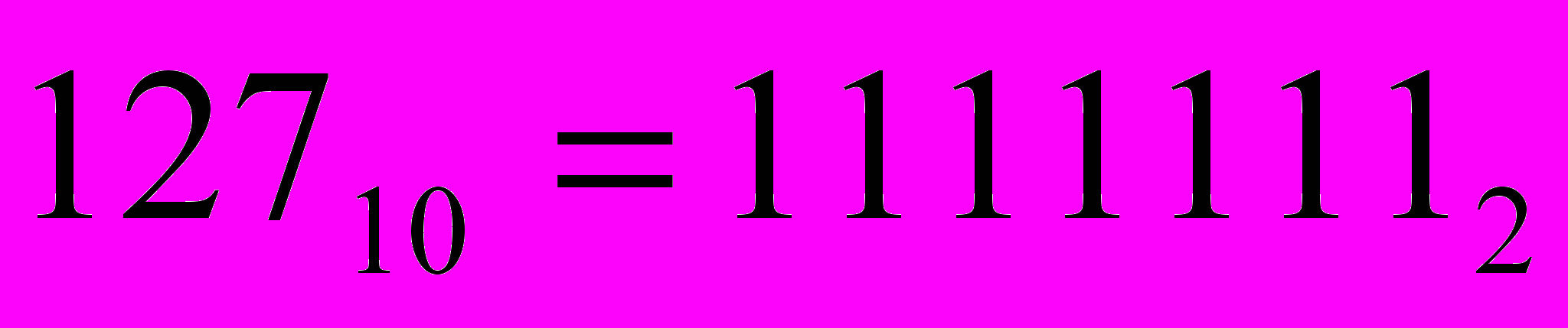
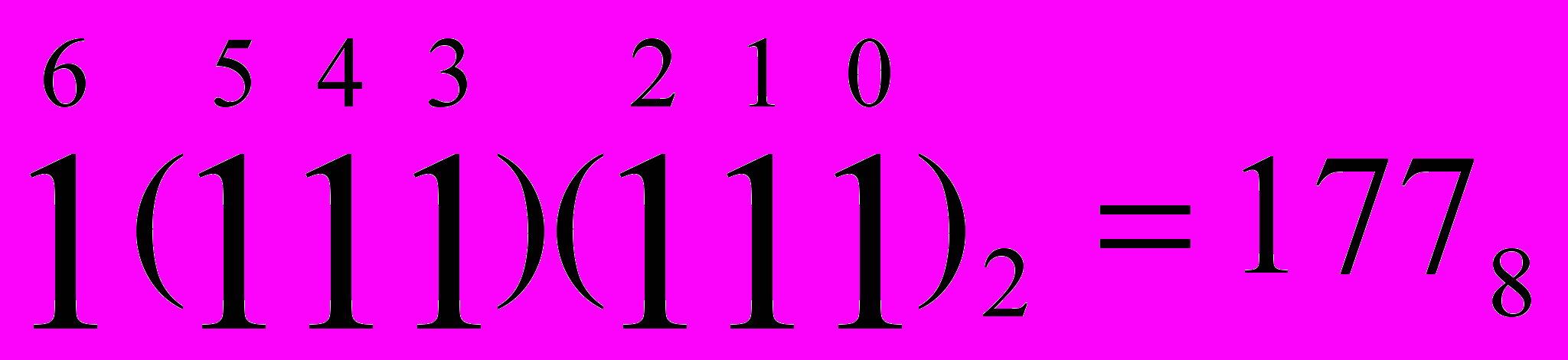
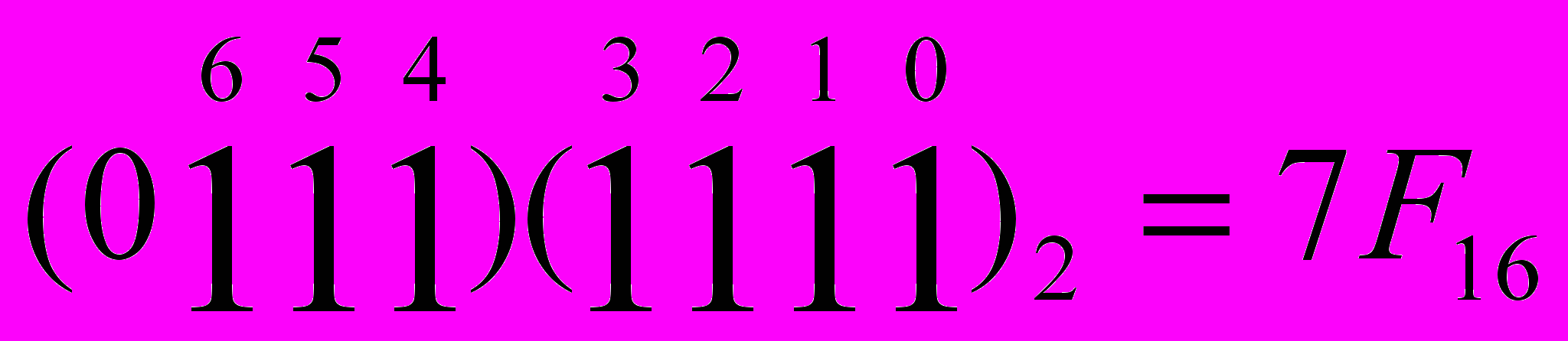ример:
