Это методическое пособие предназначено для желающих самостоятельно научиться решать задачи по основным разделам предмета на языках Бейсик и Паскаль. Предлагаемая методика включает
| Вид материала | Методическое пособие |
СодержаниеII.2.Логические высказывания Высказывания, записанные на II.3.Основные законы математической логики |
- Учебно-методическое пособие таганрог 2005 ббк 67. 01 Составитель, 578.81kb.
- Курс. 01;Мпк. 01;3 методическое пособие по курсовой работе методика воспитательной, 230.31kb.
- Методика преподавания хореографических дисциплин Учебно-методическое пособие для специальности, 1490.89kb.
- Ниязов Олег Нургалиевич Ниязов О. Н. Н60 методическое пособие, 75.1kb.
- Учебно-методическое пособие Йошкар-Ола, 2009 ббк п 6 удк 636, 3772.57kb.
- Учебно-методическое пособие и ситуационные задачи по урологии для студентов волгоград,, 482.99kb.
- Панасенко Александр Иванович, профессор кафедры органической и биологической химии, 259.01kb.
- Учебное пособие по курсу «управление банковским продуктом» Составитель: к э. н., доцент, 955.86kb.
- Предлагаемая работа представляет собой попытку в краткой форме изложить теоретический, 1296.91kb.
- Российской федерации, 664.65kb.
II.2.Логические высказывания
| Высказывания, записанные на естественном языке | Высказывания, записанные на языке алгебры логики |
| 1. Не А; неверно, что А; А не имеет места. | Ā |
| 2. А и В; как А, так и В; не только А, но и В; А вместе с В; А, несмотря на В; А в то время, как В | А В |
| 3 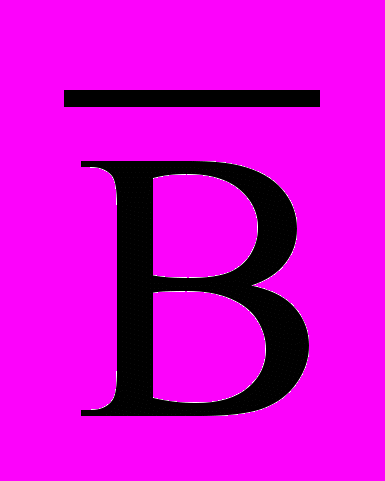 . А, но не В; . А, но не В;не В, а А | А |
| 4. А или В; А или В, или оба. | А В |
| 5 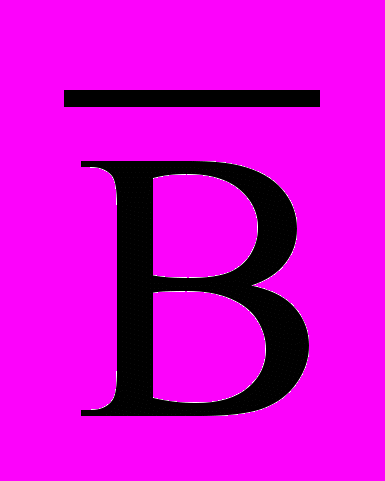 . Либо А, либо В. . Либо А, либо В. | А Ā В |
| 6 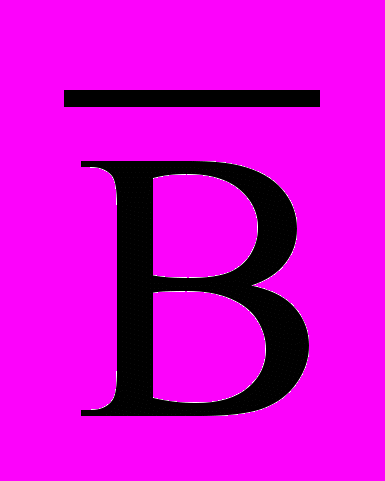  . Либо А, либо В и С . Либо А, либо В и С | А Ā В С |
| 7  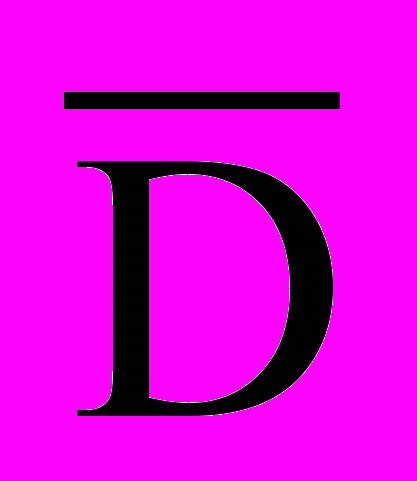 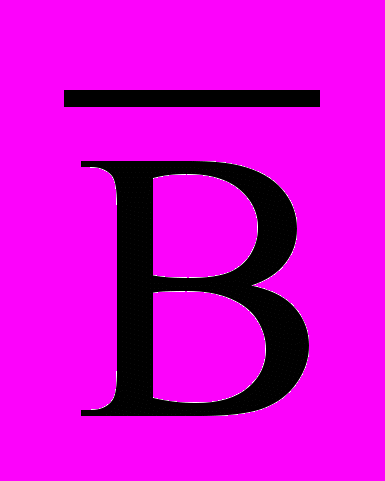 . Либо А и В, либо С и D . Либо А и В, либо С и D | А В Ā С D |
| 8. Если А, то В; А только, если В; А только тогда, когда В; А достаточно для В; А только при условии, что В; В необходимо для А; А значит В; для В достаточно А; А влечет В; для А необходимо В; из А следует В; В тогда, когда А | АВ |
| 9. А эквивалентно В; А тогда и только тогда, когда В; А если и только если В; А необходимо и достаточно для В. | АВ АВ |
II.3.Основные законы математической логики
| Законы алгебры логики | Законы, записанные на языке алгебры логики |
| 1. Закон тождества | АВ |
| 2. Закон противоречия | А Ā=0 |
| 3. Закон исключения третьего | А Ā=1 |
| 4 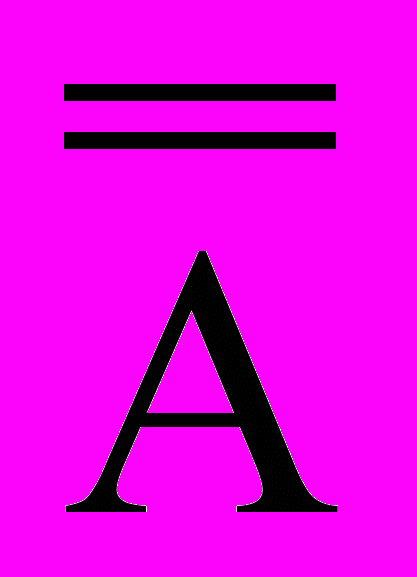 . Закон двойного отрицания . Закон двойного отрицания | А |
| 5. Коммутативный закон | А В = В А А В = В А |
| 6. Ассоциативный закон | (А В)С = А(ВС) = АВС (А ВС = А (ВС) = АВС |
| 7. Дистрибутивный закон | А(ВС) = (АВ) (АС) А (ВС) = (АВ) (АС) |
| 8. Закон поглощения | А(АВ) = А А (АВ) = А |
| 9. Закон идемпотентности | АА = А АА=А |
| 10. Законы исключения констант | А1= 1; А0= А А1=А; А0= 0 |
| 1 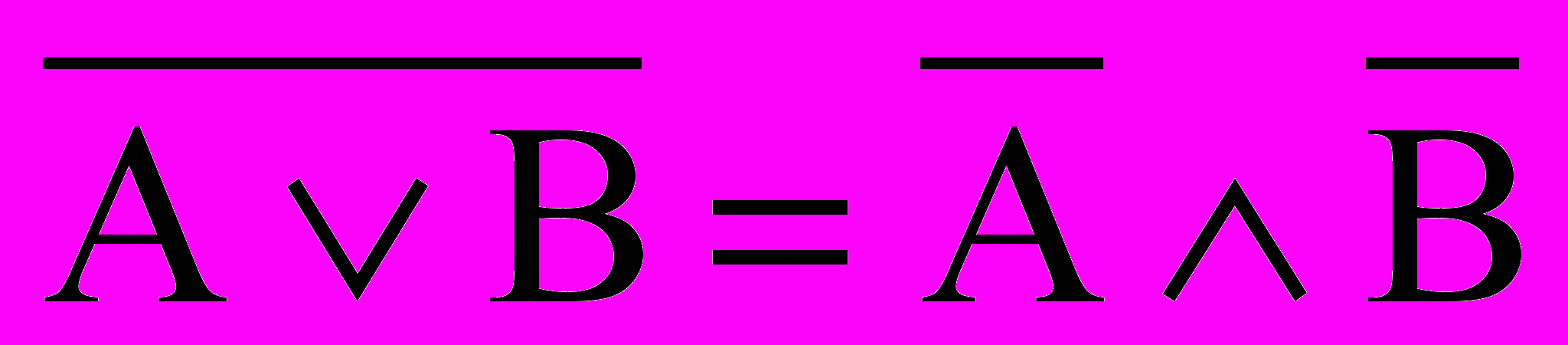 1. Отрицание дизъюнкций 1. Отрицание дизъюнкций | |
| 1 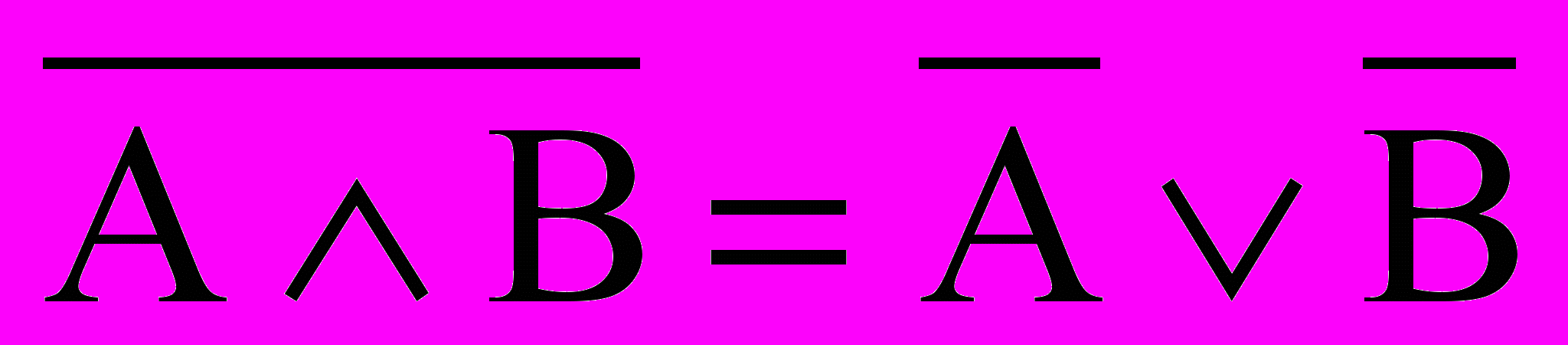 2. Отрицание конъюнкций 2. Отрицание конъюнкций | |
| 13. Закон исключения (или закон склеивания) | (АВ)( ĀВ) = В (АВ)( ĀВ) = В |
