Это методическое пособие предназначено для желающих самостоятельно научиться решать задачи по основным разделам предмета на языках Бейсик и Паскаль. Предлагаемая методика включает
| Вид материала | Методическое пособие |
СодержаниеII.4.Основные понятия математической логики Математическая логика II.5.Задачи уровня II.6.Задачи уровня II.7.Задачи уровня 1 комната - "В этой комнате сидит тигр" |
- Учебно-методическое пособие таганрог 2005 ббк 67. 01 Составитель, 578.81kb.
- Курс. 01;Мпк. 01;3 методическое пособие по курсовой работе методика воспитательной, 230.31kb.
- Методика преподавания хореографических дисциплин Учебно-методическое пособие для специальности, 1490.89kb.
- Ниязов Олег Нургалиевич Ниязов О. Н. Н60 методическое пособие, 75.1kb.
- Учебно-методическое пособие Йошкар-Ола, 2009 ббк п 6 удк 636, 3772.57kb.
- Учебно-методическое пособие и ситуационные задачи по урологии для студентов волгоград,, 482.99kb.
- Панасенко Александр Иванович, профессор кафедры органической и биологической химии, 259.01kb.
- Учебное пособие по курсу «управление банковским продуктом» Составитель: к э. н., доцент, 955.86kb.
- Предлагаемая работа представляет собой попытку в краткой форме изложить теоретический, 1296.91kb.
- Российской федерации, 664.65kb.
II.4.Основные понятия математической логики
| Суждение | - это некоторое высказывание, которое может быть истинным или ложным |
| Утверждение | - это суждение, которое требуется доказать или опровергнуть |
| Рассуждение | - это цепочка взаимосвязанных суждений, фактов, общих положений и умозаключений, получаемых из других суждений по определенным правилам вывода |
| Дедукция | - это рассуждения от общего к частному |
| Индукция | - это рассуждения от частного к общему |
| Логика | - это наука о формах и законах человеческого мышления и, в частности, о законах доказательных рассуждений |
| Математическая логика | - изучает только рассуждения со строго определенными объектами и суждениями, для которых возможно однозначно решить, истинны они или ложны |
II.5.Задачи уровня
- На олимпиаде по ИВТ участвуют Аня, Вика, Саша и Дима. Болельщики высказали следующие предложения:
- первым будет Саша:
- второй будет Аня, Дима будет третий:
- второй будет Аня, Дима будет четвертый.
Оказалось, в каждом предложении одно - истинно, другое - ложно.
Какое место занял каждый ученик?
- перевести на язык алгебры логики:
неверно, что если погода пасмурная, то дождь идет тогда и только тогда, когда нет ветра.
- Алеша, Боря и Гриша нашли в земле сосуд. Алеша предположил, что это греческий сосуд, Боря, что сосуд финикийский, Гриша - не греческий. Каждый мальчик прав только в одном случае.
- Проверить равнозначность рассуждений:
- если бригада отлично выполнит работу, то получит премию;
- бригада не получила премию, значит, ее работа не была отличной.
- Есть два подозреваемых А и В. У следователя имеются показания свидетелей. Первый свидетель утверждает, что А невиновен, второй свидетель утверждает, что В невиновен, третий свидетель утверждает, что показание третьего свидетеля ложно.
Следствие установило, что четвертый свидетель прав. Кто виновен?
- Вычислить значение логического выражения
F=A or B and C, если A=21(16); B=35(10); C=48(8)
- Построить таблицу истинности для логической функции
(
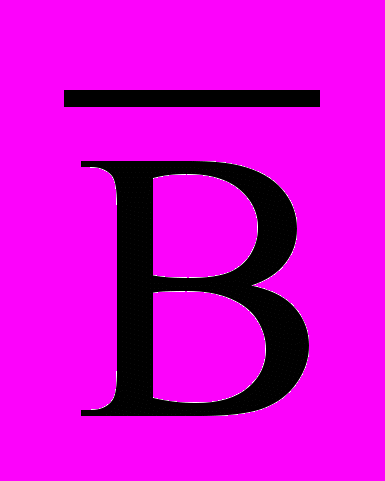А (СВ)) (В+ )8. Дана логическая функция F=(А )( ĀВ)
II.6.Задачи уровня
- Кто из друзей собирает марки? Иван, Петр, Алексей, Николай или Борис?
Если Борис собирает, то Иван и Николай собирают;
если Иван собирает то и Петр собирает;
из двух друзей - Петра и Алексея - собирает только один;
Алексей собирает лишь тогда, когда Николай собирает;
по крайней мере Николай или Борис собирают.
- Кто участвовал в соревнованиях?
Если Иванов не участвовал или Петров участвовал, то Сидоров не участвовал;
если Иванов не участвовал, то Сидоров не участвовал.
- Определить, истинны ли следующие высказывания:
- если 3*3=9, то 33=51;
- если 20 делится на 5, то 20 делится на 4;
- 30 делится на 5 тогда и только тогда, когда 30 делится на 6;
- если 8 делится на 2, то 8 делится на 4;
- если я беру зонт, то идет дождь;
- 25 делится на 5 тогда и только тогда, когда 25 делится на 15.
- Определить значения истинности Т и Р при условии, что:
"Если 3 - простое число, то Т" - истинное высказывание;
"Если Р, то 3 - составное число" - истинное высказывание;
"Если 3 - простое число, то Р" - ложное высказывание;
"Если Т, то 3 - составное число" - ложное высказывание;
"Т↔(4<5)" - истинное высказывание;
"Р↔ (4>5)" - истинное высказывание;
"Т↔ (4>5)" - ложное высказывание;
"Р↔ (4<5)" - ложное высказывание.
II.7.Задачи уровня
- Даны сложные высказывания:
а) если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны;
б) если расстояние от центра окружности до прямой меньше радиуса окружности (d< r), то прямая и окружность имеют две общие точки;
в) я позавтракаю и, если будет тепло, пойду на реку.
Каждое простое высказывание, входящее в сложное, обозначьте буквой и запишите их в символьной форме.
- Дайте обоснованный ответ.
Экзамен сдавали 4 абитуриента А, В, С, Д. Известно:
- для того, чтобы А не сдал или В сдал, необходимо, чтобы С сдал и Д не сдал;
- чтобы С не сдал, а В сдал, необходимо, чтобы А не сдал или Д сдал;
- неверно: чтобы не сдал А, достаточно, чтобы не сдал Д.
Кто сдал экзамен?
- На вопрос, кто из трех абитуриентов А, В, С может работать на персональном компьютере, был получен ответ:
"Если может работать В, то может работать С, но неверно, что если может работать А, то может работать С". Кто из трех абитуриентов может работать на компьютере?
- Узнику были предоставлены на выбор три комнаты. В одной - принцесса, в других - тигры. На дверях комнат таблички с надписями:
1 комната - "В этой комнате сидит тигр";
2 комната - "В этой комнате находится принцесса";
3 комната - "Тигр сидит в комнате два".
Король сообщил узнику, что одно из этих утверждений является истинным. В какой из этих комнат находится принцесса?