Мариупольская общеобразовательная школа I-III ступеней №41 Уроки математики в 6 классе по теме

Вид материала

Содержание

Цель урока
Оценочный лист.
Работа в парах.
Ученики получают на каждую парту алгоритм в виде карточки – схемы.
Урок № 3. Тема: Длина окружности.
Лаборатория раскрытия тайн.
Работа в группах по 4 человека.
Затем отчет групп о проделанной работе и полученном результате.
Лаборатория практиков.

Подобный материал:

1 2 3 4

Урок № 2. Тема: Окружность. Круг.

Цель урока:

Закрепить понятия окружность и круг, их элементы (диаметр, радиус, центр); изучить алгоритм построения треугольника по трем сторонам; формировать навыки исследовательской работы, умения открывать закономерности, находить способы решения задачи в результате обобщения или конкретизации;
Развивать наглядно-образное представление о математических понятиях, внимание, наблюдательность, воображение, кругозор; умение пользоваться чертежными инструментами;
Создавать условия для воспитания навыков сотрудничества, умения слушать и работать в группах, умения анализировать свою деятельность и деятельность своих товарищей, аккуратности и старательности.

Оборудование: учебник А.Г.Мерзляк «Математика 6 класс», циркуль, цветные и простые карандаши, линейка, оценочный лист, демонстрационные карточки.

План урока:

Орг. момент. - 1 мин.
Мотивация урока. - 2 мин.
Актуализация опорных знаний. - 5 мин.
Закрепление знаний и умений.- 7 мин.
Релаксация - 2 мин.
Применений знаний в новых условиях- 10 мин.
Самостоятельная работа. - 7 мин.
Творческое задание. - 5 мин.
Домашнее задание. - 1 мин.
Рефлексия. – 2 мин.
Оценивание. - 1 мин.
Итог урока. – 2 мин

Эпиграф урока:

“Из всех фигур прекраснейшая – круг”

Пифагор

Ход урока.

1. Организационный момент.

(домашнее задание до начала урока проверяется консультантами)

Удивительная страна - Геометрия!

Фигуры и линии в ней живут,

Меряют, чертят и узнают:

Периметр, площадь, длину, ширину,

Диаметр, радиус и высоту.

Скорей собирай своих знаний багаж!

Готовь поскорее циркуль и карандаш!

2. Мотивация урока.

Я приветствую вас, сотрудников научно-исследовательского института. Сегодня на уроке мы продолжим работу в лабораториях по изучению ОГО - опознанных геометрических объектов,- окружности и круга. И нас ожидает очередное заседание. У каждого из вас на столе оценочный лист, где вы будете фиксировать свои достижения, и в конце урока оцените свою работу как сотрудники лабораторий.

Оценочный лист.

Пропуск в лаборатории	Лаборатория построений	Лаборатория исследований	Лаборатория вычислений	Лаборатория творчества	Активность на уроке	Всего баллов	Оценка
6 баллов	5 баллов	4 балла	4 балла	4 балла	1 балл	24 балла	сумму баллов раздели на 2

Девизом к сегодняшнему уроку будут слова древнегреческого математика Фалеса:

- Что есть больше всего на свете? – Пространство.

- Что быстрее всего? – Ум.

- Что мудрее всего? – Время.

- Что приятнее всего? – Достичь желаемого.

Хочется, чтобы каждый из вас на сегодняшнем уроке достиг желаемого результата.

3. Актуализация опорных знаний.

И снова, чтобы получить пропуск в лаборатории НИИ, вам необходимо пройти испытание.

Задание – разгадать кроссворд. Работа в парах.

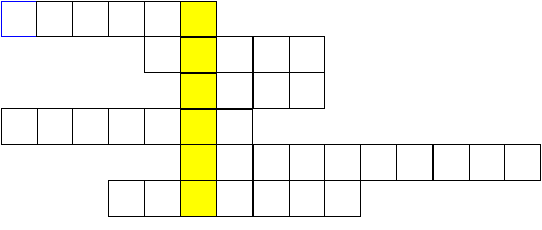
1) ОА - … (радиус)

2) О - … (центр)

3)… (круг)

4) АВ - … (диаметр)

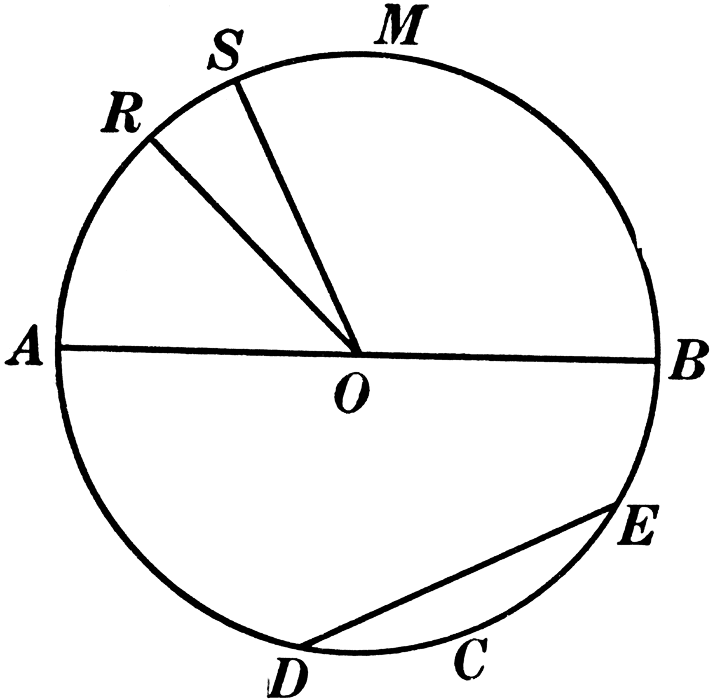
5) … - (окружность)

6) Название инструмента для вычерчивания окружностей (циркуль)

Какое слово получилось по вертикали? (сектор)

Сектор – это часть круга, ограниченная двумя радиусами.

Выполняется самопроверка. Максимальная оценка – 5 баллов. Результаты заносятся в оценочный лист.

4. Закрепление знаний и умений.

Лаборатория построений.

Пропуск получен и отправляемся в лабораторию построений. Сейчас вы будете работать в группах. Распределите позиции и пристегните бейджики:

- Организатор (организует работу в группе и следит за выполнением заданий и позиций в группе).

- Теоретик (человек, который знает теоретический материал)

- Докладчик (человек, докладывающий у доски результат работы группы).

- Хранитель времени (человек, который следит за временем, отведенным на работу в группе).

Приступайте к работе. Девиз работы: «Научился сам - научи другого».

Начертите окружность.
а) Отметить центр.
б) Отметить точку на окружности.
в) Соединить отрезком. Что получили?
г) Измерить и записать.
д) Провести диаметр, не измеряя, чему он равен.
Построить окружность с центром в точке Р, проходящую через точку Т. Провести радиус , чему он равен? Чему равен диаметр?
Построить окружность с центром в точке А и радиусом, равным расстоянию между точками М и N.
Построить окружность с диаметром 6см. Чему равен радиус?
Как найти центр круга? (у каждой группы есть модель круга из бумаги).

Учитель наблюдает за работой групп. Затем - оценивание в группе. Максимум – 5 баллов. Результаты заносятся в оценочный лист.

5. Релаксация.

Приглашаю вас в комнату психологической разгрузки.

Сядьте удобнее, закройте глаза. Представьте, что вы лежите на красивой поляне. Сделайте глубокий вдох и медленно делайте выдох, пусть всё напряжение уходит. Вокруг зелёная трава, вдалеке большой лес, поют птицы. Вы чувствуете, какая тёплая земля. Светит яркое солнышко. Один тёплый лучик упал на ваше лицо. Лицо стало тёплым и расслабилось. А луч света пошёл гулять дальше по вашему телу. Вам хорошо и приятно греться на солнышке. Вокруг зелёная трава, вдалеке большой лес, поют птицы. Вы чувствуете, какая тёплая земля. Земля вам даёт силу и уверенность. Сделайте глубокий вдох и медленно делайте выдох, пусть всё напряжение уходит. Ещё раз вдох и выдох... На счёт 5 вы вернётесь обратно. 1 – вы чувствуете, как хорошо лежать и отдыхать. 2,3,4 – у вас открываются глаза, 5 – вы возвращаетесь в НИИ полные сил и уверенности.

6. Применений знаний в новых условиях

Лаборатория исследований.

В курсе геометрии 7 класса вы познакомитесь с задачами на построение с помощью циркуля и линейки.

А сегодня в лаборатории исследований я предлагаю вам изучить алгоритм построения треугольника с данными сторонами.

Построить треугольник с данными сторонами a, b, c. (Учитель демонстрирует построение на доске).

Решение.

С помощью линейки проводим произвольную прямую и отмечаем на ней точку B.

Раствором циркуля, равным a, описываем окружность с центром B и радиусом a. Пусть С точка пересечения окружности с прямой.

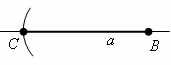
Теперь раствором циркуля, равным с, описываем окружность из центра B.

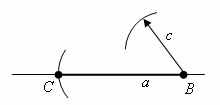
Теперь раствором циркуля, равным b, описываем окружность из центра С. Пусть A – точка пресечения этих окружностей.

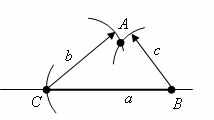
Проведем отрезки CA и BA. Полученный Δ ABC имеет стороны, равные a, b и с.

Ученики получают на каждую парту алгоритм в виде карточки – схемы.

А теперь выполните задание, работая в парах. Построить треугольник со сторонами 5 см, 6см, 4см.

Учитель консультирует тех, у кого есть затруднения при выполнении данного задания.

За данную работу оцените себя сами. Максимум – 4 баллов. Результаты заносятся в оценочный лист.

7. Самостоятельная работа.

Лаборатория вычислений.

А сейчас вас ждет очередное испытание в лаборатории вычислений.

Решите самостоятельно № 729, 731.

Затем – взаимопроверка. Сверка с верным решением, записанным на скрытой доске. Максимум – 4 баллов. Результаты заносятся в оценочный лист.

8. Творческое задание.

Лаборатория творчества.

Приглашаю вас посетить лабораторию творчества.

Окружность и круг всегда привлекали к себе внимание художников и архитекторов. С использованием окружностей можно получить очень красивые узоры. И сейчас мы создадим свою картину из кругов. ( Ученики рисуют самостоятельно картинку из кругов с помощью циркуля. Можно использовать цветные карандаши).

После этого демонстрируются картины «Круги». Оценивается всем классом и учителем. Максимум – 4 баллов. Результаты заносятся в оценочный лист.

9. Домашнее задание.

Решить № 722, 735(2), 738.

Дома вы можете также проявить свое творчество, создав картину – аппликацию из кругов. Это дополнительное задание и будет оцениваться отдельно.

10 Рефлексия.

В завершении урока поделитесь своими впечатлениями о нашем заседанием НИИ по исследованию ОГО - опознанных геометрических объектов.

Упражнение «Микрофон». (Ученики по очереди дают аргументированный ответ на один из вопросов на украинском языке).

На уроке я работал активно / пассивно
Своей работой на уроке я доволен / не доволен
Урок для меня показался коротким / длинным
За урок я не устал / устал
Мое настроение стало лучше / стало хуже
Материал урока мне был полезен / бесполезен

интересен / скучен

Домашнее задание мне кажется легким / трудным

интересно / не интересно

11. Оценивание.

Наше заседание подходит к завершению и пора подвести итоги. За активность на уроке вы получите 1 балл, который занесете в оценочный лист. Сумму всех заработанных баллов разделите на 2 и вы получите свою оценку за урок.

(Ученики подсчитывают баллы и сдают учителю оценочные листы).

12. Итоги урока.

Очередное заседание НИИ по исследованию ОГО - опознанных геометрических объектов закрыто. Сегодня мы изучали окружность и круга, познакомились с алгоритмом построения треугольника по трем сторонам с помощью циркуля и линейки, создавали «шедевры» из кругов. И, я надеюсь, эти знания вам пригодятся в дальнейшем.

Мы еще раз убедились в совершенстве окружности и круга. Недаром древние греки считали окружность совершеннейшей и «самой круглой» фигурой. И в наши дни в некоторых ситуациях, когда хотят дать особую оценку, используют слово «круглый», которое считается синонимом слова «полнейший»: круглый отличник, круглый сирота и т.п. Также считают и колесо – одно из самых замечательных изобретений человека. Наверное, весь секрет кроется в свойствах удивительной линии – окружности.

Кругла планета наша, яблоко кругло

И сердце кругло, круглота не зла,

Округлыми глазами смотрит кукла…

Я круг люблю, он выдуман хитро:

В нем нет конца,

Сыщи-ка в нем огрехи…

Недаром кругу поклонялись греки.

Урок № 3. Тема: Длина окружности.

Цель урока:

Установить зависимость между длиной окружности и её диаметром, вывести формулу длины окружности; получить значение числа π в ходе выполнения практической работы; научить применять изученные формулы при решении задач;
Активизировать познавательный интерес к предмету, развивать творческий потенциала учащихся, умение поиска информации через различные источники, сравнивать и обобщать полученные результаты, преодолевать трудности, развивать устную и письменную математическую речь;
Формировать волевые качества личности, навыки работы в парах, группе; воспитывать культуру общения, трудолюбие и самостоятельности.

Оборудование: учебник А.Г.Мерзляк «Математика 6 класс», циркуль, цветные и простые карандаши, нитки, модели 3 кругов, линейка, демонстрационные карточки, цветные карточки для рефлексии.

План урока:

Орг. момент. - 1 мин.
Мотивация урока. - 2 мин.
Актуализация опорных знаний. - 5 мин.
Изучение нового материала. - 15 мин.
Физкультминутка. - 1 мин.
Первичное закрепление изученного материала. - 10 мин
Самостоятельная работа. - 7 мин.
Рефлексия. - 1 мин.
Домашнее задание – 1 мин.
Итог урока. – 2 мин.

Ход урока.

1. Организационный момент.

Эмоциональный настрой на урок.

Дети, вам тепло? (Да!)

В классе светло? (Да!)

Прозвенел уже звонок? (Да!)

Уже закончился урок? (Нет!)

Только начался урок? (Да!)

Хотите учиться? (Да!)

Значит можно всем садиться!

2. Мотивация урока.

Приветствую всех на очередном заседании НИИ, посвященному изучению длины окружности, где мы продолжим изучение ОГО – нами опознанных геометрических объектов, окружности и круга.

Математика - наука древняя, интересная и полезная. Слово “математика” пришло к нам из древнегреческого языка, что означает “учиться”, “приобретать знания”. Математика помогает нам познавать и совершенствовать тот мир, в котором мы живем. Запуск на орбиту спутников, строительство автострад, вождение поездов, даже оклейка стен обоями,– все это и многое другое было бы просто невозможно без математических расчетов. Математика поможет нам научиться мыслить яснее и последовательнее.

Сегодня мы с вами в очередной раз убедимся в этом, и очень хочется, чтобы каждый из вас для себя сделал хотя бы небольшое, но открытие.

А девизом нашего урока будет высказывание ученого А. Маркушевича: «Через математические знания, полученные в школе, лежит широкая дорога к огромным, почти необозримым областям труда и открытий».

3. Актуализация опорных знаний.

Лаборатория теоретиков.

Фронтальная работа:

Заполните пропуски:

1. 5,64 ≈ 5,…

2. 2,477 ≈ 2,4…

3. 8,6…9 ≈ 8,65

4. 1,735 ≈ 1,…

5. 2,…6 ≈ 2,6

Найти отношение чисел:

а) 1

: 8; б) 0,2: 0,7; в) 4: 140; г) 0,4: 1,4; д) 4: 20.

Вычислите: 2

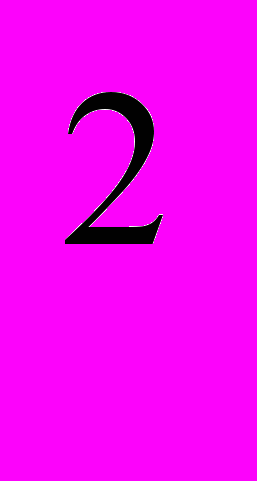, 4

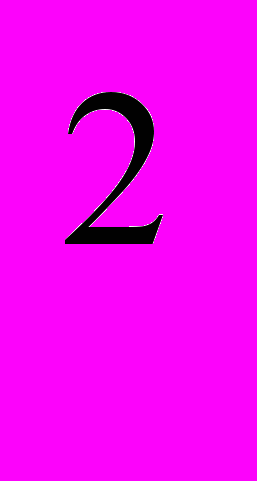, 7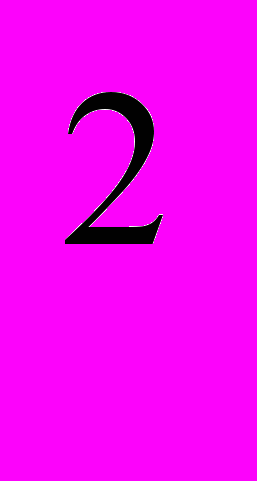

_.

По чертежу ответить на вопросы:

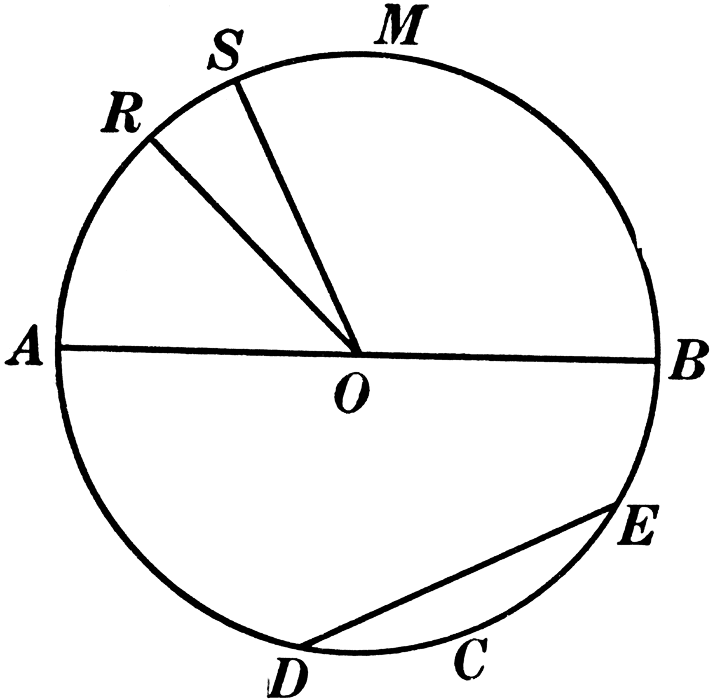
Какая геометрическая фигура изображена на чертеже?
Назовите центр окружности.
Чем является отрезок АВ?
Есть ли на чертеже еще диаметры?
Чем является отрезок ОВ?
Есть ли на чертеже еще радиусы?
Как называется отрезок DE?
Есть ли на чертеже хорды?
Какой отрезок называется хордой?
Является ли хордой диаметр?
Можно ли измерить длину радиуса?
С помощью какого измерительного прибора это можно сделать?
Какими единицами измерения будет выражен результат?
С помощью какого инструмента можно построить окружность?

4. Изучение нового материала.

Создание проблемной ситуации.

Давайте измерим длину окружности. В чем трудность? Да, к сожалению, специального прибора для измерения длины окружности нет. Но и это не останавливало человека. Предложите свой способ измерения длины окружности (обсуждение в группах).

Ниткой, веревкой удобно пользоваться для измерения длины окружности малого радиуса. А как быть, если требуется измерить длину окружности предмета круглой формы большого размера, например, трубы завода? С помощью нитки и веревки это сделать можно, но весьма трудоемко и результат таких измерений может быть неточным.

Лаборатория раскрытия тайн.

Приглашаю вас в лабораторию раскрытия тайн.

Давайте попробуем вывести формулу, по которой можно было бы вычислить длину окружности, зная ее радиус.

Работа в группах по 4 человека.

У вас на столах лежат 3 круга с отмеченным центром, а также ниточка. Как можно измерить длину окружности, которая является границей круга? (С помощью ниточки). Измерьте, пожалуйста, и запишите результат измерения в таблицу. С помощью линейки измерьте диаметр круга и результат измерения занесите в таблицу.

Найдите отношение длины окружности к ее диаметру. Округлите результат до сотых. Результаты измерений заносятся в таблицу:

№ опыта	Длина окружности (С)	Диаметр (d)	С: d
1
2
3

Затем отчет групп о проделанной работе и полученном результате.

Если измерения выполнены достаточно точно, то у всех должно получиться значение, приблизительно равное 3,1-3,2. Это число математики обозначают буквой π (пи).

Историческая справка.

Первым ввел обозначение отношения длины окружности к диаметру современным символом π английский математик Джонсон в 1706 г. В качестве символа он взял первую букву греческого слова «периферия», что в переводе означает «окружность». Введенное Джонсоном обозначение стало общеупотребительным после опубликования работ Эйлера, который воспользовался введенным символом впервые в 1736 году.

А почему это число придумали обозначать буквой π, вместо того, чтобы записывать его цифрами? (Ответы учащихся).

К сожалению, такое число π можно записать только с помощью бесконечной десятичной дроби. Ни одно натуральное число, ни одна десятичная дробь для этого не годится. Тут необходимо особое число – из тех, что называется несоизмеримым с единицей.

Число π— это бесконечная десятичная дробь. Первые восемь цифр этого числа: 3,1415926. В практических расчетах редко бывает нужно знать более трех-пяти цифр числа π.

Если со временем вы их забудете, то задайте вопрос:

Что	я	знаю	о	кругах?
3	1	4	1	6

Для запоминания большего числа знаков существуют забавные поговорки и стихи. Например, такие:

Вот и Миша, и Анюта прибежали

Пи узнать число они желали.

Треба лише постаратися і запам'ятати все як є:

три, чотирнадцять, п'ятнадцять, дев'яносто два і шість.

Историческая справка.

Еще в древности людям были известны многие геометрические фигуры, в том числе окружность и круг. Об этом свидетельствуют археологические раскопки. Еще тогда приходилось решать задачи на вычисление длины окружности. Сейчас известно, что значением числа π в разные времена считали различные числа. Так, в Древнем Египте (ок. 3500 лет назад) считали π = 3,16; древние римляне полагали, что π= 3,12. Все эти значения были определены опытным путем. Великий ученый Древней Греции Архимед определил, что значение π находится в следующих пределах 3

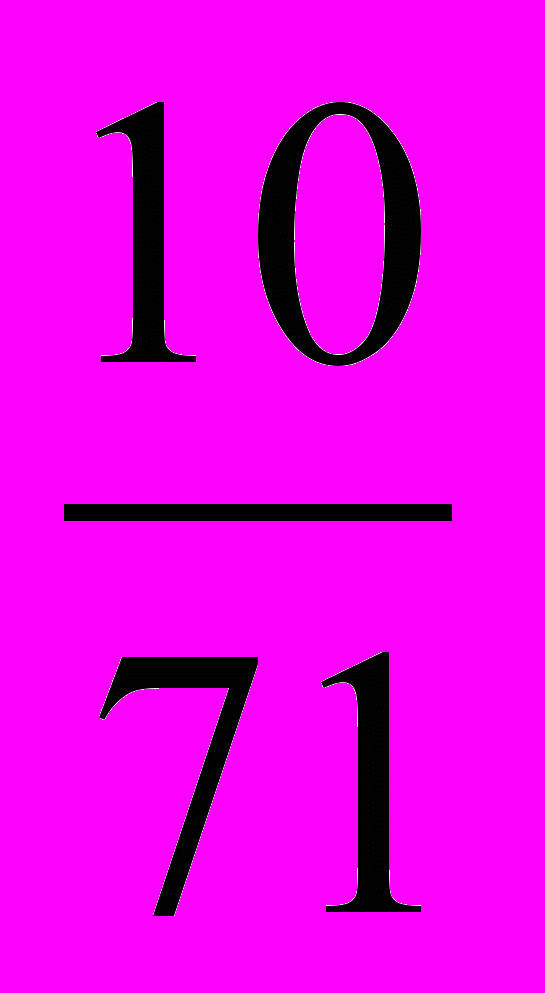<π<3

. С помощью современных электронно – вычислительных машин число π было вычислено точностью до миллиона знаков после запятой.

Итак, С: d= π, тогда С = π d.

Так как d=2r, то получаем еще одну формулу для вычисления длины окружности:

С = 2 π r.

Вывод: длина окружности вычисляется по формуле

С = 2 π r = π d, где π = 3,14.

Запишите в тетрадь формулы длины окружности.

5. Физкультминутка.

Время тратить мы не будем, поднимаем кверху руки,

Опускаем их на плечи, продолжаем дальше вместе.

Поднимаем, опускаем, от урока отдыхаем.

Руки вверх над головой, смотрим все перед собой,

Позвоночник выпрямляем, локти сводим, распрямляем,

Организм оздоровляем, кислородом наполняем.

Чтобы ноги поразмять, будем дружно приседать,

Встали, кверху потянулись, повторили, улыбнулись.

Заряд бодрости поможет нам опять урок продолжить.

6. Первичное закрепление изученного материала.

Приглашаю вас в лабораторию практиков.

Лаборатория практиков.

Работа у доски:

Задача 1. Вычислить длину окружности, диаметр которой известен (принять π =3,14).

d	3 дм	10 см	0,1 м
C

Задача 2. Вычислить длину окружности, радиус которой известен: (принять π =3,14).

R	5 дм	50 см	0,05 м
C

Blog

Мариупольская общеобразовательная школа I-III ступеней №41 Уроки математики в 6 классе по теме

Содержание