Министерство образования и науки Российской Федерации Ростовский Государственный Университет

Вид материала

Документы

Содержание Формальное решение задачи рационального разбиения на сегменты коммутируемой сети ethernet с множественными резервными каналами Ростовский государственный университет, ЮГИНФО

Подобный материал:

• Российской Федерации Министерство образования и науки Российской Федерации Государственный, 343.55kb.
• Программа 1-3 октября 2003 года Москва Организаторы и спонсоры Министерство образования, 141.3kb.
• Министерство образования и науки российской федерации федеральное агентство по образованию, 32.48kb.
• Российской Федерации Читинский государственный университет иппк рабочая программа, 177.68kb.
• Министерство образования и науки российской федерации тамбовский государственный университет, 39.54kb.
• Министерство образования и науки российской федерации тамбовский государственный университет, 60.77kb.
• Министерство образования и науки российской федерации тамбовский государственный университет, 59kb.
• Министерство образования и науки российской федерации российский государственный социальный, 183.27kb.
• Н. А. Быковой Контрольные вопросы, 24.48kb.
• Министерство образования и науки российской федерации программ, 381.21kb.

ФОРМАЛЬНОЕ РЕШЕНИЕ ЗАДАЧИ РАЦИОНАЛЬНОГО РАЗБИЕНИЯ НА СЕГМЕНТЫ КОММУТИРУЕМОЙ СЕТИ ETHERNET С МНОЖЕСТВЕННЫМИ РЕЗЕРВНЫМИ КАНАЛАМИ

Букатов А.А., Букатов С.А.

Ростовский государственный университет, ЮГИНФО

baa@rsu.ru, sbukat@aaanet.ru

В настоящей работе рассматривается формальное решение задачи оптимального разбиения на сегменты коммутируемой Ethernet сети с множественными резервными каналами, рассмотренной авторами в [1]. В этой задаче требуется разбить коммуникационный граф сети (граф связей между коммуникационными узлами) на сегменты, отделенные друг от друга маршрутизаторами (коммуникационным оборудованием 3 уровня) и не содержащие замкнутых контуров, включающих более 9 узлов. Это требуется для обеспечения условий работоспособности протокола STP (см, напр. [2]). Оптимизируемым параметром является стоимость (количество) требуемых для выполнения такого разбиения маршрутизаторов.

В качестве исходных данных задачи служат:

сеть передачи данных, заданная парой (M,L).

Здесь – множество узлов магистральной сети, в которых установлено коммуникационное оборудование;

Связи между узлами заданы матрицей,



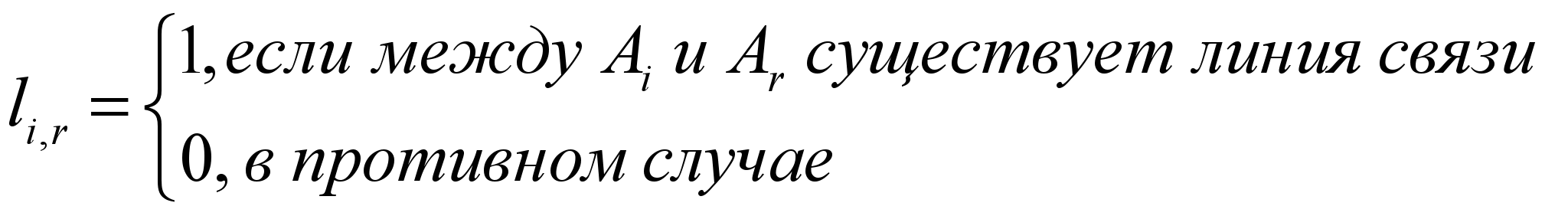
Необходимо определить количество сегментов – n и выполнить разбиение узлов по сегментам S_j 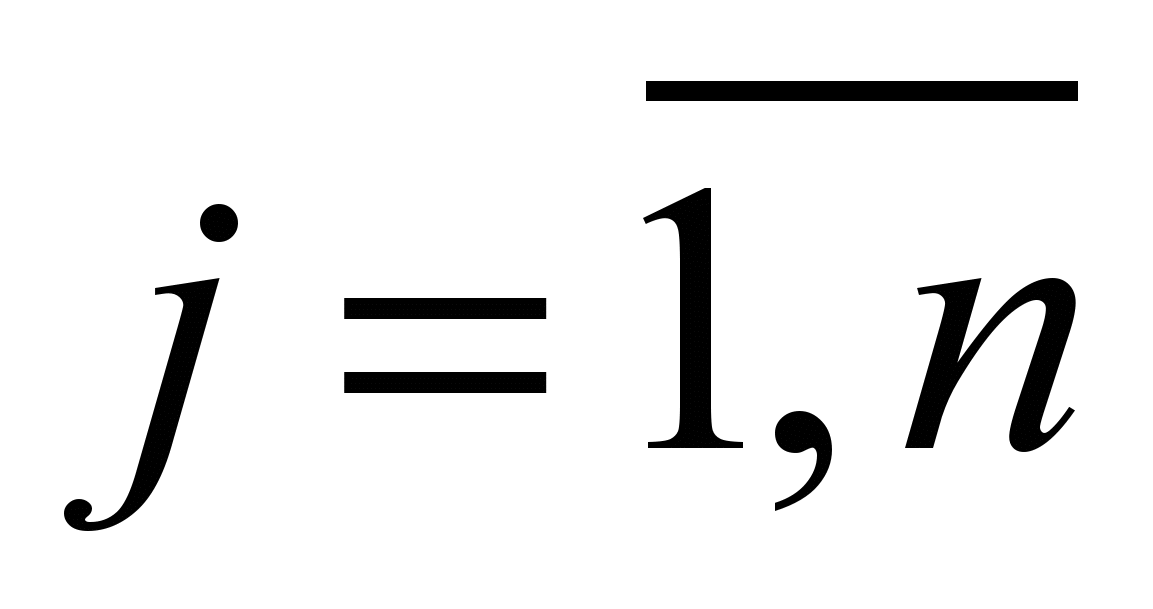, а также указать места расположения коммутационного оборудования третьего уровня (КО 3) – маршрутизаторов либо коммутаторов третьего уровня – в целях обеспечения работоспособности протокола STP [2] и минимизации затрат на КО-3.

Для построения модели вводятся следующие переменные:

x_ij – задаёт порядок распределения узлов по сегментам: x_ij =1, если i-й узел включен в j-й сегмент и x_ij=0 в противном случае, ,;

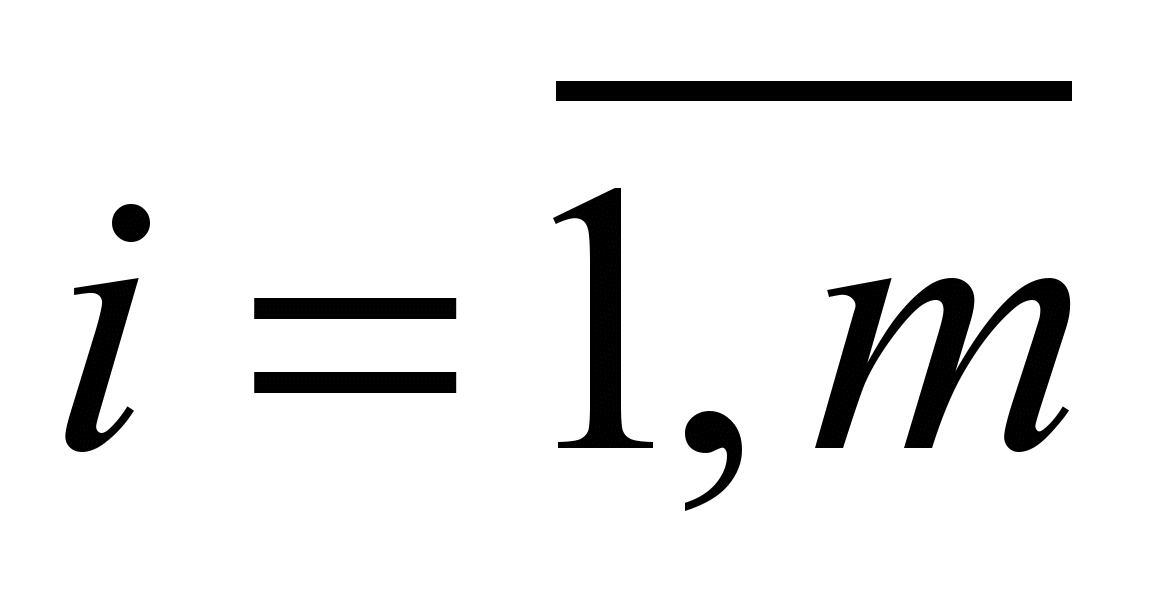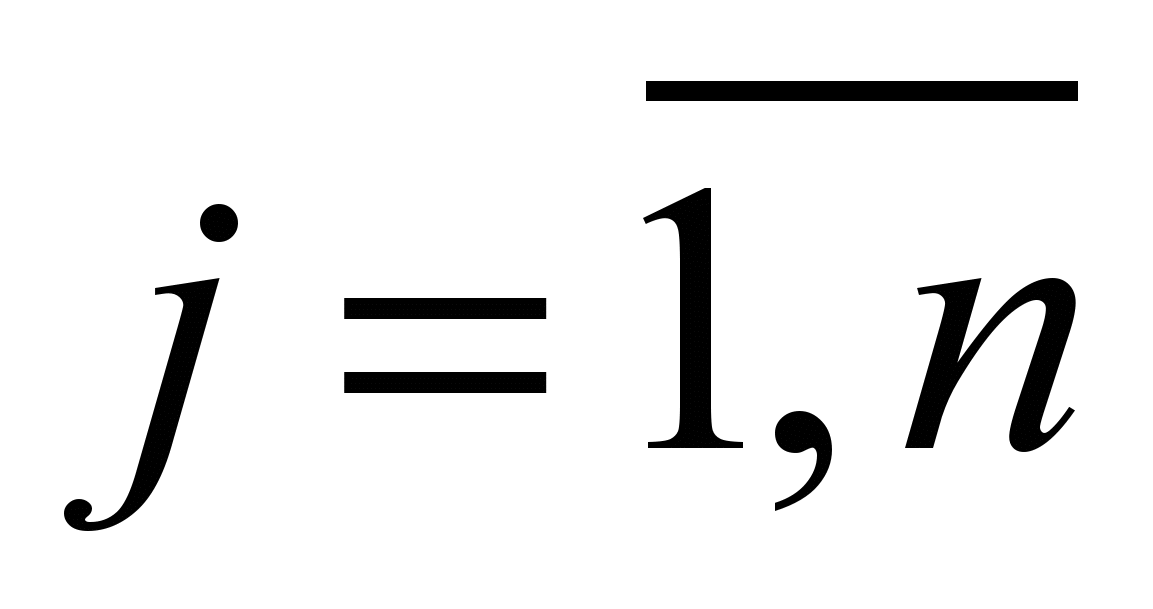z_i – выполняет определение задействованных мест размещения КО-3: z_i=1, если i–е место используется для размещения КО-3 и z_i=0 – если место в данном варианте топологии не используется, .

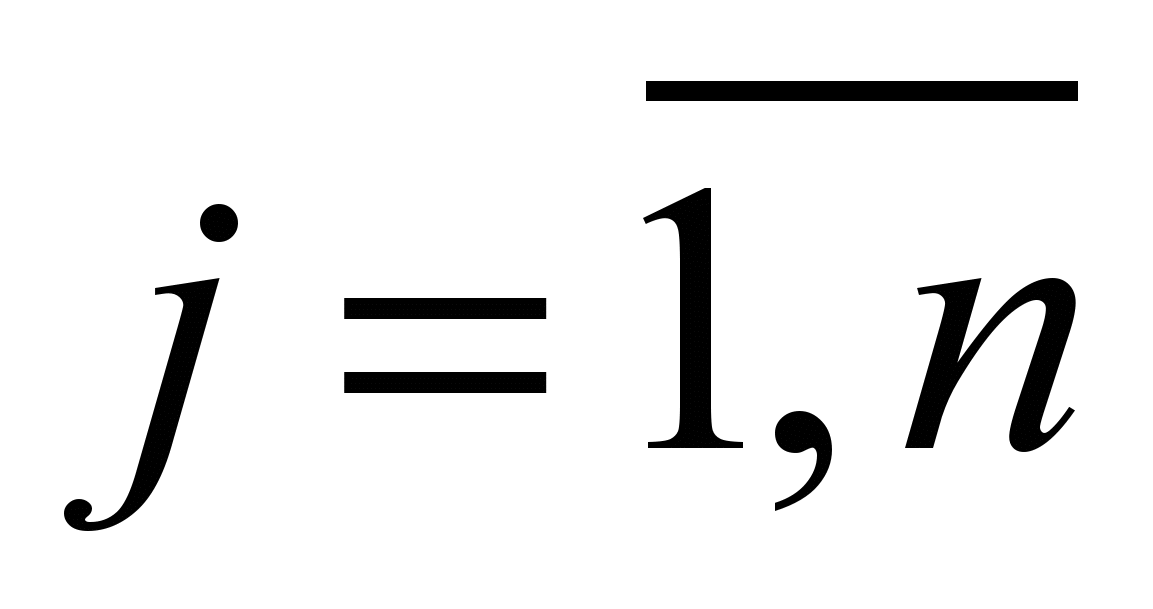Ограничениями задачи служат:

q₁: 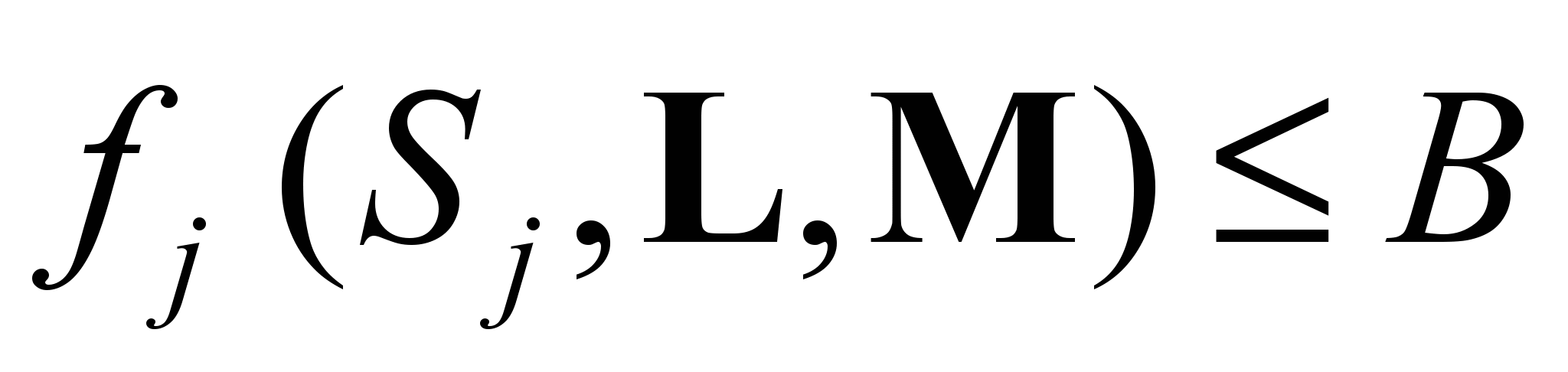– количество узлов, входящих в максимальный контур сегмента S_j магистральной сети (M, L) , ;

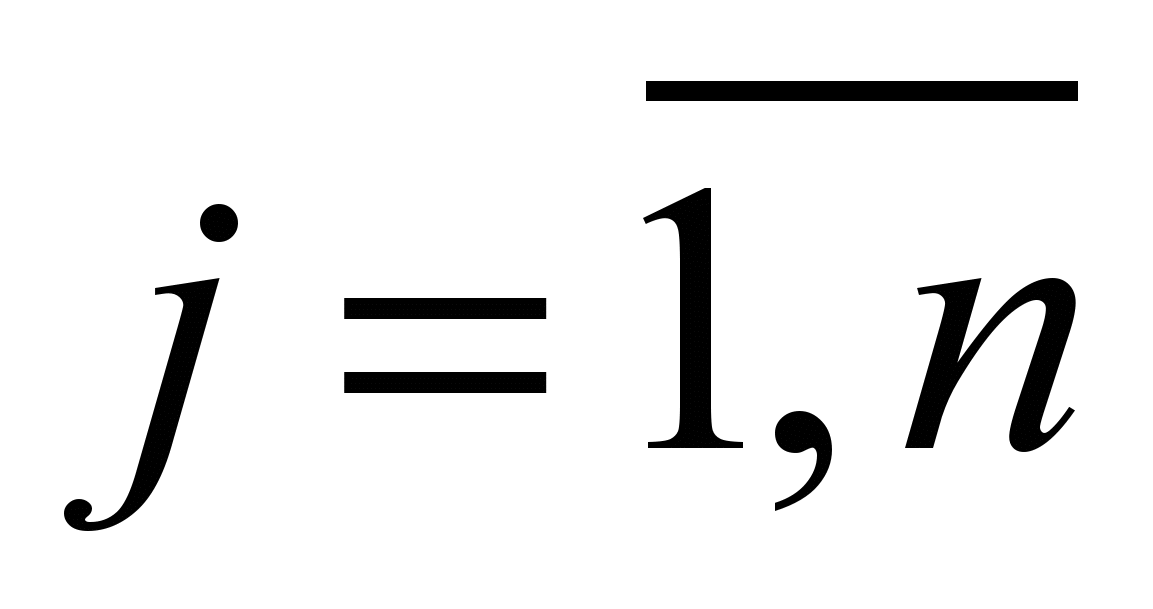q₂: – условие распределения всех узлов;

q₃: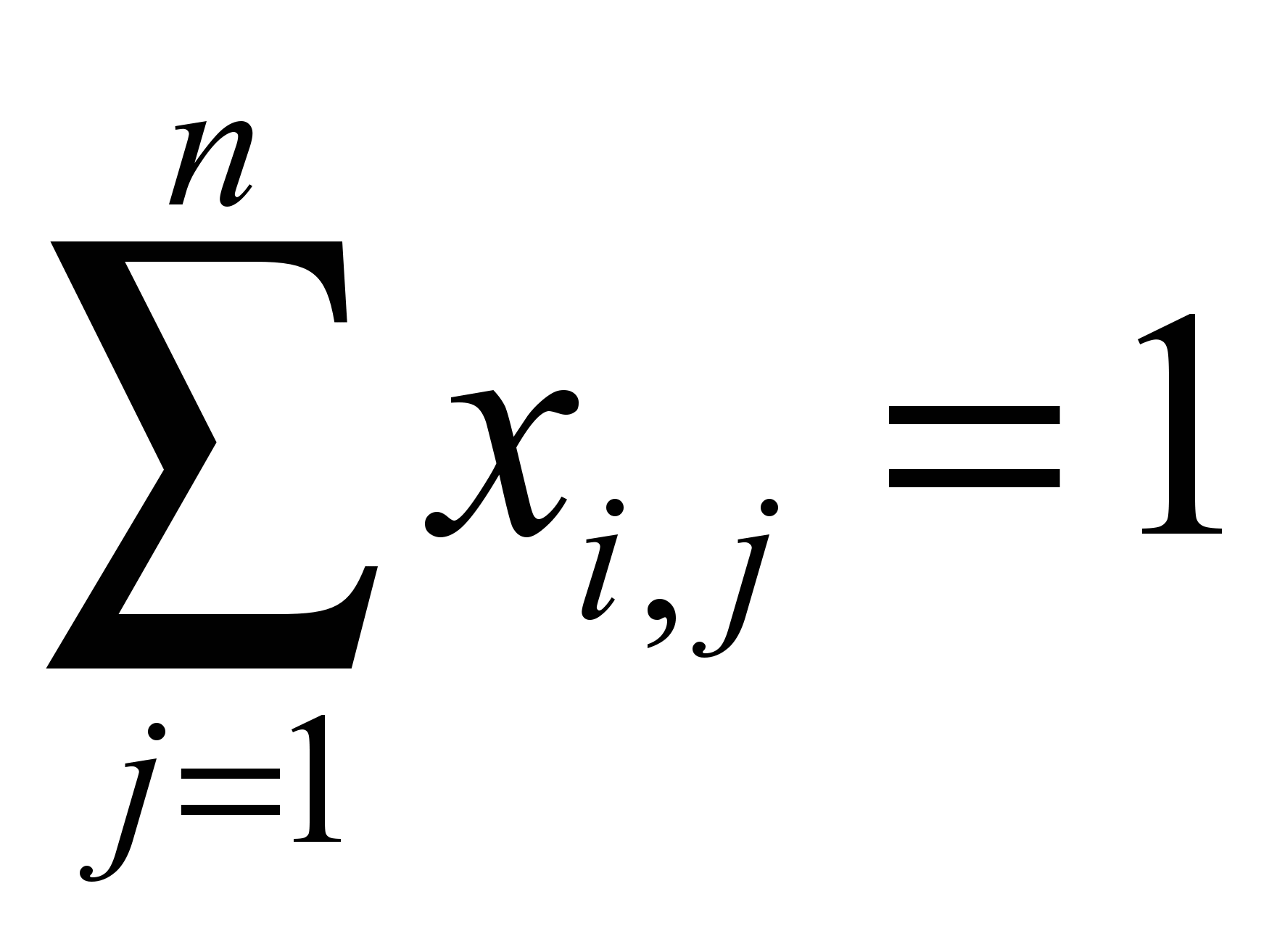, 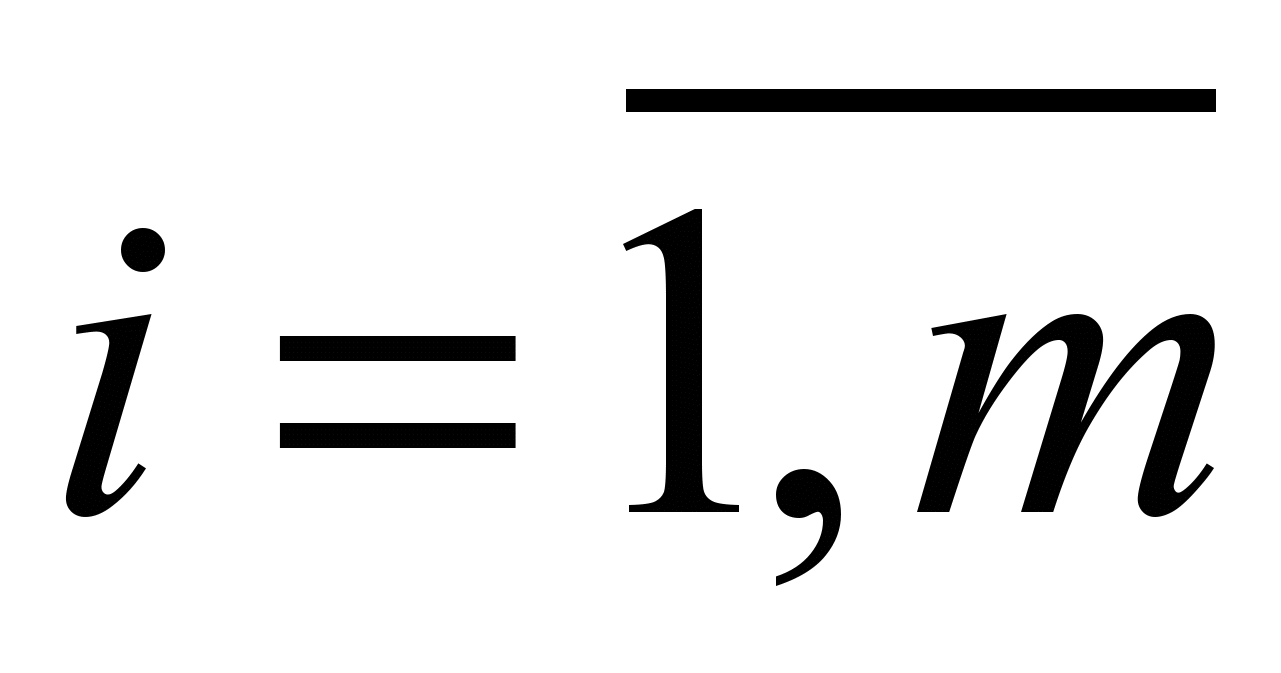– требование однократного распределения узла в сегмент;

В качестве целевой функции служит



Поставленная задача относится к классу задач дискретного программирования и характеризуется большим количеством состояний и сложным видом ограничений. Это в, первую очередь, касается ограничения q₁, для вычисления которого необходимо найти контуры максимальной длины, что, по сути, является моделированием алгоритма STA [2], заложенного в STP. Принимая во внимание, что учитываемые в задаче ограничения многократно вычисляются для оценки большого количества состояний, предлагается для решения использовать современный аппарат генетических алгоритмов [3].

Для решения поставленной задачи предлагается использовать генетический алгоритм (ГА). На сегодняшний день ГА успешно применяются при решении многих NP-сложных задач [3] и в практических приложениях, где математические модели имеют сложную структуру и использование стандартных методов типа ветвей и границ, динамического или линейного программирования затруднено. Современный ГА представляет собой адаптивный поисковый метод, применимый к широкому классу оптимизационных задач. Характерной особенностью ГА является возможность использования целевой функции при оптимизации [3], а не её оценок или приближений, так как ГА не предъявляет требований к виду целевой функции и ограничений. В процессе работы ГА обрабатывает множества альтернативных решений, организуя поиск в направлении перспективных с точки зрения используемой целевой функции и ограничений вариантов решений. Конструирование алгоритма предполагает определение таких понятий как хромосома, ген, популяция, а также оператор случайных изменений [3, 4].

В качестве хромосомы рассматривается закодированный вариант решения задачи. Этот вариант решения состоит из элементов решения – генов. Множество вариантов решения составляет популяцию.

Предлагается сконструировать хромосому с переменной структурой.

Она будет зависеть от количества сегментов в магистральной сети.

,

где гены _i представляют собой векторы, определяющие порядок распределения узлов в сегменты. , где jⁱ – номер сегмента, в который распределен i-й узел, x_ij=1. Функция bin осуществляет преобразование аргумента в двоичную форму. Таким образом, ген _i имеет вид ,, где q – количество бит, необходимое для двоичного представления числа n сегментов: , округление дробной части производится до ближайшего большего целого;

ген  определяет наличие КО-3 в месте размещения i-го узла; .

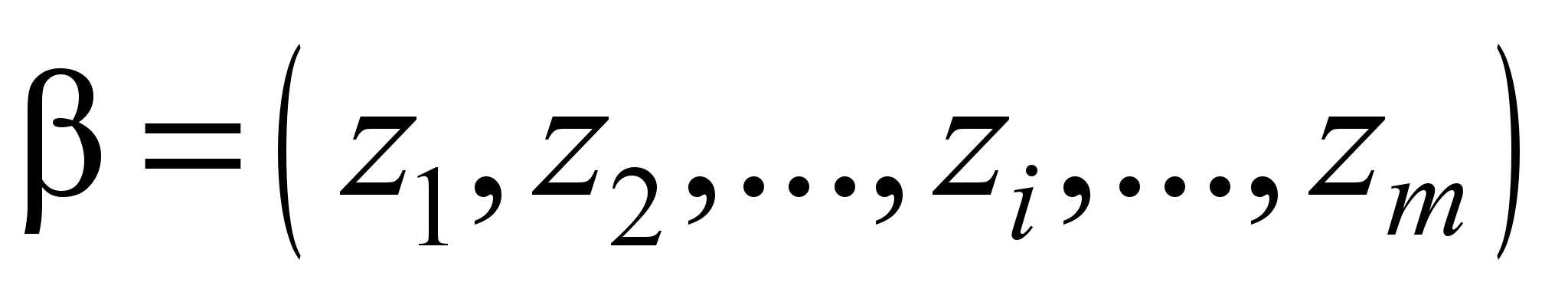Сравнение хромосом осуществляется следующим образом: из анализируемой популяции лучшей считается хромосома A_l с наименьшей величиной нарушения ограничений (A_l), а среди хромосом с равными нарушениями ограничений выбирается хромосома с меньшим значением целевой функции F(A_l).

Для определения величины нарушения ограничений (A_l) вводятся следующие переменные:

; ;



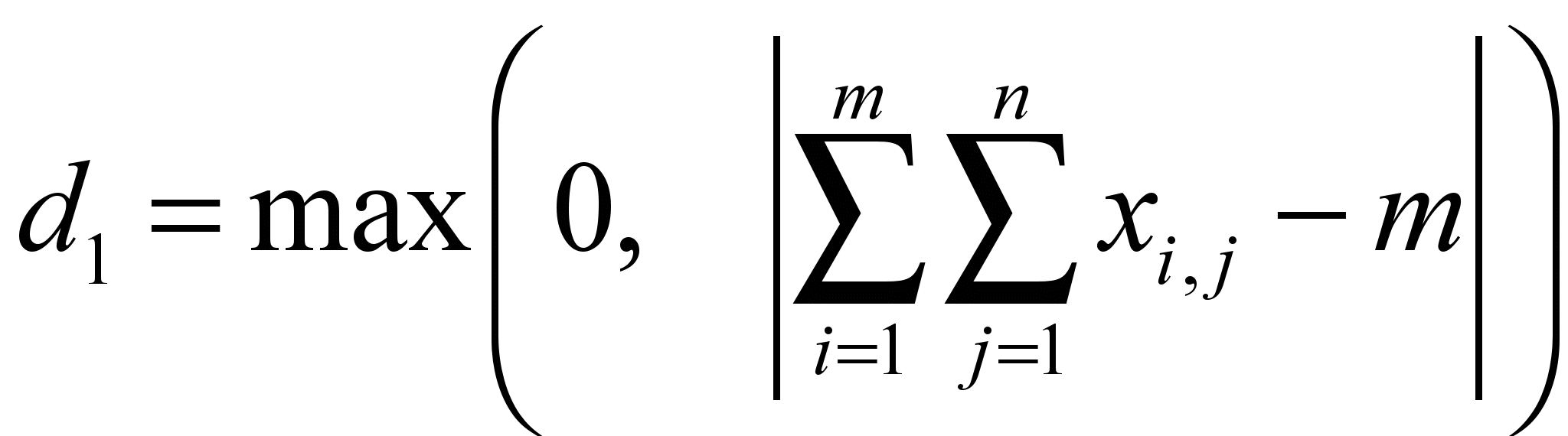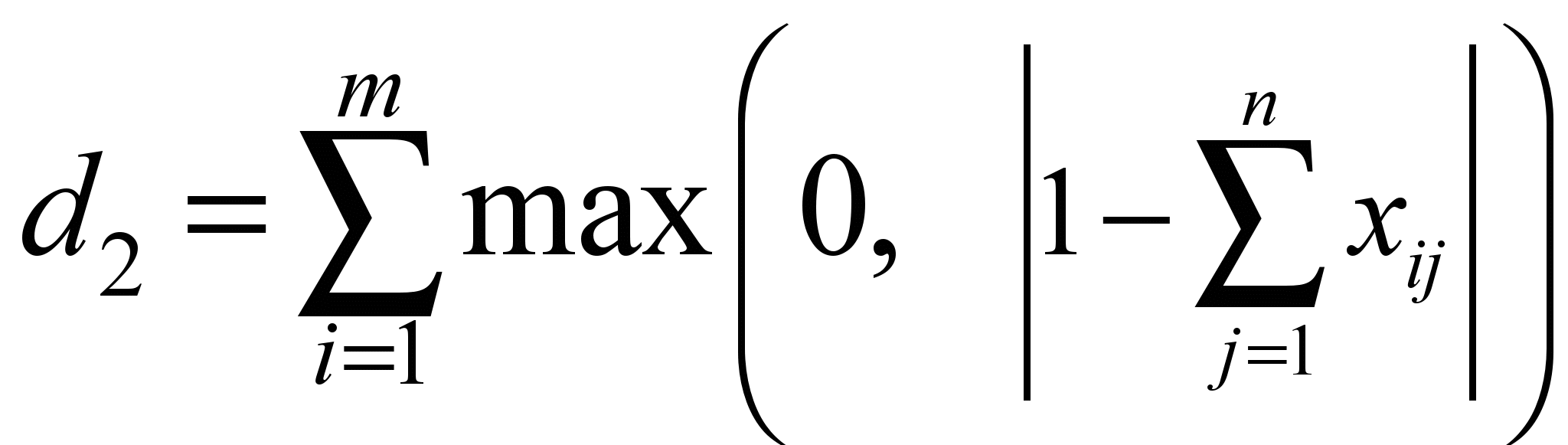Величина нарушения ограничений равна сумме введенных переменных: .

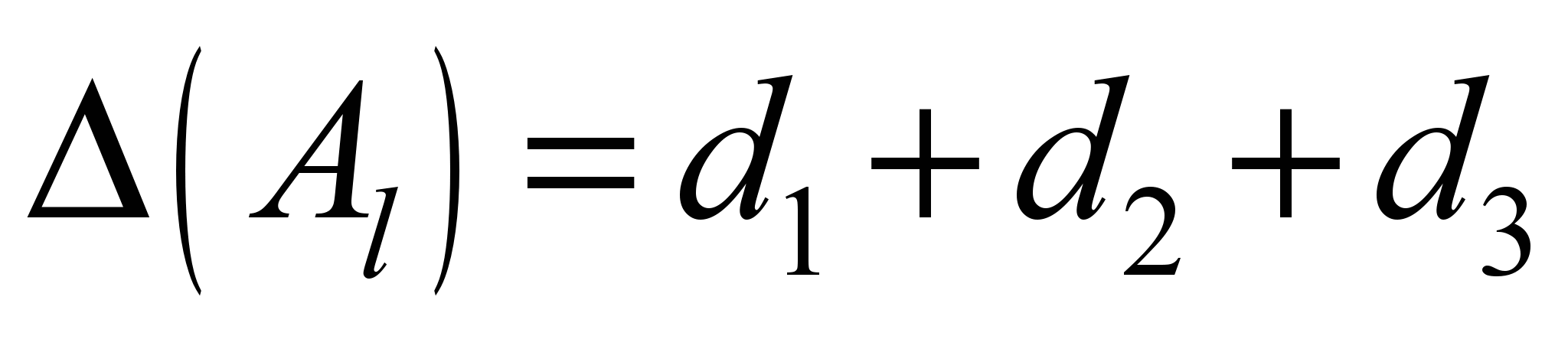В ГА для решения задачи применены операторы случайных изменений [3], которые преобразуют хромосомы, выполняют синтез новых хромосом и производят отбор перспективных для развития хромосом, а также операторы, которые производят случайные изменения, затрагивающие не всю хромосому, а один определенный ген. Это связано с тем, что на заключительной стадии работы алгоритма, когда получены хромосомы, соответствующие близким к оптимальным решениям, целесообразно провести изменения над одним геном.

В разработанном алгоритме на каждом этапе работы алгоритма увеличивается количество сегментов, на которые разбивается магистральная сеть и изменяется размерность хромосомы. В рамках итераций каждого этапа выполняются операторы случайных изменений, производится отбор хромосом-потомков и реализуется самоорганизация алгоритма. Она заключается в том, что количество выполняемых операторов на текущем шаге зависит от эффективности их применения на предыдущих шагах. То есть, по мере работы алгоритма, увеличивается доля наиболее результативных операторов в общем числе операторов, выполняемых на одном шаге. Предлагаемый алгоритм позволяет при получении первого локально-оптимального решения выполнить остановку, так как на последующих этапах возможно лишь увеличение количества сегментов, что приведет к ухудшению результата.

Литература

1. 
   Букатов А.А., Букатов С.А. Шестаков С.А. Методы рациональной организации региональных Ethernet сетей с множественными резервными каналами // Материалы X конференции представителей региональных сетей Relarn-2003, Санкт-Петербург, 2003.
   
2. Кульгин. М.В. Коммутация и маршрутизация IP/IPX трафика. М: Компьютер пресс, 1998.
   
3. Курейчик В.М. Генетические алгоритмы. Состояние. Проблемы. Перспективы // Изв. РАН. Теория и системы управления, 1999, N 1.
   
4. Минкин Ю. И., Петров А.И. Самоорганизующийся генетический алгоритм // Изв. РАН. Теория и системы управления, 2001, N 3.