Курс лекций 1999-2000 гг

Вид материала

Курс лекций

Подобный материал:

• Курс лекций для студентов заочного обучения Бурмистрова Л. А., Финансы предприятий:, 1991.45kb.
• Курс лекций. Спб, 1118.16kb.
• Курс лекций. Спб, 172.51kb.
• Курс лекций. Спб, 639.95kb.
• Цнж курс «Управление газетой», 1997 г.; «Триз-шанс» (Москва) курс «Приемы рекламы, 21.89kb.
• Курс лекций 1999-2000, 11782.85kb.
• В. Б. Аксенов Краткий курс лекций, 1098.72kb.
• Курс лекций Барнаул 2001 удк 621. 385 Хмелев В. Н., Обложкина А. Д. Материаловедение, 1417.04kb.
• Основы политологии: Курс лекций. 2-е изд., доп. Ростов на/Дону.: Феникс, 1999. 573, 14.9kb.
• Г. И. Невельского Н. Н. Жеретинцева Курс лекции, 1964.49kb.

Лекция 8

       Теперь можно было бы перейти к рассказу об образовании и распаде вторичной структуры.
       Однако прежде я хочу поговорить об основах статистической физики и термодинамики "вообще", т.к. без этого трудно рассказывать о и стабильности вторичной структуры, и о стабильности белков, и о кооперативных переходах в полипептидах и белках, и о кинетике этих переходов.
       Термодинамика дает представление о типах возможных кооперативных переходов в системах, состоящих из очень большого числа частиц. Статистическая физика позволяет указать, когда и какие переходы произойдут в рассматриваемой системе и описать детали этих переходов, исходя из свойств рассматриваемых частиц и взаимодействий между ними.

       Прежде всего мы рассмотрим основные понятия статистической физики и термодинамики  —  энтропию, температуру, свободную энергию и статистическую сумму.

       Итак, системы с большим числом степеней свободы (т.е. состоящие из большого числа молекул  —  или даже из одной большой и гибкой молекулы) описываются при помощи статистической физики. "Статистической"  —  ибо число конфигураций таких больших систем колоссально. Только один пример: если каждое из N звеньев цепи может находиться всего в двух возможных конфигурациях (например: "спиральном" и "вытянутом"), то вся N-звенная цепь имеет 2^N возможных конфигураций. То есть "нормальная" для белка цепь из 100 звеньев может иметь, по крайней мере, 2¹⁰⁰, или около 10,000,000,000,000,000,000,000,000,000,000 конфигураций. Это  —  очень много. А ведь на опыте в пробирке находятся миллиарды таких цепей,  —  не говоря о растворителе! И если бы мы захотели инвентаризовать все конфигурации этих цепей,  —  мы бы пропали навсегда. Но нас, конечно, будут интересовать более простые и разумные вещи, например,  —  средняя (т.е. статистически усредненная) спиральность цепей и то, как эта спиральность меняется с нагреванием. А замечательным свойством статистического, т.е. пренебрегающего всеми несущественными подробностям усреднения является кардинальное упрощение ситуации.

       Важнейшую роль в статистическом усреднении играет энтропия. Она говорит, сколько конфигураций системы (или, как говорят, сколько ее микроскопических состояний) соответствует наблюдаемому нами, т.е. макроскопическому (усредненному длительностью нашего наблюдения и большим числом одновременно наблюдаемых молекул) состоянию изучаемой системы. Мы уже говорили на эту тему,  —  но тогда мы рассматривали, по существу, только один частный случай: тогда число "микроскопических состояний" определялось объемом, в который была заключена молекула, а ее энтропия была пропорциональна логарифму этого объема (причем нахождение в данном объеме  — например, в данной комнате  —  и было "макроскопическим состоянием" молекулы).
       Здесь уместно ответить на естественный вопрос: почему физики предпочитают рассматривать логарифм числа микросостояний, а не само это число? Дело в том, что, если рассматривать много отдельных систем (например,  —  отдельных молекул), то мы увидим, что их объемы, энергии, числа степеней свободы при этом складываются, а количества возможных состояний  —  перемножаются. Это различие неудобно, оно сделало бы громоздким все расчеты. Но вот логарифмы чисел возможных состояний складываются при перемножении этих чисел [вы помните, что ln(AB)=ln(A)+ln(B)],  —  складываются, как энергии или объемы. Это однотипность удобна при решении задач, и к тому же операция сложения позволяет легко воспользоваться всей мощью дифференциального исчисления.

       Теперь  —  температура. Она тесно связана с энтропией: нет большого числа состояний, нет энтропии  —  нет и температуры. Для выяснения связи  —  рассмотрим замкнутую (т.е. не обменивающуюся энергией с окружением) систему. Пусть ее полная энергия равна Е, и пусть эта система находится в равновесии, т.е. все ее микросостояния, имеющие энергию Е, равновероятны (а имеющие другую энергию  —  имеют нулевую вероятность).

       Выделим теперь в этой системе "наблюдаемую малую часть" (например, отдельную молекулу в газе, или макромолекулу с окружающей ее жидкостью). Вся остальная система тогда может рассматриваться как термостат, в который погружена наша "малая часть".  
 

Замкнутая система, E=const

       Разобьем все микроскопические состояния системы на классы, различающиеся состоянием нашей "малой части". Чем больше микроскопических состояний всей системы в данном классе,  —  тем больше вероятность его (этого класса) наблюдения, т.е. тем больше вероятность наблюдения данного состояния нашей "малой части".
       Пусть наша "малая часть" фиксирована в каком-то микроскопическом состоянии (например, пусть наблюдаемая молекула в газе имеет заданное положение в пространстве и заданную скорость). Пусть она обладает при этом энергией . Поскольку вся система в целом замкнута, то полная энергия всей системы сохраняется (закон!), и энергия термостата равна E-. Пусть этой энергии соответствует M_therm(E-) возможных микросостояний термостата. Тогда вероятность наблюдения данного состояния нашей "малой части" просто пропорциональна M_therm(E-). [Замечание. Мы здесь неявно предположили, что конкретное микросостояние нашей системы не влияет на микросостояния термостата. Строго говоря, это не вполне верно (точнее: это верно только для "термостата", состоящего из разреженного идеального газа),  —  но учет явлений на границе "нашей системы" и термостата только затемнил бы все дальнейшее изложение. Для совмещения строгости и наглядности  —  можно представить себе, что наша "наблюдаемая часть" заключена в фиксированный и непроницаемый для молекул термостата объем.]
       Если число возможных состояний термостата равно M_therm(E-), то логарифм этого числа, по определению, пропорционален энтропии термостата:
 

Stherm(Е-) =  ln[Mtherm(E-)] ;

(8.1)

коэффициент  здесь вводится только для того, чтобы энтропия, как обычно, измерялась бы в единицах кал/^oK; как мы увидим позже, он окажется просто константой Больцмана.
       Энергия  "малой части" тоже должна быть относительно мала. Поэтому можно воспользоваться обычным дифференциальным разложением величины S_therm(E-) по малому параметру  [вы, конечно, помните: f(x_o+dx) = f(x_o) + (df/dx)|_xodx + 1/2(d²f/dx²)|_xo(dx)² + ... = f(x_o) + (df/dx)|_xodx при малом dx, причем (df/dx)|_xo означает, что производная df/dx берется в точке x_o]. Итак,
 

Stherm(E-) = Stherm(E)  —  (dStherm/dE)|E. .

(8.2)

[Примечание. Так как и S, и Е пропорциональны числу частиц, то dS_therm/dE от числа частиц в термостате не зависит, в то время как d²S_therm/dE² обратно пропорциональна этому числу, т.е. d²S_therm/dE²  0 в очень большом термостате; это и позволяет нам пренебречь членами порядка ²,  —  а также ³ и т.д.  —  в формуле 8.2.]
       Значит, число возможных микросостояний термостата зависит от энергии  нашей "малой части" как
 

Mtherm(E-) = exp[Stherm(E-)/] = exp[Stherm(E)/] xexp[- . {(dStherm/dE)|E/}] .

(8.3)

При этом ни общий множитель exp[S_therm(E)/] = М(Е), ни число (dS_therm/dE)|_E не зависит ни от , ни от конкретного микросостояния нашей "малой части" вообще.
       Так как число микросостояний должно расти с энергией (чем больше энергия,  —  тем большим числом способов ее можно разделить), то формула 8.3 означает просто следующее: чем больше энергии отобрала у термостата наша "малая часть", тем меньше энергии осталось у него, — и тем меньшим числом способов ее можно разделить. При этом падение числа возможных микросостояний термостата (числа способов раздела его энергии) экспоненциально зависит от энергии, содержащейся в нашей "малой части".
       Резюмируем. Вероятность наблюдения заданного микросостояния нашей "малой части" (молекулы и т.п.) пропорциональна exp[-^.{(dS_therm/dE)|_E/}], где   —  энергия этой "малой части", а величина (dS_therm/dE)|_E/ зависит не от "малой части", а только от окружающей ее среды.
       Но, по формуле Больцмана, вероятность пребывания молекулы в заданном состоянии с энергией  пропорциональна exp(-/k_ВT) [где T  —  температура, а k_В  —  константа Больцмана]! Сравнивая тождественные выражения exp[-^.{(dS_therm /dE)|_E/}] и exp(-/_BT),  —  видим, что
 

(dStherm/dE)|E = 1/Т ,

(8.4)

а "" в формулах 8.1 и 8.3  —  это та же константа Больцмана (k_B),  —  если, как обычно, энергия измеряется в джоулях (или в калориях), температура  —  в ^оК, а энтропия  —  в Дж/^оК (или в кал/^оК).

       Формулы 8.1 и 8.4, определяющие температуру как величину, обратную скорости изменения энтропии S (или логарифма числа микросостояний) с энергией Е системы,  —  основные формулы статистической физики и термодинамики.
       Они показывают, в частности, что ln[M(E+k_ВT)] = S(E+k_ВT)/k _В = [S(E) + (k_ВТ)(1/T)]/k _В = ln[M(E)]+1,  —  то есть при увеличении энергии на k_ВT число микросостояний растет в "e" (=2.72) раз, т.е. примерно втрое,  —  независимо от размеров системы, действующих в ней сил и т.д.
       Они означают также, что, зная число микросостояний любой большой системы ("термостата") при разных ее энергиях (или, как говорят, "плотность энергетического спектра" системы),  —  а точнее, зная зависимость логарифма плотности энергетического спектра системы от энергии,  —  мы можем найти температуру, соответствующую каждой энергии этой системы. Соответствующий график показан на Рис.8-1.
 
 
 
 



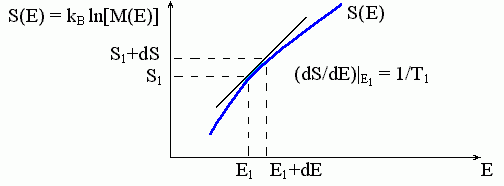
       Рис.8-1. Определение температуры большой системы. Зависимость энтропии S этой системы от ее энергии E показана жирной кривой. Наклон этой кривой, dS/dE, определяет температуру T, соответствующую данной энергии E. М(E)  —  число микросостояний с заданной энергией Е, т.е. плотность спектра энергий состояний системы.
 
 

       Надо только, чтобы микросостояний было очень много  —  производную dS/dE можно, естественно, брать только тогда, когда в малом (по сравнению с k_BT) интервале энергий находится много микросостояний системы. Именно поэтому температура появляется только в науках, рассматривающих огромное число возможных микросостояний.

       Продолжим рассмотрение системы, заключенной в фиксированный и непроницаемый для молекул термостата объем (через стенки которого она, однако, может обмениваться энергией с этим термостатом, температура которого равна Т).
       Формулы 8.1 и 8.3 показывают, что вероятность пребывания нашей системы в заданном микросостоянии i с энергией _i при температуре Т есть
 

wi(Т) = exp(-i/kBT) / Z(Т),

(8.5)

где

Z(Т) = j exp(-j/kBT)  —

(8.6)

это нормировочный коэффициент, учитывающий, что сумма вероятностей всех состояний, _j w_j, должна быть равна 1 (сумма _j здесь и выше берется по всем возможным микросостояниям j рассматриваемой "малой системы").

       Величина Z называется статистической суммой для рассматриваемой системы. Зная ее, можно вычислить по формуле 8.5 вероятность каждого из микросостояний этой системы при заданной температуре,  —  и, далее, ее среднюю энергию при этой температуре
 

E(Т) = jwj.j

(8.7)

и ее энтропию

S(Т) =  — kBjwj.ln(wj) .

(8.8)

Обратите внимание, что формула 8.8 усредняет ln(w_j) по всем сосояниям системы, j, с учетом их (состояний) вероятностей w_j. Она есть прямое обобщение давно знакомого нам (см. формулу 8.1) определения энтропии S = k_B^.ln[M(Е)] на случай, когда все состояния системы имеют самые разные вероятности,  —   а не только две, следовавшие тогда из закона сохранения энергии: w_j = 1/M(E) при E_j=Е и w_j=0 при E_j  Е.

       Статистическая сумма играет очень важную роль в статистической физике, так как величина Z(Т) позволяет прямо вычислить свободную энергию системы, находящейся в фиксированном объеме
 

F(T) = E(T) - TS(T) = j wj.{j + kBT.ln(wj)} = j wj.{j + kBT.(-j/kBT - ln[Z(T)]} = -kBT.ln[Z(T)]

(8.9)

(в предпоследнем равенстве мы воспользовались формулой 8.5). Затем можно прямо найти энтропию системы: S(T) =  —dF/dT (мы с этой формулой уже встречались, но проверьте ее самостоятельно, исходя из определений, даваемых формулами 8.9, 8.6, 8.5 и 8.8), а затем  —  и ее энергию E(T)  F(T) + TS(T) = F(T) - T(dF/dT).

       Существенные, но второстепенные замечания.

       1) Внутренняя температура "малой системы" T_in равна температуре термостата Т. Это следует из того, что, согласно приведенным выше определениям и уравнениям, T_in  dE(T)/dS(T) = d[F(T)-T(dF/dT)]/d(-dF/dT) = [dF/dT-T(d²F/dT²)-dF/dT]dT/ (—  d²F/dT²)dT = T.
       2) Полная энергия складывается из кинетической и потенциальной. Первая зависит только от скоростей частиц, а вторая  —  только от их места в пространстве, но не от скоростей. "Микросостояние" каждой частицы задается ее координатой в пространстве и ее скоростью. В классической (не квантовой) механике сочетание скоростей и координат может быть любым (и, как мы знаем, квантовое соотношение Гайзенберга, vx~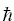/m,  —  при комнатной температуре  —  ограничивает сочетание скоростей и координат только у очень легких частиц  —  электронов). Это значит, что вероятности координат и скоростей можно "расцепить", т.е. w(_кинет+ _коорд) ~ exp(-_кинет/k _BT) x exp(-_коорд/k _BT). Продолжая несложные вычисления (предлагаю их сделать самим!), легко увидеть, что свободные энергии, энергии и энтропии тоже можно "расцепить" на кинетические и координатные части, т.е. F = F^кинет. + F^коорд. и т.д. Важно, что кинетические части не зависят от конфигурации системы (фактически, они дают только постоянный вклад в теплоемкость)  —  и их можно отбросить при изучении конформационных превращений. Поэтому в дальнейшем мы будем говорить только о конфигурационных (или конформационных) энергетических спектрах, энергиях, энтропиях и т.д.
       3) Выше мы суммировали по микросостояниям  —  но в рамках классической механики мы можем с тем же успехом интегрировать по координатам и скоростям, задающим микросостояние каждой частицы.
       4) Равновесная температура может быть только положительной. Иначе интегрирование вероятностей по скоростям, т.е. 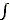ехр(-mv²/2kT)dv, обращается в бесконечность на больших скоростях  —  и система "взрывается".
       Поэтому стабильное состояние никак не может наблюдаться в тех областях конформационного энергетического спектра, где его плотность (и, значит, энтропия системы) падает с ростом ее энергии: этим областям соответствует Т<0 (см. формулы 8.4 и 8.1 и Рис.8-2а).
       5) Величина k_BT измеряется в единицах типа "энергия на частицу" или "энергия на моль (=6.02x10²³) частиц". Если бы люди с самого начала выражали бы температуру в энергетических единицах, константа Больцмана "k_B" не потребовалась бы вообще. Однако история сложилась так, что сначала ввели температурную единицу  —  "градус"  —  а потом уже поняли, что "градус" можно всегда пересчитать, конвертировать в "энергию в расчете на частицу": для этого достаточно умножить его (градус) на некоторую константу  —  "константу Больцмана". Соответственно, размерность k_B  —  "энергия_на_частицу/градус". Величина k_B зависит о того, в чем выражается энергия  —  то ли в "джоуль_на_частицу", то ли в "кал_на_моль частиц". Согласно измерению энергетической величины градуса, k_B = 1.38x10^-23 (джоуль/частицу)/градус. Однако k_B можно выразить и по-иному - в расчете не на штуку, а на моль частиц: 1.38x10^-23 (джоуль/частицу)/градус = 1.38x10^-23 (джоуль x [6.02x10²³]/[6.02x10²³ частиц])/градус = [1.38 x 10^-23 x 6.02x10²³] (джоуль/моль_частиц)/градус = 8.31 (Дж/моль)/градус = 1.99 (кал/моль)/градус. Последнюю величину — 1.99 (кал/моль)/^оК — традиционно именуют "газовой постоянной" R.
       6) Удельная энтропия часто выражается в энтропийных единицах, "э.ед": э.ед. = (кал/моль)/^оК  k_B/2. Стало быть, энтропии в 1 э.ед. соответствует е^1/2  1.65 состояний системы в расчете на частицу.
 
 
 
 



       Рис.8-2. Участки графика S(E), которым не может соответствовать никакое стабильное состояние системы. (а) Участки, где энтропия S(E) падает с ростом энергии Е: здесь Т = 1/(dS/dE) < 0. (б) "Вогнутый" участок зависимости S от E: здесь в точке касания (где dS/dE=1/T₁) свободная энергия F=E-TS не меньше, а больше, чем на соседних с ней участках кривой S(E); ср. с Рис.8-3.
 
 

       Теперь, наконец, мы рассмотрим конформационные превращения. Именно для их грамотного рассмотрения мы и повторяли азы статистической физики и термодинамики.

       Конформационные превращения бывают постепенные ("континуальные") и резкие ("фазовые"). Попробуем разобраться в их различии, используя графики плотности энергетических состояний  —  вроде тех, что представлены на Рис.8-1. Для этого прежде всего надо научиться находить на графике стабильное состояние  —  или состояния  —   нашей системы при заданной температуре среды.

       Пусть нам задано число M(E) состояний нашей системы ("макромолекулы") при каждой ее энергии Е, а также температура Т₁ окружающей среды ("термостата"). Как, зная график энтропии S(E) = k_B ln[M(E)] и Т₁, найти на графике точку, соответствующую стабильному состоянию нашей системы? Температура Т₁ показывает, какой наклон dS/dE должен быть в той точке графика, которая нас интересует: здесь dS/dE = 1/T₁  —  ведь температура у нашей макромолекулы та же, что и у среды.
       Но, вообще говоря, таких точек  —   точек, где график имеет наклон 1/T₁  —  может быть несколько (см. ниже, Рис.8-5). Какая из них отвечает стабильному состоянию? Рассмотрим касательную к графику в точке Е₁, где dS/dE|_Е1 = 1/T₁. Уравнение такой касательной таково: S-S(E₁) = (E-E₁)/T₁, или: E-T₁S = E₁-T₁S(E₁). Величина F₁ = E₁-T₁S(E₁)  —  это просто свободная энергия при температуре T₁. Вдоль касательной, как мы видим, величина (E-T₁S) неизменна. Всюду слева от касательной величина E- T₁S ниже, а всюду справа  —  выше, чем на касательной (Рис.8-3).
 
 
 



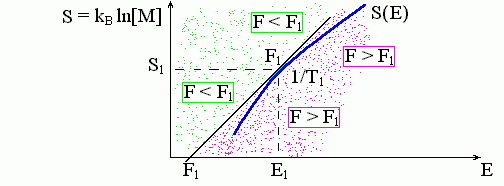
       Рис.8-3. Графическое определение свободной энергии. Зависимость энтропии S от энергии E показана жирной кривой S(E). Наклон этой кривой, dS/dE, определяет температуру T. M(E)  —  плотность спектра энергий состояний системы. F₁  —  свободная энергия, соответствующая данному энергетическому спектру при температуре Т₁. Величина F = E-T₁S постоянна вдоль касательной и равна F₁. Левее этой касательной  —  F = E-T₁S < F₁, правее касательной,  —  F = E-T₁S > F₁. Так как кривая S(E) здесь выпукла, т.е. лежит правее и ниже касательной, то точка касания отвечает минимуму свободной энергии при температуре T₁. Дальнейшие пояснения  —  в тексте.
 
 

       Последнее означает, в частности, что "вогнутым" участкам зависимости S от E (Рис.8-2б) стабильное состояние соответствовать никак не может: здесь в точке касания F не меньше, а больше, чем на соседних с ней участках кривой S(E).
       Если кривая S(E)  —  всюду выпукла, то ее наклон все падает по мере увеличения энергии Е. Тогда каждому наклону 1/Т отвечает только одна точка кривой (Рис.8-1, 8-4),  —  то есть она, эта точка, и отвечает стабильному состоянию при данной температуре Т. С изменением температуры эта точка постепенно движется, а система  —  постепенно ("градуально") меняет свое термодинамическое состояние, т.е. энтропию и энергию (Рис.8-4).
 
 
 



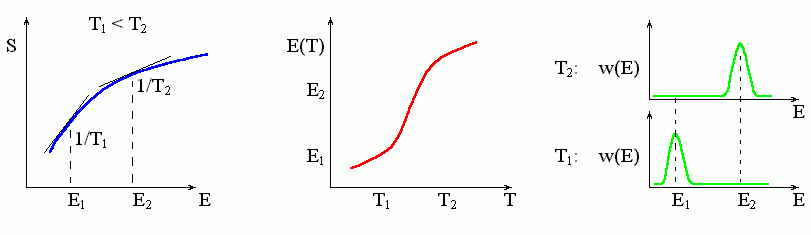
       Рис.8-4. Градуальное изменение состояния системы с изменением температуры. Для этого необходимо, чтобы кривая S(E) была выпукла. Зная зависимость S(E) (слева), можно найти зависимости Т(Е) и, далее, Е(Т); последняя показана в центре рисунка. Справа: w(E)  —  функция распределение молекул по энергиям, т.е. вероятность иметь энергию Е при заданной температуре T; вероятность w(E) пропорциональна exp[-(E-TS(E))/k_BT].
 
 

       Если наклон кривой S(T) то падает, то растет по мере увеличения энергии Е (Рис.8-5),  —  то касательных с одинаковым наклоном к этой кривой может быть несколько,  —  и касание самой левой из них (той, у которой F меньше) выделяет стабильное состояние. При этом до какой-то температуры T^* "лучшей" будет касательная в районе малых энергий, после T^*  —  "лучшей" будет касательная в районе больших энергий.
 
 
 



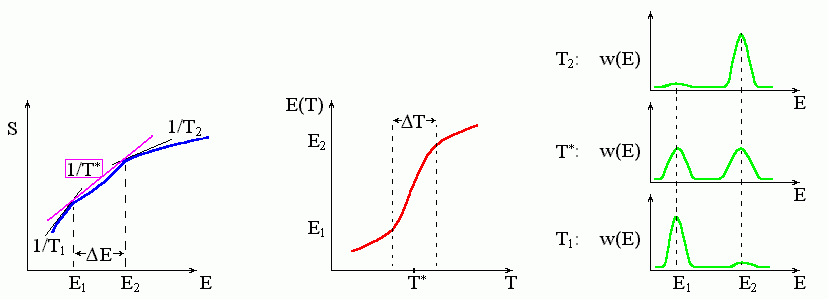
       Рис.8-5. Фазовый переход "все-или-ничего" (аналог фазового перехода первого рода в макроскопических телах) характеризуется резким изменением состояния системы при изменении температуры. Для этого необходимо, чтобы кривая S(E) имела бы вогнутый участок: в центре его свободная энергия выше, чем на его краях (см. Рис.8-2б). Переход происходит в узком диапазоне (T) температур, отвечающем сосуществованию (т.е. примерно равной вероятности) низко- и высокоэнергетичного состояния. Касательные соответствуют: температуре середины перехода T^*, а также Т₁ < T^* и Т₂ > T^*. Обратите внимание, что температура T^* перехода типа "все-или-ничего" (т.е. фазового перехода первого рода) совпадает именно с серединой резкого изменения энергии и с максимальным раздвоением функции распределения по состояниям, w(E).
 
 

       При температурах, близких к T^*, высоко- и низкоэнергетичные структуры будут сосуществовать. И  —  что наиболее важно  —  структуры со "средними" энергиями не будут проявляться: из-за "прогиба" кривой соответствующие этим состояниям точки графика лежат справа от касательной, т.е. их свободная энергия  —   выше, чем у структур, соответствующих точкам касания, а вероятность проявления  —  ничтожна. Говорят тогда, что два стабильных состояния разделены "свободно-энергетическим барьером". В этих условиях и протекает переход типа "все-или-ничего", который в макроскопических системах называется фазовым переходом первого рода.
       Здесь я хочу сразу оценить величину температурного интервала сосуществования высоко- и низкоэнергетичных структур. В середине перехода, при температуре Т^*, свободная энергия низкоэнергетичной фазы, F₁(T^*) = E₁-T^*S₁, равна свободной энергии высокоэнергетичной фазы, F₂(T^*) = E₂-T^*S₂, т.е. в середине перехода
 

(E2  —  E1) = T*(S2  —  S1) .

(8.10)

       При небольшом (на Т) сдвиге температуры от T^* свободные энергии фаз немного меняются, так что разность свободных энергий фаз составляет F = F₁(T^*+T) - F₂(T^*+T) = T (S₂ - S₁). Фазы сосуществуют (т.е. они примерно равновероятны  —  скажем, соотношение их вероятностей меняется от 10:1 в пользу первой до 1:10 в пользу второй фазы), пока ехр(-F/k _BT^*) лежит между 10 и 1/10, т.е. пока F/k_BT^* находится где-то от -2 до +2. В этой области |T| < 2k_BT^*/(S₂-S₁).Значит, температурный интервал сосуществования фаз есть
 

T  [2kBT*/(S2-S1)] - [-2kBT*/(S2-S1)] = 4kBT*/(S2-S1) = 4T*[kBT*/(E2-E1)]

(8.11)

       Рассмотрим поучительный численный пример. Если T^*~300^оК (т.е. k_BT^*~0.6 ккал/моль), а E₂-E₁ составляет, как то характерно для плавления белков, порядка 50 ккал/моль [т.е. 50/(6x10²³) ~ 10^-22 килокалорий_на_штуку], то T  —  порядка десяти градусов. Если же E₂-E₁ составляет порядка 50 килокалорий_на_штуку (как при плавлении льдины размером с бутылку), то T  —  порядка 10^-23 градуса.
       Иными словами, для фазовых переходов типа "все-или-ничего" в малых системах и  —  в гораздо большей степени  —  для фазовых переходов первого рода в макроскопических системах,  —  характерен резкий скачок энергии в узком диапазоне температур. В макроскопических системах этот диапазон практически бесконечно узок, а для макромолекул он охватывает несколько градусов, т.е. тоже узок по сравнению с "диапазоном наблюдения", обычно охватывающим от 0^оС до 100^оС. А вот в небольших олигопептидах резкого скачка нет  —  здесь диапазон изменения энергии может охватывать все "экспериментальное окошко" исследуемых температур.

       Несколько слов о фазовых переходах второго рода. Если для переходов первого рода характерен скачок энергии системы (и ее энтропии, объема и плотности), то для переходов второго рода характерен лишь излом зависимости скорости изменения энергии с температурой,  —  иными словами, скачок теплоемкости.
       Подчеркиваю, что переход второго рода происходит в точке излома (Рис.8-6), а вовсе не посередине часто идущей за ним более или менее "S-образной" зависимости энергии (или другого наблюдаемого параметра) от температуры.
 
 
 



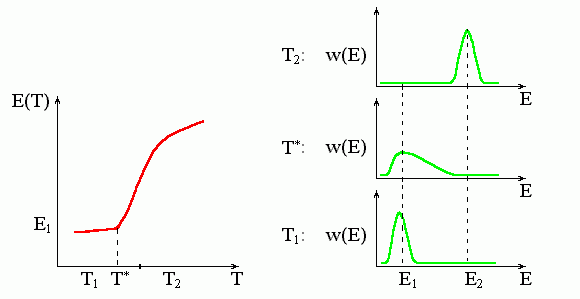
       Рис.8-6. Характерная зависимость энергии, E(T), и функции распределения, w(E), при фазовом переходе второго рода. T^* — температура этого фазового перехода. При этой температуре функция распределения молекул по энергиям, w(E), резко уширяется, и энергия начинает (или кончает —  смотря откуда смотреть) резко изменяться. Обратите внимание, что температура фазового перехода второго рода T^* совпадает именно с началом (а не с серединой) резкого изменения энергии.
 
 

       На рисунках 8-4  —  8-6 я специально представил случаи, когда энергия системы сначала меняется медленно с изменением температуры, потом  —  резко, а потом  —  снова медленно. Как вы видите, такое "S-образное" поведение Е(Т) совместимо и с фазовым переходом первого рода, и с градуальным изменением системы при отсутствии какого-либо фазового перехода вообще, и с градуальным изменением, начало которому кладет фазовый переход второго рода.
       Я прошу обратить на это особое внимание, так как среди не-физиков существуют два непонятно откуда взявшихся предрассудка: что "переход" соответствует именно середине всякого S-образного изменения, и что если этот "переход" не первого рода  —  значит второго. Это не так!
       Обратите внимание: хотя кривые Е(Т) на рисунках 8-4  —  8-6 выглядят, в общем, одинаково, — поведение кривых распределения по энергиям, w(Е), при переходе первого рода (т.е. типа "все-или- ничего") выглядит совсем не так, как при всех остальных переходах. Для переходов типа "все-или-ничего"  —  и только для них  —  характерно наличие двух пиков у w(Е), т.е. сосуществование двух фаз. Поэтому для выяснения того, как  —  прыжком или постепенно  —   происходит переход между двумя крайними состояниями,  —  недостаточно увидеть, что энергия или какой-то наблюдаемый параметр резко меняется в узком диапазоне температур. Здесь нужны дополнительные измерения, которые мы рассмотрим в одной из дальнейших лекций.

       В заключение поговорим о кинетике конформационных превращений. Точнее  —  о том, почему некоторые превращения идут очень медленно. Что здесь значит "медленно"? Предположим, вы знаете время элементарного шага по ходу процесса. Например: один остаток включается во вторичную структуру за 1 наносекунду (нс). Вы знаете также, что в цепи  —  1000 звеньев. А процесс идет не за 1000 нс, а за 1000 секунд. Это и есть "медленно": на порядки медленнее, чем можно ожидать, зная время элементарного шага и число таких шагов. Надо понять  —  почему...

       "Медленность" процессов порой связана с медленностью диффузии при высокой вязкости. Однако часто  —  подчеркиваю, не всегда, но часто  —  медленность процесса связана с преодолением высокого свободно-энергетического барьера. Особенно это типично для переходов типа "все или ничего", где свободно-энергетический барьер разделяет две фазы (Рис.8-5); здесь он всегда значителен. Такой барьер очень похож на активационный барьер в химических реакциях,  —  только в данном случае он имеет и энергетическую, и энтропийную составляющие. Напомню, как оценивается скорость такой "барьерной" реакции согласно классической теории переходных состояний.

       Рассмотрим простейший процесс, по ходу которого система переходит из состояния А в состояние В. Пусть на пути процесса "АВ" есть один "барьер" # (Рис.8-7), и ни на этом пути, ни "сбоку" от него нет никаких "ловушек" (Рис.8-8: состояний Л, более стабильных, чем исходное A, но менее стабильных, чем конечное B; наличие ловушек усложняет процесс, но не меняет его принципиально).
 
 
 



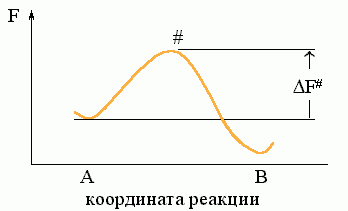
       Рис.8-7. Преодоление свободно-энергетического ("активационного") барьера # при переходе из состояния "А" в состояние "В". F^#  —  свободная энергия барьера (перехoдного состояния).
 
 
 



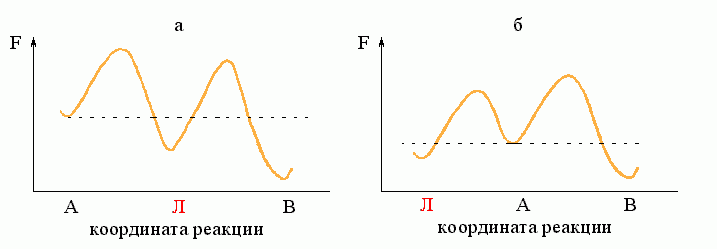
       Рис.8-8. "Ловушка": ею может быть как интермедиат "Л" (а), так и побочное (для реакции АВ) состояние "Л" (б). Для наличия кинетической "ловушки" важно только, что она более стабильна, чем исходное состояние "А", но менее стабильна, чем конечное состояние "В", и что на пути из "Л" в "В" находится более высокий свободно-энергетический барьер, чем на пути из А в Л.
 
 

       Тогда скорость процесса определяется (1) населенностью барьерного ("перехдного") состояния, и (2) скоростью перехода из барьерного в "за-барьерное" состояние.
       Если F^#  —  свободная энергия барьера, отсчитанная от свободной энергии начального состояния, причем F^# >> k_BT, и "ловушек" (Рис.8-8) нет, а в начальном состоянии находится n "частиц" (синонимы: молекул, систем и т.д.),  —  то на барьере, в каждый момент времени, находится n^# ~ n^.exp(-F^#/k_BT) частиц. Пусть каждая из этих на-барьерных частиц переходит за барьер за время  (время элементарного шага реакции). Тогда за время порядка  за барьер перейдут все n^# на-барьерных частиц. На то, чтобы за барьер перевалили бы все n частиц  —  понадобится n/n^# шагов, т.е. время порядка
 

t ~ (n/n#) ~ exp(+F#/kBT)

(8.12)

При наличии "ловушки", Л, таким же образом оценивается время перехода из А в Л и из Л в В.

       Уточнение. Если на пути из А в В находится не одно, а s последовательных промежуточных состояний с со свободной энергией, близкой к F^#,  —  то скорость процесса замедляется в s² раз по сравнению с оценкой (8.12). Это замедление связано с диффузией частиц по верхушке барьера. Однако обычно этот диффузионный фактор не играет существенной роли.