Курс лекций 1999-2000 гг

Вид материала

Содержание

Вероятность быть в состоянии с энергией Е
Вероятность где-то в объеме "б"
F, а самому

Подобный материал:

1 2 3 4 5 6 7 8 9 ... 20

Лекция 4

       До сих пор мы не учитывали водного окружения белков. Пора восполнить этот пробел.

       Вода — весьма своеобразный растворитель. Прежде всего — она кипит и затвердевает при аномально высоких, для ее малого молекулярного веса, температурах. Действительно, вода — Н₂О — кипит при 373^оК, а твердеет при 273^оК, в то время как О₂ кипит при 90^оК и твердеет при 54^оК; Н₂ кипит при всего 20^оК и плавится при 4^оК; СН₄ кипит при 114^оК, и т.д. То, что структуры воды и льда с трудом разрушаются теплом, показывает, что молекулы воды чем-то очень сильно связаны между собой.
       Это "что-то" — связь между О и Н атомами молекул Н₂О (именно между О и Н, так как и О₂, и Н₂ в отдельности легко кипят и плавятся). Эта связь называется водородной связью.
       Водородные связи наблюдаются не только в воде. Они наблюдаются всегда, когда водород химически связан с одним электроотрицательным (т.е. притягивающим электрон) атомом и при этом приближается к другому электроотрицательному атому. Примеры: O—H : : : O, N—H : : : O, N—H : : : N. Но С-H группа, например, водородных связей не образует: атом С — недостаточно электроотрицательный атом.
       Основные особенности воды как растворителя связаны с наличием в ней мощных водородных связей.

       Водородная связь молекул воды носит электрическую природу. То, что она связана именно с электронами и зарядами, а не с ядрами водородных атомов, прямо следует из того, что температуры и теплоты кипения и плавления легкой (Н₂О) и тяжелой (D₂О) воды практически совпадают, — несмотря на двукратное различие в массах ядер D и Н.
       Молекула воды полярна. Это значит, что на ее атомах есть небольшие ("парциальные") электрические заряды: на электроотрицательном О — отрицательный, на Н — положительный. Распределение зарядов и электронных облаков на этих атомах выглядит так:

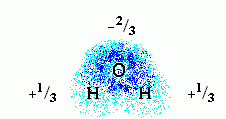
       Здесь плотность электронного облака показана плотностью точек, а цифры показывают парциальный заряд атомов этой полярной молекулы. Заряд этот выражен в долях от протонного заряда. У протона, в этих единицах, заряд, естественно, равен +1, а у электрона 1. В целом молекула воды имеет заряд 0.
       Заряды на полярных атомах появляются в результате того, что электроотрицательные атомы O оттягивают электронные облака от соседних Н атомов. В результате на последних возникают небольшие положительные заряды, а на O — отрицательный заряд.

       Как вы помните, заряды q₁ и q₂ на расстоянии r взаимодействуют в вакууме с энергией

U = q₁q₂/r.

(4.1)

В вакууме заряды взаимодействуют очень сильно. Энергия взаимодействия двух единичных (т.е. протонных или электронных) зарядов на расстоянии 1

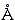близка к 330 ккал/моль (запомните эту цифру: она нам пригодится для разных дальнейших оценок), а на более реалистичном (учитывая Вандерваальсово отталкивание атомов) расстоянии 3

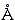эта энергия близка к 110 ккал/моль. Энергия взаимодействия единичных зарядов — это характерная энергия химической связи; она в сотни раз больше, чем характерная тепловая энергия kT или характерная энергия Вандерваальсового взаимодействия атомов.
Парциальные заряды молекулы воды меньше и потому взаимодействуют слабее — с энергией порядка 10 ккал/моль на расстоянии 3

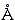, но и такой энергии хватает на то, чтобы, при притяжении Н к О, "промять" электронные оболочки атомов. Особенно этот эффект "проминания" облаков существенен для атомов водорода: здесь электронная оболочка Н, и так состоявшая всего из одного электрона, оттянута к О атому, так что смять ее особенно легко. Смять электронную оболочку, скажем, О атома много труднее — вокруг ядра О вращается 8 "своих" электронов, да еще какую-то часть электронного облака атом О (в Н₂О) оттягивает у соседних водородов.
Легкость проминания электронного облака у Н атома и превращает обычное электростатическое взаимодействие в водородную связь. Это относится ко всем водородным связям, из которых нас будут интересовать следующие, встречающиеся в белках связи: O—H : : : O, N—H : : : O, N—H : : : N.
Итак, электронное облако при Н атоме — самое слабое, и оно сильно сминается при притяжении парциального положительного заряда Н к парциальному отрицательному заряду O (или N) атома. В результате ядро Н подходит к ядру О или N не на 2.35 — 2.75

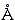(как то было бы при Вандерваальсовом взаимодействии, о котором мы говорили на прошлой лекции), а заметно ближе — на расстояние 1.8 — 2.1

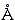(эти данные получены из кристаллов малых молекул).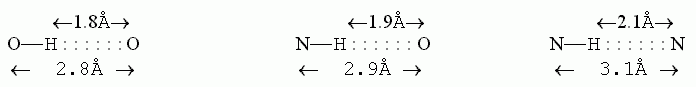

При таком сближении и возникает водородная связь (или Н-связь). Н-атом (или, точнее, О-Н или N-Н группа) называется донором водородной связи, а тот О или N атом, к которому этот Н приближается, называется акцептором водородной связи.
Обратите внимание, что наблюдающееся в кристаллах при образовании Н-связи расстояние между О и/или N атомами донора и акцептора близко к 3.0

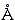(например, во льду расстояние между ними равно 2.8

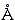). Это соответствует оптимальному Вандерваальсовому расстоянию между О и/или N атомами — т.е. наличие стоящего между ними Н атома не приводит к увеличению расстояния между донорным О (или N) и акцепторным О (или N) атомами: Н атом их не расталкивает, а связывает.

У каждой Н-связи один донор и один акцептор. При этом Н почти всегда выступает донором только одной Н-связи, а О может быть акцептором двух Н-связей. В последнем случае возникает "вилочковая" водородная связь.

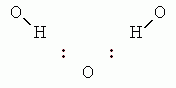
Так как при образовании "вилочки" сильно сближаются два Н-атома (с зарядом +¹/₃ каждый), то ее суммарная энергия меньше, чем удвоенная энергия одинарной (как на предыдущей схеме) Н-связи.
В отличие от Вандерваальсова взаимодействия, водородная связь весьма чувствительна к направлению — особенно к направлению донорной группы. Обычно валентная связь донора (N-H или О-Н) прямо смотрит на тот акцептор (О или N атом), с коим водородная связь образуется:

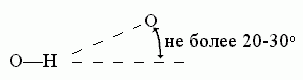
К ориентации акцепторной группировки водородная связь значительно менее чувствительна:

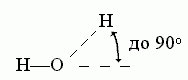
Энергия водородной связи составляет около 5 ккал/моль. Эта оценка базируется на сравнении экспериментальных теплот испарения сходных соединений, из которых одни могут завязывать водородные связи, а другие — нет. Например, теплота испарения диметилэфира — Н₃С-О-СН₃ — составляет около 5 ккал/моль, а теплота испарения спирта — СН₃-СН₂-ОН — около 10 ккал/моль. Эти вещества состоят из одних и тех же атомов — т.е. Вандерваальсовы взаимодействия в них практически одинаковы — но спирт может завязывать водородную связь, а диметилэфир — нет (у него нет О-Н группы!). Каждая ОН группа может быть донором только одной Н-связи, а ее О может такую связь акцептировать. Так как у каждой Н-связи должен быть один донор и акцептор, в спирте приходится по одной Н-связи на молекулу, т.е. цена одной водородной связи — около 10 ккал/моль - 5 ккал/моль = 5 ккал/моль.
Такая же оценка получается из теплоты испарения льда (680 кал/г = 680 кал/(1/18 моль) = 12 ккал/моль). Из них пара ккал/моль приходится на Вандерваальсовы взаимодействия — как видно из испарения малых молекул типа метана (СН₄) или О₂. На Н-связи остается около 10 ккал/моль. Во льду приходится по две водородных связи на молекулу Н₂О, т.к. Н₂О, со своими двумя ОН группами, может быть донором двух Н-связей (и столько же она может акцептировать своим О атомом). Значит, опять получается — примерно — (10 ккал/моль)/2 = 5 ккал/моль.

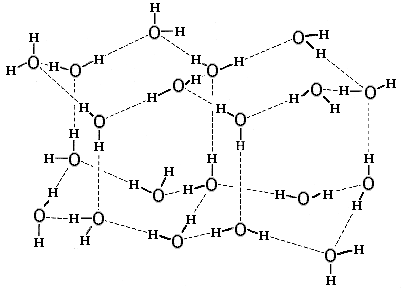
       Рис.4-1. Нормальный лед. Пунктир — Н-связи. В ажурной структуре льда видны небольшие полости, окруженные молекулами Н₂О. Картинка взята из [6].

       Структура нормального льда диктуется Н-связями (Рис.4-1): она хороша для геометрии этих связей (О-Н смотрит прямо на О), но не очень хороша для плотного Вандерваальсового контакта молекул Н₂О. Поэтому структура льда ажурна, в нем молекулы Н₂О обволакивают микроскопические (размером меньше молекулы Н₂О) поры. Ажурность структуры льда приводит к двум хорошо известным эффектам: (1) лед менее плотен, чем вода, он плавает в ней; и (2) под сильным давлением — например, лезвия конька — лед подплавляется.
       Большинство из существующих во льду (Рис.4-1) водородных связей сохраняется и в жидкой воде. Это следует из малости теплоты плавления льда (80 кал/г) по сравнению с теплотой кипения воды (600 кал/г при 0^оС). Можно было бы сказать, что в жидкой воде рвется только 80/(600+80) = 12% из существующих во льду Н-связей. Однако эта картина — что часть водородных связей в воде разорвана, а часть сохранена — неточна: скорее, все водородные связи в воде разбалтываются. Это хорошо иллюстрируется следующими экспериментальными данными.
       На приведенном внизу Рисунке 4-2, кривая 1 соответствует максимуму инфракрасного спектра поглощения групп О-Н во льду (где все Н-связи завязаны); кривая 2 соответствует максимуму инфракрасного спектра поглощения групп О-Н отдельных молекул Н₂О, растворенных в CCl₄ (где Н-связей нет — раствор Н₂О в CCl₄ слишком разбавлен); а кривая 3 соответствует спектру поглощения жидкой воды. Если бы в жидкой воде было бы два сорта О-Н групп — образующие водородные связи и не образующие их — и одни О-Н группы в воде колебались бы так же (с той же частотой), как во льду (где они образуют Н-связи), а другие — как в окружении CCl₄ (где они Н-связей не образуют). Тогда спектр воды имел бы два максимума, соответствующие двум состояниям О-Н групп, двум их характерным частотам колебаний: с какой частотой группа колеблется, с такой и поглощает свет. Но "двухмаксимумная" картина не наблюдается! Вместо нее на кривой 3 мы видим один, очень размытый максимум, простирающийся от максимума кривой 1 до максимума кривой 2. Это значит, что все О-Н группы в жидкой воде завязывают водородные связи — но все эти связи разболтаны, причем по-разному.
       Это показывает, что картина, в которой часть водородных связей в воде разорвана, а часть сохранена,  строго говоря, неверна. Однако она столь проста и удобна для описания термодинамических свойств воды, что ею широко пользуются — и мы тоже будем к ней обращаться. Но надо иметь в виду, что она не точна.

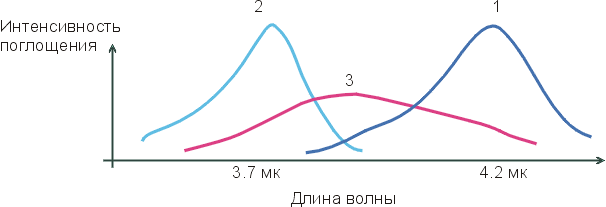
       Рис.4-2. Характерный вид инфракрасных спектров поглощения О-Н групп во льду (1), в окружении CCl₄ (2) и в жидкой воде (3).

       Обратимся теперь к взаимодействию белковой цепи с водой.
       Как и вода, остов белковой цепи полярен. Точнее — полярны входящие в остов пептидные группы. В целом остов белковой цепи имеет заряд 0, но распределение зарядов на его атомах (здесь опять заряд каждого атома выражен в долях от протонного заряда) выглядит так:

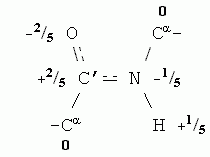
       Парциальные заряды содержат и некоторые боковые группы, например, Ser (его боковая группа — -СН₂-ОН — похожа на спирт). Еще более полярны заряженные аминокислотные остатки: заряд +1 присущ основаниям, входящим в боковые группы остатков Arg, Lys и His, когда они находятся в ионизованной форме (при примерно нейтральных рН), а у ионизованных кислотных боковых групп, Asp и Glu, заряд равен -1.

       И пептидные группы главной цепи, и полярные боковые группы выступают донорами и акцепторами водородных связей. Они могут завязывать водородные связи друг с другом или с молекулами воды — и практически все они завязывают такие связи, так как энергия водородных связей — 5 ккал/моль — раз в десять превосходит энергию теплового движения, т.е. тепловое движение не может разрушить эти связи — разве что время от времени оно случайно нарушает малую часть из них.

       Если внутримолекулярная связь между донором (D) и акцептором (А) водородной связи в белке завязывается в водном окружении, то эта связь замещает две водородные связи белка с молекулами воды (которые были до того, т.к. свято место пусто не бывает); и при этом еще создается одна связь между оторвавшимися молекулами воды:

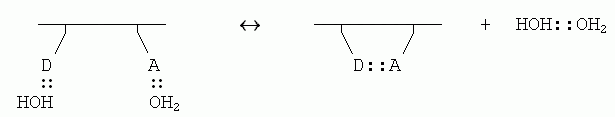
       Энергетический баланс этой реакции близок к нулю: две Н-связи было, две стало. Однако энтропия воды возрастает, так как вода больше не привязана к белковой цепи и связанные Н-связью молекулы могут плавать где хочется (а энтропия именно и связана с множественностью состояний системы). При этом рост энтропии за счет освобождения димера воды от белка — примерно такой же, как рост энтропии при уходе молекулы Н₂О изо льда в жидкую воду (в обоих случаях одна частица обретает свободу плавать).
       Энтропийный эффект выхода молекулы Н₂О изо льда в воду можно оценить следующим образом. Как известно, в точке плавления (для льда — при 0^оС, т.е. при 273^оК) энтропийный выигрыш от плавления как раз компенсирует энергетический проигрыш от него. А этот проигрыш нам известен: 80 кал/г, т.е. 80 Х 18 = 1440 кал/моль (18 - молекулярный вес Н₂О).
       Значит, вследствие роста энтропии свободная энергия системы "белок в воде" падает, — примерно на 1.5 килокалории на каждый моль формирующихся внутрибелковых водородных связей D:::A.
       Эта выделенная водой свободная энергия может полностью или частично скомпенсировать рост свободной энергии, сопровождающий падение энтропии при фиксации групп D и А связью D:::A (раньше они болтались как хотели, а теперь, связанные, — не могут). Позже мы увидим, что падение свободной энергии воды примерно компенсирует энтропию необходимой для образования водородной связи (N-H:::O) фиксации мономера во вторичных структурах полипептидных цепей. В результате регулярная вторичная структура полипептидов в воде находится как раз на грани стабильности.

       Итак, страшные слова — "энтропия" и "свободная энергия" — произнесены. Мой опыт показывает, что "энтропию" нормальный студент-биолог знает на слух (он слышал, что это — мера множественности состояний, мера беспорядка), а свободную энергию представляет совсем смутно... Так как нам понятие "свободная энергия" понадобится часто, я хочу уделить ей несколько минут сейчас, а потом, когда будет необходимо, поговорить о ней — и об энтропии — еще подробнее.

       Начнем с простого примера: пусть молекула может находиться в двух состояниях, "а" и "б", например, — здесь, в этой комнате, на высоте 200 м от уровня моря ("а"), и в монастыре Далай-Ламы, в Гималаях, на высоте 5 км ("б"). Как соотносятся вероятности этих двух состояний — при условии, что мы следим за нашей молекулой так долго, что она успеет побывать и здесь, и там?
       Обычно все помнят формулу Больцмана, которая гласит:

Вероятность быть в состоянии с энергией Е пропорциональна exp(-E/kT).

(4.2)

Физический смысл этой формулы заключается в том, что теплота окружающей среды (столкновения с другими молекулами) в определенной степени (в среднем — пропорционально температуре среды T) возбуждает нашу молекулу, и это позволяет ей забираться в область более или менее высоких энергий. Все это мы подробнее обсудим позже, а пока я позволю себе надеяться, что вы эту формулу помните. Напомню только, что k — это постоянная Больцмана, а T — абсолютная температура в градусах Кельвина.
Применительно к интересующему нас вопросу — как соотносятся вероятности пребывания молекулы на разных высотах — формула Больцмана сводится к барометрическому соотношению

[Вероятность быть на высоте б] относится к [вероятности быть на высоте а]

как exp(-E_б/kT) относится к exp(-E_а/kT) ,

(4.3)

где E_а — энергия молекулы в состоянии "а" (т.е. "здесь"), E_б — в состоянии "б" ("на высоте 5 км"), а T — абсолютная температура (для простоты, будем считать, что с высотой она не меняется).
       Из-за силы тяжести энергия молекулы "здесь" ниже, чем "на высоте 5 км"; так что, согласно Больцману, "на высоте 5 км" молекула будет проводить меньше времени, чем "здесь" [раза в полтора-два меньше; посчитайте сами при T=300^K, вспомнив, что E=mgh, где m — средняя масса молекулы воздуха (30 дальтон = 30 г/моль), g10м/с² — ускорение свободного падения, h5км — разность высот, а постоянная Больцмана k равна 1.38x10^ Джоуля/градус (Дж = кгxм^/сек^ = 0.24 кал) в расчете на частицу, т.е. 2 кал/град в расчете на моль (6x10^) частиц. Напомню, что R = 2 (кал/моль)/град. называется "газовой постоянной"].
       То есть молекул на высоте в 5 км будет раза в два поменьше, чем здесь. Точнее — поменьше в равных единицах объема, например — внутри легких (в чем легко убедиться, попробовав подышать на разных высотах). Однако в сумме число молекул в монастыре Далай-Ламы больше, чем в этой комнате: его монастырь куда больше, чем наша комната. То есть там молекула может находиться в большем числе положений — для свободно летающей молекулы воздуха это число пропорционально объему помещения. Физики говорят в этом случае, что в том монастыре возможно куда больше микросостояний молекулы, чем в нашей комнате. Поэтому вероятность того, что наша молекула находится где-то в монастыре Далай-Ламы, относится к вероятности того, что она находится где-то в этой комнате, как

[ Вероятность где-то в объеме "б"] : [вероятность где-то в объеме "а"] =

= [V_бexp(-E_б/kT)] : [V_аexp(-E_а/kT)]

Здесь V_а — объем суммы состояний "а" ("нашей комнаты"), а V_б — объем суммы состояний "б" ("его монастыря"). Вспомнив элементарную институтскую математику, а именно, что Vможно представить как exp(lnV), эту формулу можно переписать как

[Вероятность где-то в объеме б] : [вероятность где-то в объеме а] =

= [exp(-E_б/kT + lnV_б)] : [exp(-E_а/kT + lnV_а)] =

= [exp(-(E_б — Txk lnV_б)/kT)] : [exp(-(E_а — Txk lnV_а)/kT)]

Последняя формула очень напоминает формулу (4.3), формулу Больцмана, но только она относится не к единице объема, а ко всему объему системы, и — внимание! — вместо энергий Е в ней стоят величины E — Txk lnV. Так вот, величина F = E — Txk lnV называется свободной энергией нашей молекулы воздуха при заданном объеме V и температуре T. А величина S = k lnV называется энтропией нашей молекулы в объеме V.
       Это — в данном конкретном случае, когда "число доступных состояний" — это просто доступный для молекулы объем V (V_а — "нашей комнаты", V_б — "его монастыря").
       В общем случае, энтропия S просто равна k x [логарифм числа доступных состояний]. А свободная энергия F связана с энергией Е, энтропией S и температурой Т системы согласно общей формуле

F = E — TS

(4.4)

Из двух состояний стабильнее, т.е. вероятнее то, у которого свободная энергия ниже:

[Вероятность_где-то_в_объеме_"б"] : [вероятность_где-то_в_объеме_"а"] =

= exp(-F_б/kT):exp(-F_а/kT) = exp[-(F_б-F_а)/kT]

(4.5)

       Иными словами, более стабильному состоянию системы отвечает то, где ниже F, а самому стабильному состоянию системы (при заданной температуре и фиксированном объеме этой системы) отвечает минимум свободной энергии F.

       Таким образом — "свободная энергия" — это естественное расширение обычного понятия "энергии" на случай, когда система обменивается теплом с окружающей средой. Напомню: если тело не обменивается теплом со средой, его стабильное состояние отвечает минимуму его энергии (или, проще: все, что может упасть — падает). А окружающее тепло делает стабильными определенные флуктуации, прыжки — такие, которые минимизируют свободную энергию тела. То есть приток тепла возбуждает молекулы системы, они начинают захватывать многочисленные состояния с более высокой энергией (т.е. их энтропия растет) — и, в результате, молекулы воздуха летают, а не падают на землю.

       Спустимся, однако, с Гималаев к белкам.
       Итак — каков же баланс энергий, энтропий и свободных энергий в разобранном нами примере образования водородной связи в белковой цепи? Для полной наглядности, сравним ход процесса в разных условиях:

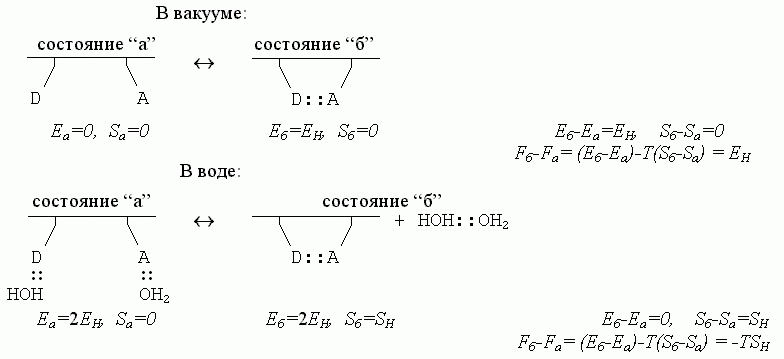
       Здесь E_H < 0 - энергия Н-связи, а S_H > 0 — энтропия перемещений и вращения свободного тела, т.е. свободной молекулы Н₂О или свободного димера НОH::OH₂. Водородные связи — воды с водой, воды с белком — стабильны, когда E_H-TS_H < 0 (а если E_H-TS_H > 0, т.е. если они нестабильны, — то есть в этом случае перед нами была бы уже не жидкая вода, а пар).
       Сравнение приведенных выше схем показывает, что водородные связи в белковой цепи как бы становятся — за счет изменения энтропии связывающейся воды — менее стабильными в водном окружении, чем в вакууме; действительно, в водном окружении их свободная энергия есть F_б-F_а = -ТS_H , — то есть она меньше, чем в вакууме, где F_б-F_а=E_H.

       Еще раз хочу подчеркнуть, что причина этого видимого ослабления — в том, что в водном окружении образовавшаяся внутри белковой цепи Н-связь замещает собой связь цепи с водой. И по той же причине водородные связи, стабилизующие структуру белка в воде носят энтропийную, а не энергетическую природу: энергии двух состояний цепи (с внутрицепочечной связью и без нее) примерно равны, и из этих двух состояний с примерно равной энергией стабильнее та, где выше энтропия, т.е. где больше число микросостояний. А их больше у оторванной молекулы воды, чем у связанной.

       Обратите внимание: водородные связи в белковой цепи (в водном окружении) носят энтропийную, а не энергетическую природу именно потому, что энергия Н-связей очень высока: раз так, "свободные" от связей в белке доноры и акцепторы водородных связей в цепи всегда на деле не свободны от всех связей вообще, а связаны с водой. Оторвавшиеся же от белка — при образовании внутрибелковой Н-связи — молекулы Н₂О тут же связываются друг с другом, так что энергия компенсируется, и свободно-энергетический выигрыш Н-связей в белке идет только от множественности возможных микросостояний оторвавшихся молекул воды. Правда, чтобы связаться друг с другом, молекулы Н₂О должны пожертвовать часть своей обретенной свободы, часть энтропии — но лучше уж потерять небольшую энтропию, чем большую энергию!

       То, что (1) молекулы воды сильно связаны друг с другом водородными связями; и (2) то, что эти связи образуются только при определенной взаимной ориентации молекул Н₂О — определяет специфику воды как растворителя. Это приводит к разным интересным эффектам. Подробнее мы об этом поговорим в двух следующих лекциях.

Blog

Курс лекций 1999-2000 гг

Содержание

Лекция 4