И. К. Беляевский маркетинговое исследование
| Вид материала | Исследование |
- Маркетинговое Агентство Step by Step 1 25047, г. Москва, ул. Чаянова, дом 15, корп., 41.45kb.
- А. Л. Абаев маркетинговое исследование, 395.17kb.
- 1. Выберите фирму, маркетинговое исследование которой Вы предпочитаете провести, 124.25kb.
- Курсового проекта актуальна, так как маркетинговое исследование – это исследовательская, 216.2kb.
- Маркетинговое Агентство Step by Step 125047, г. Москва, ул. Чаянова, д. 15/5 Тел. (495)250-61-74, 50.77kb.
- Маркетинговое исследование Маркетинговое исследование рынка запасных частей для легковых, 280.38kb.
- Тематика курсовых работ Разработка программы маркетингового исследования. Разработка, 27.44kb.
- Разработка программы маркетингового исследования. Разработка спецификации на маркетинговое, 27.82kb.
- Маркетинговое исследование потребителей городаБерезники, 37.08kb.
- Как провести маркетинговое иследование, 72.08kb.
4.4. Анализ тенденций и устойчивости развития
рыночной конъюнктуры
Важным элементом конъюнктурного анализа служит характеристика динамики исследуемого явления. Рынок, как мы уже указывали, - явление динамическое, он непрерывно изменяется, и время выступает в качестве абсциссы экономической кривой, отражающей тенденции развития рынка.
Тенденция развития рынка - экономическое и статистическое понятие, характеризующее закономерность изменения его основных параметров во времени.
Общее направление (вектор) развития и средняя скорость изменения погашают случайные отклонения от общего курса. Термин тенденция происходит от лат. tendere - направляться, стремиться. На основе количественных оценок и моделей динамики рынка даются качественные характеристики изменения рыночной ситуации: растущий/развивающийся рынок, стабильный рынок, сокращающийся рынок и т.д.
Для определения вектора и скорости развития рынка строятся динамические ряды показателей, характеризующих основные параметры рынка, а затем исчисляются темпы роста или прироста (базисные и цепные):
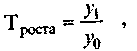 (4.15)
(4.15)где у0 и у1 - уровни динамического ряда соответственно базисного
и текущего периодов.
В табл. 4.15 приведены данные, характеризующие развитие рынка товара Q (цифры условные).
Таблица 4.15
Динамика основных параметров рынка товара Q
| периоды | Поставка, Тыс.т. | Продажа в розницу, тыс.т. | Цена, руб. кг | Товарный запас, дней | % к базисному периоду | |||
| поставка | продажа | цена | Товарный запас | |||||
| 1-й | 50 | 44 | 12 | 5 | 100 | 100 | 100 | 100 |
| 2-й | 60 | 46 | 16 | 8 | 120 | 104,5 | 133,3 | 160 |
| 3-й | 70 | 49 | 20 | 14 | 140 | 111,4 | 166,7 | 280 |
| 4-й | 66 | 36 | 40 | 21 | 132 | 81,8 | 333,3 | 420 |
| 5-й | 55 | 31 | 45 | 12 | 110 | 70,5 | 375,0 | 240 |
| 6-й | 46 | 30 | 45 | 12 | 92 | 68,2 | 375,0 | 240 |
Картина весьма противоречивая. Вероятно, рыночными структурами не было учтено повышение цен и его влияние на спрос. В результате до 3-го периода наращивалась поставка товаров. В результате росли запасы, что явилось индикацией усиления разбалансированности рынка. На основании данной информации можно более обоснованно судить о развитии ситуации на рынке, чем по неформальным данным торговых корреспондентов.
В тех случаях, когда изучаемое явление рынка представляет собой сложную агрегированную величину (например, товарооборот, состоящий из совокупности разнородных товаров), характеристика динамики количественных показателей достигается с помощью агрегатных или средних индексов, в частности, индекса физического объема товарооборота (т.е. оценки изменения стоимости товаров в сопоставимых ценах) и общего индекса цен1:
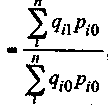 (4.16)
(4.16)где qi0 и qi1 - количество проданного i-го товара соответственно в базисном
и текущем периодах;
рi0 - цена i-го товара в базисном периоде.
Существует ряд способов исчисления индекса физического объема товарооборота. Они описаны в учебнике, на который мы ссылаемся. В данном пособии приводится наиболее простой и доступный метод, который может быть использован в том случае, когда исследователь располагает данными о продаже товаров в натуральном выражении и о ценах на них.
Пример. Данные о продаже и ценах трех товаров за два периода приведены в табл. 4.16 (цифры условные).
Таблица 4.16
Расчет индекса физического объема товарооборота
| Товар | Базисный период | Текущий период | Количество текущего периода в ценах базисного, тыс.руб. | ||||
| количество, т | Цена, руб. за 1 кг | Товарооборот, тыс. руб. | количество, т | Цена, руб. за 1 кг | Товарооборот, тыс. руб | ||
| qi0 | рi0 | qi0 рi0 | qi1 | рi1 | qi1 рi1 | qi1 рi0 | |
| А | 1 | 2 | 3 (гр.1 х гр.2) | 4 | 5 | 6 (гр.1 х гр.5) | 7 (гр.5 х гр.2) |
| 1-й | 500 | 12 | 600 | 300 | 24 | 7200 | 3600 |
| 2-й | 200 | 10 | 2000 | 200 | 10 | 2000 | 2000 |
| 3-й | 300 | 25 | 7500 | 600 | 15 | 9000 | 15 000 |
| | - | - | 15 500 | - | - | 18 200 | 20 600 |
Индекс товарооборота (в фактических ценах) исчисляется как отношение итога гр. 6 к итогу гр. 3:
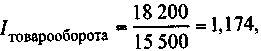
т.е. денежная выручка продавца увеличилась на 17,4%. Индекс физического объема товарооборота исчисляется как отношение итога гр. 7 к итогу гр. 3:
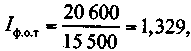
т.е. объем продажи товаров (в сопоставимых ценах) вырос на 32,9%.
Тенденции развития рынка определяются на основе анализа изменения основных своих параметров (поставки, продажи, цен, товарных запасов). Визуально рассматриваются динамические ряды темпов роста или их графические изображения (диаграммы), и на этой основе дается описательная характеристика тенденций. Иногда используется так называемый метод технического сглаживания уровней динамического ряда. Фактические данные (эмпирические уровни) наносятся на график, а после этого проводится линия, на глаз осредняющая все колебания. Такой метод широко применяется в анализе биржевой конъюнктуры, когда требуются моментальные выводы о тенденции развития рынка. Применяется еще достаточно простой, но не очень точный метод, известный в теории статистики как метод механического сглаживания, к которому мы еще вернемся в анализе сезонных колебаний.
Более надежный способ выявления основной тенденции развития рынка заключается в построении и графическом изображении трендовых моделей (так называемый метод статистического, или аналитического, выравнивания).
Тренд - графическое или математическое выражение закономерности динамического развития, т.е. отражение основной тенденции изменений изучаемого явления.
Данный метод имеет то преимущество, что определяет не только вектор, но и скорость развития, а также отражает его характер: ускорение (степенная и показательная кривая, парабола и-го порядка), рост с замедлением (полулогарифмическая кривая), спад с замедлением (гипербола), равномерное развитие (прямая) и т.д. Сущность данного метода заключается в том, что изменение явления (например, продажи товара) рассматривается как функция времени:
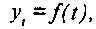 (4.17)
(4.17)где t- номер уровня (периода, даты) динамического ряда.
Более подробно об этом методе вы можете прочесть в любом учебнике по теории статистики1.
Для построения трендовых моделей используются уравнения, отбираемые по минимуму остаточной дисперсии. Ниже приводятся общие формулы соответствующих уравнений:
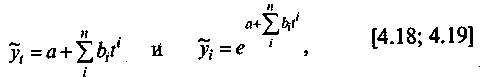
где уi - выровненное (сглаженное) значение уровней динамического ряда;
а - свободный член уравнения, экономически не интерпретируемый;
bi - i-е параметры уравнения, характеризующие скорость или ускорение развития рынка;
е - основание натурального логарифма;
t - номер уровня динамического ряда (периода, даты);
n - число i-х параметров в уравнении.
Для расчета параметров трендовых моделей используются стандартные программы ПЭВМ, а для линейных и линеаризированных моделей можно использовать систему нормальных уравнений, которая в общем виде имеет следующий вид:
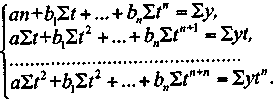 (4.20)
(4.20)Однако практически использовать систему нормальных уравнений можно только ограниченно: для моделей, построенных по функции не более чем второго порядка. В противном случае придется решать больше трех уравнений. Расчет можно упростить, если использовать следующие формулы сумм значений t с первой по четвертую степень:
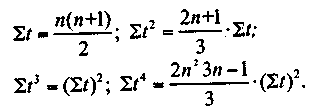 (4.21, 4.22, 4.23, 4.24)
(4.21, 4.22, 4.23, 4.24)К числу наиболее употребительных трендовых моделей относятся следующие:
1. Линейная (прямая):
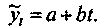 (4.25)
(4.25)Данное уравнение позволяет определить вектор развития: параметр b с плюсом - рост, b с минусом - спад. Он указывает на то, что рынок развивался равномерно, без ускорения или замедления. Модель тренда по линейной функции отражена на рис. 4.5.
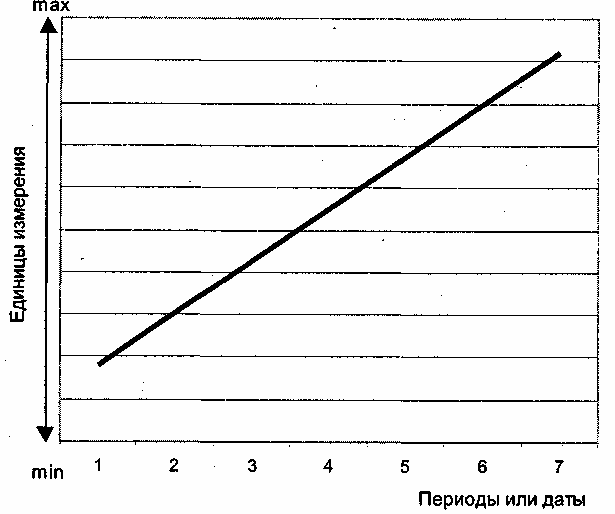
Рис. 4.5. Трендовая модель тенденции развития рынка по прямой
2. Парабола 2-го порядка
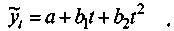 (4.26)
(4.26) Данная модель позволяет выявить не только скорость развития b1, но и его ускорение (b2). В зависимости от знаков параметров определяется вектор развития (рост, спад, ускорение, замедление). Поэтому возможно применение данной модели в широком диапазоне примеров.
Не следует забывать, что криволинейную тенденцию часто хорошо аппроксимирует парабола более высокого, чем второй, порядка:
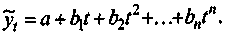
Параболический рост, а затем спад отражены на рис.4.6
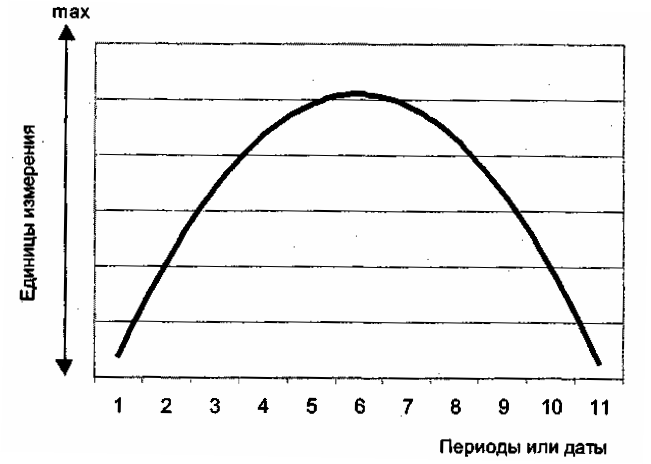
Рис. 4.6. Модель тенденции развития рынка по параболе 2-го порядка
3. Экспонента
В тех случаях, когда прирост зависит от величины основания функции, обычно используют сглаживание по экспоненциальной кривой (экспоненте). Она обычно отражает нарастание приростов. Ее формула:
У̃t = аеbt, а в линеаризированном виде: lg yt = lg a + bt (4.28; 4.29)
Моделирование тренда по экспоненте в графической форме представлено на рис. 4.7.
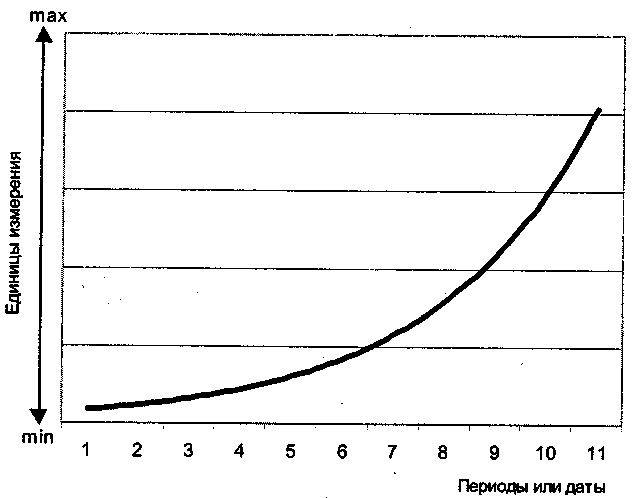
Рис. 4.7. Трендовая модель тенденции развития рынка по экспоненте
4. Степенная и показательная функции
На практике чаще встречаются тенденции, которые можно отразить уравнениями степенной и показательной функций:
 (4.30, 4.31)
(4.30, 4.31)(уравнения могут быть представлены в линейном виде):
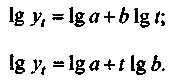 (4.32, 4.33)
(4.32, 4.33)В частности, показательная функция используется для сглаживания, когда цепные темпы роста динамического ряда более или менее постоянны.
Модель тренда по показательной функции в графической форме отражена на рис. 4.8.
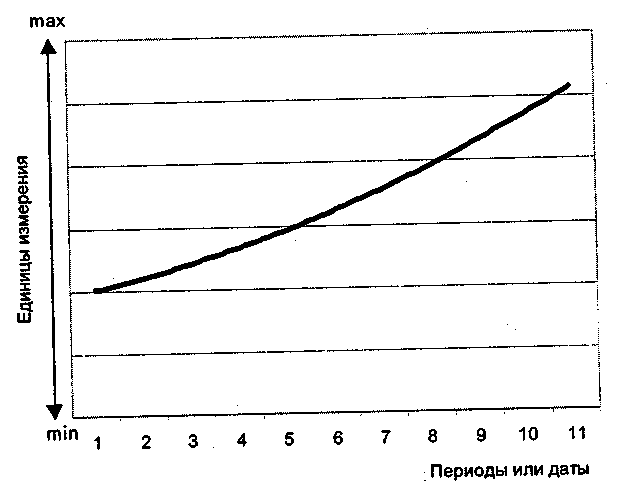
Рис. 4.8. Трендовая модель тенденции развития рынка по
показательной функции
5. Логарифмическая (полулогарифмическая) функция
Если равномерный или даже ускоренный рост параметров рынка сменяется замедлением или затуханием развития, то такую тенденцию достаточно надежно отражает логарифмическая функция типа
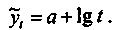 (.34)
(.34)В графической форме подобная трендовая модель показана на рис. 4.9.
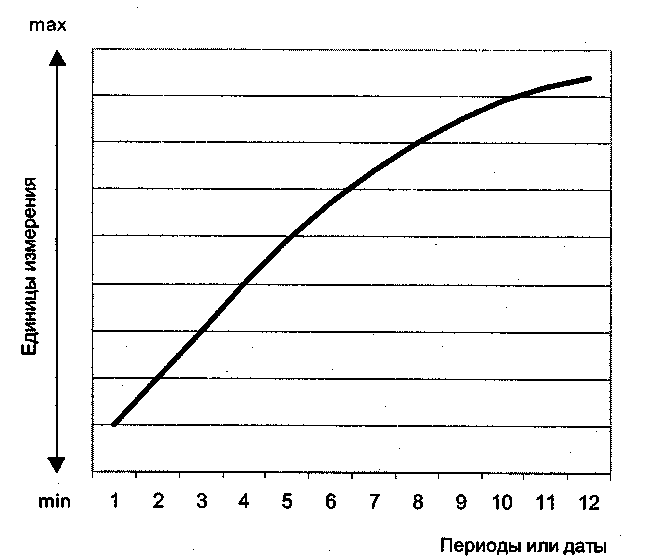
Рис. 4.9. Трендовая модель тенденции развития рынка по логарифмической функции
6. Гипербола
Тенденция к сокращению параметров рынка (спад) отражается каждой из рассмотренных функций в зависимости от характера изменения. При этом меняются знаки в уравнениях - с плюса на минус. Однако моделирование процесса сжатия рынка, если происходит спад с нарастающим замедлением к концу периода, хорошо отражается функцией гиперболы:
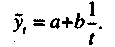 (4.35)
(4.35)Графическая форма модели тренда показана на рис. 4.10.
Трендовые модели используются также для краткосрочных прогнозов, когда есть вероятность инерционного развития рынка. Исходят из того, что сложившиеся в прошлом тенденции при соответствующих условиях можно распространить (экстраполировать) на прогнозируемый период. В формулу уравнения подставляется номер последующего периода (прогнозируемого: / + 1 и т.д.). Для долгосрочного периода, когда существенно меняются рыночные условия и окружающая среда, этот метод мало подходит. Несколько позже мы рассмотрим проблему составления прогноза.
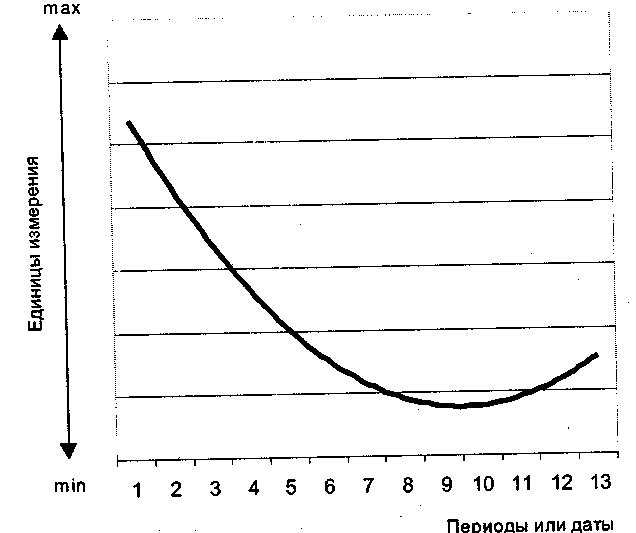
Рис. 4.10. Трендовая модель тенденции развития рынка по гиперболе
Пример. Оценка тенденции равномерного развития рынка. Данные об изменении цены товара X приведены в табл. 4.17.
Несмотря на значительные колебания цены в отдельные месяцы, в целом за все изучаемое время она выросла в 3 раза. В среднем за месяц она увеличивалась на 10,6% (за базу принят 1-й месяц). Расчет среднего темпа роста ведется по следующей формуле1:
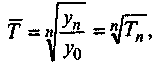 (4.36)
(4.36)где Т̃ - средний за все периоды темп роста (чаще его называют среднегодовым темпом), в нашем примере исчислен корень 11-й степени.
Таблица 4.17
Динамика цены товара X
| Месяцы, t | Цена товара, X, yi | Произведение, yt | Темпы роста, % | |
| базисные | цепные | |||
| 1 | 20 | 20 | 100 | - |
| 2 | 8 | 16 | 40 | 40 |
| 3 | 30 | 90 | 150 | 375 |
| 4 | 12 | 48 | 60 | 40 |
| 5 | 40 | 200 | 200 | 333 |
| 6 | 22 | 132 | 110 | 55 |
| 7 | 48 | 336 | 240 | 218 |
| 8 | 31 | 248 | 155 | 65 |
| 9 | 58 | 522 | 290 | 187 |
| 10 | 50 | 500 | 250 | . 86 |
| 11 | 70 | 770 | 350 | 140 |
| 12 | 61 | 732 | 305 | 87 |
| I | 450 | 3614 | - | - |
Расчет также может быть выполнен по формуле:
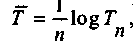 (4.36а)
(4.36а)где Тn- темп роста за весь период:
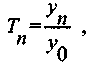 (4.36б)
(4.36б)где уn и у0 - соответственно уровни динамического ряда за последний
и начальный (базисный) периоды;
n - число периодов (дат, уровней), не считая базисного.
Средний абсолютный прирост цены за весь период равен
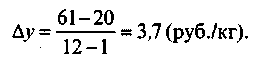
Однако, эта формула игнорирует все уровни ряда, за исключением начального и конечного. Используем одну из моделей тренда, наилучшим образом аппроксимирующую эмпирические значения уровней динамического ряда. В данном случае нет основания считать, что товарооборот растет с ускорением. Поэтому мы выбираем для отражения основной тенденции линейную модель тренда. Результат ее расчета на ПЭВМ был приведен на рис. 4.11, где показаны эмпирические данные и их трендовая линия, выражающая общую тенденцию развития.
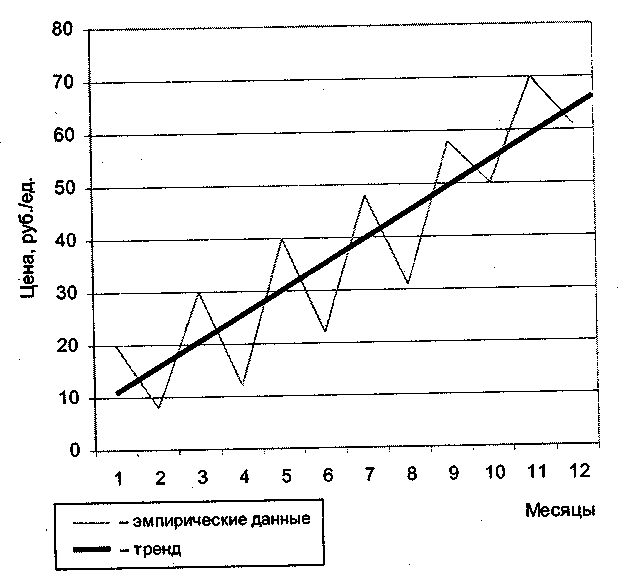
Рис. 4.11. Тенденция роста цены
Данные, приведенные в таблице, указывают на отсутствие ускорения или замедления роста цены. Поэтому мы вправе воспользоваться линейной функцией для выявления основной тенденции развития. Расчет на ЭВМ позволил построить следующую модель:
ỹt = 6,18 + 4,82/ (руб./кг) .
Это означает, что средний прирост цены за период с учетом всех колебаний составлял 4,8 руб./кг.
К этому же результату мы придем, если выполним расчет «вручную», не используя компьютер, а опираясь на формулы 4.20- 4.22. В этом случае суммы номеров месяцев и их квадратов составят:
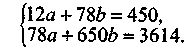
Система нормальных уравнений будет выглядеть следующим образом:
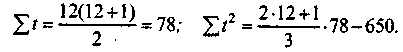
Решив ее, получим, что b = 4,82, а = 6,18, т.е. параметры модели те же, что и вычисленные ЭВМ.
Стихийность рынка, действие случайных, непредсказуемых факторов проявляется в колебаниях его параметров, в их отклонениях от линии нормального развития. Рыночные колебания имеют два вектора: динамический (колебания во времени) и пространственный (колебания по предприятиям, по территории). В первом случае наблюдаются рассмотренные ранее отклонения от основной тенденции развития, во втором - от среднего уровня состояния рынка. Чем меньше размах колебаний, т.е. чем устойчивее рынок и его развитие, тем надежнее его оценки и прогнозы, тем ниже риск маркетинговых мероприятий. Характеристика устойчивости развития рынка является важным этапом конъюнктурного анализа.
Как выявить колебания основных параметров рынка, каким образом измерить их интенсивность и тем самым определить степень устойчивости рынка? Техническая (графическая) характеристика способна визуально обратить наше внимание на неравномерное или, наоборот, на равномерное развитие рынка. В первом случае график покажет ломаную линию динамики, а во втором - линию, близкую к прямой. Рисунок отразит и размах колебаний. Однако это неформальная оценка, не позволяющая смоделировать процесс, выразить его количественно, сравнить с базисным периодом или с другим рынком.
Напомним, что линия тренда как бы осредняет колебания, равно удалена (в идеале) от точек, характеризующих эмпирические уровни динамического ряда. Это дает возможность использовать трендовую модель в целях измерения устойчивости развития рынка во времени. Определяется средний размер отклонений от тенденции развития, выраженной линией тренда.
В процессе анализа динамической устойчивости рынка нельзя использовать обычный коэффициент вариации, поскольку, чем выше скорость развития и больше угол возвышения тренда, тем больше будет отклонение от средней и соответственно больше коэффициент вариации, даже при полной равномерности развития. Посмотрите следующие два графика, которые иллюстрируют данное положение и доказывают неприемлемость определения отклонения от среднего уровня при оценке динамической устойчивости развития рынка (рис. 4.12):
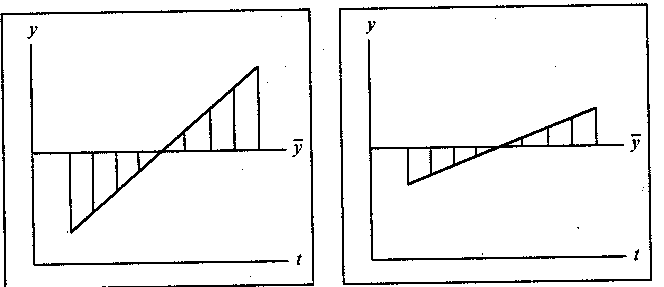
А. Высокие темпы роста Б. Низкие темпы роста
Рис. 4.12. Отклонение тренда от среднего уровня
И в том и в другом случае развитие было равномерным: оно выражено прямой линией. Однако в первом случае (А) темпы роста были высокими, соответственно отклонение от средней оказывается большим. Во втором случае (Б) темпы были невысокими, соответственно отклонение от среднего уровня незначительно.
Устойчивость (или как ее антипод - колеблемость) развития рынка во времени проявляется в характере отклонений фактических уровней развития от основной тенденции, т.е. от тренда. Это позволяет измерять устойчивость развития рынка известным в анализе динамики показателем - коэффициентом аппроксимации. Исчисляется среднеквадратическое отклонение эмпирических уровней от тренда (yi-yt):
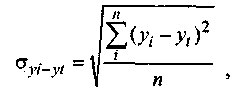 (4.37)
(4.37)где yi-yt - среднеквадратическое отклонение эмпирических уровней динамического
ряда от тренда;
уi - i-й уровень динамического ряда;
уt - сглаженный i-й уровень динамического ряда (тренд);
n - число i-х уровней динамического ряда.
Все же нельзя забывать, что среднеквадратическое отклонение выражено в именованных числах, и его результат зависит от размерности уровней динамического ряда. Поэтому следует выразить его в процентах к среднему уровню. Такой показатель называется коэффициентом аппроксимации (от лат. арргохтаге -приближаться):
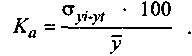 (4.38)
(4.38)Именно этот показатель, варьирующий в диапазоне между 100% и 0, отражает степень устойчивости развития рынка.
Продолжим пример. Данные о динамике продажи товара за 6 месяцев из табл. 4.17 перенесены в табл. 4.18. В нее же включены данные, полученные после подстановки в уравнение тренда значений времени (t):
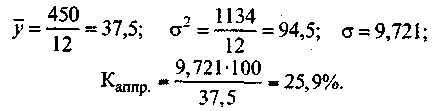
По отклонениям от тренда была исчислена остаточная дисперсия, а затем среднеквадратическое отклонение эмпирических данных от тренда. Для того чтобы стандартизовать эту величину, было исчислено ее процентное отношение к среднему уровню ряда (коэффициент аппроксимации). Он составил почти 26%. Это означает, что рынок развивался неустойчиво, в своем развитии цены колебались в значительной степени.
Однако чаще развитие рынка приобретает нелинейный характер. Рассмотрим пример, когда динамика товарооборота аппроксимирована уравнением параболы 2-го порядка (рис. 4.13):
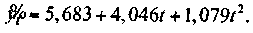
Таблица 4.18
Расчет устойчивости роста цены товара X
| Месяцы, t | Цены, руб. /кг, yi | Выровненное значение, yt | Квадрат отклонений (yi - yt)2 |
| 1 20 11 81 2 8 16 64 3 30 21 81 4 12 25 169 5 40 30 100 6 22 35 169 7 48 40 64 8 31 45 196 9 58 50 64 10 50 54 16 11 70 59 121 12 61 64 9 450 450 1134 | |||
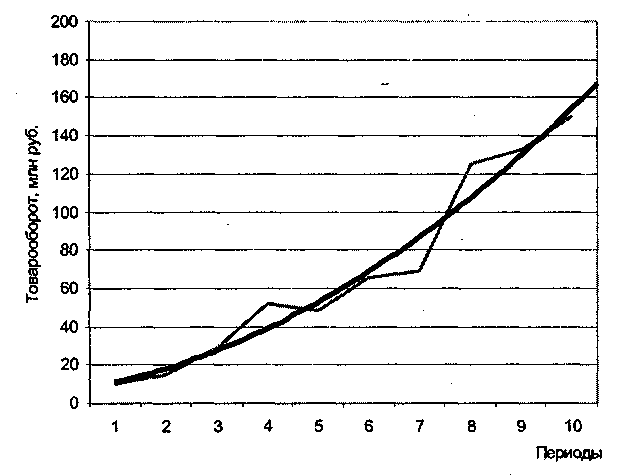
Рис. 4.13. Устойчивость нелинейного развития рынка
Диаграмма показывает, что развитие рынка происходило недостаточно устойчиво. Расчет коэффициента аппроксимации подтвердил этот вывод. Его значение составило 42,3%.
Как видно, анализ тенденций и колеблемости рынка - это достаточно трудоемкий процесс, требующий сбора соответствующей информации, построения динамических рядов, статистических расчетов (как правило, с использованием электронно-вычислительной техники). Для оперативных целей наряду с графическим (техническим) методом характеристики тенденций и устойчивости рынка и методами механического сглаживания, также не требующими сложных расчетов, рекомендуется использовать уже упоминавшийся специфический конъюнктурный метод тестирования.
В практике конъюнктурного анализа получили большое распространение тенденциальные опросы, являющиеся по существу вариантом экспертного исследования (см. 2.4). Именно на их основе разрабатываются конъюнктурные тесты, которые представляют собой средние арифметические из трех возможных оценок сложившейся тенденции развития рынка: рост (подъем), стабильность, понижение (спад), каждой из которых присваивается соответствующий балл. В результате дается обобщающая оценка тенденций развития рынка.
Конечно, любые качественные характеристики рынка носят отпечаток субъективности, но в них можно включать и объективные показатели: темп роста товарооборота (Т), уровень устойчивости (Ка), степень деловой активности. На рис. 4.14. показаны варианты оценки состояния рынка и перехода из одной ситуации в другую.
Не менее важна характеристика колеблемости рынка в статике, в территориально-экономическом пространстве, например вариация цен по предприятиям, выступающим со своими товарами на рынке. Сильные колебания, в частности, могут указывать на проявления ценовой конкуренции или на неустойчивость рыночной ситуации, часто обусловленную дифференциацией спроса. Так, в пределах одного и того же города наиболее высокие цены обычно отмечаются в центре; в «спальных» районах цены, как правило, ниже; самые низкие цены складываются в производственных зонах (табл. 4.19).
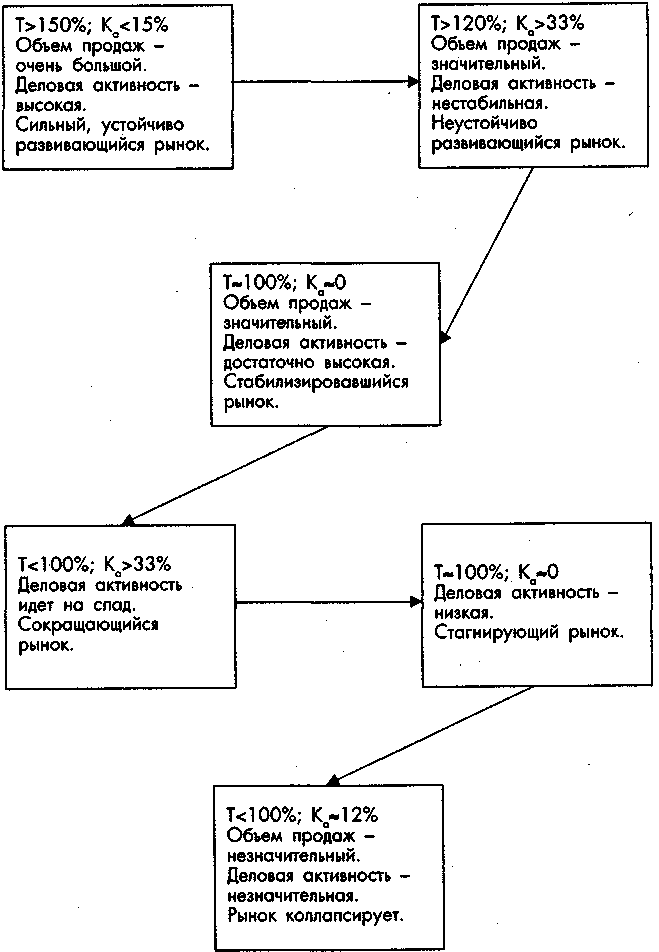
Рис. 4.14. Варианты оценки рыночной ситуации
Таблица 4.19
Группировка предприятий по уровню цен на товар
| Группы с уровнем цен | В них предприятий | |
| единиц | % к итогу | |
| Низким | 22 | 5 |
| Средним | 387 | 86 |
| Высоким | 41 | 9 |
| Итого | 450 | 100 |
В зависимости от распределения предприятий дается оценка степени различий рыночных параметров: чем больше доля средней группы, тем устойчивее рынок. Например, низкие цены были отмечены всего на 5% предприятий, высокие - на 9%, а на остальных предприятиях цены были на среднем уровне. Проиллюстрируем пример диаграммой (рис. 4.15).
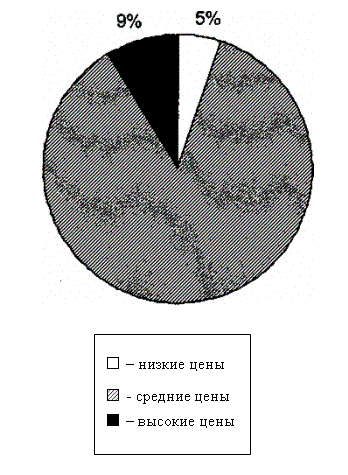
Рис. 4.15. Структура торговых предприятий по уровню цен на товар
Секторная диаграмма наглядно показала, что по параметру цен рынок находится в устойчивом состоянии. Другое дело, если каждая группа занимает в совокупности значительное место. Например, низкий уровень цен отмечался на 20% предприятий, средний - на 32% и высокий - на 48%.
Если в первом случае всего на 14% предприятий цены отклонялись от среднего уровня, то во втором примере средняя по ценам группа предприятий уже не преобладает над другими, которые занимают значительное место в совокупности. Это указывает на существенную неравномерность в состоянии рынка (по данному параметру).
Существует еще одна возможность наглядной характеристики колеблемости параметров рынка в экономическом пространстве на определенную дату, т.е. в статике: отложить на графике фактические значения параметров и изобразить линию, характеризующую средний уровень. Рассмотрим соответствующий пример (рис. 4.16).
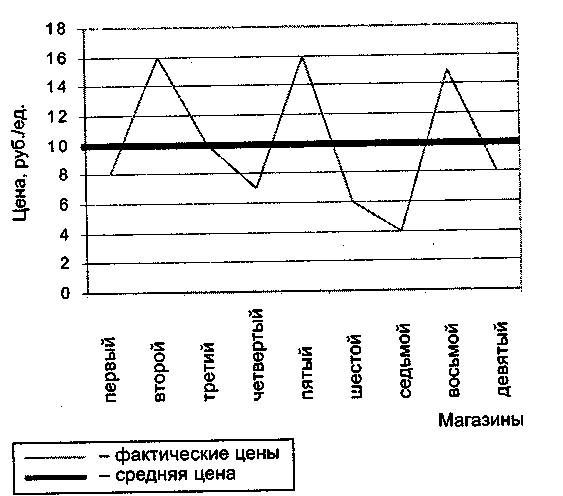
Рис. 4.16. Вариация цен по магазинам
Формализованные оценки колеблемости показателей рынка в статике, в частности в географическом или экономическом пространстве (или по регионам, или по конкурирующим фирмам, или по собственным предприятиям - торговым единицам и т.п.), осуществляются с помощью следующей формулы:
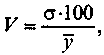 (4.39)
(4.39)где V - коэффициент вариации (стандартизованный в процентах к среднему уровню
по территории или по предприятиям);
- среднеквадратическое отклонение, исчисляемое по формуле
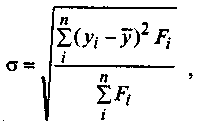 (4.40)
(4.40)где n - число i-х единиц (предприятий, регионов);
Fi - «вес», характеризующий размер i-й единицы (товарооборот, численность
населения и т.п.);
yi - параметр рынка i-го предприятия (или региона);
y̅ - среднее значение параметра (средний уровень), исчисляемое по формуле
средней арифметической взвешенной:
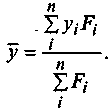 (4.41)
(4.41)В тех случаях, когда взвешивание невозможно осуществить или когда структура более или менее однородна, допустимо прибегать к косвенным характеристикам (например, использовать показатели размерности, в регионах - численность населения, на предприятиях -торговую площадь, число работающих и т.п.) или в крайнем случае использовать невзвешенные средние.
Приведем в качестве примера таблицу, на основе данных которой была построена диаграмма вариации цен по предприятиям (табл. 4.20, цифры условные).
Таблица 4.20
Данные о ценах на 1 апреля 1999 г. и о товарообороте за апрель
по 10 магазинам
| № п/п | Цена товара X, руб./ед. - y | Продано, тыс. ед. F | Произведение, yF | (уi – y)2 |
| А | 1 | 2 | 3 | 4 |
| 1 | 8 | 250 | 2000 | 3802,5 |
| 2 | 16 | 520 | 5120 | 13784,2 |
| 3 | 10 | 480 | 4810 | 1732,8 |
| 4 | 7 | 200 | 1400 | 4802,0 |
| 5 | 16 | 500 | 8000 | 1 805,0 |
| 6 | 6 | 180 | 1080 | 6265,8 |
| 7 | 4 | 50 | 200 | 3120,5 |
| 8 | 16 | 600 | 9000 | 5766,0 |
| 9 | 8 | 250 | 1760 | 3346,2 |
| 2 | - | 3000 | 33 370 | 44425,0 |
Предварительно было рассчитано как отношение итога гр. 3 таблицы на итог гр. 2 среднее по всем магазинам значение варьирующей цены:
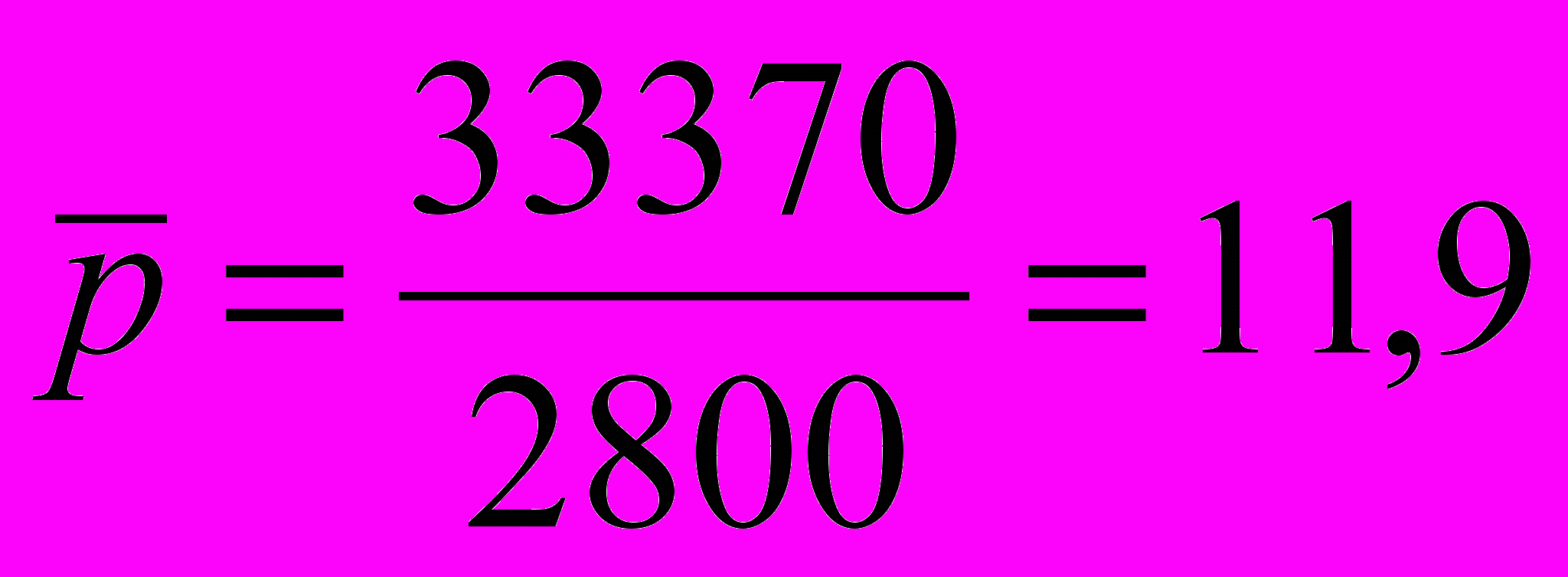 (руб./ед.)
(руб./ед.)Затем исчисляются дисперсия (отношение итога гр. 4 к итогу гр. 2), а из нее - среднеквадратическое отклонение:
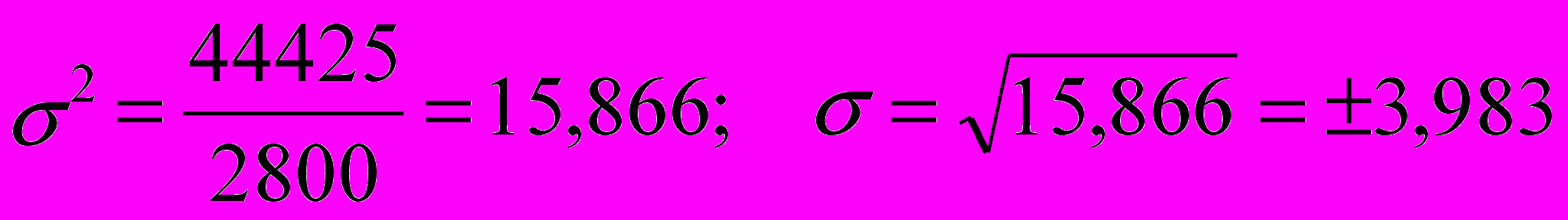 (руб./ед.)
(руб./ед.)В стандартизованном виде вариацию цен отражает коэффициент вариации:
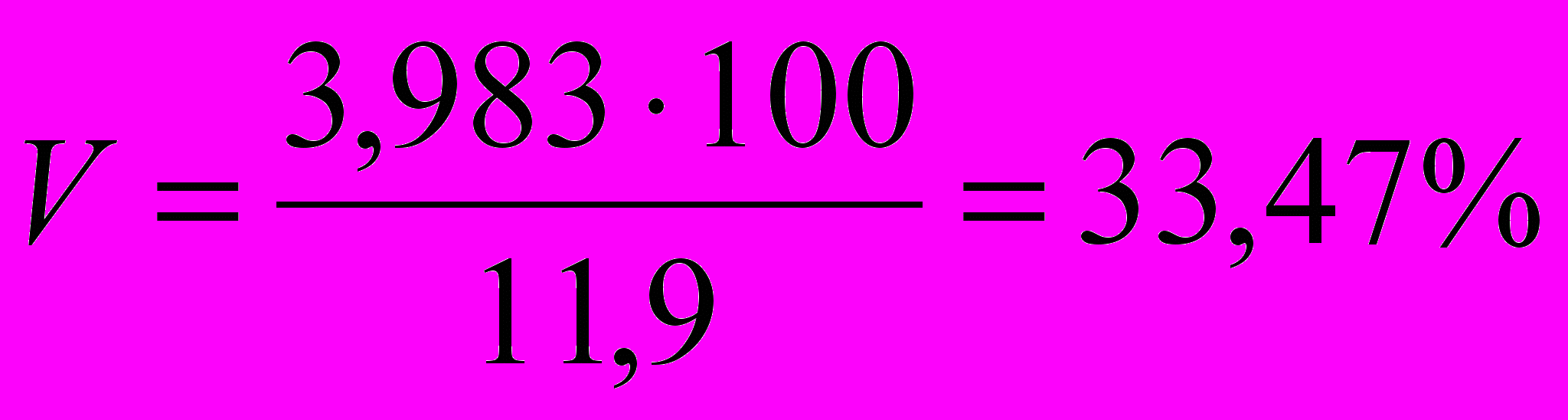 ,
,а это означает, что имеет место высокая колеблемость цен по предприятиям, выступающим на рынке.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. В чем заключается цель изучения тенденций развития рынка?
2. Какими показателями можно охарактеризовать устойчивость/неустойчивость развития рынка в динамике и статике (по территории, по предприятиям и т.п.)?
3. Что собой представляет трендовая модель развития рынка?
4. Каковы различия экономической интерпретации прямолинейной и криволинейной трендовых моделей развития рынка?
5. Можно ли охарактеризовать изменение товарооборота фирмы, исключив влияние динамики цен?
ТЕСТЫ
1. Основная тенденция развития рынка - это:
а) закономерность изменения его параметров во времени;
б) развитие товарооборота в соответствии с ранее намеченным планом;
в) динамика товарооборота, цен и товарных запасов.
2. Индекс физического объема товарооборота может быть использован в конъюнктурном анализе:
а) для измерения скорости продажи объема многоструктурной товарной массы;
б) для оценки сбалансированности рынка;
в) для оценки устойчивости рынка.
3. Техническое сглаживание уровней динамического ряда является:
а) сглаживанием эмпирических данных с помощью специальной техники;
б) оценка тенденции развития «на глазок» без использования эмпирических данных;
в) проведение трендовой линии визуально, таким образом, чтобы она была равноудалена от всех точек эмпирических данных.
4. Какая модель тренда отражает сокращение продажи с постепенным замедлением падения:
а) уравнения прямой линии;
б) уравнения степенной кривой;
в) гиперболы.
5. Экстраполяция - это:
а) логический вывод о дальнейшем развитии параметров
рынка;
б) балансовый способ определения неизвестных данных;
в) подстановка в уравнение тренда номера следующего периода/даты.
