Geum.ru

Фгоу впо мгуп учебно-методический комплекс мсис пуховский 2011 Федеральное государственное образовательное учреждение высшего профессионального образования «московский государственный университет природообустройства»

Вид материалаУчебно-методический комплекс

Содержание


Значения  при различных числах измерения n
Распределение Стьюдента. Значения
Задача 3. Обработка результатов многократных измерений. Поиск скрытой закономерности по критерию Аббе
Примечание, предварительно требуется провести экстраполяцию данных справочной таблицы к числу дат в задании
Дайте определение класса точности, найдите в учебнике варианты обозначения классов точности приборов и их использование для расч
Министерство сельского хозяйства российской федерации
Подобный материал:
1   2   3   4   5   6

Значения  при различных числах измерения n





n
q = 1 – 
n
q = 1 – 


0,10

0,05

0,025

0,01

0,10

0,05

0,025

0,01

3
1,406
1,412
1,414
1,414
15
2,326
2,493
2,638
2,808

4
1,645
1,689
1,710
1,723
16
2,354
2,523
2,670
2,837

5
1,731
1,869
1,917
1,955
17
2,380
2,551
2,701
2,871

6
1,894
1,996
2,067
2,130
18
2,404
2,557
2.728
2,903

7
1,974
2,093
2,182
2,265
19
2,426
2,600
2,754
2,932

8
2,041
2,172
2,273
2,374
20
2,447
2,623
2,778
2,959

9
2,097
2,237
2,349
2,464
21
2,467
2,644
2,801
2,984

10
2.146
2,294
2,414
2,540
22
2,486
2,664
2,823
3,008

11
2.190
2,383
2,470
2,606
23
2,504
2.683
2,843
3,030

12
2,229
2.387
2,519
2,663
24
2,520
2,701
2,862
3,051

13
2,264
2,426
2,562
2,714
25
2,537
2,717
2,880
3,071

14
2,297
2,461
2,602
2,759

















  • В соответствии с правилами оформления результатов измерений рассчитайте доверительный интервал с использованием коэффициентов Стьюдента (Доверительную вероятность принимать равной 0,95).

Распределение Стьюдента. Значения

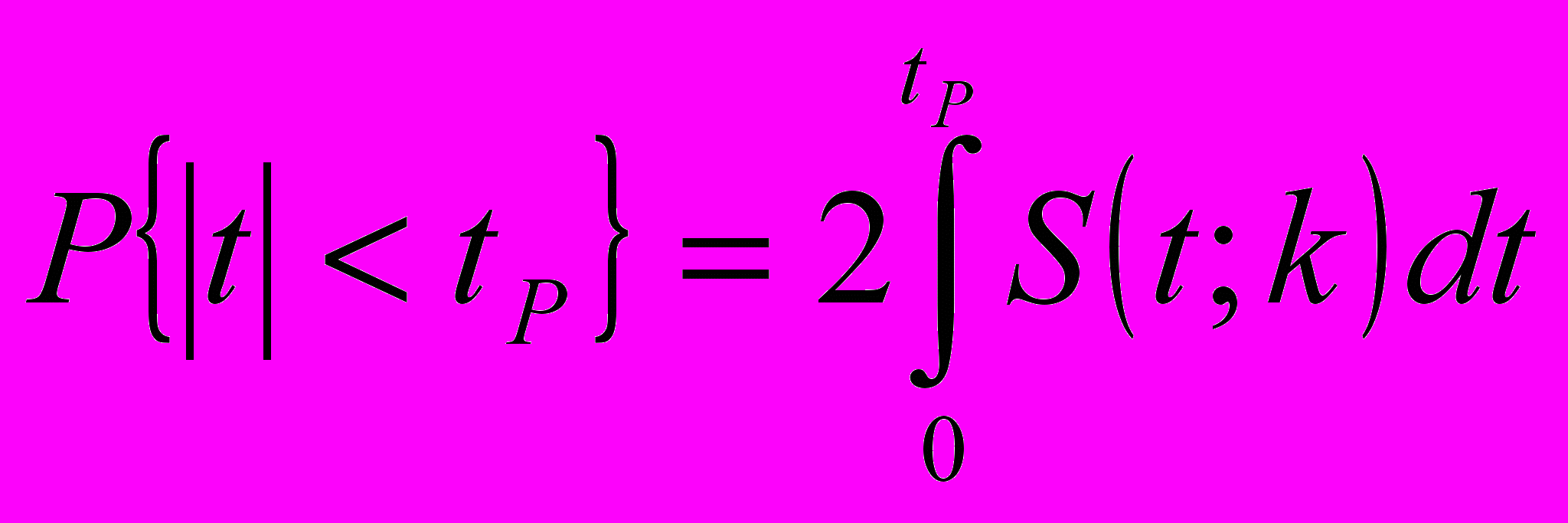
k
P


0,90

0,95

0,98

0,99

1
6,314
12,706
31,821
63,657

2
2,920
4,303
6,965
9,925

3
2,353
3,182
4,541
5,841

4
2,132
2,776
3,747
4,604

5
2,015
2,571
3,365
4,032

6
1,943
2,447
3,143
3,707

7
1,895
2,365
2,998
3,499

8
1,860
2,306
2,896
3,355

9
1,833
2,262
2,821
3,250

10
1,812
2,228
2,764
3,169

11
1,796
2,201
2,718
3,106

12
1,782
2,179
2,681
3,055

13
1,771
2,160
2,650
3,012

14
1,761
2,145
2,624
2,977

15
1,753
2,131
2,602
2,947



Задача 3. Обработка результатов многократных измерений. Поиск скрытой закономерности по критерию Аббе


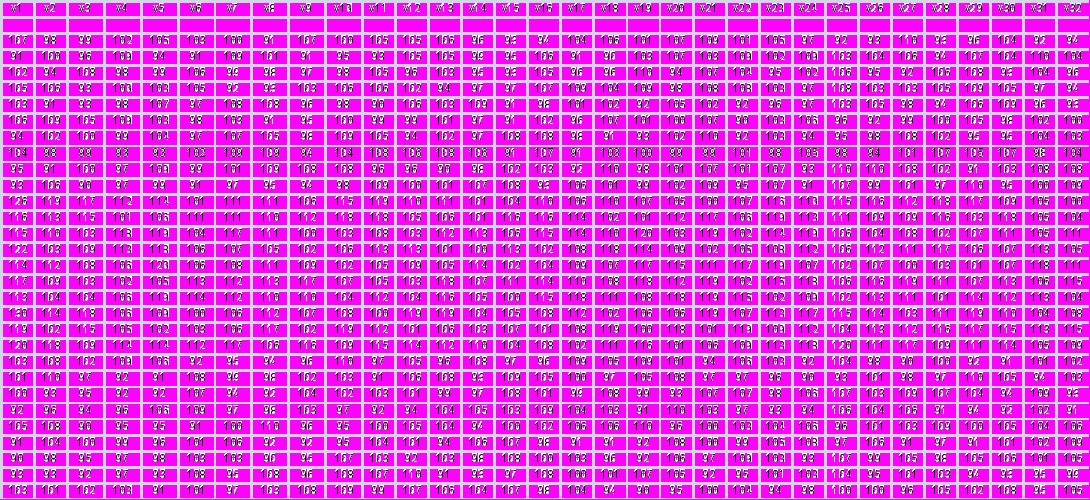Исходные данные для вариантов приведены в таблице.
  1. Построить график и визуально оценить наличие скрытой закономерности
  2. Рассчитать критерий Аббе и сравнить его с табличным значением для выбранного уровня значимости и сделать заключение о наличии или отсутствии систематической погрешности.

Примечание, предварительно требуется провести экстраполяцию данных справочной таблицы к числу дат в задании

справочная таблица



n*
Значения критерия Аббе при уровне значимости


0,001

0,01

0,05

4
0,295
0,313
0,390

5
0,208
0,269
0,410

6
0,182
0,281
0,445

7
0,185
0,307
0,468

8
0,202
0,331
0,491

9
0,221
0,354
0,512

10
0,241
0,376
0,531

11
0,260
0,396
0,548

12
0,278
0,414
0,564

13
0,295
0,431
0,578

14
0,311
0,447
0,591

15
0,327
0,461
0,603

16
0,341
0,474
0,614

17
0,355
0,487
0,624

18
0,368
0,499
0,633

19
0,381
0,510
0,642

20
0,393
0,520
0,650

* n – число измерений

Задача 4. Обработка результатов однократных измерений с учётом метрологических характеристик приборов


Дайте определение класса точности, найдите в учебнике варианты обозначения классов точности приборов и их использование для расчета погрешности


Var1. Микроамперметр на 100 мкА имеет шкалу в 200 делений. Определите цену деления и возможную допускаемую погрешность в делениях шкалы, если на шкале прибора имеется обозначение класса точности 1,0.


Var2. Сравните относительные погрешности измерений давления в 100 кПа пружинными манометрами классов точности 0,2 и 1,0 с пределами измерений на 600 и 100 кПа соответственно.


Var3. Вычислите относительную погрешность измерения скорости ветра, если предел допускаемой основной погрешности у анемометра, которым производились измерения, составляет =±(0,1+0,05V) м/с, а измеренное значение составило 2 м/с.


Var4. Вычислите абсолютную и относительную погрешности измерения давления в 100 кПа пружинным манометром класса точности 0,2 с пределом измерений на 600 кПа.


Var5. Класс точности некоторого прибора обозначен как 2,5/1,5. Какой погрешности соответствует эта форма записи? Напишите выражение для предела допускаемой погрешности, соответствующее этому обозначению класса точности.


Var6. Микроамперметр на 100 мкА имеет шкалу в 200 делений и класс точности 1,0. Определите цену деления. Вычислите возможную допускаемую погрешность (в мкА). Вычислите относительную погрешность прибора при измеренном значении, равном 50 мкА.


Var7. Указатель отсчётного устройства вольтметра с диапазоном измерения от 0 до 200 вольт класса точности 0,5 показывает 150 В. Чему с учётом погрешности прибора равно измеряемое напряжение?


Var8. Вычислите относительную погрешность измерения скорости ветра, если предел допускаемой основной погрешности у анемометра, которым производились измерения, составляет =±(0,1+0,05V) м/с, а измеренное значение составило 4 м/с.


Var9. Вычислите абсолютную и относительную погрешности измерения давления в 100 кПа пружинным манометром класса точности 1,0 с пределом измерений на 100 кПа.


Var10. Класс точности некоторого прибора обозначен как 6,0/5,0. Какой погрешности соответствует эта форма записи? Напишите выражение для предела допускаемой погрешности, соответствующее этому обозначению класса точности.


Var11. Микроамперметр на 100 мкА имеет шкалу в 200 делений и класс точности 1,0. Определите цену деления. Вычислите возможную допускаемую погрешность (в мкА). Вычислите относительную погрешность прибора при измеренном значении, равном 10 мкА.


Var12. Указатель отсчётного устройства ампервольтметра класса точности 0,02/0,01 со шкалой от -50 до +50 А показывает 10 А. Чему с учётом погрешности прибора равна измеряемая сила тока?.


Var13. Вычислите относительную погрешность измерения скорости ветра, если предел допускаемой основной погрешности у анемометра, которым производились измерения, составляет =±(0,1+0,05V) м/с, а измеренное значение составило 5 м/с.


Var14. Вычислите абсолютную и относительную погрешности измерения давления в 300 кПа пружинным манометром класса точности 0,2 с пределом измерений на 600 кПа.


Var15. Класс точности некоторого прибора обозначен как 1,5/1,0. Какой погрешности соответствует эта форма записи? Напишите выражение для предела допускаемой погрешности, соответствующее этому обозначению класса точности.


Var16. Указатель отсчётного устойства амперметра класса точности 1,5 с равномерной шкалой от -5 до +20 А показывает 15 А. Чему равна измеряемая сила тока?




Var17. Указатель отсчётного устройства мегаомметра класса точности 2,5 с неравномерной шкалой показывает 50 МОм. Чему равно измеряемое сопротивление?


Var18. Измеренное значение скорости ветра, полученное с помощью крыльчатого анемометра, составило 0,6 м/с. Предел допускаемой погрешности при различных скоростях ветра представлен в таблице "Сведения о поверке" из паспорта анемометра крыльчатого АСО-3 ГОСТ 6376−74 паспорт П6.2.781.003 ПС.


Величина

[скорость направленного воздушного потока, м/с]

Номинальная
предельного отклонения

0,3

0,4

0,8

1,5

4

5
±0,115

±0,12

±0,14

±0,175

±0,3

±0,35


Проведя линейную интерполяцию, представьте результат измерения с учётом погрешности прибора. Вычислите также относительную погрешность.


Var19. Вычислите абсолютную и относительную погрешности измерения давления в 50 кПа пружинным манометром класса точности 1,0 с пределом измерений на 100 кПа.


Var20. Класс точности некоторого прибора обозначен как 6,0/1,0. Какой погрешности соответствует эта форма записи? Напишите выражение для предела допускаемой погрешности, соответствующее этому обозначению класса точности.




Var21. Класс точности некоторого прибора обозначен как 6,0 . Какой погрешности соответствует эта форма записи?


Var22. Класс точности некоторого прибора обозначен как 2,0 . Какой погрешности соответствует эта форма записи? Какие особенности может иметь шкала данного прибора?


Var23. Определить погрешность определения относительной влажности воздуха аспирационным психрометром, если её измеренное значение составило 40%, а температура окружающего воздуха в момент производства измерений была 5 0С.


Температура воздуха С
Относительная влажность, %

100
60
20
10

Погрешность в измерении относительной влажности, % к измеряемой величине

30

20

10

0

−5

−10
±1,5

±2

±3

±4

±5

±7
±2

±3

±4

±6

±9

±12
±5

±7

±11

±17

±25

±35
±9

±14

±20

±35

±50

±70


Var24. Цифровой частотометр класса точности 2,0 с номинальной частотой 50 Гц показывает 49 Гц. Чему равна измеряемая частота?




Var25. Класс точности некоторого прибора обозначен как 4 . Какой погрешности соответствует эта форма записи?


Var26. Класс точности некоторого прибора обозначен как 6,0 . Какой погрешности соответствует эта форма записи? Какие особенности может иметь шкала данного прибора?


Задача 5. Методы стандартизации

Для var1…20

При параметрировании размеров некоторого изделия был применен ряд:

var1: 1; 2,5; 5; 7,5; 10; 12,5 …

var2: 1,5; 3; 4,5; 6; 7,5 …

var3: 3; 6; 9; 12; 15 …

var4: 50; 60; 70; 80; 90 …

var5: 30; 35; 40; 45; 50 …

var6: 0,2; 0,4; 0,6; 0,8; 1; 2; 3; 4; 5; 10; 15; 20 …

var7: 1; 1,5; 2; 2,5; 3; 6; 9; 12; 15; 20; 25; 30 …

var8: 80; 85; 90; 95; 100; 110; 120; 130; 140; 150; 175; 200; 225 …

var9: 10; 20; 30; 40; 50; 75; 100; 125; 150; 200; 250; 300 …

var10: 6; 7; 8; 9; 10; 12; 14; 16; 18; 20; 24; 28; 32 …

var11: 1; 4; 16; 64; 256 …

var12: 1; 8; 64; 512; 4096 …

var13: 10; 20; 40; 80; 160 …

var14: 10; 50; 250; 1250; 6250 …

var15: 120; 240; 480; 960; 1920 …

var16: 1,00; 1,60; 2,50; 4,00; 6,30; 10,00 …

var17: 1,00; 1,25; 1,60; 2,00; 2,50; 3,15; 4,00; 5,00; 6,30; 8,00; 10,00 …

var18: 1,00; 1,12; 1,25; 1,40; 1,60; 1,80; 2,00; 2,24; 2,50; 2,80; 3,15 …

var19: 1,00; 1,06; 1,12; 1,18; 1,25; 1,32; 1,40; 1,50; 1,60; 1,70; 1,80 …

var20: 1,00; 1,12; 1,25; 1,40; 1,60; 1,80; 2,00; 2,24; 2,50; 2,80; 3,15 …


а) Установите вид прогрессии, лежащей в основе ряда.

б) Приведите расчёт абсолютной и относительной разностей между значениями начального члена ряда и следующего за ним, а также между значениями предпоследнего и последнего члена, приведённого в условии задачи. Если Ваш вариант 6, 7, 8, 9,10, 17, 18, 19,20, то дополнительно вычислите абсолютную и относительную разности между значениями 6-го и 7-го членов ряда.

в) Если Вы идентифицировали геометрическую прогрессию, то приведите расчёт её знаменателя.

г) Не является ли заданный ряд рядом Ренара? Докажите.

д) Если Вы идентифицировали простую арифметическую либо геометрическую прогрессию, то продлите ряд на три числовые значения.


Для Var21…24

При производстве нового изделия было решено использовать

var21: унифицированных деталей — 38 шт., оригинальных деталей — 12 шт;

var22: унифицированных деталей — 166 шт., оригинальных — 44 шт;

var23: унифицированных деталей — 620 шт., оригинальных— 51 шт;

var21: унифицированных деталей — 1100 шт., оригинальных— 920 шт.

Вычислите коэффициент унификации.

Для Var25…26

var25. В производстве некоторого изделия используется 62 унифицированные детали. Известно, что коэффициент унификации равен 70%. Сколько оригинальных деталей в изделии? Каково общее число деталей?

var26. В производстве некоторого изделия используются 33 унифицированные детали. Известно, что коэффициент унификации равен 40%. Сколько оригинальных деталей в изделии? Каково общее число деталей?


МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ


ФГОУ ВПО «Московский государственный университет

природообустройства»