Лекция №1 введение

Вид материала

Лекция

Содержание Количество подведенной теплоты равно Для газа массы m работа равна 3) Изотермический процесс идеального газа. Адиабатный процесс Уравнение первого закона термодинамики для адиабатного процесса имеет вид Уравнение для адиабатного процесса имеет вид Зависимости между начальными и конечными параметрами процесса. Политропный процесс. Политропный процесс Газовые смеси. Пр: атмосферный воздух, горючая смесь или рабочее тело, продукты сгорания. Для каждой газовой смеси справедливы следующие положе Закон Дальтона. Формирование 2 закона термодинамики. Условия работы тепловых машин Рассмотрим круговой цикл тепловой машины Коэффициент полезного действия данной тепловой машины определяется Обратимый цикл тепловой машины. Работа совершаемая рабочим телом вычисляется по уравнению Тепловая диаграмма Принцип возрастания энтропии ... Полное содержание

Подобный материал:

• С. В. Шадрина Лекция 5 сентября, 15: 00-16: 30, Введение в геометрию пространства модулей, 5.97kb.
• Первая лекция. Введение 6 Вторая лекция, 30.95kb.
• Текст лекций н. О. Воскресенская Оглавление Лекция 1: Введение в дисциплину. Предмет, 1185.25kb.
• А. И. Мицкевич Догматика Оглавление Введение Лекция, 2083.65kb.
• Лекция введение в экологию (В. И. Торшин), 1146.79kb.
• Конспект лекций н. О. Воскресенская Москва 2008 Оглавление: Лекция Введение в дисциплину, 567.5kb.
• План лекций педиатрический факультет 1 семестр 1 лекция. Введение в анатомию человека., 216.63kb.
• Сидоров Сергей Владимирович Планы лекций Введение в профессионально-педагогическую, 19.81kb.
• Русской Православной Церкви и их особенности. 22 сентября лекция, 30.24kb.
• План лекций: Лекция №1. Введение в тему, общие сведения. Введение, 99.54kb.

Изменение внутренней энергии

Δ U=U₂-U₁=i/2·m/μ·R (T₂-T₁)

Количество подведенной теплоты равно

q=i/2 i/2·m/μ·R ΔT

2) Изобарный процесс
P=const

d p=O

Pv=RT

v / T=const U₁/T₁=U₂/T₂ U₁/U₂=T₁/T₂

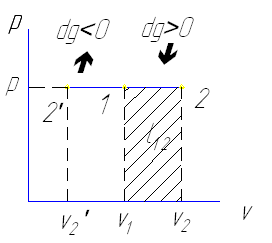
1-2 изобарное расширение dv>0 , dT >0

1-2^' изобарное сжатие dv<0 связано с уменьшением температуры dT<0

и отводе теплоты dq <0

Работа в этом процессе равна

v₂

ℓ=∫ p(v₂-v₁)=R(T₂-T₁)

v₁

Для газа массы m работа равна

L=m ℓ =mR(v₂-v₁)=p(V₂-V₁)

Изменение внутренней энергии зависит от изменения температуры и

вычисляется как в изохорном процессе.

ΔU=i/2·٧RΔT

При изобарном расширении подведенное к нему количество теплоты q расходуется на увеличение его внутренней энергии dU и на совершение газовой работы ℓ.

q=dU+ ℓ

dU=q- ℓ

Примечание:

Для изобарного расширения газа от V₁ до V₂ при котором увеличивается его Т, требуется большее количество теплоты, чем при изотермическом процессе, в котором температура газа не изменяется в ходе процесса.


3) Изотермический процесс идеального газа.

Осуществить изотермический процесс можно только при наличии

достаточно большой емкости источника теплоты данной температуры,

обеспечивающей непрерывный подвод теплоты к телу в течение всего

процесса, при постоянной температуре.

T=const dT=0

Pv=RT

Pv=const

P₁v₁=P₂v₂

P₁ / P₂=v₂/v₁



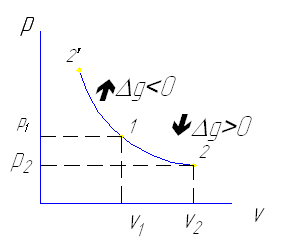
1-2 изотермическое расширение dv>0 , dp<0

1-2^' -изотермическое сжатие dv<0 , dq<0 , dp>0

При изотермическом процессе внутренняя энергия

ΔU=i/2·٧·R·ΔT

ΔU=O

Согласно 1 закону термодинамики в изотермическом процессе количество

подведенной теплоты Q полностью расходуется на совершение работы .

q=ℓ

v₂ v₂ v₂

ℓ =∫ p dv=∫ RT/v·dv= RT ∫ dv/v= RT(ℓnv₂- ℓnv₁)= RTℓn v₂/v₁= RTℓn p₂/p₁

v₁ v₁ v₁

Pv=RT

P=RT/v

Адиабатный процесс

Термодинамический процесс в тепло изолированной системе т.е. в системе

которая не обменивается теплотой с окружающими телами.

Для наиболее эффективного преобразования внутренней энергии газа,

совершаемую им работу следует предотвратить возможные потери

внутренней энергии в результате теплоотдачи окружающими телами ,

поэтому систему тепло изолируют .

q=0 dq=O

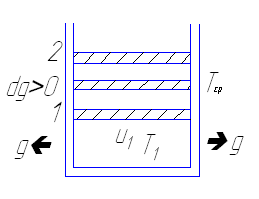Лекция № 9

Но даже если система недостаточно тепло изолирована до при быстром протекании процесса расширения или сжатия газа, теплообмен между данной системой и окружающими телами не успевает произойти за малый промежуток времени и процесс с некоторыми допущениями можно считать адиабатным.

Адиабатный процесс широко распространен.

Уравнение первого закона термодинамики для адиабатного процесса имеет вид:

0=dU+dℓ

т.к.g=0

dU=-dℓ или

ΔU=-ℓ

При адиабатном расширении работа совершается за счет уменьшения внуртенней энергии газа (температура понижается по сравнению с первоначальной)

ΔU=i/2·m/μ·R·ΔT=C_v· ΔT= C_v·(T₂-T₁)

ℓ= - ΔU= C_v·(T₁-T₂)

Работа газа в адиабатном процессе достаточно просто выражается через температуры Т₁ и Т₂ начального и конечного состояния.



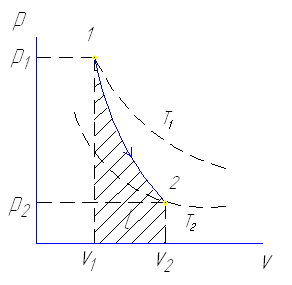
Изменение температуры газа адиабатном процессе приводит к тому, что его давление уменьшается более резко.

При адиабатном сжатии одновременно с резким ростом давления происходит повышение температуры.

Резкое нагревание воздуха при адиабатном сжатии используются в двигателях внутреннего сгорания.

При сжатии поршнем воздуха находящего в цилиндре двигателя его температура значительно возрастает до 600-850º С.

Впрыскивание жидкого топлива в конце такта сжатия приводит к его воспламенению и соответственно к резкому возрастанию давления рабочего тела вызывающему рабочий ход поршня в противоположном направлении.

Уравнение для адиабатного процесса имеет вид:

Pv^к=const – уравнение Пуассона

где к- показатель адиабаты.

к= С_р/ C_v

к_{1 ат}=1,67

к_{2 ат}=1,4

к_мн.ат=1,33

Зависимости между начальными и конечными параметрами процесса.

P и v

P₂/P₁=(v₁/ v₂)^к

T и v

T₂/ T₁= (v₁/ v₂)^к

T и P

T₂/ T₁=(P₂/P₁)^k-1/k


Работа 1 кг газа определяется по формуле:


ℓ= C_v· (T₁-T₂)

ℓ=R/k-1 · (T₁-T₂) T₁ и T₂

ℓ=1/ k-1 · (P₁v₁- P₂v₂) без T

ℓ= P₁v₁/ k-1· (1-(P₂/ P₁)^k-1/k) без T и v₂


L=m·ℓ

mv=V

L=1/ k-1 · (P₁V₁- P₂V₂) без T

L= P₁V₁/ k-1· (1-(P₂/ P₁) ^k-1/k) без T и V₂

L= mR/k-1 · (T₁-T₂) T₁ и T₂

L= mR´/k-1 · (T₁-T₂)

mR´=R

Политропный процесс.

Получился от сочетания двух греческих слов “поли”-много, “тропос”-путь.

Политропный процесс является обобщающим ранее рассмотренных 4 процессов.

Политропный процесс-это термодинамический процесс при котором остается постоянная теплоемкость.

Примеры политропных процессов с=const.

1. Изобарный процесс c=C_p
   
2. Изохорный процесс c=C_v
   
3. Изотермический процесс c=±∞
   
4. Адиабатный процесс c=0
   

Политропа - это кривая представляющая политропный процесс графически. Уравнение политропы для идеального газа.

Pvⁿ=const

где n-показатель политропы n=c-c_p/с-с_v

При различных значениях показателей политропы из уравнения политропы следует уравнение изопроцессов.

1. n=0 p=const
   

2) n=1 pv=const

3) n=k pv^k=const

4) n=±∞ v=const

В зависимости между начальными и конечными параметрами процесса, аналогичны зависимостям при адиабатном процессе, при условии замены показателей адиабаты на показатели политропы.

P₂/ P₁=(v₁/ v₂)ⁿ

ℓ= R/n-1 · (T₁-T₂)

Газовые смеси.

Газовой смесью называется смесь отдельных газов, химически не реагирующих между собой, т.е. каждый газ смеси полностью сохраняет свои свойства и занимает весь объем смеси.

Пр: атмосферный воздух, горючая смесь или рабочее тело, продукты сгорания.

Для каждой газовой смеси справедливы следующие положения:

1. Каждый газ входящий в смесь имеет температуру равную температуре смеси;
   
2. Любой из газов входящих в смесь распространяется по всему объему смеси и поэтому объем каждого газа равен объем всей смеси;
   
3. Каждый из газов входящий в смесь подчиняется своему уравнению состояния. Смесь в целом является как бы новым газом и подчиняется своему уравнению состоянию.
   

Закон Дальтона.

Давление смеси идеальных газов равно сумме парциальных давлений входящих в состав его газов.

P_см=P₁+ P₂+…..+P_n=∑P_i

Парциальным называется давление которое окажет газ входящая в смесь если он один будет занимать весь объем смеси при той же температуре.

Способы задания газовых смесей.

1. массовыми долями;
   
2. объемными долями;
   
3. мольными долями.
   

1) Массовой долей газа входящего в смесь называется отношение массы этого газа к массе смеси.

m₁=M₁/M_см

m₂=M₂/M_см

M₁₂- массы отдельных газов

M_см- масса смеси

M_см =∑M_i

∑m_i=1

2)Объемной долей газа входящего в смесь, называется отношение приведенного парциального объема (V₁,V_2,V_i) этого газа к объему смеси V_см

r₁= V₁/ V_см

r₂= V₂/ V_см

r_i- объемная доля газа

Приведенный объем можно представить в виде: если из сосуда где находится смесь удалить все газы, кроме данного и оставшийся газ сжать до давления смеси сохранив температуру , то его объем будет приведенным (или парциальным)

Определение парциального давления композиционной смеси если известен его объем

P_i/ P= V_i/ V

P V_i= P_iV

P_i=PV_i/V=r_ip

3) мольные доли

Лекция № 10

2 закон термодинамики

Введение

Существуют различные виды энергии механическая, внутренняя, электромагнитная, ядерная и др.

Энергия от греческого energeia -действие, деятельность.

Энергия-мера различных форм движения материи.

Взаимные превращения различных видов энергии происходят при переходе движения материи из одних форм в другие.

Данные превращения могут осуществляться различными способами. В термической термодинамике рассматривают два способа передачи энергии: механическая работа и теплота. Теплота и работа не являются равноценными формами передачи энергии. Работа может быть преобразована в любой вид энергии. Теплоту без промежуточного превращения в работу можно лишь использовать для увеличения внутренней энергии тела.

Причем в работу теплота может быть преобразована только при соблюдении определенных условий.

Возможность преобразования теплоты в работу, а также максимально возможное превращение работы в теплоту определяется 2 законом термодинамики.

Формирование 2 закона термодинамики.

1 закон термодинамики заключает, что не возможно построить машину, которая не смогла образовывать энергию.

Допущение:

1. Он не накладывает ограничений на возможность превращения энергии из одного вида в другую. При единственном условии, что бы общее количество теплоты было эквивалентно общему количеству работы. Это верно для превращения работы. L-Q. Работа совершенная над системой идет на увеличение ее внутренней энергии и выделение некоторого количества теплоты Q. Тело всегда можно нагреть трением, при этом получается количество энергии в форме тепла, точно равная проделанной работе. Электрическая энергия может быть превращена в теплоту при прохождении электрического тока через сопротивление. Однако существуют ограничения при превращении теплоты в работу. Если бы этого не было то можно было построить машину, которая путем охлаждения окружающих тел превращала взятую температуру в работу т.к. запас тепловой энергии содержащейся в воде и атмосфере и земле практически не ограничен Такая машина была эквивалентна вечному двигателю, Такую гипотетическую машину называют вечным двигателем второго рода
   

2 закон термодинамики исключает построение вечного двигателя второго рода.

Кельвин 1851 г.дал следующую формулировку 2 закона термодинамики: невозможен процесс, единственным конечным результатом которого будет превращение в работу всей теплоты извлеченного и теплового источника.

Из всей теплоты подведенного от “горячего” источника (нагревателя), только часть ее может быть преобразована в работу, остальная часть должна быть отведена в “холодный” источник (охладитель)

2. Первый закон термодинамики не устанавливает направления протекания тепловых процессов, также он не может отличить обратимые процессы от необратимых.
   

Однако как показывает опыт тепловые процессы могут протекать в одном направлении.

Пр : при тепловом контакте двух тел с различными температурами тепловой поток направлен в сторону более холодного тела. Подобные процессы называются необратимыми.

Немецкий физик Клаудиус дал другую формулировку 2 закона термодинамики: невозможен процесс, единственным конечным результатом которого будет переход теплоты от холодного тела к телу с более высокой температурой.

Теплота не может самопроизвольно (без некоторого дополнительного процесса) переходить от тела с данной температурой к телу с более высокой температурой.

2 закон термодинамики связан непосредственно необратимостью реальных процессов.

Реальные процессы можно считать обратимыми только с некоторыми допущениями.

Обратимыми процессами, называют процессы перехода системы из одного равновесного состояния в другое, который можно провести в обратном направлении через туже последовательность промежуточных состояний. При этом сама система и окружающие тела возвращаются к исходному состоянию.

Обратимая и необратимая тепловая машина

Тепловой машиной называется устройство позволяющее производить работу при периодическом процессе теплообмена между системой (рабочим телом) и источником теплоты. Такая машина может быть обратимой так и необратимой в зависимости от того обратимыми или необратимыми являются процессы в цикле действия машины.

Любой процесс превращения какого либо вида энергии в тепловую является необратимым процессом, т.е. он не может быть осуществлен полностью в обратном направлении.

Как показывают наблюдения все виды энергии в конечном счете превращаются в теплоту которая затем рассеивается.

Мера этого рассеивания была названа энтропия, чем больше рассеивается (обесценивается) энергия тем больше увеличивается энтропия системы.

Энергия и энтропия являются неотъемлемыми свойствами материи причем энергия есть мера движения материи, а энтропия мера рассеивания (деградации) энергии.

Общим свойством всех необратимых процессов является то, что они протекают в термодинамически неравновесной системе. И в результате этих процессов система стремится к состоянию термодинамического равновесия.

Лекция № 11

Круговые процессы или циклы.

Условия работы тепловых машин.

Для того чтобы тепловая машина совершала полезную работу необходимо выполнить следующие условия:

1. Необходимо иметь рабочее тело – это тело по средствам которого осуществляется взаимное превращение теплоты и работы.
   
2. Необходимо наличие двух источников теплоты с различными температурами: нагреватель или верхний источник теплоты (ВИТ) и холодильник или нижний источник теплоты (НИТ)
   
3. Работа тепловой машины должна быть цикличной, т.е. рабочее тело совершая ряд процессов должно возвращаться в исходное состояние
   

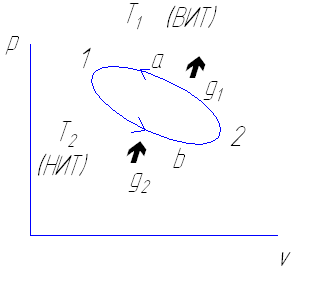
Рассмотрим круговой цикл тепловой машины.




В процессе расширения 1-а-2 от верхнего источника теплоты с температурой Т₁ и рабочему телу подводится теплота в количестве g₁ при этом совершается положительная работа расширения ℓ₁ численно равная площади под линией процесса

ℓ₁₌S_{1 a 2 V2 V1}

В процессе сжатия 2-b-1 от рабочего тела отводится теплота в количестве g₂ к нижнему источнику теплоты с температурой T₂ . В этом процессе затрачивается работа ℓ₂ (работа отрицательная) равная площади

ℓ₂=S_{2 V1 V2 1b}

Согласно первому закону термодинамики подводимая к системе теплота идет на увеличение внутренней энергии и совершения работы

g₁=ΔU+ ℓ₁

-g₂= ΔU- ℓ₂

Сложив уравнения, с учетом того, что изменение внутренней энергии за цикл равно нулю получим

g₁-g₂= ℓ₁- ℓ₂= ℓ_ц

где ℓ_ц - полезная работа за цикл

ℓ_ц=S_1a2b1

Чтобы машина совершала полезную работу работа затраченная на сжатие в процессе 2b1 должна быть меньше работы расширения в процессе 1a2, т.е. ℓ₁> ℓ₂

Чтобы этого достичь необходимо вместе со сжатием охлаждать рабочее тело отнимая у него некоторое количество теплоты g₂

Если при сжатии не охлаждать рабочее тело то процесс пойдет по пути 2а1 и на сжатие будет затрачена таже самая работа равная ℓ₁ которая была получена в процессе расширения



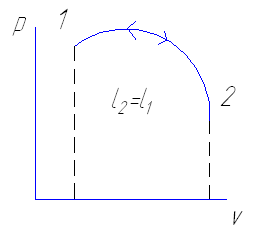
ℓ_ц= ℓ₁- ℓ₂=0

Таким образом повторяя последовательность цикла 1-а-2-b-1 с подводом и отводом теплоты можно получить непрерывно действующую тепловую машину

Коэффициент полезного действия данной тепловой машины определяется

Ŋ_t= ℓ_ц/g₁= ℓ₁- ℓ₂/g₁= g₁-g₂/g₁=1- g₂/g₁

Коэффициент полезного действия тепловой машины всегда меньше 1, т. к. не вся теплота подведенная к рабочему телу превращается в работу. Часть этой теплоты в количестве g₂ необходимо отводить к холодному источнику т.е. в окружающую среду.

Таким образом доказана формулировка 2 закона термодинамики: полное превращение теплоты в работу по средствам тепловой машины не возможно.

Обратимый цикл тепловой машины.

Представим схему обратного цикла.



Пусть имеется верхний источник теплоты с температурой Т₁ и холодный источник (НИТ) с температурой Т_2. Имеется рабочее тело.

В процессе сжатия 2 а 1 от рабочего тела к горячему источнику отводится количество теплоты g₁

При расширении 1 b 2 от холодного источника к рабочему телу подводится количество теплоты g₂ . Причем g₁ > g₂

Для того чтобы цикл возможен необходимо затратить работу ℓ_ц= ℓ_сжат- ℓ_расш

При этом отведенная от рабочего тела g₁ будет больше подведенной к рабочему телу g₂ на величину затраченной работы.

g₁= g₂+ ℓ_ц

Степень совершенства такого цикла оценивается холодным коэффициентом ε_t представляющим отношением количества теплоты g₂ взятого у холодного источника к затраченной работе ℓ_ц


ε_t= g₂/ ℓ_ц= g₂/ g₁- g₂

Энтропия.

Работа совершаемая рабочим телом вычисляется по уравнению:

v₂

ℓ=∫ p dv=p(v₂-v₁)

v₁



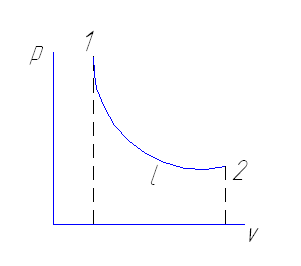
Работа совершается тогда когда изменяется объем. Давление может оставаться постоянным


ℓ= p(v₂-v₁)



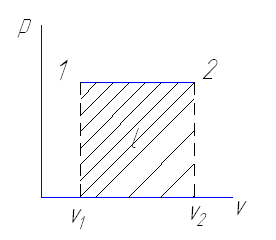
Однако если P=0, то работа равна ℓ=0


Работа является одним из видов обмена энергией термодинамической системы с внешней средой, также обмен энергии может происходить в виде передачи теплоты g значение теплоты, также как и работы можно подсчитать в виде интеграла совпадающий по форме с интегралом работы.

Давление определяет возможность совершения механической работы, а температура является очевидным признаком возможности передачи энергии в виде теплоты.

Параметр который изменяется только от количества переданной теплоты (также как объем при совершении работы) был предложен Клаузисом в 1852 г и назван энтропией (S^´) (Дж/К)

s-удельная энтропия (Дж/кг·К)


Энтропия также как и внутренняя энергия однозначна функция состояния системы и играет важную роль в термодинамике.

Энтропия не может быть измерена каким либо образом и определяется только расчетным путем (также как потенциальная энергия)

Лекция № 12

V₂

ℓ=∫ p dv

V₁

S₂

g=∫ T dS

S₁

dg=T dS

При dS>0 теплота в термодинамической системе подводится (dg>0)

При dS<0 теплота отводится dg<0

Тепловая диаграмма

Графическое представление процесса в системе координат S,T называется тепловой диаграммой.

Тепловая диаграмма имеет широкое распространение при решении ТД задач и при исследовании процессов и циклов.

S,T диаграмма используется для графического определения теплоты в процессе.


TdS=dg

s₁

g=∫ TdS

s₂


Физический смысл имеет не значение энтропии системы, а разность ΔS=S₂-S₁, в двух состояниях системы.


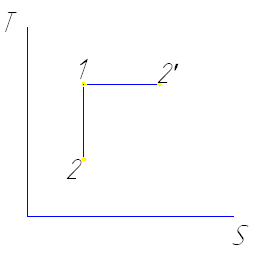
ΔS=0

Δg=0

1-2^' T=const


Изохора и изобара изображаются логарифмическими кривымы



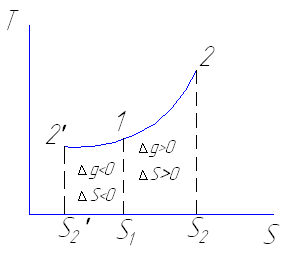
Принцип возрастания энтропии

Любые процессы в изолированной системе увеличивают ее энтропию, этот принцип следствие свойства возрастания энтропии при протекании в ней необратимых процессов.

Неравенство Готлиба: ΔS≥0, т.е. энтропия изолированной системы не убывает не при каких совершаемых ею процессах. Величина энтропии в обратимых процессах изолированной ТДС остается постоянной dS=0.

Энтропия изолированной системы в ходе совершения необратимого процесса dS>0.

Если ТДС не является изолированной, т.е. обменивается теплотой с внешней средой, то её энтропия может вести себя любым образом, если теплота от системы отводится, то энтропия уменьшается и наоборот.

Заключение: работоспособность ТДС зависит от величины энтропии системы, чем больше энтропия системы, тем сложнее совершить работу с помощью данной системы. Потребуется либо передать большее количество теплоты (g₁), либо потребуется более низкая температура холодного источника.

Необратимые процессы происходящие в изолированной системе приводят к уменьшению возможной работы (потере работоспособности энергии системы), хотя сама энергия системы в соответствии с первым законом термодинамики остается неизменной. Потерю работоспособности называют также обесцениванием или деградации энергии. То есть энтропию можно рассматривать как меру потери работоспособности энергии системы.

Чем больше значение энтропии системы тем меньше работоспособность энергии системы. Энтропия и энергия – важнейшие параметры системы. Энергия характеризует меру движения материи, энтропия характеризует потерю работоспособности системы.

Цикл Карно.

Прямой цикл.

В 1824 г. Карно предложил этот цикл. Наивыгоднейший теоретический цикл теплового двигателя, преобразующий максимальное количество теплоты в работу был предложен французским ученым Сади Карно. Он состоит из двух обратимых изотермических и двух обратимых адиабатных процессов.

Изотермический и адиабатный процессы являются самыми выгодными процессами для получения максимальной работы.



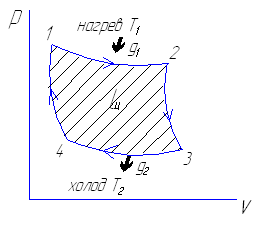
В изотермическом процессе 1-2 вся теплота g₂ подводимая к рабочему телу превращается в работу, а адиабатный процесс 2-3 протекает без потерь тепла, т.к. отсутствует теплообмен с внешней средой (работа совершается за счет уменьшения внутренней энергии рабочего тела) Получение уравнения для вычисления термодинамического КПД (ŋ_t) цикла Карно.

ŋ_t=1-T₂/T₁

Карно доказал, что невозможно превращения теплоты в работу в случае равенства температур верхнего и нижнего источника теплоты.

Карно дал следующую формулировку 2 закона термодинамики: теплота только тогда может быть преобразована в работу, когда имеется перепад температур.

Обратный цикл Карно.

Цикл Карно движется в обратном направлении против часовой стрелки, может быть использован для того, чтобы извлечь некоторое количество теплоты, от источника с более низкой температурой путем поглощения определенного количества работы от внешнего источника. Как и у обычной тепловой машины значительно ниже чем термический КПД машины по циклу Карно, потому что в реале холод. Машина также как и в тепловой всегда происходят необратимые процессы (трение, потеря тепла)

Цикл Карно в тепловой диаграмме.

КПД цикла Карно.



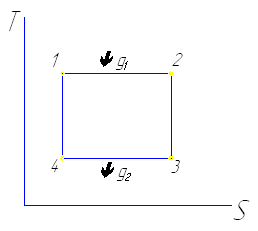
1-2 изотермическое расширение

2-3 адиабатное расширение

dS=0, т.к. dg=0

3-4 изотермическое сжатие (отводится количество теплоты g₂)

g₂=T₂ (S₂-S₁)= T₂ ΔS

4-1 адиабатное сжатие ℓ→ΔT

g₁-g₂= ℓ₁- ℓ₂= ℓ_ц

ŋ_t= ℓ_ц/ g₁= g₁-g₂/ g₁= T₁ ΔS- T₂ ΔS/ T₁ ΔS=T₁-T₂/T₁=1-T₂/T₁


g₁= T₁ ΔS

g₂= T₂ ΔS

Лекция № 13

Математическое выражение 2 закона термодинамики.

2 закона термодинамики в дифференциальной форме

dS≥dg/T

dS – бесконечно малое превращение энтропии

dg- бесконечно малое количество теплоты


Знак равенства в данном выражении относится к обратимым процессам, знак неравенства к необратимым.

Отсюда следует, что:

1. энтропия изолированной термодинамической системы при обратимых процессах не изменяется dS=0
   
2. энтропия изолированной системы при необратимых процессах возрастает dS>0.
   

2 закона термодинамики в интегральной форме

2

ΔS=S₂-S₁=∫ dg/T

1

Вычисление энтропии.

т.к. имеет физический смысл изменение энтропии, а не фактическое значение для термодинамики имеет значение рассчитывать изменение энтропии между двумя произвольными состояниями.

ΔS=S₂-S₁=С_v ln T₂/T₁+R ln v₂/v₁

S₂-S₁= С_p ln T₂/T₁- R ln p₂/p₁

S₂-S₁= С_v ln p₂/p₁+ С_p ln v₂/v₁

S= С_p ln T –R ln p + R ln R+a

S= С_p ln T –R ln p

S= С_v ln T +R ln v

Вычисление энтропии

В изохорных процессах

S₂-S₁=С_v ln T₂/T₁



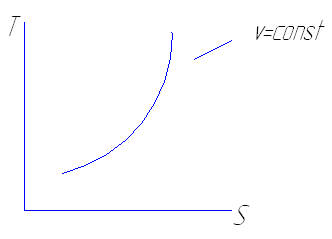
В изобарных процессах

S₂-S₁= С_p ln T₂/T₁



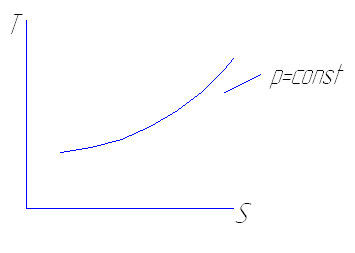
В изотермических процессах

S₂-S₁= R ln v₂/v₁= R ln p₂/p₁

В политропных процессах

S₂-S₁=с ln T₂/T₁

С- теплоемкость политропного процесса.