Решение статически неопределимых систем методом сил
| Вид материала | Решение |
СодержаниеПримеры систем многих частиц част Совокупность фотонов- квазичастиц 2Методы описания поведения систем многих частиц: Динамический Статический метод Термодинамический метод |
- Сопротивление композиционных материалов, 28.35kb.
- Статически определимые конструкции, 172.38kb.
- Решение систем нелинейных алгебраических уравнений, 20.84kb.
- Неравенств и, если «да», то найдите общее решение и частное решение двумя способами:, 11.47kb.
- Программа обсуждена на заседании кафедры Математики фнти, 45.62kb.
- Решение алгебраических уравнений высоких степеней. Решение нелинейных уравнений методом, 9.13kb.
- Решение систем линейных уравнений методом крамера, 19.06kb.
- Курсовая работа «Дифференциальные уравнения» Задача №1 (3 задачи), 8.81kb.
- 1. Решение нелинейного уравнения методом Ньютона-Рафсона, 156.67kb.
- Тема: «решение систем линейных алгебраических уравнений методом гаусса», 52.92kb.
Решение статически неопределимых систем методом сил
- Двухосное напряжённое состояние. Напряжения на наклонных площадках. Главные площадки и главные напряжения.
- Практический метод расчёта стержней на устойчивость. Зависимость от величины гибкости стержня.
- Расчёт стержней при ударном действии нагрузки.
- Растяжение и сжатие с изгибом.
- Ударное действие нагрузки. Динамический коэффициент.
- Секториальные координаты и секториальные динамические характеристики сечения.
- Продольный и поперечный удар по стержню
- Уравнение силовой плоскости
- Расчёт балок на прочность при изгибе. Условия прочности по наибольшим нормальным и наибольшим касательным напряжениям. Подбор сечений балок.
- Косой изгиб. Напряжённо-деформированное состояние при косом изгибе.
- Касательные напряжения в балках прямоугольного и двутаврового сечения при изгиб.
- Перемножение эпюр по методу Верещагина.
- Напряжённое состояние в окрестности точки тела. Напряжения на гранях прямоугольного параллелепипеда. Уравнения равновесия Навье. Закон парности касательных напряжений.
- Случай нагружения стержней Mкр, Мизг, и N.
- Продольно-поперечный изгиб стержней. Метод начальных параметров.
- Определение напряжений при кручении стержней круглого поперечного сечения.
- Дифференциальные зависимости между M, Q, q при поперечном изгибе балок. Понятие о чистом изгибе.
- Теории прочности.
- Определение критических сил с помощью энергетического метода.
- Расчёт балки на упругом основании конечной длинны.
- Обобщённый закон Гука при трёхосном напряжённом состоянии. Физический смысл величин, входящих в закон Гука.
- Расширенное понятие метода Мора
- Расчёты на прочность. Метод предельных состояний и метод допускаемых напряжений. Проверка прочности и подбор сечений при центральном растяжении и сжатии.
- Внецентренное сжатие (растяжение)
- Продольный и поперечный удар по стержню.
- Сложные сопротивления. Различные случаи сложного сопротивления.
- Касательные напряжения в поперечных сечениях балок при изгибе и их эпюры. Формула Журавского и физический смысл входящих в неё величин.
- Понятие об устойчивости. Формула Эйлера для критической силы. Влияние способа закрепления стержней на величину критической силы.
- Главные площадки и главные напряжения. Три вида напряжённого состояния. Наибольшие касательные напряжения.
- Продольно-поперечный изгиб стержней. Решение уравнения продольно-поперечного изгиба стержней методом начальных параметров.
- Определение угла закручивания стержней с круглым поперечным сечением.
- Нормальные напряжения в поперечных сечениях балки при изгибе и их эпюры. Основные гипотезы теории изгиба балок.
- Постановка задачи об изгибе балки на упругом основании.
- Перемещения и деформации в точке тела, их обозначения, правила знаков и физический смысл.
- Метод начальных параметров определения прогибов при изгибе балки
- Зависимости между моментами инерции относительно параллельных осей.
- Определение температурных смещений в системах.
- главные площадки и главные напряжения. Три вида напряжённого состояния. Наибольшие касательные напряжения.
- Теорема о взаимности виртуальных работ.
- Главные оси и моменты инерции.
- Определение смещений в статически неопределимых системах. Кинематические проверки.
- Понятие о чистом сдвиге. Закон Гука при сдвиге.
- Дифференциальное уравнение изогнутой оси балки. Метод непосредственного интегрирования.
- Статические моменты и центр тяжести поперечных сечений стержней. Моменты инерции и моменты сопротивления изгибу.
- Расчёт бесконечной балки на упругом основании.
- Связь между деформациями и перемещениями. Соотношения Коши. Физический смысл величин, входящих в эти соотношения.
- Метод Мора, определения перемещений в сечениях.
- Определение напряжений, деформаций и перемещений при центральном растяжении (сжатии) стержней. Закон Гука. коэффициент Пуассона.
Тепловое излучение
Тела, нагретые до достаточно высокой температуры, приобретают способность светиться. По мере уменьшения температуры изменяется не только интенсивность излучения но и его спектральный состав. В нём всё сильнее обнаруживается преобладание длинных волн – красных и инфракрасных.
Электромагнитное излучение, возникающее за счёт внутренней энергии излучающего тела и зависящее только от температуры называется тепловым излучением.
Если энергия расходуемая на излучение не восполняется теплом, то излучение с течением времени уменьшается и температура постепенно понижается.
Единственное излучение, способное находиться в равновесии с веществом. Равновесное излучение. Устанавливается в адиабатно - замкнутой теплоизолированной системе (теплоизолированной)
1
Предмет статической физики и термодинамики.
Изучается состояние и поведение систем многих частиц, в зависимости от состояния/поведения частиц, образующих систему.
Примеры систем многих частиц част:
- Макроскопические тела, как совокупности структурных частиц: молекул, атомов, ионов с валентными электронами (в газах концентрация n=1019см-3, в жидкостях 23)
- Электромагнитное излучение, в частности свет, - совокупность фотонов – фотонный газ.
- Совокупность фотонов- квазичастиц, соответствующих тепловым колебаниям кристаллической решётки; энергия тепловых колебаний квантуется, и её можно представить как совокупность порций энергии hv.
- Совокупность электронов в атоме.
- Совокупность протонов в ядрах атомов.
- Совокупность нейтронов в ядрах атомов.
- Совокупности различных квазичастиц.
2
Методы описания поведения систем многих частиц:
Динамический – аналогичен методам динамики. Мгновенное состояние системы описывается координатами и скоростями частиц системы. Состояние описанное столь детально, в каждый момент времени называется динамическим или микросостоянием. Неосуществимо из-за большого числа частиц, при нормальном состоянии газа каждая частица испытывает 109 столкновений в сек.
Статический метод – состояние частиц характеризуется средними значениями механических величин, которые одинаковы для всех частиц и постоянны, если состояние системы не изменяется, в то время как состояния отдельных частиц будут разными, переменными, случайными. Средние значения рассчитываются на основе функций распределения частиц по состояниям: Максвелла-Больцмана, Бозе-Эйнштейна, Ферми-Дирака.
Термодинамический метод – состояние системы описывается величинами, характеризующими
состояние системы в целом: давление газа p, объём V, температура Т, концентрация молекул n, масса m, внутренняя энергия U, энтропия S, напряжённости электрического и магнитного полей. Состояние, описанное такими методами называется макросостоянием. Значения обусловлены совокупным поведением частиц, из которых состоит система.(Например температура – степень нагретости определяется средней кинетической энергией молекул Wк.с.
Термодинамические параметры системы непрерывно и хаотично меняются со временем, такие изменения называются флуктуациями. Среднее же значение параметров стремиться к определённому пределу. Параметры бывают внешние и внутренние. Система называется открытой, если она может взаимодействовать с внешней средой. Равновесное состояние – постоянные внешние условия, неизменные параметры и отсутствие потоков.
3
Средняя арифметическая скорость молекул в газах.
 при условии что Ni молекул имеют скорость vi, отношение wi=Ni/N вероятность того, что молекула движется со скоростью vi, вероятность того что скорость молекулы лежит в интервале dv близи v: dw_v=dN_v/N, тогда скорость молекул
при условии что Ni молекул имеют скорость vi, отношение wi=Ni/N вероятность того, что молекула движется со скоростью vi, вероятность того что скорость молекулы лежит в интервале dv близи v: dw_v=dN_v/N, тогда скорость молекул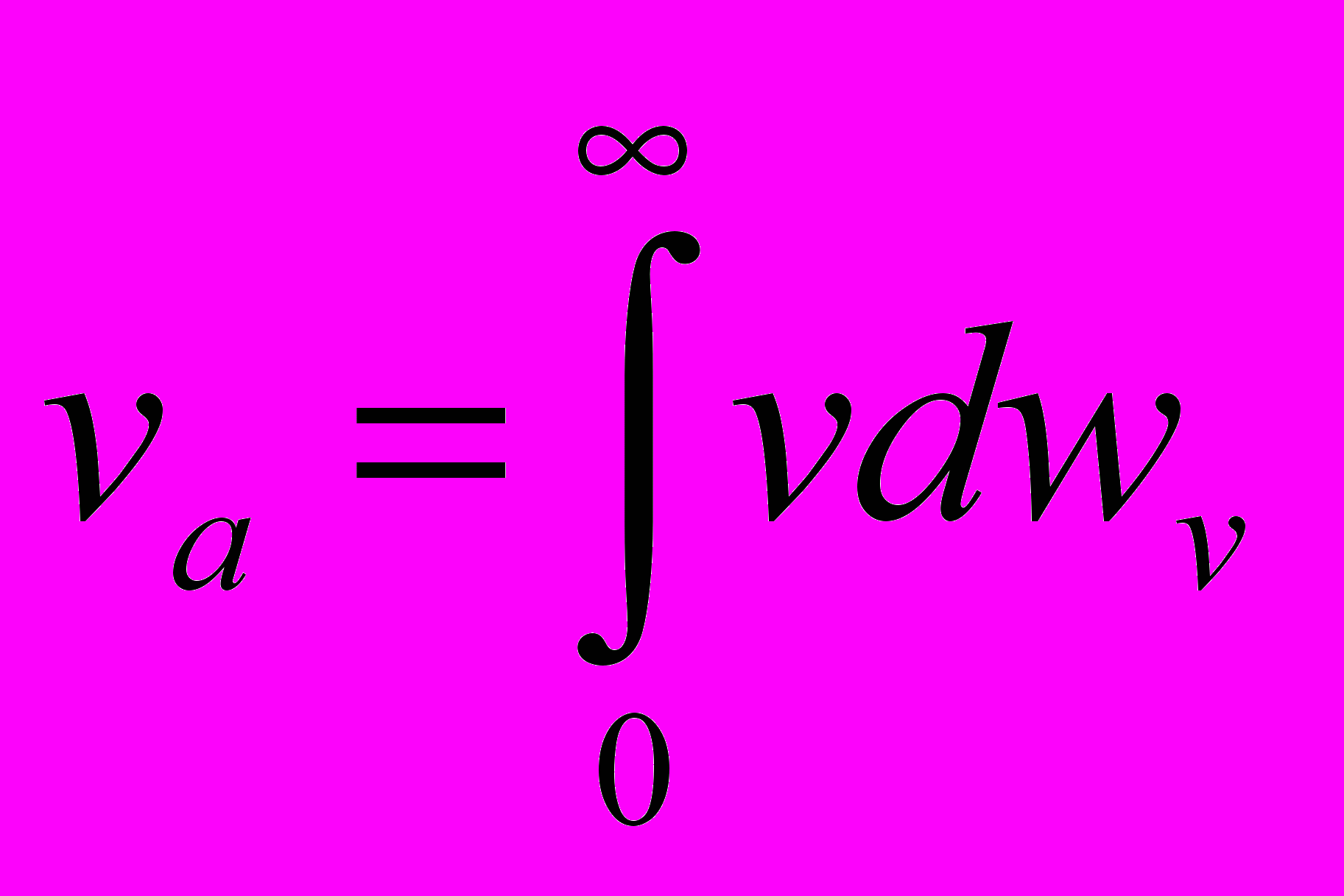 . Функция F(v) = вероятность того, что молекула имеет скорость в единичном интервале скоростей вблизи v, показывает какая это часть молекул
. Функция F(v) = вероятность того, что молекула имеет скорость в единичном интервале скоростей вблизи v, показывает какая это часть молекул 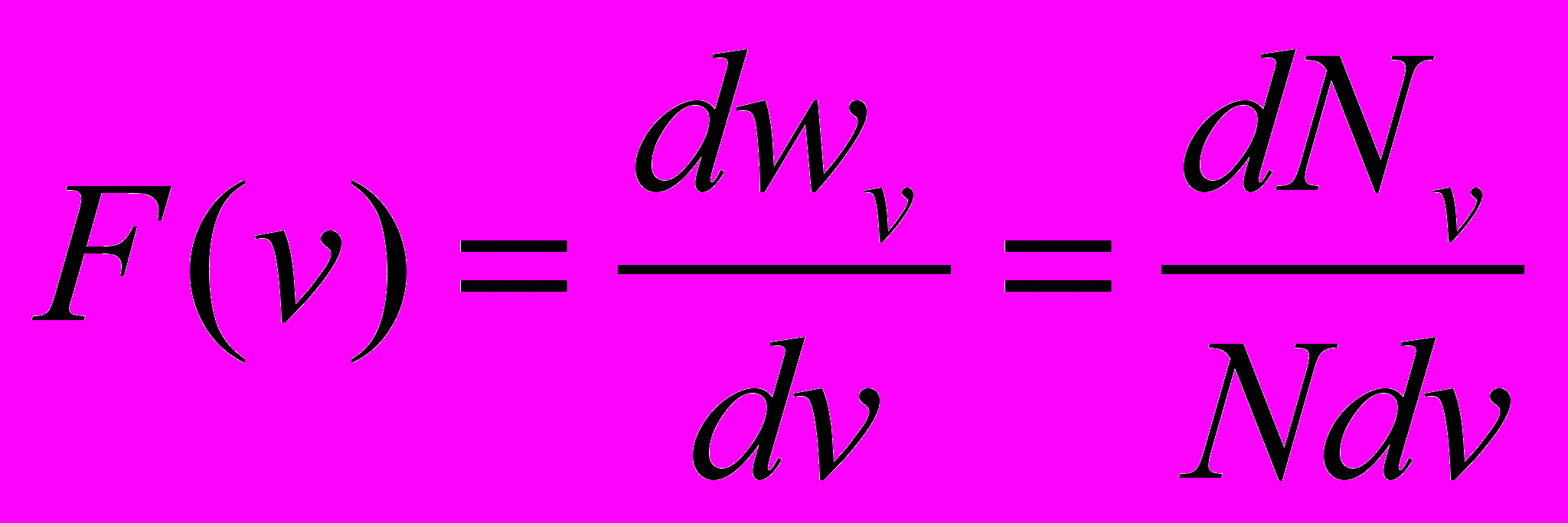 - функция распределения молекул по скоростям (абс) Для идеальных газов dw_v=F(v)dv, v_a=int(0,∞)(vF(v)dv), аналогично средн арифм, вводится ср кв.
- функция распределения молекул по скоростям (абс) Для идеальных газов dw_v=F(v)dv, v_a=int(0,∞)(vF(v)dv), аналогично средн арифм, вводится ср кв. 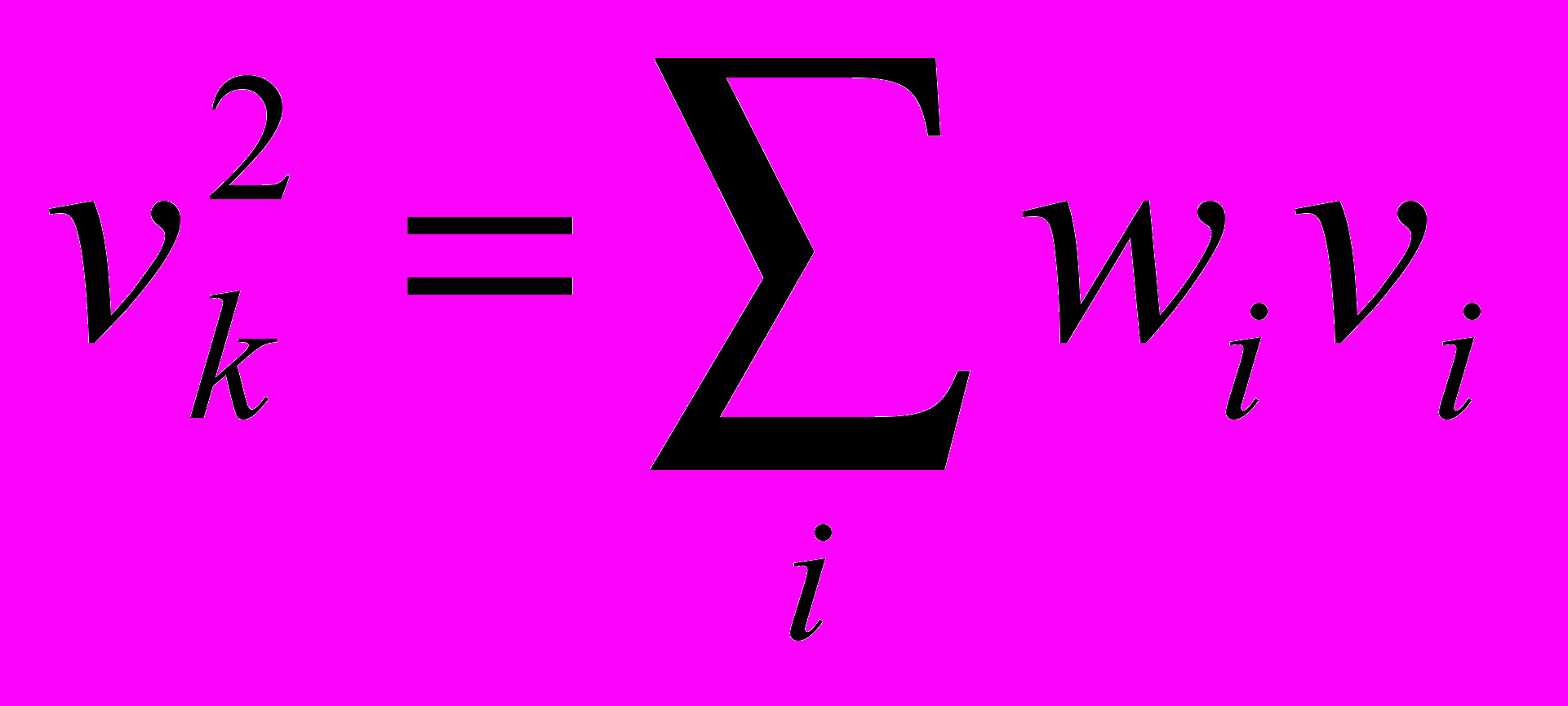 ,
,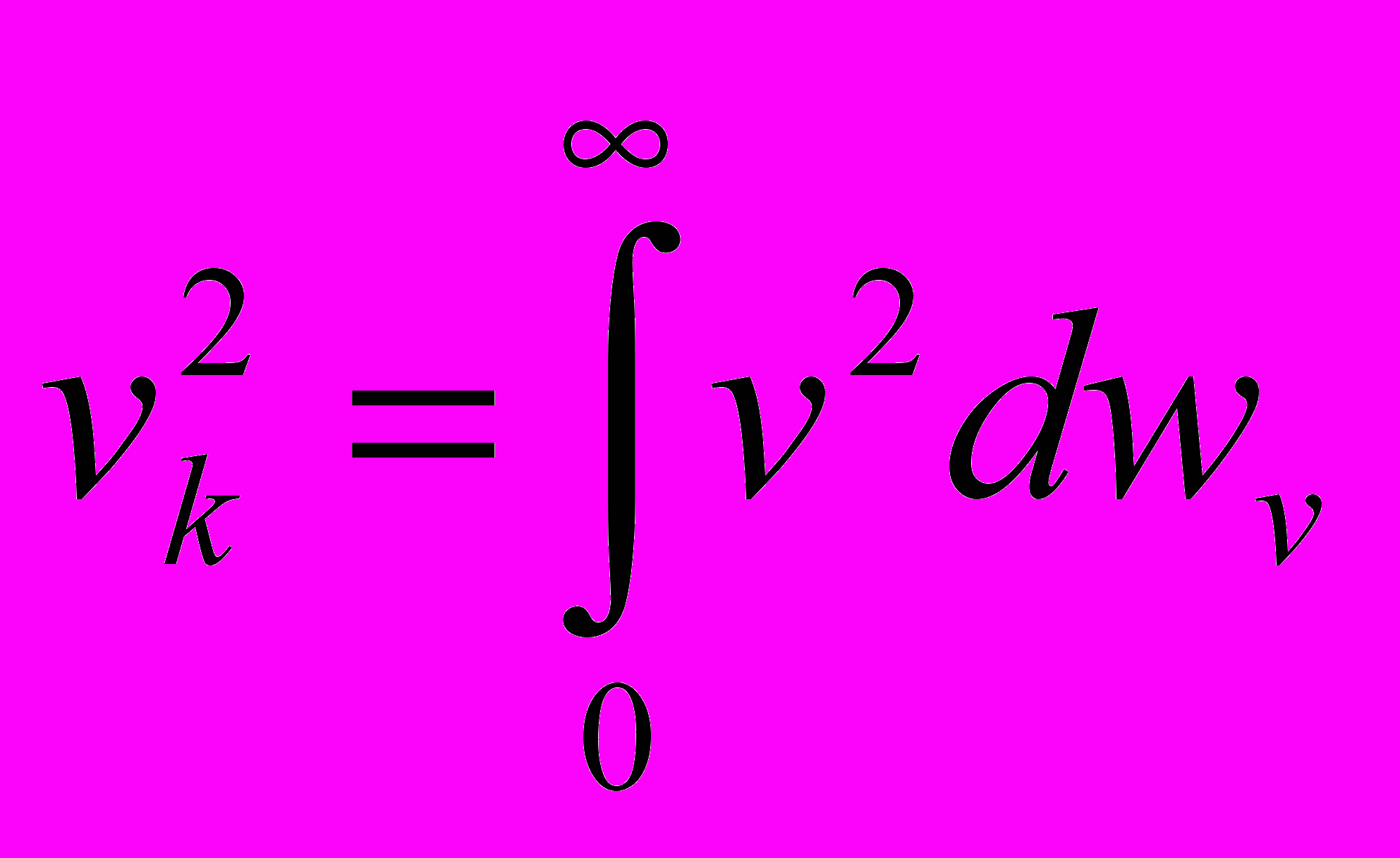 .
.v_k2=int(0,∞)(v2*F(v)dv), Средняя кв ск определяет среднюю кинетическую энергию молекул. Wк.с.=1/2m*v_k2=1/Nsumm(j)(Wkj)=1/Nsumm(j)((1/2)mv_j2)=(1/2)m(1/N)summ(j)(v_j2)
Давление газа на площадь поршня S, с грузом Р: p=P/S Объём становится внутренним параметром, так как положение поршня с грузом зависит от внутреннего давления.
Ур-ние Менделеева-Клайперона
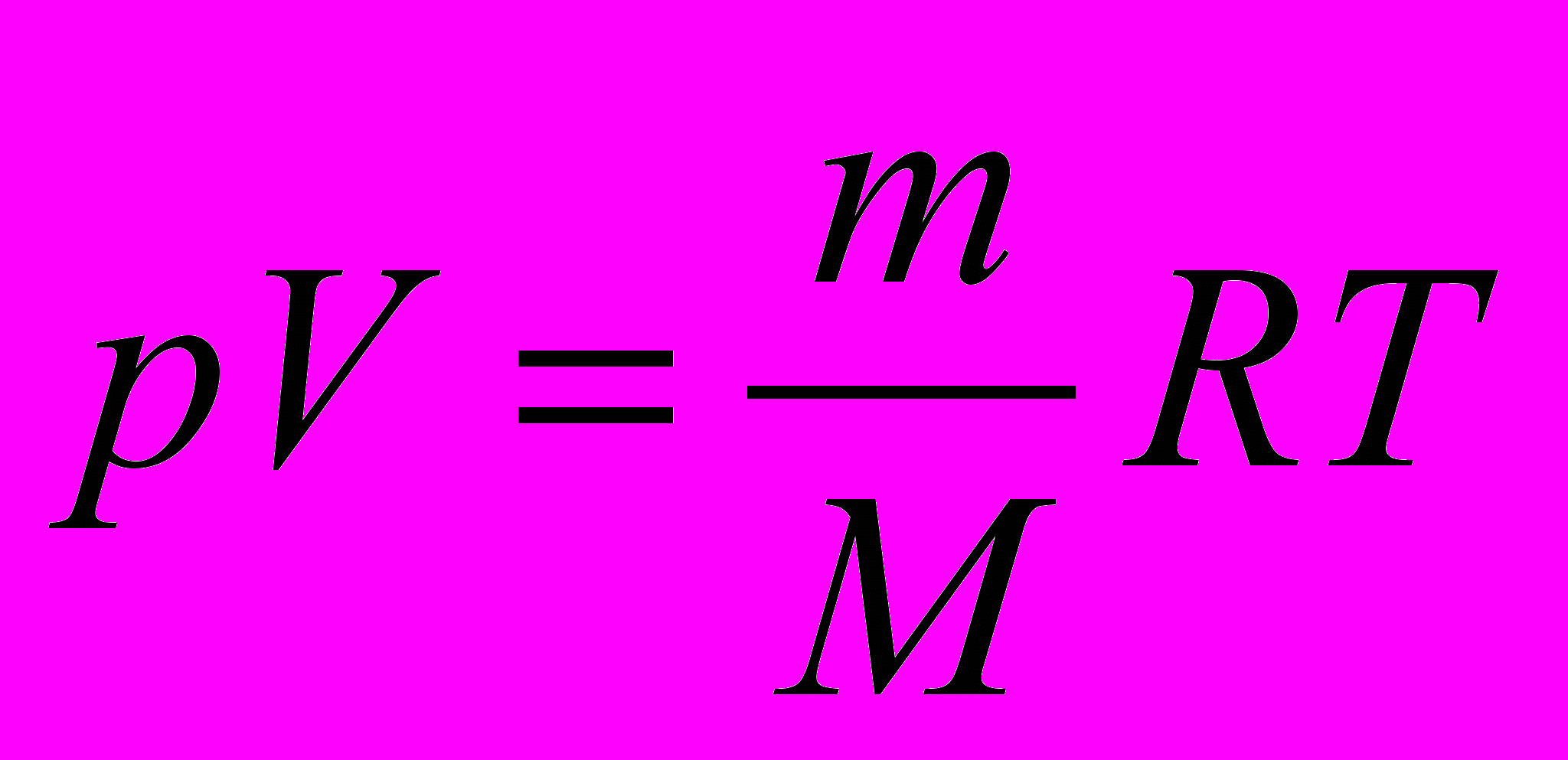
4
Молекулярно кинетическое строение вещества.
Основные положения МКТ
- Любое вещество состоит из молекул и имеет дискретное строение (обьясняется сжимаемостью). Молекула –наименьшая частица вещества, обладающая химическими свойствами в-ва. Эффективный диаметр10-10 м, масса 10-26кг.
- Молекулы непрерывно и хаотично движутся. Т определяется средней кинетической энергией движения молекул, хаотичное движение называется тепловым. Характер движения различен в разных агрегатных состояниях. Подтверждается броуновским движением и диффузией. (Броуновское движение – движение мелких твёрдых частиц, взвешенных в жидкости или газе. Диффузия – самопроизвольное проявление веществ друг в друге или самопроизвольное выравнивание концентрации вещества.)
- Молекулы взаимодействуют друг с другом. В зависимости от расстояния преобладает сила притяжения или сила отталкивания.
Агрегатные состояния вещества.
Твёрдое – молекулы вещества сильно связаны между собой и препятствуют деформации тела, совершают колебания около узлов кристаллической решетки.
Жидкое – совершают колебания около центров равновесия и редко меняют своё положение.
Газообразное – хаотично движутся.
Плазменное.
5
Взаимодействие молекул.
Молекулы состоят из + ядер и – электронов. Взаимодействие между молекулами электромагнитного происхождения. Между молекулами могут иметь место все виды хим. Связей (ионные, ковалентные, металл., водородн.)Межмолекулярные силы взаимодействия (Ван-дер-Ваальса.) различной природы (ориентационная, индукционная, дисперсная, отталкивающая.) Описываются приближёнными формулами с определёнными границами справедливости.
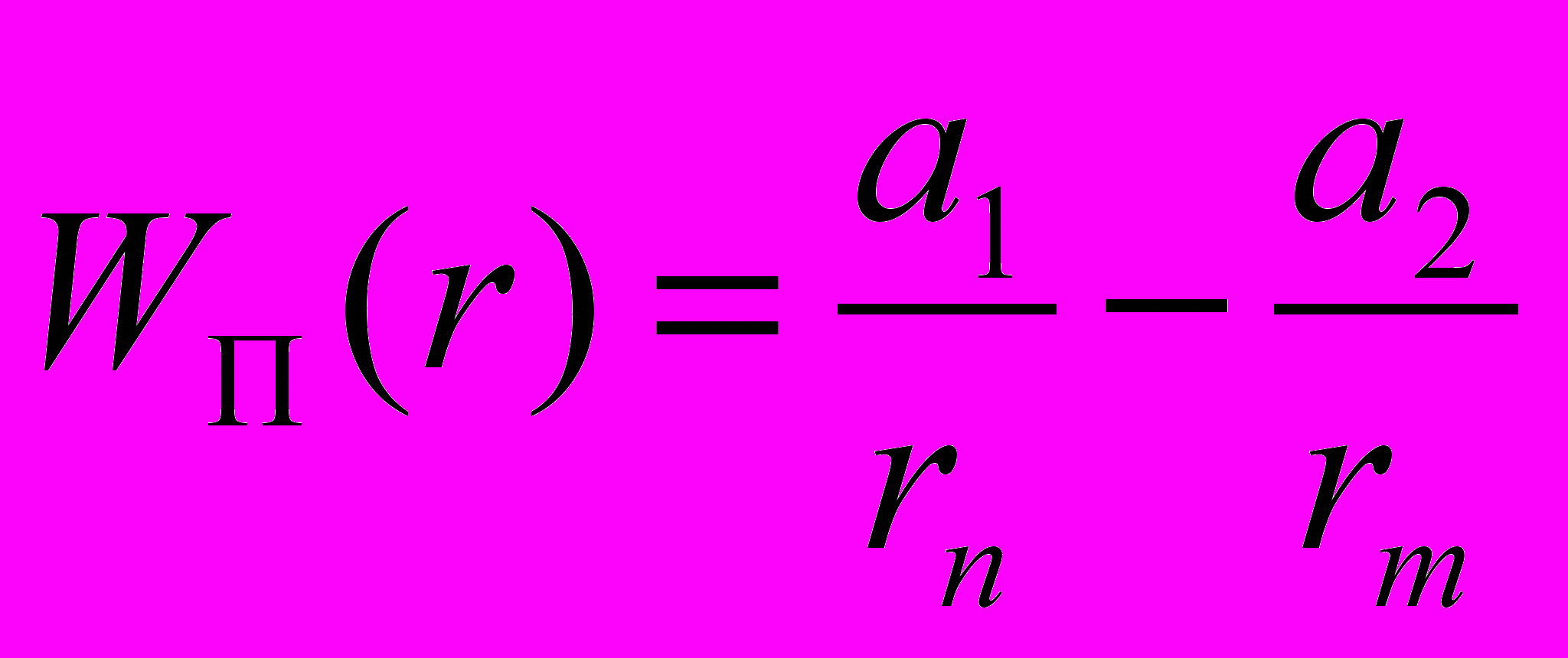 , a1,a2,n,m – выбираются из требования наилучшей апроксимизации реального потенциала. В большинстве случаев m=12, n=6, а1,а2 – подбираются для конкретных молекул. Между молекулами одновременно действуют силы притяжения и отталкивания.
, a1,a2,n,m – выбираются из требования наилучшей апроксимизации реального потенциала. В большинстве случаев m=12, n=6, а1,а2 – подбираются для конкретных молекул. Между молекулами одновременно действуют силы притяжения и отталкивания. Графики.
Газ Ван-дер-Ваальса – модель реального газа.
Соответствует модели твёрдых шаров. Силы отталкивания учитываются тем, что размеры молекул конечны. Проявляются эти силы только в момент столкновения. Между столкновениями молекула движется по инерции прямолинейно.
Модель идеального газа
Пренебрегают взаимодействиями молекул на расстоянии. Диаметр молекул равен нулю. Молекулы могут сближаться до расстояния, равного 0. Взаимодействуют только при столкновении.
Длинна свободного пробега молекул в газах.
Будем находить как отношение среднего пути, пройденного молекулой со скоростью v_o.c за время delta t к среднему числу столкновений с остальными молекулами за это время.
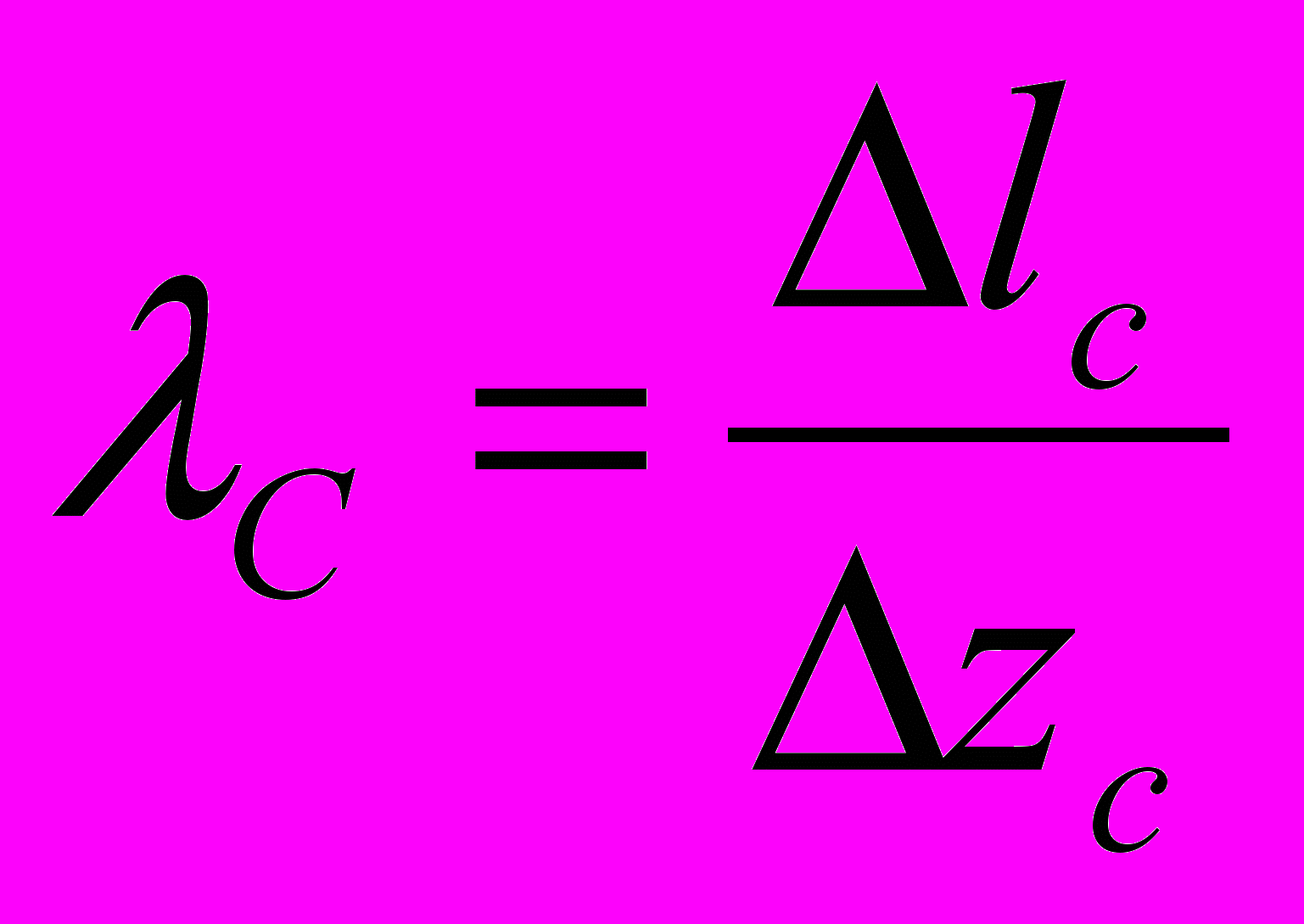 ,если средняя арифметическая скорость молекулы равна v_a, то путь delta l_c = v_a*delta t. Воспользуемся моделью газа Ван-дер-Ваальса. Среднее число столкновений равно среднему числу остальных в объёме. Delta z_c=n*V, Где V – объём ломанного цилиндра описанного сферой ограждения S (2d) за время t. V=(pi*d2)*v_o.c*delta t, где v_o.c*delta t –высота цилиндра, а sigm=(pi*d2) , тогда delta z_c==(pi*d2)*v_o.c*delta t*n, v_oc=sqrt(2)v_a, тогда delta z_c, а за ед времени z_c=delta z_c/delta t=...
,если средняя арифметическая скорость молекулы равна v_a, то путь delta l_c = v_a*delta t. Воспользуемся моделью газа Ван-дер-Ваальса. Среднее число столкновений равно среднему числу остальных в объёме. Delta z_c=n*V, Где V – объём ломанного цилиндра описанного сферой ограждения S (2d) за время t. V=(pi*d2)*v_o.c*delta t, где v_o.c*delta t –высота цилиндра, а sigm=(pi*d2) , тогда delta z_c==(pi*d2)*v_o.c*delta t*n, v_oc=sqrt(2)v_a, тогда delta z_c, а за ед времени z_c=delta z_c/delta t=...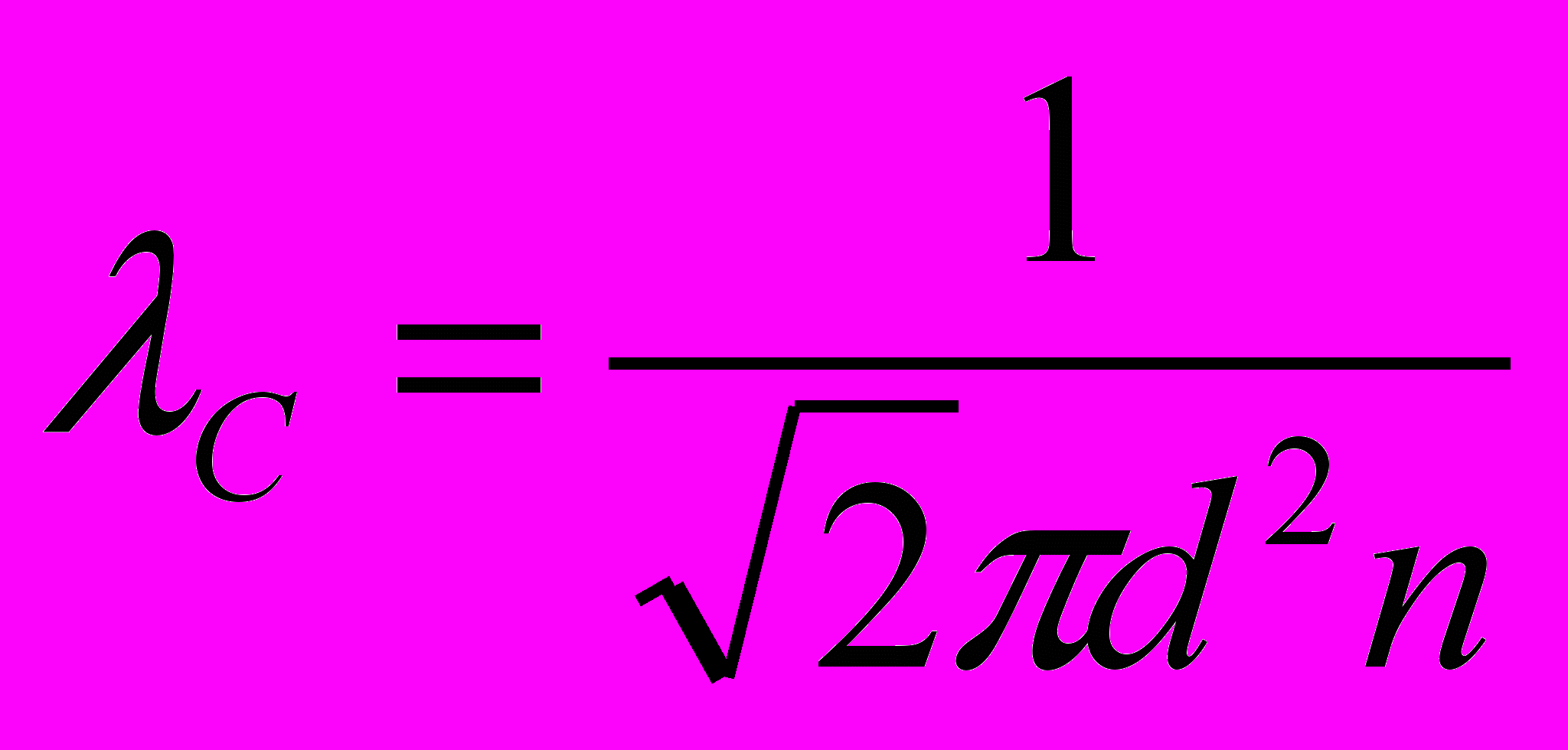 , z=v_a/lambda_c
, z=v_a/lambda_c6
Основное уравнение МКТ.
Уравнение, выражающее связь давления идеального газа со средними значениями характеристик молекул, называется осн ур МКТ.
Вводится давление (мех напр) p=dF_д/dS, -модуль нормальной силы, действующей на участок поверхности, при равном распределении: p=Fд/S, давление на стенки сосуда по 2 з-ну Ньютона Fд=delta p_x/delta t, p=delta p_x/(S*delta t) –давление равно импульсу передаваемому молекулами газа единице площади поверхности сосуда за единицу времени. Изменение импульса при ударе о стенку: delta p_x=m_M*v_x-(-m_M*v_x)=2m_M*v_x, если молекула летит под углом к стенке то изменение импульса по оси у =0, давление Fy=0.Ударения молекул о стенки будут проходить через промежуток времени delta t , необходимого для того, чтобы молекуле пересечь сосуд и вернуться обратно 2l. Delta t=2l/v_x. Средняя сила
Fi=delta p_xi/delta t=1m_M*v_xi2/2l=m_M*v_xi2/l, сила со стороны всех молекул: F=summ(Fi)=(m_M/l)*summ(i)(v_xi2) среднее значение квадрата х составляющей скорости: v_xc2=1/Nsumm(v_xi2), F=..., квадрат любой скорости равен сумме квадратов проекций, для v_k2=v_...c2, так как молеклы движутся хаотически, все эти проекции равны. И v_xc2=1/3v_k2, подставим в F=..., тогда p=F/S=..., получим основное уравнение динамики, выражающее давление идеального газа через концентрацию и среднюю квадратичную скорость молекул p=1/3nm_Mv_k2, p пропорц n, p m_M, p v_k2, можно записать в виде p=2/3nWk.c.п. – средняя скорость поступательного движения молекул.
7
Связь средней кинетической энергии молекул с абс температурой, согласно закону распределения энергии по степеням свободы.
Ур-ние Менделеева-Клайперона
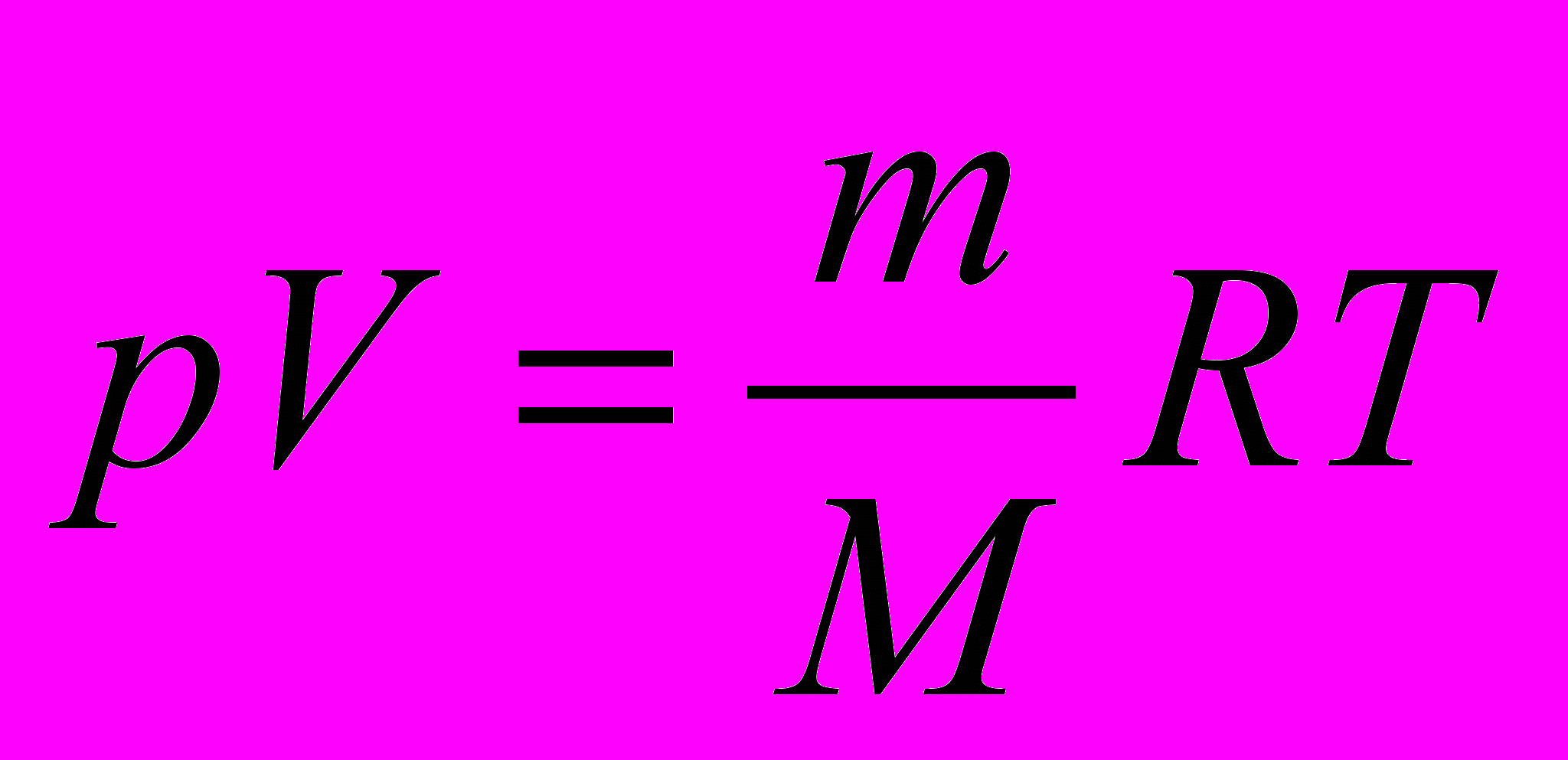 - уравнение состояния идеального газа.
- уравнение состояния идеального газа.При учёте соотношений p=m/v=nm_M, M=m_M*Na, R=kNa, принимает вид: p=nkT, с учётом формулы p=2/3n Wk.c.п., получим Wk.c.п.=3/2kT Также энергия связана кроме поступательного движения ещё и с вращательным и колебанием атомов. Позволяет вычислить её закон распределения энергии по степеням свободы.
При любом числе степеней свободы молекулы три из них поступательные. Wксп=1/2mv_k2=1/2mvxc2+..yc..zc=Wxc+Wyz+Wzc, Wxc=Wyc=Wzc=1/3Wксп=1/2kT, Wвращ=1/2J_12*omega_c2 Wкс=i’/2kT, Wc(полн)=i/2kT где i’=iпост+iвр+iкол, i=iпост+iвр+2iкол
С точки зрения МКТ температура определятся средней кинетической энергией теплового движения отдельных молекул тела, а не внутренней (тепловой энергией тела) Uт=NWкс=m/MNa(i’/2)kT=i’/2m/MRT
8
Уравнение состояния.f(p,V,T) – функциональная зависимость, которая называется термическим уравнением состояния тела. Примерами являются Ур-ния Менделеева-Клапейрона и В-д-В.
На основе опытных законов Бойля-Мариотта, Гей-Люссака и Шарля, описывающих соответственно изотермический, изобарный и изохорный процессы изменения состояния идеальных газов, было получено уравнение состояния.
Ур-ние Менделеева-Клайперона
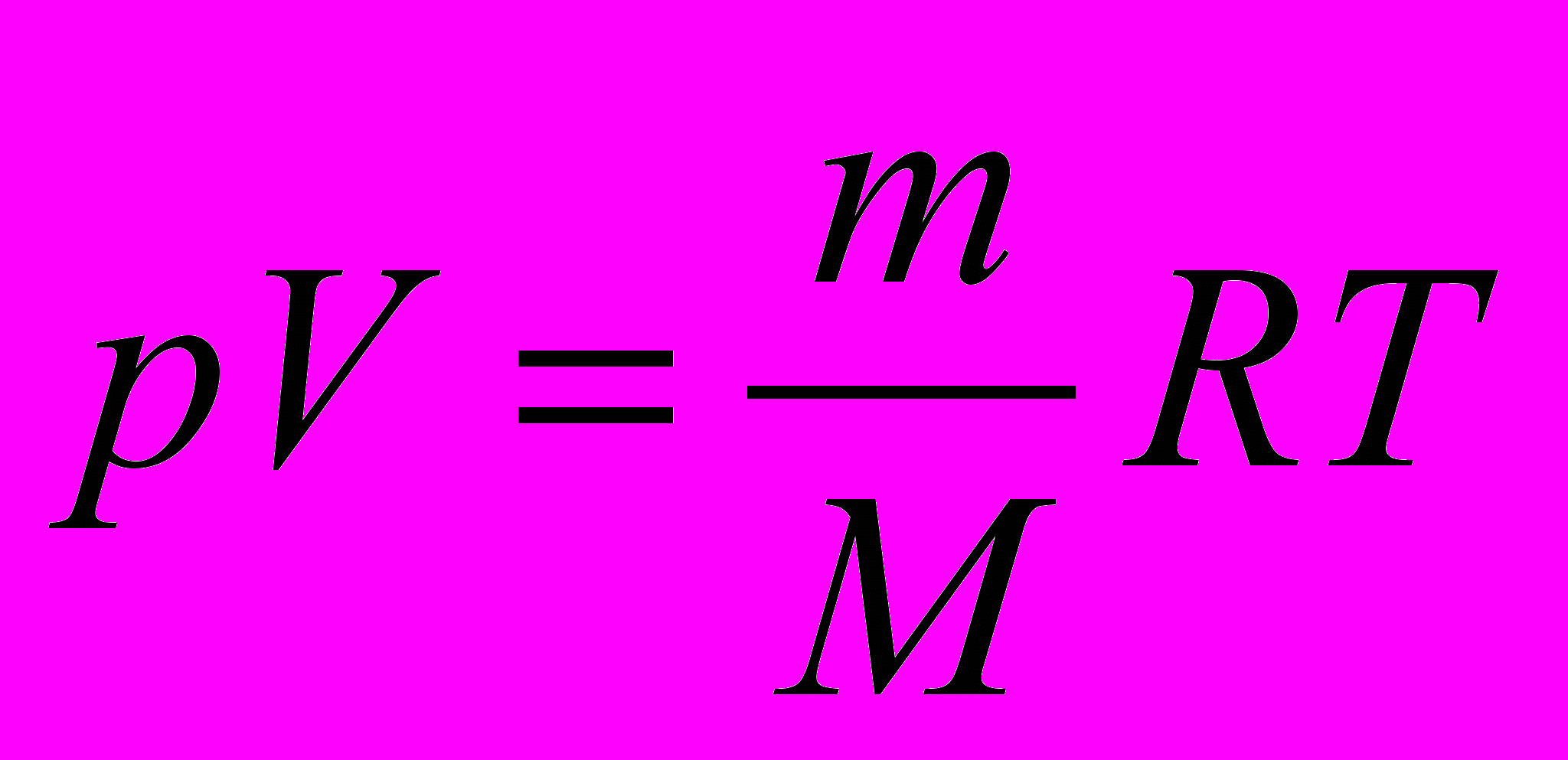 При учёте соотношений p=m/v=nm_M, M=m_M*Na, R=kNa, принимает вид: p=nkT, с учётом формулы p=2/3n Wk.c.п., получим Wk.c.п.=3/2kT(вывод закона) Для данной массы и молекулярной масс = пост, можно запистать:
При учёте соотношений p=m/v=nm_M, M=m_M*Na, R=kNa, принимает вид: p=nkT, с учётом формулы p=2/3n Wk.c.п., получим Wk.c.п.=3/2kT(вывод закона) Для данной массы и молекулярной масс = пост, можно запистать: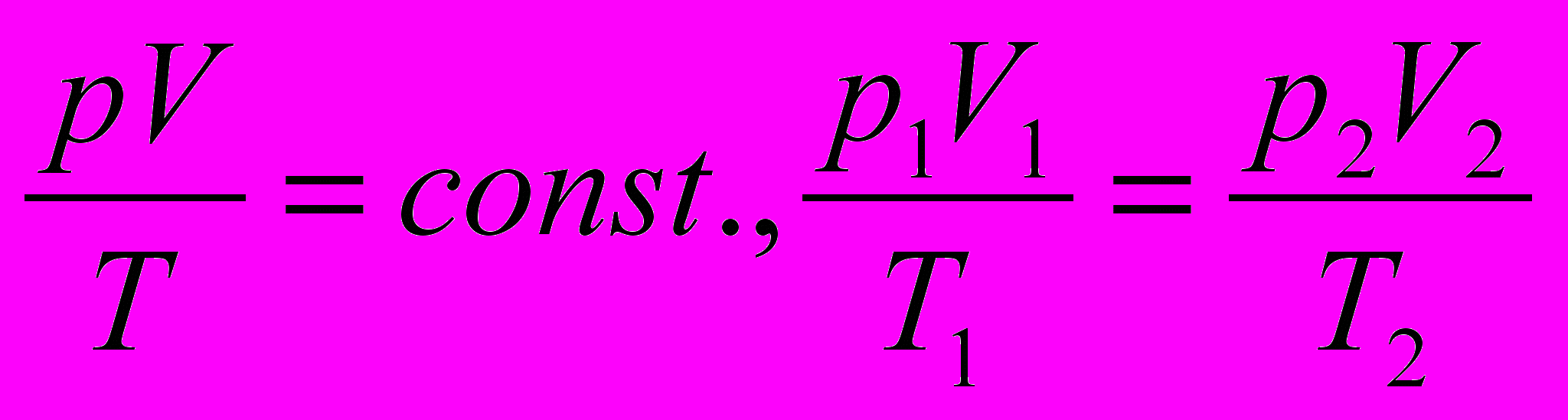
Ур-ние Вдв. Для реальных газов уравнения менд-к. выпоняется до тех пор, пока давление не слишком высоко. При высоком давлении обьём газа меньше, соответствующего объёма идеального газа.
Для реального газа оказывается недоступным объём, из-за других молекул (V-delta V) delta V=(m/M)b, где b-поправка на недост V в расчёте на 1 моль газа. B=4NaV_M, с учётом введённой поправки, уравнение состояния газа примет вид (Ур сост Клаузиуса0 p(v-(m/M)b)=(m/M)RT давление с учётом поправки delta p + p, тогда: (p+(m2*a)/(M2/V2))V=m/MRT, где а – постоянная, характерная для газа. (p+(m2*a)/(M2/V2))*(v-(m/M)b)= m/MRT –ур-ние Ван-дер-Ваальса.
Изотермы реального газа и ВДВ
Получаем Ур-ние умножив ВДВ на V2 и раскрыв скобки – описвающее поведение газов –изотермы.
9
Внутренняя энергия и способы её изменения.
Энергия, которая связана со всевозможными движениями частиц и их взаимодействием, энергию покой частиц называют внутренней. Внутреннюю энергию макроскопической системы можно представить как сумму кинетических энергий теплового движения молекул (поступ, вращ, кин эн атомов), потенциальных энергий взаимодействий молекул между собой, потенциальную энергию вз атомов в многоатом мол и кристаллах и внутренних энергий атомов.
Внутренняя энергия явл функцией состояния системы.ЕWki Wпi Wпai Ui, чаще всго изучаются процессы при которых u=конст, и её отбрасывают. ,В модели идеального газа также отбрасывают пот эн вз, т.к. вз на расстоянии не учит., для одноат идел газа Wпаi=0, U=EWki
U=NWc, где Wc средняя энергия молекул, а N=m/M Na, при учёте степеней свободы и i/2m/M RT.,для ВДВ U=m/Mc_vT-m2/M2 a/V
Изменяется за счёт мех энергии при соверш раб над телом.
За счёт внутр энергии других тел при теплообмене.
Теплопередача за счёт теплопроводности, конвекции, электромагнитного излучения.
Первый закон тд.
При изменении внутренней энергии системы за счёт внутренней энергии других тел (притеплообмене, за счет мех эн др тел, изменение внутренней энергии системы dU равно сумме количества теплоты, сообщённого системе dQ и работы dA’ над системой. ΔU=Q+A’ (A=-A’)
Q=delta U+A при изох проц Cv=dQv/dt=dU/dt, отношение Cv/Cp=гамма=i+2/i –показатель адиабаты.
Количество теплоты и теплоёмкость. Q- энергия, переданная системе при теплообмене. C=dQ/dt, Суд= C/m, Q=mCуд(T2-T1) C-молярн=MC/m, Q идёт не только на нагревание но и на соверщ работы. Теплоёмкость ид газов при пост объёме cv= im/2MR cv=Cv*M/m
Работа газа dA=pdV – при изм обьёма A=int(V1-V2)(pdV)
10
Обратимые и необратимые процессы.
Можно считать равновесным процесс., (квазистатическим, квазиравновесным), протекающий настолько медленно, что отклонения от параметров системы от равновесных, пренебрежимо мало.(последовательность равновесных состояний. При изменении направления равновесного процесса система будет проходить те же равновесные состояния что при прямом ходе, поэтому их называют обратимыми. (любое промеж состояние явл сост термодинам равновесия и не зав от напр)Такие процессы не вызывают изменений в окр среде и могут прох самопроизвольно.
Реальные процессы, в природе протекают с конечной скоростью и сопровождаются рассеиванием энергии за счёт трения, теплопров, и т.д., и явл необрат., для их возвр в исх сост, необх компенс процесс, связ с остат изм.
11
Энтропия системы.
Энтропией системы для обратимого процесса называют S=klnP, где Р –термодинам вероятность макросостояния, к – пост Больцмана. (величина, приращение кот = отнош получ сист в ходе обр проц теплоты к Т системы.
Число различных микросостояний delta N, посредством которого осуществляется данное макросостояние, называется тд вероятностью. deltaN=P, Все микросостояния системы равновероятны. Тогда возможно всего 4 распределения. Полная хаотичность приводит к тому, что все распределения встречаются одинаково часто. Вероятность какого либо одного события w1=1/N –мат вероятность макросост. .таблица. Пусть есть сосуд, разделённый на две части, и две молекулы, помеченные. dS=dQ/T – формула Больцмана, выражающая связь энтропии в термодинамике с энтропией в статистич физике. Энтропия изолированной системы возрастает.
Энтропия – степень беспорядочности состояния макросистемы.
Энтропию также можно записать в виде: ds=CvdT/T+(p/T)dV=m/McvdT/T+pdV/Tисп ф-лу М-К, получим: m/M(cvdT/T+RdV/V), при изотерм delta S=Q/T изохорном =m/M*c_v*ln(T2/T1)
При изобарном =m/M*c_p*ln(T2/T1), при адиабатном =0=int(1,2)(dQ/dT) при круговом, инт от дС (1,1) =0
12
Закон распределения по скоростям теплового движения молекул газа в состоянии термодинамического
равновесия называется распределением Максвелла.dn=n0f(u)*4pi*u2du=n0F(u)du F(u)=4*pi*u2f(u)
F(u)=dn/n0du - функция распределения. -Доля молекул модули скоростей которых находятся в шаровом
слое единичной толщины. - ф-я распределения молекул газа по модулям их скоростей.F(u)du=dn/n0-
вероятность того, что модуль скорости молекул заключён между u и u+du Интеграл от
ф-ии от 0 до беск. =1 (любая молекула имеет к-л абс значение скорости u, поэтому если просуммировать
все доли молекул им абс ск то получим 1. Ф-я f(u) - имеет тот же смысл, но явлется функцией
распределения, отнесённой к йод интервалу объёмов d(omega)=4*pi*u2du.
F(u)=((m0/2*pi*k*T)(3/2))*e(m0*u2/(2kT)) закон распределения молекул по скоростям -то же самое,
только умноженное на 4i*u2du Можно найти наиболее вероятную скорость uв, запишем максимум ф-ции
F(u) [(d/du)*(e(........)*u2] при u=uв =0 nогда uв =sqrt(2kt/m0)=sqrt(2RT/M)=vкв*sqrt(2/3)
ср арифмет скорость =vкв*sqrt(8/3pi)
13
Явления переноса - потоки энергии, вещества, импульса упроядоченного
движения частиц, характерные для неравновесных состояний газов.
Теплопроводность возникает при наличии разности температур,
вызванной к-л внешними причинами. При этом молекулы газа в разных
местах его объёма имеют разные кинетические энергии и хаотическое
тепловое движение молекул приводит к направленному переносу внутренней
энергии тела. Молекулы, попавшие из более нагретых частей объёма, попадая
в более холодные, отдают часть своей энергии окр. частицам. И наоборот.
Происходит это за счёт соударений.
Внутреннее трени - вязкость, связанное с возникновением сил трения
между слоями газа или жидкости, перемещающимися параллельно друг другу,
с разл по модулю скоростями. Со стороны слоя дв быстрее возникает ускор
сила. Силы трения напр по касательной. С т.з. МКТ причиной вязкости является
наложение упорядоченного движения слоёв газа с различными скоростями и
хаотичного теплового движения молекул.
Диффузией явление самопроизвольного взаимного проникновения и перемещения частиц двух
соприкасающихся газов (жидкостей, тв. Тел). В химически чистых газах при постоянной
температуре диффузия возникает вледствие неодинаковой плотности в различных частях газа.
Для смеси газов диффузия взывается различием концентрации отдельных газов в различных
частях объёма смеси. При постоянной температуре явление диффузии заключается в переносе
массы газа из мест с большей концентрацией в места с меньшей.
Все явления возникают в результате нарушения полной хаотичности движения молекул.
Это вызванно направленным воздействием на газ, в случае диффузии приводящее к
к неоднородной плотности, теплопроводности - к разной температуре по объёму. Это сопровождается
отклонением от Максвелловского распределения по скоростям. Этими отклонениями
обьясняется направленный перенос массы, импульса и внутренней энергии в газах.
14
получаем ln(p)-ln(p0)=-gMh/(RT) или p=p0e(gMh/(RT))- барометрическая формула. h= (RT/GM)ln(p0/p)
на позволяет получить соотношение между концентрациями газа на различных высотах Используем уравнение
Найдём закон изменения давления идеального газа с высотой в однородном поле тяготения.
Пусть газ находиться в состоянии термодинамического равновесия, так что его температура Т везде
одинакова. Выделим на высоте h столб abcd газа высотой dh и площадью основания, равной 1
Разность давлений p и P+dp на верхнее и нижнее основание на соотв высотах h и h+dh равна
гидростатическому давлению (ro)gdh столба. -Dp=(ro)gdh. D(ro)=(pM/RT)gdh или
d(ro)/p=-(gM/RT)dh. Интегрируя это выражение по всоте от 0 до h и по давлению от p0 до p,
получаем ln(p)-ln(p0)=-gMh/(RT) или p=p0e(gMh/(RT))- барометрическая формула. h= (RT/GM)ln(p0/p)
на позволяет получить соотношение между концентрациями газа на различных высотах Используем уравнение
состояния идеального газа p=n0kT, n0 - концентрация молекул газа. При постоянной Т имеем:
p/p0=n0/n00 где n00 конц молекул газа при давл р0 на высоте =0 заменяя R/M = k/m0, где м0 -
масса молекулы газа, получаем n0=n00*e(mgh/kT) при Е->unlimited, n0->n00 - повышение температуры
приводит к выравниванию концентрации газа при т стрем к нулю Келв, н0 стрем к нулю, молекулы под действием
силы тяжести, опускаются на дно сосуда. Наша атмосфера существует лишшь благодаря тепловому движению частиц
воздуха. Если учесть, что Wп=mgh, потенциальная энергия молекулы в однородном поле тяготения вблизи земли,
то формулу можно переписать в виде n0=n00(-Wп/kT) - математическое выражение закона больцмана для
распределения частиц во внешнем потенциальном поле. Справедлив для любого п поля
14
Квантовая природа света.
Квантовая гипотеза Планка привела к предствлению о том, что свет испускается и
поглощается отдельными порциями - квантами.
Явление вырывания электронов из твёрдых и жидких веществ под действием света
получило название внешнего фотоэффекта. Законы фэ 1максимальная начальная скорость
фотоэлектронов определяется частотой света и не зависит от его интенсивности.
2. Для каждого вещества существует красная граница фотоэффекта, т.е. Минимальная
частота v0 света при которой ещё возможен вн фэ (зависит от химической природы
вещества и состояния его поверхности). 3. Число фотоэлектронов n, вырываемых из
катода за единицу времени, пропорционально интенсивности света, т.е. Фототок
насыщения пропорционален энергетической освещённости катода Е (закон Столетова).
Фотоэффект практически безинерционален.
Множество опытов служит доказательством квантовой природы света, но также мн-во
оптических явлений свидетельствует о волновых его свойствах. Свойства непрерывности
характернык для электромагнитного поля световой волны не исключают свойств дискретности,
характерных для световых квантов- фотонов. Свет одновременно обладает обеими свойствами.
В проявлении этих свойств имеется определённая закономерность: С уменьшением длинны
волны (увеличением частоты) всё более отчётливо сказываются квантовые свойства света.
С этим связанно существование красной границы.
Гипотеза Де Бройля - корпускулярно волновая двойственность характерна не только для света.
Pф=h/(lambda) предположил, что это соотношение имеет универсальный характер для любых
частц, обладающих импульсом р: (lambda)=h/p -формула Де Бройля, для частицы
массой м, движущейся со скоростью, меньшей скорости света, (l)=h/(mv), если частица
имеет кинетическую энергию, учитывая что p=sqrt(2mW), то
(l)=h/sqrt(2mW)
14
Основная задача квантовой механики:
Найти уравнения по которым можно, по начальным условиям и заданным силам найти для любого
момента времени координаты тела и его скорость. Так как состояние частцы
в данный момент времени задаётся волновой функцией (PSI)(x,y,z,t)
уравнение Шрёдингера -(h/i)(de(psi)/det=(-h2/2m)delta(Psi)+U(x,y,z,t)(Psi),
delta=d2/dx2+d2/dy2+d2/dz2-оператор Лапласа., где U()-потенциальная энергия частицы в силовом поле.
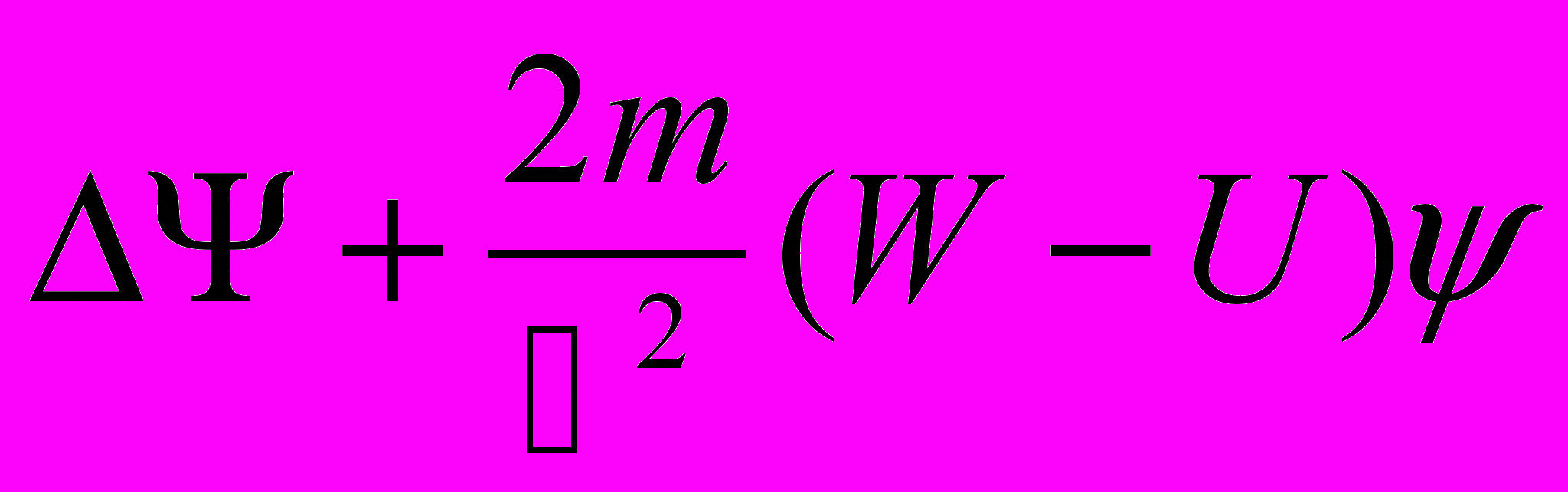 - стационарное Ур-ние Шредингера.
- стационарное Ур-ние Шредингера.15
Теория Бора для водородоподобных систем.
1постул Существуют стационарные состояния атома в которых он не излучает энергию.
Правило квантования орбит бора.
В стационарном состоянии атома, электрон, двигаясь по круговой орбите,
Должен иметь квантовые значения момента импульса., удовлетворяющие условию:
Ln=m_evr=nh(c крестом) масса Эл, скорость Эл, радиус его орб.
2. при переходе атома из одного стационарного состояния в другое, испускается или поглощается один фотон.
Правило частот Бора: - Изменение энергии атома, связанное с выделением или поглощением фотона, пропорционально частоте v: delta W=hню
Боровские орбиты электрона представляют собой геометрическое место точек, в которых с наибольшей вероятностью может быть обнаружен электрон.
16
Ядерная модель атома Резерфорда. На основании опытов по рассеванию альфа чтастиц тонкими металлическими фольгами. Согласно модели в ядре атома, малой по сравнению со всем атомом области, с размерами 10в-15 сосредоточен весь его положительный заряд и практически вся масса атома. Вокруг атома в области с лин разм 10в-10, движутся электроны, масса которых составляет лишь весьма малую часть массы. Также называтся планетарной. Атому свойственна исключительная устойчивость, орбиты электронов стационарны.Атом излучает энергию только при определённых условиях, излучение имеет линейчатый спектр Предполагали что атом постоянно должен терять энергию при излучении и должен быть неустойчивым, и имеет только непрерывный спектр.
17
Принцип Паули или принцип исключения. – в любом атоме не может быть двух электронов, находящихся в одинаковом стационарном состоянии, определяемых набором квантовых чисел- главного l(1…3=spdf…n-1) орбитального n магнитного m спинового m_S
Пространственное квантование – момент импульса электрона может иметь лишь такие ориентации в пространстве, при которых проекция на ось з вектора момента импульса Li на направление Z внешнего поля принимает квантовые значения кратные постоянной Планка.
Liz=mh(x) где m – магнитное квантовое число, где v=(...+-l)
Энергетические уровни зависят только от главного квантового числа. N=n_r(радиальн кв ч)+l+1
17
Таблица Менделеева.
1.порядков номер хим элемента равен общему числу электронов в атоме данного элемента.
2.состояние электронов в атоме определяется набором квантовых чисел, Распределение электронов в атомах должно удовлетворять принципу минимума энергии атома: с возрастанием числа электронов каждый следующий должен занять возможное энергетическое состояние с наименьшей энергией.
3.заполненеие электронами энергетических состояний должно происходить в соответствии с принципом Паули.
