Ие и его эффективное использование: системы управления базами данных, персональные информационные системы, системы управления проектами, системы деловой графики
| Вид материала | Документы |
- Планирование продаж планирование производства формирование графика выпуска продукции, 382.65kb.
- Тема Базы данных. Системы управления базами даннях (12 часов), 116.1kb.
- Программа дисциплины Системы управления базами данных Семестры, 22.73kb.
- Вопросы к государственному экзамену по специальности «Информационные системы и технологии», 39.93kb.
- Системы управления базами данных, 313.7kb.
- Реферат Дипломный проект 79 с., 3 разд., 6 рис., 17 табл., 18 источников, 7 Приложений, 565.68kb.
- Развитие объектно-ориентированных систем управления базами данных, 122.52kb.
- Информационные технологии управления лекция 6 Информационные системы планирования (бюджетирования), 41.66kb.
- Календарно-сетевое планирование и управление «Методология» управления проектами Управление, 10.14kb.
- Календарно-сетевое планирование и управление «Методология» управления проектами Управление, 9.71kb.
8. Сетевые методы планирования и управления
Сетевой анализ включает ряд приемов, которые используются при планировании и претворении в жизнь взаимосвязанных мероприятий. Эти приемы особенно полезны при управлении проектом, когда использование сетевых графиков помогает осуществлять контроль за проектами, направлять ресурсы туда, где это необходимо, и отслеживать затраты. На практике приемы анализа временной последовательности операций особенно целесообразны при осуществлении сложных проектов, включающих проведение многих сотен операций.
Рис. 8.1. Операция
транспортировки
Сетевой график включает в себя операции и события. Каждую операцию можно отобразить с помощью стрелки. События, показывающие начало и окончание каждой операции, обозначаются кружками и обычно прономерованы. Например, транспортировка товаров с завода на склад обозначается операцией А: (рис.8.1). Кружок 1 означает начало операции А, т.е. товары можно отправлять, а кружок 2 — окончание операции А, т.е. транспортировка товаров завершена. Единичные события, представленные кружками, могут обозначать начало или окончание как одного, так и нескольких единичных операций.
Сетевой график — это графическое отображение связей между различными операциями. Чтобы составить сетевой график, необходимо иметь следующую информацию:
- перечень требуемых мероприятий;
- взаимозависимость мероприятий, т.е. их очередность.
При построении сетевых графиков необходимо, чтобы по каждому мероприятию номер кружка, обозначающего его начало, был меньше номера окончания мероприятия.
Важнейшим параметром управления проектом является его общая продолжительность. Ее можно рассчитать по сетевому графику, при условии, что известна продолжительность каждого мероприятия, требуемого в соответствии с проектом.
Таблица 8.1
| Меропри-ятия | Очеред-ность | Продолжитель-ность (недель) |
| А | - | 5 |
| Б | - | 4 |
| В | Б | 2 |
| Г | Б | 6 |
| Д | А, В | 7 |
| Е | Г | 1 |
Рис. 8.2
Пример. Рассмотрим проект из шести мероприятий (А, Б, В, Г, Д и Е). Продолжительность каждого мероприятия приведено в табл. 8.11.
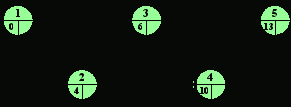
Рис. 8.3
На сетевом графике (рис. 8.2) указывается продолжительность каждого мероприятия. Чтобы найти общую продолжительность проекта, необходимо определить самое раннее и самое позднее время в каждом из кружков сетевого графика. Эти значения обычно вписываются в каждый кружок наряду с номером события (рис. 8.3). В кружок первого события в проекте ставиться ноль. Самое раннее время по последующим событиям рассчитывается путем прибавления продолжительности мероприятия к самому раннему времени предшествовавшего события. Если два или более мероприятия ведут к одному событию, тогда самое раннее время рассчитывается по каждому маршруту, и берется наибольшее полученное значение. Как видно из рисунка, наш проект может быть завершен в течении тринадцати недель.
Рис. 8.4
Далее рассчитывается самое позднее время по каждому событию в соответствии со следующем алгоритмом (рис. 8.4). В последнем кружке проекта самое позднее время события равно самому раннему времени события. Самое позднее время предшествующих событий рассчитывается путем вычитания продолжительности мероприятия из последующего самого позднего времени события. Если два или более мероприятий отходят от одного события, то рассчитывается самое позднее время по каждому маршруту, и берется наименьшее полученное значение.
Анализ методом критического пути заключается в определении того маршрута в сетевом графике, который особым образом влияет на общую продолжительность. Действие на этом маршруте называются критическими действиями. Такие действия не имеют гибкости, если проект должен закончиться в срок. Любое отклонение от времени начала, продолжительности или времени окончания критического действия неизбежно повлияет на общую продолжительность проекта. В сетевом графике критическое действие можно определить следующим образом (рис.8.5):
- самое раннее и самое позднее время начала одинаково;
- самое раннее и самое позднее время окончания одинаково;
-
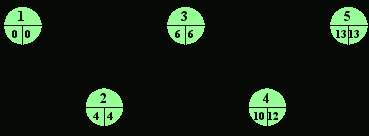
Рис. 8.5
разница между временем начала и окончания равна продолжительности действия.
На сетевом графике критические действия обозначаются маркированной стрелкой. В нашем примере общая продолжительность проекта составляет тринадцать недель, а критический путь — БВД. Все другие действия не являются критическими. То есть, если сократить продолжительность любого из действий А, Г или Е, то это не скажется на общей продолжительности проекта. Так, действие А не является критическим, т.к. оно может начаться в неделю 0 и закончиться в неделю 6, что в итоге составляет шесть дней, тогда как для выполнения действия требуется только пять дней. В то же время, если изменить продолжительность любого из критических действий (Б, В или Д), то это скажется на общей продолжительности проекта.
Резерв времени — это количественный показатель подвижности или запасного времени по каждому действию в сетевом графике. Критические действия - не гибкие и поэтому имеют резерв времени, равный нулю. Существует три вида резерва времени.
Суммарный резерв времени — качественный показатель времени, на которое может быть задержано завершение действия без ущерба для общих сроков проекта.
Суммарный резерв = самое позднее время окончания –
– самое раннее время начала – продолжительность
Свободный резерв времени - количественный показатель времени, на которое может быть задержано завершения действия без ущерба для общих сроков проекта и времени начала последующих действий.
Свободный резерв = самое раннее время окончания –
– самое раннее время начала – продолжительность
Независимый резерв времени - количественный показатель времени, на которое завершение действия может быть задержано без ущерба для общих сроков проекта, а также времени начала последующих действий или времени окончания предшествующих действий.
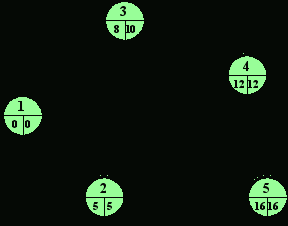
Рис. 8.6
П
Независимый резерв = самое раннее время окончания –
– самое позднее время начала – продолжительность
ример. Рассмотрим следующий сетевой график (рис.8.6). Продолжительность действия указана в неделях, также выделены критические действия. Расчет резервов времени по эти действиям приведены в табл.8.2. Рассмотрим действие А. Его можно задержать до четырех недель (как это указано в столбце суммарного резерва времени) без ущерба для общих сроков проекта. Однако действие А можно задержать только до двух недель (как показывает свободный резерв времени) без ущерба для времени начала последующих действий. Для действия Е все виды резерва времени одинаковы (8 недель), что говорит о том, что продолжительность этого действия можно увеличить до 8 недель без ущерба для общих сроков проекта, а также сроков других действий. Заметим, что все значения резерва времени по критическим действиям (Б, Д и Ж) равны нулю, что указывает на то, что любое увеличение продолжительности этих действий повлияет на продолжительность всего проекта.
Таблица 8.2
| Дейст-вия | Продол-житель-ность (недели) (1) | Самое раннее время начала (2) | Самое позднее время начала (3) | Самое раннее время оконча-ния (4) | Самое позднее время оконча-ния (5) | Суммар-ный резерв времени (5)-(2)-(1) | Свобод-ный резерв времени (4)-(2)-(1) | Незави-симый резерв времени (4)-(3)-(1) |
| А | 6 | 0 | 0 | 8 | 10 | 4 | 2 | 2 |
| Б | 5 | 0 | 0 | 5 | 5 | 0 | 0 | 0 |
| В | 3 | 5 | 5 | 8 | 10 | 2 | 0 | 0 |
| Г | 2 | 8 | 10 | 12 | 12 | 2 | 2 | 0 |
| Д | 7 | 5 | 5 | 12 | 12 | 0 | 0 | 0 |
| Е | 3 | 5 | 5 | 16 | 16 | 8 | 8 | 8 |
| Ж | 4 | 12 | 12 | 16 | 16 | 0 | 0 | 0 |
График Ганта иначе отображает совокупность действий. На нем отмечается время начала и окончания действия, и с его помощью легко видно, какие из действий должны проходить в любой временной точке. Этот график особенно полезен при планировании ресурсов. Рассмотрим график Ганта для нашего примера (рис.8.7). График содержит самое раннее время начала и продолжительность каждого действия (сплошная линия), а также значения суммарного резерва времени по каждому действию (пунктир).
Рис. 8.7
Таблица 8.3
| Действие | Потребность в рабочей силе |
| А | 2 |
| Б | 1 |
| В | 3 |
| Г | 2 |
| Д | 2 |
| Е | 3 |
| Ж | 1 |
Предположим, что для выполнения каждого действия в установленные сроки требуется определенное количество персонала, представленное в табл.8.3.
При этом предполагается, что работники относятся к однородней группе и что для действий по проекту требуются одни и те же профессиональные навыки. Потребности в рабочей силе по каждой неделе проекта можно отобразить в виде гистограммы (рис.8.8а).
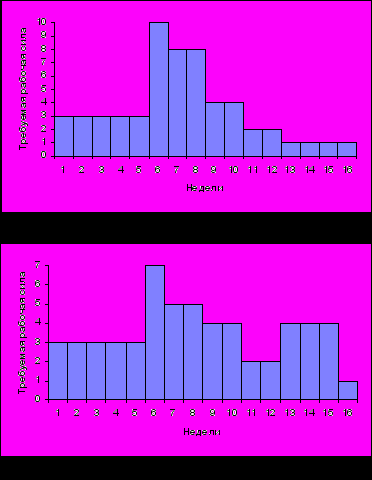
Рис. 8.8
Максимальные потребности в рабочей силе (10 единиц) приходиться на неделю 6. Можно уменьшить эти потребности путем перепланирования действий по графику Ганта. Например, действие Е можно закончить в любое время вплоть до недели 16. Если действие Е начинается в 12 неделю вместо 5, то получится скорректированная потребность в рабочей силе (рис.8.8б). В этом случае максимальная потребность в рабочей силе составляет 7 единиц персонала.
Аналогично, изменение времени начала других действий может еще больше снизить потребности в рабочей силе (например, можно задержать на неделю начало действий В и Г). В данном случае основным подходом к управлению проектом является выравнивание потребности в ресурсах, например в рабочей силе, на протяжении всего проекта.
Другой подход связан с возможностью сокращения продолжительности проекта за счет использования дополнительных ресурсов или внеурочного времени. В этом случае возникают дополнительные расходы. Задача состоит в минимизации этих расходов путем сравнения стоимости сокращения каждого действия до получения желаемого уровня продолжительности проекта.
Таблица 8.14
| Действие | Очередность | Оценочная продолжительность (дней) | ||
| | | Наиболее вероятная | Оптимистическая | Пессимистическая |
| А | - | 9 | 8 | 16 |
| Б | А | 8 | 7 | 9 |
| В | - | 4 | 3 | 5 |
| Г | В | 5 | 5 | 5 |
| Д | В | 8 | 7 | 15 |
| Е | Д | 3 | 2 | 4 |
На практике часто невозможно спрогнозировать точную продолжительность каждого действия в рамках проекта. Например, при осуществлении строительных проектов воздействие на продолжительность действий может оказывать укомплектованность персоналом и оборудованием, погода и другие факторы. Метод оценки и пересмотра планов (ПЕРТ) заключается в вероятностной оценки проекта при этом определяются крайние сроки каждого действия и их наиболее вероятная продолжительность. По каждому действию определяется наиболее вероятная, максимально возможная (пессимистическая) и минимально возможная (оптимистическая) продолжительность. Далее оцениваются ожидаемая продолжительность действия, а также возможный разброс (среднеквадратичное отклонение). Ожидаемая продолжительность и среднеквадратичное отклонение продолжительности всего проекта могут быть получены путем сочетания ожидаемых значений и среднеквадратичных отклонений всех критических действий. Так, если действия А, Б и В являются критическими с ожидаемыми значениями ЕА, ЕБ и ЕВ и среднеквадратическими отклонениями А, Б и В, то общая продолжительность проекта определяется следующим образом:
Ожидаемая продолжительность проекта = ЕА + ЕБ + ЕВ,
Среднеквадратичное отклонение =
.Рассмотрим следующий пример (табл.8.14).
Рассчитаем ожидаемую производительность каждого действия (рис.8.9):
ЕА = (8 +4 9 + 16) 6 =60 6 = 10 дней
ЕБ= (7 +4 8 + 9) 6 = 8 дней
ЕВ = (3 +4 4 + 5) 6 = 4 дня
ЕГ = (5 +4 5 + 5) 6 = 5 дней
ЕД = (7 +4 8 + 15) 6 = 9 дней
ЕЕ = (2 +4 3 + 4) 6 = 3 дня
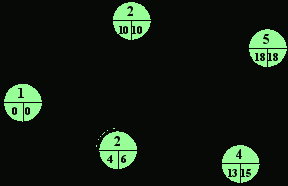
Рис. 8.9
На основании этих данных строиться сетевой график из которого видно, что критическими являются действия А и Б.
Для действия А ЕА = 10 дней, А = (16 - 8) 6 = 1,33 дня. Для действия Б ЕБ = 8 дней, Б = (9 - 7) 6 = 0,33 дня. Ожидаемая продолжительность проекта: 10 + 8 = 18 дней со среднеквадратическим отклонением:
=
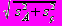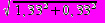= 1,37 дня. Эти значения можно использовать при дальнейшем анализе проекта. Например, можно определить вероятность того, что продолжительность проекта превысит 20 дней. Используя таблицы нормального распределения, можно найти, что данная вероятность равна 7,2 %.В целом методы сетевого анализа дают руководителю мощный инструмент планирования проекта и управления им. Для многих руководителей - это самые важные методы количественного анализа хозяйственной деятельности применительно к управлению людскими и другими ресурсами.