Решить систему уравнений 3-мя способами

Вид материала

Решение

Подобный материал:

• Системы линейных уравнений, 63.47kb.
• Обработка информации на ЭВМ. Урок Этапы решения задач на ЭВМ, 110.78kb.
• Лабораторная работа, 124.91kb.
• Контрольная работа по курсу «Линейной алгебры и математического программирования», 99.84kb.
• Лекция № Тема 1: Системы линейных алгебраических уравнений. Метод Гаусса решения систем, 50.61kb.
• Статья Тема: «Уравнения высших степеней с параметрами», 55.64kb.
• Задание: Составить систему уравнений по законам Кирхгофа для расчета токов ветвей., 17.99kb.
• Лабораторная работа 1 Методы решения задач линейной алгебры, 32.21kb.
• Контрольная работа по линейной алгебре и аналитической геометрии «Системы линейных, 383.4kb.
• Неравенств и, если «да», то найдите общее решение и частное решение двумя способами:, 11.47kb.

Решить систему уравнений 3-мя способами.

1. Методом Гаусса,
   
2. средствами матричного исчисления,
   
3. по формулам Крамера.
   

Решение:



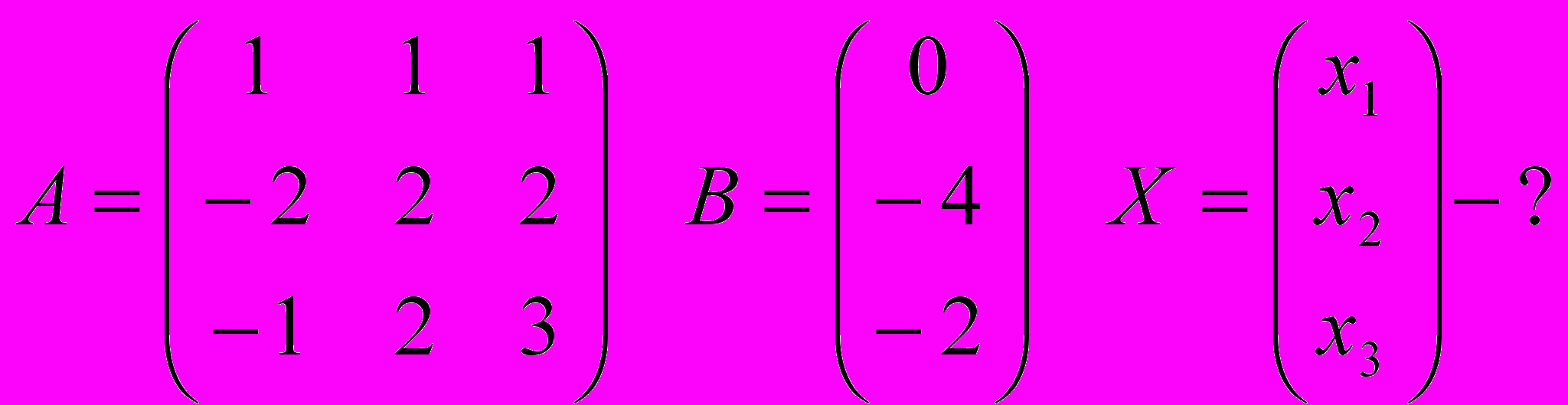
1. Метод Гаусса.

Выпишем расширенную матрицу системы и произведем над ней элементарные преобразования.




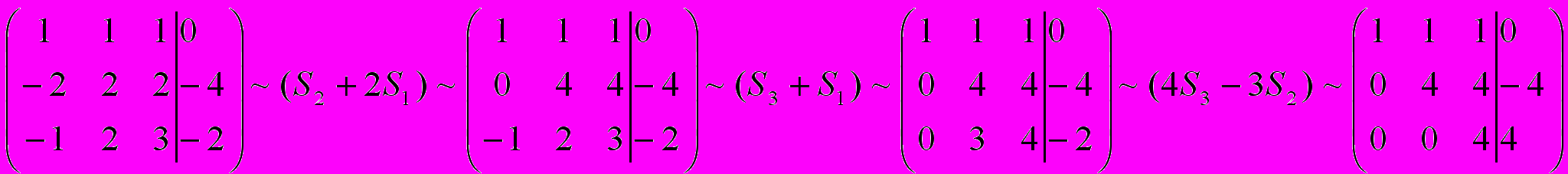
Значит исходная система равносильна системе:



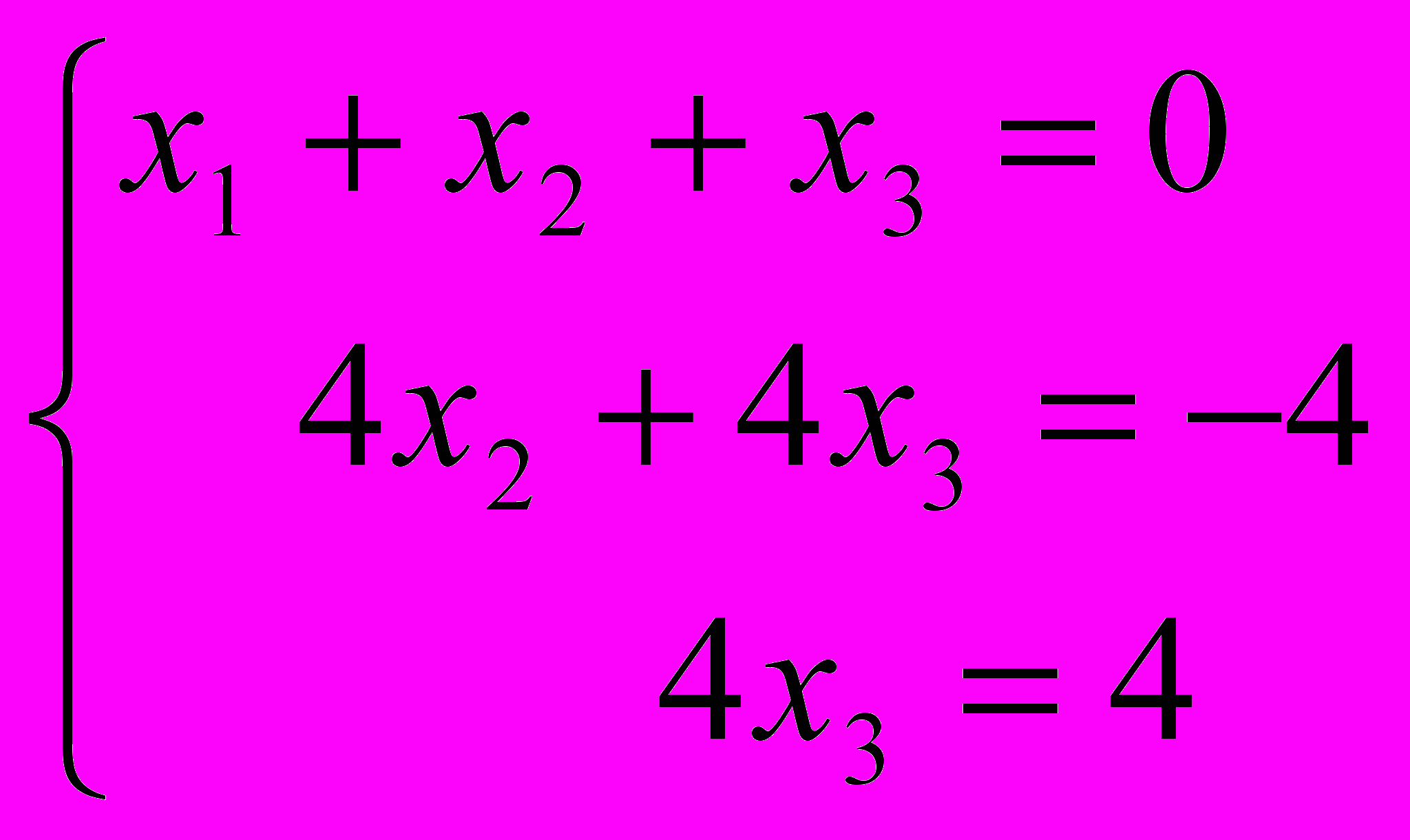
Выполняем обратный ход:

Ответ:

2) Средствами матричного исчисления:



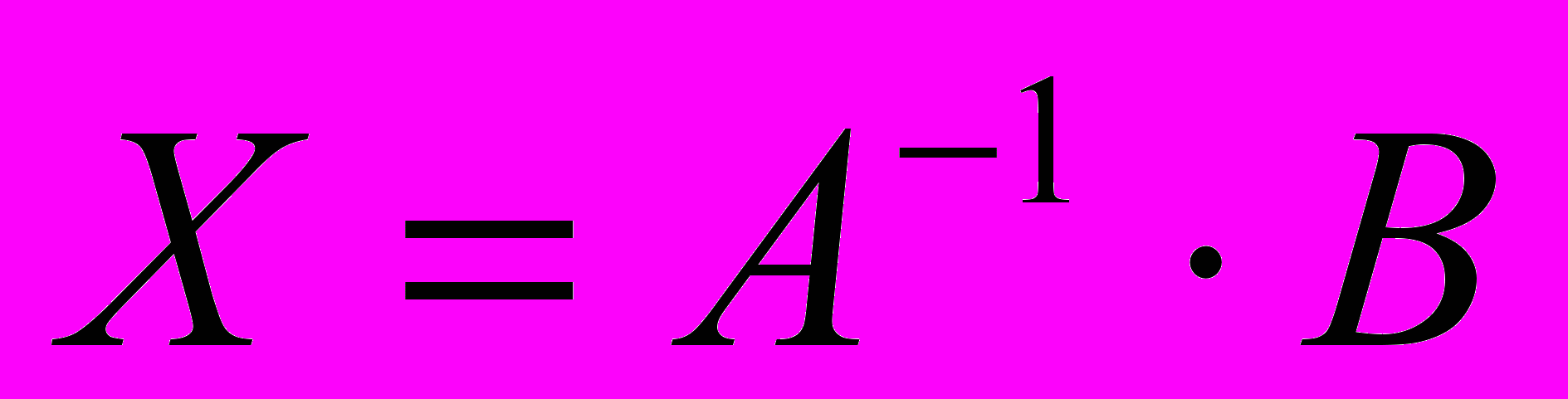
Найдем обратную матрицу 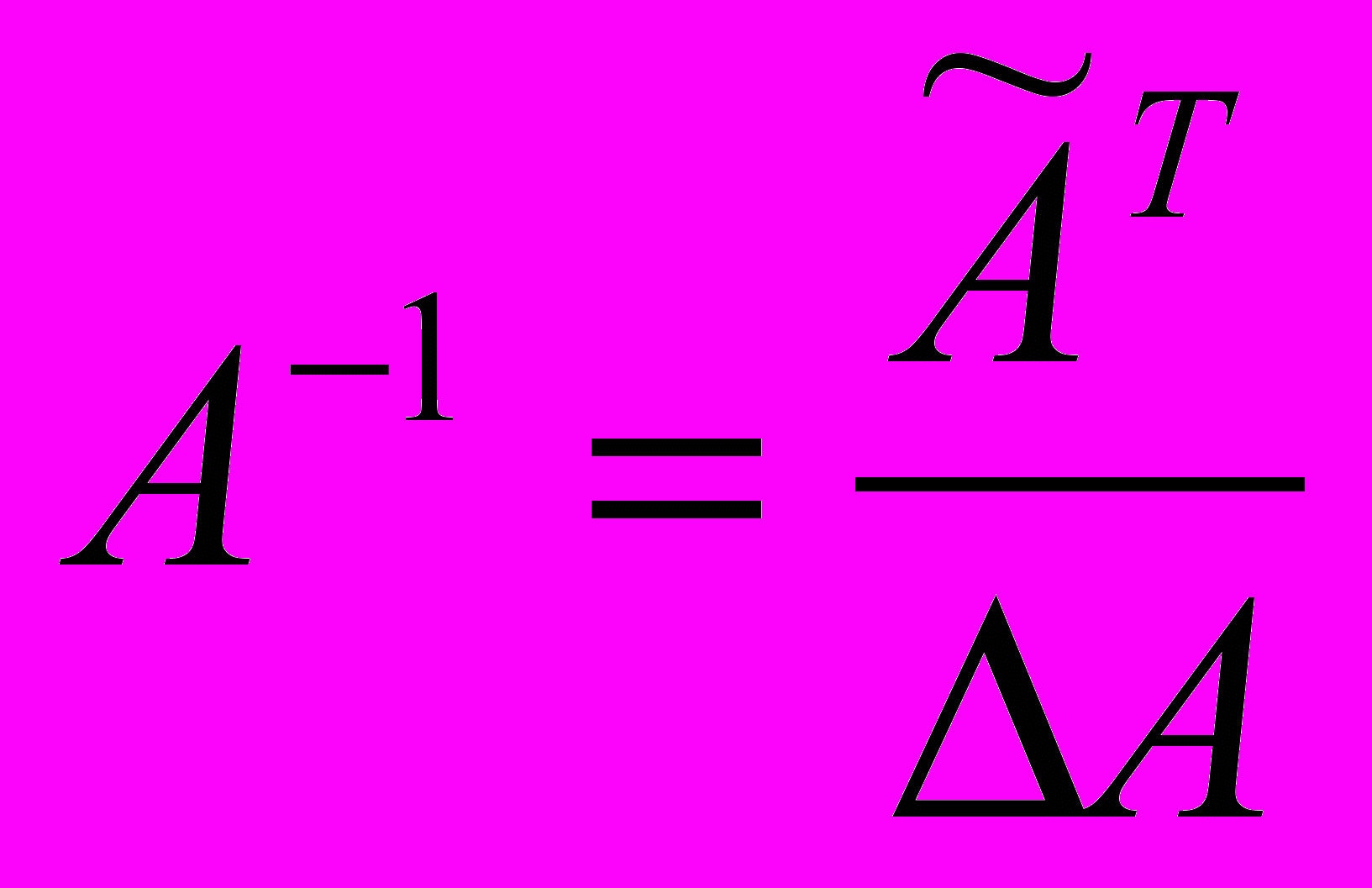. Составим матрицу алгебраических дополнений :









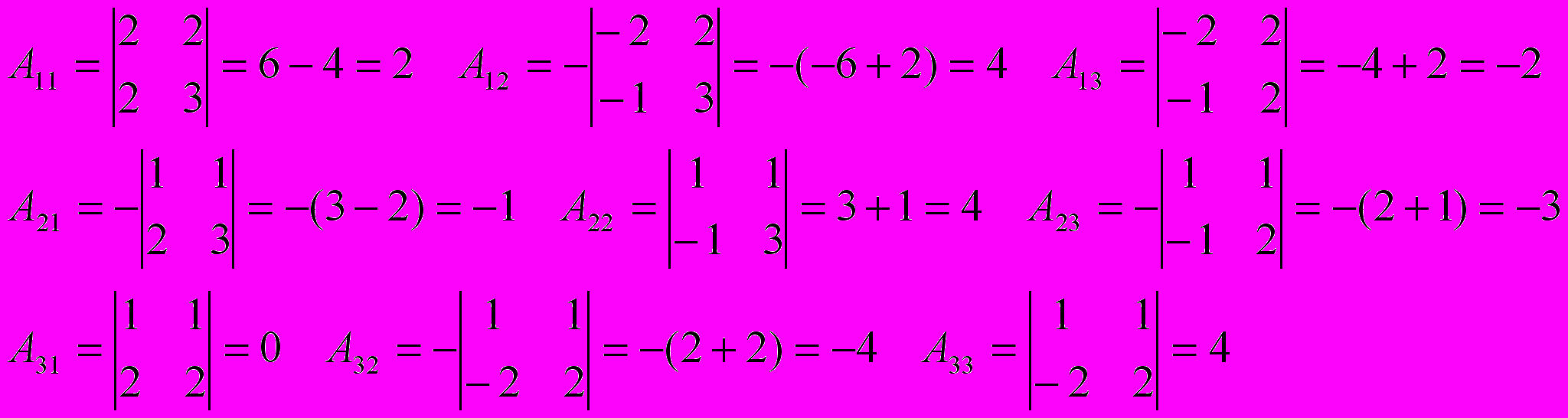
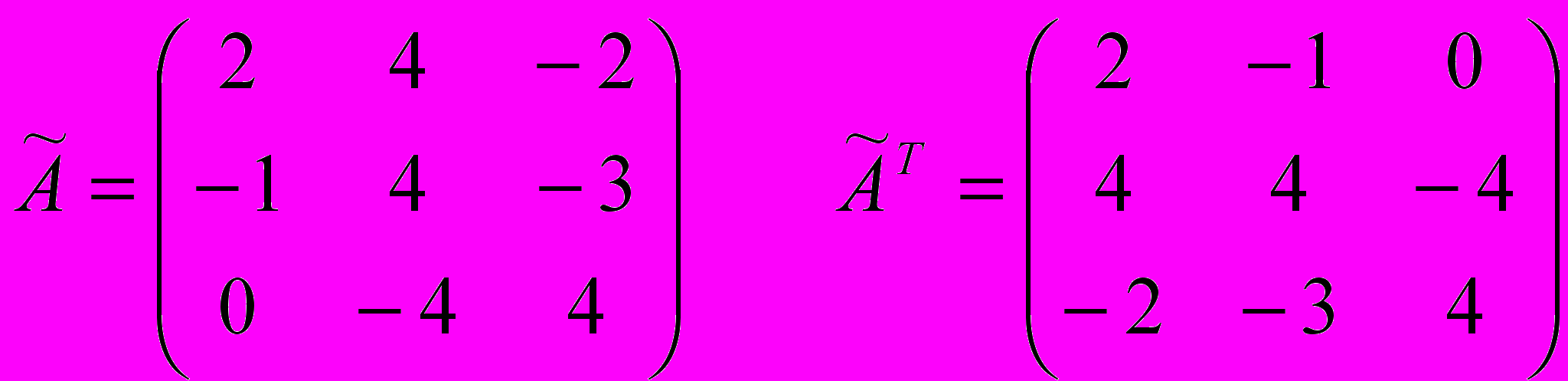
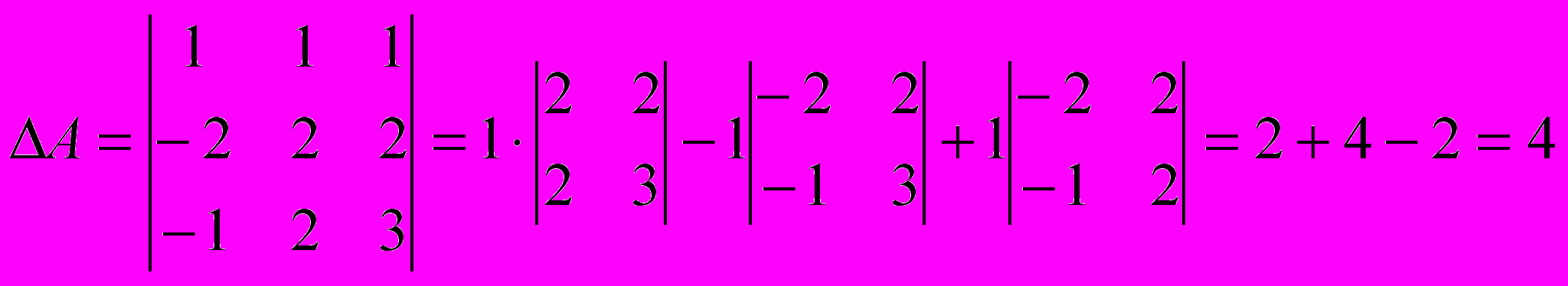
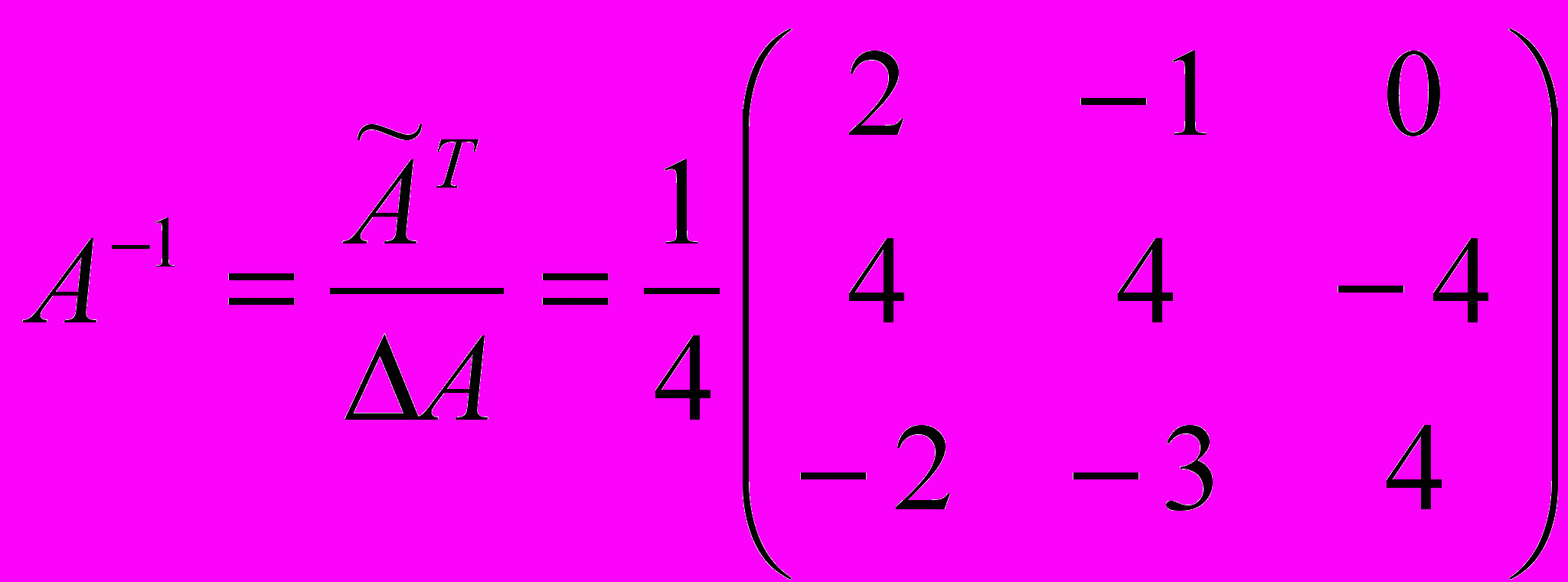
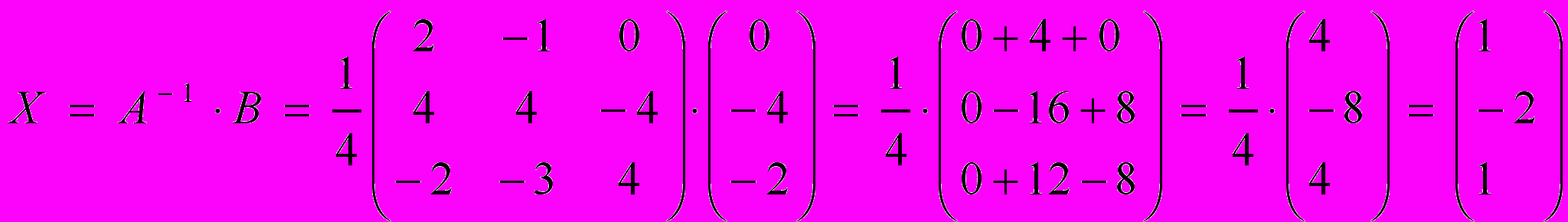Ответ:

3) По формулам Крамера




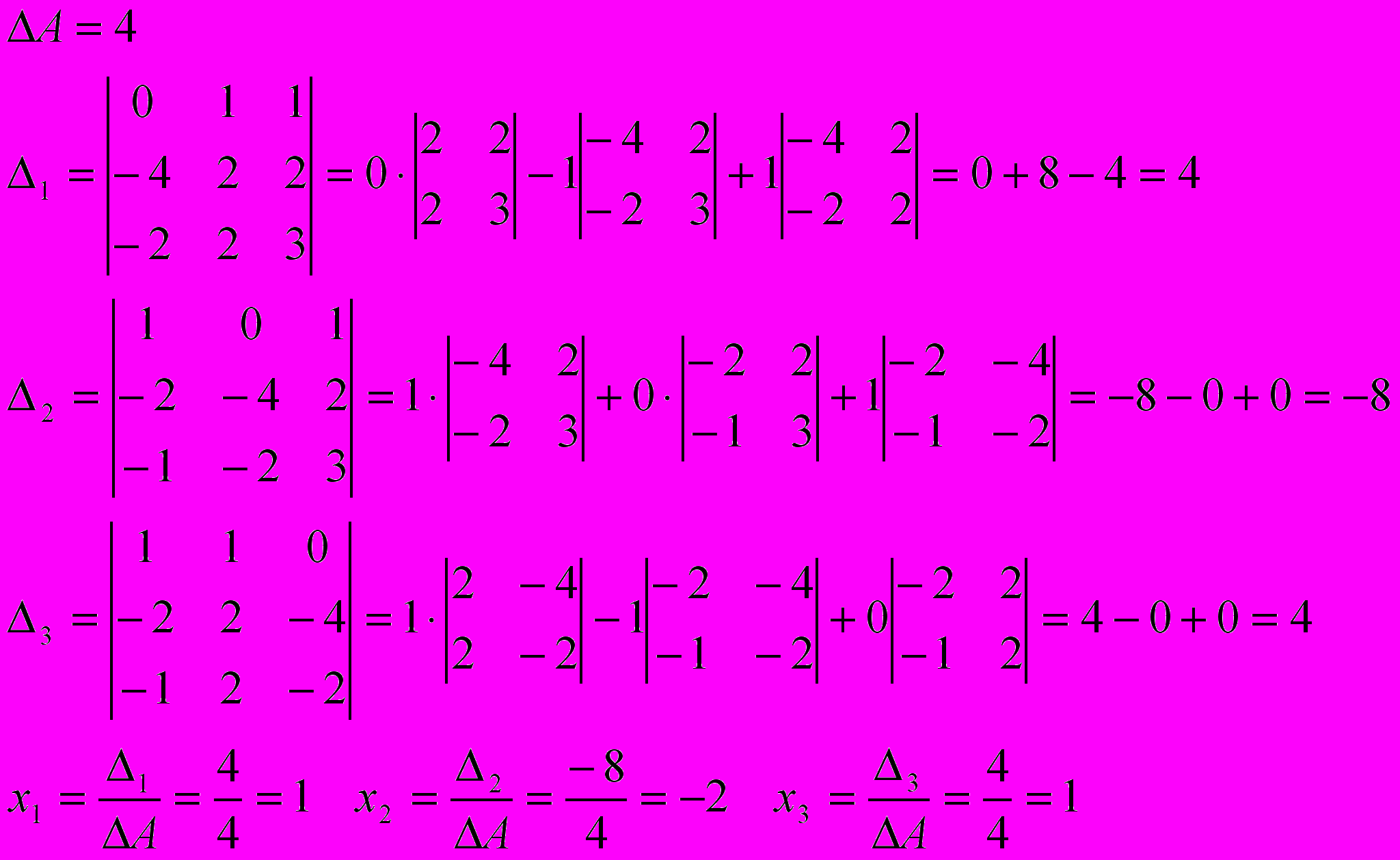
Ответ: