Рабочая программа по дисциплине: «Математика» специальность: 110201 Агрономия

«Утверждаю»

Зав. кафедрой __________О.А. Саввина

«___» _____________2006 г.

РАБОЧАЯ ПРОГРАММА

по дисциплине:	«Математика»
специальность:	110201 – Агрономия
квалификация:	учёный агроном
форма обучения:	заочная
срок обучения:	6 лет
факультет:	сельскохозяйственный
кафедра:	математического анализа и элементарной математики
курс:	I, II
семестр:	1,2,3
лекций:	44 часа
практических занятий: контрольная работа:	30 часов 1, 2, 3 семестры
экзамен:	3 семестр
зачёт:	1, 2 семестры
самостоятельная работа:	326 часов
всего часов:	400 часов

Елец – 2006


Рабочая программа разработана на основе ГОС по специальности 110201 – Агрономия номер государственной регистрации __________________

на кафедре математического анализа и элементарной математики.


Рабочая программа рассмотрена на заседании кафедры (протокол №_____, от «___» ______________2005 г.)


Зав. кафедрой_______________ (О.А Саввина)


Рабочая программа утверждена методическим советом университета (факультета) (протокол №______ от «__» _______ 200__г.)


Председатель методического совета ______________ (В.Н. Воропаев)


Рабочую программу составил С.В. Щербатых

I. ОРГАНИЗАЦИОННО-МЕТОДИЧЕСКИЙ РАЗДЕЛ

1.1. пояснительная записка

Основная цель курса: подготовка высококвалифицированного специалиста – агронома.

Данная программа призвана обеспечить профессиональную подготовку специалистов за счёт системности и действенности знаний, дальнейшей работы по углублению и расширению математических знаний.

Основные задачи изучения курса математики состоят в том, чтобы:

1. раскрыть студентам мировоззренческое значение математики, углубить их представления о роли и месте математики в изучении окружающего мира;
   
2. дать студентам необходимые математические знания, сформировать умения, необходимые для глубокого овладения его содержанием;
   
3. показать возможность применения математического материала к решению прикладных задач;
   
4. способствовать формированию стохастического мышления;
   
5. развивать умение самостоятельной работы с учебными пособиями и другой научной и математической литературой.
   

Указанные цель и задачи в основном определяют содержание данного курса математики.

Базисными понятиями курса математики являются понятия множества, матрицы, определителя, вектора, функции, предела, производной, интеграла, ряда, дифференциального уравнения, соединений, вероятности, случайной величины, математического ожидания, дисперсии, функции распределения, выборочных и генеральных средних, статистических гипотез, уравнения регрессии, коэффициента корреляции и регрессии.

Сельскохозяйственные науки, в частности агрономическая, строятся на анализе зависимостей, существую­щих в природе, на статистических и иных законах. Математика является тем универсальным средством, с помощью которого можно описать реально существующие зависимости и использо­вать их в дальнейшем для научных прогнозов явлений и про­цессов.

Специалисты сельского хозяйства, как и другие специалис­ты, используют методы математической статистики. Здесь су­щественное значение имеет правильный выбор математической модели изучаемого явления, т.е. так называемой производст­венной функции, отражающей основные особенности рассмат­риваемого процесса. Дальнейшее исследование этой функции позволяет найти скорость её изменения, решить задачи наилуч­шего использования ресурсов, получения максимального уро­жая, определения максимальной прибыли и минимума затрат на производство единицы продукции и другие задачи.

Для успешного овладения агрономической специаль­ностью также важно знать законы физики, генетики, биоло­гии, химии, экономики. Все эти науки в той или иной мере ис­пользуют математику, что лишний раз говорит о пользе серьез­ного изучения курса математики.

Следует отметить, что математическая статистика даёт единственный математически обоснованный аппарат для решения задач управления процессов и прогнозирования при отсутствии явных закономерностей в изучаемых сельскохозяйственных процессах. Из этого следует важность, и необходимость изучения раздела на сельскохозяйственном факультете.

Методы статистического исследования имеют важное прикладное значение. Большинство рассматриваемых методов являются непараметрическими, что значительно расширяет их возможности по сравнению с традиционными параметрическими методами. Все методы рекомендуется рассматривать на реальных данных, полученных в сельскохозяйственной практике.

Выборочное наблюдение – решает задачу обобщения на всю совокупность результатов, полученных при изучении её части.

Проверка статистических гипотез – позволяет ответить на вопрос о достоверности принимаемого решения.

Корреляционно-регрессионный анализ – позволяет выявить связи и построить модели зависимостей.

Перечисленные методы основываются на теоретических положениях теории вероятностей и являются классическими.

2. Требования к уровню освоения содержания
   

дисциплины.

Студенты должны
Знать:	Уметь:
Определения и свойства теоретико-множественных операций и отношений, определение разбиения множества на классы, определение прямого произведения множеств.	Выполнять теоретико-множествен-ные операции над конечными и бесконечными множествами, находить прямое произведение множеств.
Понятия множеств: N, Z, Q, I, R, С; определения и свойства операций в данных множествах.	Записывать комплексные числа в алгебраической, тригонометрической и показательной формах; выполнять основные операции над числами из множества С.
Понятия матрицы, определителя, обратной матрицы, системы линейных уравнений.	Выполнять простейшие операции над матрицами и определителями; вычислять значения определителей; решать системы уравнений 1-ой степени в матричной форме и с помощью формул Крамера.
Определения вектора, векторного и смешанного произведений, формул для расчёта расстояний между точками и от точки до плоскости, уравнение окружности.	Выполнять операции над векторами; задавать прямые и плоскости; находить векторное и смешанное произведения векторов, расстояния между точками и от точки до плоскости; выяснять взаимное расположение прямых и плоскостей; задавать окружность.
Понятие линейного программирования.	Применять методы линейного программирования к задачам оптимизации сельскохозяйственного производства.
Определение и способы задания функций; понятие предела, производной, экстремума, точек перегиба, первообразной, неопределённого, определённого и несобственного интегралов, методов их вычисления; определения числового, функционального, степенного и тригонометрического рядов.	Задавать функции, находить их область определения и область значения; находить пределы, производные, первообразные, неопределённые, определённые и несобственные интегралы; исследовать функции с помощью производной; устанавливать сходимость несобственных интегралов; исследовать ряды на сходимость; раскладывать функции в ряд Тейлора и ряд Фурье.
Понятие дифференциального уравнения, основные виды дифференциальных уравнений.	Решать различные виды дифференциальных уравнений; составлять дифференциальные уравнения по тексту задачи.
Основные правила и методы решения комбинаторных задач.	Решать простейшие комбинаторные задачи.
Определения и свойства вероятности, определение и виды событий, их комбинации, формулировки теорем сложения и умножения, их следствий.	Решать простейшие задачи на определение вероятности события; применять теоремы сложения и умножения и их следствий для определения неизвестной вероятности.
Формулировки теорем о независимых повторных испытаниях, условия их применения.	Грамотно использовать теоремы о независимых повторных испытаниях в конкретных ситуациях.
Понятия случайной величины, её виды, понятие закона распределения случайной величины, способы задания и основные виды.	Составлять законы распределения для дискретной случайной величины, определять её вид.
Основные числовые характеристики дискретной случайной величины, их вероятностный смысл и свойства	Вычислять числовые характеристики дискретной случайной величины различными способами.
Способы задания непрерывных случайных величин, понятие интегральной и дифференциальной функции распределения, их основные свойства и графическое представление, определения числовых характеристик непрерывных случайных величин.	Решать задачи на нахождение интегральной и дифференциальной функции распределения, находить неизвестные параметры распределения, числовые характеристики непрерывных случайных величин.
Определение функции нормального распределения, вероятностный смысл параметров, её определяющих, изменение графика функции в зависимости от изменения параметров распределения.	Использовать нормальное распределение для решения сельскохозяйственных задач.
Неравенство П.Л. Чебышёва, различные трактовки закона больших чисел.	Применять неравенство П.Л. Чебышёва, теоремы Я. Бернулли и П.Л. Чебышёва к описанию реальных процессов.
Основные положения выборочного метода.	Находить выборочные характеристики по эмпирическому распределению.
Основные способы определения оценок параметров.	Решать задачи точечного и интервального оценивания параметров распределения.
Определение статистической гипотезы, критериев согласия.	Использовать статистические гипотезы при проверке согласования теоретических и эмпирических сведений, полученных в результате наблюдений и экспериментов.
Знать основные положения корреляционного и регрессионного анализа.	Находить коэффициенты парной и множественной корреляции; составлять уравнения регрессии; оценивать параметры уравнения регрессии методом наименьших квадратов.

II. СОДЕРЖАНИЕ ДИСЦИПЛИНЫ «МАТЕМАТИКА»

2.1. Основные разделы дисциплины.

1. Элементы теории множеств.
   
2. Матрицы и определители.
   
3. Аналитическая геометрия.
   
4. Линейное программирование.
   
5. Элементы математического анализа.
   
6. Простейшие дифференциальные уравнения.
   
7. Элементы комбинаторики.
   
8. Случайные события.
   
9. Случайные величины.
   
10. Анализ вариационных рядов. Выборочный метод.
    
11. Статистические оценки параметров распределения.
    
12. Проверка статистических гипотез.
    
13. Элементарные сведения из теории корреляции и регрессионного анализа.
    

2.2. Темы и их содержание.

1. Элементы теории множеств
   

Множества, способы задания множеств. Подмножества. Равенство множеств. Универсальное множество. Круги Эйлера. Операции пересечения, объединения, разности двух множеств, дополнение множества до универсального. Свойства операций над множествами. Декартово (прямое) произведение множеств, его свойства.

Числовые множества: N, Z, Q, I, R. Расширение понятия числа – множество С. Понятие комплексного числа, его представление. Действия над числами из С.

2. Матрицы и определители
   

Понятие матрицы. Действия над матрицами.

Определители. Обратная матрица. Матричная запись и матричное решение системы уравнений 1-ой степени. Формулы Крамера.

3. Аналитическая геометрия
   

Векторы на плоскости. Прямая, способы её задания. Взаимное расположение прямых на плоскости. Окружность.

Векторы в пространстве. Плоскость, способы её задания. Задание прямой в пространстве. Векторное произведение. Смешанное произведение векторов. Взаимное расположение двух плоскостей, прямой и плоскости. Расстояния между двумя точками, от точки до плоскости.

4. Линейное программирование
   

Понятие линейного программирования. Применение методов линейного программирования к задачам оптимизации сельскохозяйственного производства.

5. Элементы математического анализа
   

Понятие функции. Способы задания функций. Область определения и область значения функции. Понятие о производственных функциях в сельском хозяйстве.

Понятие последовательности. Предел последовательности. Основные теоремы о пределах последовательностей. Предел функции. Основные теоремы о пределах функций. Замечательные пределы. Непрерывность функции.

Понятие производной, её геометрический, механический, биологический и химический смыслы. Правила дифференцирования функций и производные элементарных функций.

Применение производной: возрастание и убывание функций, экстремумы; наибольшее и наименьшее значения функции на отрезке; выпуклость и вогнутость графика функции, точки перегиба; построение графиков функций.

Понятие функции нескольких переменных. Непрерывность функции нескольких переменных. Дифференцирование функций нескольких переменных. Экстремумы функций нескольких переменных.

Первообразная функция и неопределенный интеграл. Основные методы интегрирования. Понятие определенного интеграла. Несобственные интегралы и их сходимость.

Числовые ряды, их основные свойства. Функциональные и степенные ряды, области их сходимости. Разложение функций в степенные ряды. Ряд Тейлора. Тригонометрические ряды. Разложение функций в ряд Фурье.

6. Простейшие дифференциальные уравнения
   

Понятие дифференциального уравнения. Дифференциальные уравнения первого порядка, их частные случаи: уравнения с разделяющимися переменными, линейные дифференциальные уравнения.

Дифференциальные уравнения второго порядка, допускающие понижение порядка.

7. Элементы комбинаторики
   

Перебор возможных вариантов, «дерево» вариантов. Правила умножения и сложения. Перестановки, размещения и сочетания с повторениями и без повторений.

8. Случайные события
   

Предмет теории вероятностей. Понятие случайного, достоверного, невозможного событий. Классическое, геометрическое, статистическое и аксиоматическое определения вероятности. Сумма и произведение событий. Совместные, несовместные, зависимые, независимые, противоположные события. Теоремы сложения и умножения вероятностей. Формула полной вероятности, формула Байеса. Повторение опытов. Формула Я. Бернулли. Наивероятнейшее число наступления событий. Интегральная и дифференциальная теоремы Лапласа. Формула Пуассона.

9. Случайные величины
   

Понятие дискретной и непрерывной случайной величины. Закон распределения дискретной случайной величины, его виды. Биномиальное распределение и распределение Пуассона. Числовые характеристики случайных величин. Математическое ожидание и его свойства. Дисперсия дискретной случайной величины и ее свойства. Среднее квадратичное отклонение. Одинаково распределённые взаимно независимые случайные величины.

Определение интегральной функции распределения. Свойства и график интегральной функции распределения. Дифференциальная функция распределения. Нахождение интегральной функции распределения по известной дифференциальной. Свойства дифференциальной функции распределения. Числовые характеристики непрерывных случайных величин. Нормальный закон распределения. Закон больших чисел: неравенство Чебышёва, теорема Чебышёва, теорема Бернулли.

10. Анализ вариационных рядов. Выборочный метод
    

Предмет и задачи математической статистики. Эмпирический закон распределения. Вариационные ряды. Графическое изображение вариационных рядов.

11. Статистические оценки параметров распределения
    

Статистические оценки параметров распределения. Требования, предъявляемые к оценкам параметров. Несмещённость, состоятельность, эффективность точечных оценок. Понятие генеральной и выборочной средней, моды, медианы. Размах. Понятие генеральной и выборочной дисперсии, выборочного среднего квадратичного отклонения, коэффициента вариации. Точечная оценка генеральной средней. Точечная оценка генеральной дисперсии. Исправленная дисперсия. Интервальные оценки параметров распределения. Доверительный интервал и доверительная вероятность. Интервальная оценка математического ожидания при известном , неизвестном . Интервальная оценка генерального среднего квадратичного отклонения по исправленному.

12. Проверка статистических гипотез
    

Понятие статистической гипотезы. Ошибки первого и второго рода. Мощность критерия. Статистический критерий. Параметрические и непараметрические статистические гипотезы. Выбор критической области.

Алгоритм проверки параметрической гипотезы, алгоритм проверки непараметрической гипотезы. Критерии согласия. Критерии Пирсона, Фишера, Стьюдента.

13. Элементарные сведения из теории корреляции и регрессионного анализа
    

Функциональная, статистическая и корреляционная зависимости. Определение формы связи. Коэффициент корреляции и его свойства. Множественная корреляция.

Основные положения регрессионного анализа. Эмпирическое уравнение регрессии. Виды уравнений регрессии. Оценка параметров уравнения регрессии методом наименьших квадратов.


III. Рабочая программа учебной дисциплины «Математика»

1. Распределение часов курса по видам и темам работ.
   

№	Наименование тем и разделов		Всего часов	Аудиторные занятия			Самостоятельная работа
				лк	пр	лб
Установочная сессия
I	Элементы теории множеств
	Множества, способы задания множеств. Подмножества. Равенство множеств. Универсальное множество. Круги Эйлера. Операции пересечения, объединения, разности двух множеств, дополнение множества до универсального. Свойства операций над множествами. Декартово произведение множеств, его свойства.	25		4	3	-	18
	Числовые множества: N, Z, Q, I, R. Расширение понятия числа – множество С. Понятие комплексного числа, его представление. Действия над числами из С.	20		-	-	-	20
II	Матрицы и определители
	Понятие матрицы. Действия над матрицами. Определители. Обратная матрица. Матричная запись и матричное решение системы уравнений 1-ой степени. Формулы Крамера.		16	2	2	-	12
III	Аналитическая геометрия
	Векторы на плоскости. Прямая, способы её задания. Взаимное расположение прямых на плоскости. Окружность.		6	-	-	-	6
	Векторы в пространстве. Плоскость, способы её задания. Задание прямой в пространстве. Векторное произведение. Смешанное произведение векторов. Взаимное расположение двух плоскостей, прямой и плоскости. Расстояния между двумя точками, от точки до плоскости.		11	2	1	-	8
	ВСЕГО		78	8	6	-	64
1 семестр
IV	Линейное программирование
	Понятие линейного программирования. Применение методов линейного программирования к задачам оптимизации сельскохозяйственного производства.		10	-	-	-	10
V	Элементы математического анализа
	Понятие функции. Способы задания функций. Область определения и область значения функции. Понятие о производственных функциях в сельском хозяйстве.		6	-	-	-	6
	Понятие последовательности. Предел последовательности. Основные теоремы о пределах последовательностей. Предел функции. Основные теоремы о пределах функций. Замечательные пределы. Непрерывность функции.		9	2	1	-	6
	Понятие производной, её геометрический, механический, биологический и химический смыслы.		8	2	1	-	5
	Правила дифференцирования функций и производные элементарных функций		8	2	1	-	5
	Применение производной: возрастание и убывание функций, экстремумы; наибольшее и наименьшее значения функции на отрезке; выпуклость и вогнутость графика функции, точки перегиба; построение графиков функций.		17	2	1	-	14
	Понятие функции нескольких переменных. Непрерывность функции нескольких переменных. Дифференцирование функций нескольких переменных. Экстремумы функций нескольких переменных.		10	-	-	-	10
	Первообразная функции и неопределённый интеграл. Основные методы интегрирования.		11	2	1	-	8
	Понятие определённого интеграла. Несобственные интегралы и их сходимость.		9	2	1	-	6
	Числовые ряды, их основные свойства. Функциональные и степенные ряды, области их сходимости. Разложение функций в степенные ряды. Ряд Тейлора.		8	-	-	-	8
	Тригонометрические ряды. Разложение функций в ряд Фурье.		8	-	-	-	8
	Контрольная работа		2	-	2	-	-
			106	12	8	-	86
2 семестр
VI	Простейшие дифференциальные уравнения
	Понятие дифференциального уравнения. Дифференциальные уравнения первого порядка, их частные случаи: уравнения с разделяющимися переменными, линейные дифференциальные уравнения.		16	2	2	-	12
VII	Элементы комбинаторики
	Перебор возможных вариантов, «дерево» вариантов. Правила умножения и сложения. Перестановки, размещения и сочетания с повторениями и без повторений.		14	-	-	-	14
VIII	Случайные события
	Предмет теории вероятностей. Понятие случайного, достоверного, невозможного событий. Классическое, геометрическое, статистическое и аксиоматическое определения вероятности. Совместные, несовместные, зависимые, независимые, противоположные события. Сумма и произведение событий. Теоремы сложения и умножения вероятностей. Формула полной вероятности, формула Байеса.		15	2	1	-	12
	Повторение опытов. Формула Я. Бернулли. Наивероятнейшее число наступления событий. Интегральная и дифференциальная теоремы Лапласа. Формула Пуассона.		13	2	1	-	10
IX	Случайные величины
	Понятие дискретной и непрерывной случайной величины. Закон распределения дискретной случайной величины, его виды. Биномиальное распределение и распределение Пуассона.		12	2	-	-	10
	Числовые характеристики случайных величин. Математическое ожидание и его свойства. Дисперсия дискретной случайной величины и её свойства. Среднее квадратичное отклонение. Одинаково распределённые взаимно независимые случайные величины.		14	2	1	-	11
	Определение интегральной функции распределения. Свойства и график интегральной функции распределения. Дифференциальная функция распределения. Нахождение интегральной функции распределения по известной дифференциальной. Свойства дифференциальной функции распределения.		14	2	1	-	11
	Числовые характеристики непрерывных случайных величин. Нормальный закон распределения. Закон больших чисел: неравенство Чебышёва, теорема Чебышёва, теорема Бернулли.		14	2	-	-	12
	Контрольная работа		2	-	2	-	-
	ВСЕГО		114	14	8	-	92
3 семестр
X	Анализ вариационных рядов. Выборочный метод
	Предмет и задачи математической статистики. Эмпирический закон распределения. Вариационные ряды. Графическое изображение вариационных рядов.		14	1	1	-	12
	Статистические оценки параметров распределения. Требования, предъявляемые к оценкам параметров. Несмещённость, состоятельность, эффективность точечных оценок. Понятие генеральной и выборочной средней, моды, медианы. Размах. Понятие генеральной и выборочной дисперсии, выборочного среднего квадратичного отклонения, коэффициента вариации. Точечная оценка генеральной средней. Точечная оценка генеральной дисперсии. Исправленная дисперсия.		17	2	1	-	14
	Интервальные оценки параметров распределения. Доверительный интервал и доверительная вероятность. Интервальная оценка математического ожидания при известном , неизвестном . Интервальная оценка генерального среднего квадратичного отклонения по исправленному.		15	2	1	-	12
XI	Проверка статистических гипотез
	Понятие статистической гипотезы. Ошибки первого и второго рода. Мощность критерия. Статистический критерий. Параметрические и непараметрические статистические гипотезы. Выбор критической области. Алгоритм проверки параметрической гипотезы, алгоритм проверки непараметрической гипотезы. Критерии согласия. Критерии Пирсона, Фишера, Стьюдента.		22	3	1	-	18
XII	Элементарные сведения из теории корреляции и регрессионного анализа
	Функциональная, статистическая и корреляционная зависимости. Определение формы связи. Коэффициент корреляции и его свойства. Множественная корреляция.		16	1	1	-	14
	Основные положения регрессионного анализа. Эмпирическое уравнение регрессии. Виды уравнений регрессии. Оценка параметров уравнения регрессии методом наименьших квадратов.		16	1	1	-	14
	Контрольная работа		2	-	2	-	-
	ВСЕГО		102	10	8	-	84
	ВСЕГО ПО КУРСУ		400	44	30	-	326

IV. УЧЕБНО-МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ КУРСА

4.1. Типовые контрольные работы

1 семестр

Контрольная работа.

1. Докажите следующее равенство. Рассмотрите его геометрическую интерпретацию с помощью кругов Эйлера.
   

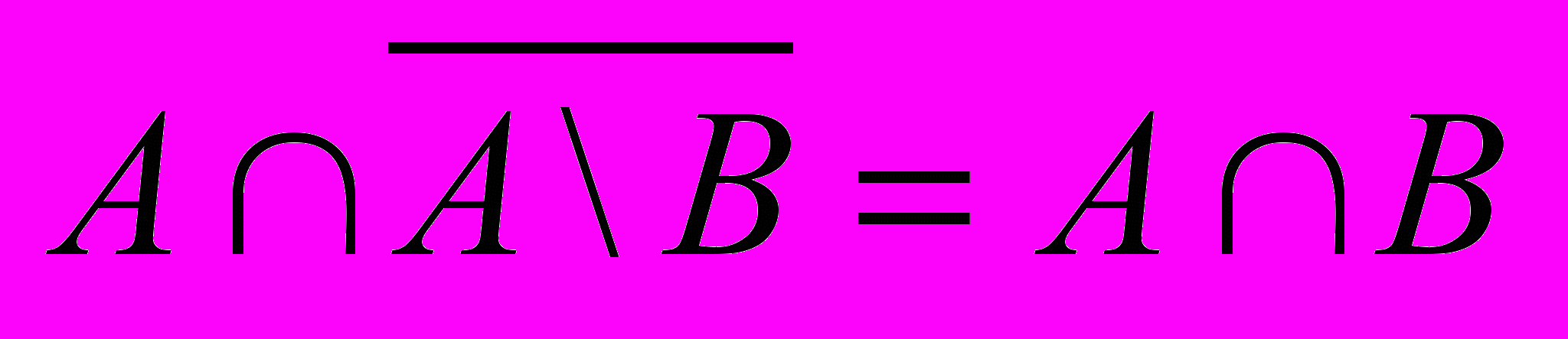
2. С помощью формул Крамера решите систему уравнений.



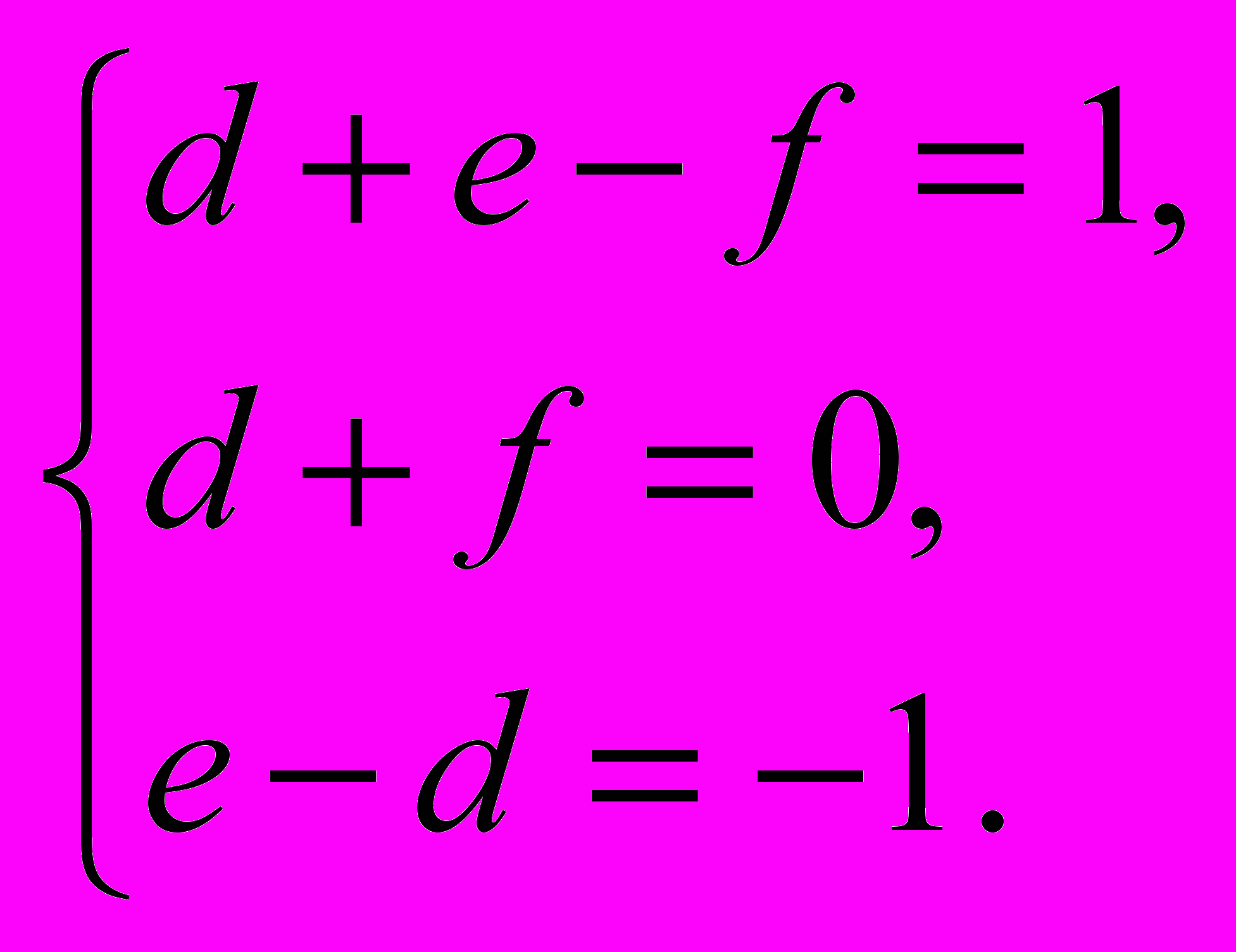
3. Зависимость урожая картофеля у (ц/га) от фотосинтетического потенциала х (%) выражается прямой, проходящей через начало координат и точку (2; 450). Запишите уравнение зависимости.

4. Вычислить предел функции:

.


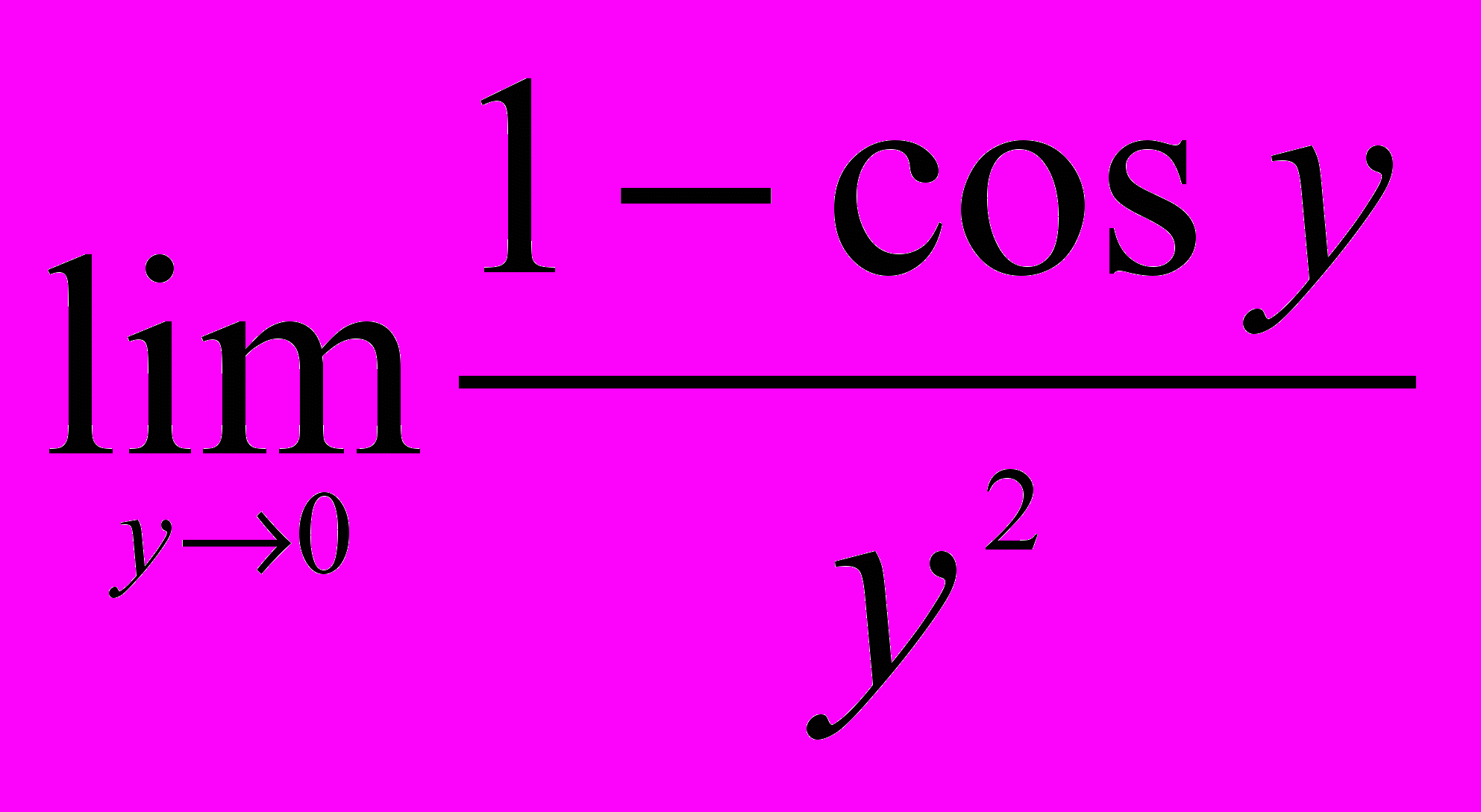5. Применяя формулу Ньютона-Лейбница вычислите определённый интеграл:

.


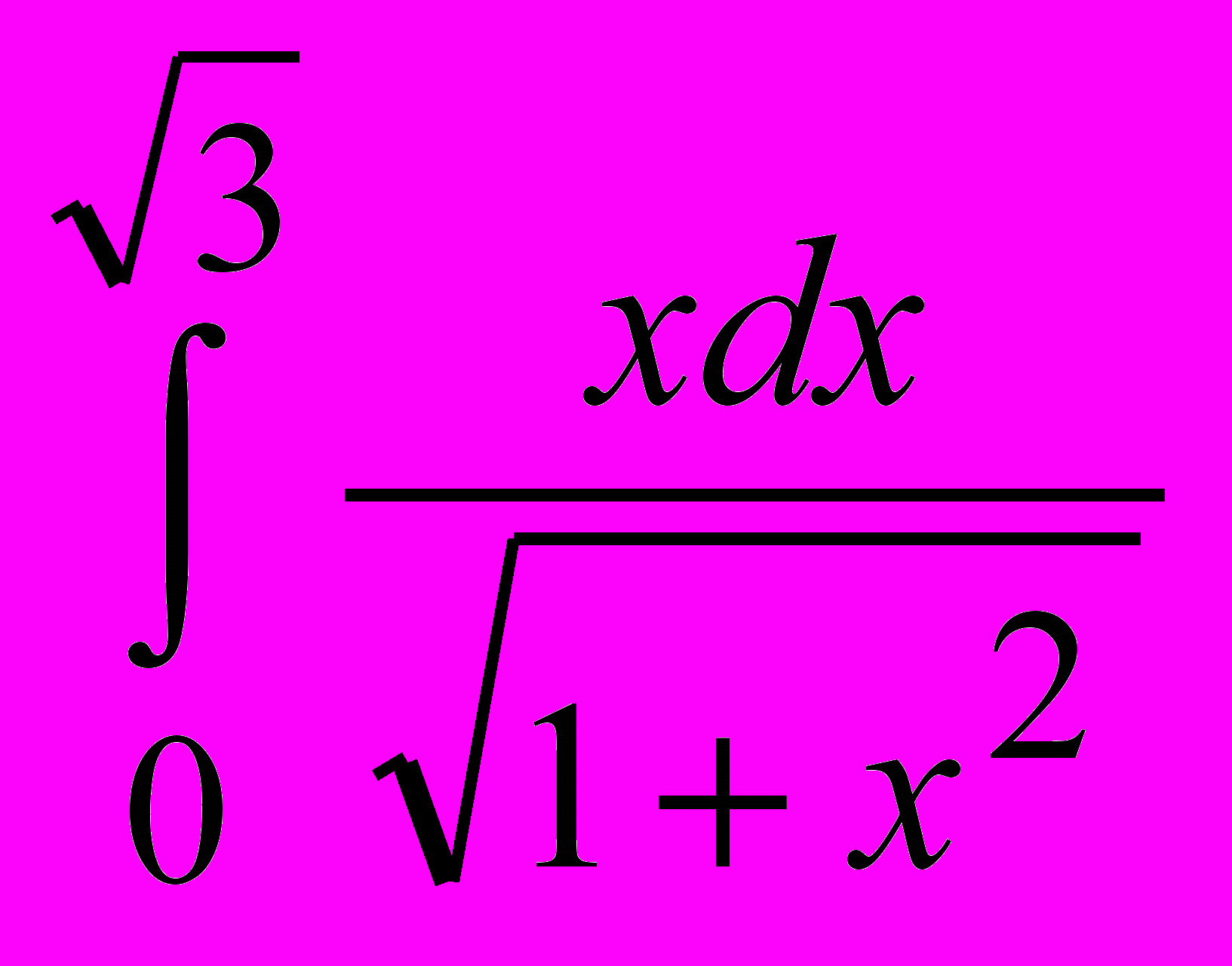2 семестр

Контрольная работа.

1. Решите уравнение:

.

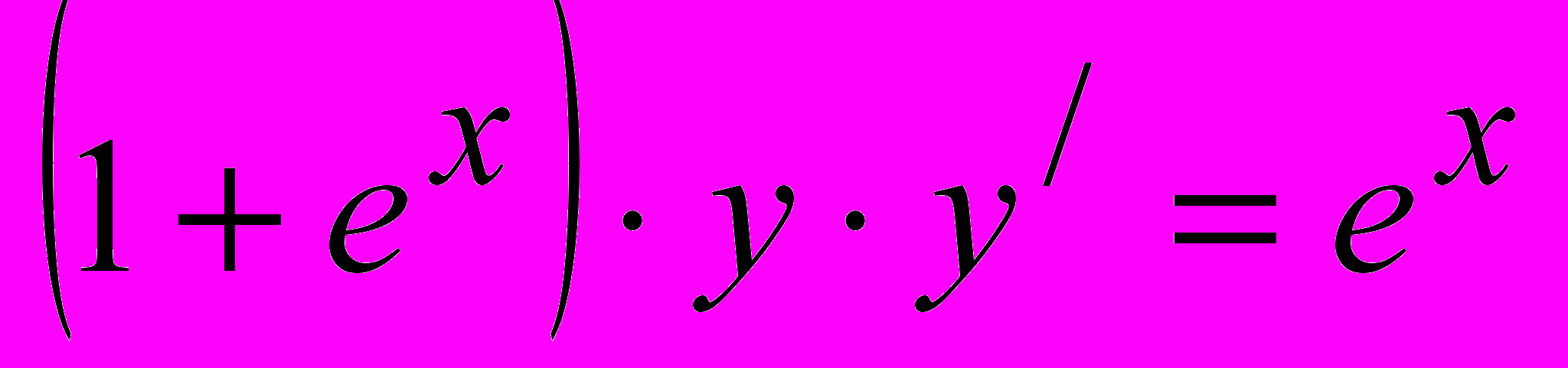2. Пусть всхожесть семян оценивается вероятностью 70%. Какова вероятность того, что из двух посеянных семян взойдёт какое-либо одно?

3. У клевера красного сорта Пермский местный бывает в среднем 84% позднеспелых растений. Какова вероятность того, что 75 растений из 100 растений клевера, отобранных случайным образом, являются позднеспелыми?

4. Для посева заготовлены семена 4 сортов пшеницы. Причём, 20% всех семян 1-го сорта, 30% – 2-го сорта, 10% – 3-го сорта и 40% – 4-го сорта. Вероятность того, что из зерна вырастет колос, содержащий не менее 40 зёрен, для первого сорта равна 0,5, для второго – 0,3, для третьего – 0,2, для четвёртого – 0,1. Найти вероятность того, что наудачу взятое зерно даст колос, содержащий не менее 40 зёрен.

5. Урожайность озимой пшеницы по совокупности участков распределяется по нормальному закону с параметрами: 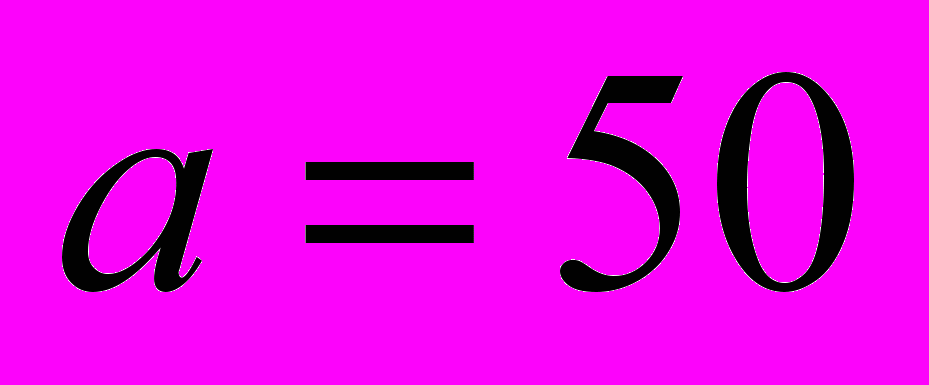ц/га, 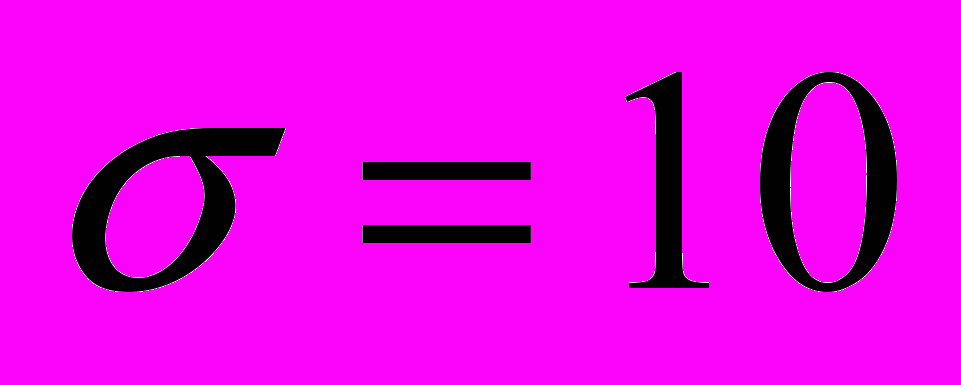ц/га. Определить: а) какой процент участков будет иметь урожайность свыше 40 ц/га; б) процент участков с урожайностью от 45 до 60 ц/га.


3 семестр

Контрольная работа.

1. Пусть дан ряд распределения хозяйств по количеству рабочих на 100 га сельскохозяйственных угодий (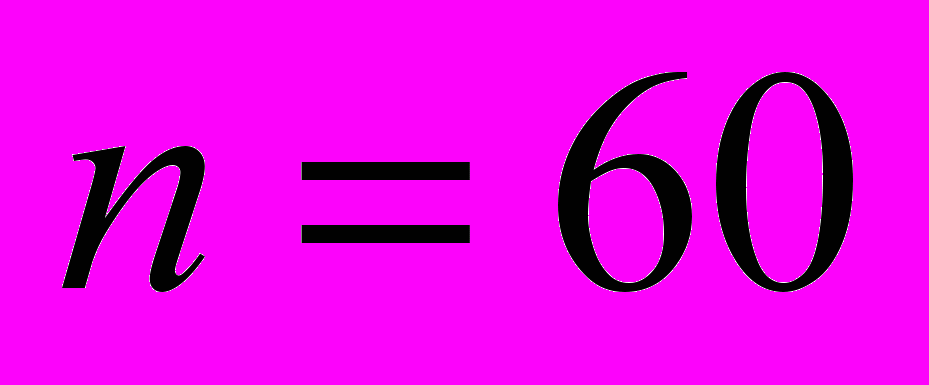): 12, 6, 8, 6, 10, 11, 7, 10, 12, 8, 7, 7, 6, 7, 8, 6, 11, 9, 11, 9, 10, 11, 9, 10, 7, 8, 8, 8, 11, 9, 8, 7, 5, 9, 7, 7, 14, 11, 9, 8, 7, 4, 7, 5, 5, 10, 7, 7, 5, 8, 10, 10, 15, 10, 10, 13, 12, 11, 15, 6. Построить интервальный вариационный ряд и гистограмму распределения частот.

2. По следующим данным: длина листьев садовой земляники (см): 5,2; 5,6; 7,1; 6,6; 8,6; 8,2; 7,7; 7,8 найдите выборочную среднюю, размах, медиану, выборочную дисперсию, среднее квадратичное отклонение и коэффициент вариации.

3. При самоопылении гороха, полученного от скрещивания растений с жёлтыми гладкими и зелёными морщинистыми семенами было получено: 876 растений с жёлтыми гладкими, 321 – с жёлтыми морщинистыми, 298 – с зелёными гладкими и 115 – с зелёными морщинистыми семенами. Можно ли утверждать, что подобное расщепление подчиняется 3-му закону Г.Менделя (дигибридное скрещивание)?


4.2. Вопросы для самостоятельного изучения

Установочная сессия

1. Числовые множества: N, Z, Q, I, R. Расширение понятия числа – множество С.
   
2. Понятие комплексного числа, его представление.
   
3. Действия над числами из С: сложение и вычитание в алгебраической и тригонометрической формах.
   
4. Действия над числами из С: умножение и деление в алгебраической и тригонометрической формах.
   
5. Действия над числами из С: возведение в степень и извлечение корня. Векторы на плоскости. Прямая, способы её задания.
   
6. Взаимное расположение прямых на плоскости. Окружность.
   

1 семестр

1. Понятие линейного программирования.
   
2. Применение методов линейного программирования к задачам оптимизации сельскохозяйственного производства.
   
3. Понятие функции. Способы задания функций.
   
4. Область определения и область значения функции.
   
5. Понятие о производственных функциях в сельском хозяйстве.
   
6. Понятие функции нескольких переменных.
   
7. Непрерывность функции нескольких переменных.
   
8. Дифференцирование функций нескольких переменных.
   
9. Экстремумы функций нескольких переменных.
   
10. Числовые ряды, их основные свойства.
    
11. Функциональные и степенные ряды, области их сходимости.
    
12. Разложение функций в степенные ряды. Ряд Тейлора.
    
13. Тригонометрические ряды. Разложение функций в ряд Фурье.
    

2 семестр

1. Перебор возможных вариантов, «дерево» вариантов. Правила умножения и сложения.
   
2. Перестановки, размещения и сочетания с повторениями и без повторений.
   

4.3. Примерный перечень вопросов для подготовки

к экзамену (зачёту)

1 семестр (зачёт)

7. Множества, способы задания множеств. Подмножества. Равенство множеств. Универсальное множество. Круги Эйлера.
   
8. Операции пересечения, объединения, разности двух множеств, дополнение множества до универсального. Свойства операций над множествами.
   
9. Декартово произведение множеств, его свойства.
   
10. Числовые множества: N, Z, Q, I, R. Расширение понятия числа – множество С.
    
11. Понятие комплексного числа, его представление.
    
12. Действия над числами из С: сложение и вычитание в алгебраической форме; умножение и деление в алгебраической и тригонометрической формах.
    
13. Действия над числами из С: возведение в степень и извлечение корня.
    
14. Понятие матрицы. Действия над матрицами.
    
15. Определители. Обратная матрица.
    
16. Матричная запись и матричное решение системы уравнений 1-ой степени. Формулы Крамера.
    
17. Векторы на плоскости. Прямая, способы её задания.
    
18. Взаимное расположение прямых на плоскости. Окружность.
    
19. Векторы в пространстве. Плоскость, способы её задания.
    
20. Задание прямой в пространстве.
    
21. Векторное произведение.
    
22. Смешанное произведение векторов.
    
23. Взаимное расположение двух плоскостей, прямой и плоскости.
    
24. Расстояния между двумя точками, от точки до плоскости.
    
25. Понятие линейного программирования.
    
26. Применение методов линейного программирования к задачам оптимизации сельскохозяйственного производства.
    
27. Понятие функции. Способы задания функций.
    
28. Область определения и область значения функции.
    
29. Понятие о производственных функциях в сельском хозяйстве.
    
30. Понятие последовательности. Предел последовательности.
    
31. Основные теоремы о пределах последовательностей.
    
32. Предел функции. Основные теоремы о пределах функций.
    
33. Замечательные пределы.
    
34. Непрерывность функции.
    
35. Понятие производной, её геометрический и механический смыслы.
    
36. Понятие производной, её биологический и химический смыслы.
    
37. Правила дифференцирования функций и производные элементарных функций.
    
38. Возрастание и убывание функций, экстремумы.
    
39. Наибольшее и наименьшее значения функции на отрезке.
    
40. Выпуклость и вогнутость графика функции, точки перегиба.
    
41. Первообразная функция и неопределённый интеграл.
    
42. Основные методы интегрирования.
    
43. Понятие определённого интеграла.
    
44. Несобственные интегралы и их сходимость.
    
45. Числовые ряды, их основные свойства.
    
46. Функциональные и степенные ряды, области их сходимости.
    
47. Разложение функций в степенные ряды. Ряд Тейлора.
    
48. Тригонометрические ряды. Разложение функций в ряд Фурье.
    

2 семестр (зачёт)

1. Понятие дифференциального уравнения. Дифференциальные уравнения с разделяющимися переменными.
   
2. Линейные дифференциальные уравнения.
   
3. Перебор возможных вариантов, «дерево» вариантов. Правила умножения и сложения.
   
4. Перестановки, размещения и сочетания с повторениями и без повторений.
   
5. Предмет теории вероятностей, основные понятия теории вероятностей. Классическое и статистическое определения вероятности.
   
6. Геометрическое и аксиоматическое определения вероятности.
   
7. Сумма событий, теорема сложения вероятностей.
   
8. Произведение событий. Теорема умножения вероятностей.
   
9. Формула полной вероятности.
   
10. Формула Байеса.
    
11. Повторение испытаний. Формула Бернулли.
    
12. Наивероятнейшее число наступление событий.
    
13. Локальная и интегральная теоремы Лапласа.
    
14. Вероятность отклонения относительной частоты от постоянной вероятности в независимых испытаниях.
    
15. Виды случайных величин. Закон распределения дискретной случайной величины.
    
16. Виды распределений. Биномиальное распределение.
    
17. Виды распределений. Распределение Пуассона.
    
18. Математическое ожидание ДСВ. Вероятностный смысл М(Х).
    
19. Свойства математического ожидания.
    
20. Дисперсия дискретной случайной величины.
    
21. Свойства дисперсии.
    
22. Среднее квадратичное отклонение. Среднее квадратичное отклонение суммы взаимно независимых случайных величин.
    
23. Одинаково распределённые взаимно независимые случайные величины.
    
24. Интегральная функция распределения, её свойства и график.
    
25. Дифференциальная функция распределения, её свойства.
    
26. Вероятность попадания НСВ в заданный интервал.
    
27. Нахождение интегральной функции распределения по её дифференциальной функции распределения.
    
28. Числовые характеристики непрерывных случайных величин.
    
29. Нормальное распределение. Кривая нормального распределения.
    
30. Формулы для определения вероятностей 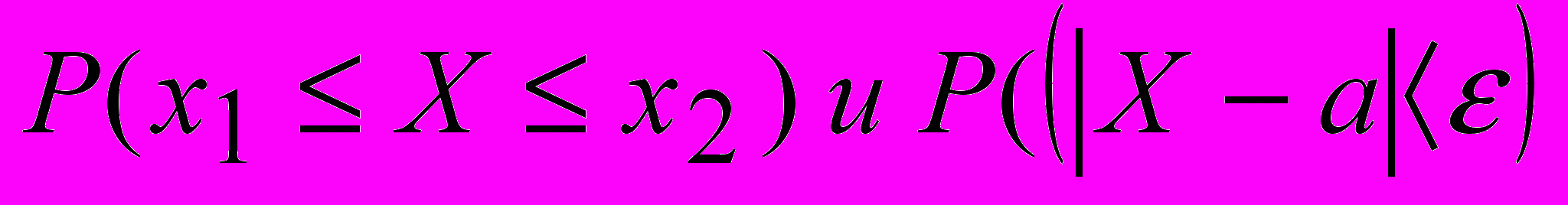, где Х – нормально распределенная случайная величина.
    
31. Закон больших чисел.
    

3 семестр (экзамен)

1. Предмет математической статистики. Задачи статистики. Характеристика совокупности.
   
2. Эмпирический закон распределения величин. Дискретный вариационный ряд.
   
3. Эмпирический закон распределения величин. Интервальный вариационный ряд. Гистограмма.
   
4. Понятие генеральной и выборочной средней.
   
5. Мода, медиана, размах.
   
6. Понятие генеральной и выборочной дисперсии.
   
7. Понятие выборочного среднего квадратичного отклонения, коэффициента вариации.
   
8. Статистические оценки параметров распределения. Требования, предъявляемые к оценкам параметров.
   
9. Несмещенность и состоятельность выборочной средней.
   
10. Оценка дисперсии по выборке. Исправленная дисперсия.
    
11. Интервальная оценка. Доверительный интервал. Доверительная вероятность.
    
12. Интервальная оценка математического ожидания по известному .
    
13. Интервальная оценка математического ожидания по неизвестному .
    
14. Интервальная оценка генерального среднего квадратичного отклонения по исправленному среднему квадратичному отклонению.
    
15. Понятие о статистической гипотезе. Общая постановка задачи проверки статистических гипотез.
    
16. Выбор критической области.
    
17. Алгоритм проверки параметрической гипотезы (на примере критерия Стьюдента).
    
18. Алгоритм проверки непараметрической гипотезы (на примере критерия Пирсона).
    
19. Алгоритм проверки статистических гипотез с помощью углового преобразования Фишера.
    
20. Функциональная, статистическая и корреляционная зависимости.
    
21. Линейный коэффициент корреляции. Свойства коэффициента корреляции.
    
22. Линейный коэффициент корреляции. Основные формулы для расчета коэффициента корреляции.
    
23. Множественная корреляция.
    
24. Основные положения регрессионного анализа. Эмпирическое уравнение регрессии.
    
25. Виды уравнений регрессии.
    
26. Оценка параметров уравнения регрессии методом наименьших квадратов.
    

4.4. Список рекомендуемой литературы

Основная литература

1. Баврин, И.И. Высшая математика [Текст]: учеб. для студ. естественнонаучных специальностей пед. вузов / И.И. Баврин. – М.: Издательский центр «Академия»; Высшая школа, 2000.
   
2. Владимирский, Б.М. Математические методы в биологии [Текст]: учебное пособие для студентов вузов обучающимся по специальности «биология» / Б.М. Владимирский. – Ростов: Изд. Ростовского университета, 1983.
   
3. Вентцель, Е.С. Теория вероятностей [Текст]: учебное пособие / Е.С. Вентцель.  М.: Высшая школа, 2001.
   
4. Гнеденко Б.С. Курс теории вероятностей [Текст]: учебник для ВУЗов.  М.: УРСС, 2006.
   
5. Гнеденко, Б.В. Элементарное введение в теорию вероятностей [Текст] / Б.В. Гнеденко, А.Я. Хинчин. – М.: Наука, 1982.
   
6. Гмурман, В.Е. Теория вероятностей и математическая статистика [Текст] / В.Е. Гмурман.  М.: Высшая школа, 2003.
   
7. Гмурман, В.Е. Руководство к решению задач по теории вероятностей и математической статистике [Текст] / В.Е. Гмурман.  М.: Высшая школа, 2003.
   
8. Гусак, А.А. Теория вероятностей [Текст]: справочное пособие к решению задач / А.А. Гусак, Е.А. Бричикова. – Изд-е 4-е, стереотип. – Мн.: ТетраСистемс, 2003.
   
9. Зайцев, И.А. Высшая математика [Текст]: учеб. для сельскохозяйственных вузов / И.А. Зайцев. – 3-е изд., испр. – М.: Дрофа, 2004.
   
10. Золотаревская, Д.И. Теория вероятностей: Задачи с решениями [Текст]: учебное пособие / Д.И. Золотаревская. – изд. 2-е, перераб. и доп. – М.: Едиториал УРСС, 2003.
    
11. Ильин, В.А. Высшая математика [Текст]: учеб. / В.А. Ильин, А.В. Куркина. – 2-е изд., перераб. и доп. – М.: ТК Велби, Изд-во Проспект, 2005.
    
12. Колемаев, В.А. Теория вероятностей и математическая статистика [Текст]: учебник / В.А. Колемаев, В.Н. Калинина. – М.: ИНФРА-М, 2001
    
13. Лакин, Г.Ф. Биометрия [Текст]: учеб. пособие для биологич. спец. Вузов / Г.Ф. Лакин. – 3-е изд., перераб. и доп. – М.: Высшая школа, 1980.
    
14. Сборник задач по математике: теория вероятностей и математическая статистика [Текст]: учебное пособие для вузов / под ред. А.В. Ефимова– М.: Наука, 1990.
    
15. Колмогоров, А.Н. Введение в теорию вероятностей [Текст] / А.Н. Колмогоров и др. – М.: Наука, 1982.
    

Дополнительная литература

1. Горелова, Г.В. Теория вероятностей и математическая статистика в примерах и задачах с применением Excel [Текст]: учебное пособие для вузов / Г.В. Горелова, И.А. Кацко. – издание 2-е испр. и доп. – Ростов н/Д: Феникс, 2002.
   
2. Гринин, А.С. Математическое моделирование в экологии [Текст]: учеб. пособие для вузов / А.С. Гринин, Н.А. Орехов, В.Н. Новиков. – М.: ЮНИТИ-ДАНА, 2003.
   
3. Данко, П.Е. Высшая математика в упражнениях и задачах. Ч.II [Текст]: учеб. пособие для студентов втузов / П.Е. Данко, А.Г. Попов, Т.Я. Кожевников.  М.: Высшая школа, 1999.
   
4. Зеленцов, Б.П. Основы теории вероятностей [Текст] / Б.П. Зеленцов // Соросовский образовательный журнал, 2001. – №10. – с.115-121.
   
5. Общий курс высшей математики для экономистов [Текст]: учебник / под ред. В.И. Ермакова. – М.: ИНФРА-М, 2000.
   
6. Феллер, В. Введение в теорию вероятностей и ее приложения. В 2 т. [Текст] / В. Феллер.  М.: Мир, 1984.
   
7. Чубарев, А.М. Невероятная вероятность (О прикладном значении теории вероятностей) [Текст] / А.М. Чубарев, В.С. Холодный. – М.: «Знание», 1976.
   
8. Шипачёв, В.С. Задачник по высшей математике [Текст]: учеб. пособие для вузов / В.С. Шипачёв. – М.: Высшая школа, 1998.
   
9. Шипачёв, В.С. Основы высшей математики [Текст]: учеб. пособие для вузов / В.С. Шипачёв. – М.: Высшая школа, 2001.
   
10. Щербатых, С.В. Случайность вокруг нас (учебно-методический комплекс элективного курса) [Текст]: учебно-методическое пособие / С.В. Щербатых. – Елец: ЕГУ им. И.А. Бунина, 2005.