Ax=y Произведем некоторое преобразование координат С: cax=Cy

Вид материала

Лекция

Содержание Характеры неприводимых представлений

Подобный материал:

• Программа курса «Общая физика. Механика», 33.84kb.
• Программа вступительного экзамена по специальности в магистратуру физического факультета, 209.43kb.
• Ії приймання навігаційної інформації, обчислювання координат супутників, обчислювання, 175.51kb.
• Лекция 4 аксонометрические проекции. Многогранные и кривые поверхности, 219.26kb.
• Положение камеры Преобразования, определяющие положение и ориентацию объекта в мировой, 105.74kb.
• Урок лекция по геометрии в 10 классе по теме «Декартовы координаты в пространстве», 53.59kb.
• Решить систему уравнений 3-мя способами, 7.16kb.
• Тема: Карти. Атласи. Визначення географічних координат, 313.96kb.
• Суть метода координат, 16.15kb.
• Урок-подорож, 108.55kb.

Лекция 9

R  x

A – матрица

Ax=y

Произведем некоторое преобразование координат С:

CAx=Cy

CAC^-1Cx=Cy



- матрица в преобразованных координатах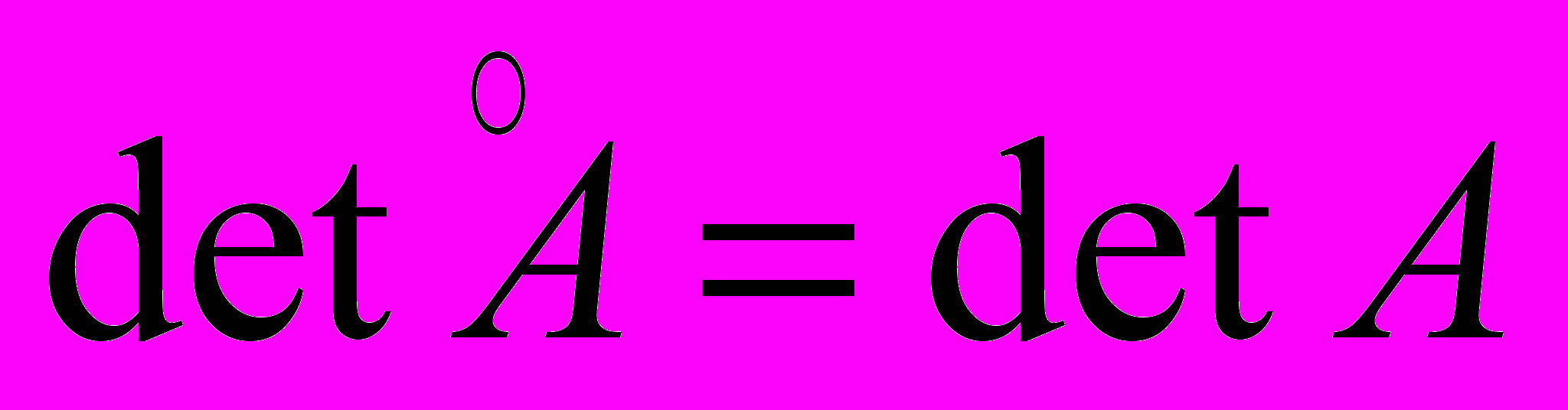



Определитель матрицы инвариантен относительно преобразования координат. Кроме того, след матрицы инвариантен относительно преобразования.

След матрицы - - сумма диагональных элементов матрицы. Sp – (spur (нем.) – след.) = tr – (trace).





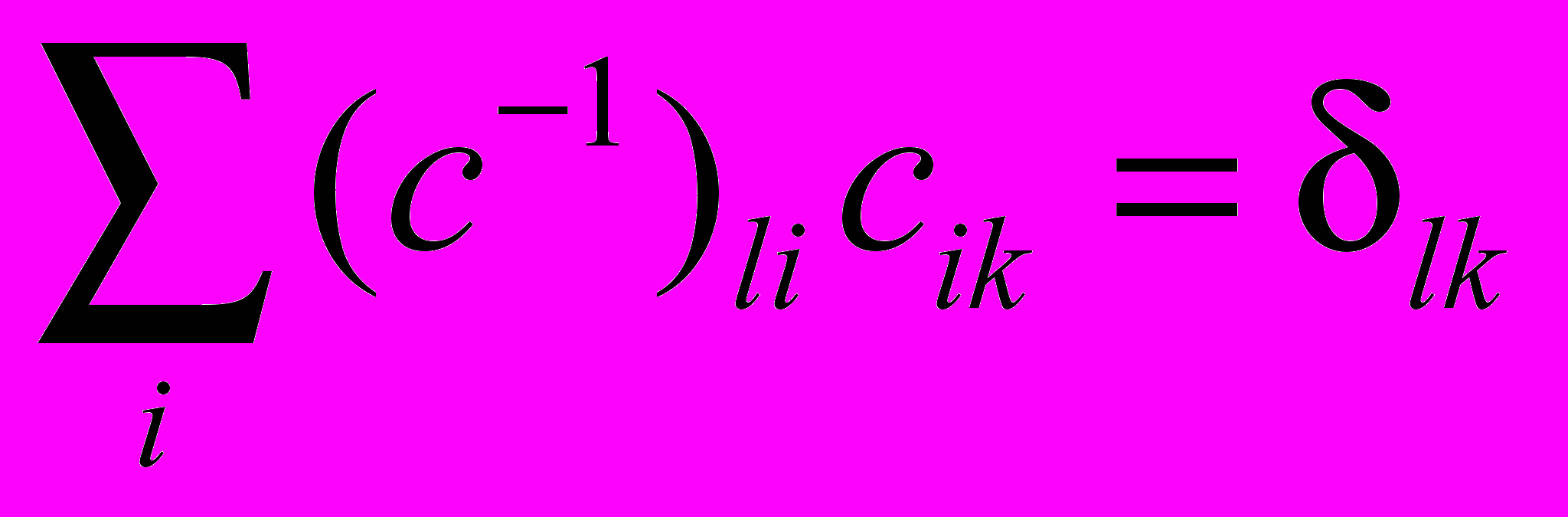
Этот инвариант называется характером матрицы.

T_g  A  χ(A) – ставим в соответствие матрице её характер.

Из всех преобразований выбираем унитарные матрицы (они не меняют длины векторов). В R_n ортогональные матрицы не меняют длин векторов.

Рассмотрим (x,y)  (O_x,O_y)=(x,O^TO_y)

При соответствующем выборе базиса матрицу можно свести к виду:



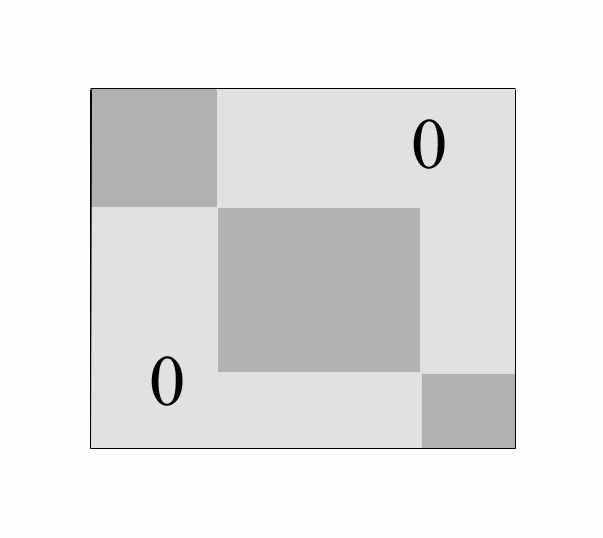
Эту операцию можно проводить до определенного момента. Матрица неприводимого представления – матрица, которую уже нельзя привести к такому виду.





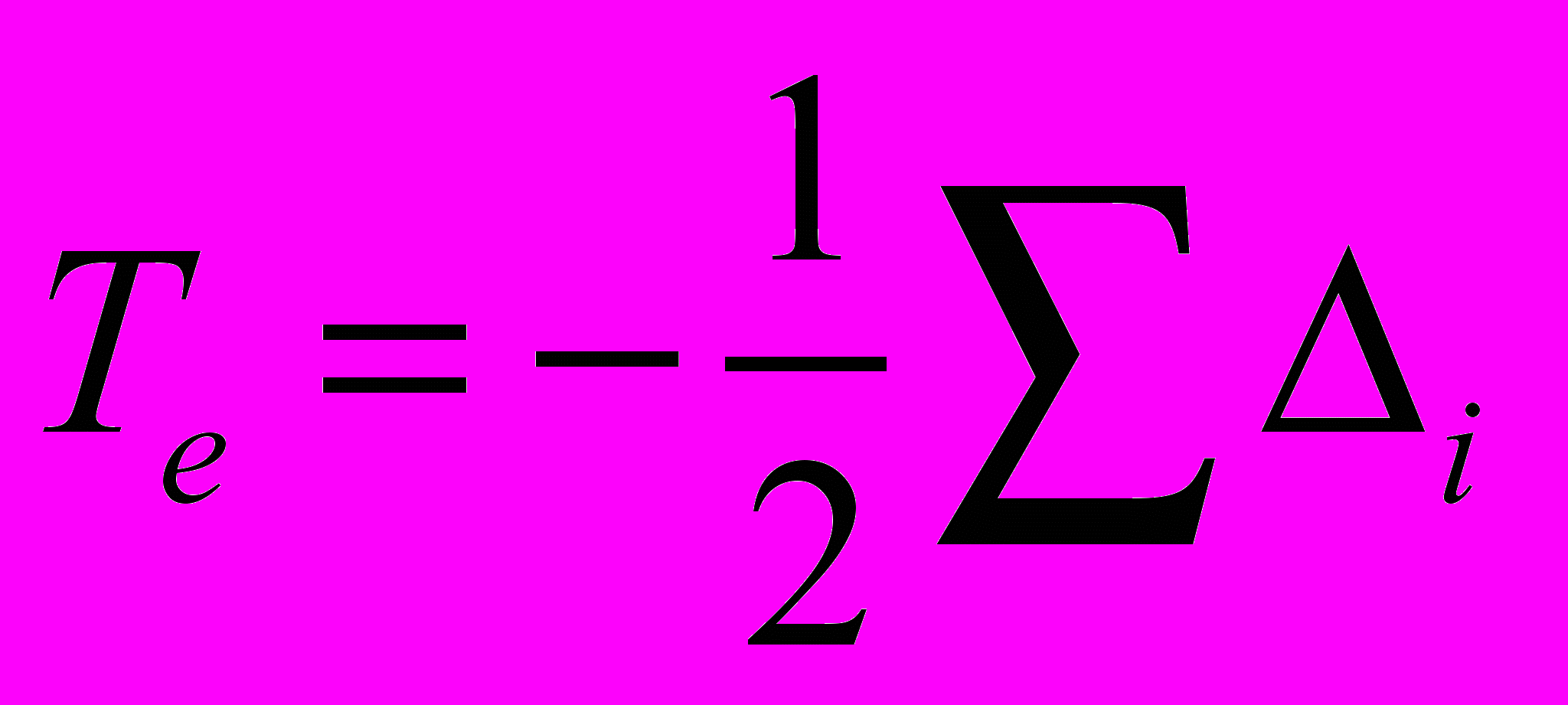
Рассмотрим первые производные:



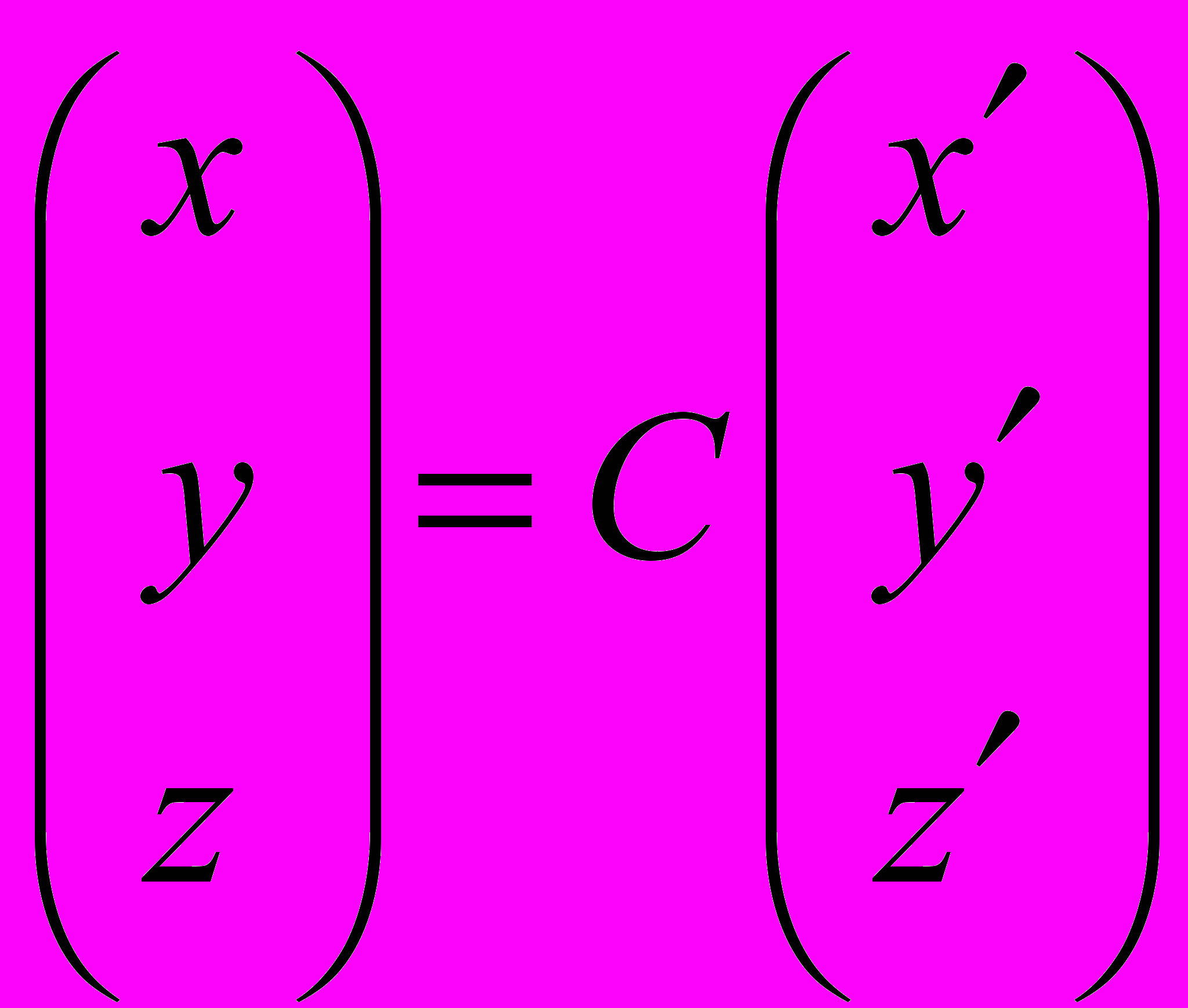
, откуда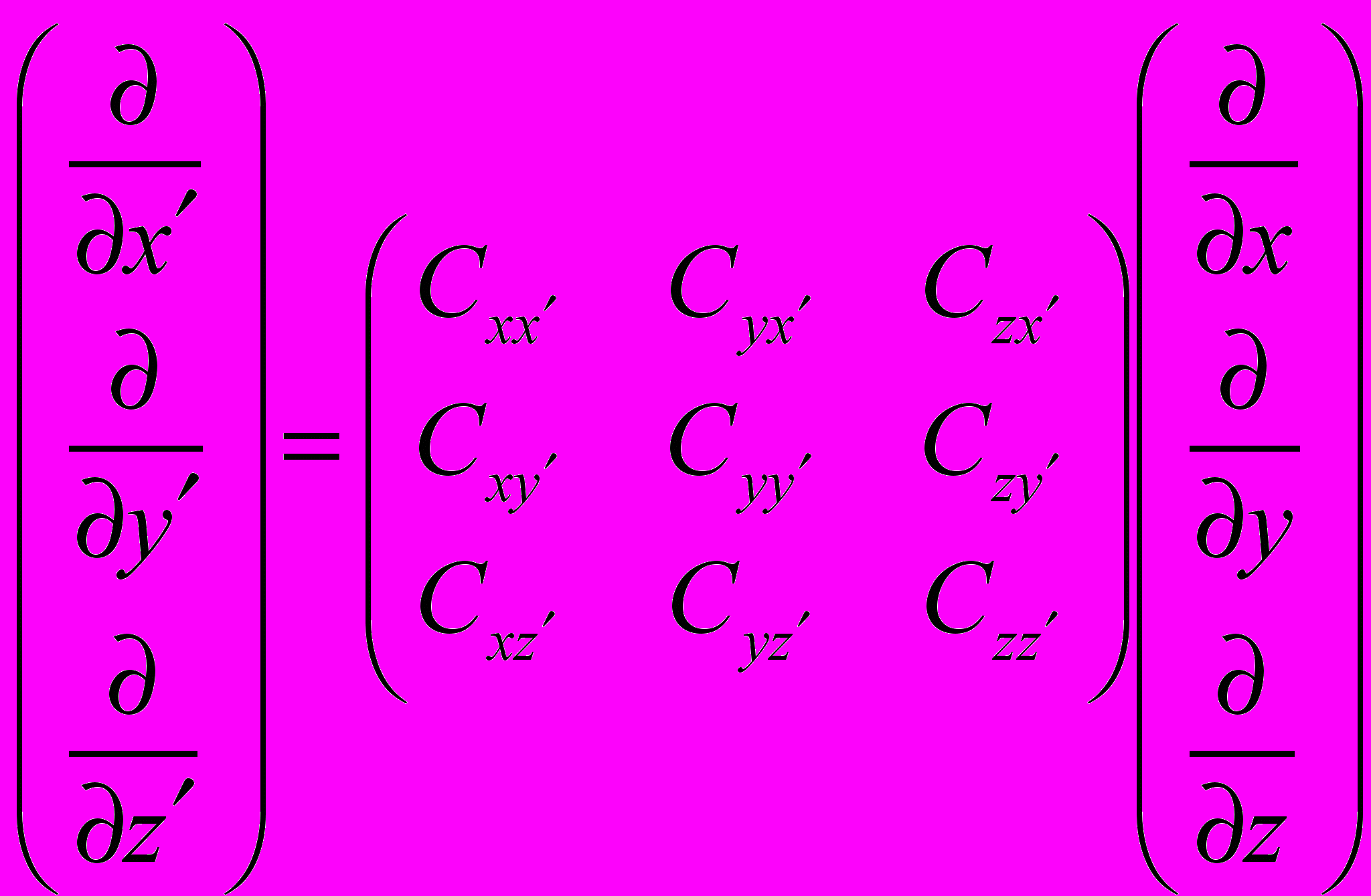



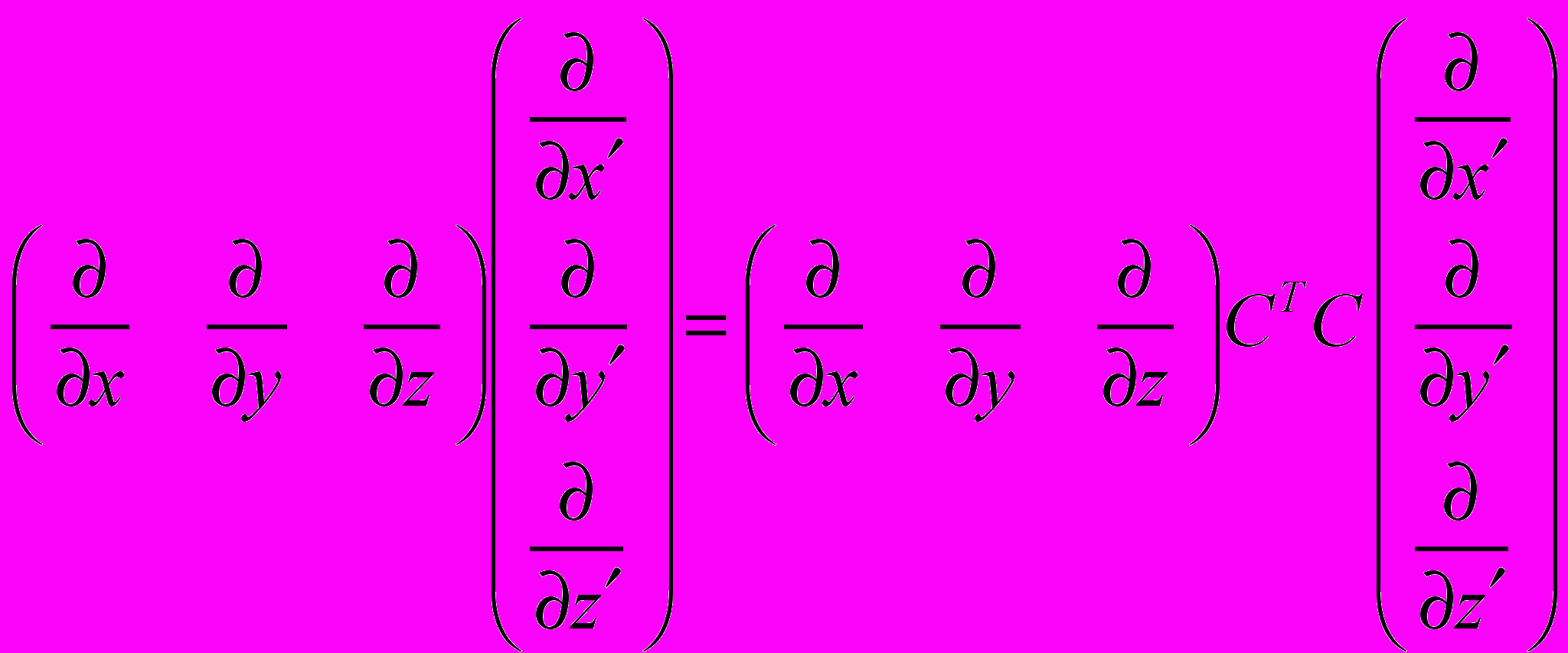, где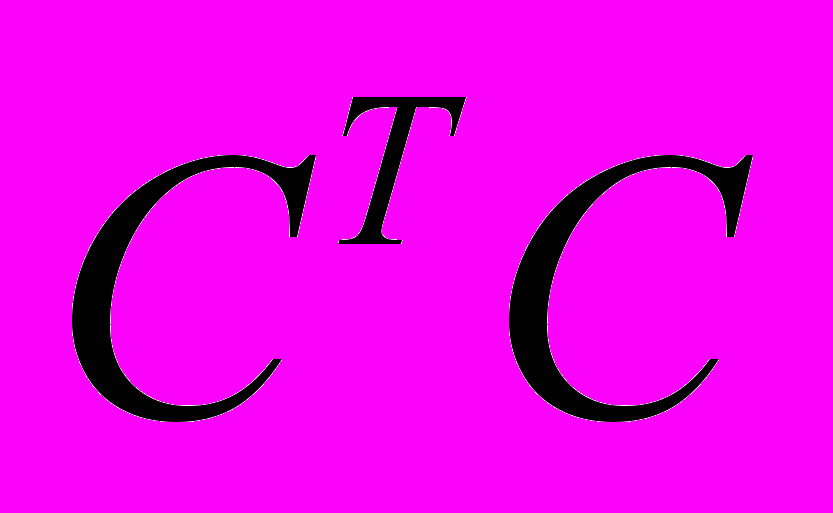

- единичная матрица.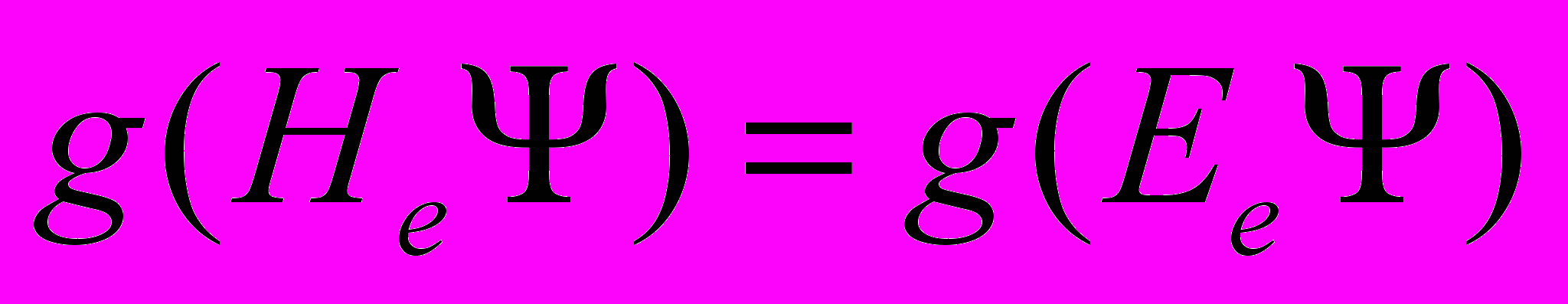











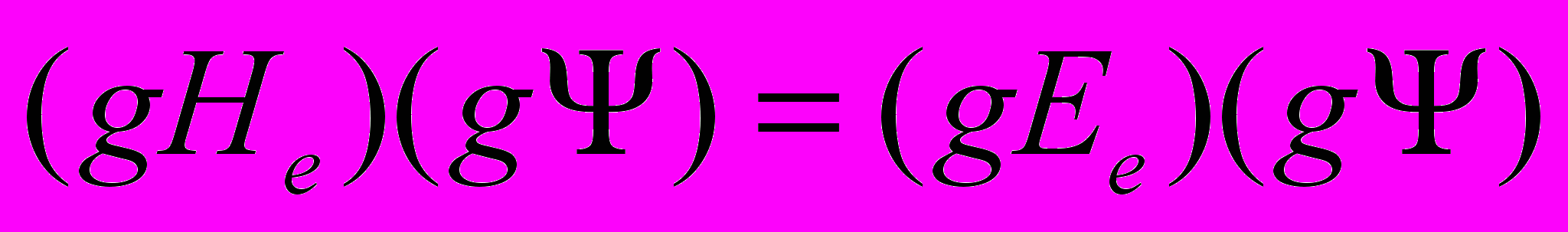
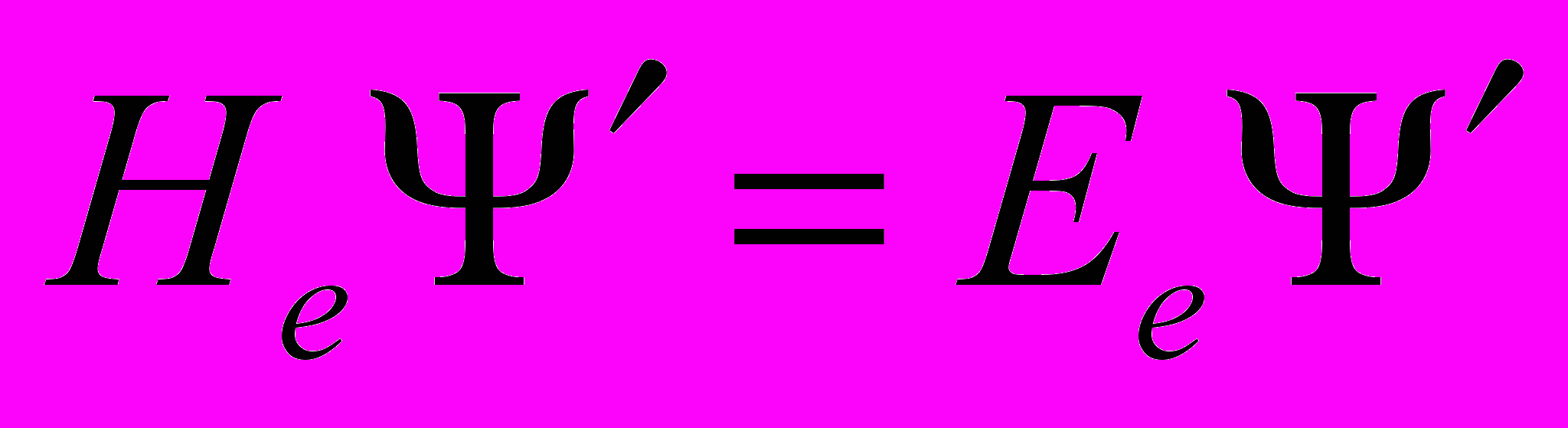
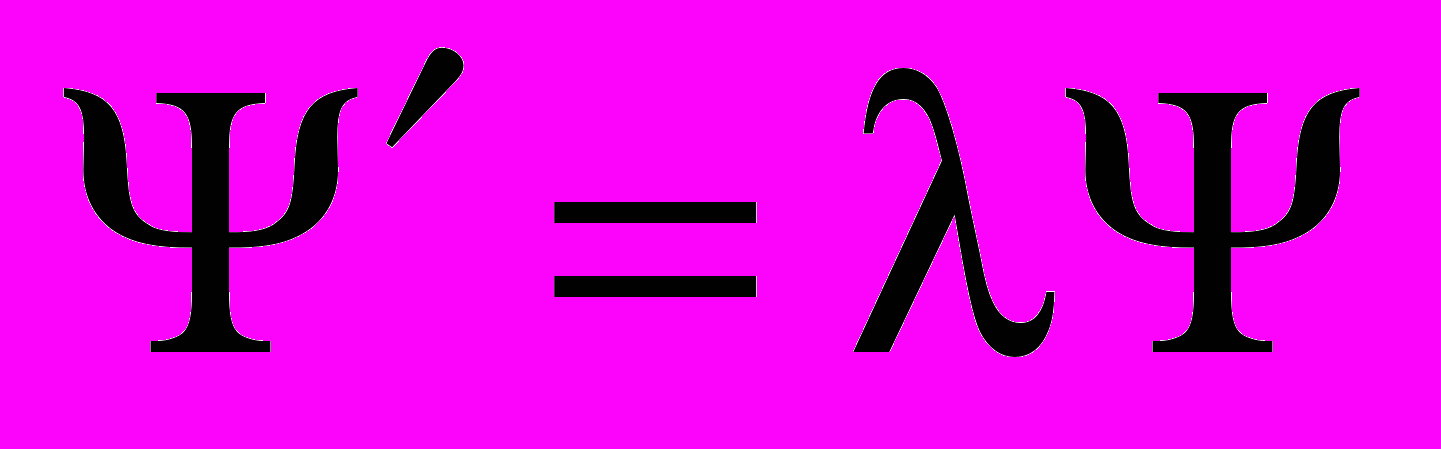
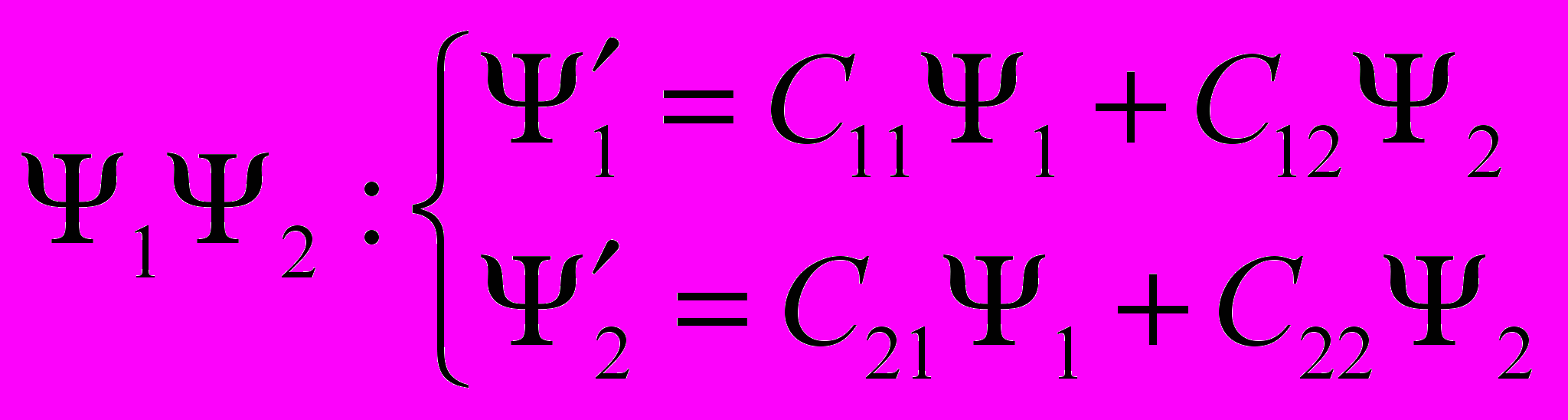
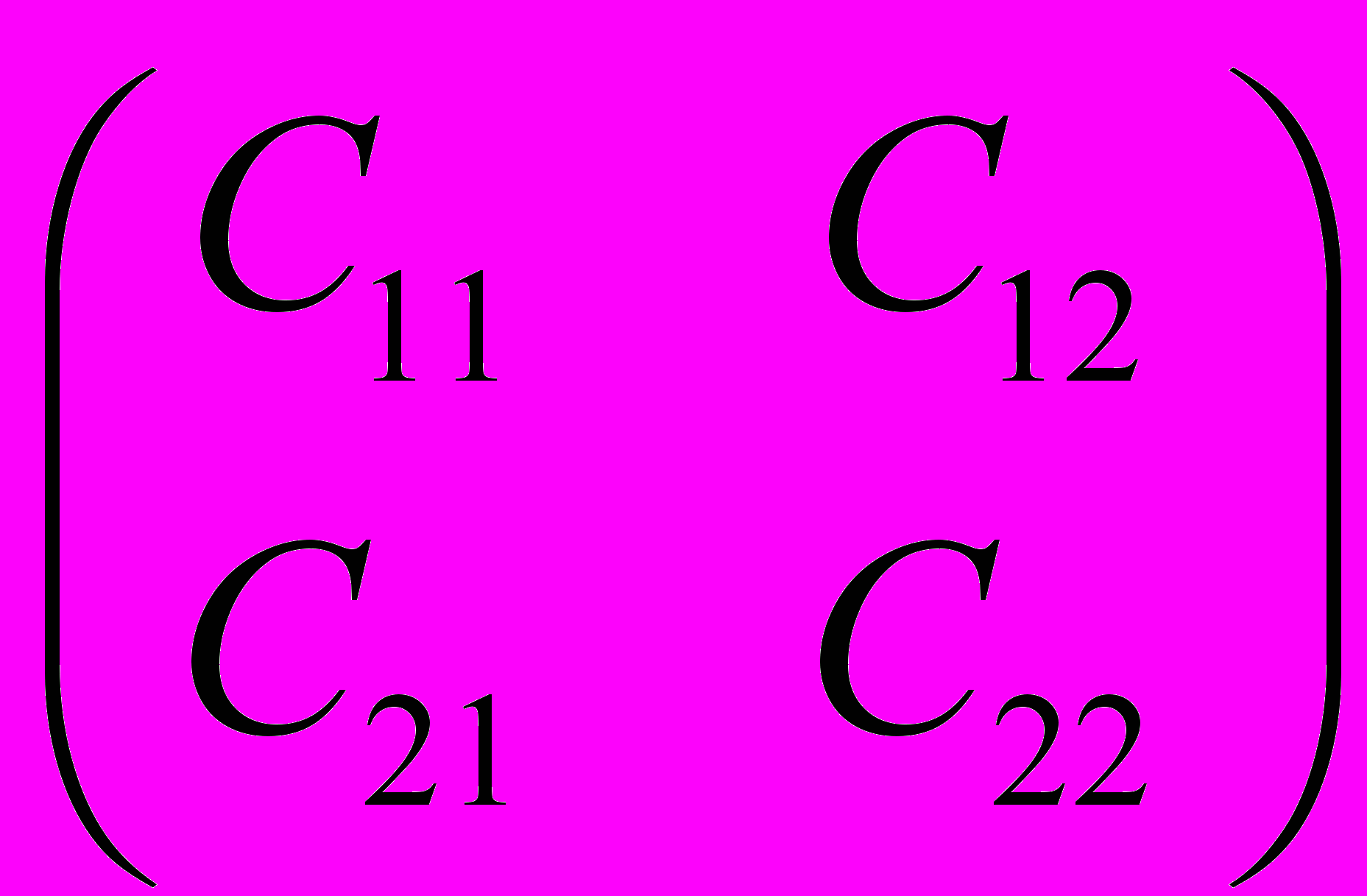- задает преобразование исходных функций под действием преобразований симметрии в новых функциях.

Например, матрица поворота вокруг оси z на угол φ:



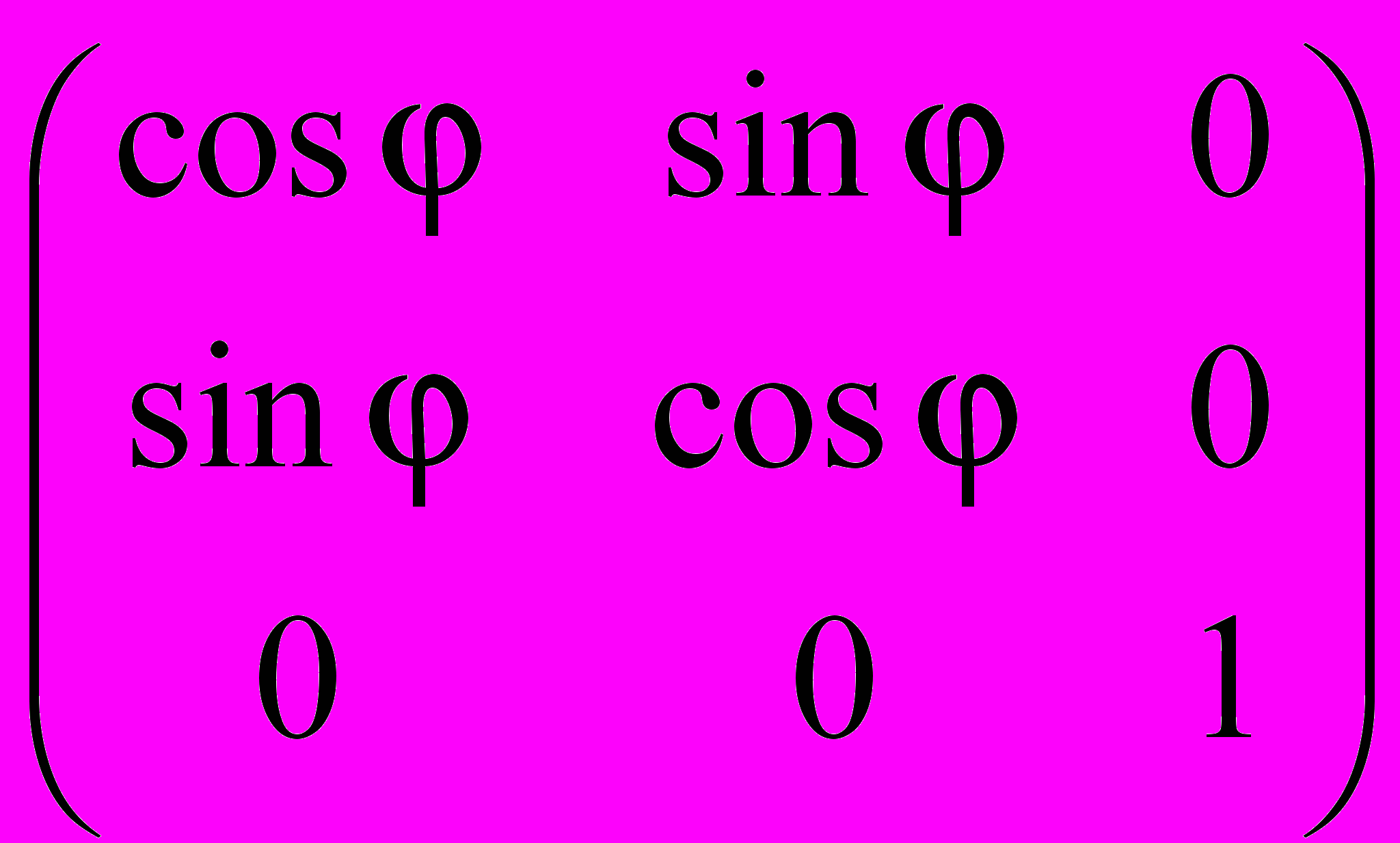
Данная матрица не сводится к блочно-диагональному виду.

Характеры неприводимых представлений:

Пусть есть два разных неприводимых представления T₁ и T₂ и g₁, g₂,…,g_N – совокупность операций симметрии и каждому элементу этой группы в этом представлении соответствуют матрицы





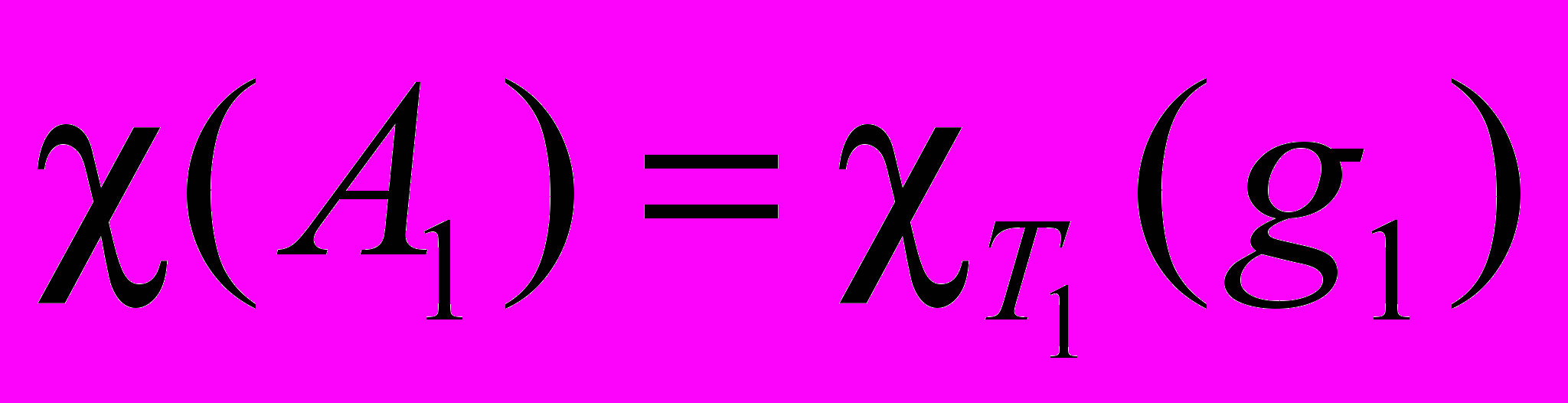
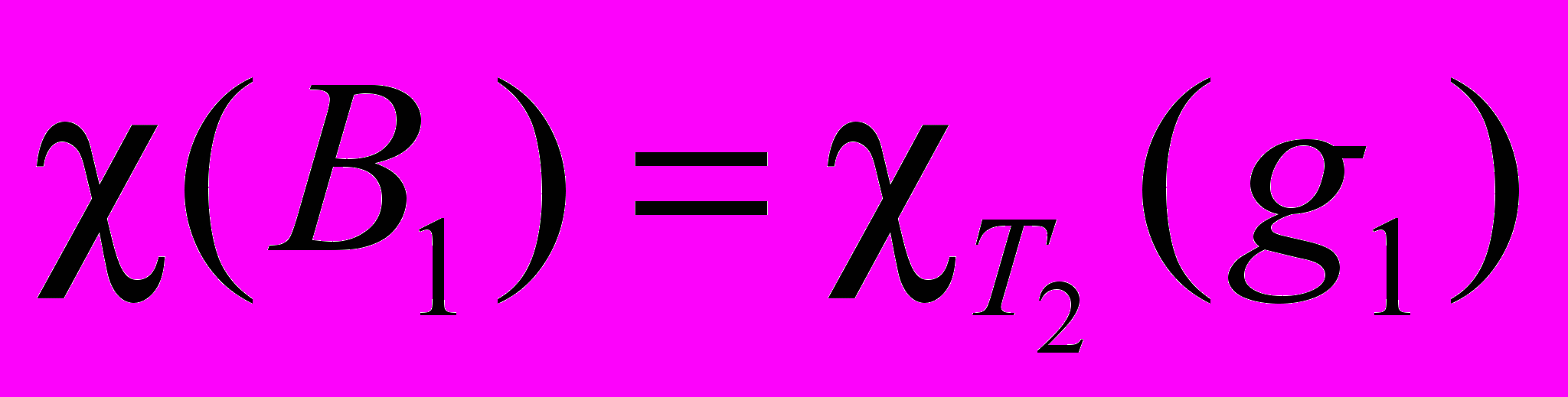, то

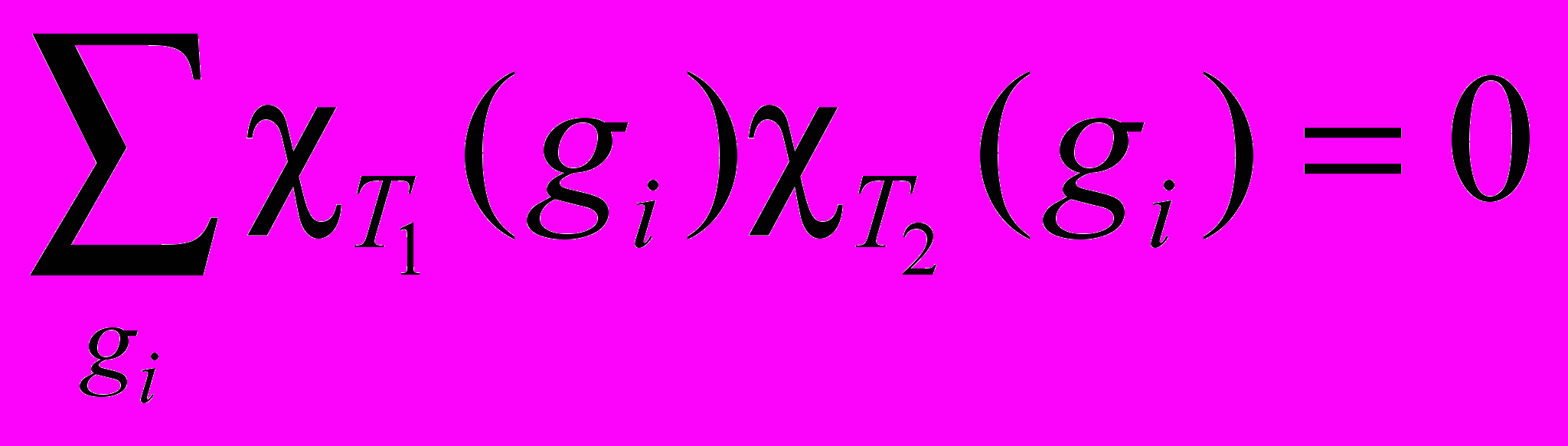или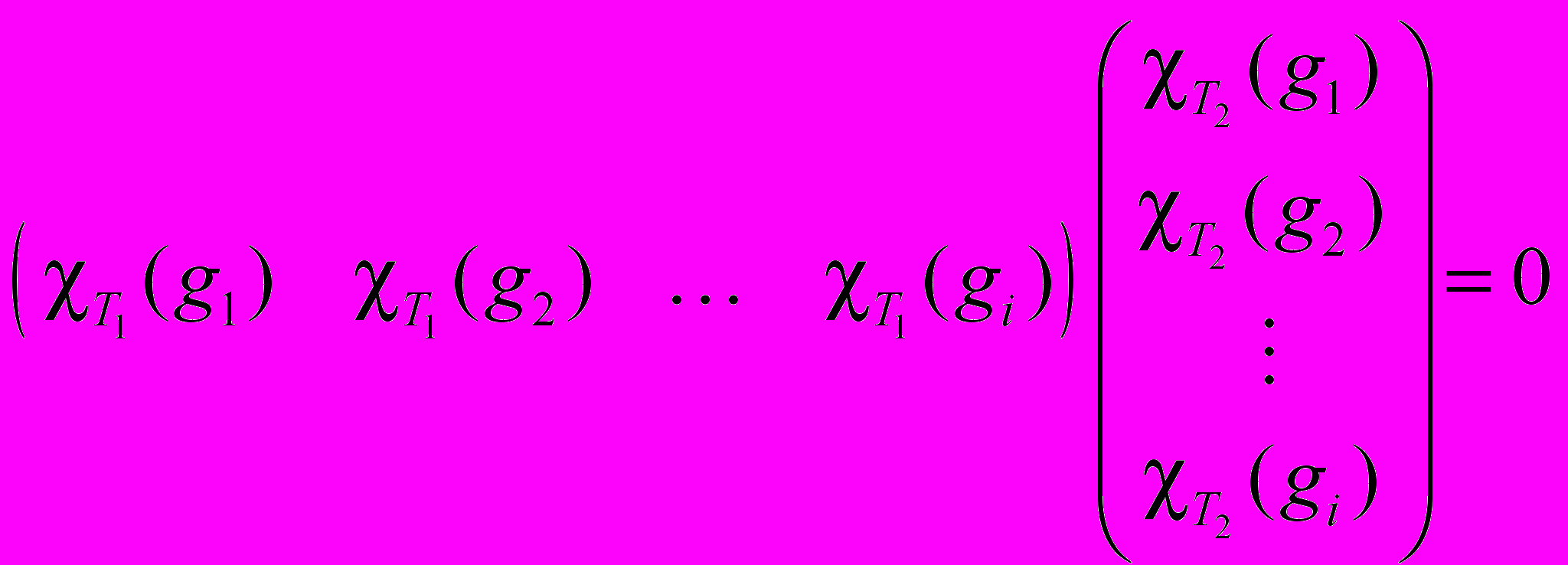

, т.е.

характеры двух неприводимых представлений взаимоортогональны.

Если имеется неприводимое представление, которое можно разложить на два или более неприводимых представлений, то характер этого представления:



При использовании материалов лекции ссылка на students.chemport.ru обязательна.