Лекция 4 аксонометрические проекции. Многогранные и кривые поверхности

Вид материала

Лекция

Содержание OXYZ (рис.53). Построим горизотальную проекцию а X, Y, Z натуральными ко­ор­ди­на­тами точки А, а х Виды аксонометрических проекций. Р). Так как плоскость Р Прямоугольная аксонометрия Прямоугольная диметрическая аксонометрия. 0,94. Таким образом, действительные коэффициенты искажения k 3. Косоугольная аксонометрия Косоугольная горизонтальная изометрическая аксонометрия. Общие сведения о многогранниках SA, называемой образующей MN остается параллельной сама себе, то получается призматическая V и проецируется на нее в истинную величину – в прямоугольник. Основания проецируются на плоскость Н К на переднем ребре и точка М Пирамида и ее развертка. Н в диагонали квадрата abсd О осей выбрано в центре основания, а ось оz 6. Общие сведения о кривых поверхностях Линей­чатые поверхности 5. Построение проекций кривых поверхностей ... Полное содержание

Подобный материал:

• 3 Виды поверхностеЙ и их проекции, 84.24kb.
• Учебно-методический комплекс по дисциплине опд. Ф. 01. 01 «Начертательная геометрия., 480.75kb.
• 3D графика это процесс создания объемной модели при помощи специальных компьютерных, 110.51kb.
• Реферат по дисциплине "Инженерная и компьютерная графика" на тему: Кривые линии и поверхности, 15.15kb.
• С. Н. Хвостик Сумский государственный университет, 198.55kb.
• Выбор картографической проекции теоретические основы выбора картографической проекции, 375.04kb.
• Закон убывающей предельной полезности 12 > Эффект дохода и эффект замещения 13 > Кривые, 260.03kb.
• Муниципальное общеобразовательное учреждение, 259.67kb.
• Эффекты эйнштейна и шапиро в контексте экспериметальных исследований, 718.48kb.
• Черкасова Татьяна Павловна, к э. н, 2006г лекция, 143.84kb.

Лекция 4


АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ.

МНОГОГРАННЫЕ И КРИВЫЕ ПОВЕРХНОСТИ


П л а н


1. Сущность аксонометрических проекций и их виды

2. Прямоугольная аксонометрия

3. Косоугольная аксонометрия

4. Общие сведения о многогранниках

5. Построение проекций многогранника и развертка

6. Общие сведения о кривых поверхностях

7. Построения проекций кривых поверхностей и развертка

1. Сущность построения аксонометрических проекций
   

Отнесем точку А пространства к натуральной системе координат ^ OXYZ (рис.53). Построим горизотальную проекцию а и тем самым закрепим поло­жение точки А относительно системы координат. Спроецируем затем точки А и а вместе с осями координат в направлении s на произ­вольную плоскость Р. Натуральная система координат OXYZ спроецируется в аксонометрическую систему oxyz точки А и а соответственно в точки А_p и а_p.

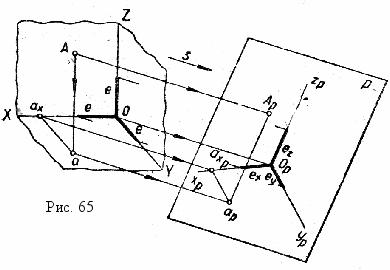
П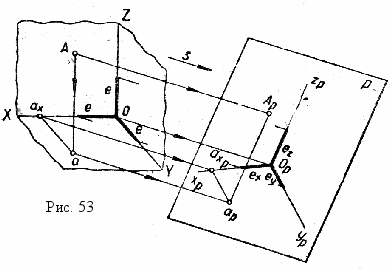лоскость Р назы­ва­ют плоскостью ак­со­но­мет­рических про­ек­ций, прямые О_pX_p, О_pУ_p, О_pZ_p аксономет­

ри­ческими осями, точ­ку А_p «первичной» ак­со­нометрической и точ­ку а_р вторичной го­ри­зонтальной проек­ция­ми точки А.

Назовем ^ X, Y, Z натуральными ко­ор­ди­на­тами точки А, а х_р, у_р, z_р аксономет­ри­чес­кими координатами.

Пространственная координатная ломаная Оа_хаА натуральной системы спроецируется в плоскую координатную ломаную Оpа_хp,а_рА_p аксо­но­мет­ри­ческой системы. Отрезки натуральной координатной ломаной параллельны соответствующим осям координат, поэтому и отрезки аксонометрической координатной ломаной оказываются параллельными аксонометрическим осям, т.е. а_хp,а_р ║ ОpУ_p и а_рА_p║ ОpZ_p.

Если принять координатные плоскости хOу, хOz., УOz за плоскости проекций Н, V и W и спроецировать на них с помощью прямоугольных лучей точку А (рис.53), то получится горизонтальная а, фронтальная а' и профильная а'' проекции этой точки соответственно. При проецировании всей системы на аксонометрическую плоскость проекций Р спроецируется вместе с ориг­и­на­лом и ее прямоугольные проекции. В результате аксонометрическое изоб­ра­же­ние становится обратимым.

^ Виды аксонометрических проекций. Зададимся натуральным масштабом е (натуральной единицей изме­рения) и отложим ею на всех трех прямоугольных осях (рис. 65). При проеци­ро­вании натуральных осей координат в аксонометрические полу­чаются аксонометрические масштабы е_х, е_у, е_г. Аксонометриче­ские масштабы в общем случае не равны натуральному, так как при проецировании проис­ходит определенное искажение.

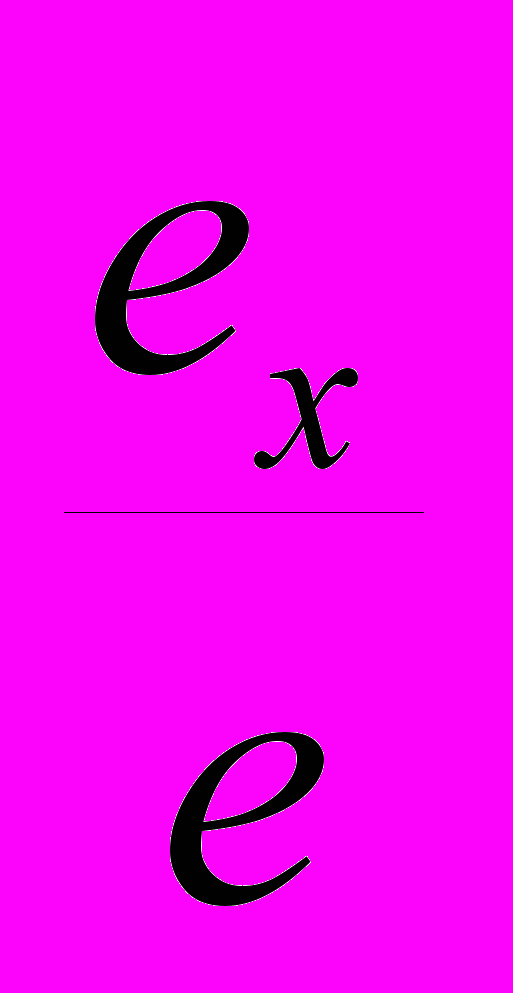
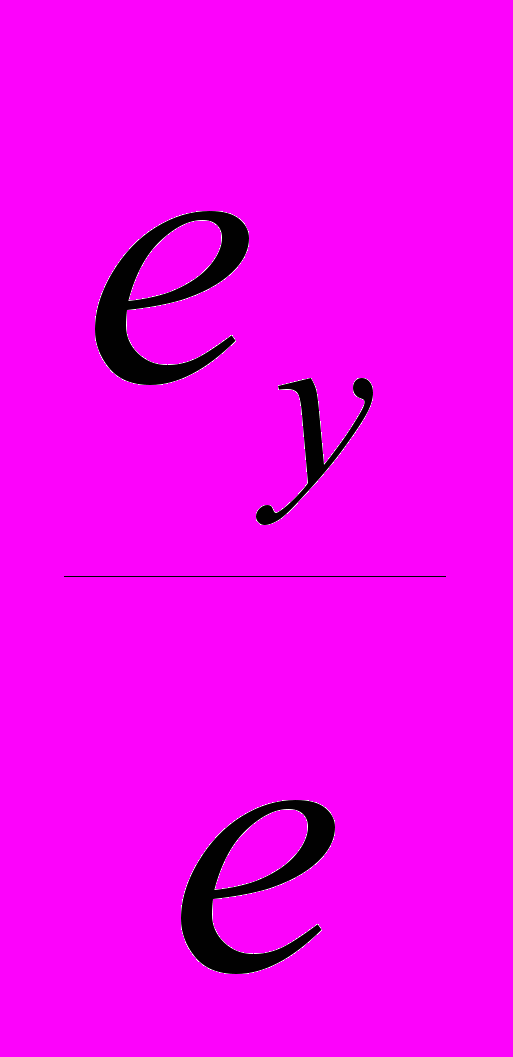
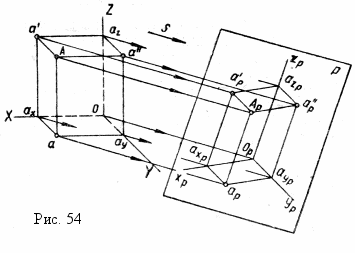
О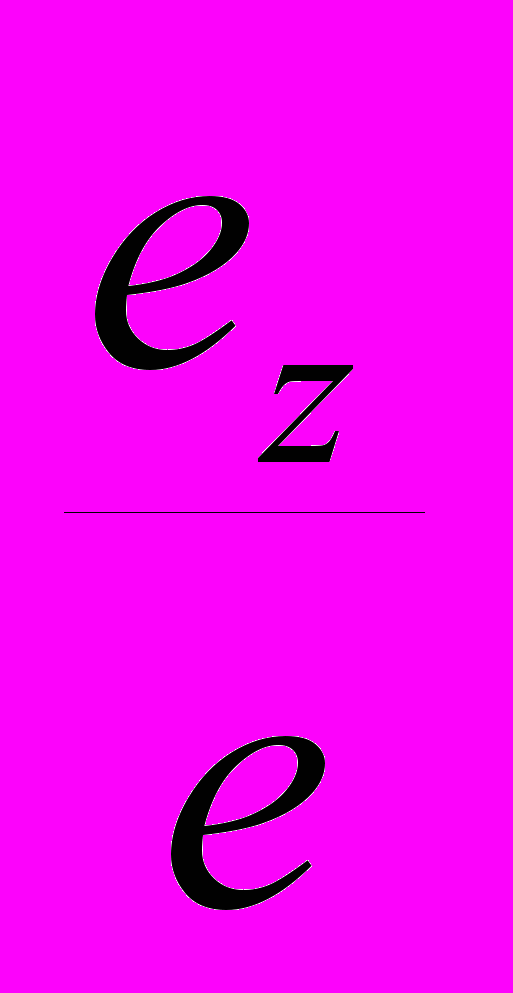тношения аксонометрических масштабов к натуральному называют коэффициентами искажения по осям (k). Таким образом, коэффициент искажения по оси ох k_x= , по оси оу k_y= и по оси oz. оу k_z= .

Следовательно, для получения аксонометрических координат заданной точки А необходимо умножить каждую ее натураль­ную координату на коэффициент искажения вдоль соответствую­щей оси, учитывая, что x_p=O_pax_p=x·k_x, y_P=ax_pa_p=y·k_y и z_p=a_pA_p=z·kp. Ломаная линия 0_Рах_ра_рА_р позволяет по­строить аксонометрическую проекцию заданной точки по ее ко­ординатам (рис. 54).

В зависимости от соотно­шения коэффициентов искаже­ния по осям различают следу­ющие виды аксонометри­чес­ких про­екций:

1) изометрические k_x = k_y = k_z (коэффициенты искажения по осям одинаковы);

2) диметрические k_x= k _z≠ k_y (равны коэффициенты искаже­ния по двум осям);

3) триметрические к_х≠к_у≠к_г (коэффициенты искажения по осям раз­ные).

В зависимости от направления проецирования различают два вида аксонометрических проекций:

1) прямоугольные – проецирующие лучи перпендикулярны плоскости аксонометрических проекций (sP);

2) косоугольные – проецирующий луч составляет острый угол с плос­костью проекций (s не перпендикулярен ^ Р).

Так как плоскость Р может занимать любое положение, а проецирующий луч иметь с ней любой угол, то аксонометричес­ких проекций может быть очень много.

Для практических целей стандартом отобраны из них лишь те, которые обладают наилучшей наглядностью и просты по по­строению.

ГОСТ 2.317–69 «Аксонометрические проекции» рекомендует применять следующие пять видов аксонометрических проекций:

1) прямоугольную изометрическую;

2) прямоугольную диметрическую;

3) косоугольную фронтальную изометрическую;

4) косоугольную горизонтальную изометрическую;

5) косоугольную фронтальную диметрическую.

2. ^ Прямоугольная аксонометрия
   

Изометрическая аксонометрия. В изометрической проекции коэффициенты искажения по всем трем осям одина­ковые, т. е. k_x=k_y=k_z. Если подставить их в уравнение




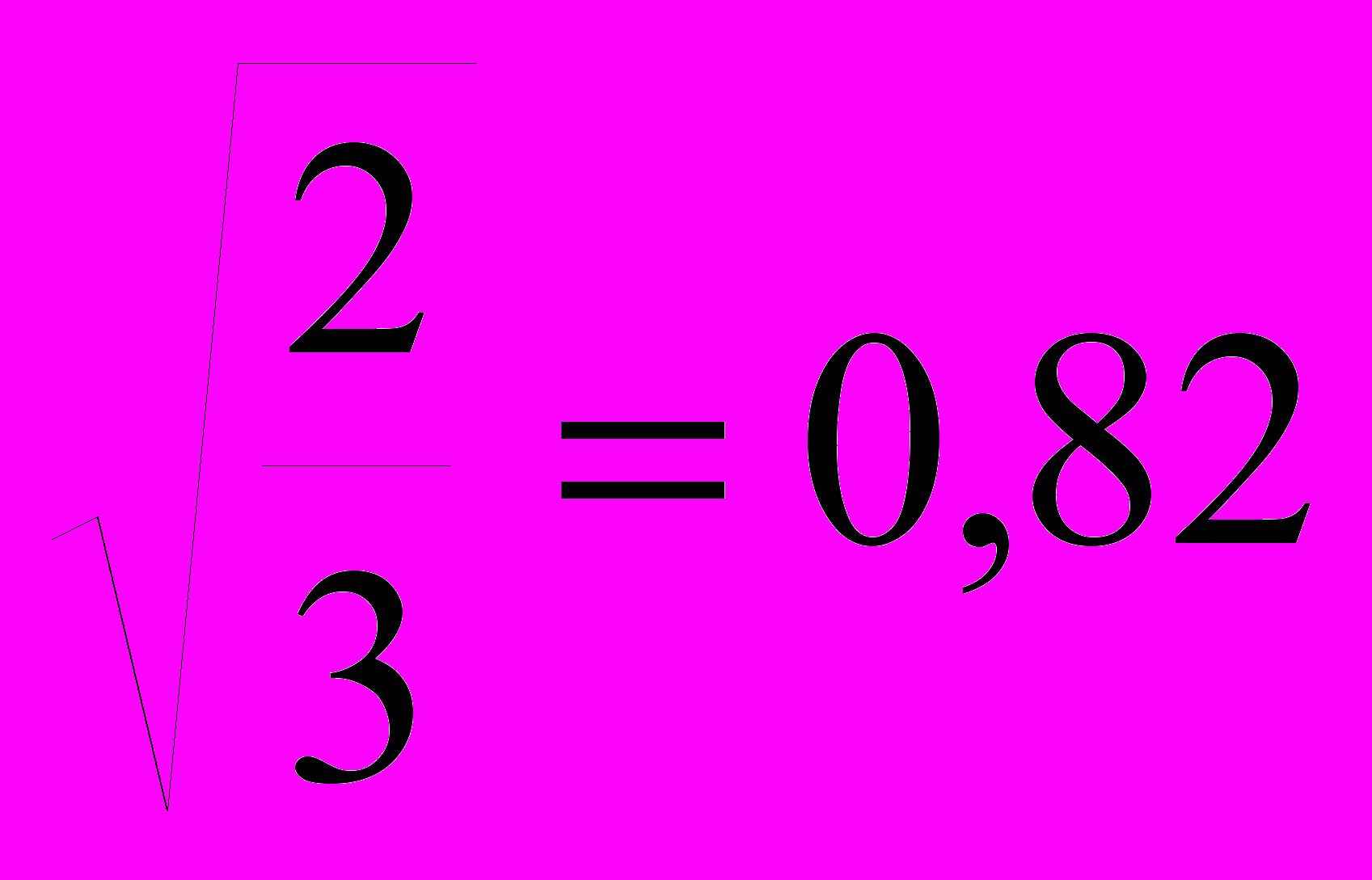
K_x²+ K_y²+ K_z²=2, то получится 3k_x²=2 или K_x= .


Это значит, что при изображении предмета в изометриче­ской проекции необходимо его размеры вдоль осей О_рх_р, О_ру_р и OpZ_p брать равными 0,82 истинной величины.

В прямоугольной изометрической проекции треугольник сле­дов Р_хРуР_z равносторонний. Следовательно, аксонометрические оси, являющиеся его высотами, располагаются под углами 120° друг к другу (рис. 55, а).

В дальнейшем будем аксонометрические оси обозначать без индексов, одной строчной буквой: х, у, z, как принято по ГОСТ 2.317—69.

На практике при построении изображений в аксонометриче­ской проекции использовать действительные коэффициенты ис­кажения затруднительно, поэтому их заменяют приведенными коэффициентами, т. е. приравненными к единице: К_х=К_у=Kz=1 (будем обозначать их заглавными

буквами). В этом случае изображение получается увеличенное в = 1,22 раза.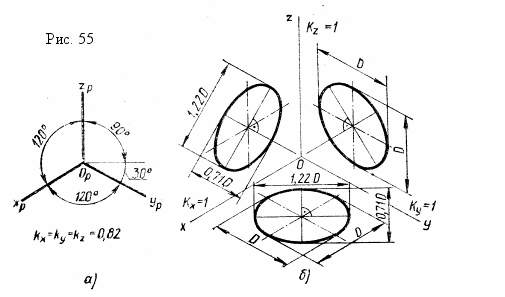




Однако на наглядности такое увеличение не отражается, по­строение же с применением приведенных коэффициентов иска­жения значительно упрощается, так как при откладывании размеров вдоль осей исключаются дополнительные расчеты.

Оси эллипсов — изображений окружностей, лежащих в плос­костях Н, V и W (или им параллельных),– имеют определенные размеры и положение относительно аксонометрических осей (рис. 55,6). Так, большая ось эллипса – изображения окруж­ности, лежащей в плоскости Н,– всегда перпенди­ку­лярна оси оz, а малая — ей параллельна. Большая ось эллипса — изобра­жения окружности, лежащей в плоскости V, – перпендикулярна оси оу, а эллип­са – изображения окружности, лежащей в плоско­сти W,– перпенди­куляр­на оси ох.

При использовании действительных коэффициентов искаже­ния большая ось эллипса равна диаметру (D) изображаемой окружности, а малая ось — 0,58D. Если применяются приведен­ные коэффициенты искажения, то размеры осей эллипса уве­личиваются в 1,22 раза и получаются равными: большая ось — 1,22 D, а малая ось — 0,71D (см. рис. 55).

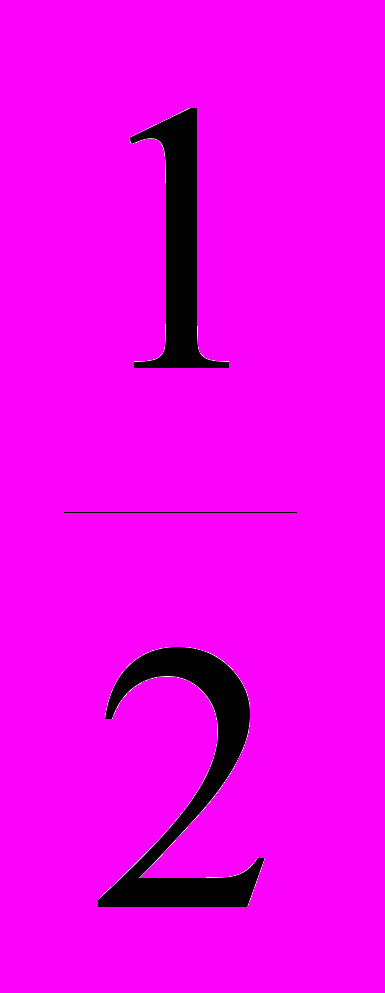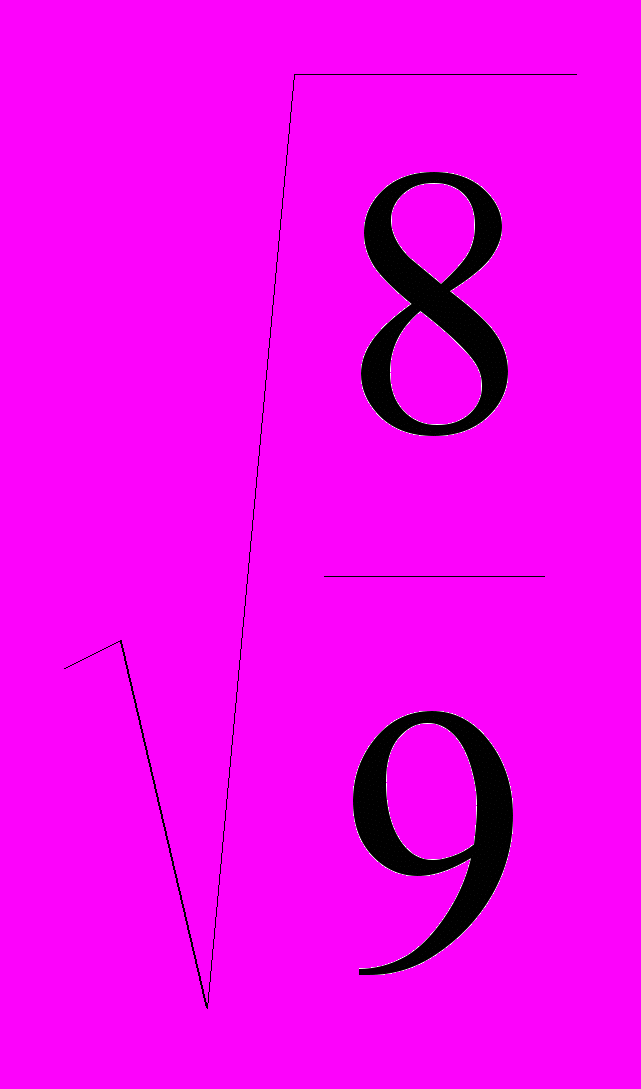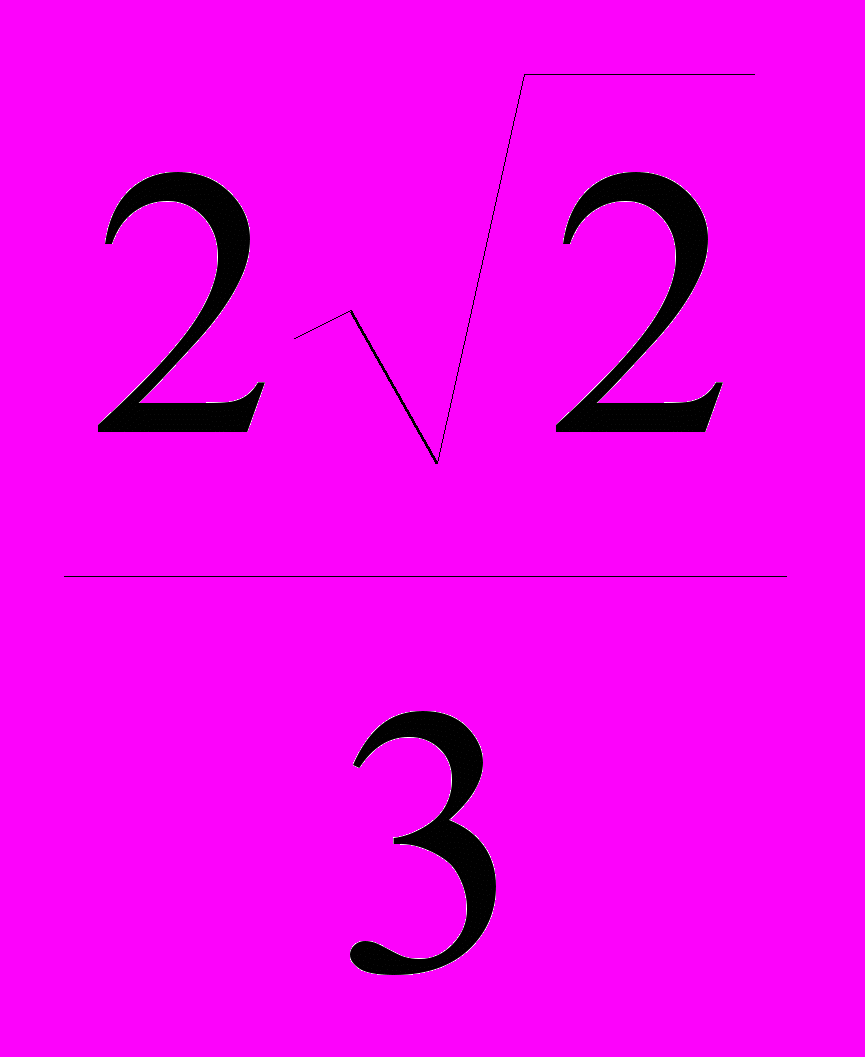^ Прямоугольная диметрическая аксонометрия. В диметрической проекции два коэффициента искажения одинаковые, а третий может быть любым. Наиболее удобна для практических целей и наглядна прямоугольная диметрическая проекция, у которой коэффициенты искажения k_x=k_z и k_y=k_x. Если подставить их в уравнение k_x²=k_y²⁼k_z²=2, то получится k_x²+k_x²+ =2, или 9k_x²=8, откуда k_x ===^ 0,94.

Таким образом, действительные коэффициенты искажения k_x=k_z=0,94 и к_у=0,47. Это значит, что, изображая предмет в прямоугольной диметрической проекции, необходимо его раз­меры вдоль осей ох и оz брать равными 0,94, а вдоль оси оу – равными 0,47 истинной величины (рис.56).

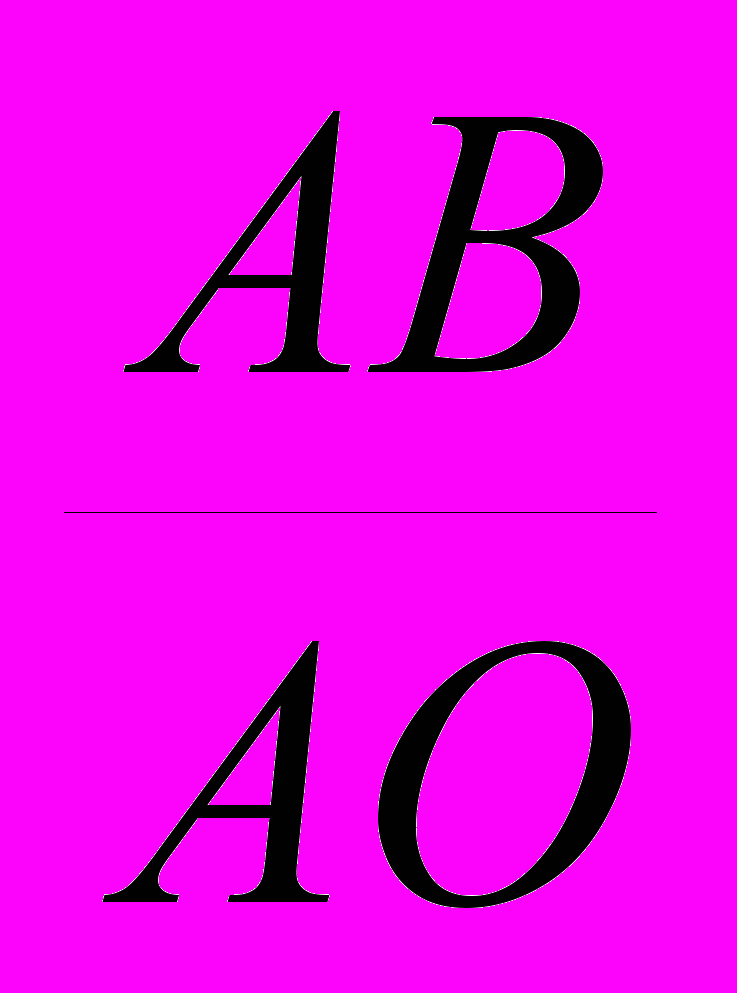
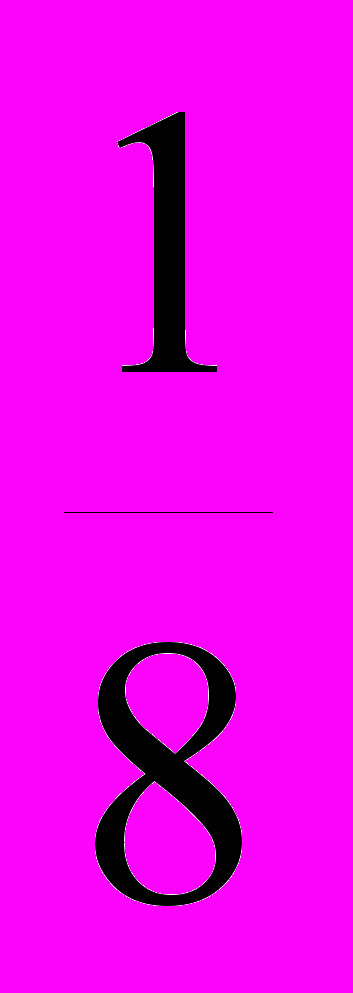
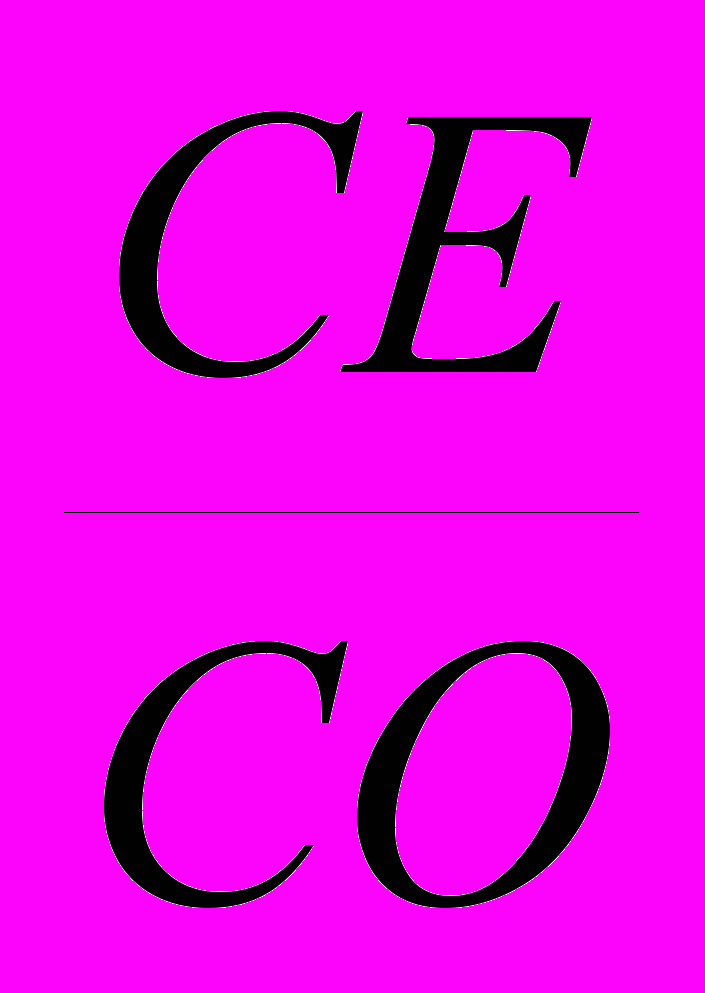
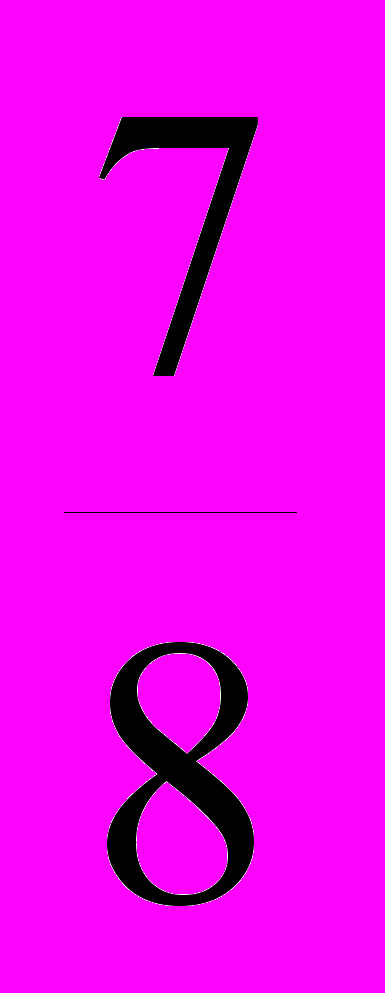
П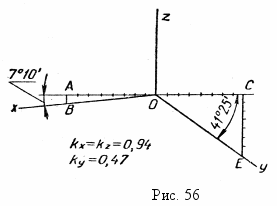ри таких коэффициентах искажения угол между аксономет­рическими осями ох и оz равен 97°10', а между осями оу и оz равен 131^о25'. Ось оу направлена по биссектрисе угла xOz. Если про­вести прямую, перпен-дикулярную оси оz, то оси ох и оу будут рас­полагаться к ней соответственно под углами 7°10' и 41^о25' (рис. 56). Эти углы можно по­строить при помощи прямоугольных треугольников АВО и СЕО, у которых катеты имеют отно­шение, = , = .


На практике использовать действительные коэффициенты ис­ка­же­ния трудно, поэтому их заменяют приведенными коэффи­циентами, принимая K_x = K_z=1 и К_у=0,5. В этом случае изображе­ние полу­чается увеличенным в 1,06 ра­за. Однако на его нагляд­нос­ти такое увеличение не отра­жается. Построения же по осям с применением приведенных коэффициентов значительно упрощаются, так как исключаются дополнительные расчеты.


^ 3. КОСОУГОЛЬНАЯ АКСОНОМЕТРИЯ


Фронтальная изометрическая проекция. Этот вид аксономет­рических проекций получается в случае, если плоскость Р рас­положена параллельно плоскости V (фронтально). Тогда угол между аксонометрическими осями ох н оz равен 90°, а коэффи­циенты искажения по этим осям равны 1, k_x=k_z=1.

Направление проецирования в этом случае выбирают та­ким, чтобы коэффициент искажения по оси оу тоже был равен 1 (k_y=1), а сама ось располагалась под углом 45° к продолжению оси ох (рис. 57, а).




Во фронтальной изометрической проекции окружности, ле­жащие в плоскостях, параллельных плоскости V, проецируются на аксонометрии­ческую плоскость в окружности, а лежащие в плоскостях, параллельных горизонтальной и профильной плос­костям проекций,– в эллипсы Одина­ковой формы (рис. 57,б). Большая ось этих эллипсов равна 1,3D малая – 0,54D.

Допускается применять фронтальные изометрические проек­ции с углами наклона оси оу, равными 30 или 60°.

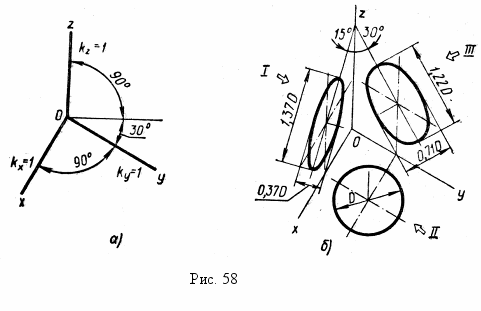
^ Косоугольная горизонтальная изометрическая аксонометрия. Этот вид аксоно­метрических проекций получается в случае, когда плоскость Р расположена параллельно плоскости Н (горизонтально). При таком положении плоскости Р угол между аксонометрическими осями ох и оу равен 90°, а коэффициенты искажения по осям ох и оу равны 1, т. е. k_x=k_v=1.

Направление проецирования в этом случае выбирают таким, чтобы коэффициент искажения по оси oz тоже был равен 1 (k_z=1), а углы между ося­ми соответствовали рис.58, а.

В горизонтальной изометрической проекции окружности, ле­жащие в плос­костях, параллельных плоскости Н, проецируются на аксоно­мет­ри-чес­кую плоскость проекций в окружности, а ле­жащие в плоскостях; парал­лельных фронтальной и профиль­ной плоскостям проекций,— в эллипсы (Рис. 58, б). Большая ось эллипса I равна 1,37D, а малая ось — 0,37 D; большая ось эллипса III равна 1,22D, а малая ось — 0,71 D.

Допускается применять горизонтальные изометрические про­екции с углами наклона оси оу, равными 45 или 60°, сохраняя угол менаду осями ох и оу, равным 90°.





Косоугольная фронтальная диметрическая аксонометрия. Фронтальная косо­угольная диметрическая проекция отличается от фронтальной косоугольной изометрической коэффициентом искажения по оси оу, который равен (к_у = ) и формой эллипсов, в кото­рые проеци­ру­ются окружности.

Положение аксонометрических осей показано на рис. 59, а. Угол наклона оси оу равен 45°, но допускается применять и фрон­тальные диметрические проекции с углом наклона оси оу, рав­ным 30 или 60°.





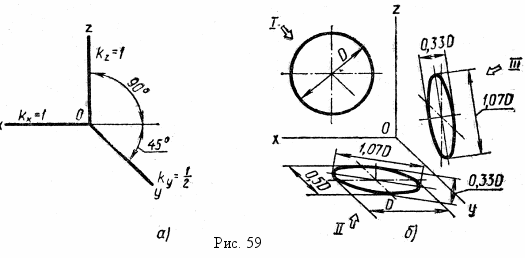
Во фронтальной диметрической проекции окружности, лежа­щие в плоскостях, параллельных фронтальной плоскости проек­ций, проецируются на аксонометрическую плоскость проекций в окружности, а лежащие в горизонтальных и профильных плос­костях– в эллипсы (рис. 59,6). Большая ось эллипсов II и III равна 1,07D, а малая ось – 0,33D.

3. ^ Общие сведения о многогранниках
   

Многогранником называется тело, ограниченное плоскими многоуголь­ни-ка­ми. Стороны многоугольников называются реб­рами, а заключенные между ни­ми плоские многоугольники — гранями. Вершины граней являются верши­на­ми многогранника.

Многогранники подразделяются на правильные (например, тетраэдр, куб) и неправильные (например, наклонные призма и пирамида). У правильного многогранника все грани, ребра и углы соответственно равны между собой.

И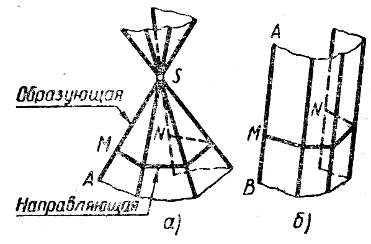з многогранных поверхностей рассмотрим только пирами­дальные и призматические.

Пирамидальную поверх­ность (рис. 60) можно рассмат­ривать как поверх­ность, полу-ченную перемещением прямой ^ SA, называемой образующей,

по направляющей ломаной

MN, если эта образующая во всех своих положениях про­ходит через одну точку S. Если

о
Рис. 60
бразующая АВ во время движения по ло­маной ^ MN остается параллельной сама

себе, то получается призматическая поверхность (рис.60). При пересечении зам­кнутой пирамидальной по­верх­ности плоскостью, не проходящей через вершину S, получается многогранник, называемый пира­мидой. Многоугольник, полученный в секущей плоскости, назы­вается основанием пирамиды. Боковые грани пирамиды пред­ставляют собой треугольники. Пирамиду называют правиль­ной, если основанием являя­ет­ся правильный многоугольник, а ее высота проходит через центр этого мно­гоугольника.

При пересечении замкнутой призматической поверхности дву­мя взаимно параллельными плоскостями получается многогран­ник, называемый призмой. Многоугольники, получаемые в секу­щих плоскостях, – основания призмы. Боковые грани призмы представляют собой параллелограммы. Призма прямая, если ее боковые ребра перпендикулярны основаниям. Прямая приз­ма, осно­ванием которой является прямоугольник, называется параллелепипедом. Прямая призма правильная, если ее основа­ние – правильный многоугольник.

Общее название призмы и пирамиды определяется формой их основания, например треугольная пирамида (рис. 61) или треугольная призма (рис. 62).




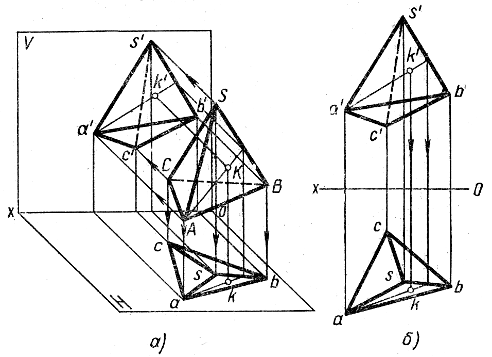
Рис. 61

4. 
   
5. 
   
6. 
   
7. 
   
8. 
   

9. Построение проекций многогранника и развертка
   

На чертеже построение проек­ций многогранника сводится к по­строению проекций его вершин и соединению их отрезками прямых (рис.61). Поскольку плоскости (грани) принято считать непрозрач­ными, то проекции некоторых ребер и граней будут невидимыми. Неви­димые ребра определяют при помо­щи конку­рирующих точек и по­казывают штриховыми линиями. Очерк многогран­ни­ка всегда будет видимым.

Недостающие проекции точки, лежащей на поверхности мно­гогранника, строят следующим образом:

1) через заданную проекцию точки проводят проекцию про­извольной прямой, принадлежащей соответствующей грани;

2) находят вторую проекцию этой прямой;

3) с помощью линии связи находят недостающую проекцию точки на найденной проекции прямой.

На рис. 61 показано построение горизонтальной проек­ции k точки К, лежащей на грани SAB, по заданной фронталь­ной проекции k'.

Призма и ее развертка. На рис. 62 показаны чертеж, аксо­нометрическая проекция призмы и развертка ее поверхности. По чертежу нетрудно установить форму и положение призмы. Призма треугольная, правильная, ее боковые ребра (и грани) перпендикулярны к плоскости Н, а основания – равносторон­ние треугольники, расположенные в горизонтальных плоскостях.

Задняя грань призмы параллельна плоскости ^ V и проецируется на нее в истинную величину – в прямоугольник. Основания проецируются на плоскость Н в истинную величину – в тре­угольник abc. Стороны этого треугольника одновременно явля­ются горизонтальными проекциями боковых граней.

Построение аксонометрической проекции призмы начинают с нанесения на чертеже (рис.62 а) осей прямоугольных коор­динат, к которым относят призму. Затем строят аксонометри­ческие оси и аксонометрическую проекцию нижнего основания по координатам вершин с учетом коэффициентов искажения (рис. 62 б). Из вершин фигуры основания проводят прямые параллельно оси оz и откладывают на них высоту призмы, опре­делив ее по фронтальной проекции, получают аксонометрические проекции ребер. Соединяя найденные точки отрез­ками прямых, завершают построение призмы в аксонометрической проекции. На рис. 62, б построена фронтальная косоугольная диметрическая проекция призмы.





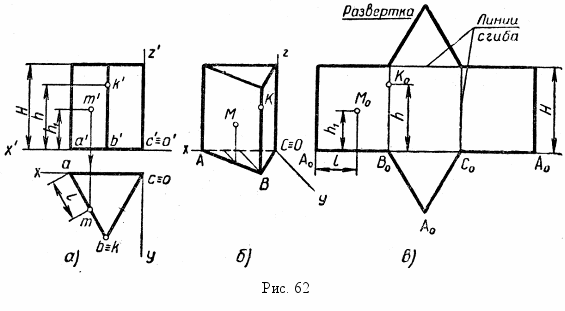
Разверткой поверхности многогранника называется плоская фигура, получающаяся в результате совмещения с плоскостью всех его граней. Чертежи разверток необходимы при изготовле­нии моделей и изделий из листового материала.

Построение развертки поверхности многогранника сводится к построению изображений граней в истинную величину. Это легко осуществить путем определения длины ребер многогран­ника, а в случае необходимости и длины диагоналей граней. Полная развертка поверхности призмы состоит из развертки ее боковой поверхности и оснований. Боковые грани прямой треугольной призмы – прямоугольники, поэтому развертка ее боковой поверхности пред­став­ляет собой прямоугольник, длина которого равна периметру основания, а вы­сота – высоте приз­мы (рис. 62, в) к развертке боковой поверх­ности при­страива­ют основания призмы – равносторонние треугольники.

На поверхности призмы построены две точки: точка ^ К на переднем ребре и точка М на левой грани. Соответствующие им точки Ко и М₀ нанесены и на развертку. Точку Ко строят по высоте h, а точку М₀ определяют с помощью высоты h₁ и рас­стояния l от одной из вертикальных сторон (ребер) грани, взя­того с горизонтальной проекции.

^ Пирамида и ее развертка. На рис. 75 даны чертеж, аксонометрическая проекция и развертка поверх­ности пирамиды по чертежу устанавливают, что пирамида четырехугольная, правильная, так как ее основание ABCD – квадрат, лежащий в горизонтальной плоскости, а высота OS проецируется в центр основания. Две стороны основания – AD и ВС – параллельнь плоскости V. Боковые грани – равные между собой равнобедренные треугольники, причем наклонены к плоскости Н под одинаковыми углами. Левая и правая грани – фронтально-проецирующие.

Пирамида проецируется на плоскость V в треугольник. Боковые ребра равны между собой и проецируются на плоскость ^ Н в диагонали квадрата abсd, являющегося горизонтальной проекцией основания. Ни одна из проекций боковых ребер и граней не равна их истинной величине.

Для удобства построения аксонометрической проекции начало ^ О осей выбрано в центре основания, а ось оz совмещена с высотой пирамиды. На рис. 63, б показано построение фронтальной косоугольной диметрической проекции пирамиды Сначала изображено основание: вдоль оси ох симметрично О отложен отрезок, равный длине стороны основания, а вдоль





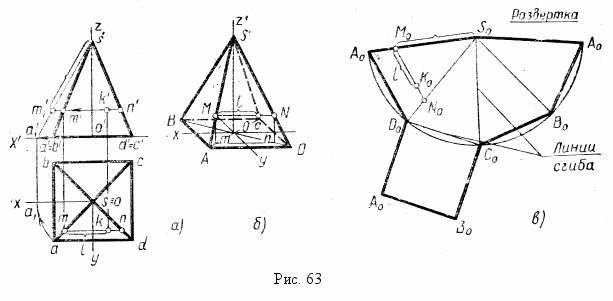
оси оу – половине ее длины. Через полученные на осях ох и оу точки проведены прямые, парал­лель­ные этим осям, до взаимного их пересечения, в результате чего найдены вер­шины А, В, С и D основания. Затем вдоль оси оz от точки О отложена высо­та OS пирамиды. Точка S соединена с точками А, В, С и D осно­вания. Аналогично строят и другие виды аксонометрических проекций пирамиды.

Построение развертки боковой поверхности пирамиды сво­дится к построению по трем сторонам примыкающих друг к дру­гу треугольников (боковых граней) с общей вершиной So (рис. 63, в). Длину бокового ребра (стороны треугольника) можно определить любым способом, например способом враще­ния (рис. 63, а). Затем из произвольной точки S₀ радиусом, равным длине ребра, проводят дугу и строят четыре хорды, равные стороне основания пирамиды. Соединив концы хорд с точкой So, получают развертку боковой поверхности пира­миды. К одному из треугольников пристраивают изображение основания.

Если ребра имеют разную длину, то для построения разверт­ки пирамиды необходимо найти длину каждого ребра в отдель­ности.

Аксонометрическую проекцию точки, лежащей на поверх­ности пирамиды, строят по координатам или при помощи вспо­могательной прямой. На рис. 63 показано построение точки К, лежащей на передней грани пирамиды. Для построения орто­гональных проекций k и k', аксонометрической проекции К и точ­ки К_о на развертке использована горизонталь MN грани. На аксоно­мет­ри­чес­кой проекции (рис. 63, б) сначала найдена вторичная проекция тп го­ри­зон­та­ли, а затем – проекция MN. Точка К находится на расстоянии I от точки М, которое изме­ряется по горизонтальной проекции горизонтали (рис. 63, б). На развертке прямую M_оN_о определяют, откладывая от точки S₀ отрезки S_оM_о и S_оN_о равные натуральной величине соответст­венно s' m' и s m (рис.63, а).


^ 6. Общие сведения о кривых поверхностях


В начертательной геометрии все поверхности исследуют по чертежу. Для простоты изображения кривую поверхность рассматривают как совокупность последовательных положений какой-либо линии — образующей, движущейся в пространстве по определенному закону. Закон перемещения образующей за­дают неподвижными прямыми или кривыми — направляющими линия­ми.

Способы образования кривой по­верхности движением линии могут быть различны. Например, поверх­ность кругового цилиндра может быть образована двумя способами: вращением прямой АВ вокруг па­раллельной ей неподвижной оси или поступательным движением ок­ружности, центр которой перемещается по прямой (оси), перпендикулярной к плоскости окружно­сти (рис. 64).

По виду образующей по­верх­ности разделяют на линей­чатые и нелинейчатые. ^ Линей­чатые поверхности получа­ются в резуль­тате переме­щения прямой линии. Однако необхо­димо иметь в виду, что любая поверх­ность может быть получена несколь­кими способа­ми, так как обра­зующие можно принять за на­правляющие. Поэто­му линейчатая поверхность может быть полу­чена и перемещением кривой линии по прямым направляю­щим. Ли­нейчатая поверх­ность в общем случае образуется дви­жением прямолинейной образу­ющей по трем криволинейным направ­ляющим. Нелинейчатые поверх­нос­ти могут быть получе­ны только в результате перемещения кривой линии (сфера, парабалоид и др.), они относятся к неразвертывающимся – их нельзя совместить с плоскостью без разрывов и складок.

Линейчатые поверхности разделяют на развертывающиеся и неразвер­ты­ваю­щиеся.

К развертывающимся поверхностям относятся конические, цилиндри-ческие и торсы (поверхности с ребром возврата).

Коническая поверхность (рис. 65, а) образуется движением прямой, про-ходящей через неподвижную точку S (вершину) и скользящей по разомкнутой или замкнутой кри­вой MN. Если направляющей служит произвольная кривая, окружность, эллипс и др., получается коническая поверхность соответ­ственно произвольного вида, круговая, эллиптическая и др. Образующие проходят в обе стороны от вершины S, по­этому коническая поверх­ность имеет две полости.




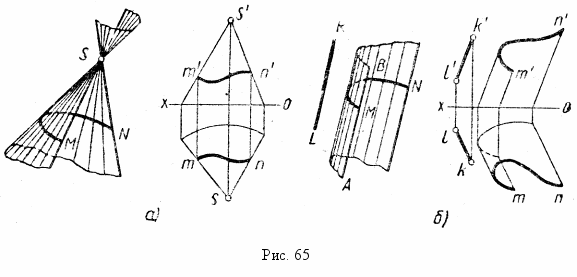
Цилиндрическая поверхность (рис. 65, б) обра­зуется движением прямой АВ, скользящей по разомкнутой или замкнутой кривой параллельно заданному направлению KL. В зависимости от направляющей цилиндрические поверх­ности могут быть произвольного вида, круговые, эллиптические и др.


^ 5. Построение проекций кривых поверхностей

и развертка


Прямой круглый цилиндр и его развертка. Прямой круговой цилиндр с осью, перпендикуляр­ной какой-либо плос-кости проекций, проецируется на нее в окружность диаметра, равного диа­метру основания. На другие плоскости проекций – в прямоугольники, высота которых равна высоте цилиндра, а ширина – диаметру основания. На рис. 66 даны чертеж, прямоугольная изометрическая проекция и раз­вертка поверхности прямого кругового цилиндра, ось которого перпендикулярна плоскости Н. Горизон­тальную проекцию а точ­ки А, лежащей на цилиндрической поверх­нос-ти, по заданной фронтальной проекции а' находят при помощи линии связи на окружности, в которую проецируется поверхность на плос­кость Н.

Строить аксонометрическую проекцию начинают с изобра­жения нижнего основания (рис. 66, б). Затем вдоль оси оz откладывают высоту и строят аксономет­ри­ческую проекцию верх­него основания. Завершают построение изображением контур­ных образующих. Точку А переносят на аксономет­рическую проекцию при помощи координат х, у, z, взятых с ортогональ­ных проекций.

Развертка поверхности цилиндра состоит из прямоугольника (боковой поверхности) и двух кругов (оснований цилиндра) (рис. 66, в). Длина прямоу­голь­ника равна πD (где D – диа­метр основания), а высота – высоте цилиндра.




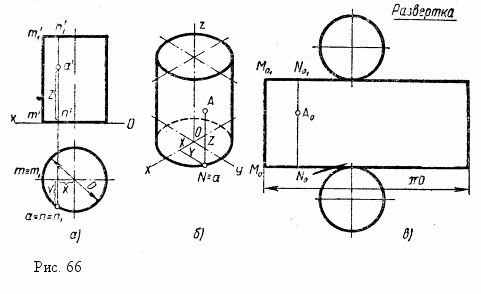
Для нахождения на развертке точки ^ А, лежащей на поверх­ности цилиндра, используют образующую NN₁, проходящую че­рез нее. Для этого откладывают отрезок M₀N_o, равный дуге MN, изображенной в истинную величину на гори­зон­тальной проекции. На развертке точку A_о, соответствующую точке A, по­лу­ча­ют, отложив отрезок N₀A₀, равный п'а'.

Прямой круглый конус и его развертка. Прямой круговой конус c осью, перпендикулярной какой-либо плоскости проекций, проецируется на эту плоскость в окружность диаметра, равного диаметру основания. На две другие плоскости проекций он проецируется в равнобедренные треугольники, высота которых равна высоте конуса, а основа­ние – диаметру основания конуса. На рис. 67 даны чертеж, прямоугольная изо­мет­рическая проекция и развертка поверхно­сти прямого кругового конуса с осью, перпендикулярной плос­кости Н. Проекции точек, лежащих на поверх­ности конуса, на­ходят при помощи образующих и параллелей (рис. 67, а).

Аксонометрическую проекцию конуса строят аналогично про­екции ци­линдра. Сначала изображают основание конуса, затем откладывают на оси оz вы­соту. Завершают построение проведе­нием проекций контурных образующих (рис. 67, б). Аксоно­метрические проекции точек, лежащих на поверхности конуса, строят по координатам, часто привлекая и образующие, на ко­торых лежат эти точки.

Развертка поверхности конуса состоит из кругового сектора (боковой по­верх­ности) и круга (основания) (рис. 67 в). Ра­диус сектора равен длине образу­ющей конуса, а длина его ду­ги— длине окружности основания. Угол сектора α= 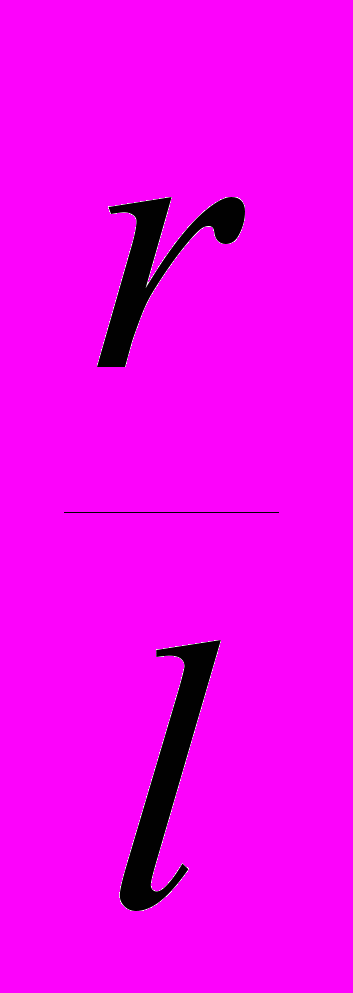360°, где r – радиус основания и l — длина образующей.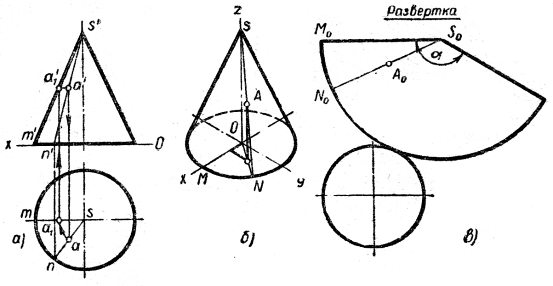




Рис. 67

Для построения на развертке точки Л, лежащей на поверх­ности конуса, используют образующую NS, проходящую через эту точку. Для этого на развертке откладывают дугу M₀N₀, рав­ную дуге MN основания конуса. Точку А₀ на развертке получа­ют, отложив на N₀S₀ отрезок S_QA₀, равный отрезку s'a₁', опре­деляющему расстояние точки А от вершины конуса S (найден­ному способом вращения).