С. Н. Хвостик Сумский государственный университет

Вид материала

Содержание

Рисунок 2 – Тенденции в использовании методов временной дискретизации для моделирования процесса резания
Рисунок 3 – Общий алгоритм решения задачи
Рисунок 4 – Граничные условия и нагрузки
Рисунок 5 – Влияние величины фаски износа на проекции силы резания
Рисунок 7 - Влияние параметров коэффициента трения на форму и размеры стружки:  = 5, V = 300 м/мин, a= 0.150 мм

Подобный материал:

УДК [621.9.025:621.9.01].001.57

Имитационная Модель
прямоугольного свободного резания

В.А. Залога, д-р техн. наук; Д.В. Криворучко, канд. техн. наук;
С.Н. Хвостик

Сумский государственный университет

В статье описана конечноэлементная модель процесса прямоугольного резания, реализованная методом явного решения уравнения движения. Показано, что наибольшая ошибка прогнозирования с помощью данной модели наблюдается в проекции Py силы резания и обусловлена априорным выбором параметров модели трения и неточным учетом силы на задней поверхности.

В работе представлены результаты научно-исследовательской работы, посвященной моделированию методом конечных элементов процесса прямоугольного резания. Важность решения этой задачи обозначил в своем докладе на XIV Международном научно-техническом семинаре «Интерпартнер-2005» проф. Весткемпер Э. (Германия), подчеркнув, что создание виртуальных производств является одним из приоритетных научно-исследовательских направлений в Европе, финансируемых за счет седьмой основной рабочей программы Европейского союза.

Существенные усилия ученых, особенно в последние годы, направлены на решение задачи моделирования процесса резания.
Используются а

налитические, экспериментальные методы, имитационные методы на основе метода конечных элементов (МКЭ) и методы искусственного интеллекта [1047 1]. В этих условиях метод конечных элементов имеет преимущество, благодаря своей универсальности, наглядности и информативности. Среди задач, которые могут быть решены этим методом, следует назвать задачи математического моделирования процесса пластической деформации, т.е. моделирования процесса стружкообразования, оценки напряженно-деформированного состояния (НДС) режущего клина (лезвия) и на этой о

снове оптимизации конструктивных элементов и условий эксплуатации режущего инструмента, прогнозирования остаточных напряжений в обработанной поверхности, прогнозирования величины заусенца и др.

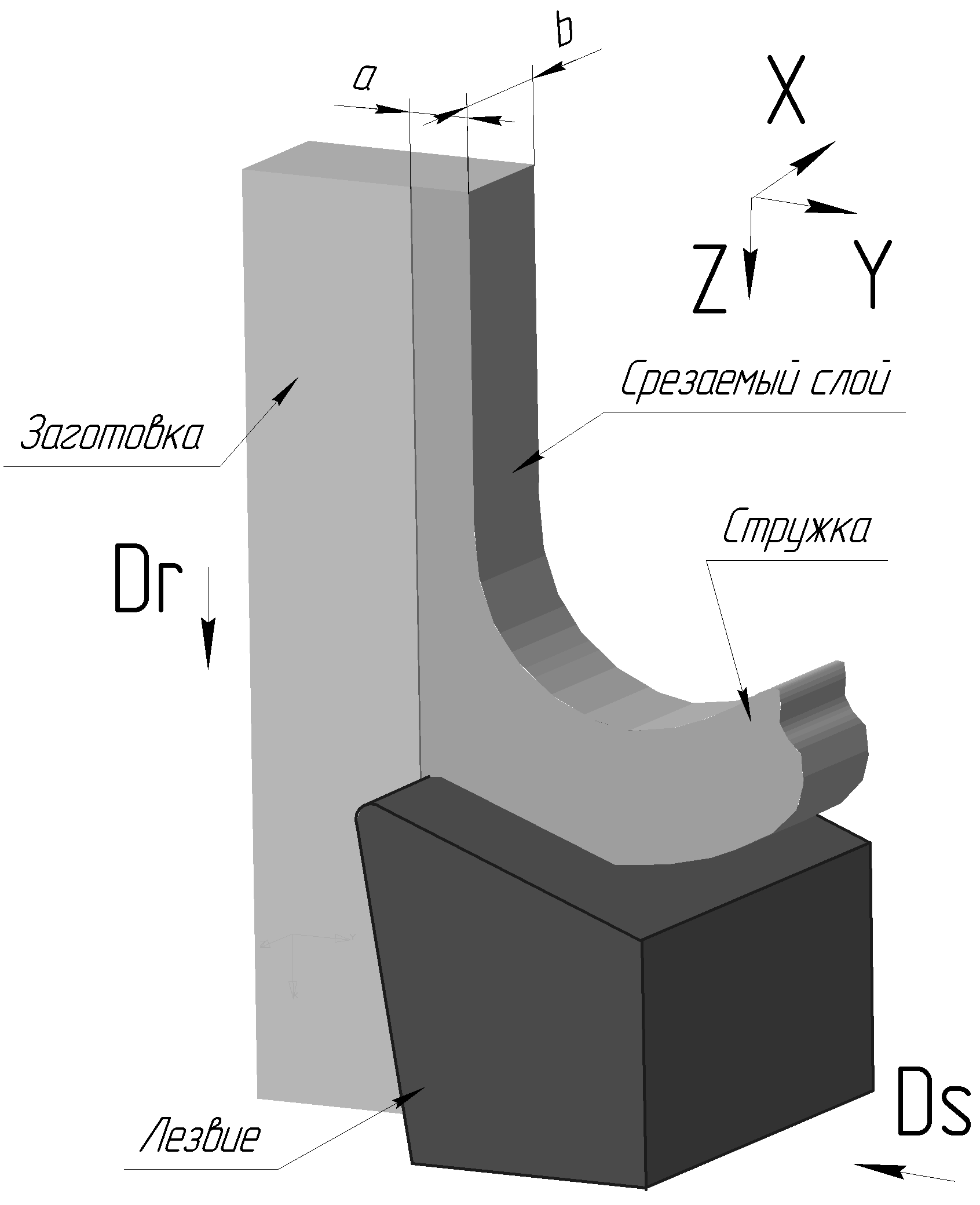
В данной работе была поставлена задача прогнозирования формы стружки, распределения напряжений и деформаций в заготовке и инструменте при прямоугольном резании стали твердосплавным инструментом (рис. 1).

Для решения этой задачи должны быть заданы следующие исходные данные:

а) геометрию инструмента: , ,  по ГОСТу 25762;

б) элементы режима резания: V, S, b, причем для свободного прямоугольного резания a=S;

в) реологическую модель обрабатываемого материала;

г) модель трения.

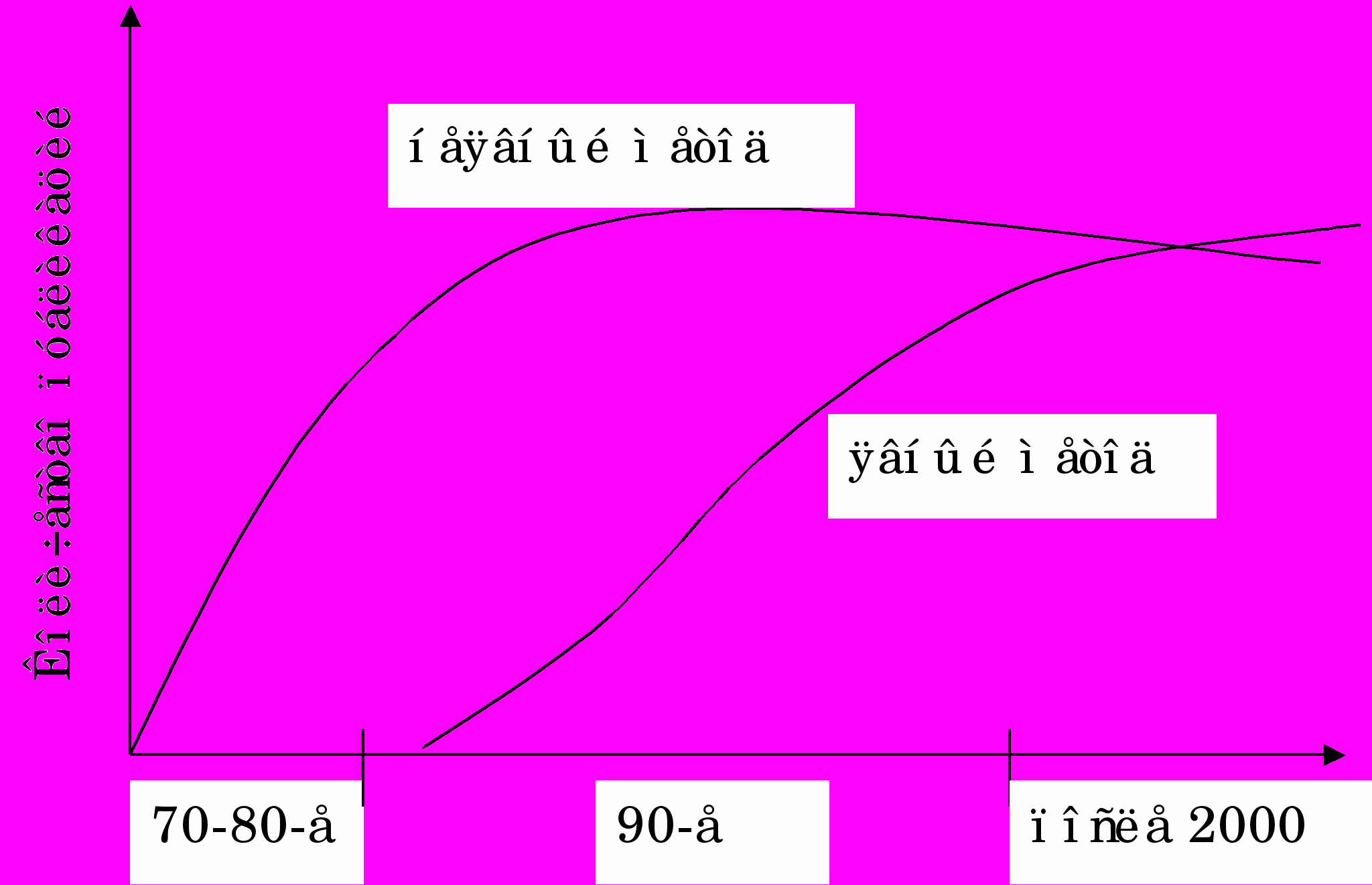
Рисунок 2 – Тенденции в использовании методов временной дискретизации для моделирования процесса резания

Таблица 1 - Методы временной дискретизации, реализованные в коммерческих программных продуктах КЭ прочностных расчетов или используемые для КЭ моделирования процесса резания

Явный	Неявный
LS-DYNA	ANSYS
ABAQUS-Explicit	ABAQUS-Implicit
AdventEdge	MSC. Marc
	DEFORM2D

Как показано в работе [187 2], процесс резания в общем случае является нестационарным процессом и, следовательно, задача его моделирования также должна решаться во времени. В этом случае решение методом КЭ предполагает временную дискретизацию. Обзор литературы показал, что от выбора метода временной дискретизации существенно зависит не только время решения задачи, но и численная устойчивость решения. Известно два метода временной дискретизации: явный и неявный (табл.1).

Явный метод временной дискретизации является условно-стабильным, т.е. решение есть всегда, если шаг по времени меньше критического периода времени, т.е. времени, необходимого звуковой волне для прохождения наименьшего КЭ. Это быстрый метод, но скорость вычислений ограничена шагом по времени. Решение методом явной временной дискретизации динамическое, т.е. перемещения рассчитываются из уравнения второго закона Ньютона. Это эффективный метод, поскольку матрица масс всегда собрана и поэтому нет необходимости решать систему уравнений для ее сборки. Очевидно, это более затратный метод для моделирования установившегося стружкообразования, но является наиболее эффективным при решении высоконелинейных задач динамики, и особенно в тех случаях, когда можно пренебречь инерционными силами. При этом увеличение шага по времени можно достичь искусственным увеличением плотности материала.

Шаг по времени в методе неявной временной дискретизации определяется только желаемой точностью получаемого решения и условием сходимости. Однако требуется решение системы уравнений, часто нелинейных, что может приводить иногда к численной неустойчивости. Для решения системы уравнений широко используется метод Ньютона-Рафсона, который может использоваться как с учетом, так и без учета инерции, т.е. без учета второго закона Ньютона. Такой метод временной дискретизации наиболее подходит для моделирования процесса установившегося стружкообразования.

Проведенный авторами анализ литературных источников свидетельствует о том, что неявный метод временной дискретизации для моделирования процессов резания имел преимущественное применение в 90-х годах прошлого века, а в настоящее время исследователи отдают предпочтение явному методу временной дискретизации (рис. 2). В связи с этим в данной работе был использован именно явный метод временной дискретизации.

Общий алгоритм решения задачи представлен на рис. 3. Процесс вычисления представляет собой итерационную процедуру, содержащую два независимых цикла по времени. Основной цикл (блоки 3,4,5) выполняется с малым шагом по времени и обеспечивает вычисление поля напряжений и деформаций в инструменте и заготовке. Вспомогательный

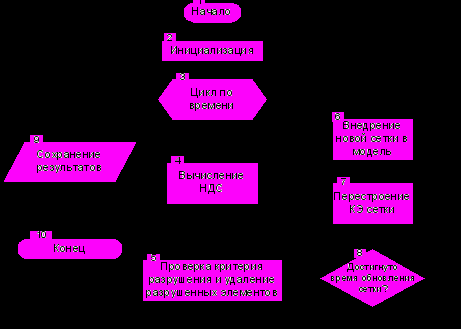
Рисунок 3 – Общий алгоритм решения задачи

цикл (блоки 6,7,8) выполняется с шагом, по крайней мере в 10² раз большем, чем основной цикл и реализует перестроение КЭ сетки. Несмотря на споры в литературе относительно корректности такого подхода [1065 3], это, по-видимому, единственный универсальный способ восстановления качества КЭ сетки и обеспечения численной устойчивости вычислений [982 4].

Ввиду важности остановимся на математическом описании основного цикла. В основу модели было положено фундаментальное уравнение движения точек твердого тела, которое можно записать в виде [1217 5]:

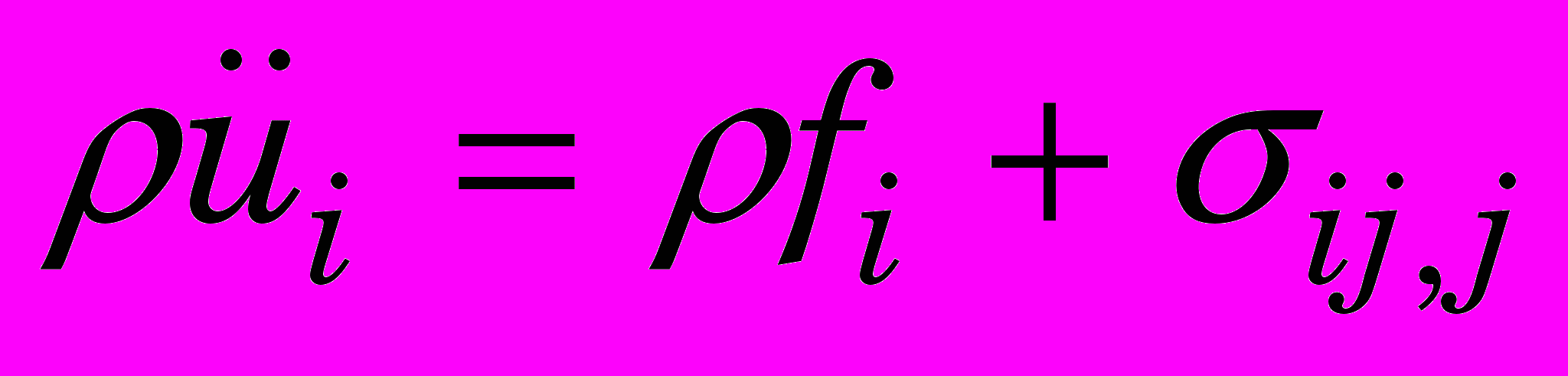, (0)

где

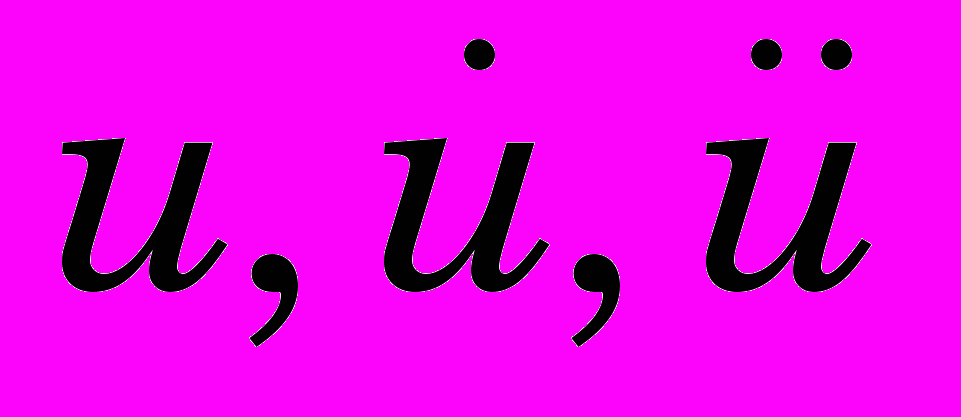- соответственно векторы перемещения точек твердого тела, их скорость и ускорение;

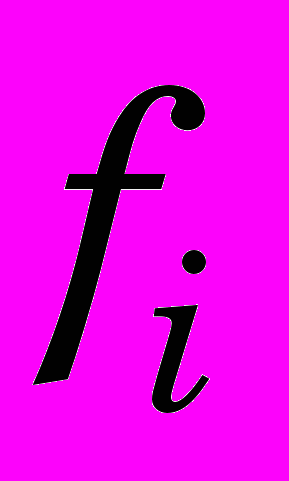- плотность объемных сил;  - плотность в данный момент времени;

- компоненты тензора напряжений Коши.

Граничные условия математически формулируются в виде:

в силах на границе тела -

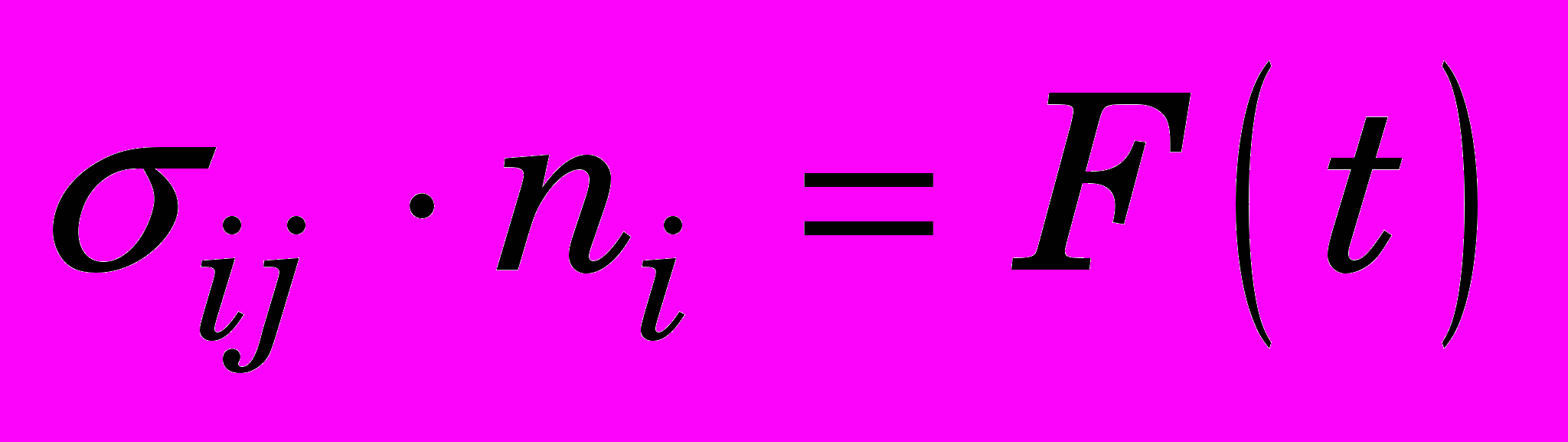; (0)

в перемещениях на границе тела

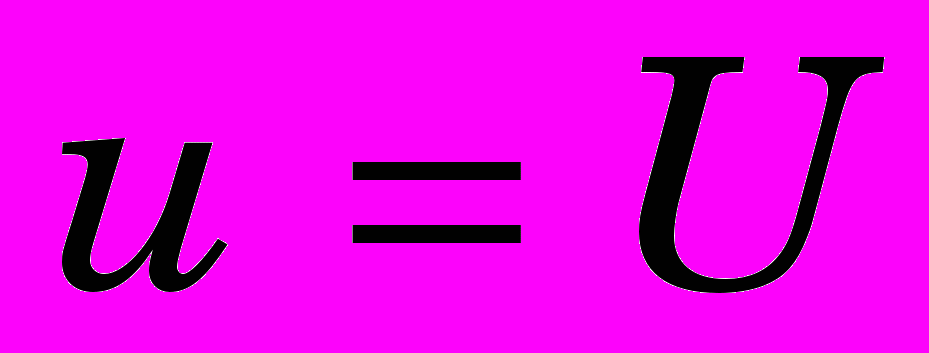; (0)

в силах на контактной границе

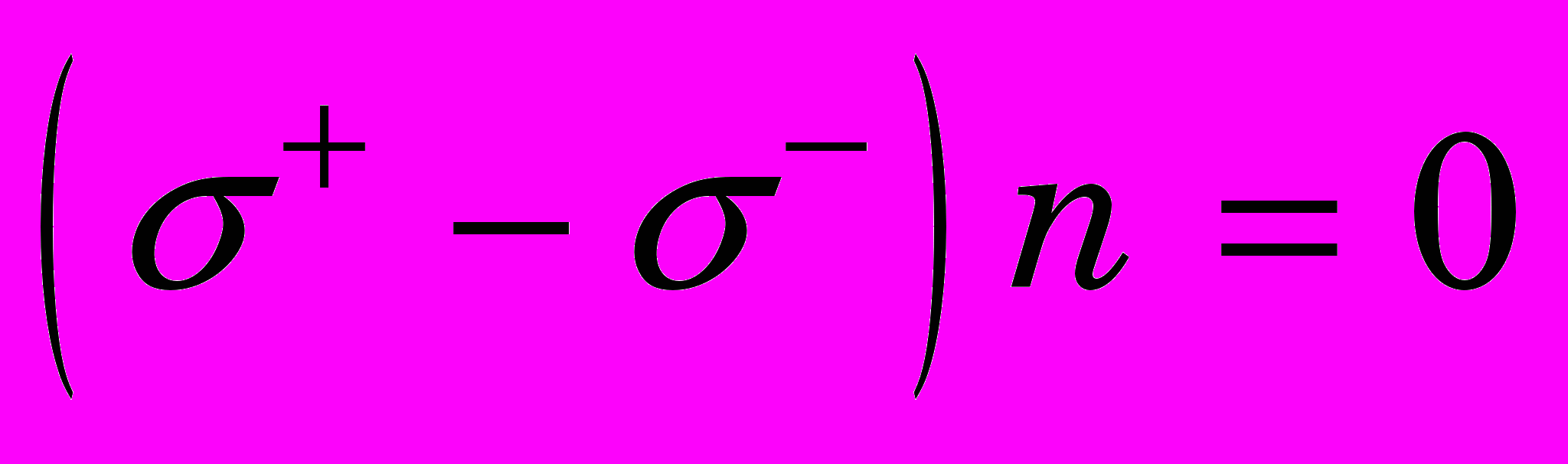при

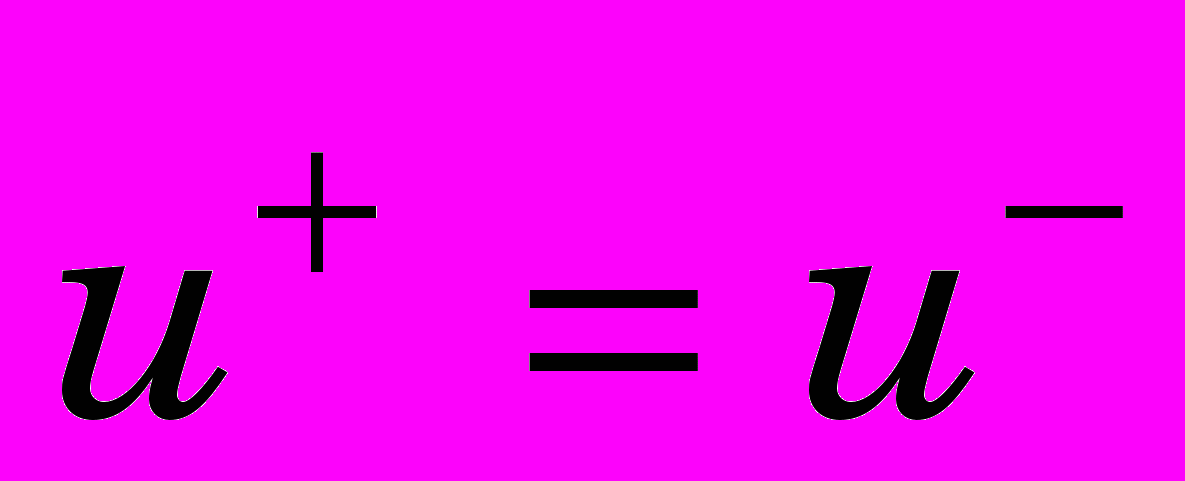. (0)

Уравнение сохранения массы

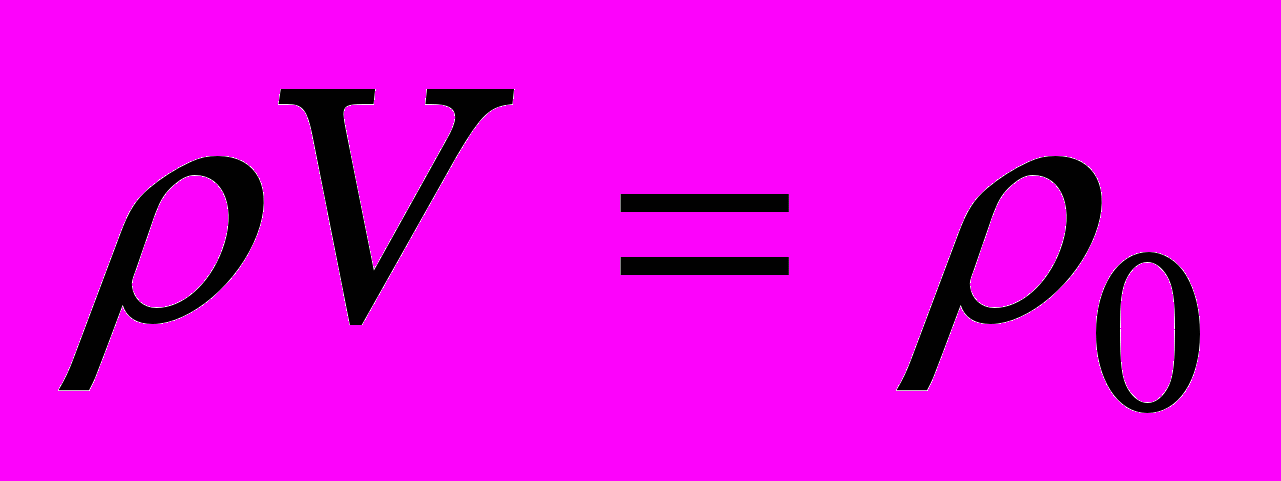, (0)

где

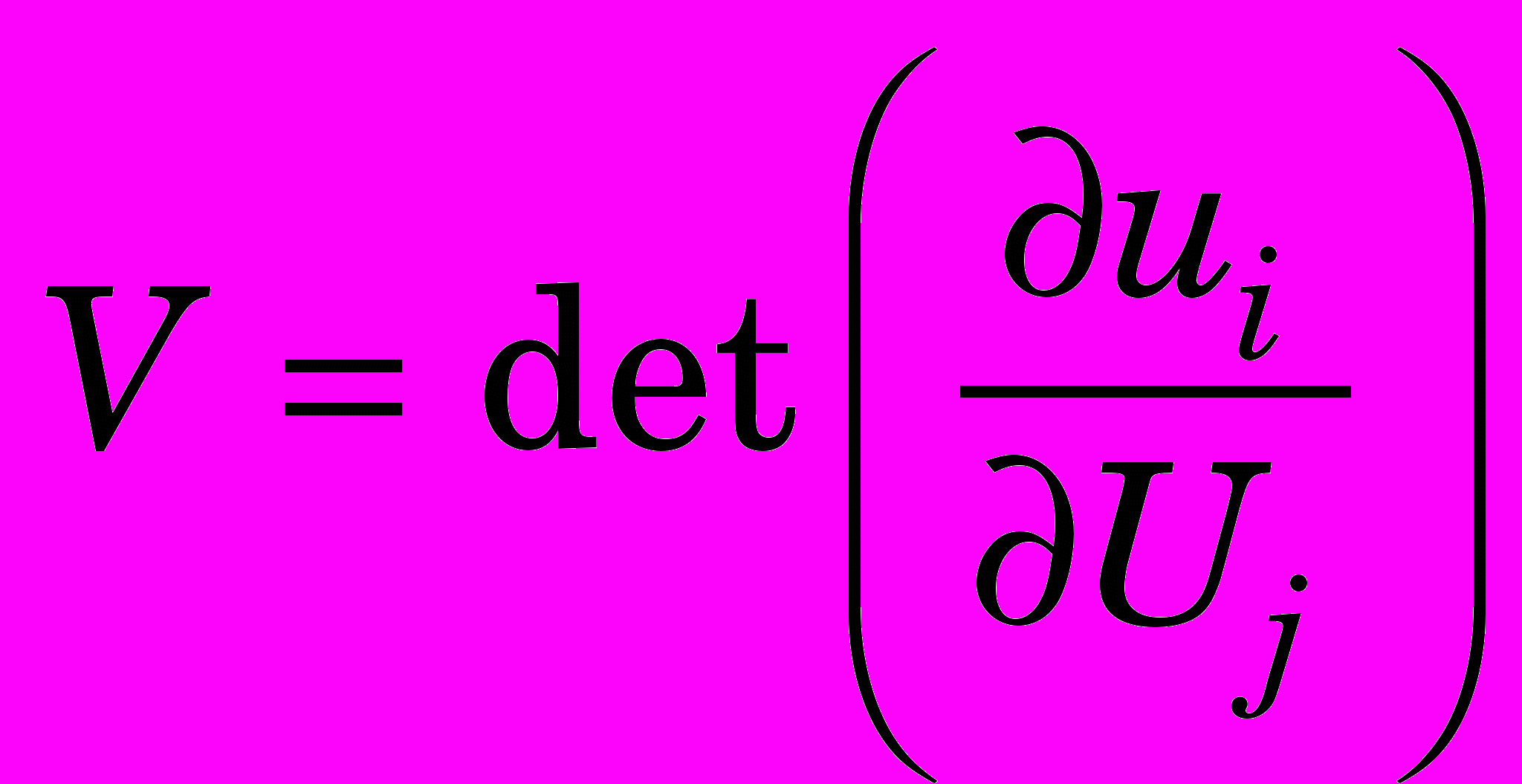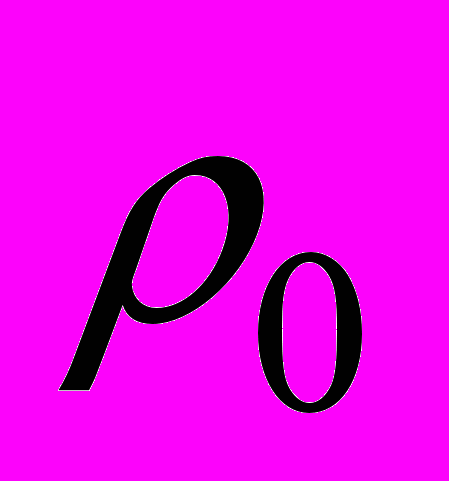- начальная плотность материала.

Уравнение энергии

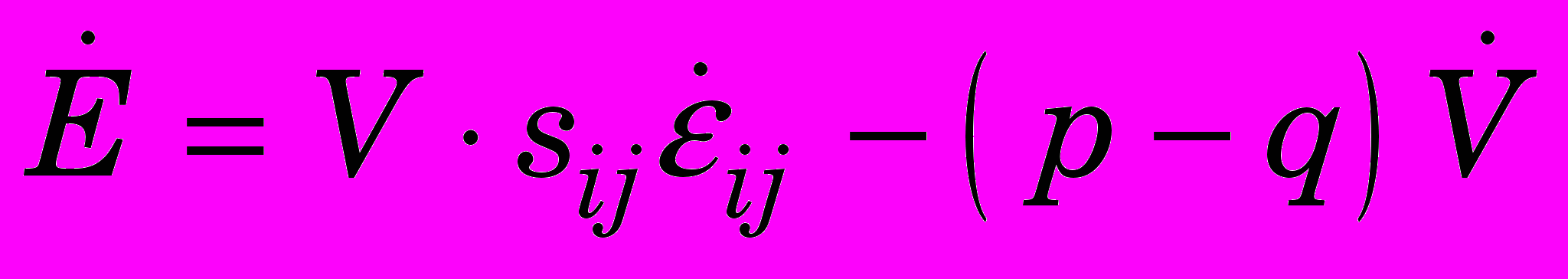, (0)

где

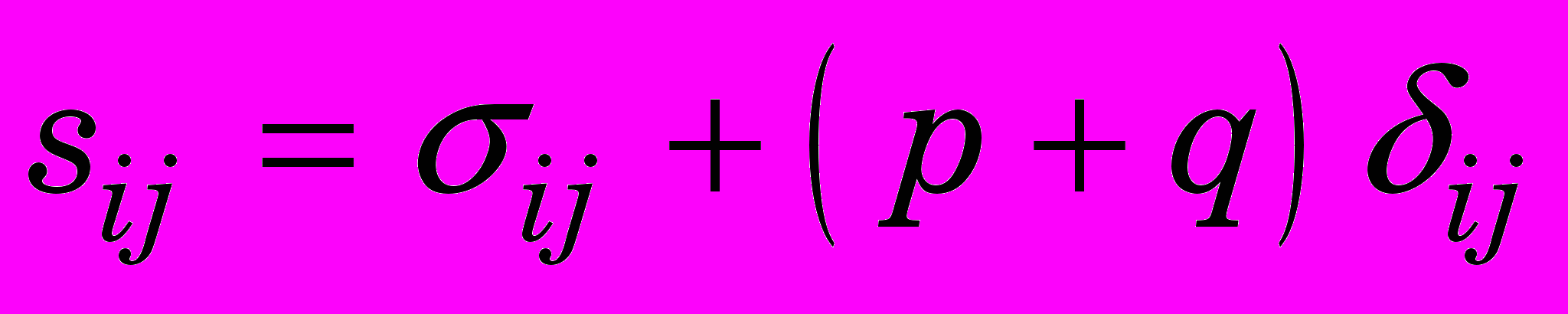компоненты девиатора тензора напряжений Коши;

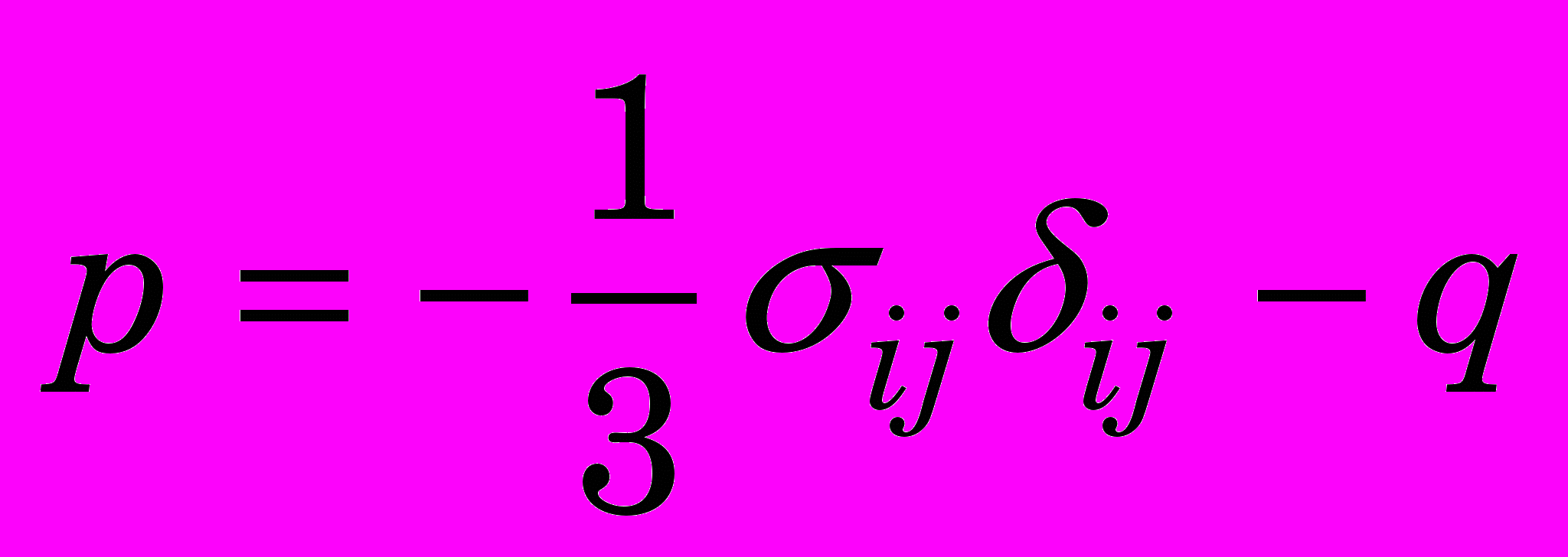гидростатическое давление (отрицательное при растяжении);

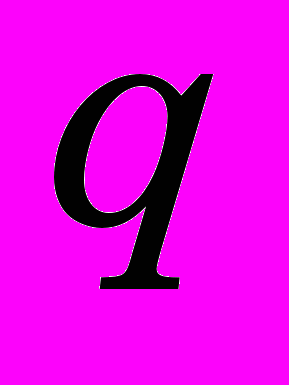объемная вязкость;

- символ Кронекера;

- компоненты тензора скорости деформации.

В работе принято допущение о плоской деформации, хорошо подтверждающееся экспериментом [351 6]. Это требует, чтобы u_z=0, _z = 0, b=1. В работе использованы четырехузловые КЭ. Силы, действующие на твердое тело, можно определить по формуле [1217 5]

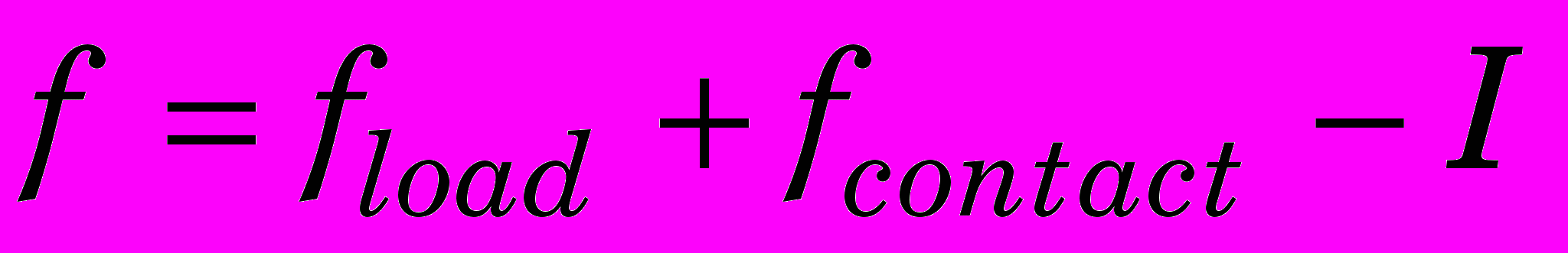, (0)

где

- приведенные к узлам КЭ сетки объемные и внешние силы, действующие на тело;

- приведенные к узлам КЭ сетки силы на контактной границе тела;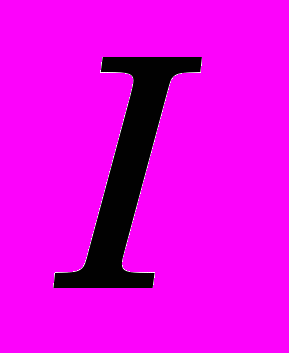

- внутренние силы.

Основываясь на указанных фундаментальных уравнениях, численное вычисление перемещений узлов твердого тела может быть выполнено с помощью следующей итерационной процедуры.

Пусть в начальный момент времени во всех точках моделируемого тела

;

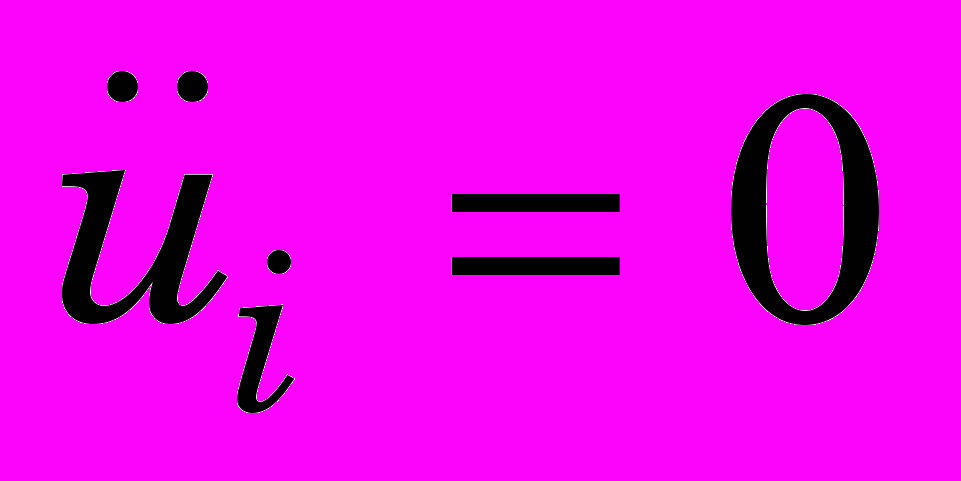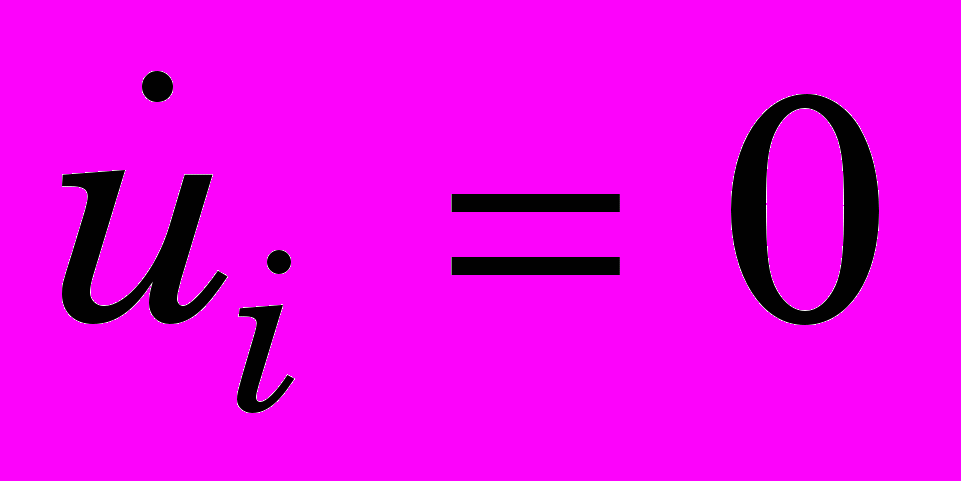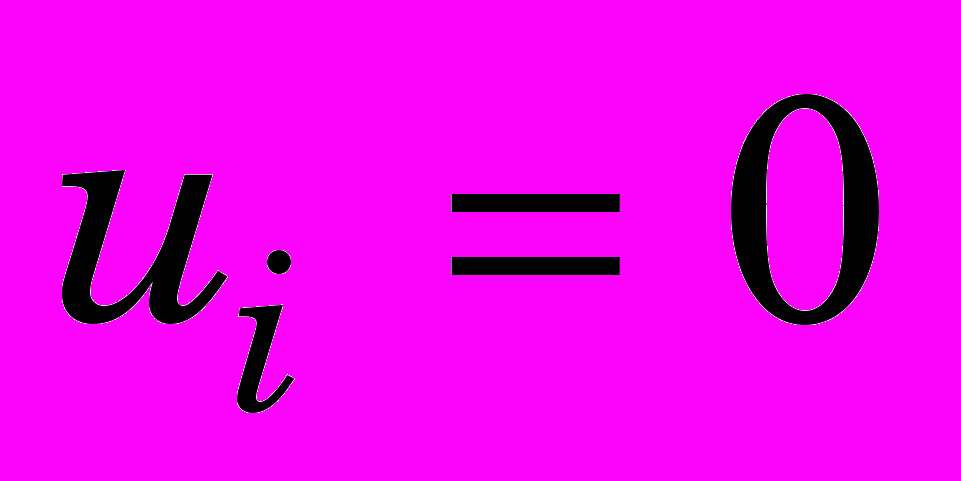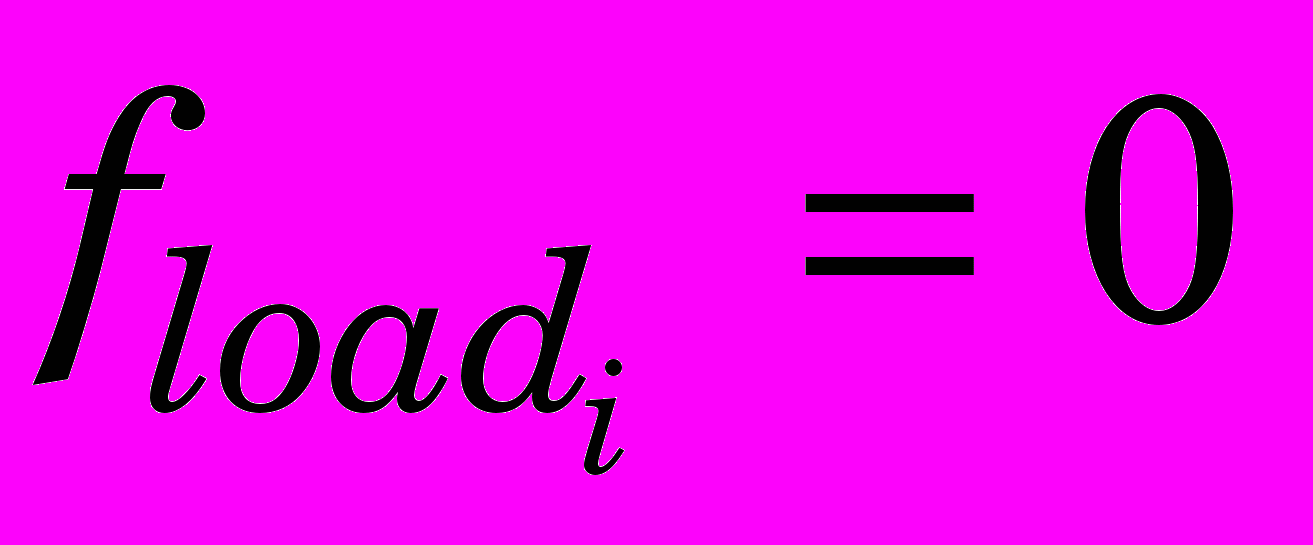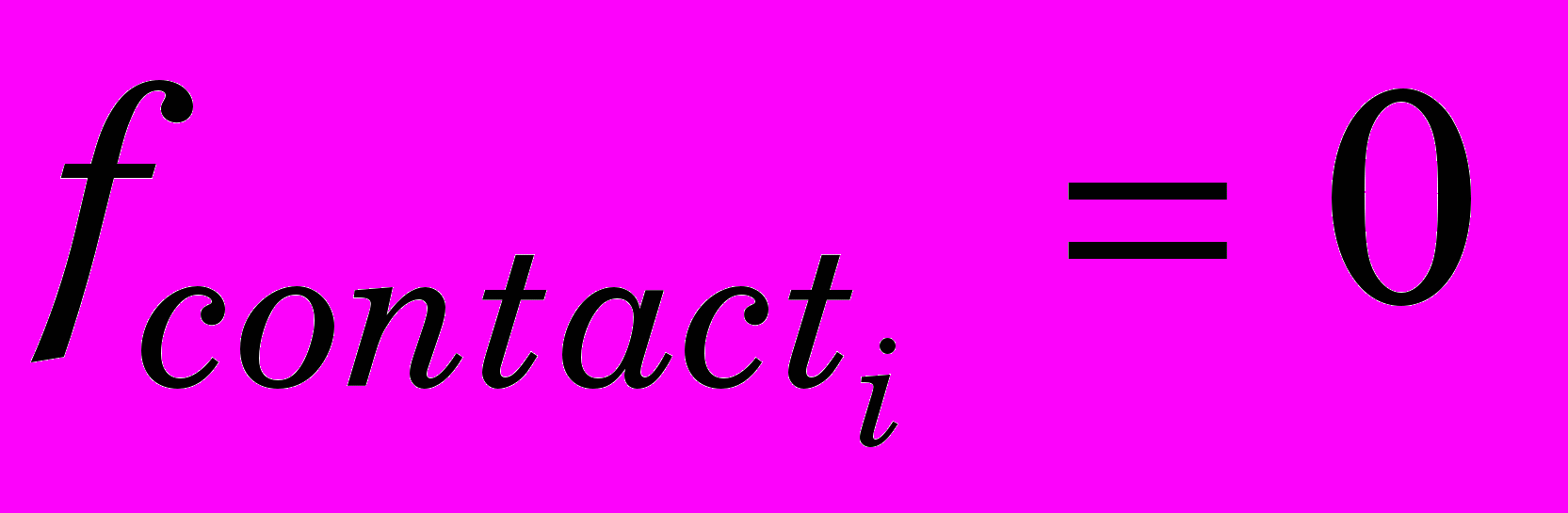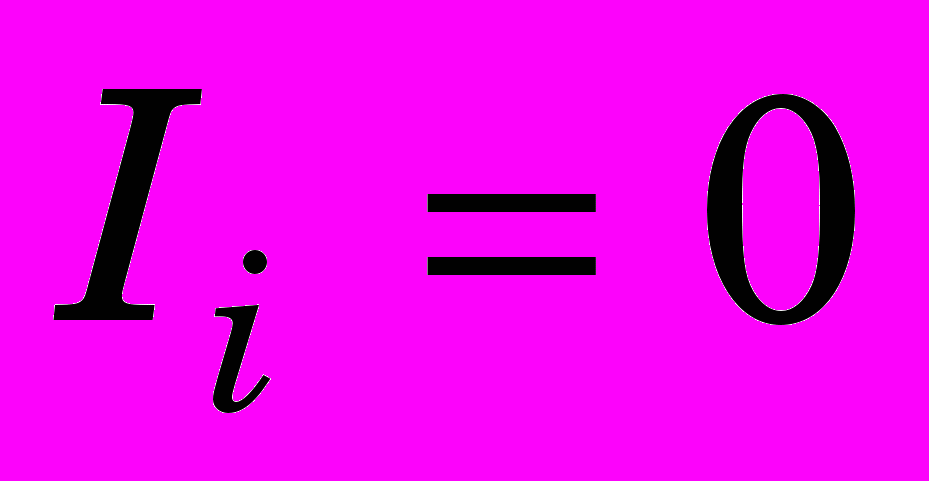. (0)

Найдем перемещение точек тела через некоторый бесконечно малый промежуток времени t. Для этого зададим кинематические граничные условия и нагрузки, определенные по условиям задачи в данный момент времени:

;

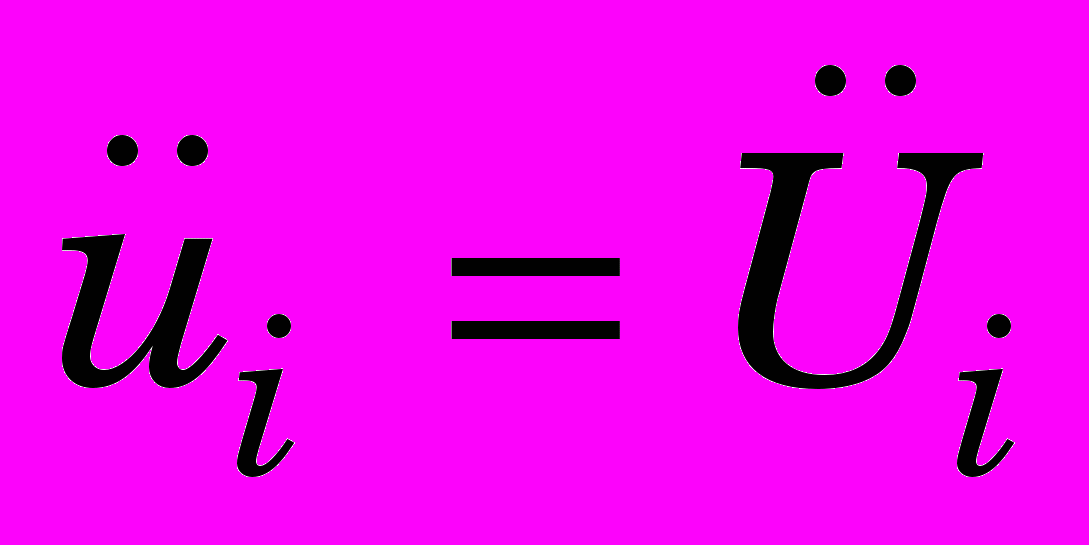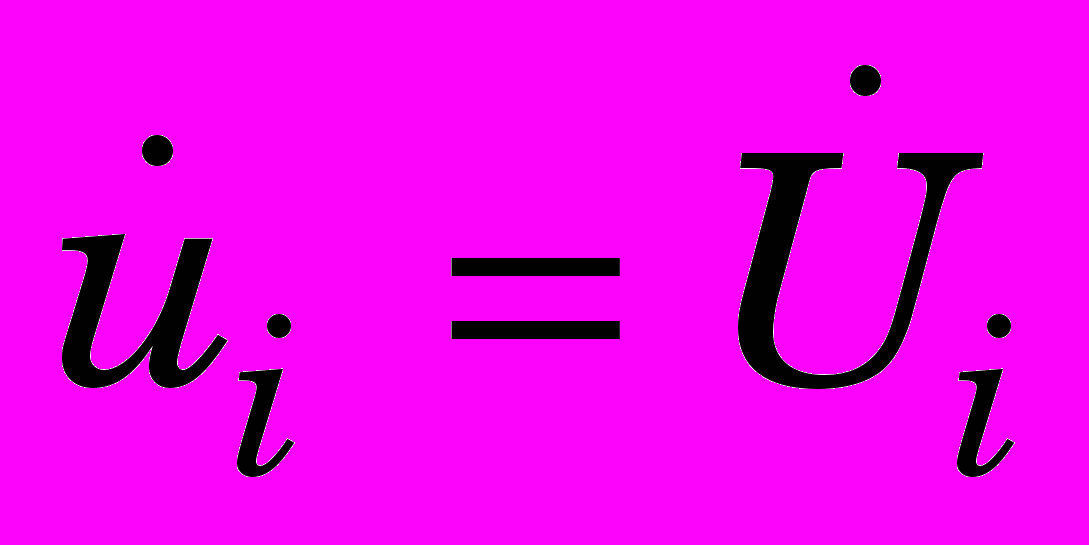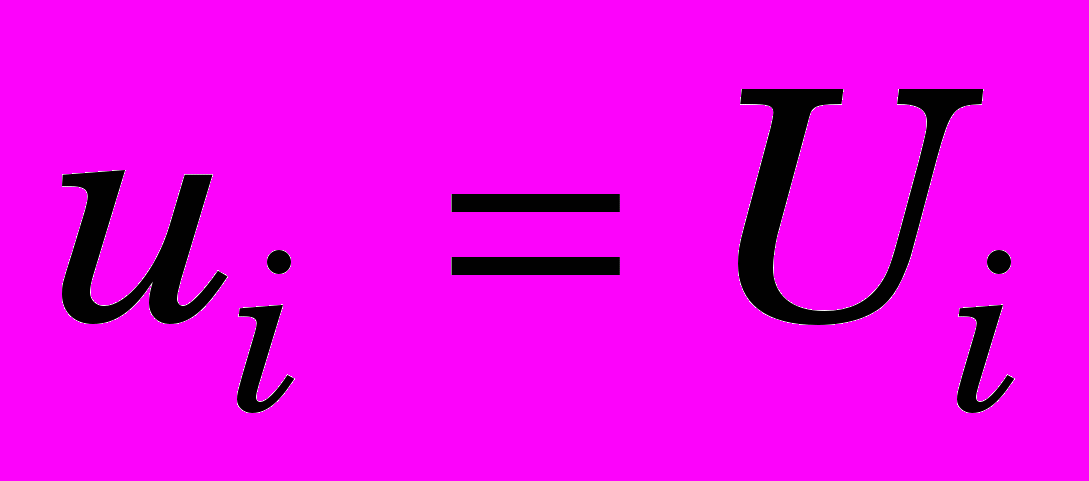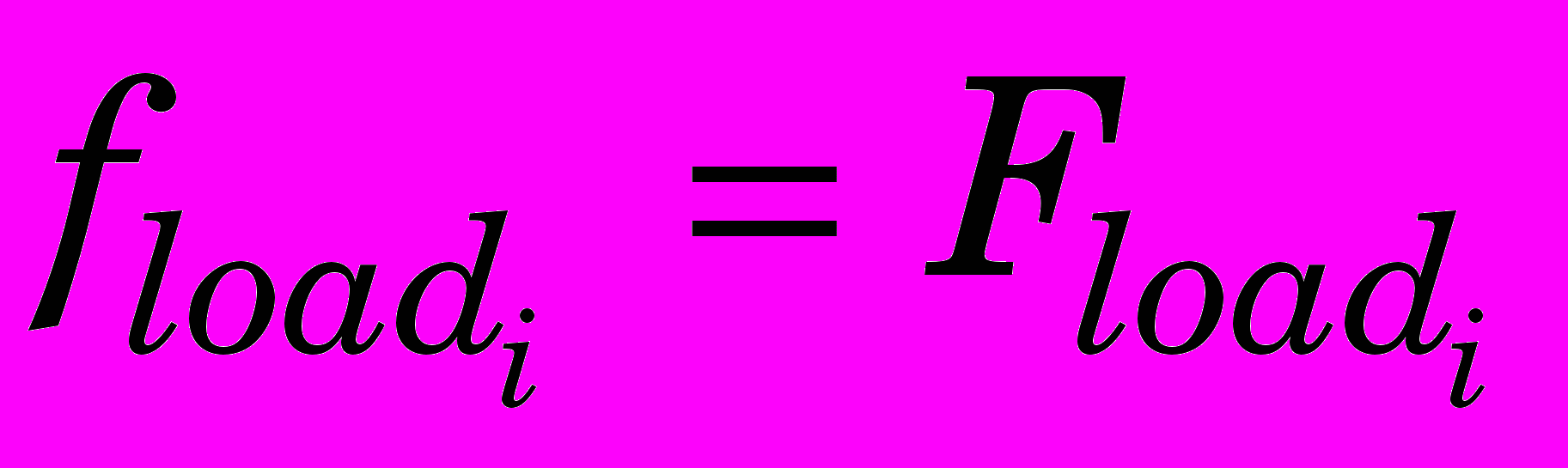. (0)

По уравнению (1) вычислим вектор ускорений:

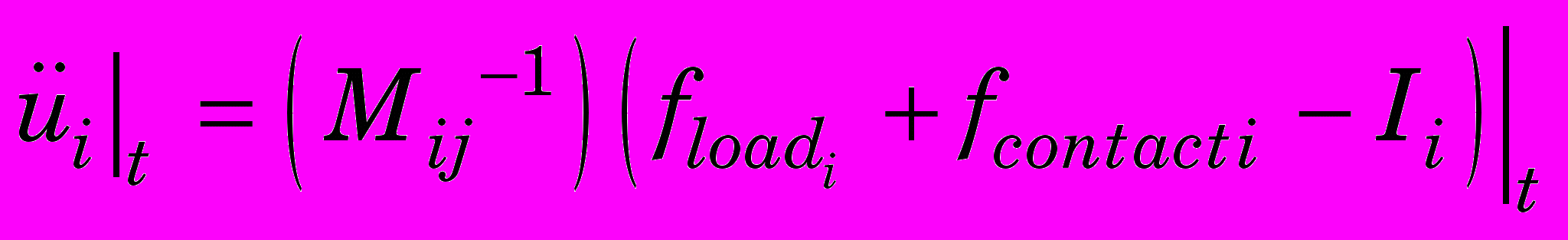, (0)

где M – матрица масс.

Далее вычисляем вектор скоростей, выполняя интегрирование методом центральных разностей:

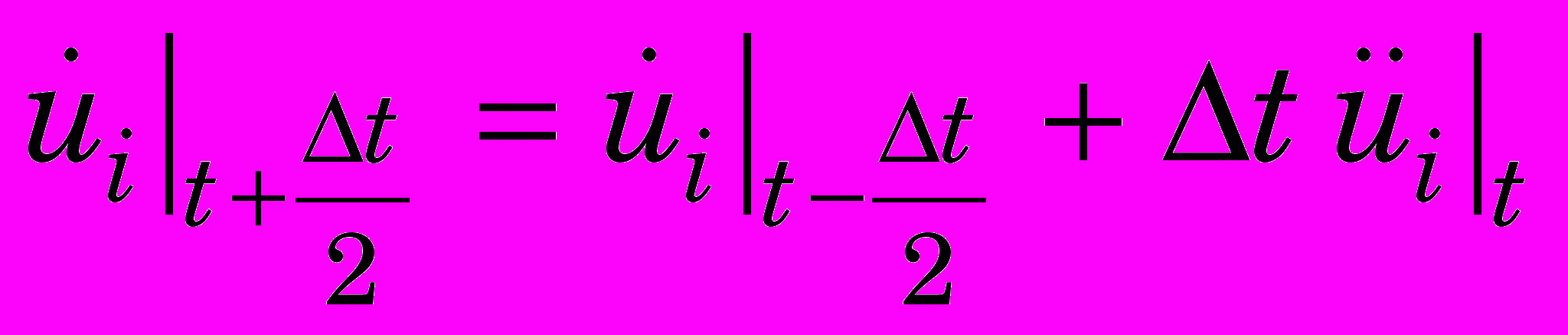. (0)

Поступая аналогично, вычисляем вектор перемещений точек тела:

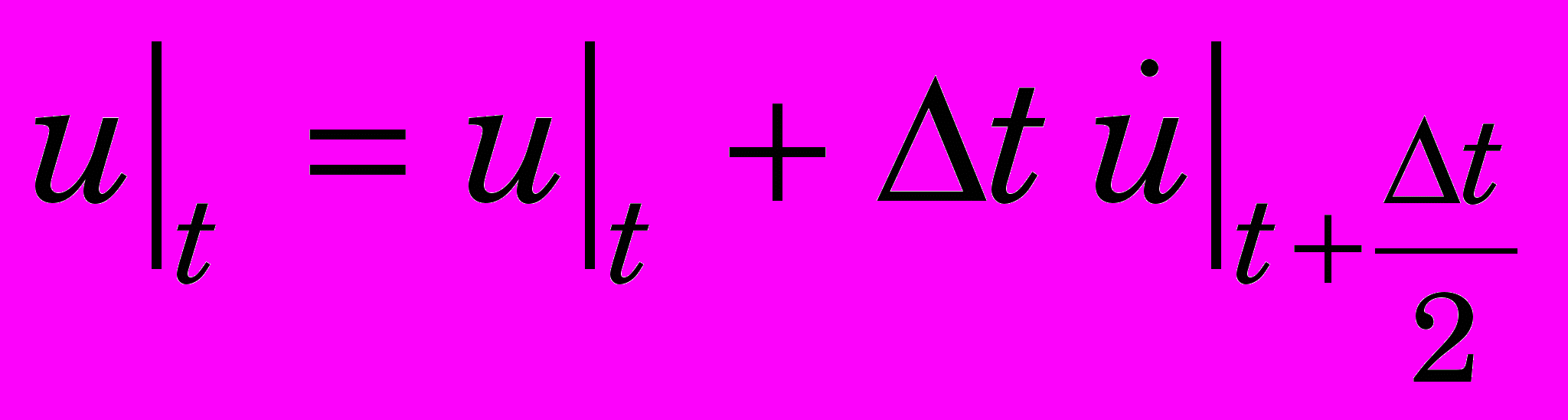. (0)

Очевидно, что перемещения точек тела вызовут силовую реакцию со стороны тела в виде внутренних сил I, которые пока остаются неизвестными. Для их определения вычислим тензор скоростей деформаций:

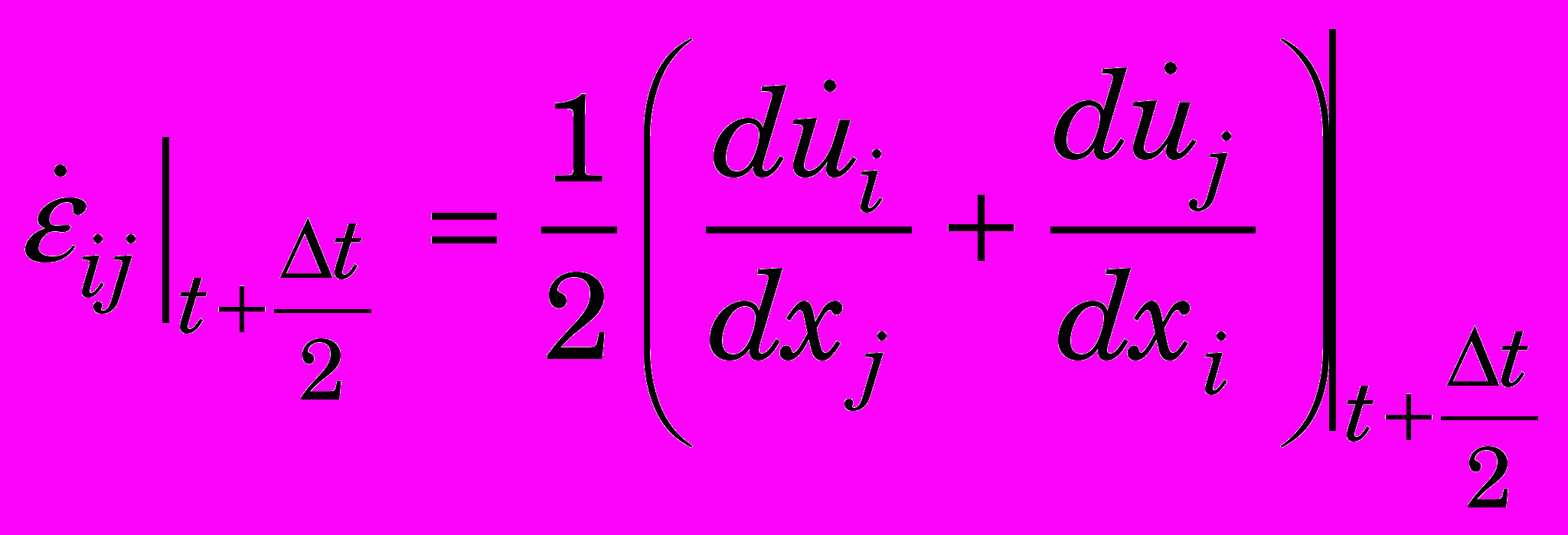. (0)

Выполняем декомпозицию:

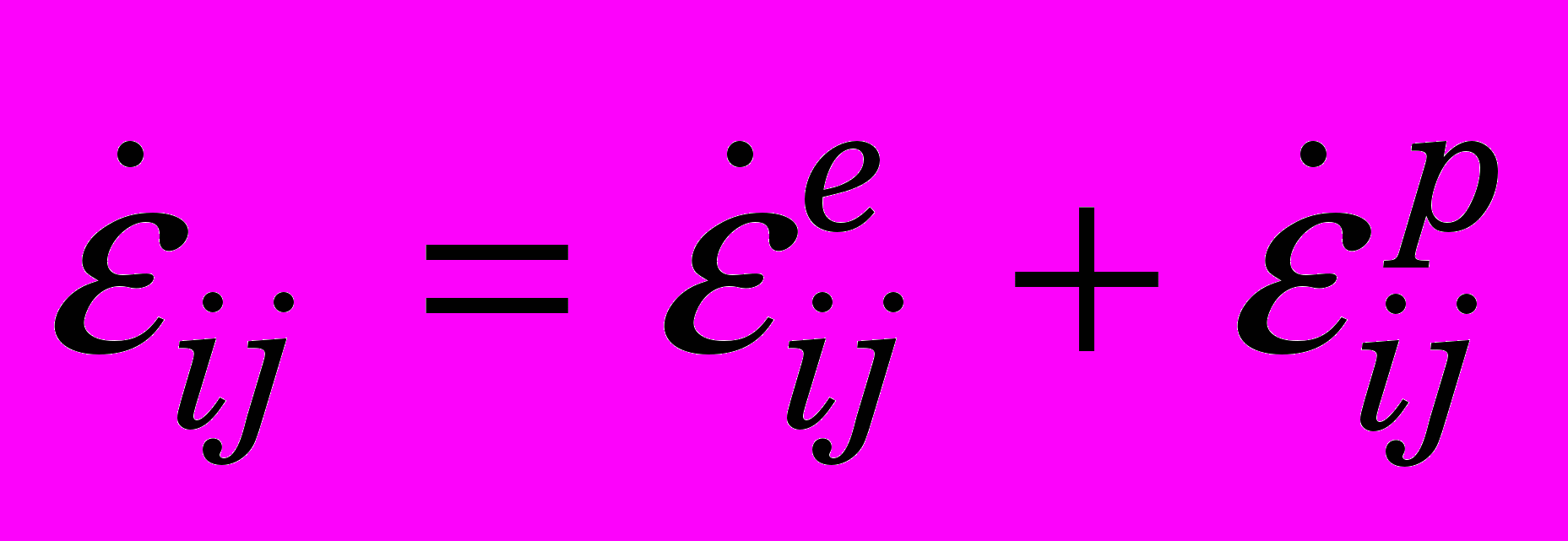, (0)

где

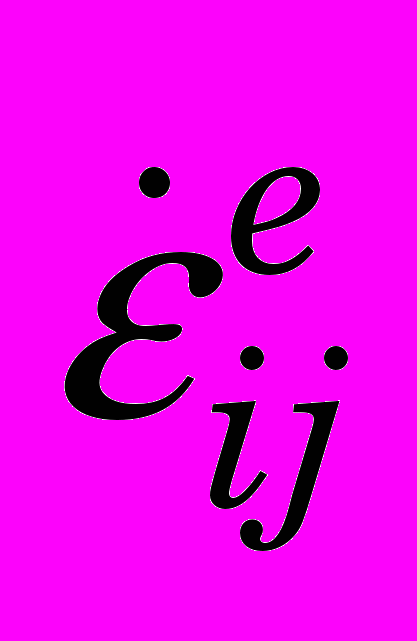- тензор скоростей упругих деформаций;

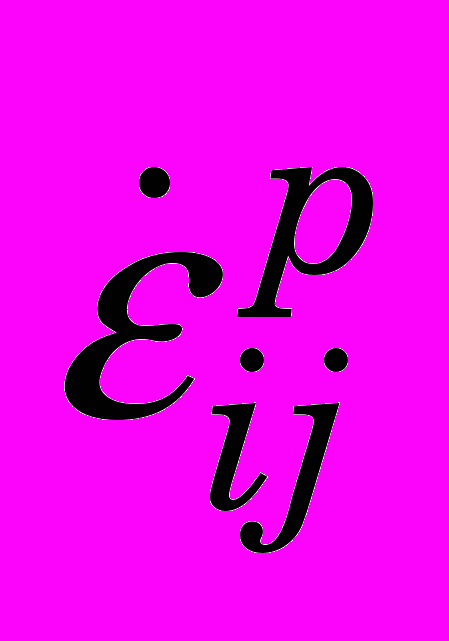- тензор скоростей пластических деформаций.

Тогда приращение любой составляющей деформаций

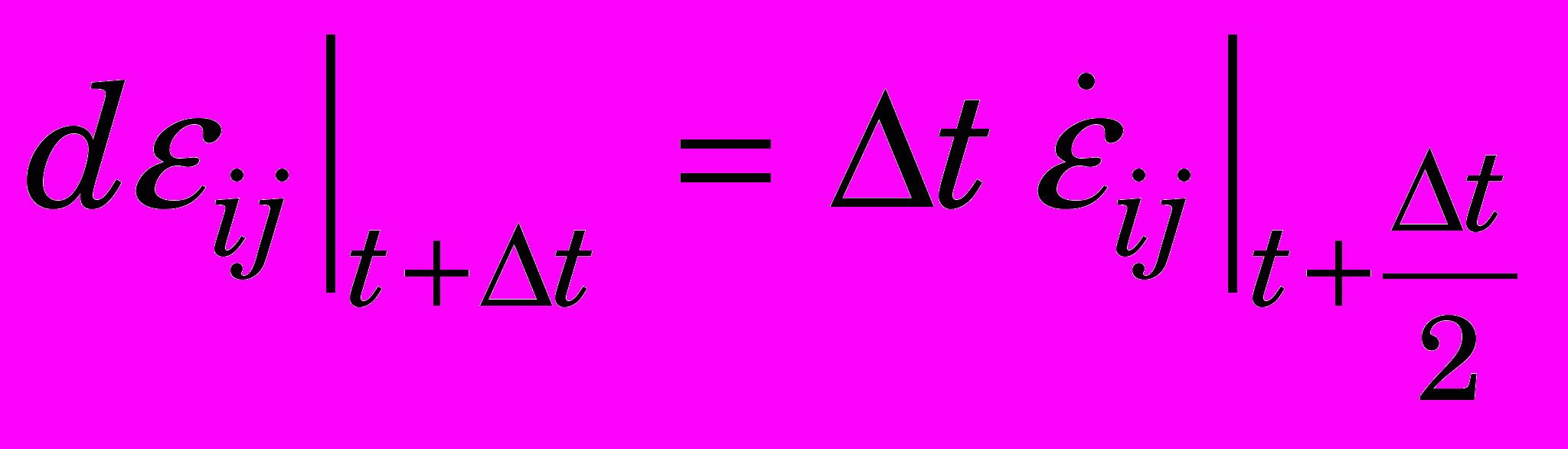. (0)

Величина любой составляющей деформации:

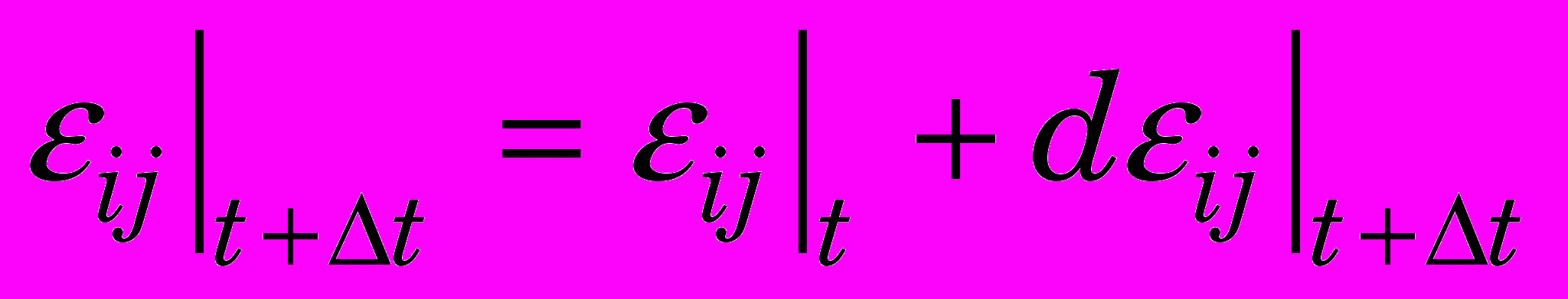. (0)

Учитывая большие скорости деформации в зоне стружкообразования при практически применяемых скоростях резания [339 7], принято допущение об адиабатическом характере деформации. Тогда температура, возникающая при такой деформации, может быть вычислена как

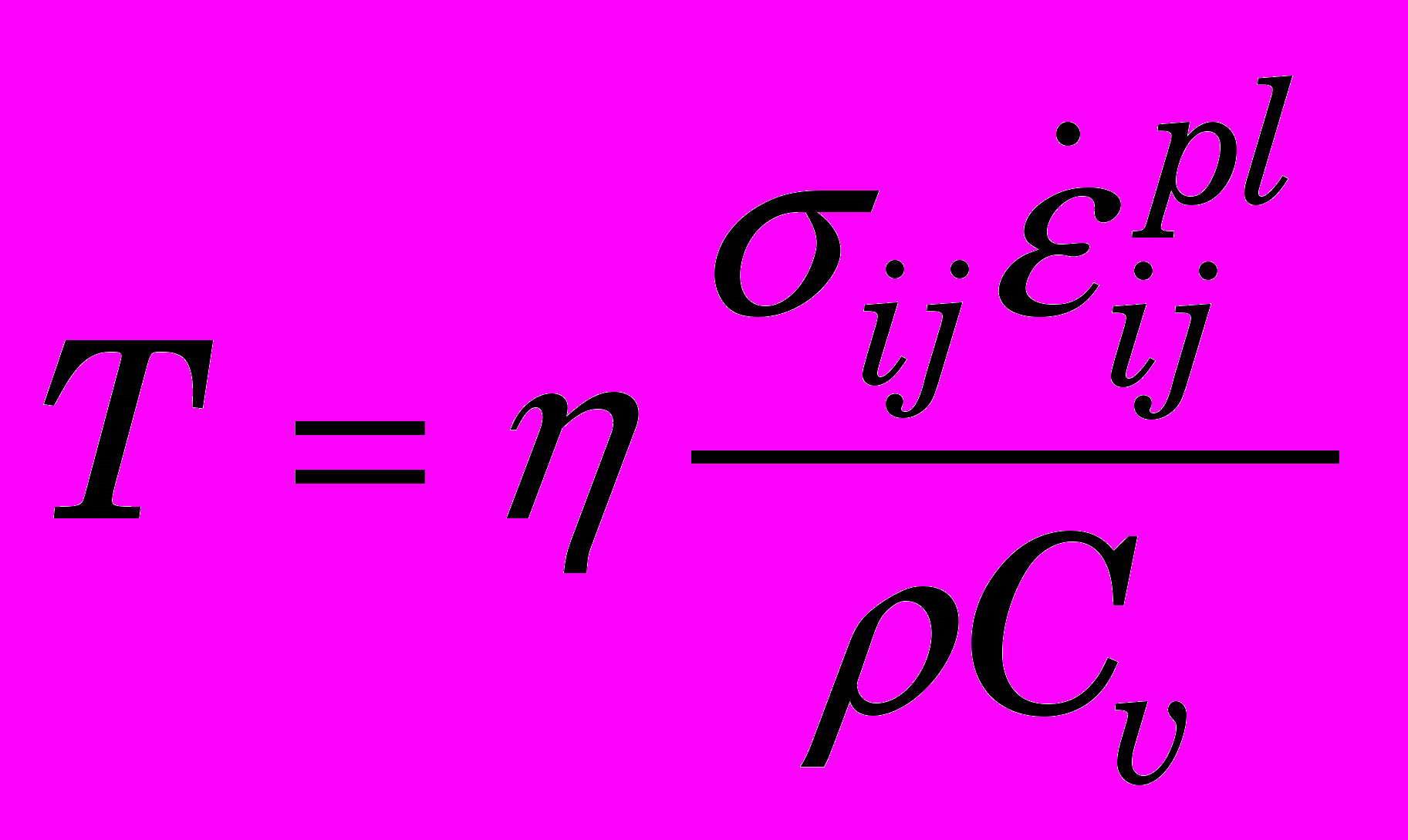. (0)

Применяя реологическую модель (уравнение состояния) материала деформируемого тела [1112 8], вычисляем напряжения в узлах КЭ:

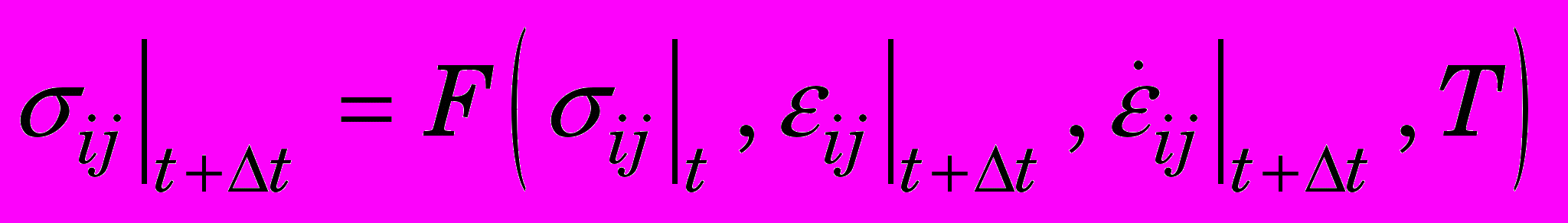, (0)

осуществляем сборку внутренних сил в узлах

.

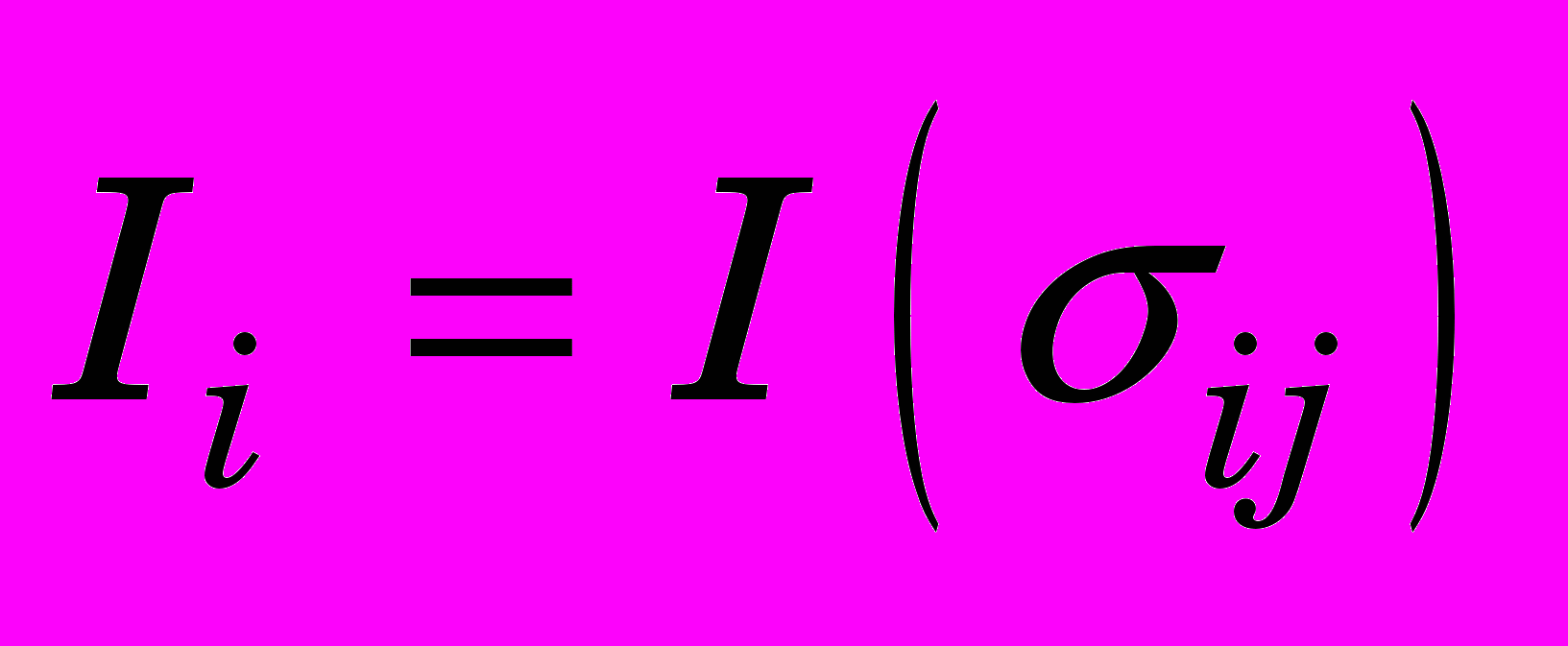Реологическая модель упругих деформаций представлена в данной работе обобщенным законом Гука. Данная реологическая модель применяется для расчета напряжений как в инструменте, так и в заготовке. Заготовка также деформируется пластически. Как показали предыдущие исследования, уравнение состояния в форме Джонсона – Кука [986 9] описывает для этого случая эксперимент наилучшим образом:

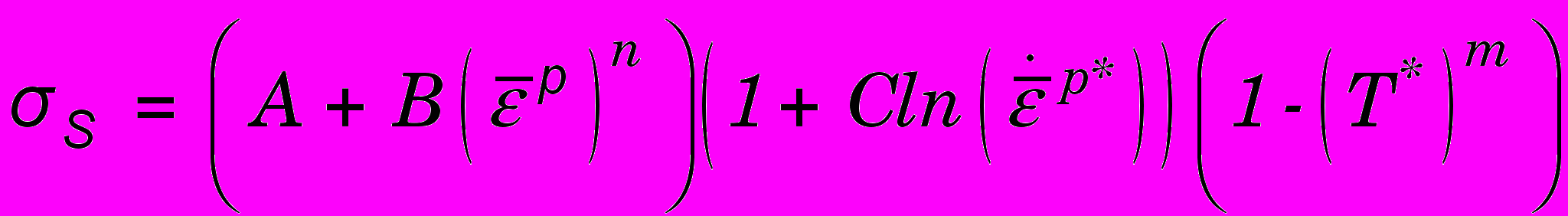, (0)

где

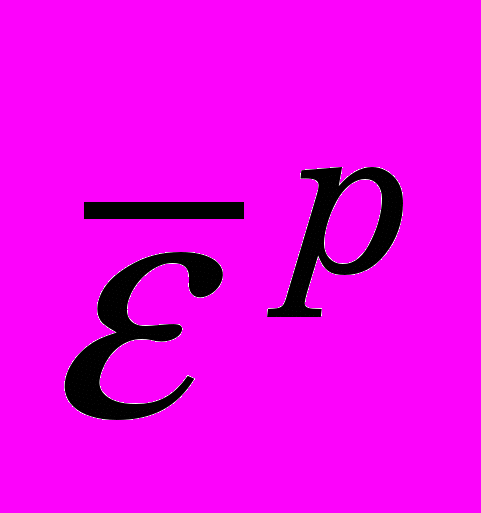- величина интенсивности пластической деформации;

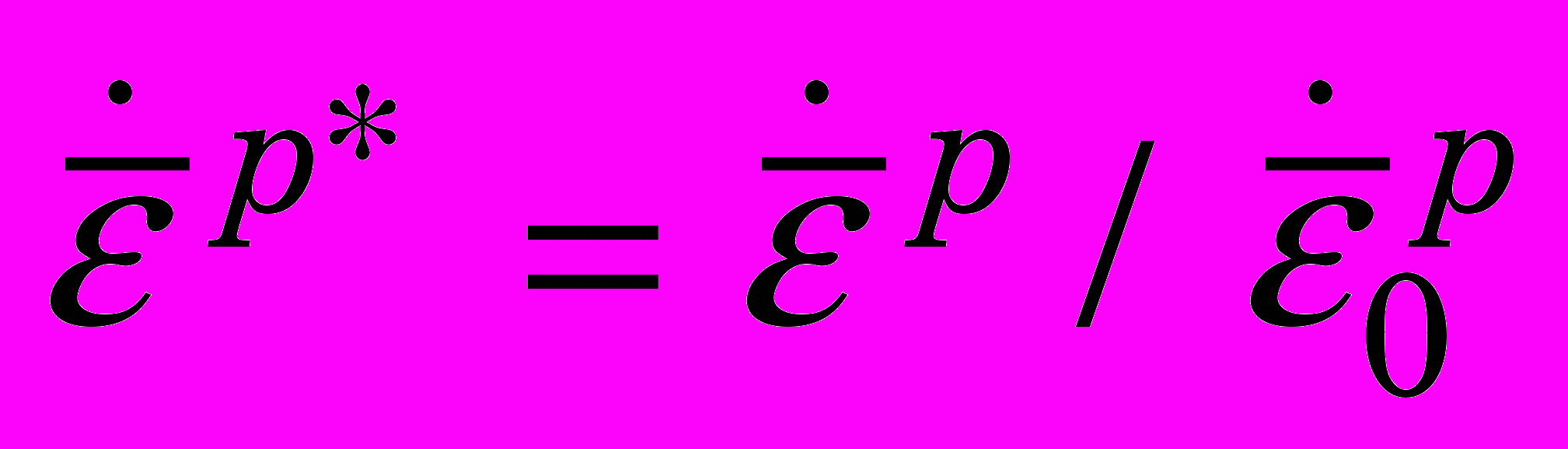- интенсивность скорости пластической деформации;

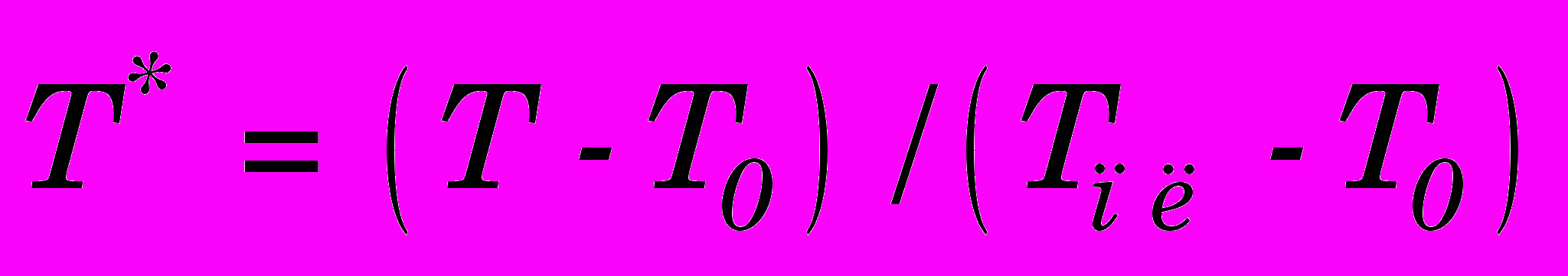- гомологическая температура.

После этого определяем силы на границе контакта. Решение контактной задачи и определение сил на контактной границе

выполняются методом штрафов [5]. Контактные касательные напряжения вычислялись по модели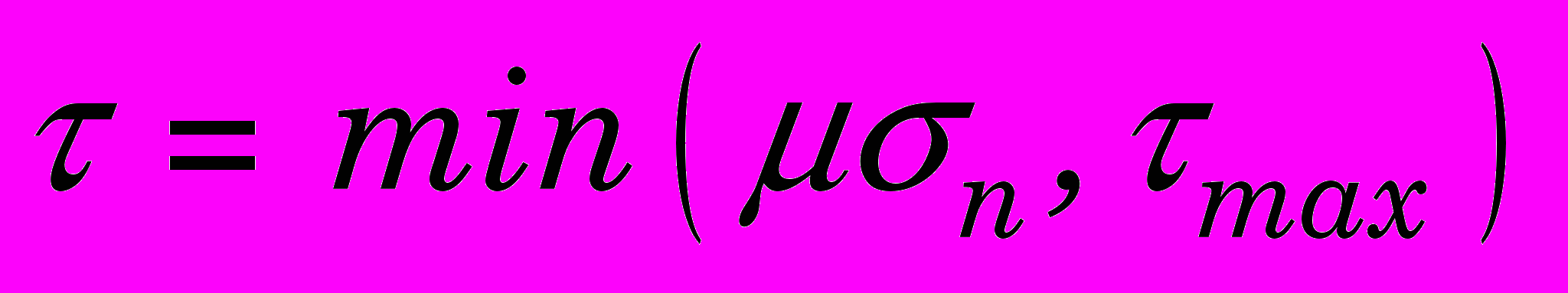

, (0)

где  - коэффициент трения;

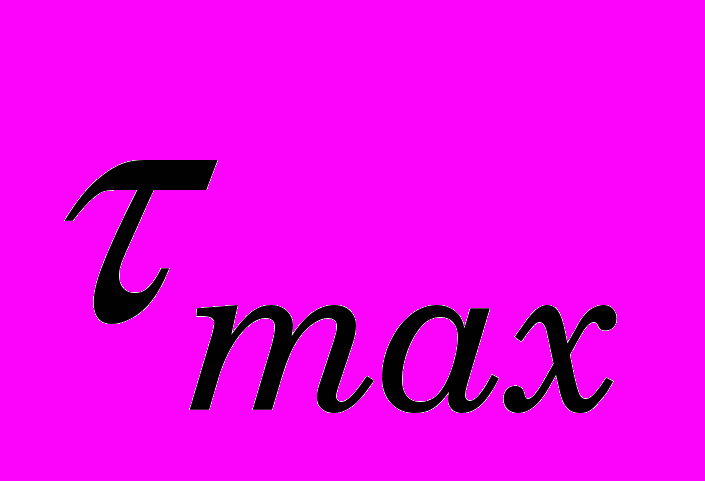- максимальные контактные напряжения;

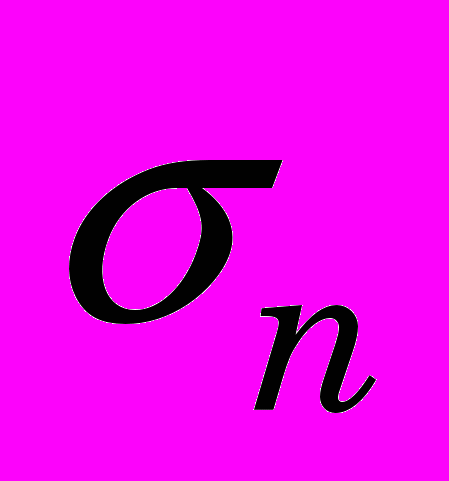- нормальные напряжения на контактной площадке.

Далее проверяется выполнение критерия разрушения в каждом КЭ заготовки. В данной работе в качестве критерия разрушения пластического материала принят критерий накопленных пластических деформаций в форме Джонсона-Кука [1218 1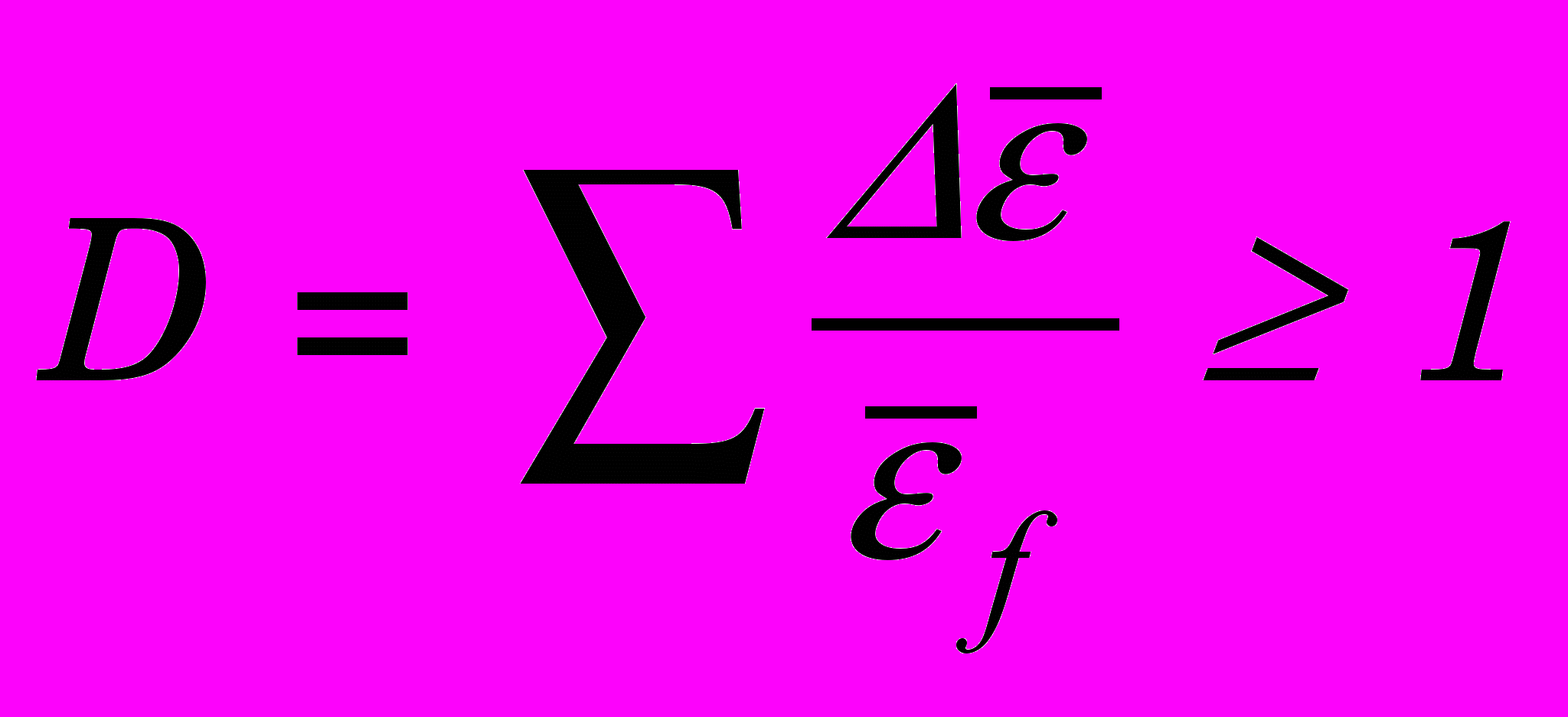0]:

, (0)

где

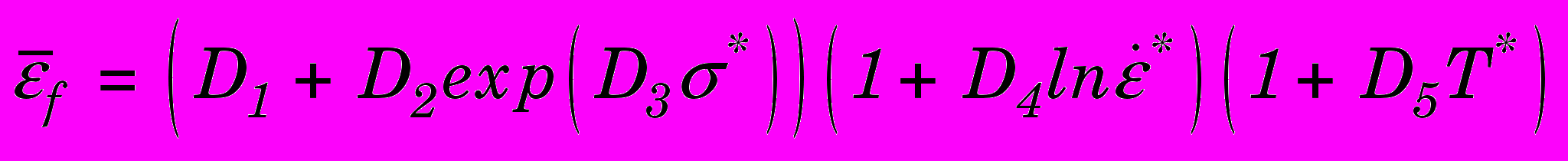- предельная величина накопленных пластических деформаций;

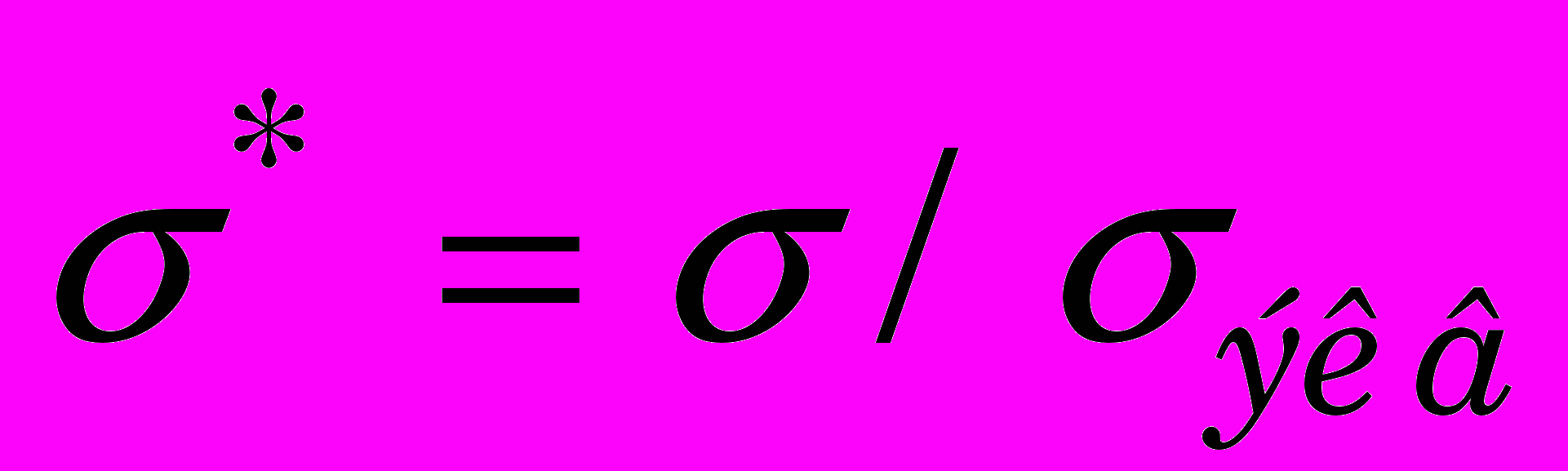;  – гидростатическое давление; _экв- эквивалентные напряжения по фон Мизесу. В тех КЭ, где условие (0) выполняется, тензор напряжений Коши устанавливается равным 0 и в КЭ удаляются сетки.

Далее текущее время t увеличивается на шаг интегрирования t и вычисления повторяются.

Максимальный шаг интегрирования определяется формулой

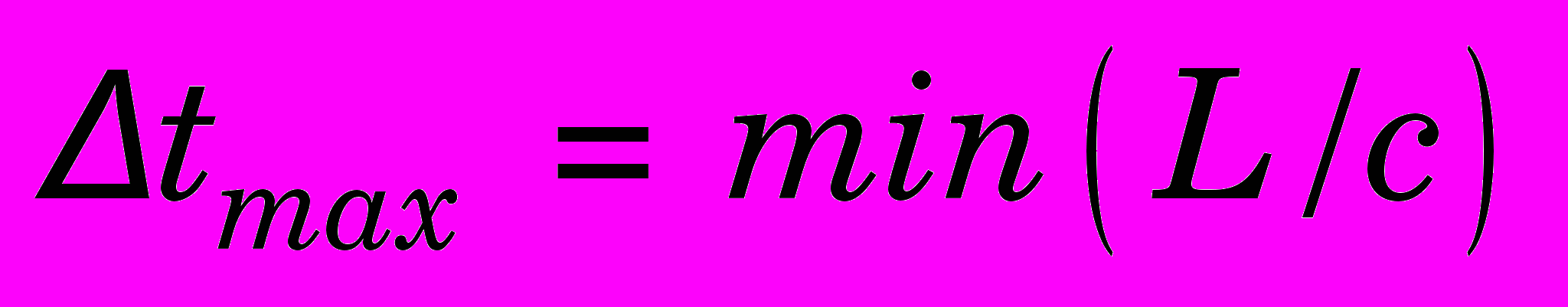, где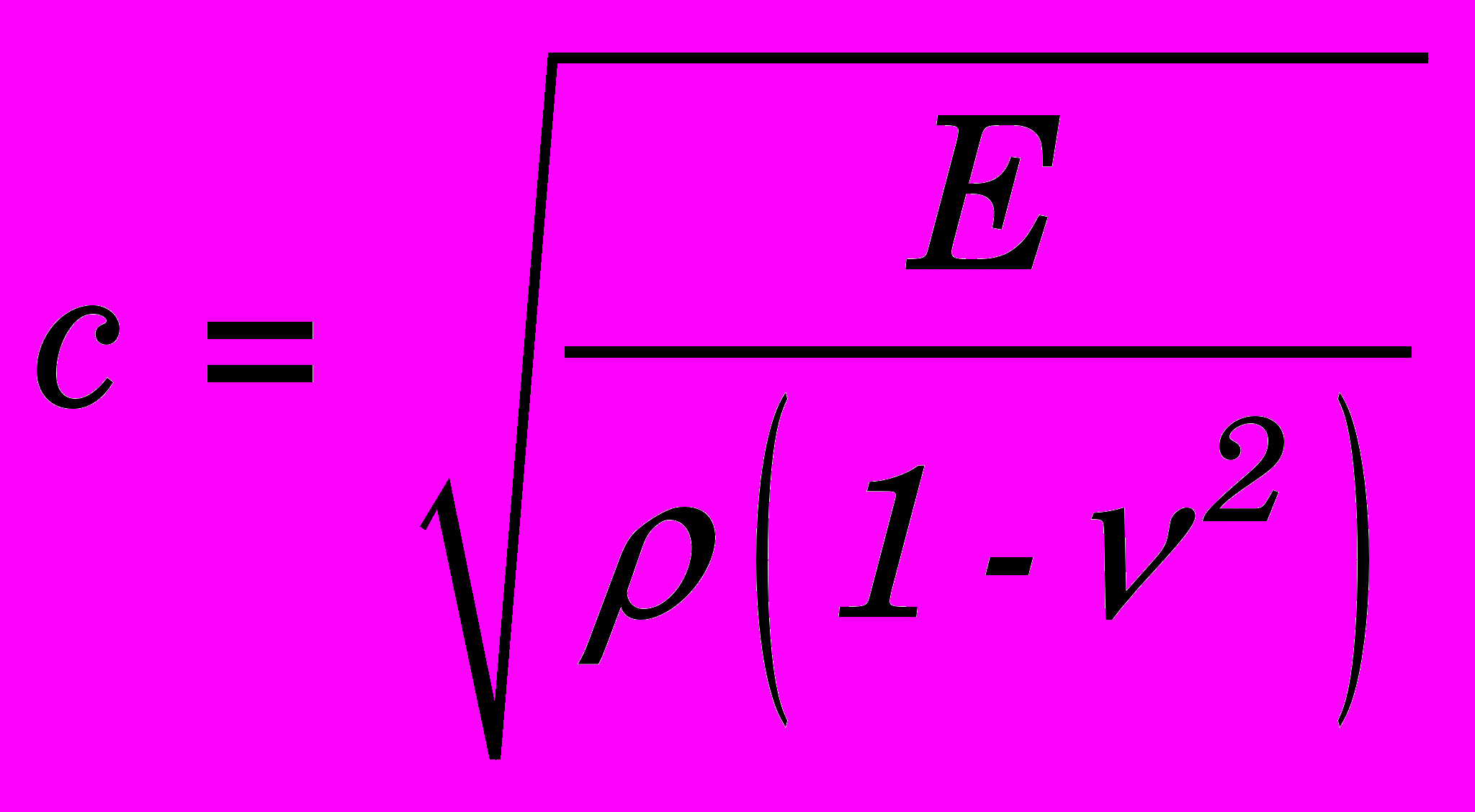

– скорость плоской звуковой волны в материале;

- характерный размер КЭ.

Практическая реализация модели в данной работе осуществлена с помощью линейных четырехугольных конечных элементов. В случае решения задачи с явной дискретизацией по времени эти КЭ обеспечивают хорошую сходимость по сравнению с треугольными и большую скорость вычислений по сравнению с четырехугольными КЭ высших порядков (рис. 4).

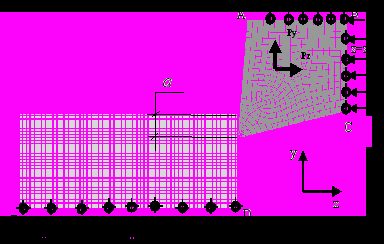
Рисунок 4 – Граничные условия и нагрузки

Выполнялось сгущение КЭ сетки инструмента в области режущей кромки, причем так, чтобы минимальный размер любого элемента был не меньше размера элемента в заготовке. Для обеспечения максимальной скорости решения в заготовке генерировалась равномерная КЭ-сетка. Граничные условия в данном случае были заданы закреплением основания заготовки в направлении оси y и z, а также закреплением границы инструмента в направлении оси у. Перемещение инструмента относительно заготовки было задано перемещением с постоянной скоростью правой (по схеме) границы инструмента. Начальные условия были заданы в виде постоянной комнатной температуры по всему объему инструмента и заготовки, а также нулевыми скоростями всех узлов.

Рассмотрим реализацию модели для случая резания стали 45 твердостью 196±5НВ инструментом из твердых сплавов K68 и KC9010 корпорации KENAMETAL. Задний угол лезвия 10, радиус округления режущей кромки – 0.02мм, величина фаски износа – 0 мм.

Механические свойства инструментального материала [147 11]: E=580 ГПа, =0.3,  = 11200 кг/м³. Механические свойства обрабатываемого материала [1058 12, 1082 13]: E=200 ГПа, =0.3,  = 7850 кг/м³, A=553.1 МПа, B=600.8 МПа, n=0.234, C=0.0134, m=1, D₁=1.5, D₂=3.44, D₃=-2.12, D₄=0, D5=0.

В качестве первого приближения примем по рекомендации работы [1031 14] такие параметры модели трения: =0.1, _max = 0.6_S = 0.6_S/

=
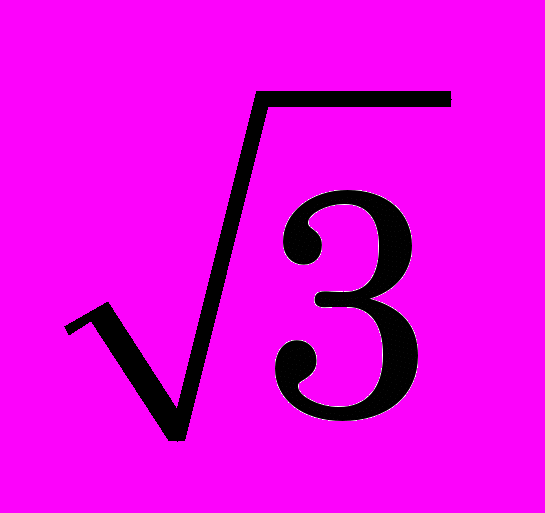=400 МПа, где _S принято равным 1150 МПа.

Экспериментальные данные о силе резания и других показателях процесса представлены в работе [1091 15].

Анимация процесса образования стружки при прерывистом резании, полученная в результате расчета модели из 5634 узлов и 4986 элементов представлена на рис. 6. Видно наличие области сдвига, локализованной в узкой области. Также наблюдаются распространение пластических деформаций под обработанную поверхность, завивание стружки и образование заусенца. Таким образом, данная картина качественно соответствует наблюдаемой в эксперименте.

Рисунок 5 – Влияние величины фаски износа на проекции силы резания

К

оличественное сравнение результатов моделирования с экспериментом представлено в таблице 2. Видно, что расхождение проекции Pz с экспериментом редко превышает 20%, в то время как расхождение в проекции Py значительно больше 20%. Видно также, что коэффициент утолщения стружки К_а также занижен, причем чем меньше скорость, тем больше. Такая ситуация может быть обусловлена, по мнению авторов, двумя причинами: априорным выбором параметров модели трения и неточным определением силы на задней поверхности.

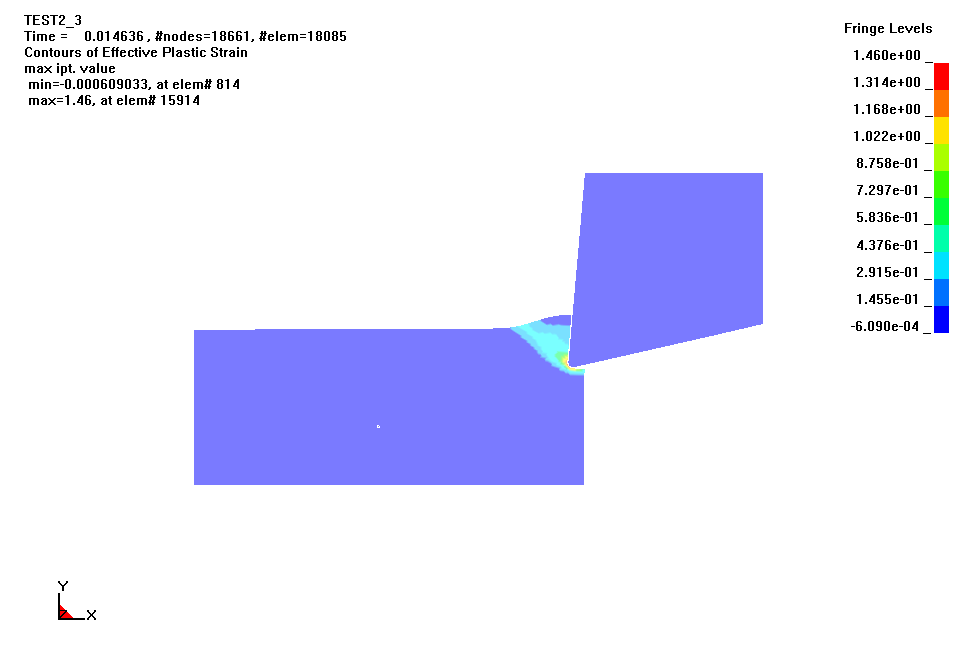
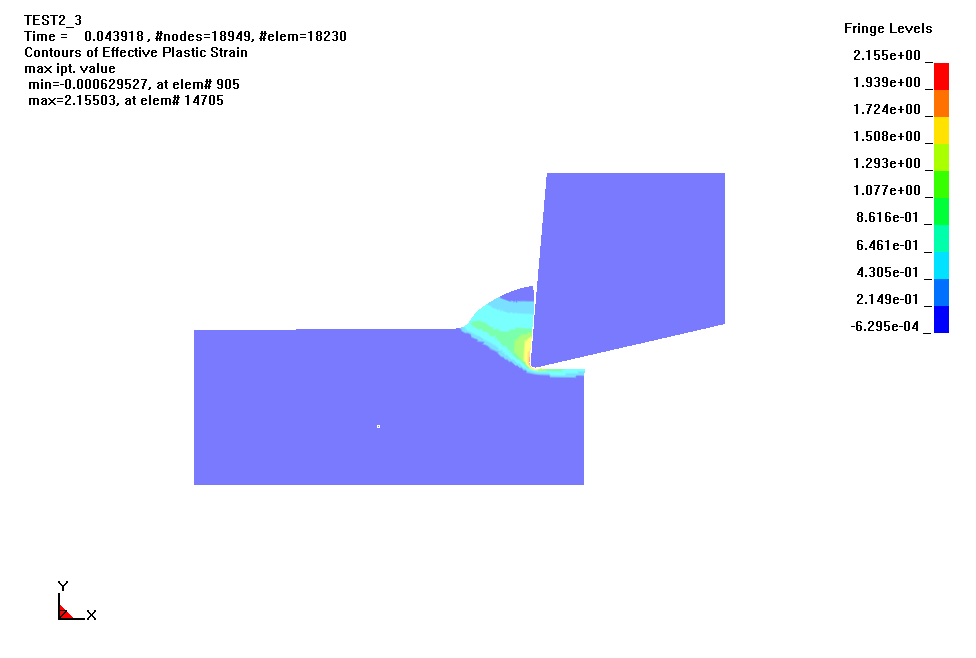
t=0.015 c. t=0.044 c. t=0.086 c.

Y

Z

0.5 мм

t=0.148 c. t=0.211 c. t=0.251 c.

Рисунок 6 - Процесс образования стружки при резании стали 45 инструментом твердого сплава со скоростью резания

V = 300 м/мин и толщиной среза a = 0.150 мм

Параметры трения  = 0.1, _max = 400 МПа. Геометрия лезвия:  = 5, =13, =0.02 мм

Таблица 2–Результаты экспериментальной проверки разработанной модели

№ п/п	V, м/мин	S, мм/об	, 	C_l, мм	К_a			Pz, Н				Py, Н
					Эксп.	КЭ	Ошибка, %	Эксп.	КЭ	Ошибка, %		Эксп.	КЭ	Ошибка, %
5	200	0,15	-7	0,27	3,15	2,05	-35	621±10	504±40		19	500±10	201±17	59,8
					2,6		-21	587±10			14	444±21		54,7
1		0,15	5	0,21	2,72	1,9	-30	561±45	416±16		26	383±37	76±20	80
					2,6		-27	519±36			20	334±31		77,24
6		0,30	-7	0,57	2,3	2,1	-9	1048±100	1012±28		3,4	680±89	352±32	48,23
					2,4		-13	1058±50			4,35	669±60		47,38
3		0,30	5	0,435	2,4	1,9	-21	940±55	832±16		11,5	473±57	106±26	77,6
					2,2		-14	875±92			4,9	430±55		75,3
7	300	0,15	-7	0,26	3,6	2,1	-42	596±74	508±20		14,7	452±72	184±16	59,3
					2,5		-16	534±39			4,8	377±38		51,2
2		0,15	5	0,22	2,6	1,9	-27	536±14	420±12		21,6	324±16	80±20	74,2
					2,2		-14	500±15			16	294±16		75,3
8		0,30	-7	0,58	2,3	2,1	-9	1029±14	1008±32		2	618±13	288±32	53,4
					2,2		-5	961±46			-4,89	538±53		46,5
4		0,30	5	0,44	2,3	1,9	-18	877±61	880±160		-0,34	400±50	70±34	82,5
					2,05		-7	847±30			-3,89	370±21		81

Примечания: 1 Верхнее значение приведено для инструментального материала K68, нижнее - для KC9010

2 С₁– длина контакта на передней поверхности

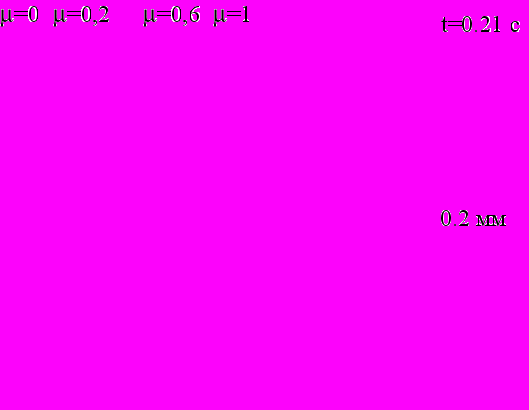
Действительно, проведенные расчеты показали, что увеличение фаски износа на задней поверхности приводит к существенному увеличению проекции Py (рис. 6), а изменение коэффициента трения значительно изменяет форму и размеры стружки (рис. 7).

Рисунок 7 - Влияние параметров коэффициента трения на форму и размеры стружки:  = 5, V = 300 м/мин, a= 0.150 мм

Поэтому прогнозирование истинных значений силы на задней поверхности и параметров модели трения, отвечающих сложившимся в зоне стружкообразования термомеханическим условиям, является необходимым для получения адекватной конечно-элементной модели процесса резания.

SUMMARY

In article explicit finite element model of orthogonal cutting is described. It is shown, that the greatest error of prediction with the aim of the given model is observed in cutting force projection Py and caused by an aprioristic choice of friction model parameters and the inexact account of force on a tool clearance face.

Список литературы

Kalhori V. Modeling and simulation of mechanical cutting: Doctoral thesis. -Lulea: Lulea university of technology, 2001. -103 c.
Залога В. А., Криворучко Д. В. Классификация факторов, определяющих нестационарность процессов резания, и их влияние на выходные параметры механической обработки//Вестник ХГПУ: Серия НРСТ. -Харьков: ХГТУ, 2000. -Вып. 77. -C. 35- 38.
Bil H. , Tekkaya A. E., Kılıç E. S. Finite Element Modeling of Machining: A Comparison of Different Approaches with Experiments//Proceedings of the 7th CIRP International Workshop on Modeling of Machining Operations. -2004.
Marusich T. D., Ortiz M. Modelling and Simulation of High-Speed Machining//Int. J. Num. Meth. Eng. -1995. -Т. 38. -C. 3675- 3694.
Hallquist J. O. LS-DYNA Theoretical manual. -Livermore: LSTC, 1998. -498 c.
Развитие науки о резании металлов/Н. Н. Зорев, Г. И. Грановский, М. Н. Ларин и др. -М.: Машиностроение, 1967. -415 c.
Розенберг А. М., Розенберг О. А. Механика пластического деформирования в процессах резания и деформирующего протягивания. -К.: Наукова думка, 1990. -320 c.
Залога В. А., Криворучко Д. В. Обзор способов экспериментального определения параметров уравнения состояния пластических материалов для моделирования методом конечных элементов их механической обработки//Резание и инструмент в технологических системах. -2005. -№ 69. -C. 193- 202.
Johnson G. R., Cook W. H. A Constitutive Model and Data for Metals Subjected to Large Strains, High Strain Rates and High Temperatures//Proceedings of the 7th int. Symp. on Ballistics. -1983. -C. 541- 547.
Johnson G. R., Cook W. H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures//Engng Fracture Mechanics. -1985. -C. 31- 48.
Резников А. Н., Резников Л. А. Тепловые процессы в технологических системах. -М.: Машиностроение, 1990. -288 c.
Adibi-Sedeh A. H., Vaziri M. , Pednekar V. и др.и др. Investigation of the Effect of Using Different Material Models on Finite Element Simulations of Machining//Proceedings of the 8th CIRP International Workshop on Modeling of Machining Operations. -2005. -C. 215- 224.
Jaspers S. P., Dautzenberg J. H. Material behavior in conditions similar to metal cutting: ﬂow stress in the primary shear zone//Journal of Material Processing Technology. -2002. -Т. 122. -C. 322- 330.
Sartkulvanich P. , Altan T. , Göcmen A. Effects of flow stress and friction models in finite element simulation of orthogonal cutting — A sensitivity analysis//Machining Science and Technology. -2005. -№ 9. -C. 1- 26.
Ivester R. W., Kennedy M. , Davies M. A. Assessment of Machining Models: Progress Report//www.mel.nist.gov/div822/amm. -Gaithersburg: National Institute of Standard and Metrology, 2000.

Поступила в редакцию 5 декабря 2005 г.

Blog

С. Н. Хвостик Сумский государственный университет

Содержание