Суть метода координат

Вид материала

Документы

Содержание Этапы решения задач методом координат

Подобный материал:

• Программа курса лекций (4 курс, 8 сем., 32 ч., экзамен) Профессор, д ф. м н., Лариса, 14.31kb.
• Задача 2, 24.83kb.
• Ії приймання навігаційної інформації, обчислювання координат супутників, обчислювання, 175.51kb.
• Лекция 4 аксонометрические проекции. Многогранные и кривые поверхности, 219.26kb.
• Положение камеры Преобразования, определяющие положение и ориентацию объекта в мировой, 105.74kb.
• Урок лекция по геометрии в 10 классе по теме «Декартовы координаты в пространстве», 53.59kb.
• Программа курса «Общая физика. Механика», 33.84kb.
• Тема: Карти. Атласи. Визначення географічних координат, 313.96kb.
• Урок-подорож, 108.55kb.
• Суть метода, 280.38kb.

Суть метода координат


Сущность метода координат как метода решения задач состоит в том, что, задавая фигуры уравнениями и выражая в координатах различные геометрические соотношения, мы можем решать геометрическую задачу средствами алгебры.

Метод координат – это универсальный метод. Он обеспечивает тесную связь между алгеброй и геометрией, которые, соединяясь, дают «богатые плоды», какие они не могли бы дать, оставаясь разделенными.

В некоторых случаях метод координат дает возможность строить доказательства и решать многие задачи более рационально, красиво, чем чисто геометрическими способами.

Этапы решения задач методом координат

Чтобы решать задачи методом координат необходимо выполнение 3 этапов:

I – перевод задачи на координатный (аналитический) язык;

II – преобразование аналитического выражения;

III – обратный перевод, т. е. перевод с координатного языка на язык, в терминах которого сформулирована задача.


Задача. В треугольнике ABC: AC=b, AB=c, ВС=а, BD - медиана. Докажите, что .

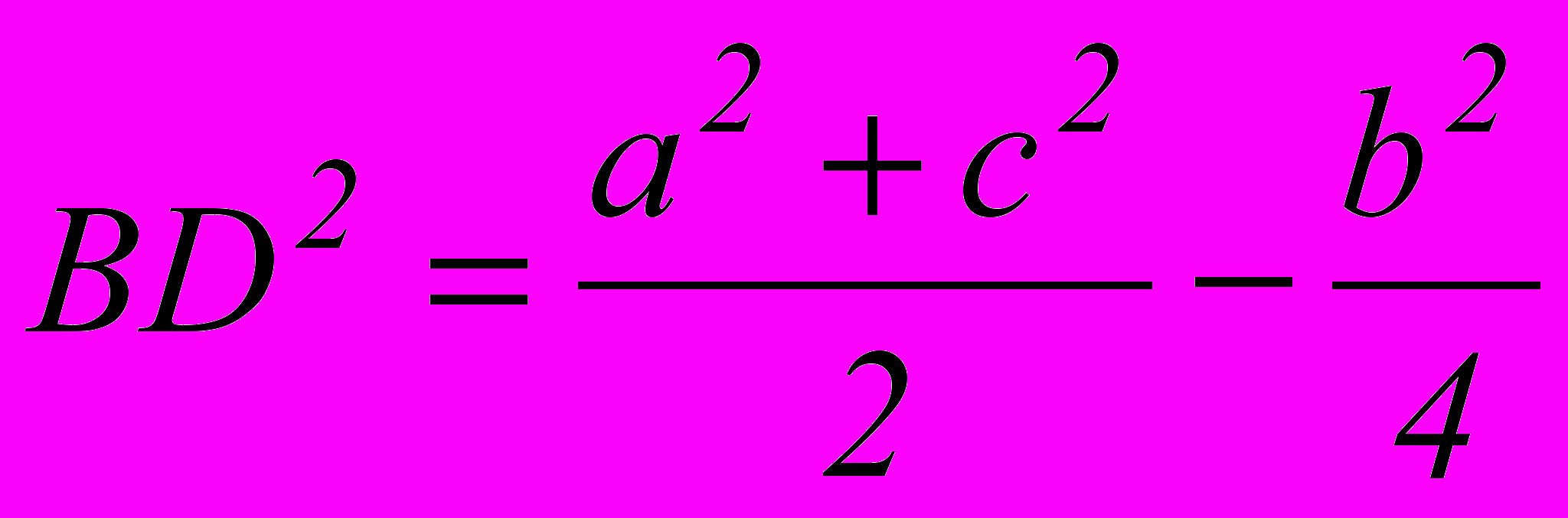I этап.

Выберем систему координат так, чтобы точка А служила началом координат, а осью Ох - прямая АС (рис.).

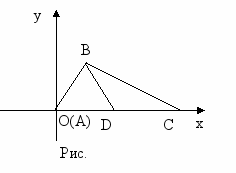(!!! Важно оптимально выбирать систему координат, т. е. так, чтобы наиболее просто находить координаты данных точек).

В выбранной системе координат точки А, С и D имеют следующие координаты: А(0,0), D(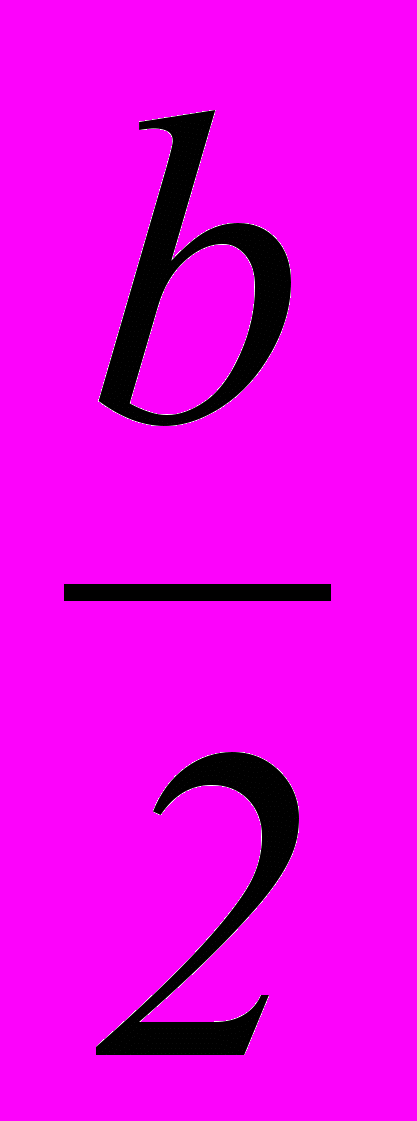,0) и С(b,0).

II этап.

Обозначим координаты точки В через х и у. Тогда используя формулу для нахождения расстояний между двумя точками, заданными своими координатами, получаем:

с²= х²+у², a²= (x-b)²+y². (1)

По той же формуле 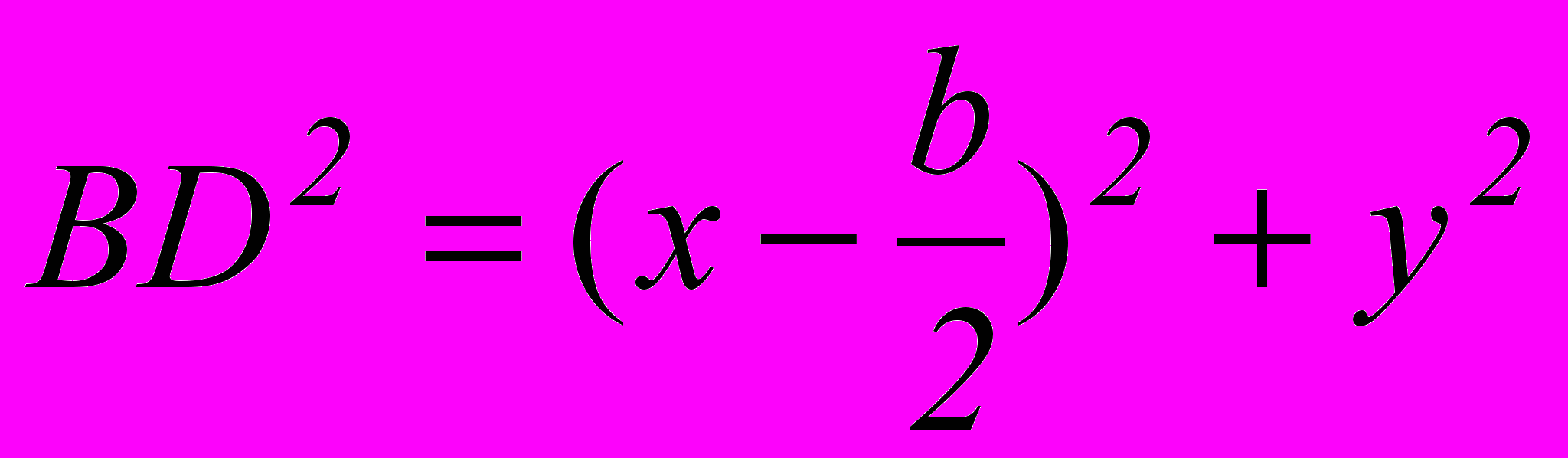. (2)

Решив систему уравнений (1), найдем х и у:

; .

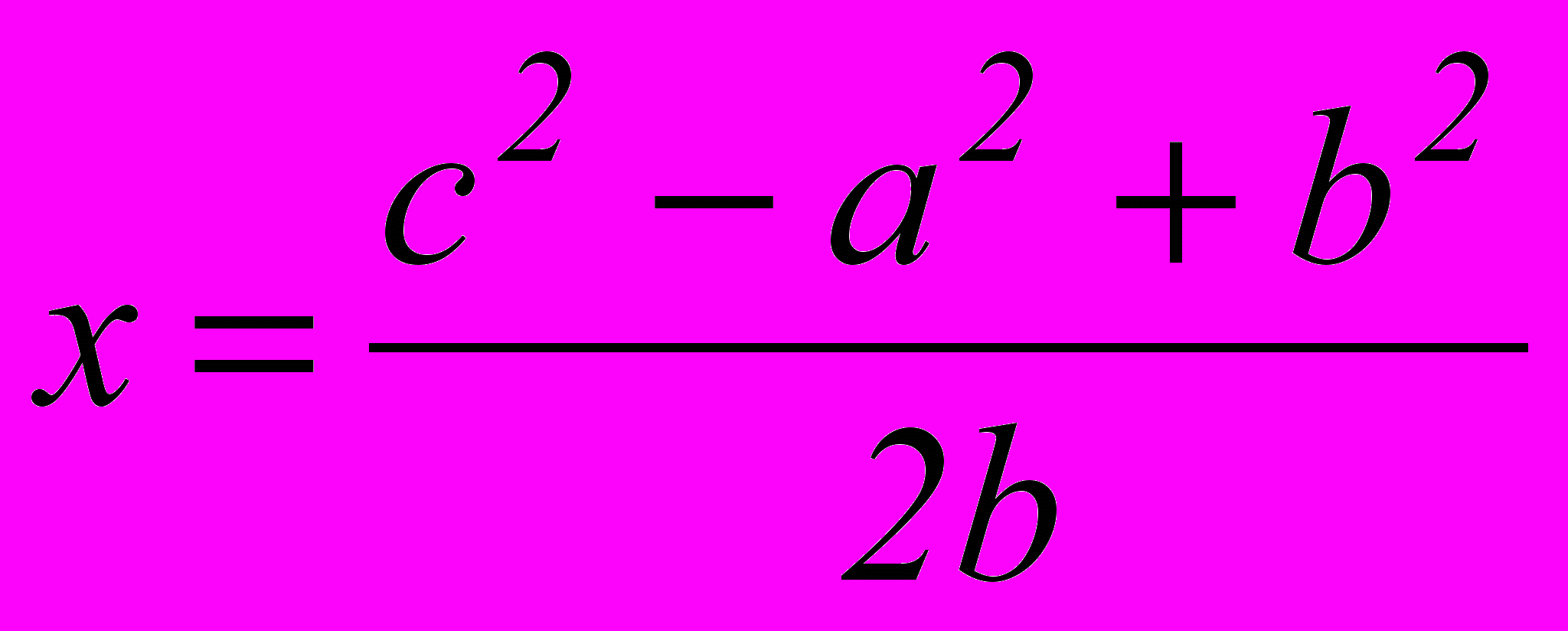Подставляя результат в формулу (2), получаем: .

.
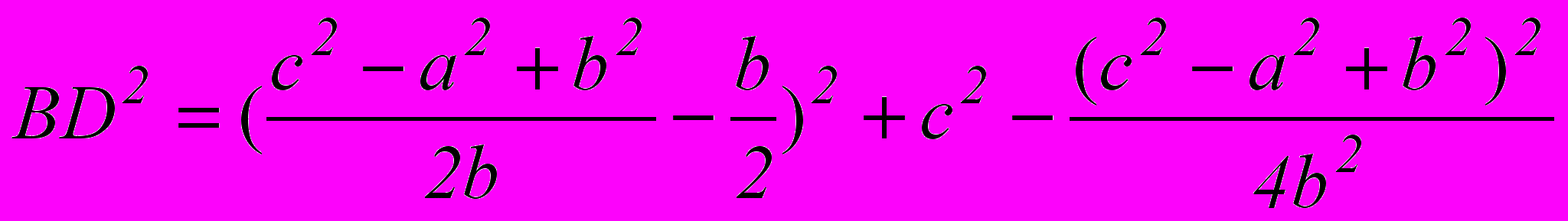