Задача 2

Вид материала

Задача

Содержание Совет: потребуются формулы двойного аргумента из тригонометрии) R – радиус описанной окружности, r

Подобный материал:

• Программа курса лекций «Математические методы и модели исследования операций», 27.98kb.
• Т. М. Боровська кандидат технічних наук, доцент І. С. Колесник, 118.17kb.
• Разновозрастная итоговая проектная задача 1-4 классы, 87.27kb.
• Программа дисциплины Алгоритмы на графах Семестр, 13.21kb.
• Гиперкомплексных Динамических Систем (гдс) задача, 214.67kb.
• Домашнее задание по Теории информационных процессов и систем, 267.24kb.
• Задача линейного программирования Задача о «расшивке узких мест», 5.51kb.
• Программа учебной дисциплины вариационные методы в физике (спецкурс, дисциплины, 147.31kb.
• Варианты контрольных работ контрольная работа №1 (3 семестр), 237.84kb.
• Ручаевского Дмитрия Александровича. Карасик Л. В 1997-98 уч год. Основная часть Античная, 202.33kb.

Применение скалярного произведения векторов и метода координат к доказательству геометрических и алгебраических неравенств и решению уравнений.


При решении и исследовании задач арифметики, алгебры, анализа и геометрии нередко приходится рассматривать неравенства и из системы, применять свойства неравенств.


Данная исследовательская работа ставит своей целью рассмотреть случаи применения скалярное произведение векторов для решения задач, в условии которых про векторы речи нет и их надо ввести.


Этап I

Доказательство геометрических неравенств


Задание 1. Рассмотреть понятие скалярного произведения векторов и его свойства.

Для каких векторов верно равенство ?

А такое: ?


Задача 2. Для треугольника АВС оценить сумму: соsA + cosB + cosC. (Совет: помни тему работы, введи векторы и примени свойства скалярного произведения векторов)


Задача 3. Доказать, что для любого треугольника АВС имеют место неравенства , , где R радиус описанной окружности.


Задание 4. Выведи неравенство, похожее на неравенство задачи 2, но для четырехугольника. Может попробовать задействовать и углы между прямыми, содержащими противоположные стороны четырехугольника?


Задание 5. А если в сумме (задача 3) одно из слагаемых взять со знаком "-"?? А теперь в сумме рассмотреть два слагаемых со знаком "-"? ( Совет: потребуются формулы двойного аргумента из тригонометрии)


Задание 6. Доказать, что для любого треугольника АВС выполняется неравенство , где R – радиус описанной окружности, r- радиус вписанной окружности.(Совет: вероятно потребуются теоремы косинусов, синусов, формулы площадей треугольника через радиусы вписанной и описанной окружностей)

Этап II

Решение алгебраических уравнений и неравенств.

Теперь рассмотрим способы решения иррациональные уравнения и неравенства, которые стандартными способами не решаются, либо решения этих уравнений очень сложны.

Взглянув на части уравнения или неравенства как на длины векторов или на скалярное произведение векторов, можно решить их используя геометрический смысл предложенной ситуации.


Задание 1 Рассмотри случаи выполнения неравенства .

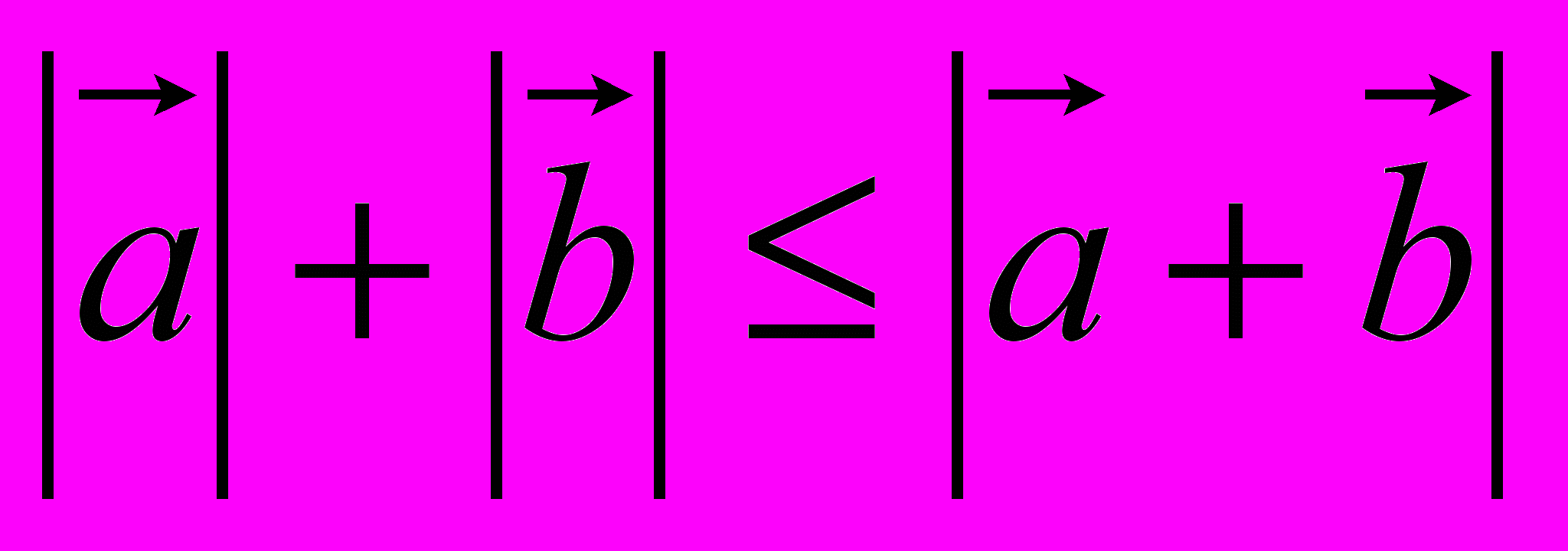Задание 2. Рассмотри условия выполнения этого неравенства

Задание 3. Примени полученные результаты для решения уравнений и неравенств:

1. .

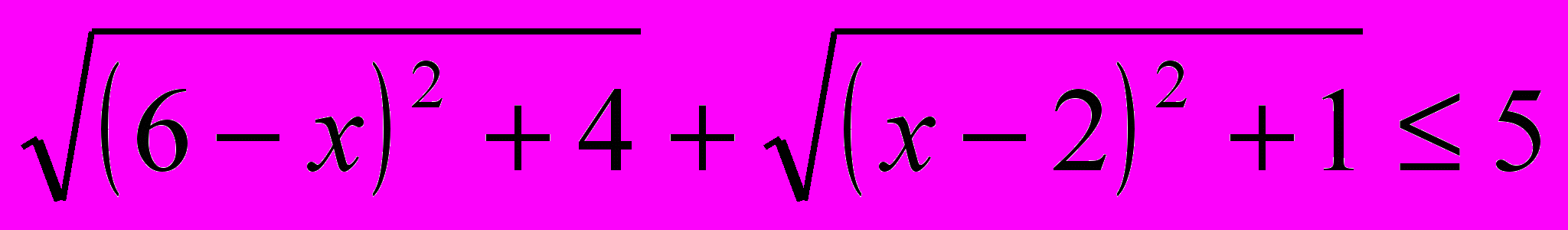2. ,

3. .

4. .

5. .


Задание 4. В этих задачах постарайся увидеть возможность применения т. Пифагора.

1. Доказать. Если , то .

2. Доказать. Если , то .


Задание 5. Составь свои уравнения и неравенства решение которых основано на рассмотренных геометрических фактах.


Этап III

Все изученное, доказанное и рассмотренное надо собрать в одном документе с рисунками и оформить в соответствии с требованиями к исследовательской работе.