Часть физики, которая изучает за­кономерности механического движения и причи­ны, вызывающие или изменяющие это движение

Вид материала

Документы

Содержание Средней путевой скоростью Свободным падением 3. Модуль вектора перемещения материальной точки, скорость которой изменяется по закону υ=2 - 2t (м/с), через 4 с

Подобный материал:

• Кинематика, 366.47kb.
• Домашнее задание по физики на 1 сессию 9 класс, 123.67kb.
• Методика изучения прямолинейного равномерного движения в курсе физики полной средней, 19.55kb.
• Тематическое планирование курса физики в 10 классе, 68.52kb.
• Урок решения задач по теме «Относительность механического движения», 28.22kb.
• Момент количества движения системы, 47.81kb.
• Возрастная психология развивающаяся отрасль психологической науки, 966.39kb.
• Повторительно-обобщающий курс, 864.61kb.
• Конспект урока физики Тема: Механическое движение и его виды, 84.19kb.
• 1. Предмет макроэкономики. Методы и принципы макроэкономического анализа, 799.49kb.

Механическое движение.

Механика - часть физики, которая изучает за­кономерности механического движения и причи­ны, вызывающие или изменяющие это движение.

Механическим называется движение, при кото­ром изменяется взаимное расположение тел (или частей тел) друг относительно друга.

Механика Галилея-Ньютона называется клас­сической механикой. В ней изучаются законы дви­жения макроскопических тел, скорости которых малы по сравнению со скоростью света в вакууме. Законы движения макроскопических тел со скоро­стями, сравнимыми со скоростью света в вакууме, изучаются релятивистской механикой, основанной на специальной теории относительности, сформу­лированной А. Эйнштейном в 1905 г. Для описания движения микроскопических тел (отдельных ато­мов и элементарных частиц) законы классической механики неприменимы - они заменяются закона­ми квантовой механики.

Классическая механика делится на три раздела: 1) кинематику; 2) динамику; 3) статику.

Кинематика изучает движение тел, не рассмат­ривая причины, вызвавшие это движение.

Динамика изучает законы движения тел и причины, которые вызывают или изменяют это дви­жение. Статика изучает условия равновесия тел.

Материальной точкой называется тело, линей­ными размерами которого в данной задаче можно пренебречь.

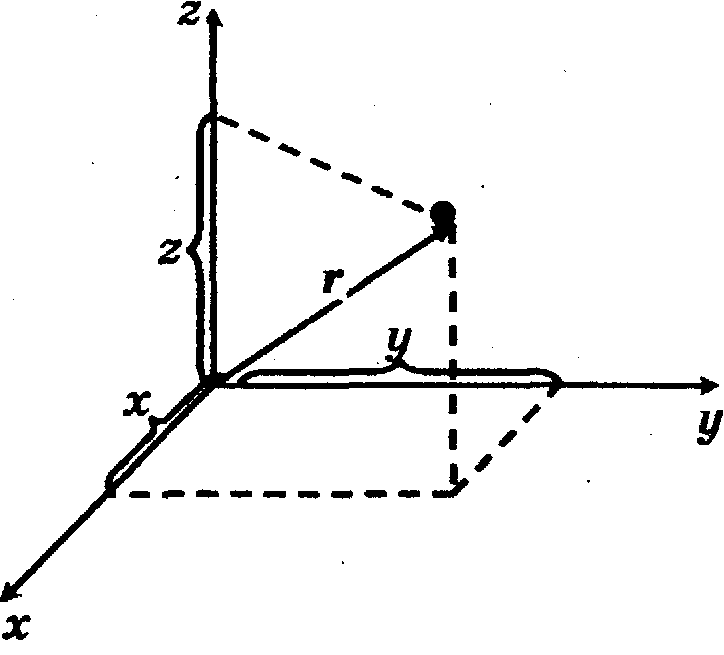
Системой отсчета называется система коорди­нат, жестко связанная с телом отсчета и с введен­ным в нее определенным масштабом времени. По­ложение материальной точки в пространстве при этом определяется радиусом - вектором г . r = xi + yj + zk, где х, у, z - координаты материальной точки (про­екции радиуса - вектора г на оси координат); i, j,k - единичные вектора, направление которых со­впадает с выбранным направлением соответствую­щих осей системы координат, а модули которых равны единице. Тогда движение материальной точки определя­ется тремя скалярными уравнениями

x = x(t). y = y(t)_t z = z(t), или одним эквивалентным векторным уравнением r = r(t).

Эти уравнения называ­ются кинематическими уравнениями движения материальной точки.

Поступательным называется такое движение, при котором любая прямая, проведенная через

тело, перемещается параллельно самой себе.

Параметры кинематики поступательного движения

1. Перемещение .

Перемещением материальной точки называет­ся вектор, начало которого совпадает с начальным положением тела, а конец - с конечным .

2. Длина пути S.

Длиной пути S называется сумма длин всех уча­стков траектории, пройденных телом за рассмат­риваемый промежуток времени с начала отсчета времени. При прямолинейном движении вектор перемещения совпадает с соответствующим участ­ком траектории, и модуль перемещения || будет равен пройденному пути S. [S] - м.

3. Время t.

Время t - скалярная величина, характеризую­щая длительность и последовательность событий. [t] = c.

4. Скорость V.

4.1. Мгновенная скорость V.

Мгновенной скоростью V называется предел от­ношения перемещения к тому промежутку време­ни, в течение которого это перемещение произош­ло, при стремлении промежутка времени к нулю:Вектор мгновенной скорости направлен по ка­сательной к траектории в сторону движения. Физический смысл скорости: скорость Равномерным называется движение, при кото­ром тело за любые равные промежутки времени совершает равные перемещения. Для равномерно­го движения и

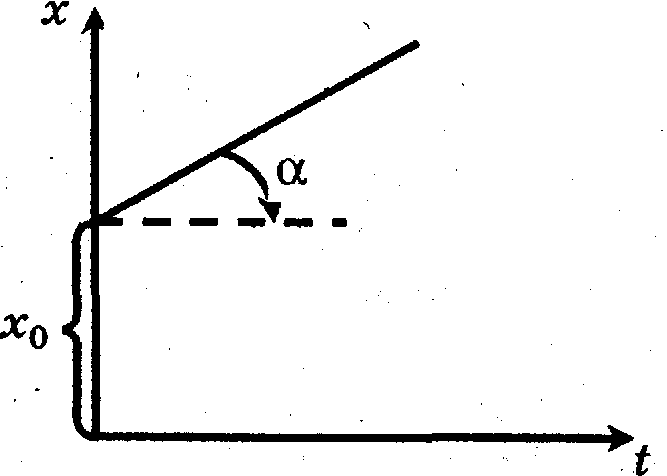
С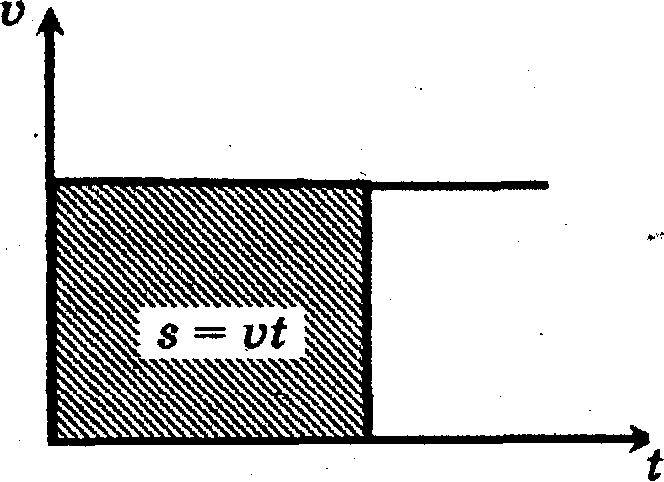ледовательно, при равномерном движении путь от времени зависит прямо пропорционально. В начальный момент времени пройденный путь "всегда равен нулю и с течением времени он может только увеличиваться . Координата же в начальный момент времени может быть и не рав­на нулю и с течением времени может как увеличиваться, так и уменьшаться (заходя даже в область отрицательных значений). Тангенс угла наклона графика зависимости пути от времени (или координаты от времени) к положительному направ­лению оси времени численно равен скорости.

Скорость при равномерном движении постоян­на, а площадь под графиком зависимости скорос­ти от времени численно равна пройденному пути .


4.2. Средняя скорость.

Средней скоростью перемещения называется физическая величина, равная отношения вектора перемещения точки к промежутку времени, в течение которого это перемещение про­изошло:

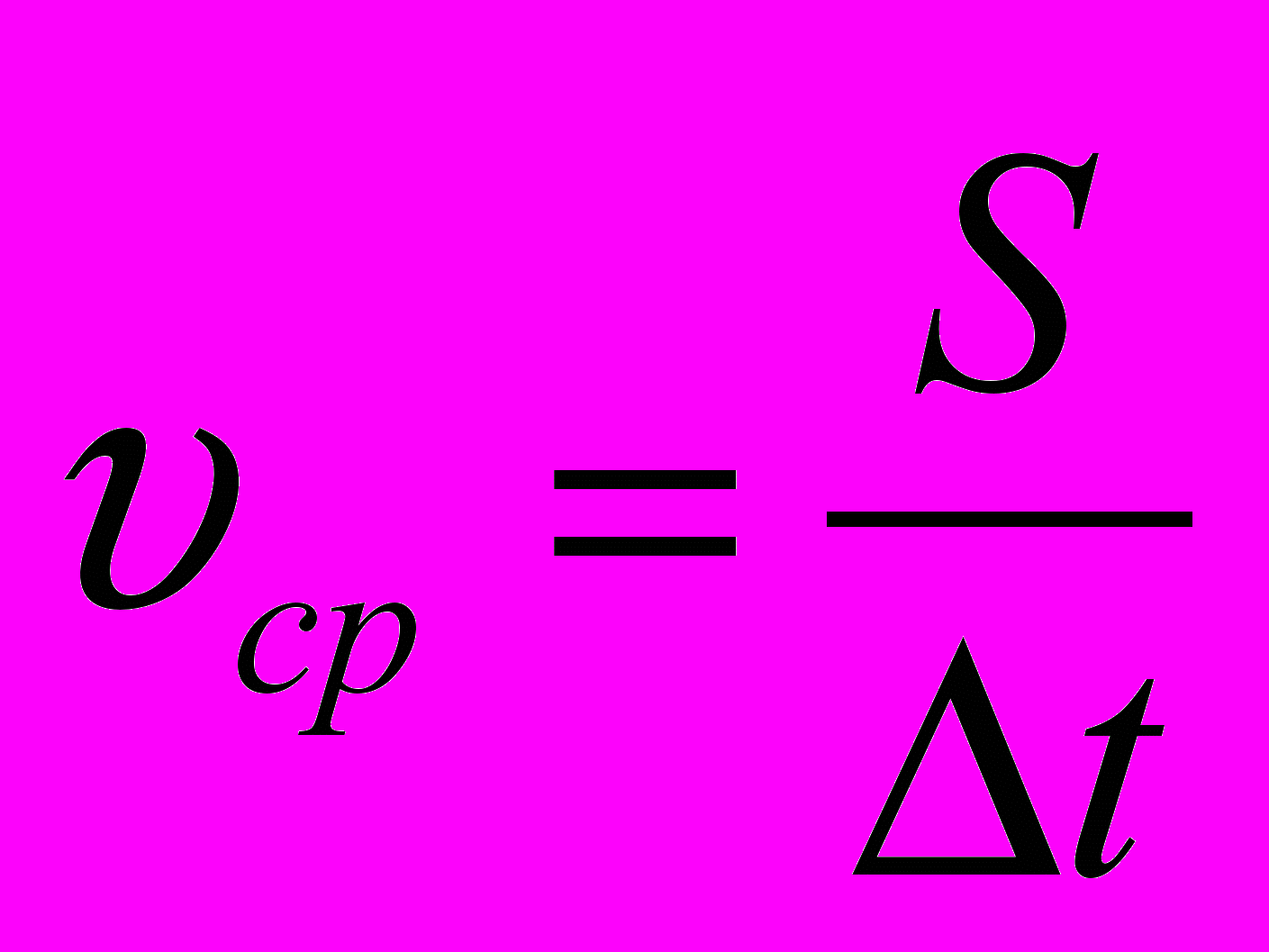
Направление вектора средней скорости совпада­ет с направлением вектора перемещения.

Средней путевой скоростью называется физи­ческая величина, равная отношению длины пройденного за данный промежуток времени пути к этому промежутку времени: Средняя путевая скорость всегда положитель­на. [ υ] = м/с.

5. Ускорение а.

Ускорением называется отношение изменения скорости к тому промежут­ку времени, в течение которого это изменение про­изошло: 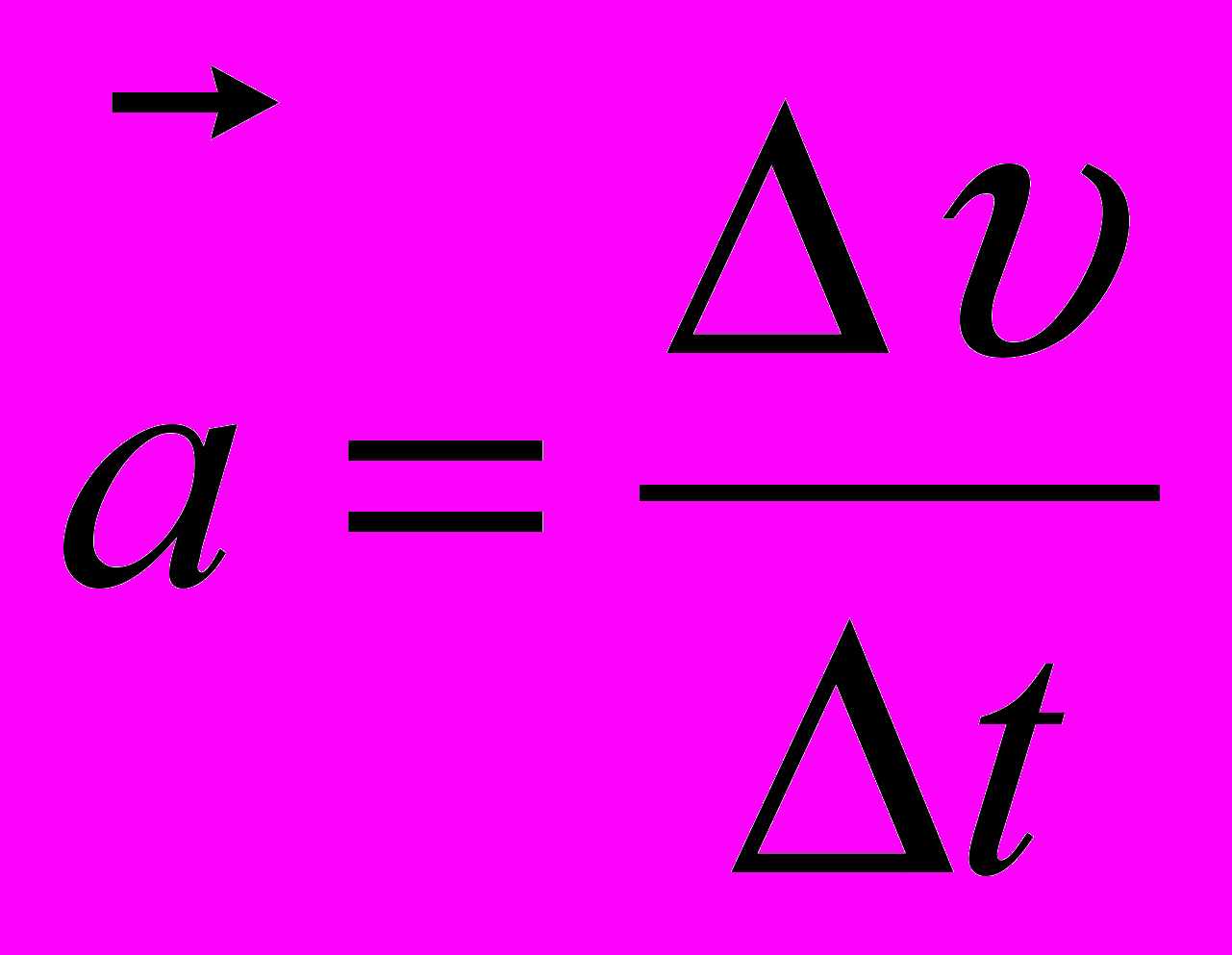; [а] = м/с².

Направлено ускорение всегда вдоль изменения скорости . Физичес­кий смысл ускорения: ускорение есть количественная характеристика (мера) быстроты изме­нения скорости.

Равнопеременным называется такое движение, при котором скорость тела за любые равные промежутки времени меня­ется одинаково. Для такого движения т. е. скорость от времени зависит прямо пропорци­онально, а пройденный путь и координа­та тела 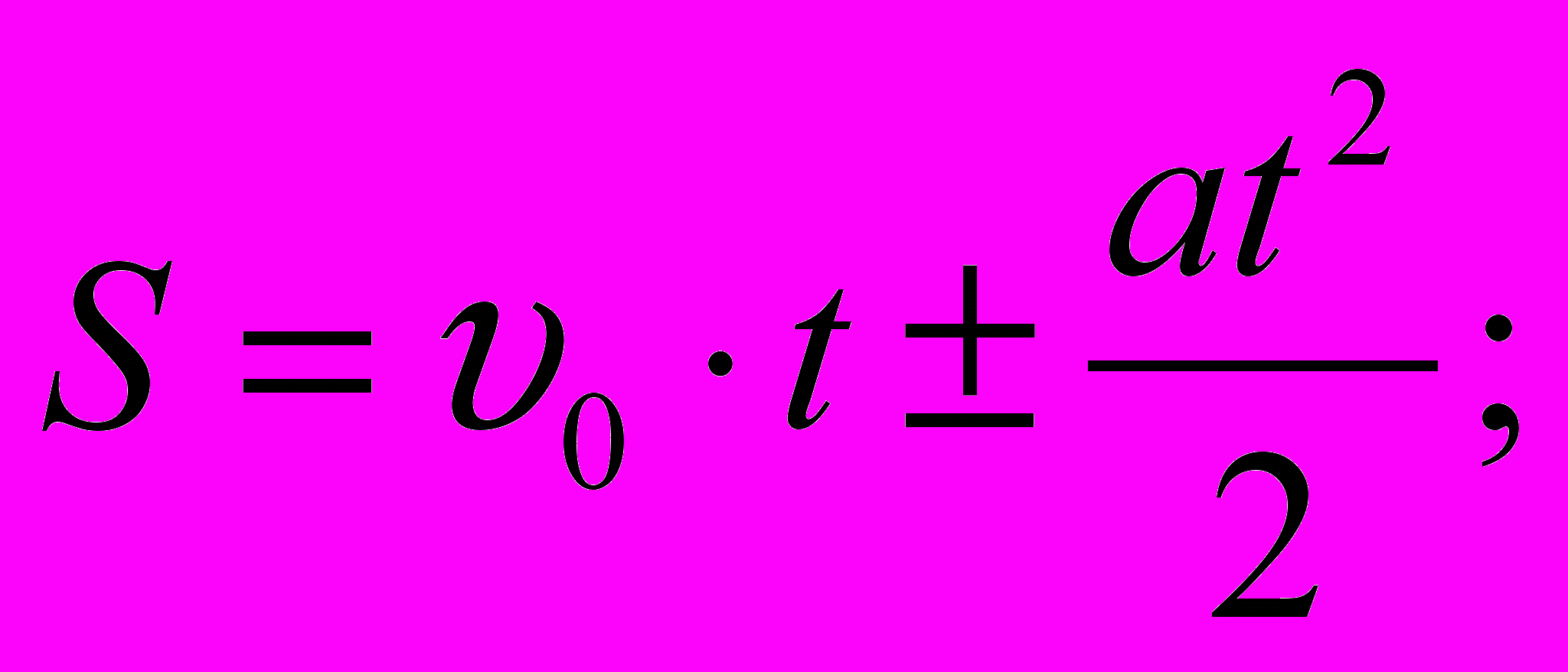на участках траектории, где движение равноуско­ренное, а > 0; на участках траектории, где движе­ние равнозамедленное, а < 0. Длина всего пути равна сумме длин всех участков траектории, прой­денных телом за рассматриваемый промежуток времени.



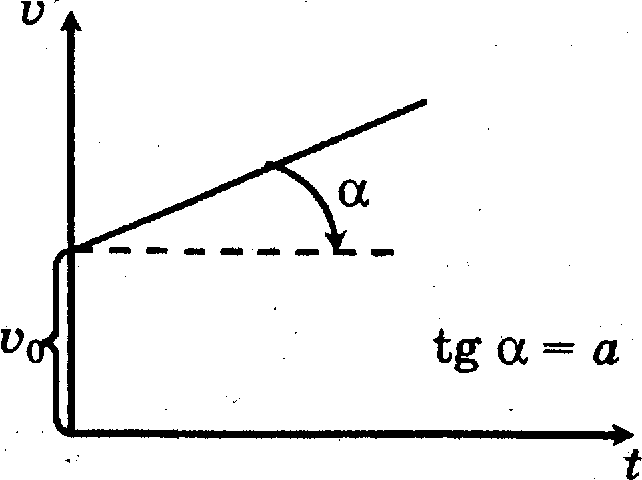
Это значит, что путь от времени при равнопере­менном движении зависит

квадратично . Тангенс угла наклона графика зависимости скоро­сти от

времени к положительному направлению оси времени численно равен

ускорению.

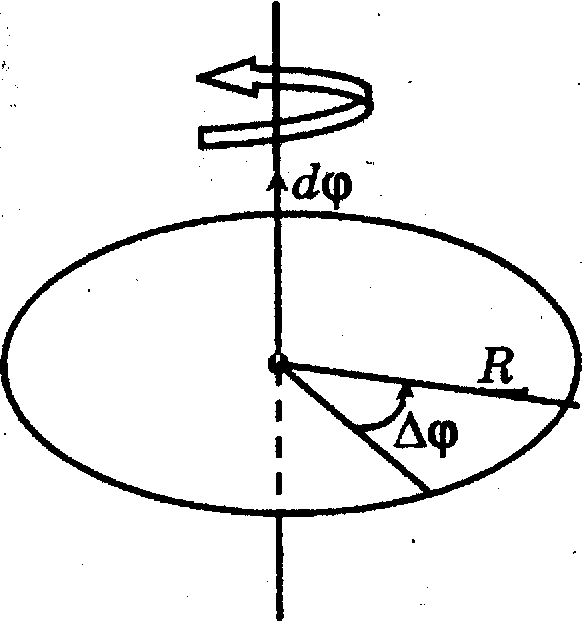
В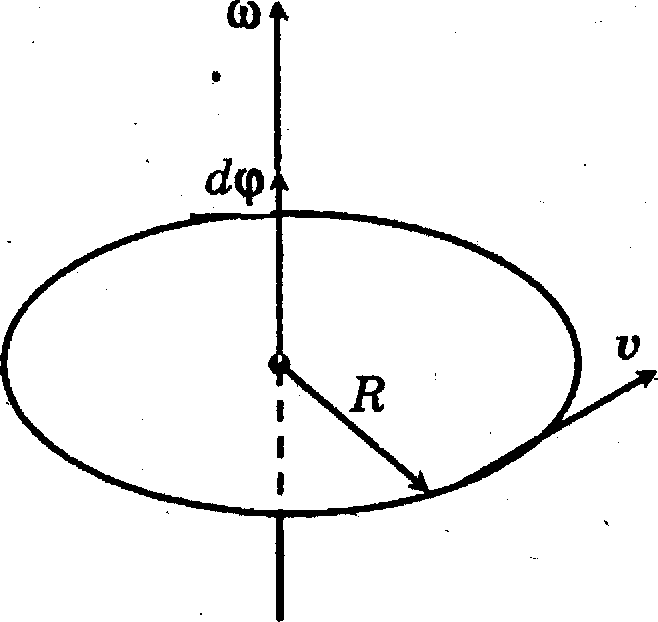ращательным называется такое движение, при котором все точки тела описывают окружно­сти, центры которых лежат на одной прямой. Эта прямая называется осью вращения. Равномерным движением по окружности называется движение с постоянной по модулю скоростью. При равномерном движении материальной точки по окружности радиус – вектор поворачивается за любые равные промежутки времени на равные углы . Угол поворота равен отношению длины дуги 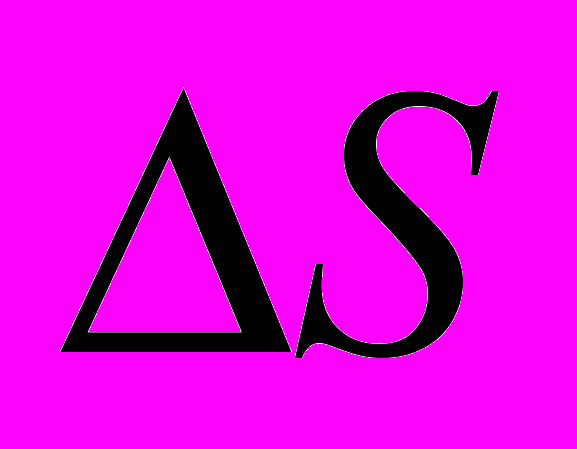, на которую он опирается, к радиусу окружности R: 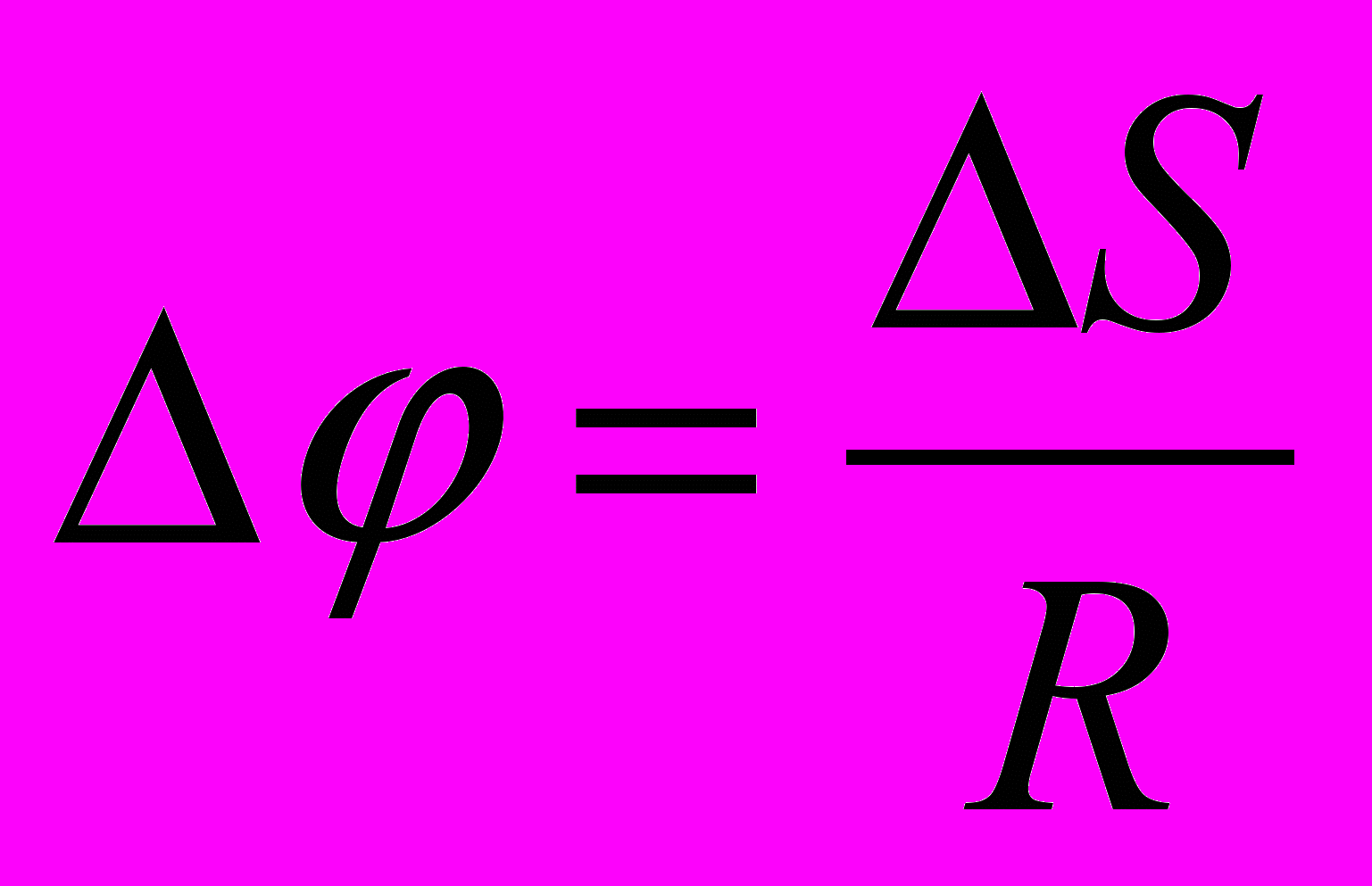. Угловой скоростью называется отноше­ние угла поворота к тому промежутку времени, в течение которого этот поворот произошел: .


Линей­ная скорость точки



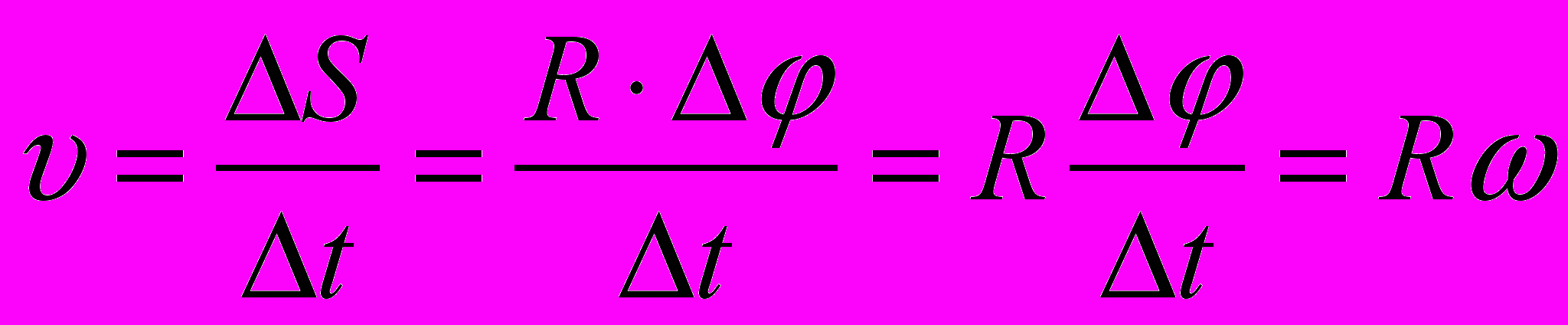
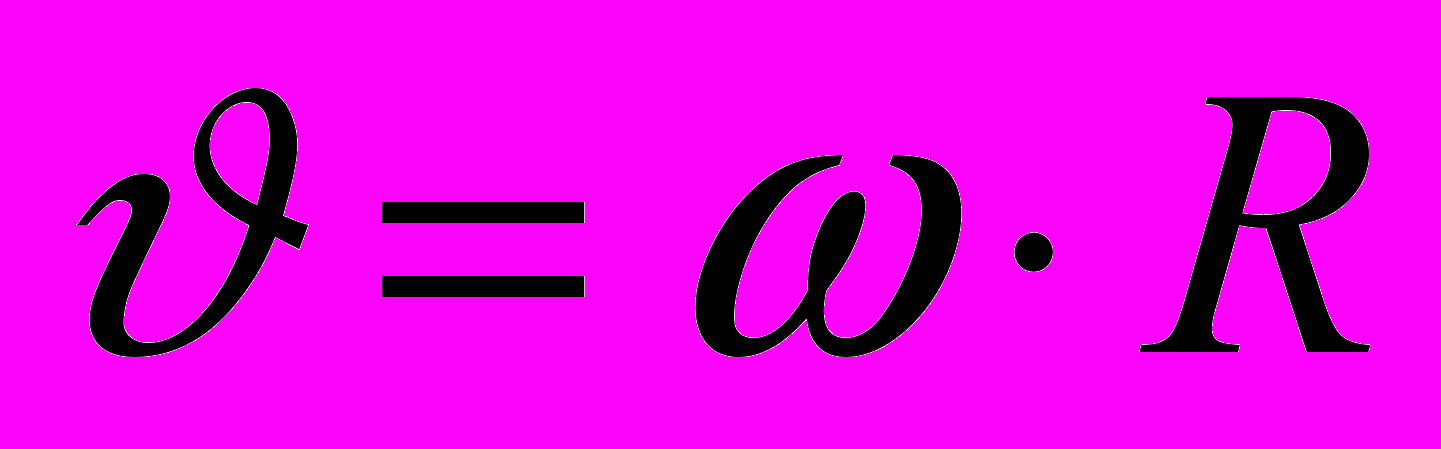
Если = const, то вращение равномерное, и его можно ха­рактеризовать периодом вращения Т - временем, за которое точка совершает один полный оборот, т. е. ее радиус - вектор поворачивается на угол 2π. Так как промежуток времени t = Т соответству­ет то , откуда

Т =. Частота равна числу полных оборотов в единицу времени : 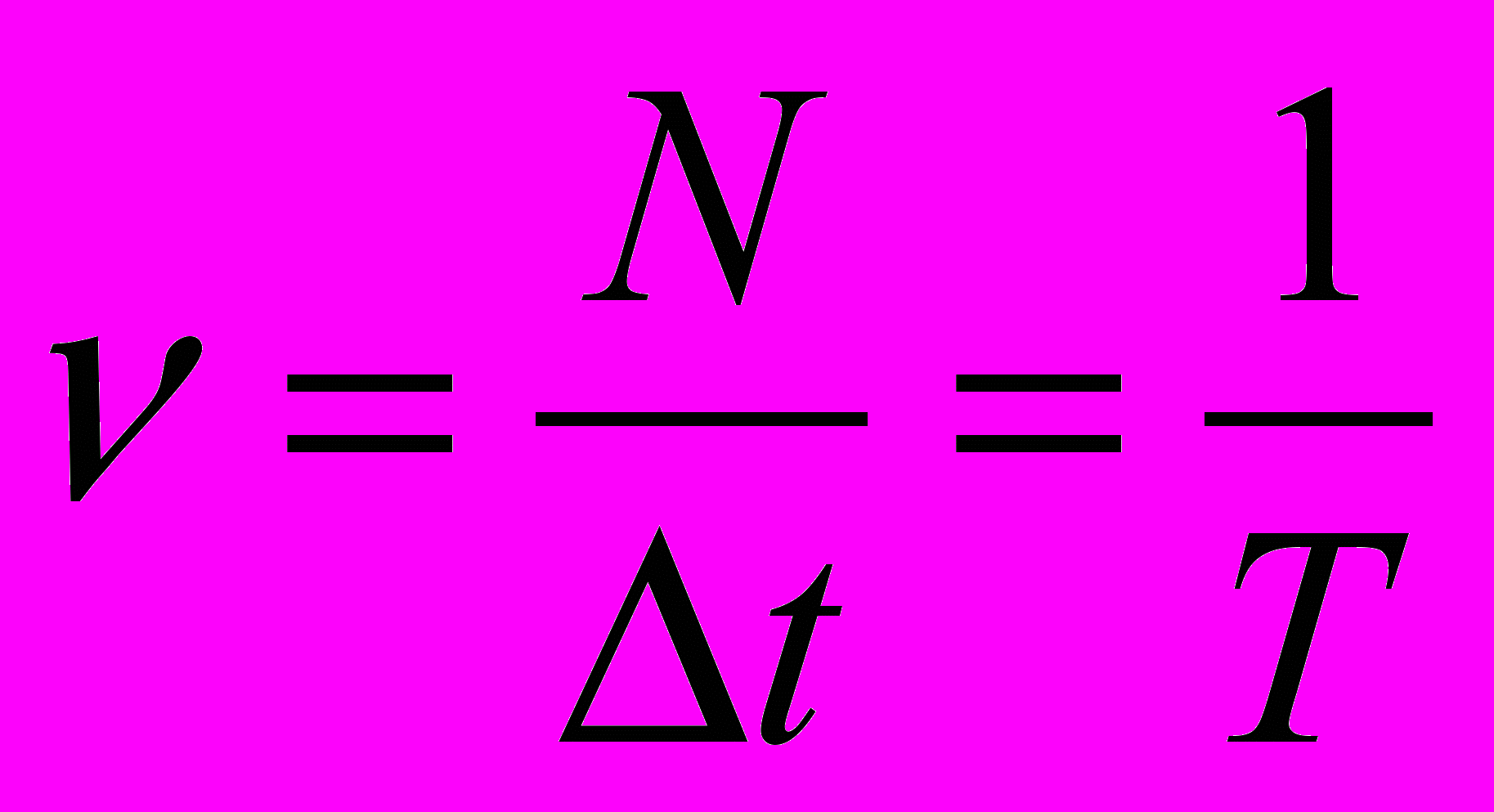, тогда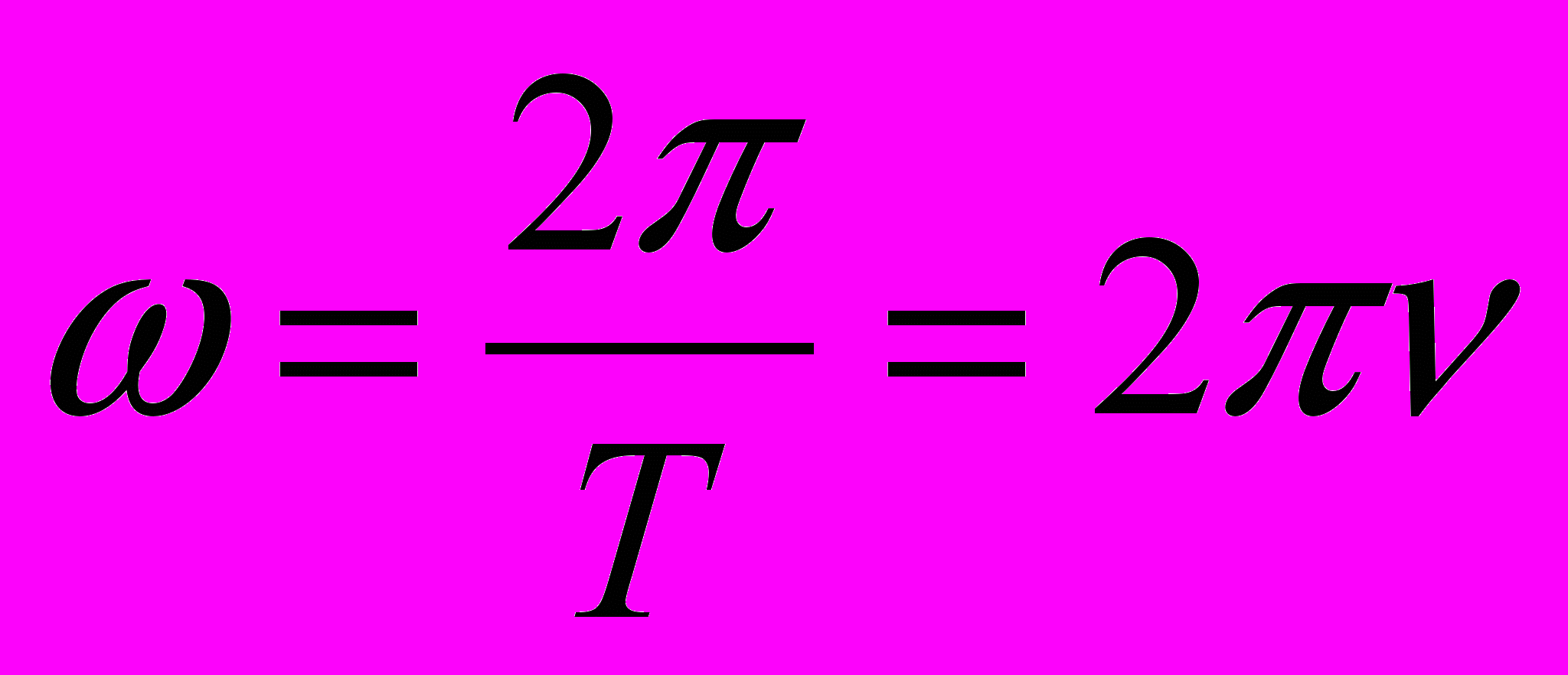

Движение по криволинейной траектории – всегда движение с переменным ускорением, отвечающим за изменение направления скорости. Это нормальное или центростремительное ускорение (направлено к центру окружности), численно равное:

Связь между линейными и угловы­ми величинами выражается следующими формулами:



Свободным падением - называется движение тела только под влиянием притяжения к Земле. Ускорение g, с которым движется вблизи поверхности Земли материальная точка, называется ускорением свободного падения. Оно не зависит от массы точки.


Примеры решения задач.

1.Модуль перемещения материальной точки, начавшей двигаться по окружности из точки А и совершившей за 2,5 с 2,5 полных оборота, равен: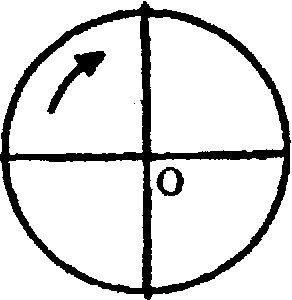

1) 5 R; 2) 2R; 3) 0; 4) R; 5) 2,5R

Совершив 2,5 полных оборо­та, материальная точка из точки А переместится в точ­ку В, расстояние от А до В равно двум радиусам, поэто­му модуль вектора переме­щения равен 2R.


2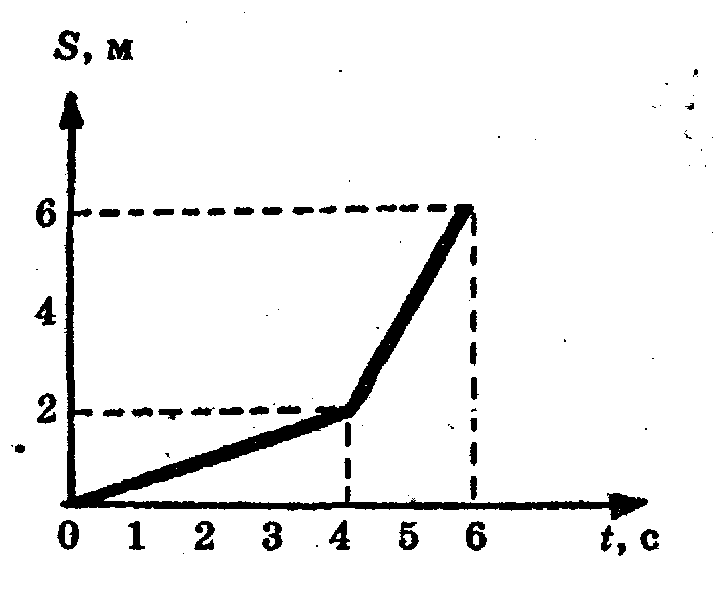.На графике изображена за­висимость пройденного пути от времени для прямолиней­ного движения материальной точки. Средняя ско­рость точки за 6 с равна:

1) 1 м/с: 2) 1,5 м/с; 3) 1,75 м/с; 4) 1,25 м/с; 5) 1,125 м/с.

Для подсчета средней скорости необходимо весь пройденный путь (6 м) разделить на все время движения (6 с).


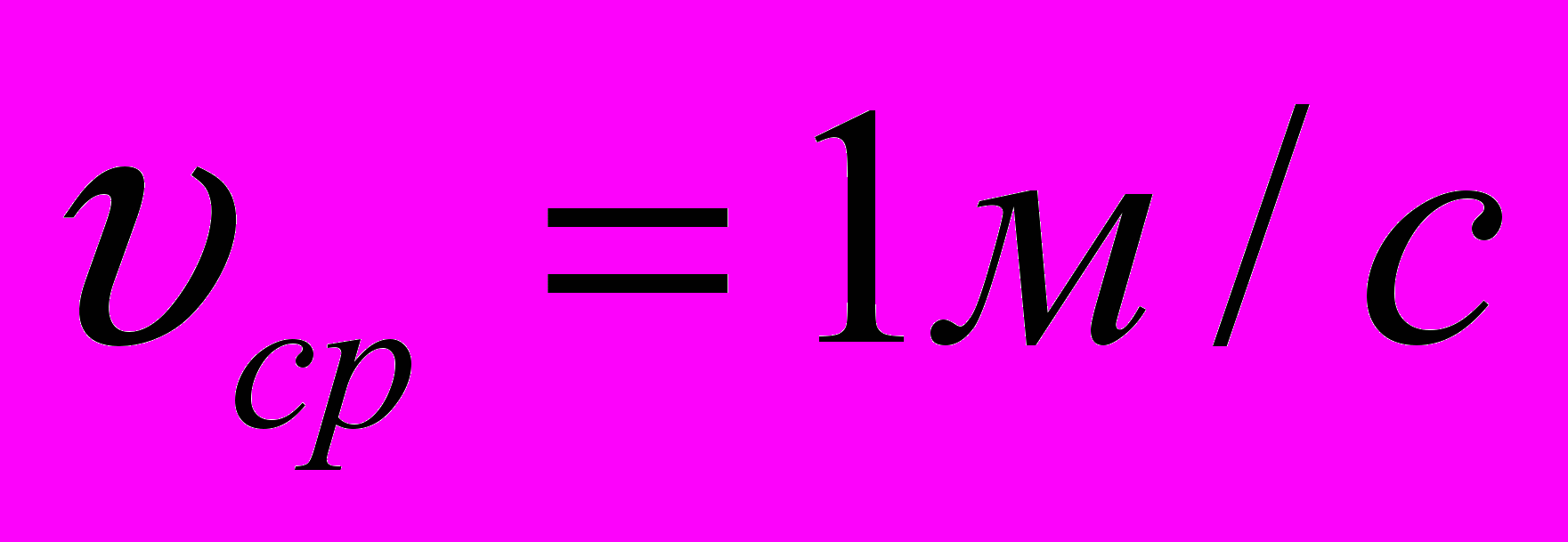
3. Модуль вектора перемещения материальной точки, скорость которой изменяется по закону υ=2 - 2t (м/с), через 4 с после начала движения равен

1) 8м; 2) 10 м; 3) 0; 4) 4 м; 5) 16 м.

Координата точки описывается уравнением , а скорость — уравнением .

Из приведенного уравнения ясно, что υ₀ = 2 м/с, а а = -2 м/с². Поэто­му уравнение для координаты принимает вид х = х_о + 2t - t². Для t = 0 х₁ = х₀; для t = 4 с х₂ = х₀ + 8 - 16 = х₀ - 8м. В данном случае модуль вектора перемещения

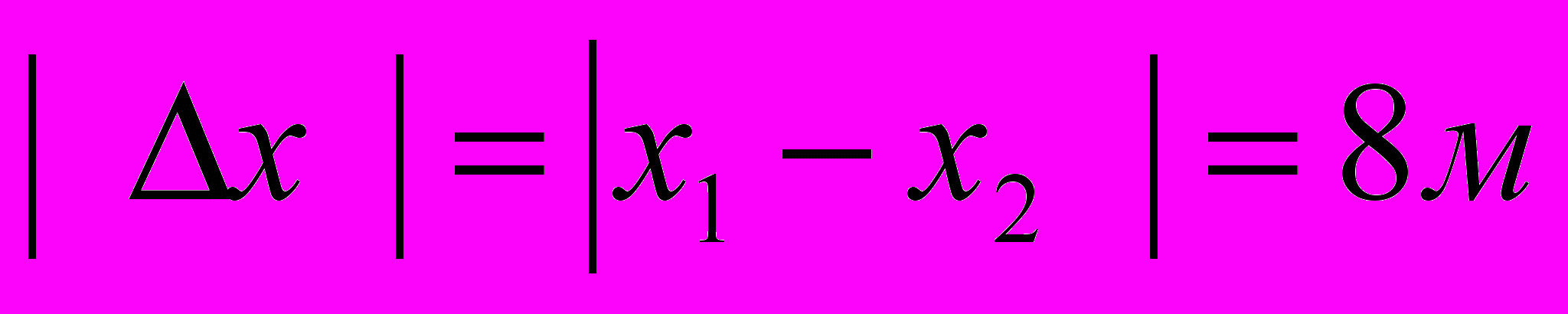
4. Равноускоренное движение материальной точки — это такое движение, при котором

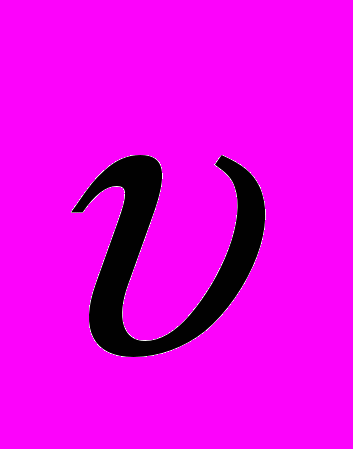1) = const; 2) а = const; 3) = const;

4) = const; 5) = .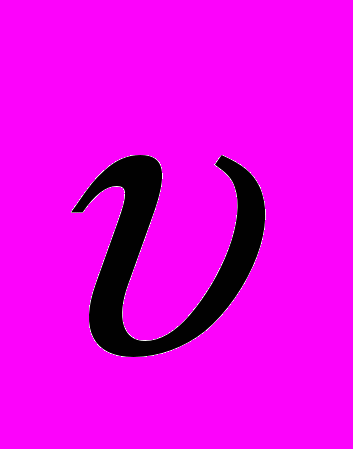

Равноускоренное движение — это движение с постоянным ускорением, причем вектор ускорения не должен менять­ся ни по модулю, ни по направлению. Верный ответ: = const.

5. Изменение модуля скорости тела, двигающегося по ок­ружности со скоростью, численно равной 5 м/с, при прохождении четверти окружности равно:

1) 5 / 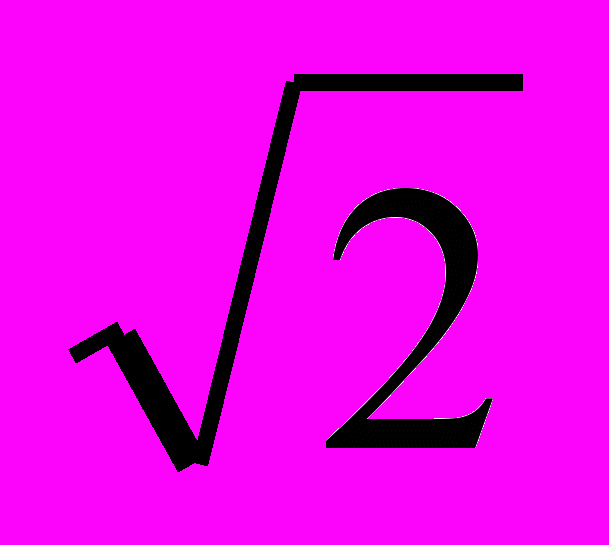м/с; 2) 10 м/с; 3) 0 м/с 4) 5 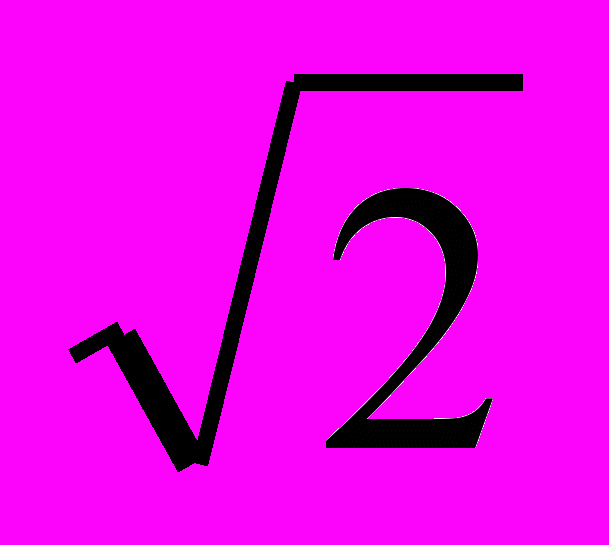м/с; 5) 2,5 м/с.

Решение. При равномерном движении тела по окружности модуль его скорости не меняется. Поэтому изменение модуля ско­рости равно нулю.

6. Материальная точка движется по окружности с посто­янной по величине скоростью. Линейную скорость точ­ки увеличили в 2 раза, и период обращения увеличи­ли в 2 раза. При этом центростремительное ускорение точки:

1) увеличилось в 4 раза; 2) увеличилось в 2 раза; 3)не изменилось; 4) уменьшилось в 2 раза;

Решение. Центростремительное ускорение равно

Если увеличилось в 2 раза, а Т тоже увели­чили в 2 раза, то центростремительное ускорение не изме­нилось.

7. Отношение центростремительных ускорений а ₁/а ₂ двух материальных точек, движущихся с одинаковы-

ми линейными скоростями по окружностям радиусов R ₁ и R ₂ причем R ₁ = 3 R ₂ , равно:

1)1/9; 2)1/3; 3)1; 4)3; 5)9.

Решение. Центростремительное ускорение находится по формуле 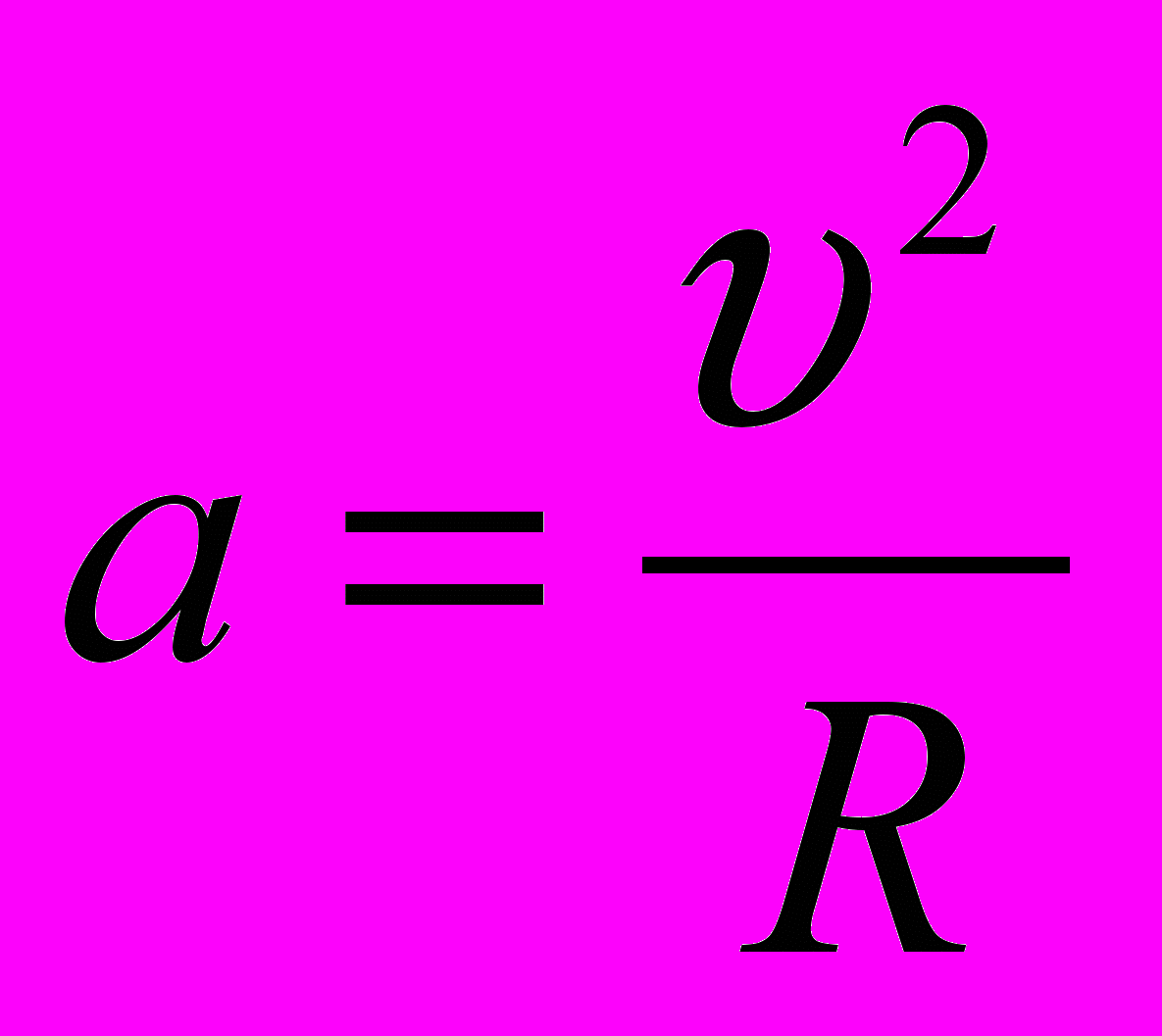. Так как скорости одинаковы, а радиус уменьша­ется в 3 раза, то ускорение увеличивается во столько же раз.

8. Если мяч, брошенный вертикально вверх, упал на зем­лю через 3 с, то величина скорости мяча в момент па­дения равна:

1)5 м/с; 2) 10 м/с; 3) 15 м/с; 4) 20 м/с; 5) 30 м/с.

Мяч 1,5 с поднимается и 1,5 с спускается. Модуль скорос­ти в момент падения равен начальной скорости мяча. За­кон изменения скорости (ось направлена вверх) . Время подъема . Отсюда начальная и конечные скорости равны .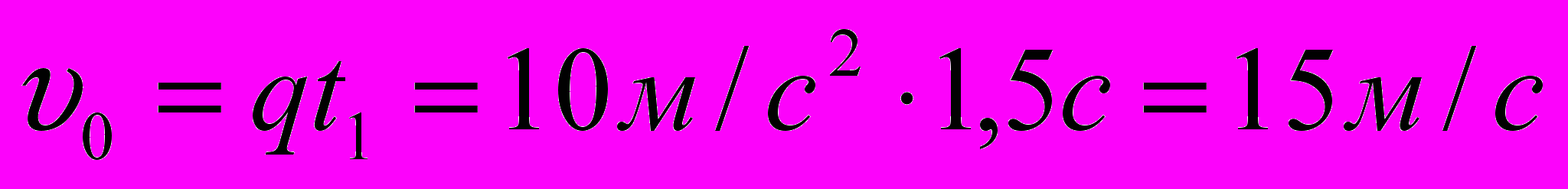


Контрольная работа № 1

Перемещение. Скорость. Равномерное прямолинейное движение. Свободное падение.

1. Двигаясь равномерно, велосипедист проезжает 40 м за 4 с. Какой путь он проедет при движении с той же скоро­стью за 20 с?

А. 30 м. Б. 50 м. В. 200 м.

2. На рисунке 1 приведен график движения мотоциклис­та. Определите по графику путь, пройденный мотоцик­листом в промежуток времени от 2 до 4 с.

А. 6 м. Б. 2 м. В. 10 м.

3. На рисунке 2 представлены графики движения трех тел. Какой из этих графиков соответствует движению с большей скоростью?

А. 1. Б. 2. В. 3.

4. По графику движения, представленному на рисунке 3, определите скорость тела.

А. 1 м/с. Б. 3 м/с. В. 9 м/с.

5. Определите, какой из графиков (рис. 4) соответствует равноускоренному движению тела.

А. 1. Б. 2. В. 3.

6. По графику зависимости скорости от времени (рис. 5) определите ускорение тела.

А. 5 м/с². Б. 1 м/с². В. 2 м/с².

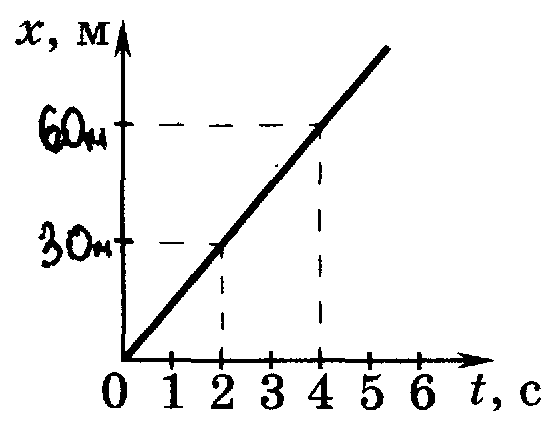Рис.1

Рис.2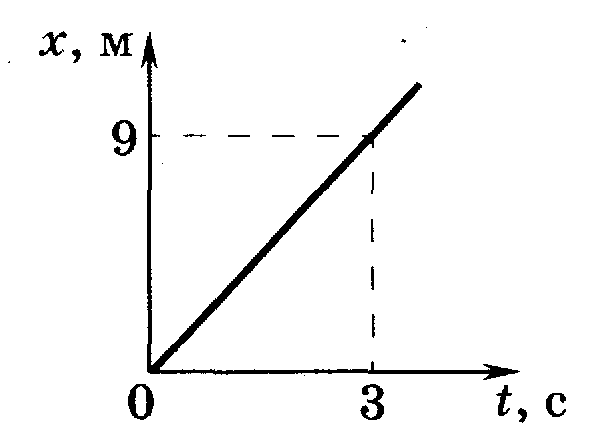

Рис.3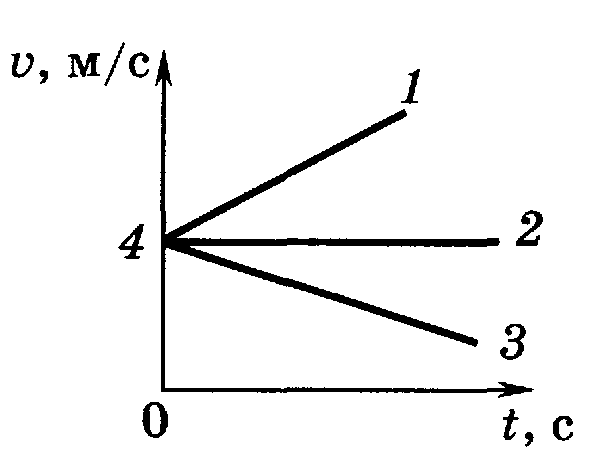

Рис.4

Рис.5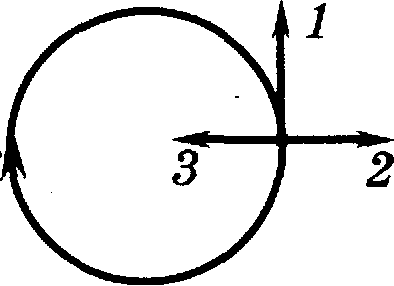

Рис.6

7. Две автомашины движутся по дороге с постоянными скоростями 10 и 15 м/с. Начальное расстояние между машинами равно 1 км. Определите, за какое время вто­рая машина догонит первую.

А. 50 с. Б. 80 с. В. 200 с.

8. Мотоциклист совершает поворот по круговой траекто­рии радиусом 50 м с постоянной по модулю скоростью 10 м/с. Каково ускорение мотоциклиста?

А. 1 м/с². Б. 3 м/с². В. 2 м/с².

9. Тело движется равномерно по окруж­ности по часовой стрелке (рис. 6). Как направлен вектор ускорения при таком движении?

А. 1. В. 3. Б. 2

10. Тело движется равномерно по окруж­ности по часовой стрелке (рис. 6). Как направлен вектор ускорения при таком движении?

А. 1. В. 3. Б. 2

11. Какова частота вращения тела, движущегося по ок­ружности радиусом 5 м со скоростью 5 м/с?

А. 2 Гц. Б. 0,5 Гц. В. 4 Гц.

12. Тело движется по окружности радиусом 4 м со скоростью 10 м/с. Определите пери­од вращения тела.

А. 0,8 с В. 2 с. Б. 1с.

13. Трамвайный вагон движется на повороте по закругле­нию радиусом 40 м. Рассчитайте скорость трамвая, если центростремительное ускорение равно 0,4 м/с².

А. 2 м/с. Б. 1 м/с. В. 4 м/с.

14. После старта гоночный автомобиль достиг скорости 360 км/ч за 25 с. Определите расстояние, пройденное ав­томобилем за это время.

А. 1250 м. Б. 1400 м. В. 1500 м.

15.Катер плывет против течения реки. Какова скорость кате­ра относительно берега, если скорость катера относительно во­ды 4 м/с, а скорость течения реки 3 м/с?

А. 7 м/с. Б. 5 м/с. В. 1<м/с.

16. Поезд прошел первые 40 км со скоростью 80 км/ч, а сле­дующие 50 км — со скоростью 100 км/ч. Определите среднюю скорость поезда на всем пути.

А. 95 км/ч. Б. 85 км/ч. В. 90 км/ч.

17. Чему равна скорость свободно падающего тела через 2 с после начала падения, если ₀ = 0?

А. 20 м/с. Б. 10 м/с. В. 30 м/с.

18. С какой высоты был сброшен предмет, если он упал на землю через 2 с ?

А. 30 м. Б. 20 м. В. 10 м.

19. Рассчитайте время свободного падения тела с высоты 20 м.

А. 1с. Б. 3 с. В. 2 с.

20. Тело брошено вертикально вверх со скоростью 30 м/с. Какова максимальная высота подъема тела?

А. 45 м. Б. 50 м. В. 90 м.,

При решении задач принять g = 10 м/с²