Geum.ru

Момент количества движения системы

Вид материалаЛекция

Содержание


Длина такого математического маятника, период колебаний которого равен периоду колебаний физического маятника, называется привед
Подобный материал:
Лекция №4

МОМЕНТ КОЛИЧЕСТВА ДВИЖЕНИЯ СИСТЕМЫ

Количество движения характеризует только поступательное движение тела. Для описания вращательного движения необходимо ввести понятие момента вектора относительно какой-либо точки или оси. Для одной материальной точки сделаем это также, как и в случае силы:

Момент количества движения системы относительно неподвижного центра О (кинетический момент) равен геометрической сумме моментов количества движения всех материальных точек системы относительно этого центра.











Рассмотрим некоторые частные случаи определения главного момента.
  1. При поступательном движении твёрдого тела кинетический момент равен:


Но при поступательном движении скорость всех точек тела равна скорости центра масс , т.е.


  1. При вращательном движении тела вокруг неподвижной оси определение сводится к определению проекций кинетического момента . Найдем наиболее важную из проекций: Суммируя по всем точкам получаем:


Кинетический момент тела относительно оси равен произведению осевого момента инерции на угловую скорость




Проекции на другие оси определяются аналогичным образом и равны: будут определены в лекции №6.


Если ось вращения - главная ось инерции ( и кинетический момент направлении вдоль оси вращения.

Для системы тел, вращающихся вокруг оси z с угловыми скоростями - соотв. момент инерции.
  1. При плоскопараллельном движении все точки тела перемещаются параллельно некоторой неподвижной плоскости (x o y). В этом случае


кинетический момент тела относительно неподвижной оси равен сумме кинетического момента тела относительно оси , ей параллельной и проходящей через центр масс с, и момента главного вектора количества движения тела , приложенного в центре масс, относительно оси


- 1-ая теорема Кенига.

Теорема об изменении момента количества движения системы (кинетического момента)


Пусть система состоит из n материальных точек , имеющих скорости и находящихся под действием внешних и внутренних сил 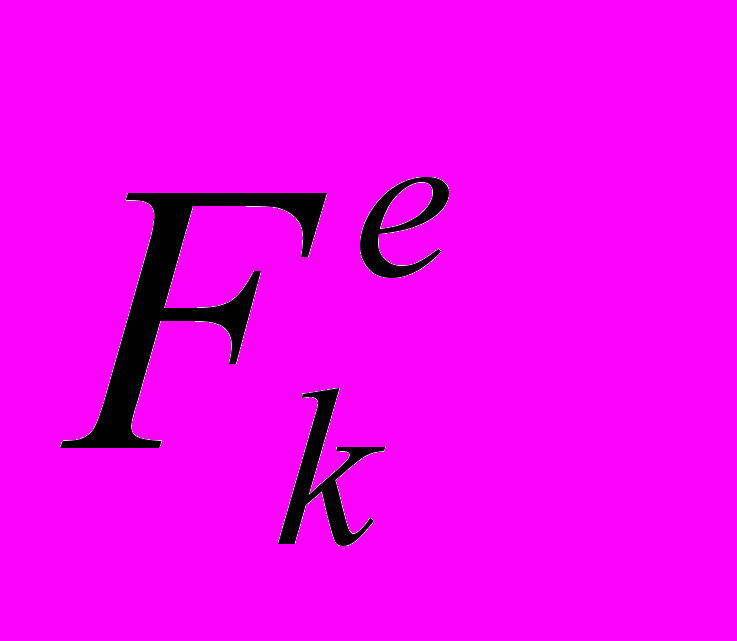, 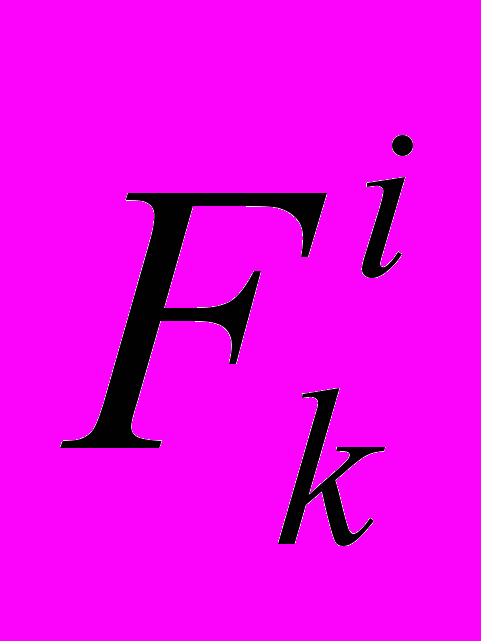. Для одной материальной точки момент количества движения относительно центра О равен: Продифференцируем это соотношение по времени: , т.е. первое векторное произведение равно нулю (векторы параллельны). Во втором члене , т.е. он равен

Суммируя по всем точкам системы, получаем:



(т.к.

Но (свойство внутренних сил системы), поэтому



Производная по времени кинетического момента системы относительно некоторого неподвижного центра равна геометрической сумме моментов внешних сил относительно этого центра.


Проектируя на оси координат, получаем:



Теорема моментов относительно центра масс





Для осей , движущихся поступательно вместе с центром масс, теорема моментов имеет тот же вид, что и относительно неподвижных осей.


Закон сохранения момента количества движения системы.
  1. Сумма моментов всех внешних сил системы относительно центра О равна нулю:

Если сумма моментов всех внешних сил относительно некоторого неподвижного центра равна нулю, то момент количества движения системы относительно этого центра (кинетический момент ) есть величина постоянная (по модулю и направлению).

2)

Элементарная теория гироскопа, гирокомпас, навигационные приборы. Вращательное движение твёрдого тела

Пусть твёрдое тело вращается вокруг неподвижной оси z под действием заданных внешних сил.



Реакции моментов не дают, т.к. линии их действия проходят через ось. называется вращающимся моментом. , поэтому: или , или .

Произведение осевого момента инерции на угловое ускорение равно вращающему моменту. Чем больше момент инерции, тем меньше угловое ускорение, т.е. при вращательном движении момент инерции играет ту же роль, что и масса при поступательном. Зная вращающий момент , можно определить закон вращения тела.

1) (равномерное вращение)

2) (равноускоренное вращение)

Обычно

Физический маятник Голландский физик Гюйгенс (1629-1695)

Физическим маятником называется твёрдое тело, колеблющееся относительно неподвижной горизонтальной оси под действием силы тяжести.


При поэтому - уравнение малых колебаний физического маятника.

(теорема Гюйгенса-Штейнера)

- период колебаний математического маятника

- приведенная длина физического маятника.

Точка К называется центром колебаний. Длина такого математического маятника, период колебаний которого равен периоду колебаний физического маятника, называется приведенной длиной физического маятника.
Плоскопараллельное движение твёрдого тела

Рассматривалось в кинематике (это такое движение, при котором все точки тел перемещаются параллельно некоторой неподвижной плоскости). При описании плоскопараллельного движения, которое слагается из поступательного вместе с некоторым полюсом и вращательного относительно этого полюса, в качестве полюса можно выбрать любую точку. Теперь за полюс выбираем центр масс. Пусть на тело действуют внешние силы . Уравнение движения центра масс тела имеет вид: . Вращательное движение можно описать с помощью теоремы об изменении кинетического момента относительно оси, проходящей через центр масс:

Окончательно получаем: - дифференциальные уравнения плоскопараллельного движения твёрдого тела.

При естественном способе задания движения, когда траектория движения центра масс известна, удобнее пользоваться уравнениями движения в проекциях на касательную, нормаль и бинормаль




S-Солнце

Траектория планеты Земля

Плоскость траектории=плоскость эклиптики

Ось Мира параллельна оси вращения Земли.