Экспериментальная работа учительницы начальных классов Кукморской гимназии №1 имени Ч. Т. Айтматова Зиатдиновой Н. М

Вид материала

Содержание

В одной книге 36 страниц, в другой – 18 страниц. Во сколько раз больше страниц в первой книге, чем во второй?

Подобный материал:

-----------------------------------------------

Кукморская гимназия №1 им.Ч.Т.Айтматова

Экспериментальная работа учительницы начальных классов Кукморской гимназии № 1 имени Ч.Т.Айтматова Зиатдиновой Н.М.

---------------------------------------

---------------------------------------

Формирование логического мышления младших школьников на уроках математики

------------------ 2 ------------------

---------------------------------------

ВВЕДЕНИЕ

Математика имеет неограниченные возможности в развитии интеллекта школьника. Математические задачи, накопленные и проведенные в ходе многолетней педагогической практики, позволяет эффективно развивать различные стороны психической деятельности человек: внимание, воображение, фантазию, образное и понятное мышление, зрительную, слуховую и смысловую память. В методической литературе за развивающими задачами закрепились специальные названия: задачи на соображение, логические задачи, задачи с «изюминкой», задачи на смекалку и др.

Цель формирования логического мышления на уроках математики – помочь учащимся в полной мере проявить свои способности, развить инициативу, самостоятельность, творческий потенциал; повысить эффективность обучения математике, актуализация резервов мыслительных процессов.

Задачи таких уроков: интеллектуальное развитие младших школьников, формирование культуры самостоятельности мышления, предупреждение неуспеваемости сохранения здоровья. Логические задачи почти всегда носят занимательный характер и этим привлекают даже тех, кто не любит математику. И главное, их

решение развивает логическое мышление, что способствует успешному изучению основ любой другой науки.

-----------------3--------------------

---------------------------------------

ГЛАВА 1.1. Формирование

логического мышления

Формирование логического мышления – важная составная часть педагогического процесса. Помочь учащимся в полной мере проявить свои способности, развить инициативу, самостоятельность, творческий потенциал – одна из основных задач современной школы. Успешная реализация этой задачи во многом зависит от сформированности у учащихся познавательных интересов.

Математика дает реальные предпосылки для развития логического мышления. Задача учителя – полнее использовать эти возможности при обучении детей математике. Однако конкретной программы логических приемов мышления, которые должны быть сформированы при изучении данного предмета, нет. В результате работа над развитием логического мышления идет без знания системы необходимых приемов, без знания их содержания и последовательности формирования.

Ученье – процесс двусторонний: работают дети, работает учитель; он ведет за собой учащихся, руководит их умственной деятельностью, организует и направляет ее.

Традиционно проблема развития познавательного интереса

-------------------4------------------

---------------------------------------

ребенка решается средствами занимательности в обучении математике. Однако следует больше использовать так называемую «внутреннюю» занимательность самой математики, тесно связанную с изучаемым учебным материалом, и врожденную любознательность маленьких детей. Внутренняя занимательность - появление необычных, нестандартных ситуации с уже знакомыми детям понятиями, возникновение новых «почему» там, где, казалось бы, все ясно и понятно (но только на первый взгляд). Это, наконец, проникновение в методику элементов игровой деятельности, которая, естественно, присуща ребенку. Чему нужно научить ребенка при обучении математики? Размышлять, объяснять получаемые результаты, сравнивать, высказывать догадки, проверять, правильные ли они, наблюдать, обобщать и делать выводы.

Линия на развитие познавательных интересов учащихся достаточно четко прослеживается в учебниках математики: в них есть упражнения, направленные на развитие внимания, наблюдательности, памяти. Однако, работая в начальных классах около 30 лет, я все больше убеждаюсь, что необходимы дополнительные задания развивающего характера, задания логического характера, задания, требующие применения знаний в новых условиях. Такие задания включаю в задания в определенной системе. Используя индуктивного рассуждения, веду учащихся к

-------------------5------------------

---------------------------------------

цели подмечать закономерности, сходство и различия с простых упражнений, постепенно усложняя их. С этой целью подбираю серию упражнений с постепенным повышением уровня трудности.

ГЛАВА 1.2. Логические мышления при решениях примеров

В I классе предлагаю задания, направленные на развитие наблюдательности, которые тесно связаны с такими приемами логического мышления, как анализ, сравнение, синтез и обобщение, например:

1. Чем отличаются и чем похожи данные выражения?

2 + 5 3 + 2 6 - 3 8 - 3

2 + 6 4 + 2 7 - 3 9 - 4

2. Найди результат, пользуясь решенным примером:

3 + 5 = 8

3 + 6 =

3 + 7 =

3 + 8 =

3. Сравни числа, записанные в первом и втором столбиках. Сумма чисел в первом столбике равна 18. Как быстро можно найти сумму чисел, записанных во втором столбике?

-------------------6------------------

---------------------------------------

3 13

4 14

5 15

6 16

Учащиеся отвечают, что во втором столбике каждое из данных чисел на 10 больше соответствующего однозначного числа первого столбика. Таких чисел 4, значит, сумма будет больше 10 – 4. Она равна 18 + 40 = 58.

4. Продолжи данный ряд чисел:

3, 5, 7, 9,…

1, 4, 7, …

2, 4, 7, 9, 12,…

1, 4, 2, 5, 3,…

В процессе изучения нумерации чисел очень часто предлагаю сравнивать два числа, например: 16 и 36. И сколько разных ответов услышишь! Для выполнения таких заданий ученик должен не только владеть запасом определенных терминов и понятий, но и уметь устанавливать между ними взаимосвязь, проявить наблюдательность, проанализировать полученные данные. А это способствует не только осознанному усвоению материала, но и умственному развитию.

В III и IV классах предлагаю различные задания для самостоятельного выявления закономерностей, зависимотей и

-------------------7------------------

---------------------------------------

формулировки обобщения. Для этой цели использую задания:

1. сравни примеры, найди общее и сформулируй новое правило:

1) 0 + 1

2 + 3

3 + 4

4 + 5

Вывод: сумма двух последовательных чисел есть число нечетное.

2) 1 – 0

2 – 1

3 – 2

4 – 3

Вывод: если из последующего числа вычесть предыдущее, то получится 1.

3) 5 + 4 - 4

10 + 7 – 7 а + b – b = а

52 + 13 – 13

Вывод: если к любому числу прибавить и затем из него вычесть одно и то же число, то получиться первоначальное.

4) 26 : 2 ∙2

16 : 8 ∙ 8 а :b ∙ b = а

10 : 5 ∙ 5

Вывод: если любое число разделить и умножить на одно и то же число, то получится первоначальное число.

-------------------8------------------

---------------------------------------

В процессе обучения рассуждениям побуждаю учащихся поискам новых примеров, побуждающих правильность сделанного вывод, и учу сопоставлять вывод с теми фактами, на основе которых он сделан, искать и такие факты, которые могут

опровергнуть вывод, например:

Сравни выражение, найди общее в полученных неравенствах, сформулируй вывод:

2 + 3 * 2 ∙ 3

3 + 4 * 3 ∙ 4

4 + 5 * 4 ∙ 5

5 + 6 * 5 ∙ 6

Вывод: Сумма двух последовательных чисел всегда меньше произведения этих же чисел неверный, так как

0 + 1 > 0 ∙ 1; 1+ 2 > 1 – 2

2. Слагаемое 1 2 3 4 5 6

Слагаемое 5 5 5 5 5 5

Сумма

Вывод: Сумма всегда больше каждого из слагаемых – опровергается подбором фактов: 1 + 0 = 1; 2 + 0 = 2 и т. д., где суммы равны другому слагаемому.

ГЛАВА 1.3. Решение задач

-------------------9------------------

---------------------------------------

Программой по математике предусмотрено решение таких задач, которые лучше воспринимаются учащимися при сравнении и сопоставлении. Это прямые и составные задачи, задачи на увеличе-

ние и уменьшение числа на несколько единиц и в несколько раз, прямые и обратные и т.д. При сравнении прямых и обратных задач задаю следующие вопросы: Что общего и различного в условиях прямой и обратной задач? Какие величины являются искомыми? Что общего и различного в решении прямой и обратной задач? Каким действием решена каждая из задач? Почему?

Размышление одного ученика способствует развитию этого умения других учащихся.

Овладение в процессе обучения такими мыслительными операциями, как анализ и синтез, абстрагирование, конкретизация, обобщение, учащиеся более глубоко осознают изучаемый материал, учатся обосновывать свои суждения. У них формируются умения и навыки самостоятельно решать поставленные задачи, сознательно пользоваться приобретенными знаниями.

Для осущевстления преемственности между обучением в начальных классах и в средней школе провожу определенную работу по формированию умения строить правильные дедуктивные умозаключения. Для проведения дедуктивных рассуждений необходима большая подготовительная работа, направленная на сознательное усвоение общего вывода, свойства и закономерности.

-------------------10-----------------

---------------------------------------

Например, при решении задачи: В одной книге 36 страниц, в другой – 18 страниц. Во сколько раз больше страниц в первой книге, чем во второй? – рассуждение строю таким образом:

общая посылка: все задачи, в которых требуется узнать, во сколько раз одно число больше другого, решаются делением. Частная посылка: в этой задаче надо узнать, во сколько раз 36 больше 18.

Заключение: для ответа на вопрос задачи надо 36 разделить на 18. После решения примеров 5 : 5, 6 : 6, 3 ∙ 0, используя опыт работы Г. Микулиной, предлагаю детям поиграть в сказочную школу, только цифры другие, не похожие на те, которыми мы пользуемся, остались прежними только 1 и 0. Сможете ли вы решить такие примеры?

a : 1 d + 0

b : b k + 0

c : 0 k – 0

1. Разбей числа на группы, чтобы в каждой группе были числа, похожие между собой: 53, 33, 84, 22, 13, 11, 44.

(В одну группу входят числа, записанные одной цифрой, в другую – двумя разными цифрами.)

2. По какому правилу записан каждый ряд чисел? Продолжи его:

10, 30, 50, 70…

14, 34, 54, 74…

------------------11------------------

--------------------------------------ГЛАВА 1.4. Геометрический материал

На уроках математики использую задания на классификацию,

пользуясь геометрическим материалом. Второклассники с гораздо большей охотой выполняют работу на классификацию геометрических объектов, воспринимая их как занимательные задания, например:

Продолжи ряд. Какие фигуры ты здесь нарисуешь? Почему?

Сколько квадратов, треугольников, четырехугольников и т.д.?

------------------12-----------------

------------------------------------

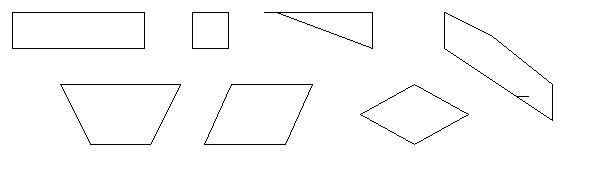
3. Чем отличаются эти фигуры, чем похожи?

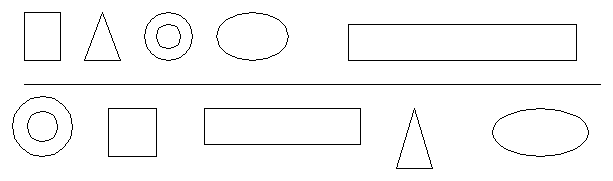
4. Рассмотрит фигуры в каждом ряду. Чем они похожи? Что

послужило основанием для разделения фигур?

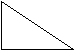
5. Какие фигуры дружат с числом 4?

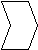
------------------13-----------------

---------------------------------------

ГЛАВА 1.5. Нестандартные задачи

Используя на уроках математики специальные задачи и задания, направленные на развитие познавательных возможностей и способностей детей. Нестандартные задачи требуют повышенного внимания к анализу условия и построения цепочки взаимосвязанных логических рассуждений.

Приведу примеры таких задач, ответ на которые необходимо логически обосновать:

В коробке лежат 5 карандашей: 2 синих и 3 красных. Сколько карандашей надо взять из коробки, не заглядывая в нее, чтобы среди них был хотя бы 1 красный карандаш?
Батон разрезали на 3 части. Сколько сделали разрезов?
Четыре мальчика купили 6 тетрадей. Каждому мальчику досталось не меньше одной тетради. Мог ли купить какой-нибудь мальчик 3 тетради?

Нестандартные задачи ввожу уже с 1-го класса: использование таких задач расширяет математический кругозор младших школьников, способствует математическому развитию и повышает качество математической подготовленности.

------------------14-----------------

---------------------------------------

ГЛАВА 1.6. Числовая логика

При изучении сложения и вычитания чисел в пределах 100 стремлюсь на каждом уроке математики отвести 5 – 10 минут на работу с заданиями, развивающими логическое и абстрактное мышление. Для этого предлагаю примеры с окошками и пропущенными знаками действий, например:

Какой знак действия нужно поставить, чтобы равенство было верным?

□ ◦ □ = 20

2. Какой знак <, >, = пропущен?

□ – 6 ◦ □ + 6

Для формирования умения проводить дедуктивные рассуж-

дения использую задания: ответь, правильны ли данные рассуждения или нет. Если нет, то почему?

1.Пианино – это музыкальный инструмент. У Вовы дома музыкальный инструмент. Значит, у него дома пианино?

2.Классные комнаты надо проветривать. Квартира – это не классная комната. Значит, квартиру не надо проветривать?

3. Если одно число при счете называют раньше, то это число меньше?

------------------15------------------

---------------------------------------

4. Верно ли, что 25 см больше, чем 2 дм5см?

Или: на одном месте пишу общие посылки, на другом – частные. Учащиеся должны установить, какой общей посылке соответствует

каждая частная посылка, и поставить около задания номер общей посылки.

ГЛАВА 1.7. Классификация

Исходя из актуальности формирования элементарных логических приемов, использую в своей работе один из необходимых видов мыслительной деятельности – прием классификации.

Применение приема классификации на уроках математики позволяет расширять имеющиеся в практике приемы работы, способствует формированию положительных мотивов в учебной деятельности, так как подобная работа содержит элементы игры и

элементы поисковой деятельности, что повышает активность учащихся и обеспечивает самостоятельное выполнение работы.

Из опыта своей работы могу выделить следующие виды заданий на классификацию:

Подготовительные задания:

Убери лишний предмет, назови лишний предмет, нарисуй фигуру такого же цвета (формы, размера), дай название группе предметов; сравни похожие рисунки, найди отличия.

------------------16------------------

---------------------------------------

2.Задания, в которых указывается основание классификации:

Разбей данные числа на группы, в первый запиши числа, которые меньше 5, во второй числа, которые больше 5:

1, 2, 3, 4, 5, 6, 7.

2) Разбей данные числа на группы, чтобы в каждой были

похожие записи:

3 + 1, 4 – 1, 5 + 1, 6 -1, 7 +1, 8 -1,…

3) Разбей данные числа на две группы – однозначные числа и

двузначные числа:

2, 7, 35, 41, 4, 8, 80, 60, 3,… и т. д.

3. Задания, в которых надо выделить объекты из данной группы

по определенному основанию, а затем указать основание для

оставшейся группы объектов:

1) Выпиши все числа, записанные двумя различными цифрами:

22, 56, 80, 66, 74, 47, 88, 31, 94, 44.

После того как учащиеся сделают это, предлагаю внимательно посмотреть на те числа, которые остались, и назвать признак, являющимся общим для них, т. е. указать основание.

Но особенно эффективными для развития логического мышления учащихся являются задания, в которых основание для классификации выбирают сами дети. Впервые такие задания ввожу во втором классе. Учащиеся уже достаточно развиты для того, чтобы оперировать более абстрактными понятиями.

------------------17------------------

---------------------------------------

В своей педагогической деятельности использую графические схемы в устном счете и при решении задач. Сначала эти схемы простые, потом их значительно усложняю.

Предлагаю такие задания:

Задай графическую схему.
Доведи до конца частично заполненные схемы.
Составь выражение по данной графической схеме.
Составь задачу по графической схеме.
Составь графическую схему по условию.

Дидактическая игра оказывает большое влияние на познавательную деятельность учащихся. Картотека игр помогает мне рационально использовать их в учебном процессе.

Заключение 1-ой главы

Изложенная мной система работы по развитию логического мы-

шления учащихся направлена на формирование умственных действий детей. Дети учатся выявлять математические закономерности и отношения, выполнять посильные обобщения, учатся делать выводы. Использование на уроках математики опорных схем, таблиц способствует лучшему усвоению материала, побуждает детей активнее мыслить.

В результате математической работы по развитию логического мышления учебная деятельность многих учеников активизировалась, качество их знаний заметно повысилось.

------------------18------------------

---------------------------------------

ГЛАВА 2.1. Актуализация резервов мыслительных операций

Современное содержание математического образования направлено главным образом на интеллектуальное развитие младших школьников, формирование культуры и самостоятельности мышления.

Данный аспект является главным в развитии личности ученика, так как мышление влияет на воспитанность человека. Достаточная подготовленность к мыслительной деятельности снимает психологические нагрузки в учении, предупреждает неуспеваемость, сохраняет здоровье.

Важнейшим фактором в развитии мыслительных операций служат педагогические системы развивающего обучения. К такой технологии относится методика обучения по УДЕ (укрупнение дидактических единиц).

Одна из основных целей технологии – создание действенных и эффективных условий для развития познавательных способностей детей, их интеллекта и творческого начала, расширение математического кругозора.

------------------19------------------

---------------------------------------

В основу УДЕ положен принцип: чтобы обучать ускоренно и при высоком уровне знаний, необходимо рассматривать целостные группы взаимосвязанных понятий.

Большой интерес представляет структура учебников. Она такова, что в триадах задач реализуется фактор дополнительности подсознательных механизмов познания.

Триада означает выполнение учеником на одном уроке:

готового упражнения;
обращение этого задания и самостоятельное обобщение решенной задачи.

Этот прием дает хороший эффект в обучении, так как он побуждает учащихся осмысливать и усваивать материал на основе более высокой логической степени обучения.

Принцип УДЕ в обучении математики реализуется следующим образом:

совместное и одновременное изучение взаимосвязанных понятий и операций;
широкое использование метода обратной задачи;
применение деформированных упражнений;
упражнение исходного упражнения посредством самостоятельного составления учеником новых заданий;
одновременная подача одной и той же математической информации на нескольких кодах.

------------------20------------------

---------------------------------------

Практика обучения показывает, что изучение действий сложения и вычитания выгодно осуществлять на одних и тех же уроках, ибо это облегчает осуществление процесса контроля. Наглядное иллюстрирование взаимно-обратных операций заставляет ученика применять рассуждение, т.е. логические средства исследования, способствующие развитию математических операций заставляет ученика применять рассуждение, т.е. логические средства исследования, способствующие развитию мыслительных операций.

Схематически четыре промежуточные операции образуют как бы замкнутый цикл в рассуждениях.

5 + 1 = 6 → 6 + 1 = 7

6 – 1 = 5 → 7 – 1 = 6

Развитие мыслительных операций основано на аналогичном попарном родстве элементарных операций, посредством которых выполняется пара сложных операций.

Вскрытию резервов мыслительной деятельности способствует применение задач, в которых противопоставляется действия первой и второй ступени: удобно при этом использовать четверки примеров:

3 + 5 = 8 5 + 3 = 8 3 ∙ 5 = 15 15 ÷ 3 = 5

8 – 5 = 3 8 – 3 = 5 5 ∙ 3 = 15 15 ÷ 5 = 3

Такие упражнения тренируют мышление.

------------------20------------------

---------------------------------------

Заключение 2-ой главы

Исходя из рассмотренного можно заключить: активная умственная деятельность – одно из основных условий, которое обеспечивает технология УДЕ. Широкое применение принципов, реализующих УДЕ, помогает постигать азы логического мышления.

ГЛАВА 3. Развитие логического мышления

ГЛАВА 3.1. Субъектизация

Субъектизация как способ обучения в первую очередь направлена на развитие интеллекта младшего школьника,

качеством, которого является логическое мышление. Учитывая это, использую данную методику в процессе обучения математике.

Приведу некоторые нестандартные задания, способствующие развитию логического мышления, которые использую на уроках математики.

------------------22------------------

---------------------------------------

1.Ответьте на вопрос задачи: «На грядке сидит 6 воробьев. К ним прилетели еще 4 воробья. Сколько воробьев осталось на грядке?». Сформулируйте самостоятельно тему сегодняшнего урока. (Неправильно сформулирован вопрос к задаче. На вопрос задачи ответить нельзя).

Сегодня цифра спряталась в дне недели, который предшествует субботе. Какая это цифра? Какова тема урока? (Цифра и число 5).
Внимательно посмотрите на запись и найдите лишнее число: 1, 3, 9, 11, 7, 5. Определите тему урока.(Двузначные числа).
Задания способствуют развитию наглядно-действенного мышления. Сначала учащиеся выполняют все действия практически, затем производят перестановку карточек мысленно. Постепенно количество карточек и перестановок увеличивается. Например: Внимательно посмотрите на карточки с геометрическими фигурами.

Какую карточку в нижнем ряду надо переставит, чтобы в обоих рядах фигуры имели одинаковый порядок. Определите тему урока.

УЧЕНИК. Карточку с квадратом надо поставить в пустой кармашек. Тогда фигуры в верхнем и нижнем рядах будут иметь одинаковый порядок. Тема сегодняшнего урока- геометрическая фигура- квадрат.

------------------23------------------

---------------------------------------

Задания способствуют формированию словесно-логического мышления. Это работа с игровым полем из 9 или 12 клеток, где можно зашифровать тему урока или новый для детей математический термин.

Например: Вспомните правило игры. Посмотрите внимательно на поле и сформулируйте тему урока. Что обозначает этот математический материал? (Алгоритм).

Задания логического характера для устного счета.

1). Игровое поле. Составление цепочек.

Посмотрите внимательно на поле. Скажите, какое действие надо выполнить, чтобы получить данный результат. Составьте числовые цепочки. Как называются такие примеры? (Зайчик может прыгать через дорожку только наискосок. Значит, из домика 7 он

может попасть в домик 2 или 4).

Двое учеников по очереди выполняют задания у доски:

зайчик из домика 7 прыгает в домик 2.

Чтобы получить число 2, надо из 7 вычесть 5. Из домика 2 зайчик попадает в домик 6. Чтобы получить число 6, надо к 2 прибавить 4 и т.д. Это круговые примеры.

Остальные учащиеся могут самостоятельно заполнять цепочки на карточках или проверять работающих у доски.

Такие работы предлагаю иногда для самостоятельной работы.

------------------24------------------

---------------------------------------

2). Эвристические задания, в которых учащиеся могут оперировать категориями все, некоторые, отдельные и устанавливать отношения между членами множеств. В таких заданиях учащиеся встречаются с тремя уровнями сложности.

ГЛАВА 3.2. Сложные задачи

На первом уровне они оперируют одним суждением, например: Рамиль и Алия решали примеры. Один решил у доски, другой в тетради. Где решила Алия примеры, если Рамиль не решал у доски?

На втором уровне учащимся необходимо сопоставлять два

суждения. Например: Камиль, Василь и Самат учили таблицу умножения. Один учил таблицу на 5, другой на 6, третий на 9. Кто, какую таблицу учил, если Камиль знал таблицу умножения на 6 и на 9, а Василь знал таблицу на 9?

Третий уровень – это задачи, в которых учащимся необходимо соотнести три суждения. Например: (На дереве сидело) Асаф, Булат, Гульназ и Чулпан выполняли задания по выбору: решить задачу, примеры, уравнение и найти периметр фигуры. Кто какое задание выполнял, если Асаф не решал уравнений, задач и примеров; Булат не решал примеров и задач, а Чулпан не решала задач?

------------------25------------------

---------------------------------------

Перебор вариантов отношений. Например: На дереве сидело 4 голубя и 6 воробьев. 5 птиц улетело. Улетел ли среди них хоть один голубь?
Установление пространственных, временных и

функциональных отношений. Например: а) Сережа шел по лестнице, шагая через две ступеньки. Он считал 1, 2, 3, 4… Когда ему нужно было сказать 5, то оказалось, что осталось одна ступенька. Сколько всего ступеней на лестнице? (14 ступеней). б) Как отличить 3 л. Жидкости, если есть емкости 7 и 2 л.?

(7 – 2 – 2 =3 л.)

5) Комбинаторные действия, т.е. умения создавать новые комбинации из имеющихся элементов. Например: а) Составьте все возможные трехзначные числа, используя цифры 5, 7, 3. б) Составьте все возможные фигуры из заданных геометрических элементов.

ГЛАВА 3.3. Логические задачи при изучении нового материала.

Нахождение закономерностей (ступенчатый счет, как в прямом, так и в обратном порядке):

22, 25, 28… 789, 63

5, 15,…,35 909, 899,…,…,869

5, 7, 35, 6, 8, 48,..

------------------26------------------

---------------------------------------

2) Знание разрядности чисел. Например: какое будет число, если в числе 427 число десятков увеличить на 2 и т.п. (Число на доске

не записывается, а задание повторяется один раз).

Составление задач по данному выражению или требованию, также задач, где известны лишь общие характеристики данных. Например: составьте задачу, где известно одно из слагаемых, а другое неизвестно.

Данис: Эльвина прочитала 9 страниц, а Сирина на 4 страницы меньше. Сколько страниц прочитали девочки вместе?

Ислам: Летом я жил у бабушки. У нее было 2 курицы- несушки. Мы с мамой купили ей на 3 курицы больше, чем у нее было. Сколько кур-несушек стало у бабушки?

Для самостоятельной работы использую задачи с поэтапным усложнением (простые - сложные – с абстрактными данными).

Сравнение вида одинаковые, разные. Например: посмотрите внимательно на рисунки, сравните их. Найдите среди данных рисунков такой, который отличается от двух других.
Задачи с мысленным нахождением двух рисунков друг на друга и их детальным сравнением. Игра «Просвет» = (условие задачи и ответ на доске или на картинке).

------------------27------------------

---------------------------------------

Условие задачи →

Ответы к задаче →

Например: определите, какое изображение получилось бы при наложении двух верхних рисунков друг на друга, и выберите ответ. Ответ обоснуйте.

Задания могут быть на определение совпадающих или несовпадающих в пространстве элементов. При решении таких задач можно использовать различные геометрические фигуры и формы для наложения.

Словестно-логические задачи.

а) Если на лист простой бумаги синего цвета положить лист копировальной бумаги красного цвета и провести по нему линию карандашом желтого цвета, то какого цвета линия будет на листе простой бумаги? (красная)

б) через 5 лет Гульшат будет столько же лет, сколько сейчас Алсу. Кто младше?

в) Через 4 года Ильсу будет на 2 года меньше, чем Ильнуру через 7 лет. Кто старше? (Ильяс)

------------------28------------------

---------------------------------------

г) Юля веселее Аси, Ася легче Сони, Соня сильнее Юли, Юля тяжелее Сони, Соня печальнее Аси, Ася слабее Юли. Кто самый веселый, самый легкий, самый сильный?

На этапе закрепления предлагаю задачи на сообразительность, где проявляется способность учащихся нестандартно мыслить и развивается интуиция. Например:

а) Трое играли в шашки. Всего сыграли три партии. Сколько партии сыграл каждый? (2).

б) На столе лежат три карандаша разной длины. Как удалить из середины самый длинный карандаш, не трогая его? (переложить крайний).

в) По улице идут два и два отца. Всего три человека. Может ли так быть?

Практически на каждом уроке и на разных его этапах использую различные задания на развитие внимания и памяти учащихся, так как без них невозможно совершенствования логического мышления.

Учащимся нравится игра на шахматной доске одной фишкой. У каждого ученика шахматное поле из 16 клеток (на плотной бумаге в прозрачном пакете, чтобы работать ручкой). Затем игровое поле только на доске, самое сложное задание – поле представляют дети мысленно и мысленно передвигают фишку. Далее можно игровое

поле увеличить до 25 клеток и продолжить работу.

------------------29------------------

---------------------------------------

Учитель диктует продвижение фишки по клеткам, Учащиеся мысленно передвигают фишку, затем рисуют на своих досках фишку там, где она остановилась. На классной доске появляется правильный ответ. Например: Учитель диктует: «2 клетки вверх, 2 клетки вниз, 1 клетка вправо, 2 клетки вверх, 1 клетка влево, 1 клетка вниз.

Если есть неправильные ответы, то необходимо фишку провести по клеткам практически, чтобы учащиеся смогли проследить ее путь.

Если же учащиеся легко справляются с такими заданиями, то их можно дополнить словами. С каждым ходом фишки можно называть слово(2 клетки вниз – самолет, 1 клетка влево – дом и т.д.).

Сначала лучше называть слова знакомые, связанные по смыслу или с чем-то легко ассоциируемые, затем более трудные.

При проверке выполнения мыслительной работы нужно показать не только, где находится фишка, но и назвать слова, которые удалось запомнить. В результате ум ребенка становится острее, а сам он – находчивее и сообразительнее.

------------------30------------------

---------------------------------------

Заключение

В результате многократных изменяющихся и усложняющихся упражнений ум ребенка становится острее, а сам он – находчивее и сообразительнее. У детей меняется подход к решению задач, он становится более гибким, особенно развивается навык по решению задач, имеющих несколько вариантов решения, задач на комбинированные действия. Рассуждение учащихся становятся последовательными, доказательными и логическими, а речь четкой, убедительной и аргументированной. Повышается интерес к предмету, формируется неординарность мышления. Умение анализировать, сравнивать, обобщать и применять задания в нестандартных ситуациях. Ведь в творческом поиске легких побед не бывает, поэтому развивается упорство в достижении поставленных целей и, что очень важно, развивается навыки самоконтроля и самооценки.

Изложенный материал использую не первый год. Результат на лицо: мои выпускники успешно продолжают обучение в средней школе и являются наиболее сильными учениками.

------------------31------------------

Blog

Экспериментальная работа учительницы начальных классов Кукморской гимназии №1 имени Ч. Т. Айтматова Зиатдиновой Н. М

Содержание