К. В. Коробова ассистент кафедры информационных технологий виу

Вид материала

Документы

Содержание 2. Основным объектом наших исследований будет конечномерное нормированное пространство X над полем действительных чисел R D называется конусом D выпукло, если с любыми своими точками оно содержит отрезок их соединяющий, т.е. х,yD [x,y]  D. 4. Модель Неймана-Гейла Состоянием равновесия

Подобный материал:

• К. В. Коробова ассистент кафедры информационных технологий, 162.68kb.
• Б. С. Губаева ассистент кафедры государственного и муниципального управления виу, 106.33kb.
• Учебное пособие для студентов, интернов, клинических ординаторов и врачей, 943.15kb.
• В. С. Хачирова ассистент кафедры гражданского права виу, аспирант Института государства, 153.78kb.
• Н. Б. Березова ассистент кафедры иностранных языков виу, 145.74kb.
• Методические указания к практическим занятиям по внутренним болезням и эндокринологии, 896.86kb.
• Выпускная работа по «Основам информационных технологий» Магистрант кафедры международного, 307.23kb.
• Нечаев Дмитрий Юрьевич, кандидат технических наук, доцент, профессор кафедры информационных, 419.94kb.
• Семенов Сергей Максимович, канд техн наук, зав кафедрой информационных систем и компьютерных, 157.7kb.
• Отчет о работе Центра информационных технологий Петрозаводского кооперативного техникума, 273.15kb.

К.В. Коробова

ассистент кафедры

информационных технологий ВИУ


ПРИЛОЖЕНИЕ ТЕОРИИ ПОЛУУПОРЯДОЧЕННЫХ ПРОСТРАНСТВ В МОДЕЛИРОВАНИИ ЭКОНОМИЧЕСКИХ ПРОЦЕССОВ


1. Математика представляет собой науку о количественных отношениях и пространственных формах действительного мира. Впервые математику, как самостоятельную науку, стали изучать в Древней Греции в VI-V вв. до нашей эры. Это было начальным периодом элементарной математики, в течение которого из арифметики появляется теория чисел, создается алгебра, геометрия Евклида.

В XVII в. развитие естествознания и техники привели к созданию методов, позволяющих изучать с помощью математики движение, преобразование геометрических фигур. Создается аналитическая геометрия, дифференциальное и интегральное исчисления. Начинается период математики переменных величин, и на первый план выдвигается понятие функции. Дальнейшее развитие математики в XIX в. привело к постановке задачи изучения возможных типов количественных отношений и пространственных форм. Изучаются математические модели, причем одна и та же математическая модель может описывать свойства несовместимых на первый взгляд явлений. Например, используя одно и тоже дифференциальное уравнение можно описать процессы роста населения и распада радиоактивного вещества. Это говорит о том, что для математики важна не природа рассматриваемых объектов, а существующие между ними отношения, в том числе и экономические.

Математическое моделирование экономической динамики и равновесия имеет многолетнюю историю. Классические модели основаны на функциональных и дифференциальных уравнениях. Некоторые разделы математики, например, теория оптимизации, развивались под воздействием необходимости математического моделирования экономических процессов. В более позднее время появились, в частности, математические модели, связанные с понятием многозначного отображения. При работе с произвольными пространствами необходимо ввести в них отношение порядка, так как элементы полуупорядоченного пространства во многом очень близки к понятию числа по своим свойствам. Включение упорядочения в исследование объектов функционального анализа значительно обогащает и разнообразит их.

Данная статья посвящена рассмотрению экономических моделей, при изучении которых используются методы и понятия теории полуупорядоченных пространств.

2. Основным объектом наших исследований будет конечномерное нормированное пространство X над полем действительных чисел R.

Центральным понятием теории полуупорядоченных пространств является понятие конуса.

Множество D называется конусом с вершиной в точке x, если для любого yD луч [x,y) содержится в множестве D.

Если задан конус К, то можно определить отношение частичного порядка следующим образом: x y тогда и только тогда, когда y-xK. При таком определении неравенство x0 означает, что xK, поэтому элементы конуса принято называть положительными.

Легко проверяется, что для этого отношения выполняются свойства рефлексивности, антисимметричности и транзитивности.

Напомним ряд математических понятий:

Множество D выпукло, если с любыми своими точками оно содержит отрезок их соединяющий, т.е. х,yD [x,y]  D.

В конечномерном нормированном пространстве X функционалом будем называть отображение p: D → R для некоторого множества D X.

Функционал p называется линейным, если D =R и α, βR, x,yX выполняется равенство p(αx + βy) = αp(x) + βp(y).

Функционал p называется непрерывным, если он непрерывен в каждой точке x множества D. А последнее означает, что ε > 0 существует U_ε(x) - такая окрестность точки x, что yU_ε(x) ∩ D выполняется неравенство |p(y)-p(x)|<.

3. Широко известны классические модели экономических систем, рассматривающих все протекающие процессы как систему линей­ных зависимостей между показателями состо­яния системы. Классическим примером линей­ного подхода к моделированию является модель "затраты—выпуск" Леонтьева¹. Эта модель сводится к решению системы линейных уравнений, причем на основании спектральной теории линейных операторов выведены условия существования и единственности ре­шения системы уравнений, описывающего положение экономического равновесия. Поми­мо квазилинейной производственной функ­ции, использующейся в модели Леонтьева, можно использовать нелинейные функции для отображения зависимостей между пока­зателями состояния. Нелинейные функции являются более гибкими в представлении процессов, происходящих в экономике. При­мером часто используемой нелинейной фун­кции является производственная функция Кобба—Дугласа вида



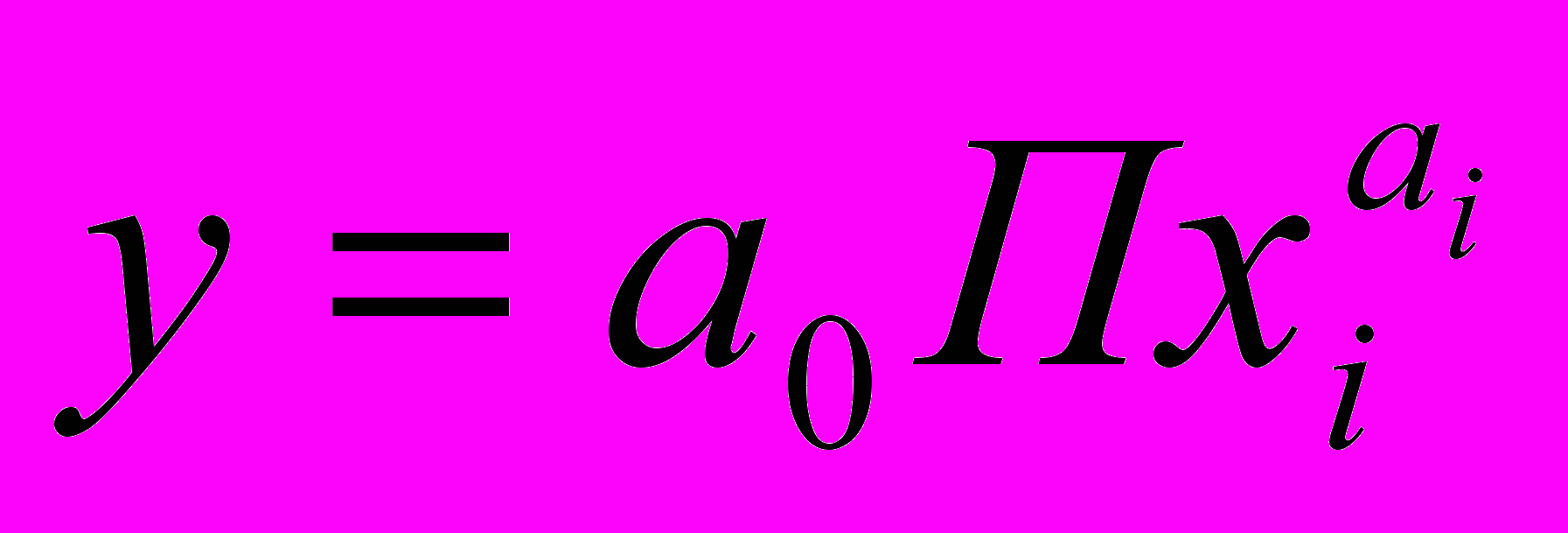
при этом нормирующие коэффициенты а₀ могут быть для простоты опущены, если их вклю­чить в единицу измерения у.

Для построения балансовой модели исполь­зуется принципиальная схема, предложенная Леонтьевым. При этом, в отличие от класси­ческого подхода, предлагается выделить ма­териальные (или количественные) и инфор­мационные (или качественные) ресурсы. С точки зрения моделирования отличие заклю­чается в том, что информационные ресурсы не дробятся в системе (на все подсистемы, использующие ресурс х., поступает одно и тоже количество х_г, называемое затратой г-го ресурса в системе). Для материальных ресурсов должно выполняться дополнительное ус­ловие равенства затраты i-го ресурса в сис­теме сумме затрат г-го ресурса во всех под­системах.

Рассматривается модель экономической системы с производственными функциями Кобба—Дугласа, иерархической структурой взаимосвязи между показателями состояния, характеризующими количества материальных ресурсов и произвольной структурой взаимо­связи между показателями состояния, опи­сывающими качественные ресурсы. Такая модель описывается следующей системой уравнений:

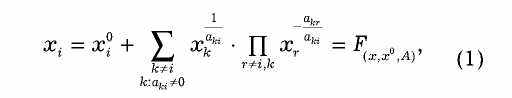где i = 1, п, А — матрица коэффициентов про­изводственной функции, x_i — ресурсы, пере­рабатываемые и производимые в системе, х⁰ — вектор ресурсов, предназначенный для потребления в случае макроэкономической модели и продажи в случае микроэкономи­ческой модели.

При изучении экономической модели очень важным является вопрос об условиях суще­ствования и единственности неподвижной точ­ки отображения (1) — положения экономи­ческого равновесия, характеризующего стабильное состояние экономики. Условия суще­ствования неподвижной точки обычно полу­чаются при применении теорем о сжимаю­щем отображении. В данном случае частные производные отображения (1) имеют сложный вид, не позволяющий применять стандартные формулировки теорем. Оказалось возможным получить достаточные условия существования равновесия в модели, опираясь на асимптоти­ческие результаты, полученные М. А. Красносельским². Эти условия накладываются на матрицу производственных коэффициентов А.

Для этого необхо­димо выделить конус в пространстве Rⁿ, на котором будет рассматриваться оператор (1). Если взять в качестве порождающего множества {х : т_i < х_i < M_i, i = 1,n}, где 0 < т_i < М_i — положительные константы, большие 0, эко­номический смысл которых может быть ин­терпретирован как границы диапазона "комплектности ресурсов в данной производствен­ной системе, тогда искомый конус будет пред­ставлять собой множество следующего вида: К = {tx : t<0, т_i < х_i < М_i, i = l,n}. Для такого конуса в работе Демченко К.С.³ доказана теорема:

Теорема. Для экономических балансовых систем вида (1) с производственными функция­ми Кобба—Дугласа, имеющими возрастающую отдачу, то есть при выполнении ограничений вида 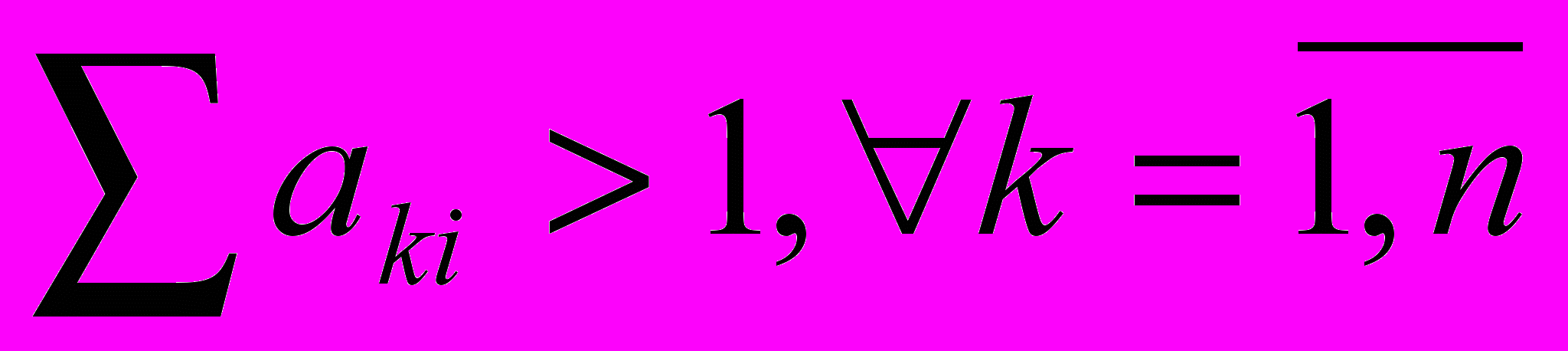положение экономичес­кого равновесия на конусе К (неподвижная точ­ка отображения (1)) существует.

При доказательстве этой теоремы используется тот факт, что конус К является нормальным, телесным и воспроизводимым. Отметим, что всеми этими свойствами обладает строго регулярный конус, поэтому в качестве порождающего множества в зависимости от экономической проблемы можно взять произвольный строго регулярный конус в пространстве Rⁿ. Общий вид таких конусов описан в работах⁴.


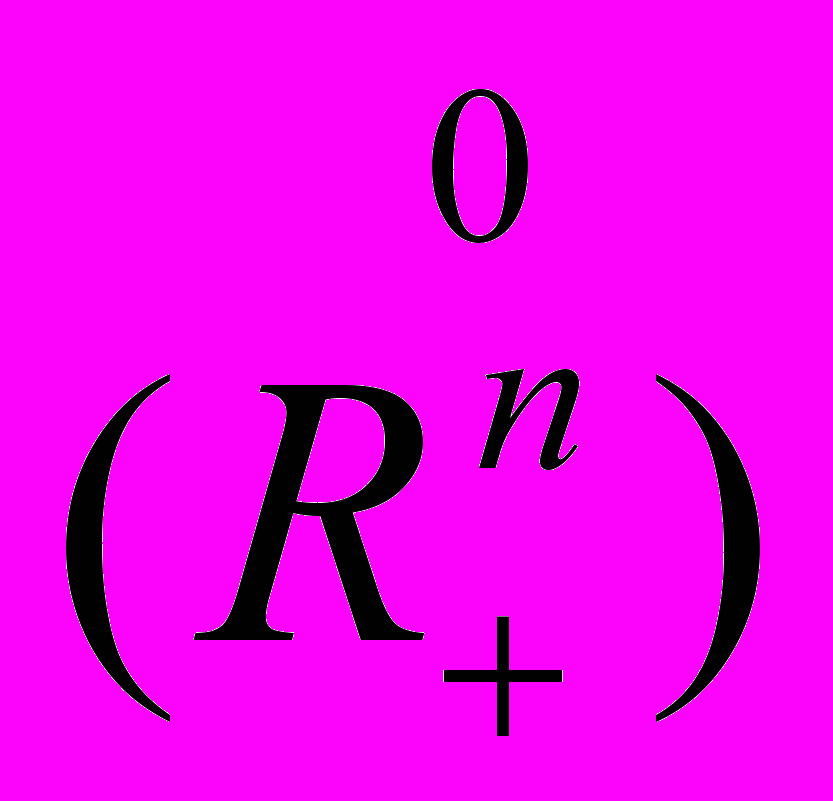4. Модель Неймана-Гейла - это такой выпуклый замкнутый конус Z ×, что у0, (0, у)Z, Pr₂Z ∩0. Модель Z назы­вается правильной, если Pr₁Z =. В дальнейшем мы рассматриваем правильные модели Неймана - Гейла.

Для пары (x, y)Z вектор x называется вектором затрат, а y - вектором выпуска. Подчеркивая этот содержательный смысл векторов, иногда пару (x,y)Z будем называть процессом.

По конусу Z можно построить многозначное отображение f: K → P(), где K = Pr₁Z, f(x) = {y| (x,y)Z}. Отображение f называется производственным отображением модели Неймана-Гейла. Известно, что конус Z - модель Неймана-Гейла тогда и только тогда, когда соответствующее отображе­ние f является квазилинейным многозначным отображением.

Состоянием равновесия модели Неймана-Гейла называется набор элементов σ= с числом  > 0, парой Z и функционалом ()*, для которых выполняются условия:

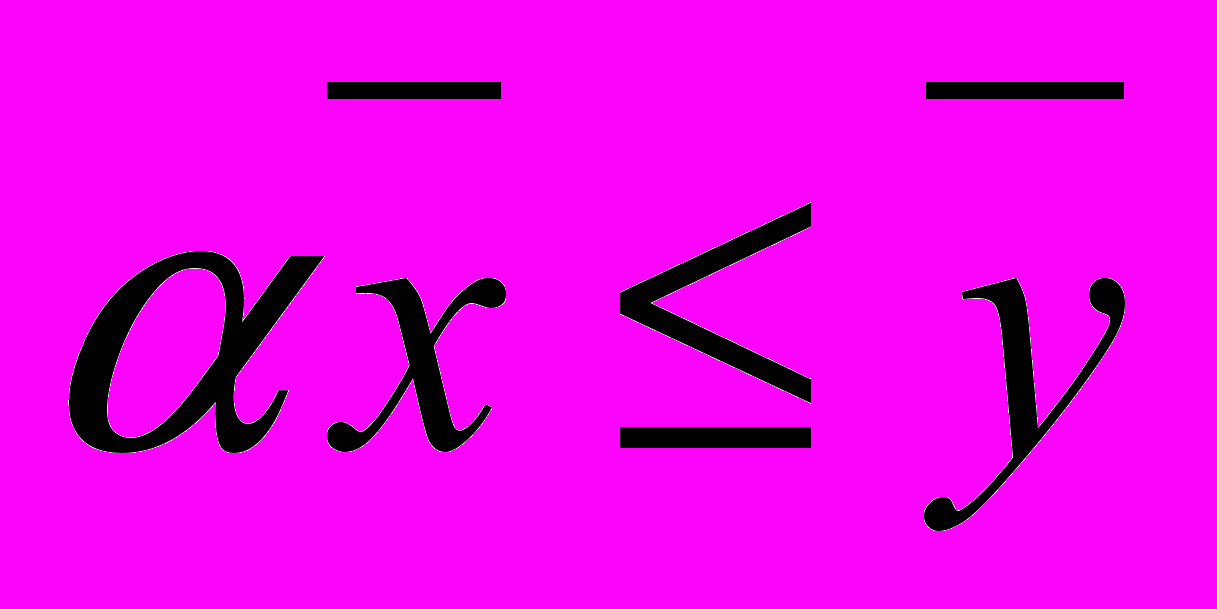1. (неравенство понимается в смысле конуса)
   
2. (x,y)Z выполняется неравенство
   

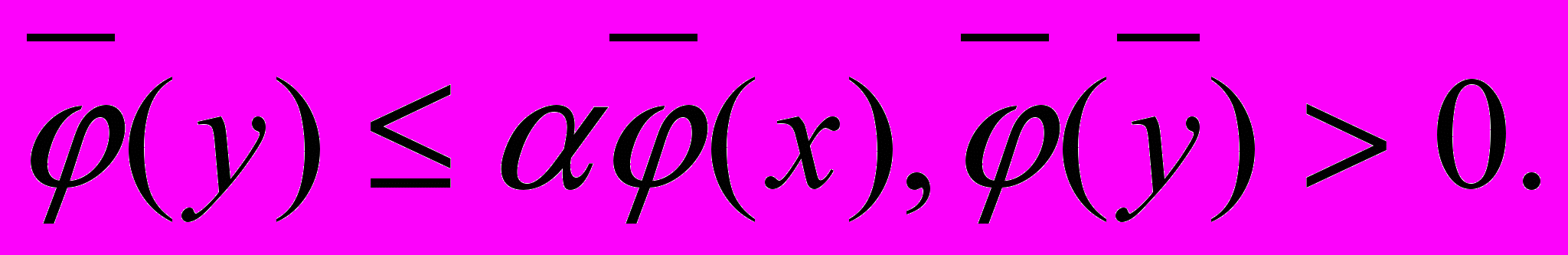
Число  =  (σ) называется темпом роста модели Неймана-Гейла Z (или производственного отображения f).

Если Z модель Неймана - Гейла, то Z' также модель Неймана - Гейла (с заменой Rⁿ на (Rⁿ)*). Тогда и для Z' можно говорить о темпах роста. Модель Z' будем называть двойственной по отношению к модели Z. Известно, что если  является темпом роста модели Неймана-Гейла Z, то 1/ является темпом роста отображения f'.

Траекторией правильной модели Неймана-Гейла Z называется последовательность (x_t)_t=0^∞ с (x_t,x_t+1)Z (то есть x_t+1f(x_t)). Содержательно это означает, что в момент времени t затраты x_t порождают продукцию x_t+1, которая полностью является затратами следующего момента времени t+1. Если в x_t учесть все экономические процессы "вокруг "моделируемого объекта, то подобные траектории описывают обшир­ный класс экономических явлений.

Конечная траектория (x_t)^T_t=0 называется оптимальной, если существует такой линейный функционал  ()*, что



где f ^T- суперпозиция отображения f с собой T раз. Пусть  - темп роста модели. Положим



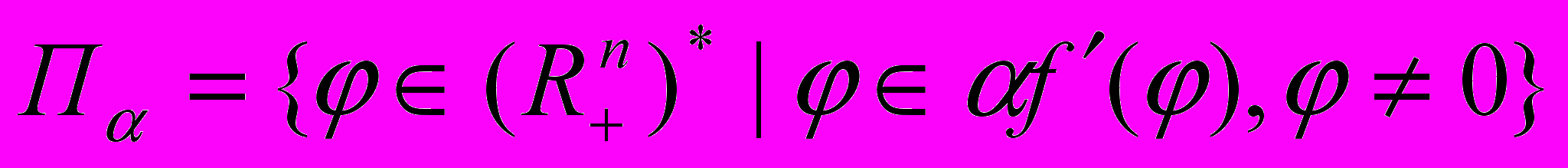
Из определения равновесия и свойств двойственного отображения f' следует, что П_{0}- это выпуклый замкнутый конус. Известно, что если  П_, то (, ^-1,…,^-t) является траекторией двойственной модели Z'.

Траектория (x_t)_t=0^∞ модели Z имеет средний темп роста , если (x_t)_t=0^∞ согласована с траекторией (, ^-1,…,^-t) при некотором r (П_), т.е. если .

Изучим асимптотику траекторий, имеющих средний темп роста . Для каждого  П_ обозначим



Множество 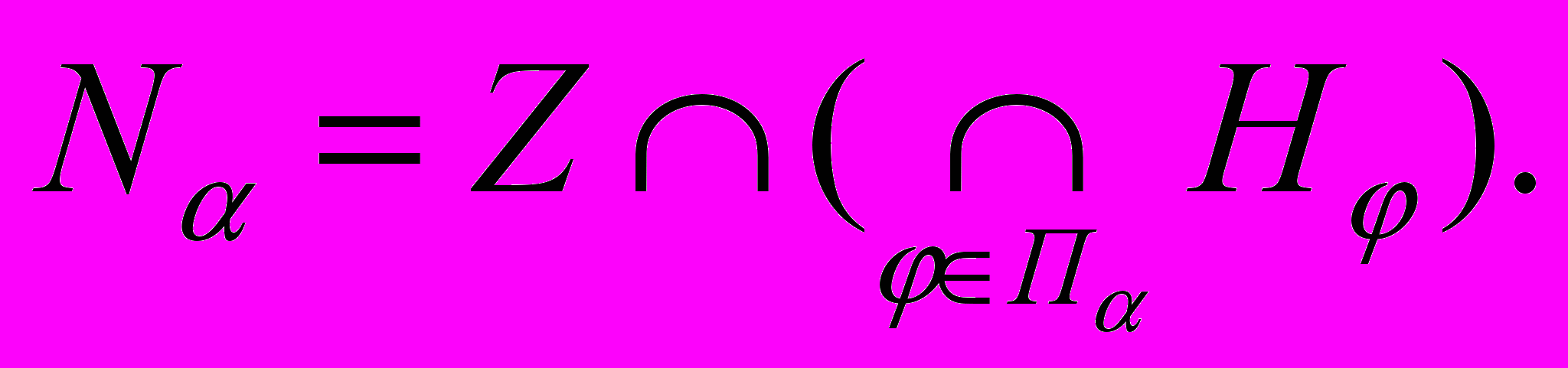называется неймановской гранью конуса Z.

Теорема о магистрали в слабой форме. Пусть  - темп роста модели Z, точка x₀ >0, функционал ψ≥0 таковы, что выполнены следующие условия:

а) из точки x₀ исходит траектория (x_t) со средним темпом ;

б) существуют положительные числа k₁, k₂ и такой функционал ri(Π_α), что k₁ ≤ψ≤ k₂.

Пусть задано положительное число ε.

Тогда для любой конечной траектории (x_t)^T_t=0, исходящей из точки x₀ и оптимальной в смысле ψ, число процессов (x_t,x_t+1), для которых

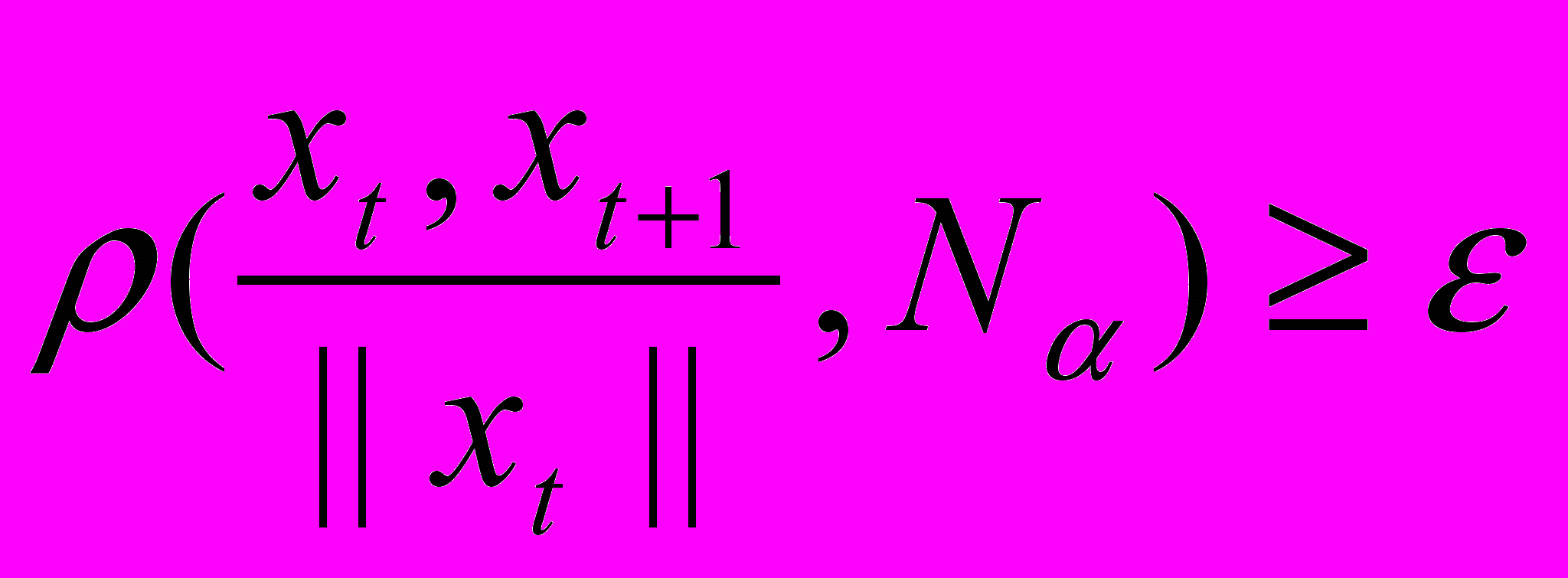не превосходит некоторого числа β, не зависящего от T.

Таким образом, не зависимо от «длины» траектории число оптимальных процессов ограничено. Заметим, что при нахождении расстояния  от элемента до конуса N_ можно воспользоваться формулами, определенными в работе автора⁵.

Таким образом, математические модели экономической динамики используют технику многозначных отображений и понятия теории полуупорядоченных пространств. Многозначные отображения позволяют создать общее описание процессов экономической динамики, а результаты, полученные в теории конусов, могут быть успешно использованы для решения проблем экономического моделирования. Сюда вкладываются модели Леоньева «затраты-выпуск» и серия моделей Неймана и Неймана-Гейла.