Программа дисциплины «Математические модели в экологии и экологическая информатика» дополнительная квалификация

Вид материала

Программа дисциплины

Содержание 4. Требования к уровню освоения содержания дисциплины 1. Разделы курса 2. Темы и краткое содержание Определение, структура, характеристики моделей Конечность модели. Упрощенность модели. Адекватность модели. Качественный анализ исследуемого процесса и построение математической (вычислительной) модели. Разработка вычислительного алгоритма. Создание программы для реализации полученного вычислительного алгоритма. Проведение расчетов на ЭВМ. Обработка результатов расчета, анализ, выводи. Модели ограниченного роста популяции с дискретным размножением Тема: Модель межвидовой конкуренции Логистическая модель межвидовой конкуренции 3. Перечень примерных контрольных вопросов и заданий для самостоятельной работы 4.Примерная тематика рефератов 5. Примерный перечень вопросов к зачету по всему курсу Тема: Модель межвидовой конкуренции. 1. Рекомендуемая литература (основная) ... Полное содержание

Подобный материал:

• Рабочая программа по дисциплине «Математические модели в экологии» для студентов дневного, 152.04kb.
• Программа курса "Математические модели естествознания и экологии", 22.79kb.
• Рабочая программа дисциплины «математические методы и модели в экологии» Код дисциплины, 129.07kb.
• Рабочая программа наименование дисциплины Математические модели в теории, 197.61kb.
• Рабочей программы учебной дисциплины математические методы и модели в экономике уровень, 37.32kb.
• Программа дисциплины «Дискретные математические модели», 241.81kb.
• Программа дисциплины «математические модели в экономике» Для направления, 156.79kb.
• Программа дисциплины «Дискретные математические модели», 224.89kb.
• Программа дисциплины «Актуальные проблемы современной экологии» дополнительная квалификация:, 138.34kb.
• Программа дисциплины «Математика (моделирование и информатика)» дополнительная квалификация:, 121.19kb.

Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

"Тобольский государственный педагогический институт им. Д.И. Менделеева"


Программа утверждена на заседании кафедры протокол № 1 от 28.09.2007

Программа дисциплины

«Математические модели в экологии и экологическая информатика»

дополнительная квалификация:

«Эколог» (в области профессиональной деятельности)»


Составители:

кандидат биологических наук, доцент кафедры зоологии, экологии и природопользования Т.В. Третьякова


кандидат физико-математических наук, доцент кафедры информатики и методики преподавания информатики

Е.В. Клименко


Тобольск 2007


Примерная программа дисциплины «Математические модели в экологии и экологическая информатика» федерального компонента цикла ОПД составлена в соответствии с Государственными требованиями к минимуму содержания и уровню профессиональной подготовки выпускника для получения дополнительной квалификации «Эколог» (в области профессиональной деятельности)».


I. Организационно-методический раздел


1. Цель курса


Назначение учебного курса «Математические модели в экологии и экологическая информатика» - профессиональная подготовка специалиста эколога (в области профессиональной деятельности), обладающего навыками построения экологических моделей природных систем и процессов и планирование деятельности в соответствии с законами функционирования и устойчивости надоргаизменных систем.

Математические модели в экологии и экологическая информатика- это раздел информатики, изучающий основы разработки, построения и анализа моделей, построенных с помощью программного обеспечения.

Основная цель предмета – научить принципам моделирования с целью создания компьютерной имитации природных систем и процессов.


2. Задачи курса

• сформировать понятия о структуре модели и принципах отражения функциональных связей внутри нее;
  
• раскрыть основные характеристики моделей;
  
• обосновать необходимость применения моделирования в современных исследованиях;
  
• сформировать необходимые практические навыки для построения моделей и их анализа в области экологии.
  

3. Место курса в профессиональной подготовке выпускника


Дисциплина направлена на подготовку специалиста эколога в области профессиональной деятельности, связанной с охраной окружающей среды для решения задач природоохранного содержания, в том числе организация, проектирование, менеджмента и осуществление экологической безопасности.


4. Требования к уровню освоения содержания дисциплины


После изучения данной дисциплины студент должен

иметь представления:

• об основных этапах развития моделирования;
  
• об основных типах моделей и их классификации;
  
• о принципах моделирования;
  

знать:

• структуру моделей и основные характеристики;
  
• основные законы и принципы моделирования;
  
• основные этапы построения моделей и их анализа;
  

уметь:

• использовать методы моделирования при решении задач в основной области профессиональной деятельности;
  
• провести декомпозицию объекта исследования;
  
• найти формальное описание объекта изучения и представить его в математическом виде;
  
• реализовать модель с помощью программного обеспечения;
  
• проводить анализ и обобщение полученных результатов;
  

владеть:

• системным подходом к решению экологических задач с использованием моделирования как метода познания;
  
• навыками принятия решений на основе полученных с помощью моделирования результатов исследований.
  

II. Содержание курса


1. Разделы курса


Раздел 1. Понятие модели. Классификация моделей. Основные этапы моделирования

История развития понятия «модель». Понятие «модель» как только к материальным объектам. Понятие «модель» как абстрактные, идеальные построения. Изоморфная теория модели с созданием Декартом и Ферма аналитической геометрии. Понятие модели в XX веке . Моделирование как теория познания, на идее которой основывается любой метод научного познания, как теоретический, так и экспериментальны. Определение, структура, характеристики моделей. Понятия "модель" В. А. Штоффа в книге "Моделирование и философия". Назначение модели. Характеристики моделей. Классификация моделей по способу возникновения. Основные этапы моделирования.


Раздел 2. Понятие вычислительного эксперимента. Этапы вычислительного эксперимента

Понятие вычислительного эксперимента как теоретическая база, его методологии и технология решения задач. Два вида эксперимента: лабораторный и натурный. Термин вычислительного эксперимента академика А.А. Самарского Математическое моделирование Основа вычислительного эксперимента является, как теоретическая база – прикладная математика, а техническая – мощные ЭВМ, Этапы вычислительного эксперимента.


Раздел 3. Компьютерное моделирование решение задач с помощью компьютерного моделирования

Общее понятие компьютерного моделирования. Компьютерное моделирование в экологи. Значение математических моделей в биологии и экологии. Цели создания математических моделей в классической экологии. Виды взаимодействий в классической экологии: взаимодействие организма и окружающей среды; взаимодействие особей внутри популяции; взаимодействие между особями разных видов (между популяциями). Модель неограниченного роста популяции с дискретным периодом размножения. Модели ограниченного роста популяции с дискретным размножением. Модель межвидовой конкуренции. Логистическая модель межвидовой конкуренции.


2. Темы и краткое содержание


Раздел 1. Понятие модели. Классификация моделей. Основные этапы моделирования

Тема: История развития понятия «модель»

Очень долго понятие «модель» относилось только к материальным объектам. Таковы, в частности представления Анаксимандра о Земле как плоском цилиндре, вокруг которого вращаются наполненные огнем полые трубки с отверстиями. Модель в этом смысле выступает как некоторая идеализация, упрощение действительности, хотя сам характер и степень упрощения, вносимые моделью, могли со временем меняться. Другими словами, первоначально моделью называли некоторое вспомогательное средство, объект, который в определенной ситуации заменял другой объект. При этом далеко не сразу была понята универсальность законов природы, всеобщность моделирования, т.е. не просто возможность, но и необходимость представлять любые наши знания в виде моделей.

Следующий шаг заключился в признании того, что моделями могут служить не только реальные объекты, но и абстрактные, идеальные построения. Так в 16 веке, модель представлялась как изоморфная теория (после создания Декартом и Ферма аналитической геометрии под моделью подразумевали теорию, которая обладает структурным подобием по отношению к дугой теории). В результате деятельности математиков, логиков и философов, занимающихся исследованием оснований математики, была создана теория моделей.

В XX веке понятие модели становится более общим, охватывающим и реальные и идеальные модели. При этом понятие абстрактной модели вышло за пределы математических моделей, стало относиться к любым знаниям и представлениям о мире. Сегодня моделирование является одной из основных категорий теории познания, на идее моделирования основывается любой метод научного познания, как теоретический, так и экспериментальный

Тема: Определение, структура, характеристики моделей

Определений модели известно достаточно много. Это объясняется тем, что определение модели также модель – разным целям требуется сопоставить разные аспекты моделей, поэтому различие в определении моделей неизбежно.

Наиболее полное определение понятия "модель" дает В. А. Штофф в своей книге "Моделирование и философия", в которой под моделью понимается такая мысленно представляемая или материально реализуемая система, которая отображая или воспроизводя объект исследования, способна заменить его так, что ее изучение дает нам новую информацию об этом объекте.

Модель (modus – мера образ, способ). Долгое время моделью некоторое вспомогательное средство способное заменять некоторый объект. В средние века под моделью понимались только материальные объекты специального типа (модель судов, карет). После создания аналитической геометрии пришло понимание, что модели могут быть абстрактные построения. 20-е века охватывает и материальные и идеальные объекты. Объектом можно считать предмет, процесс или явление.

Модель – это инструмент познания. Модель не просто отображает объект, а отображает его с какой-то целью. Следовательно, модель воспроизводит только те свойства, которые соответствуют цели исследования. На компьютере возможно создание модели таких объектов и процессов, которые невозможно изучить физически.

Назначение модели

• Изучить свойства объекта, его структуры, законов его развития и взаимодействия с окружающим миром
  
• Выбор лучшего способа управления объектом при заданных целях и критериях
  
• Программирование последствия различных воздействий на предмет
  
• Выявление новых знаний об объекте
  

Состав модели:

1. цель, ради которой производиться моделирование;
   
2. объект оригинал, который моделируется;
   
3. средства, из которых создается модель;
   
4. среда, в которой модель должна функционировать;
   
5. субъект, который управляет моделированием.
   

Рассмотрим некоторые характеристики моделей:

1. Согласованность с культурной средой. Для того чтобы модель отвечала своему назначению, необходимо, чтобы существовали условия, обеспечивающие ее функционирование. Не только модель должна приспосабливаться к среде, но и среда к модели

2. Конечность модели. Мир, частью которого мы являемся, бесконечен, как бесконечен и любой объект, не только в пространстве и времени, но и в своих связях с другими объектами, формах бытия, свойствах и тенденциях развития. Конечность характеризует любые конкретные явления и объекты, которые существуют в определенных пространственных и временных границах. Конечное – это форма проявления бесконечного, которое в свою очередь складывается из бесчисленного множества конечных объектов и явлений. Таким образом, в практике познания мира мы сталкиваемся с противоречием – необходимо познавать бесконечный мир конечными средствами. Способ преодоления этого противоречия состоит в построении моделей. Модель конечна, так как она отображает оригинал лишь в конечном числе отношений и ресурсы моделирования конечны.

3. Упрощенность модели. Упрощенность характеризует качественные различия модели и оригинала. Причиной вынужденного упрощения модели является необходимость оперирования с ней

Например: за неимением методов решения нелинейного уравнения мы линеаризуем его; в других случаях искусственно уменьшаем размерность, заменяем переменные величины постоянными, случайные – детерминированными и т.д.

4 Приближенность модели. Приближенность модели может быть очень высокой, например, уточнения числа пи производилась методами, указанными еще Архимедом: окружность заменялась многоугольником с большим числом сторон. В 1579 г. французский математик Ф.Виет вычислил пи с 9 знаками В наши дни с помощью ЭВМ число пи вычислено с точностью до миллиона знаков.

5 Адекватность модели. Модель, с помощью которой успешно достигается поставленная цель моделирования, будем называть адекватной этой цели. Модель адекватна моделируемому объекту, если полученные на ее основе результаты и выводы соответствуют реальному положению дел и неадекватна в противном случае. Основными причинами неадекватности обычно являются следующие:

а) для построения модели использовалась ошибочная теория или система идей,

б) в модели не учтена существенная информация.

Моделирование - это процесс построения, изучения и применения моделей.

1. Классификация моделей
   

Один из принципов классификации моделей состоит в соотнесении типов моделей с типами целей моделирования. Цель моделирования диктует какие стороны оригинала должны быть отражены в модели Различным целям соответствуют разные модели одного и того же объекта.

По назначению модели можно разделить на познавательн6ве и прагматические (инструментальные), что соответствует делению мелей построен, моделей на теоретические и практические. Познавательные модели являются формой организации и представления знаний, средством соединения новых знаний с имеющимися. Прагматические модели являются средством управления, организации практических действий, способом представления образцово правильных действий или их результата те являются рабочим приставлением целей.

По уровню моделирования модели можно разделить на эмпирические теоретические смешанные Эмпирические модели строятся на основе эмпирических фактов 'и зависимостей Теоретические – на основе математических описаний. Смешанные используют эмпирические зависимости и математические описания.

По способу построения модели можно разделить на материальные и идеальные. Материальные модели - это физические тела или системы. Основными разновидностями материальных моделей являются физические и аналоговые модели. При физическом моделировании реальному объекту ставится в соответствие его увеличенная или уменьшений копия. Эта копия создается на основе теории подобия, что и позволяет утверждать, что и модели сохранились требуемые свойства. Примерами таких отображений являются фотографии. масштабированные модели самолетов, кораблей, макеты зданий, шаблоны выкройки и т.д. Такое подобие называют пряным. Аналоговые модели основаны на замене исходного объекта объектом другой физической природы, обладающим аналогичным поведением, косвенном подобии (часы – аналог времени; электрический ток в подходящих цепях может моделировать транспортные потоки информации в сетях связи). Абстрактные или идеальные модели являются идеальными конструкциями построенными средствами мышления, сознания. К абстрактным моделям можно отнести языковые конструкции. На естественном языке мы можем говорить, обо всем поэтому он является универсальным средством построения любых абстрактных моделей.

По способу возникновения модели классифицируют следующим образом:

• модели, возникшие и результате прямого наблюдения, в результате прямого изучения и осмысливания (феноменологические модели);
  
• модели, возникшие в результате некоторого процесса дедукции, когда новая модель, получается как частный случай из некоторой более обшей модели (асимптотические модели);
  
• модели, возникшие в результате некоторого процесса индукции, когда новая модель является естественным обобщением «элементарных моделей» (индуктивные модели).
  

По способу поведения системы модели можно разделить на статические и динамические. Если модель отображает конкретное состояние предмета или явления (своего рода «моментальная фотография), она называется статической. Другими словами, множество состояний статической системы содержит один элемент. В курсе компьютерного моделирования один из важнейших классов статических компьютерных моделей - базы данных. Если модель отображает процесс изменения состояний во времени, то такую модель будем называть динамической. Процесс смены состояний динамической модели называется движением модели.

2. Основные этапы моделирования:
   

1. определение цели моделирования. Главное здесь – чётко сформулировать сущность проблемы, вопросы, на которые требуется получить ответы;
   
2. декомпозиция реального объекта. Выделение важнейших для цели моделирования черт и средств объекта, абстрагирование от второстепенного;
   
3. поиск формального описания. Изучение структуры объекта и основных его зависимостей. Определение основных конструкций модели, уточнение её параметров. Формирование гипотез (хотя бы предварительных) объясняющих поведение и развитие объекта;
   
4. построение математической модели и её анализ. Это этап формализации проблемы, выражение её в виде конкретных математических зависимостей и отношений;
   
5. подготовка исходной информации;
   
6. программная реализация модели, разработка алгоритмов для численного решения задачи, составление программы на ЭВМ и непосредственное проведение расчётов;
   
7. анализ численных результатов и их применение. На этом этапе встаёт вопрос о правильности и полноте результатов моделирования, об адекватности модели, о степени её практической применимости.
   

Раздел 2. Понятие вычислительного эксперимента. Этапы вычислительного эксперимента

Тема: Понятие вычислительного эксперимента

В математическом моделировании существует своя теоретическая база - его методологии и технология решения задач – вычислительный эксперимент.

Для проверки идей, гипотез, технических решений, работы новых технических конструкций ранее использовались 2 вила эксперимента: лабораторный и натурный.

Для лабораторного эксперимента требовалось создание экспериментальной установки, разработка измерительной аппаратуры и разработка методов проведения эксперимента. Чаще всего лабораторные эксперименты применялись в физике и химии.

Натурный эксперимент чаще всего применялся в технике, и суть его состояла в том, что новые аппараты подвергались различным испытаниям в целях определения их свойств, возможностей, характеристики.

Однако, натурные и лабораторные исследования часто стоят огромных денежных затрат. связаны с угрозой жизни или просто невозможны. Как быть с объектами, недоступными дли исследования, расположенными в недрах Земли или в далеком космосе? Какие процессы происходят, например, в глубинах Солнца или планет Солнечной системы? Как ведет себя материал заготовки при его термической и механической обработке? Посмотреть, «потрогать руками» то, что происходит в раскаленном добела слитке металла при прокатке на стане металлургического комбината, просто нереально. Здесь специалисту приходит на помощь особая, качественно новая форма изучения окружающей действительности - вычислительный эксперимент Термин введен академиком А.А. Самарским.

Технологию исследования математических моделей изучаемого объекта, основанную на построении и анализе с помощью электронной вычислительной техники, принято называть вычислительным экспериментом.

Основой вычислительного эксперимента является математическое моделирование, теоретическом базой - прикладная математика, а технической – мощные ЭВМ, Кроме того, для квалифицированного проведения исследовательской работы требуется знать многие разделы математики и механики, физики и химии, экологии и экономики.

Этапы вычислительного эксперимента.

1. Качественный анализ исследуемого процесса и построение математической (вычислительной) модели. На этом этапе вычислительного эксперимента из всего многообразия свойств, присущих объекту, выделяются и рассматриваются только те, которые представляют интерес в данной конкретной ситуации. Для исследуемого процесса строится математическая (вычислительная) модель, фиксирующая разделение всех факторов влияющих на объект на две группы: главные, которые учитываются; второстепенные, которые можно отбросить. Формулируются допущения или рамки применимости модели, в которых будут справедливы полученные на ее основе результаты.
   
2. Разработка вычислительного алгоритма. Второй этап вычислительного эксперимента связан с разработкой метода расчета сформулированной математической задачи, или как говорят, вычислительного алгоритма. Фактически, он представляет собой совокупность алгебраических формул, по которым ведутся вычисления, и логических условий, позволяющих установить нужную последовательность применения этих формул.
   
3. Создание программы для реализации полученного вычислительного алгоритма. Этап программирования для электронных вычислительных машин представляет собой проект подготовки кода, как правило, на языке высокого уровня, являющегося реализацией алгоритма численного решения задачи.
   
4. Проведение расчетов на ЭВМ. Этот этап вычислительного эксперимента, в чем m очень похож на лабораторный эксперимент. Только, если в лаборатории эксперимента с помощью специально построенной установки задает вопросы природе, то специалисты пи вычислительному эксперименту с помощью ЭВМ ставят эти вопросы математической модели.
   
5. Обработка результатов расчета, анализ, выводи. Результат расчета – это некоторая цифровая информация, которую необходимо расшифровать Проведение расчетов и анализ результатов - этап, требующий значительных интеллектуальных усилий и навыков по обработке, представлению и осмыслению получаемых решений.
   

Раздел 3. Компьютерное моделирование решение задач с помощью компьютерного моделирования

Тема: Общее понятие компьютерного моделирования

Под компьютерным моделированием будем понимать процесс представления информации о моделируемой системе посредством компьютера, а результат этого представления компьютерной моделью.

Компьютерное моделирование в экологи.

Математические модели в биологии и экологии используются практически с момента возникновения этом науки. Математические модели помогают установить некоторые закономерности и общие тенденции развития отдельных популяций, а также сообществ. Рассмотрим цели создания математических моделей в классической экологии:

• модели помогают проанализировать и систематизировать важные разрозненные свойства большого числа уникальных наблюдений;
  
• модели выступают в качестве универсального языка, с помощью которого может быть описано явление или процесс, и относительные свойства таких явлений становятся более понятными;
  
• модель может служить образцом «идеального объекта» или идеализированного поведения, при сравнении с которым можно оценивать и измерять реальные объекты и процессы.
  

Экология – это самостоятельный раздел биологии, изучающий взаимодействие организмов и окружающей среды. Основными понятиями в экологии является понятия особи, популяции и сообщества

Под особью понимают отдельный индивидуум, отдельный организм. Популяция - это совокупность особей одного вида, существующих в одно и тоже время и занимающих определенную территорию. Сообщество- это совокупность совместно существующих популяций.

В классической экологии рассматриваются взаимодействия нескольких видов:

• взаимодействие организма и окружающей среды;
  
• взаимодействие особей внутри популяции;
  
• взаимодействие между особями разных видов (между популяциями).
  

Тема: Модель неограниченного роста популяции с дискретным периодом размножения

Рассмотрим простейшую модель для вида с дискретными периодами размножения, в которой численность популяции в момент времени t равна N_t и численность изменяется во времени согласно величине чистой скорости воспроизводства R. Коэффициент к характеризует количество особей, которое воспроизводит отдельная особь, а также выживание уже существующих. Например, если к=4, то особь может воспроизвести четырех потомков и при этом погибнуть, или же воспроизвести трех потомков и при этом выжить.


N₀ – начальная численность популяции.

R – чистая скорость воспроизводства.

N_t+1=N_t*R, где N_t – численность популяции в некоторый момент времени t.

Пусть N₀=10, R=2, тогда

N₁= 10*2=20; N₂= 20*2=40; N₃= 40*2=80

Тогда численность популяции будет увеличиваться бесконечно.

Обнаруженную закономерность можно сформулировать так: если действие окружающей среды сказывается лишь на скорости прироста, то живые организм размножаются в геометрической прогрессии. Построенную модель называют модели: неограниченного роста в геометрической профессии.


Тема: Модели ограниченного роста популяции с дискретным размножением

В реальности популяций с неограниченным ростом не существует: ни при каких, даже самых благоприятных, условиях масса популяции не может превысить массу планеты, т.к нарушает фундаментальный закон сохранения вещества.

В реальности в какой-то момент времени начинают работать механизмы сдерживания роста популяции. Основным механизмом сдерживания является конкуренция.

Конкуренция – использование некоторого ресурса (пищи, воды, света, пространства и т.д.) каким-либо организмом, который тем самым уменьшает доступность этого ресурса для других организмов. Если организмы принадлежат к одному виду, то это внутривидовая конкуренция, если к разным – межвидовая


К – предельная плотность популяции




Рассмотрим простейший пример зависимости скорости воспроизводства от численности популяции. Точка А отражает ситуацию, в которой численность популяции близка к нулю, конкуренция при этом практически отсутствует. Следовательно, при низкой плотности популяции уравнение N_t+1=N_t*R справедливо.

Точка В отражает ситуацию, в которой численность популяции высока, высока и внутривидовая конкуренция. Фактически конкуренция настолько велика, что популяция может лишь восстанавливать свою численность в каждом поколении.

Следовательно в уравнение необходимо заменить чистую скорость воспроизводства на фактическую, которая уменьшается по мере роста популяции

a=(R-1)/К, а – коэффициент конкуренции.

Тогда: N_t+1=

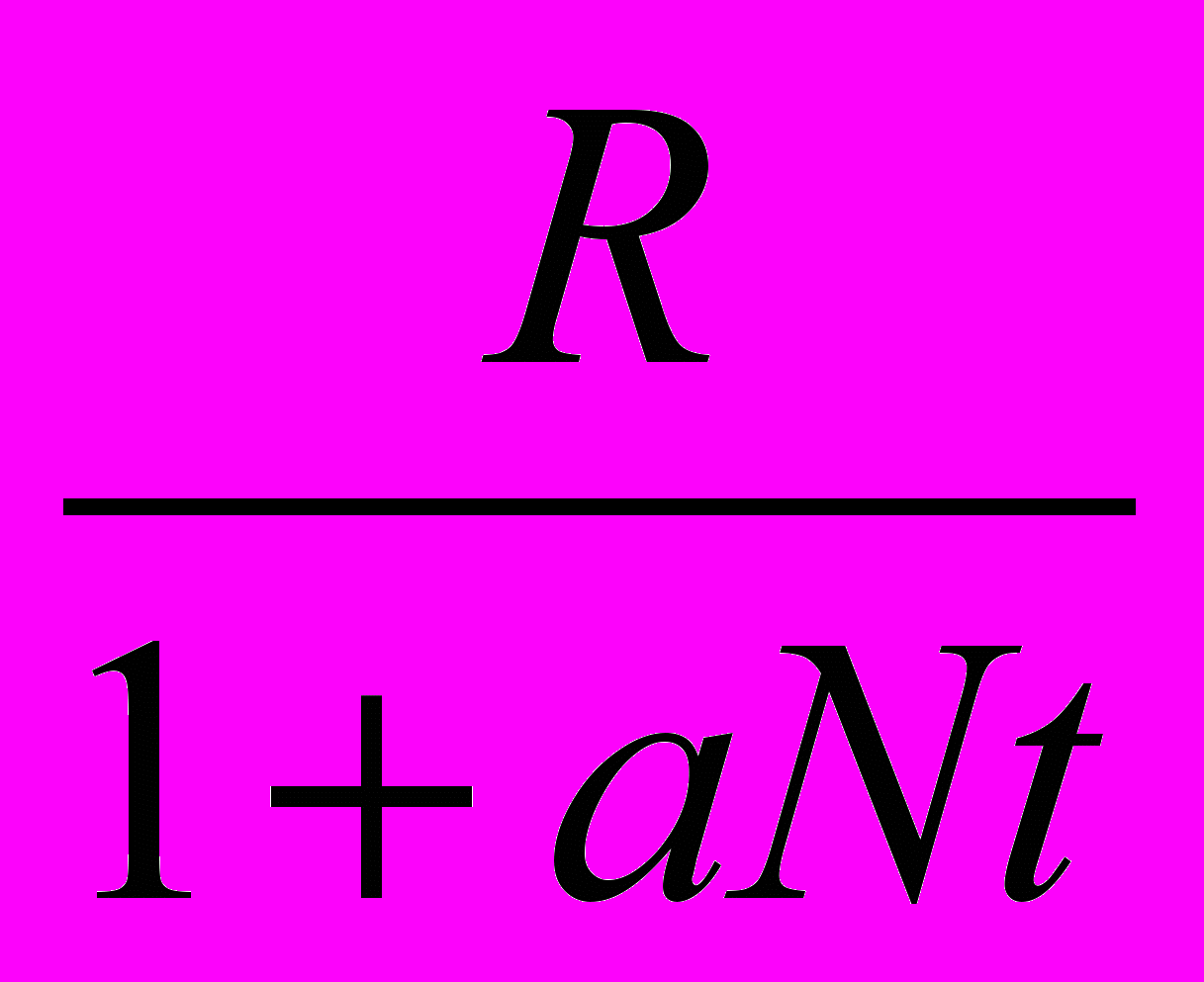
Такой тип конкуренции приводит к саморегуляции численности популяции.

Однако далеко не всегда реальная динамика популяций совпадает с данной формулой. Экологи вводят параметр b, который, определяет тип зависимости скорости роста популяции от ее численности. Окончательная формула:

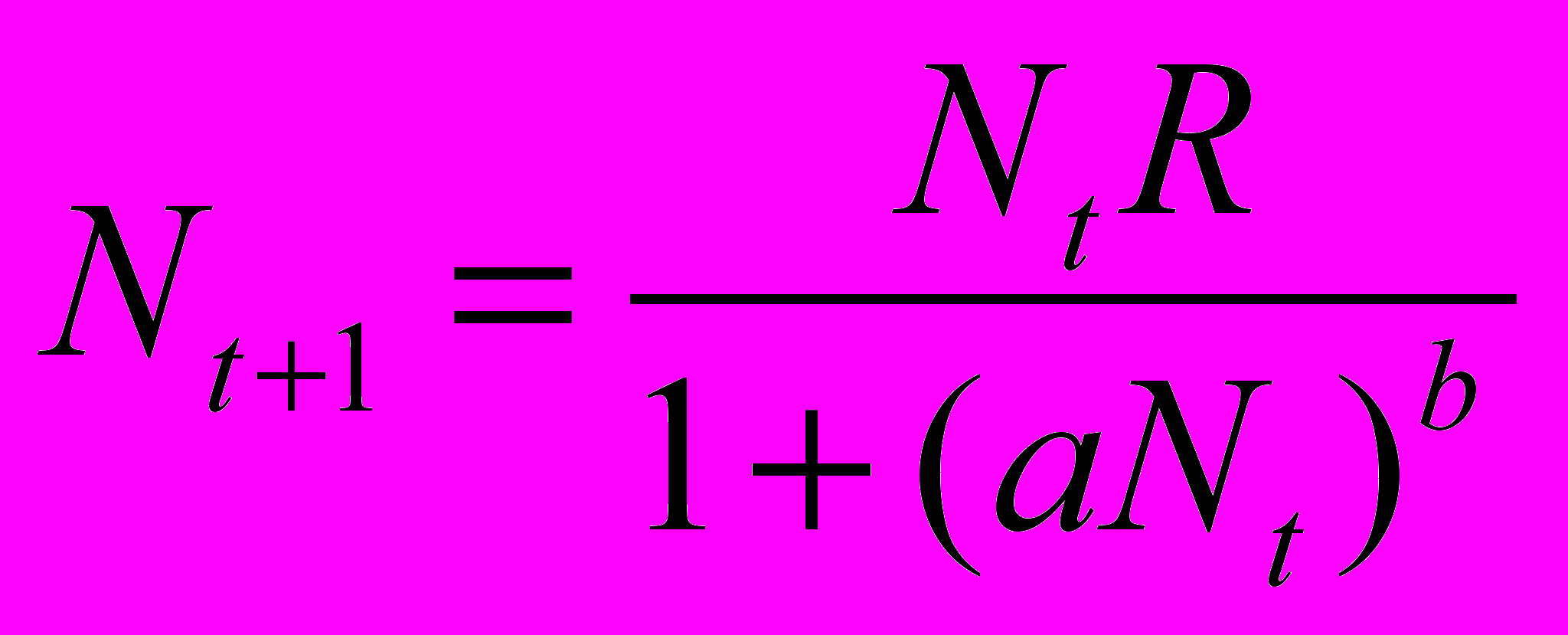
С помощью данной модели можно изучать различные динамики развития популяций.


Монотонное установление стационарной численности популяции





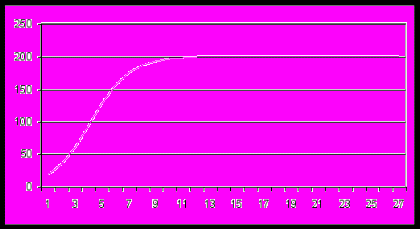
Колебательное установление численности популяции





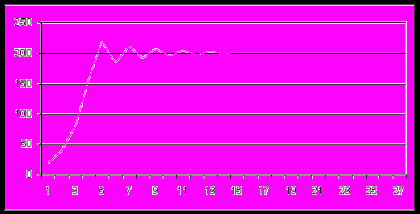
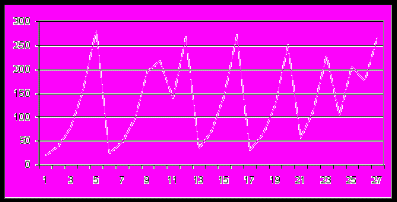
Устойчивые предельные циклы изменения численности популяции





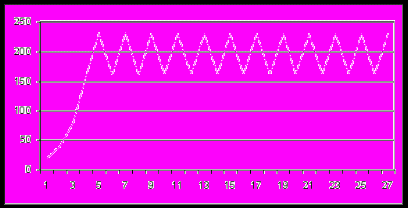
Случайные изменения численности популяции

Тема: Модель межвидовой конкуренции

Динамика изменения популяции с дискретным периодом размножения рассчитывается по формуле:

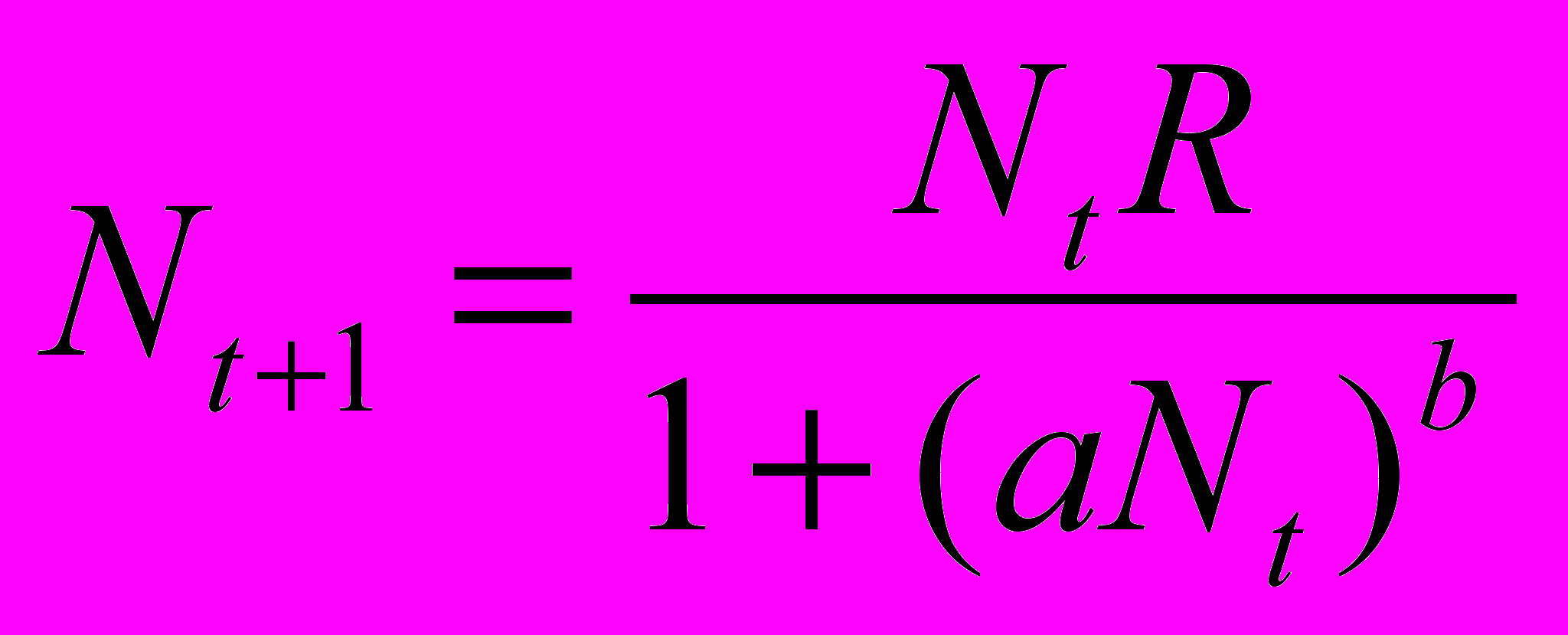
где, K -предельная плотность популяции

N₀- начальная численность популяции

а – коэффициент конкуренции

b - параметр который, определяет тип зависимости скорости роста популяции от ее численности.

Но для видов с непрерывным периодом размножения эта формула неприменима. Для исследования таких видов вводят новый параметр r – мгновенная удельная скорость численности популяции, т.е. приращение численности за единицу времени в пересчете на одну особь.

Общая формула:

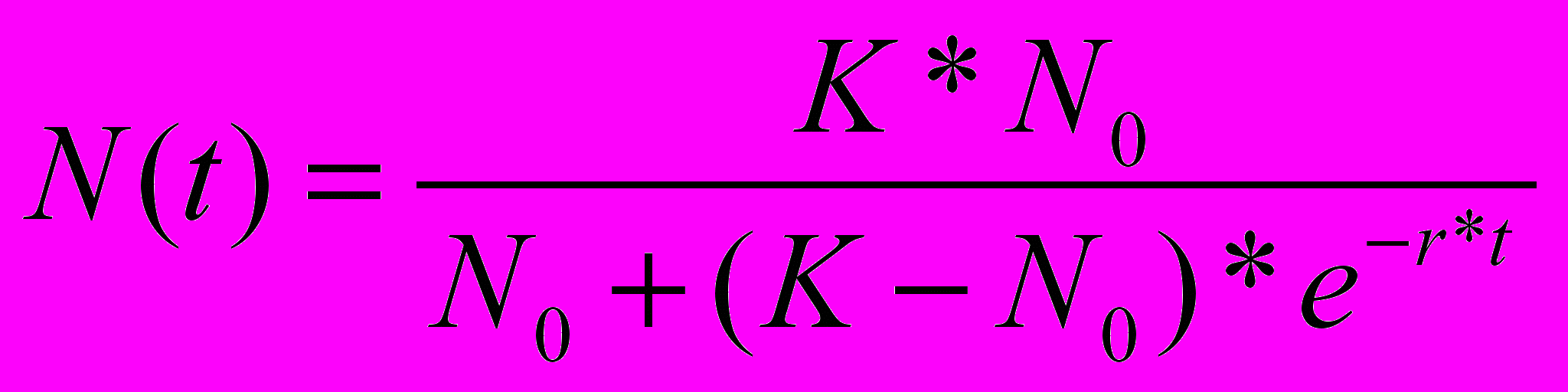
Это уравнение носит название логистического и играет большую роль в экологическом моделировании.


Тема: Логистическая модель межвидовой конкуренции

Сущность межвидовой конкуренции заключается в том, что у особей одного вида уменьшается плодовитость, выживаемость и скорость роста в результате использования того же ресурса, что и особями другого вида, причем влиянию конкуренции в той или иной мере подвергаются особи обоих видов.

Так как мы имеем дело с двумя различными популяциями, то введем соответствующие обозначения.

Пусть N₁ — численность первой популяции, a N₂ — второй. Предельные плотности популяции К₁ К₂ соответственно, мгновенная удельная скорость численности популяций – r₁ и r₂.

Необходимо понять, как же две популяции, конкурирующие между собой, влияют друг на друга. Для этого вводят специальный коэффициент конкуренции, разный для популяций, т.к. предполагается, что степень влияния у них различна. Для первой популяции – это коэффициент а₁₂, для второй а₂₁.

Для подсчета численности обеих популяций мы используем следующие формулы:

N₁ = К₁ – a₁₂*N₂

N₂ = К₂ – a₂₁*N₁

Это частный случай развития популяций. На самом деле формулы динамики популяций более сложные и используют аппарат дифференциального исчисления.


3. Перечень примерных контрольных вопросов и заданий для самостоятельной работы

1. Стадо бизонов в США в 1800 году насчитывало около 50 млн. голов, в т.ч.: половозрелые самцы в возрасте более 2 лет (ADM) - 16.8 млн. голов; половозрелые самки в возрасте более 2 лет (ADF) - 16.8 млн. голов; молодые самцы в возрасте от года до двух (YM) - 3.38 млн. голов; молодые самки в возрасте от года до двух (YF) - 3.38 млн. голов; телята в возрасте до года (BM) - 4.5 млн. голов; телочки в возрасте до года (BF) - 4.5 млн. голов.
   

67 % половозрелых самок ежегодно приносят по 1 детенышу, из которых 53 % - самцы, а 47 % - самки.40 % телят выживают в течение первого года, и лишь 30 % доживают до второго.

Среди половозрелых зверей ежегодно 0.5 % тонет, 5 % умирает от туберкулеза и 4.5 % погибает от хищников и по другим причинам. Общая ежегодная смертность среди взрослых составляет 10 %.

Кроме того, определенное количество самцов (QM) и самок (QF) ежегодно разрешено отстреливать. Стоит вопрос: как будет выглядеть популяция бизонов при данных условиях через какой-то промежуток времени? Попробуйте спрогнозировать это, введя квоту на отстрел и временной лаг.

2. Проанализировать динамику развития популяции при N₀ = 20, К=200, R=2, при b изменяющемся от 1 до 4, с шагом 1.
   

Известны ежегодные показатели рождаемости и смертности некоторой популяции. Рассчитайте, до какого возраста могут дожить особи одного поколения.

• Определите, до какого возраста доживут особи одного поколения при s = 30, х = 1000. Постройте график.
  

• Каково должно быть изначальное количество особей одного поколения, чтобы они доживали до 25 лет, при той же смертности?
  
• Каков должен быть показатель смертности, чтобы при той же рождаемости (x=1000) особи одного поколения доживали до 35 лет.
  
• Обобщите полученные результаты.
  

3. Определите, как будет меняться плотность популяции голубя в течение 5 ближайших лет, если наблюдения позволили установить, что ее плотность составляет 130 особей/га. За период размножения (раз в году) из одной кладки яиц в среднем выживает 1,3 детенышей. Смертность в среднем за год составляет 27% особей. При увеличении плотности популяции до 300 особей/га и выше, смертность составляет 50%.
   

• Введите значения исходных данных (Плотность популяции=130 и Плодовитость=1,3) и постройте в одной системе координат графики изменения плотности, рождаемости и смертности популяции голубя за 5 лет.
  
• Как изменится модель, если число самок составляет 1/3 от общего количества популяции? Если 2/3? Если ¼?
  
• Обобщите полученные результаты.
  

• Постройте график изменения численности популяции с непрерывным периодом размножения, при N=25, k = 200. R изменяется от 0,1 до 1. Обобщите результаты.
  

4. Постройте графики межвидовой конкуренции.

N₁=100, K₁=200, N₂=20, K₂=300. а₁₂ и а₂₁ изменяются от 0,1 до 1.

5. Проведите вычислительные эксперименты и ответьте на вопрос: что больше влияет на численность популяции – начальная численность, предельная плотность или коэффициент конкуренции?

6. Для производства вакцины на заводе выращивают культуру бактерий. Экспериментально установлена скорость размножения бактерий. Известно также, что при увеличении числа бактерий начинается самоотравление, причем количество погибающих бактерий пропорционально квадрату биомассы. Определенную массу забирают ежедневно на нужды производства. Требуется установить, как будет меняться масса бактерий с течением времени

Провести эксперимент при х₀ = 13000, 17000, 17500, 18000.

В программе предусмотреть возможность выхода из цикла, когда все бактерии погибнут, с указанием через сколько дней этой произойдет.

Построить модель в электронной таблице, создать графики изменения численности при этих же значениях.

Проанализировать полученные данные.


4.Примерная тематика рефератов

1. Моделирование как метод познания мира.
   
2. Достижения компьютерного моделирования на современном этапе развития.
   
3. Моделирование в экологии.
   
4. Основное программное обеспечение для реализации построения моделей.
   
5. Разработка модели «Жизнь» и ее реализация.
   
6. Разработка модели «Хищник-жертва» и ее реализация.
   
7. Имитационное моделирование.
   

5. Примерный перечень вопросов к зачету по всему курсу

1. Понятие модели. История возникновения и современное понимание термина «модель».
   
2. Моделирование как метод познания мира.
   
3. Различные подходы к классификации моделей.
   
4. Объект и система как базовые понятия компьютерного моделирования.
   
5. Цели, задачи и этапы моделирования.
   
6. Класс математических моделей и их особенности.
   
7. Вычислительный эксперимент. Этапы вычислительного эксперимента.
   
8. Типы моделей данных. Сходство и различия.
   
9. Компьютерное моделирование в экологии.
   
10. Модели динамики популяции с дискретным периодом размножения.
    
11. Модели динамики популяции с непрерывным периодом размножения. Модели развития популяций вида "жертва – хищник".
    
12. Имитационное моделирование в экологии.
    
13. Глобальные модели развития человечества.
    

III. Распределение часов курса по темам и видам работ

№ пп	Наименование тем и разделов	Всего часов	Аудиторные занятия (час)		Самостоя-тельная работа
			лекции	семинары
1	Раздел 1. Понятие модели. Классификация моделей. Основные этапы моделирования. Тема: История развития понятия «модель».	2	2	-	-
2	Тема: Определение, структура, характеристики моделей.	4	-	2	2
3	Раздел 2.Понятие вычислительного эксперимента. Этапы вычислительного эксперимента. Тема: Понятие вычислительного эксперимента.	6	2	2	2
4	Раздел 3. Компьютерное моделирование решение задач с помощью компьютерного моделирования Тема: Общее понятие компьютерного моделирования.	6	2	2	2
5	Тема: Модели ограниченного роста популяции с дискретным размножением.	4	-	2	2
6	Тема: Модель межвидовой конкуренции.	4	-	2	2
7	Тема: Логистическая модель межвидовой конкуренции.	4	-	2	2
Итого:		30	6	12	12

IV. Форма итогового контроля

зачет


V. Учебно- методическое обеспечение дисциплины


1. Рекомендуемая литература (основная)

1. Вронский, В.А. Экология: Словарь-справочник / В.А. Вронский. – Ростов н/Д.: Феникс, 2002.
   
2. Гашев, С.Н. Статистический анализ для биологов (Пакет программ «STATAN-1996») / С.Н. Гашев. – Тюмень: ТюмГУ, 1998. – 51 с.
   
3. Гершензон, В.Е. Информационные технологии в управлении качеством среды обитания: учеб. пособие / В.Е. Гершензон, Е.В. Смирнова, В.В. Элиас; под ред. В.Е. Гершензона. – М.: Академия, 2003.
   
4. Информатика. Базовый курс: учеб. пособие / под ред. С.В. Симоновича. – СПб: Питер, 2005.
   
5. Киселев, В.Н. Основы экологии: учеб. пособие / В.Н. Киселев. – Мн.: Университет, 2000.
   
6. Советов, Б.Я. Информационные технологии: учеб. для вузов / Б.Я. Советов. – М.: Высшая школа, 2005.
   
7. Экология: учеб. пособие / В.В. Денисов [и др.]. – Ростов н/Д: МарТ, 2002.
   
8. Ясманов, Н.А. Основы экологии: учеб. пособие / Н.А. Ясманов. – М.: Академия, 2003.
   

2. Рекомендуемая литература (дополнительная)

1. Биологическая кибернетика / под ред. А.Б.Когана. – М.: Высшая школа, 1972. – 384 с.
   
2. Гашев, С.Н. Млекопитающие в системе экологического мониторинга / С.Н. Гашев. – Тюмень: ТюмГУ, 2000. – 220 с.
   
3. Грейг-Смит, П. Количественная экология растений / П. Грейг-Смит. – М.: Мир, 1967. – 360 с.
   
4. Коли, Г. Анализ популяций позвоночных / Г. Коли. – М.: Мир, 1979. – 364 с.
   
5. Реймерс, Н.Ф. Экология (теории, законы, правила, принципы и гипотезы) / Н.Ф. Реймерс. – М.: Россия молодая, 1994. – 367 с.
   
6. Розанов, С.И. Системная экология / С.И. Розанов. – Ижевск: УдГУ, 1996. – 204 с.
   
7. Федоров, В.Д. Экология: учеб. пособие / В.Д. Федоров, Т.Г. Гильманов. – М.: МГУ, 1980. – 464 с.
   
8. Шилов, И.А. Экология: учеб. для вузов / И.А. Шилов. – М.: Высшая школа, 2003.
   

3. Перечень обучающих, контролирующих компьютерных программ, диафильмов, кино- и теле- фильмов, мультимедиа

Комплект мультимедийных лекций – 6 шт.