Тема урока Основные понятия

Вид материала

Урок

Содержание 1.    Актуализация опорных знаний. 3. Новая тема. Моделирование физических процессов. 1. Описание постановки задачи. Построение математической модели. 2. Компьютерный эксперимент. Задача о прямолинейном движении тела Шаг увеличения количество разбиений интервала времени Цель: Выяснить зависимость расстояния и времени полета тела от угла броска и начальной скорости. Угол броска и начальная скорост Дано: v0 - начальная скорость (м/c) a - угол бросания (радианы) Найти Задача о полете тела , брошенного под углом к горизонту (a) Начальная скорость Угол бросания Как зависит дальность полета от угла броска на Луне В) Выяснить, при каком угле броска тело улетит на наибольшее расстояние. Задача о полете тела , брошенного под углом к горизонту (в) Задача о полете тела, брошенного под углом к горизонту Промежуточные результаты Наибольшее расстояние Домашнее задание.

Подобный материал:

• Тема: Основные понятия и определения, 121.92kb.
• Тема: Основные понятия и определения, 164.71kb.
• План урока: Орг момент. Повторение изученного. Объявление темы. Изучение нового материала., 66.27kb.
• Урока Дата Тема урока Основные понятия урока, 628.93kb.
• Урока Тема урока Основные понятия, 134.98kb.
• Урока Тема урока Основные теоретические понятия, 92.1kb.
• Наименование раздела программы Тема урока Кол-во часов Тип урока, 819.25kb.
• Тема урока Задачи урока, 245.26kb.
• План урока Оргмомент Мотивационное начало урока. Объявление темы, целей урока, 75.92kb.
• Урока Тема урока Кол-во ча-сов, 513.94kb.

1.    Актуализация опорных знаний.

Письменно ответьте на вопросы.

Вариант №1.

1)     Приведите пример материальной и информационной модели автомобиля.

2)     Какая модель называется математической?

3)     Этапы решения задачи на компьютере.

Вариант №2.

1)     Приведите пример материальной и информационной модели Земного шара.

2)     Какая модель называется информационной?

3)     Какие этапы включает в себя компьютерный эксперимент?

 

2. Анализ домашней контрольной работы.

 

Загрузить файл «Задачи к урокам», лист «Домашняя контрольная работа»

Предложить учащимся прокомментировать решение задач 1,2.

 

3. Новая тема. Моделирование физических процессов.

 

Задача №1

Тело движется прямолинейно с ускорением а м/с² и начальной скоростью v м/с. Требуется определить, какой путь пройдет тело за T секунд

 

1. Описание постановки задачи. Построение математической модели.

Вы знаете ответ к этой задаче: S = v×T + aT² /2 (1)

Приведенное соотношение неоднократно проверялось в различных физических экспериментах, в том числе и вами в лабораторных работах по физике. Но всякий физический эксперимент обязательно содержит ошибки измерений. Поэтому совершенно точно формулу (1) проверить экспериментально невозможно. А чтобы вывести ее теоретически, на уроках физики, по сути дела, строилась приближенная математическая модель равноускоренного движения (хотя слово «модель», конечно, не употреблялось). Нетрудно убедиться в том, что эта модель ос­нована на следующем допущении: если интервал времени разбит на очень большое количество равных маленьких промежутков, то мы не сильно ошибемся, предполагая, что скорость тела на каждом из них постоянна (т. е. движение равномерно) и меняется «мгновенно» в конце каждого промежутка – второстепенные факторы.

Принято считать, что при неограниченном увеличении числа отрезков разбиения мы получим величину перемещения с любой точностью. Фактически это еще одно предположение, которое лежит в основе модели, приводящей к формуле (1), чем мельче отрезки разбиения, тем ближе будет результат к значению, полученному по формуле (1).

Определим, что считать исходными данными и результатами нашей модели. Ясно, что исходными являются начальная скорость v, ускорение a, время движения T – главные факторы, результатом - перемещение S.

Теперь наша цель — получить математическое соотношение, связывающее исходные данные и результат. Оно будет зависеть от того, на сколько частей мы разобьем интервал времени.

Разобьем интервал времени от 0 до T секунд на N равных частей. Величина каждой части составляет r = T/N секунд. По нашему предположению скорость тела в течение каждого из этих промежутков времени считается постоянной. В течение первых r секунд тело движется с начальной скоростью v₁ = v м/с. На следующем отрезке (от r секунд до 2г секунд) — со скоростью v₂ = v₁ + ar м/с. В течение третьего промежутка времени скорость будет равна v₃ = v₂ + ar м/с- Как видите, последовательность v₁, v₂, v₃ … является арифметической прогрессией с первым чле­ном v и разностью d = ar. Найдем путь, пройденный телом:

Воспользуемся формулой для суммы N членов арифметической прогрессии:

S=((2v+d (N- 1)) N/2) r=((2v+ar (N - 1)) N/2) r.

Раскрывая скобки и подставляя T/N вместо г, получим:

Эта формула и является математическим соотношением, свя­зывающим исходные данные и результат. Построение математи­ческой модели закончено. Вы видите, что полученная формула для S отличается от формулы (1) слагаемым — aT'²/2N, которое показывает, с какой степенью точности построенная модель описывает равноускоренное движение. Пусть a=5 м/с.

 

2. Компьютерный эксперимент.

Для моделирования будем использовать среду электронной таблицы (Файл «Задачи к урокам, лист «Прямолинейное движение»).

 

	A	B
1	Задача о прямолинейном движении тела
2	Исходные данные
3	Начальная скорость	60
4	Время движения	15
5	Шаг увеличения количество разбиений интервала времени	100

 

	A	B	С	D
6	Расчет
7	Промежуточные результаты		Результаты
8	Количество разбиений интервала	Время Движения	Начальная скорость	Дальность полета
9	100	15	60	=C9*B9+5*B9*B9/2-5*B9*B9/(2*A9)
10	=A9 + $B$5	Заполнить вниз	Заполнить вниз	Заполнить вниз
11	Заполнить вниз

 

1	Прямолинейное движение тела
2	Исходные данные
3	Начальная скорость	60
4	Время движения	15
5	Шаг изменения количества разбиений интервалов времени	100
6	Расчет
7	Промежуточные результаты		Результаты
8	Количество разбиений интервала времени	Начальная Скорость	Время Движения	Перемещение S
9	100	60	15	1456,875
10	200	60	15	1459,6875
11	300	60	15	1460,625
12	400	60	15	1461,09375
13	500	60	15	1461,375
14	600	60	15	1461,5625
15	700	60	15	1461,696429
16	800	60	15	1461,796875
17	900	60	15	1461,875
18	1000	60	15	1461,9375

 

Вывод:

Точность результата определяется количеством разбиений интервала, чем больше число измерений, тем точнее результат.

 

Задача №2

Требуется построить математическую модель физического процесса: движения тела, брошенного под углом к горизонту.

Цель: Выяснить зависимость расстояния и времени полета тела от угла броска и начальной скорости. Угол броска и начальная скорость являются главными факторами процесса моделирования.

 

1. Описание постановки. Построение математической модели

При расчете будем использовать следующие допущения (второстепенные факторы):

        Система координат имеет начало в точке бросания;

        Тело движется вблизи поверхности земли, это значит, что ускорение свободного падения постоянно и равно 9,81 м/с²

      Сопротивление воздуха не учитывается, поэтому движение по горизонтали равномерное.



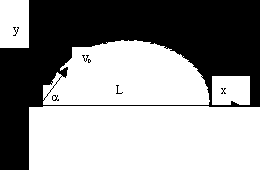
Пусть:

v₀ - начальная скорость (м/c),

a - угол бросания (радианы),

L - дальность полета (м).

Движение тела, брошенного

под углом к горизонту, описывается

формулами

 

v_x = v₀*cosa - горизонтальная составляющие начальной скорости

v_y = v₀*sina - вертикальная составляющие начальной скорости

x= v_x t - т. к. движение по горизонтали равномерное

y= v_y t (1) - т. к. движение по вертикали равноускоренно с отрицательным ускорением.

Искомым в этой задаче будет то значение x=L, при котором y=0.

Дано: v₀ - начальная скорость (м/c)

a - угол бросания (радианы)

Найти: L - дальность полета (м).

Связь: L = v_x t - дальность полета,

0 = v_y t - точка падения

v_x = v₀*cosa - горизонтальная проекция вектора скорости

v_y = v₀*sina - вертикальная проекция вектора скорости

g=9,81 - ускорение свободного падения

При: v₀ > 0, 0 < a < p/2

Подставляем в формулу (1) значение v_y. Получаем уравнение:

v₀*sina*t - gt²/2=0. Чтобы решить это уравнение выразим из формулы x= v_x t переменную t: t=x/(v₀*cosa). Подставив это значение в уравнение, получаем решение: 2v₀²*sina*cosa= g*L. Дальность полета равна: L=(v₀²*sin2a )/g, т. е. зависит от начальной скорости и угла наклона.

 

2. Компьютерный эксперимент.

Для моделирования будем использовать среду электронной таблицы (Файл «Задачи к урокам, лист «Дальность полета»).

a)    Выяснить, как зависит дальность полета от угла броска.

 

		A		B
	1	Задача о полете тела , брошенного под углом к горизонту (a)
	2	Исходные данные
	3	Начальная скорость		60
	4	Угол бросания		15
	5	Шаг увеличения угла		15
			A	B			С
6			Расчет
7			Промежуточные расчеты		Результаты
8			Угол бросания	Начальная скорость	Дальность полета
9			15	60	= ($B$92*SIN(2*A9 *3,14/180)/9,81
10			=A9 + $B$5	Заполнить вниз	Заполнить вниз
11			Заполнить вниз

Исходные данные
Начальная скорость	60
Угол бросания	15
Шаг увеличения угла	15
Расчет
Промежуточные результаты		Результаты
Угол бросания	Начальная Скорость	Дальность полета
15	60	183,40187
30	60	317,71003
45	60	366,97236
60	60	318,00213
75	60	183,90787

Выводы:

С увеличением угла бросания от 15⁰ до 45⁰ и постоянной скорости полета дальность полета увеличивается;

С увеличением угла бросания от 45⁰ до 90⁰ и постоянной скорости полета дальность полета уменьшается.


б) Выяснить, как зависит дальность полета от угла броска на Луне

(g=1,63 м/с) (Файл «Задачи к урокам, лист «Дальность полета на Луне»).

 

Как зависит дальность полета от угла броска на Луне
Исходные данные
Начальная скорость	60
Угол бросания	15
Шаг увеличения угла	15
Расчет
Промежуточные результаты		Результаты
Угол бросания	Начальная скорость	Дальность полета
15	60	1103,7867
30	60	1912,1076
45	60	2208,5883
60	60	1913,8656
75	60	1106,8321

Выводы:

Дальность полета больше, чем на Земле;

С увеличением угла бросания от 15⁰ до 45⁰ дальность полета увеличивается;

С увеличением угла бросания от 45⁰ до 90⁰ дальность полета уменьшается.

 

В) Выяснить, при каком угле броска тело улетит на наибольшее расстояние.

Необходимо определить угол броска от 30^° до 70^°, при котором дальность полета тела будет наибольшей. Какое при этом будет время полета?

(Файл «Задачи к урокам, лист «Наибольшее расстояние»).

 

	A	B
1	Задача о полете тела , брошенного под углом к горизонту (в)
2	Исходные данные
3	Начальная скорость	15
4	Угол бросания	30
5	Шаг увеличения Угла	5

 

	A	B	С
6	Расчет
7	Промежуточные расчеты		Результаты
8	Угол бросания	Начальная скорость	Дальность полета
9	30	15	=($B$92*SIN(2*A9* 3,14/180)/9,81
10	=A9 + $B$5	Заполнить вниз	Заполнить вниз
11	Заполнить вниз

 

Задача о полете тела, брошенного под углом к горизонту
Исходные данные
Начальная скорость	15
Угол бросания	30
Шаг увеличения угла	5
Расчет
Промежуточные результаты		Результаты
Угол бросания	Начальная скорость	Дальность полета	Время Полета
30	15	19,856877
35	15	21,54772
40	15	22,584509
45	15	22,935773
50	15	22,590849
55	15	21,560208
60	15	19,875133
65	15	17,586773
70	15	14,764588
Наибольшее расстояние		22,935773	1,529052

Выводы:

        Наибольшее расстояние пролетит тело при начальной скорости 15 м/c, когда угол броска будет 50°

        Время полета при этом

1,52 с.

Домашнее задание.

Знать математическую модель и программу движения тела, брошенного под углом к горизонту.

Вопросы

Изменение численности биологического вида в зависимости от рождаемости, смертности и других факторов

Ход урока

Новая тема.

Вычислительная техника открыла широчайшие возможности для изу­чения процессов, происходящих в природе и обществе. Среди задач, успешно моделируемых на компьютерах, особое место занимают эко­логические. Круг их необычайно велик. С одной стороны, это задачи развития биологических видов в природной среде, с другой — исследо­вание влияния деятельности человека на природу.

Моделирование в экологической сфере позволяет прогнозировать раз­витие биологических популяций, управлять численностью отдельных видов и предсказывать влияние факторов, угрожающих их развитию.

Определенную природную среду населяет один или несколько ви­дов живых организмов. У них может быть разная среда обитания, раз­ные источники питания, т. е. различные внешние факторы, влияющие на численность.

Жизнь некоторых популяций идет обособленно, они как бы зани­мают свою «экологическую нишу». Их численность практически не зависит от наличия соседствующих видов. Некоторые виды живых организмов хотя и не угрожают напрямую своим соседям, но имеют с ними общую среду обитания и/или одни и те же источники питания. Про такие виды говорят, что они соперни­чают друг с другом.

И наконец, живые существа могут враждовать, т. е. один вид охо­тится за другим и уничтожает его. Требуется изучить, как изменяется численность популяций в раз­ных условиях.