Тема урока Основные понятия
| Вид материала | Урок |
- Тема: Основные понятия и определения, 121.92kb.
- Тема: Основные понятия и определения, 164.71kb.
- План урока: Орг момент. Повторение изученного. Объявление темы. Изучение нового материала., 66.27kb.
- Урока Дата Тема урока Основные понятия урока, 628.93kb.
- Урока Тема урока Основные понятия, 134.98kb.
- Урока Тема урока Основные теоретические понятия, 92.1kb.
- Наименование раздела программы Тема урока Кол-во часов Тип урока, 819.25kb.
- Тема урока Задачи урока, 245.26kb.
- План урока Оргмомент Мотивационное начало урока. Объявление темы, целей урока, 75.92kb.
- Урока Тема урока Кол-во ча-сов, 513.94kb.
1. Актуализация опорных знаний.
1.1 Диктант
В письменном виде ответьте на вопросы.
Вариант №1.
- Что такое модель?
- Какая модель называется статической?
- Этапы моделирования.
Вариант №2.
- Что такое моделирование?
- Какая модель называется динамической?
- Типы моделей по способу представления.
1.2. Проверка домашнего задания
2. Новый материал.
Беседа учителя о математической модели, этапах решения задачи на компьютере. Беседа сопровождается демонстрацией презентации на экране.
Модель задачи
Пусть вам надо решить какую-либо задачу, и вы хотите воспользоваться услугами ЭВМ. С чего начать? Прежде всего, нужно разобраться, что дано, что требуется получить, как связаны исходные данные и результаты. Предположения, которые позволяют в море информации об изучаемом явлении или объекте выудить исходные данные, определить, что будет служить результатом, и какова связь между исходными данными и результатом – называют моделью задачи.
Понятие математической модели.
В моделировании есть два различных пути. Модель может быть похожей копией объекта, выполненной из другого материала, в другом масштабе, с отсутствием ряда деталей. Например, это игрушечный кораблик, самолетик, домик из кубиков и множество других известных вам натурных моделей. Модель может отображать реальность в абстрактной форме. В таком случае почти всегда привлекаются средства математики, и мы имеем дело с математической моделью:
математическая модель выражает существенные черты объекта или процесса языком уравнений и других математических средств. Собственно говоря, в историческом аспекте, сама математика обязана своим существованием тому, что пыталась отражать, т. е. моделировать, на своем специфическом языке закономерности окружающего мира.
Под математической моделью понимают систему математических соотношений – формул, уравнений, неравенств и т. д., отражающих существенные свойства объекта или процесса.
Математическое моделирование в наше время гораздо более всеобъемлюще, нежели моделирование натурное. Математический аппарат для моделирования объектов и процессов реального мира ученые использовали очень давно, но огромный толчок математическому моделированию дало появление ЭВМ, которые сегодня помогают в этой деятельности. Использование математического моделирования является самым общим методом научных исследований.
Вывод.
При математическом моделировании исследование объекта осуществляется посредством изучения модели, сформулированной на языке математики, с использованием тех или иных методов.
Простой пример: представьте себе, что нужно определить площадь поверхности письменного стола. Как обычно поступают в таком случае? Измеряют длину и ширину стола, а затем перемножают полученные числа. Это фактически означает, что реальный объект – поверхность стола – заменяется абстрактной математической моделью прямоугольником. Площадь этого прямоугольника и считается искомой.
Как видите, из всех свойств стола мы выделили три: форма поверхности (прямоугольник) и длины двух сторон. Для нас не важны ни цвет стола, ни материал, из которого он сделан, ни то, как он используется. Если бы мы решали другую задачу о столе (скажем, сколько стоит изготовление стола), то возможно, для нас важна была бы как раз эта информация.
Предположив, что поверхность стола – прямоугольник, мы легко указываем исходные данные и результат. Они связаны соотношением S=a×b. Сделанное предположение позволило “перевести” нашу задачу на язык чисел: и исходные данные, и результат – числа, а соотношение между ними задается математической формулой.
Анализировать математические модели проще и быстрее, чем экспериментально определять поведение реального объекта. Кроме того, анализ математической модели позволяет выделить наиболее существенные свойства данного объекта (процесса), на которые надо обратить особое внимание при принятии решения.
Этапы решения задач на компьютере:
1. Постановка задачи – точная формулировка условий и целей решения, описания наиболее существенных свойств объекта.
2. Построение математической модели – описания наиболее существенных свойств объекта с помощью математических формул.
3. Разработка алгоритма.
4. Запись алгоритма на языке программирования.
5. Отладка и тестирование программы на компьютере.
6. Анализ полученных результатов.
Решение задачи с помощью ЭВМ начинается с точной формулировки условий и целей решения, описания наиболее существенных свойств объекта с помощью математических формул. Для того, чтобы ЭВМ произвела необходимые вычисления и получила ответ, нужно составить для нее четкую инструкцию, строго указать необходимую последовательность действий, т. е. составить алгоритм решения задачи. Далее необходимо провести вычислительный эксперимент:
составить программу, проведя вычисления на ЭВМ;
получить и проанализировать результаты.
Ведь сколько бы свойств мы не учитывали, модель всегда основана на некотором упрощении, и трудно быть абсолютно уверенным, что модель соответствует реальной задаче. Такую уверенность можно обрести, лишь сопоставив результаты расчетов с экспериментальными фактами, теоретическими воззрениями и другой информацией об изучаемом объекте.
При этом может возникнуть необходимость уточнить математическую модель, исправляют алгоритм, проводят расчеты на ЭВМ и анализируют результаты. Так будет продолжаться до тех пор, пока анализ результатов не покажет их приемлемое соответствие знаниям об объекте.
Контрольные вопросы.
1. Что такое математическое моделирование?
2. Дайте определение математической модели.
3. Перечислите этапы решения задачи на компьютере.
Рассмотрим на примерах задачи математического моделирования.
Задача №1
Вычислить количество краски для покрытия пола в спортивном зале, используя язык программирования PASCAL.
РЕШЕНИЕ
Этапы решения задачи на ЭВМ

1. Постановка задачи
При покраске пола стараются, чтобы слой краски покрывал поверхность равномерно. Для выполнения этого задания измеряют длину пола. Это значит, что количество краски пропорционально площади, которую надо покрасить. Поэтому, для решения задачи нужно знать площадь пола. Существенным является предположение: пол имеет форму прямоугольника. Для выполнения этого задания измеряют длину, ширину пола и вычисляют его площадь. Реальный объект – пол зала – занимается прямоугольником, для которого площадь является произведением длины на ширину. При покупке краски выясняют, какую площадь можно покрыть содержимым одной банки, и вычисляют необходимое количество банок.
2. Математическая модель
Пусть A – длина пола, B - ширина пола, S1 - площадь, которую можно покрыть содержимым одной банки, N – количество банок, тогда:
площадь пола вычисляем по формуле S=A×B, а количество банок, необходимых для покраски зала, N= A×B/S1.
3. Алгоритм
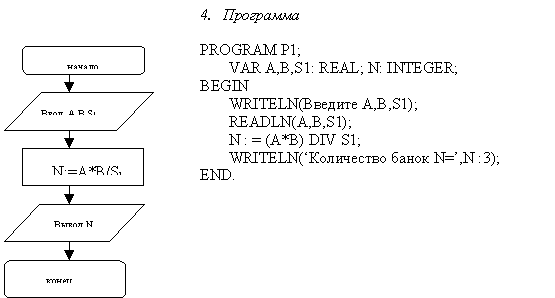
Следующие задачи предлагается решить с помощью ЭТ.
Задача №2
На научный семинар собрались ученые и обменялись друг с другом визитными карточками. Всего было роздано 210 визитных карточек. Сколько ученых приехало на семинар, если известно, что их было не более 20?
РЕШЕНИЕ
1. Постановка задачи. Математическая модель
Пусть x – количество ученых, приехавших на семинар. Т. к. в процессе обмена каждый раздает по одной карточке всем, кроме себя, то он раздаст x-1 карточку. Т. о., будет всего будет роздано n =x×(x-1) карточек.


Начнем эксперимент, последовательно вводя в ячейку B2 числа 2, 3, 4 и т. д.
В результате проведенного эксперимента получим ответ: 15 человек.
Поверим результат, решив квадратное уравнение x2 – x - 210 = 0.
Задача №3 (самостоятельно)
Участники шахматного турнира после окончания очередной партии обменивались друг с другом рукопожатиями. Всего сыграно 210 партий, значит, 210 раз противники жали друг другу руки. Сколько человек принимали участие в турнире, если каждый сыграл по одному разу со всеми остальными и известно, что участников было не более 38?
РЕШЕНИЕ
Решать задачу, используя ту же таблицу, исправив содержимое ячейки B3.
1. Математическая модель
Пусть n – количество рукопожатий, x – количество участников.

Ответ: 21 человек.
Задача №4
Знаменатель правильной дроби на 2 больше числителя. Если числитель увеличить в 5 раз, а к знаменателю прибавить 5 и сократить дробь, то в результате получится 3/2. Найти исходную дробь.
РЕШЕНИЕ
1. Постановка задачи. Математическая модель
Пусть числитель исходной дроби равен x, тогда:
X+2 - знаменатель исходной дроби;
X×5 - новый числитель
X+7 - новый знаменатель
Т. к. по условию задачи новая дробь равна после сокращения 3/2, составляем уравнение:

Математическая модель нашей задачи будет такой:

2. Компьютерный эксперимент
Реализуем нашу модель в ЭТ (Файл «Задачи к урокам», лист «Дробь»)
| | A | B | C | D |
| 1 | Модель задачи | Дроби | | |
| 2 | Числитель | ? | Новый числитель | =B2*5 |
| 3 | Знаменатель | =В2+2 | Новый знаменатель | =B3+5 |
| 4 | | | | |
| 5 | Проверка | =D3*3 | =D2*2 | |
В нашей математической модели уравнение представляет собой пропорцию. Воспользуемся основным свойством пропорции – произведение крайних членов равно произведению средних членов, т. е. 5x*2=(x+7)*3.
В ячейке B5 записано произведение средних членов, а в ячейке C5 записано произведение крайних членов. Решение задачи сводится к подбору в ячейке B2 такого числа, чтобы значения выражений в ячейках B5 и C5 совпадали. Как только это произойдет, ответ задачи получим в ячейках B2 и B3.
Проверить правильность нашей модели можно, решив линейное уравнение 5x*2=(x+7)*3, 10x=3x+21, 7x=21, x=3 – это числитель исходной дроби, тогда ее знаменатель равен 5, т е. исходная дробь 3/5
Ответ: 3/5
Задача №5 (самостоятельно)
Дана правильная дробь, знаменатель которой на 2 больше числителя. Если от числителя отнять 1, а к знаменателю прибавить 7 и сократить дробь, то в результате получится 1/2. Найти исходную дробь. (Используется таблица задачи №4, изменив соответствующим образом формулы в ячейках).
Задача №6
Через иллюминатор затонувшего корабля требуется вытащить сундук с драгоценностями. Удастся ли это сделать?
1. Описание постановки. Построение математической модели.
Иллюминатор корабля имеет форму круга, будем считать, что сундук имеет форму параллелепипеда. Чтобы вытащить сундук необходимо, чтобы диаметр иллюминатора был больше любой из трех диагоналей поверхности сундука.

Сундук можно вытаскивать через иллюминатор одной из трех боковых граней, следовательно, достаточно, чтобы диагональ иллюминатора оказалась меньше одной из трех диагоналей граней сундука, т. е. истинным было хотя бы одно из условий:
Усл1=ЕСЛИ((2*R>КОРЕНЬ(a*a+b*b));1;0)
Усл2=ЕСЛИ((2*R>КОРЕНЬ(a*a+с*с));1;0)
Усл3=ЕСЛИ((2*R>КОРЕНЬ(с*с+b*b));1;0)
2. Компьютерный эксперимент
В таблице находим сумму трех условий, если сумма равна 0, делаем вывод «Сокровища не доступны» иначе «Сокровища доступны» (Файл «Задачи к урокам», лист «Сокровища не доступны», лист «Сокровища доступны»).
| Задача о сокровищах 1. | | | | | |||
| Исходные данные | | | | | | ||
| Радиус Иллюминатора | 20 | | | | | | |
| Длина сундука | 60 | | | | | | |
| Ширина сундука | 50 | | | | | | |
| Высота сундука | 40 | | | | | | |
| Расчет | |||||||
| Промежуточные расчеты | Расчеты | | | ||||
| Радиус | Длина сундука | Ширина сундука | Высота Сундука | | | | |
| 20 | 60 | 50 | 40 | 0 | | | |
| | | | | 0 | | | |
| | | | | 0 | | | |
| | | | СУММА | 0 | | | |
| | | | ОТВЕТ | СОКРОВИЩА НЕДОСТУПНЫ | |||
| Задача о сокровищах 2. | | | | ||
| Исходные данные | | | | | |
| Радиус Иллюминатора | 20 | | | | |
| Длина сундука | 60 | | | | |
| Ширина сундука | 50 | | | | |
| Высота сундука | 40 | | | | |
| Расчет | |||||
| Промежуточные расчеты | Расчет | ||||
| Радиус | Длина сундука | Ширина сундука | Высота сундука | | |
| 20 | 25 | 25 | 40 | 1 | |
| | | | | 0 | |
| | | | | 1 | |
| | | | СУММА | 2 | |
| | | | ОТВЕТ | СОКРОВИЩА ДОСТУПНЫ | |
Домашнее задание:
1) Площадь прямоугольного треугольника равна 6 см . Найти длины катетов и гипотенузы этого треугольника, если один катет больше другого на 1 см и известно, что длина каждой из сторон не превосходит 12 см.
Составьте в тетради математическую модель этой задачи:
• выделите исходные данные;
• определите, что является результатом;
• найдите связь между исходными данными и результатом и запишите ее в виде математических соотношений (представьте в виде уравнения).
1) Повторить формулы площади боковой поверхности и объема параллелепипеда.
2) Выполнить домашнюю контрольную работу (срок выполнения 2 недели).
Задача 1 Требуется оббить входную дверь 210х92 см дерматином. Хватит ли куска дерматина 215х102 см для обивки двери, если на подгиб с каждой стороны требуется по 2 см ткани?
Задача 2 Необходимо покрасить краской панели (стены) кухонной комнаты. Сколько потребуется банок краски, если размеры кухни: 405х310х285 см, 88% площади стены занимает кафельная плитка и 1 банка краски предназначена для покраски площади 5 м2?
РЕШЕНИЕ
Задача 1
1. Постановка и математическая модель задачи.
Дано: 210см - длина двери
92см - ширина двери
2см - припуск на швы
215см - длина куска дерматина
102см - ширина куска дерматина
Определить хватит или нет куска дерматина на обивку двери.
Размеры двери с учетом припуска на швы для оклейки: 212см, 94см,
S двери = 214×96
S куска дерматина = 215×102.
Если S двери > S куска дерматина, то куска дерматина не хватит на обивку двери, дополнительно потребуется кусок дерматина размером S двери - S куска дерматина.
2. Моделирование в среде ЭТ (Файл «Задачи к урокам», лист «Домашняя контрольная работа»)
| Вариант 1. Задача об обтяжке двери дерматином | ||
| | | |
| Исходные данные | | |
| Размеры двери | | с припуском на швы |
| Длина | 210 | 214 |
| Ширина | 92 | 96 |
| ширина швов | 2 | |
| Размеры куска дерматина | | |
| Длина | 215 | |
| Ширина | 100 | |
| Расчеты: | | |
| Sдвери | 20544 | |
| Sдерматина | 21500 | |
| ОТВЕТ: | КУСКА ДЕРМАТИНА ХВАТИТ | |
Задача 2
1. Постановка и математическая модель задачи.
Дано: b – длина комнаты
a – ширина комнаты
c - высота комнаты
0,12 – часть комнаты для покраски (без кафеля)
5 м2 – площадь покраски при использовании 1 банки краски
Найти: S стен для покраски, необходимое количество банок краски.
S стен с кафелем =2с(a+b)
S стен для покраски =2с(a+b)0,12
Чтобы определить сколько потребуется банок краски, надо площадь для покраски разделить на 5 м2 т. е. S стен для покраски / 5 и результат округлить вверх.
3. Моделирование в среде ЭТ
Файл «Задачи к урокам», лист «Домашняя контрольная работа»)
| Задача 2. Окраска панелей кухни | | ||
| | | | |
| Исходные данные | | | |
| Комната | | краска | |
| Длина | 4,05 | Sпокраски 1 б. | 5 |
| Ширина | 3,10 | | |
| Высота | 2,85 | | |
| | | | |
| S стен | 4,8906 | | |
| | | | |
| Результаты | 1 | банка | |
Самостоятельная работа
1 вариант
Реализуйте модель, составленную для домашней задачи в ЭТ, проанализировав полученные результаты, найдите правильный ответ и получите ответ.
РЕШЕНИЕ.
| | A | B | C | D |
| 1 | Длина катета а | Длина катета b | Длина гипотенузы с | Площадь s |
| 2 | 1 | A2-1 | =КОРЕНЬ(A2+B2) | =1/2*A2*B2 |
| 3 | 2 | | | |
| 4 | 3 | Заполнить вниз | Заполнить вниз | Заполнить вниз |
| | Длина катета a | Длина катета b | Площадь s | Длина гипотенузы c |
| 2 | 1 | 2 | 1 | 2,236067977 |
| 3 | 2 | 3 | 3 | 3,60555128 |
| 4 | 3 | 4 | 6 | 5 |
| 5 | 4 | 5 | 10 | 6,40312424 |
| 6 | 5 | 6 | 15 | 7,81024968 |
2 вариант
Площадь прямоугольного треугольника равна 24 см2. Найти длины катетов и гипотенузы этого треугольника, если один катет на 2 см меньше другого и известно, что каждая из длин сторон треугольника не превосходит 12 см.
1. Практическая работа «Определение максимального объема коробки»
Разработать математическую модель решения задачи: имеется квадратный лист картона со стороной а. Из листа делается коробка следующим образом: по углам листа вырезаются четыре квадрата, и коробка склеивается по швам. Какова должна быть сторона вырезаемого квадрата, чтобы коробка имела наибольшую вместимость?
Реализовать модель в среде ЭТ. Выводы, расчеты отразить в тетрадях.
РЕШЕНИЕ
1. Постановка задачи
В задаче рассматривается процесс преобразования одного объекта (картонного листа) в другой (коробку). Исходный объект – картонный лист - имеет заданные размеры: длина стороны a. Созданный объект – коробка – характеризуется объемом, а вырезы – размером стороны и площадью.

| x |
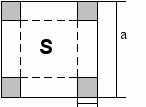
2. Математическая модель
Пусть х – длина выреза, a - длина стороны картонного листа,
тогда длина стороны дна равна а-2×х,
площадь дна равна (а-2×х)2,
объем коробки равен (а-2×х)2×x
3. Компьютерный эксперимент
Для моделирования будем использовать среду электронной таблицы (Файл «Задачи к урокам», лист «Максимальный объем коробки»).
1) Заполните область данных по образцу.
-
A
B
1
Задача о склеивании коробки
2
3
Исходные данные
4
Длина стороны
40
5
Шаг увеличения выреза
1
2) Составьте таблицу расчета со столбцами Длина выреза, Длина стороны, Площадь дна, Объем. Определите по столбцу Объем наибольший объем коробки (функция МАКС). Длину выреза изменяйте с шагом 1 см. В столбце Длина выреза определите значение выреза, соответствующее наибольшему объему коробки.
-
A
B
C
D
6
Расчет
7
Промежуточные расчеты
Результаты
8
Длина выреза
Длина стороны
Площадь дна
Объем
9
1
=$B$4 – 2*A9
=B92
=C9*A9
10
=A9 + $B$5
Заполнить вниз
Заполнить вниз
Заполнить вниз
11
Заполнить вниз
3) Проведите расчеты для разных исходных данных:
а=40 см, x=1см
a=40 см, x=0,5 см
a=6 см, x=0,1 см
Обратите внимание, что для различных значений исходного размера картонного листа понадобится разное количество расчетных строк в таблице.
Пример расчета для а=40 см.
-
7
Длина выреза
Длина стороны
Площадь дна
Объем
8
1
38
1444
1444
9
2
36
1296
2592
10
3
34
1156
3468
4) Составьте таблицу результатов расчета для различных значений исходного размера картонного листа, копируя в столбцы только значения расчетов. При копировании и переносе результатов из расчетной таблицы в ячейки анализа результатов пользуйтесь командой Специальная вставка (кнопка Только значения).
-
F
G
H
I
1
Результаты моделирования
2
Оптимальный вырез
3
Длина стороны
Шаг увеличения выреза 1 см
Шаг увеличения выреза 0,5 см
Шаг увеличения выреза 0,1 см
4
40
7
6,5
6,7
5
15
3
2,5
2,5
6
80
13
13,5
13,5
5) Проанализируйте результаты моделирования и ответьте на вопросы:
а) По столбцу Длина стороны определяем, что длина стороны коробки все время уменьшается, пока не станет равной 0. Если заполнено большее количество строк, то в них длина стороны уже меньше 0. Чем это можно объяснить? Надо ли эти строки учитывать при определении максимального объема?
б) Как изменяется оптимальный размер выреза (допустимое значение, позволяющее найти максимальный объем), если изменять шаг выреза? Чем это можно объяснить?
в) В тетрадях для лабораторных работ составьте отчет. В отчете отразите этапы решения задачи: исходные данные, расчетные формулы, результаты расчета для нескольких вариантов исходных данных. Ответьте на предложенные вопросы.
Домашнее задание.
1) Задача. Определение минимальной длины изгороди садового участка.
Садовый участок прямоугольной формы имеет площадь S. При каких размерах длины и ширины участка длина изгороди будет наименьшей? Составьте математическую модель.
2) Повторить функцию, вырабатывающую случайные числа RANDOM(X).
3) Знать формулу площади круга.
Вопросы.
1) Имитационное моделирование.
2) Применение моделирования. Моделирование случайных процессов на примере вычисления числа p. Метод Монте-Карло.
Ход урока
1. Актуализация опорных знаний.
Проверка домашнего задания. Задача “о наименьшем периметре участка”
1. Математическая модель
Пусть a – длина участка, площадь – S, тогда его ширина равна S/a. Длина изгороди есть не что иное как периметр участка, который вычисляем по формуле P=2(a+S/a).
2. Компьютерный эксперимент
Для моделирования будем использовать среду электронной таблицы (Файл «Задачи к урокам», лист «Наименьший периметр»).
1) Составим таблицу расчета со столбцами Длина участка, Ширина участка, Площадь участка, Периметр.
2) Определим по столбцу Периметр наименьший периметр участка (функция МИН).
3) Длину участка изменяйте с шагом 2 м. В столбце Длина участка определите значение длины, соответствующее наименьшему периметру участка и сделайте выводы.
-
A
B
C
D
1
Шаг изменения длины участка
2
2
Расчет
3
Промежуточные расчеты
Результаты
4
Длина участка
Площадь
Ширина участка
Периметр
5
1
300
=B5/A6
=2*(A5+C5)
6
=A5 + $B$1
Заполнить вниз
Заполнить вниз
Заполнить вниз
7
Заполнить вниз
-
A
B
C
D
1
Наименьший периметр
2
Шаг изменения длины
2
3
Расчеты
4
Длина участка
Площадь
Ширина участка
Периметр
5
1
300
300
602
6
3
300
100
206
7
5
300
60
130
8
7
300
42,85714
99,71429
9
9
300
33,33333
84,66667
10
11
300
27,27273
76,54545
11
13
300
23,07692
72,15385
12
15
300
20
70
13
17
300
17,64706
69,29412
14
19
300
15,78947
69,57895
15
21
300
14,28571
70,57143
16
23
300
13,04348
72,08696
17
Минимальное значение периметра
69,29412
Вывод:
Наименьший периметр имеет прямоугольник длина и ширина которого одинаковы, т. е. квадрат.
2. Новая тема. Имитационное моделирование.
Процессы в системе могут протекать по-разному в зависимости от условий, в которых находится система. Следить за поведением реальной системы при различных условиях, пробовать всевозможные варианты бывает трудно, а иногда и невозможно. В таких случаях выручают модели. Построив модель, можно многократно возвращаться к начальному состоянию и наблюдать за поведением модели.
Такой метод исследования систем называется имитационным моделированием. Имитационное моделирование применяют в тех случаях, когда нужно учесть возможно большее разнообразие исходных данных, изучить протекание процессов в различных условиях.
Рассмотрим пример имитационного моделирование на примере вычисления числа p (метод Монте - Карло). p = 3,1415922653... .
Теоретическая основа метода была известна давно. Однако до появления ЭВМ этот метод не мог найти сколько-нибудь широкого применения, ибо моделировать случайные величины вручную - очень трудоемкая работа.
Само название “Монте-Карло” происходит от города Монте-Карло в княжестве Монако, знаменитого своим игорным домом. Дело в том, что одним из механических приборов для получения случайных величин является рулетка.
Для вычисления площади круга единичного радиуса проведем эксперимент. Поместим данную фигуру в квадрат. Будем наугад (как говорят математики, случайным образом) бросать точки в этот квадрат. Естественно предполагать, что чем больше площадь фигуры, тем чаще в нее будут попадать точки. Представьте себе квадратный дворик и в нем детскую площадку. Каждому ясно, что во время снегопада количество снежинок, попавших на детскую площадку, пропорционально ее площади. Таким образом, можно сделать допущение: при большом числе точек, наугад выбранных внутри квадрата, доля точек, содержащихся в данной фигуре, приближенно равна отношению площади этой фигуры и площади квадрата.
Такой метод приближенного нахождения площадей фигур и носит название метода Монте-Карло.
1) Постановка задачи вычисления числа p методом Монте-Карло
Для вычисления числа p с помощью метода Монте-Карло рассмотрим круг радиуса 1 с центром в точке (1,1). Круг вписан в квадрат, SКВ=2×2=4.
Выбираем внутри квадрата N случайных точек. Выбрать точку – это значит задать ее координаты: числа x и y. Обозначим NКР - число точек, попавших при этом внутрь круга.
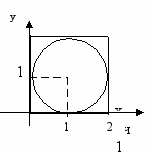
Исходными данными являются сторона квадрата, содержащего круг, и количество точек, которые мы будем случайным образом выбирать внутри квадрата. Результатом является площадь круга.
Точка принадлежит квадрату, если 0 £ x £ 2 и 0 £ y £2.
Если (x-1)2+(y-1)2 £ 1, то точка попадает в круг, иначе она вне круга. Это и есть математическое соотношение, позволяющее для каждой точки определять, лежит ли она в круге.
Геометрически очевидно, что
 , отсюда
, отсюда 
т. е.
 , т. к. Sкруга=p, получаем p =
, т. к. Sкруга=p, получаем p = (1)
(1)Формула (1) дает оценку числа p. Чем больше N, тем больше точность этой оценки. Следует заметить, что данный метод вычисления площади будет справедлив только тогда, когда случайные точки будут не "просто случайными", а еще и "равномерно разбросанными" по всему квадрату.
Для моделирования равномерно распределенных случайных чисел в интервале от 0 до 1 в языке программирования Паскаль используется датчик случайных чисел - функция RANDOM. Это специальная компьютерная программа, которая выдает последовательность случайных величин равномерно распределенных от 0 до 1.
Таким образом, суть компьютерного эксперимента заключается в обращении к функции RANDOM для получения координат точки x и у N раз. При этом определяется попадет ли точка с координатами (х, у) в круг единичного радиуса. В случае попадания увеличивается на 1 значение величины Nкруга
3) Алгоритм
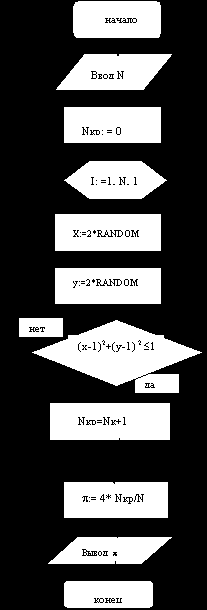
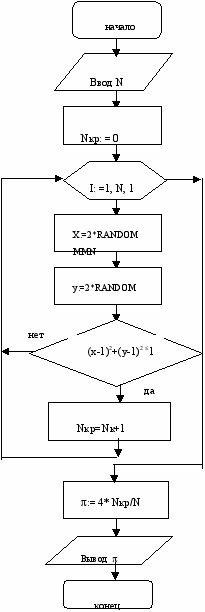
3). Программа
PROGRAM MONTE_KARLO;{ПАСКАЛЬ}
VAR I,N,N1:LONGINT;
X,Y,PI:REAL;
BEGIN
RANDOMIZE;
WRITE('Введите количество точек N=');
READLN(N);
FOR I:=1 TO N DO
BEGIN
X:=2*RANDOM;
Y:=2*RANDOM;
IF SQR(X-1)+SQR(Y-1)<=1 THEN N1:=N1+1;
END;
PI:=4*N1/N;
WRITELN('PI=',PI:15:11);
END.
4) Вычислительный эксперимент и анализ результатов
Предложить учащимся выполнить практическую работу на ЭВМ, оформить результаты в таблице и сделать соответствующие выводы. В таблице приведены примерные результаты.
-
N
Результат
50
2,8000000000
50
3,2800000000
50
3,2800000000
600
3,1400000000
600
3,1266666667
600
3,2333333333
2500
3,1408000000
2500
3,1008000000
2500
3,0784000000
5000
3,1184000000
5000
3,1280000000
5000
3,1656000000
10000
3,1404000000
10000
3,1444000000
10000
3,1588000000
1000000
3,1440640000
1000000000
3,1440640000
Выводы:
С увеличением точности вычислений увеличивается время работы программы;
Разные результаты при одном и том же количестве случайных точек зависит от того, что точки все-таки случайные;
Математическая модель, выбранная нами для решения задачи на нахождение площади (числа p) отличается от предыдущих тем, что в ней используются случайные числа (такие модели называют вероятностными, поэтому и результаты могут получиться разными.
Домашнее задание:
1) Привести примеры вероятностных моделей.
2) Повторить основные понятия и определения темы.
3) Повторить формулы равномерного и равноускоренного движения.
Вопросы.
1) Понятие главных и второстепенных факторов.
2) Моделирование физических процессов на примере моделирования полета тела, брошенного под углом к горизонту.
Ход урока
