Рабочая программа учебной дисциплины «Математический анализ» Направление подготовки
| Вид материала | Рабочая программа |
- Рабочая программа учебной дисциплины «Математический анализ» Направление подготовки, 275.11kb.
- Рабочая программа дисциплины «Математический анализ ii» Направление, 132.24kb.
- Программа учебной дисциплины математический анализ рисков в страховании Направление, 144.35kb.
- Рабочая программа дисциплины «Математический анализ» Направление подготовки, 180.51kb.
- Рабочая программа учебной дисциплины «Математический анализ» Специальность «Математические, 187.35kb.
- Аннотация рабочей программы учебной дисциплины математический анализ Направление подготовки, 95.49kb.
- Рабочая учебная программа дисциплины (модуля) Математический анализ, 233.89kb.
- Рабочая программа учебной дисциплины «психология» Направление подготовки, 808.24kb.
- Содержание рабочей программы учебной дисциплины математический анализ Направление подготовки, 67.55kb.
- Рабочая программа учебной дисциплины судебная этика Направление подготовки 030500., 197.85kb.
Министерство образования и науки Российской Федерации
ГОУВПО «Мордовский государственный университет им. Н.П.Огарёва»
Математический факультет
Кафедра математики и теоретической механики
-
«УТВЕРЖДАЮ»
_____________________
_____________________
«______»__________201_ г.
РАБОЧАЯ ПРОГРАММА УЧЕБНОЙ ДИСЦИПЛИНЫ
«Математический анализ»
Направление подготовки
230100.62 –Информатика и вычислительная техника
Профиль подготовки
____________________________________
Квалификация (степень) выпускника
Бакалавр
Форма обучения
очная
г. Саранск
2011 г.
- Цели и задачи учебной дисциплины:
Цели изучения дисциплины:
- ознакомление студентов с элементами математического аппарата, необходимого для решения теоретических и практических задач;
- ознакомление студентов с методами математического исследования прикладных вопросов;
- формирование навыков самостоятельного изучения специальной литературы, понятия о разработке математических моделей для решения практических задач;
- развитие логического мышления, навыков математического исследования явлений и процессов, связанных с профессиональной деятельностью.
Задачи изучения дисциплины:
- формирование представления о месте и роли математики в современном мире;
- формирование системы основных понятий, используемых для описания важнейших математических моделей и математических методов, и раскрытие взаимосвязи этих понятий;
- формирование навыков самостоятельной работы, организации исследовательской работы.
- Место учебной дисциплины в структуре ООП:
Дисциплина «Математика» входит в базовую часть (Б2) математического и естественнонаучного цикла. Для изучения дисциплины необходимы знания курса математики в объеме общеобразовательной средней школы.
3. Требования к результатам освоения дисциплины
Компетенции обучающегося, формируемые в результате освоения дисциплины(модуля):
Процесс изучения дисциплины направлен на формирование следующих компетенций:
- владеть культурой мышления, способен к обобщению, анализу, восприятию информации, постановке цели и выбору путей её достижения (ОК-1);
- уметь логически верно, аргументировано и ясно строить устную и письменную речь (ОК-2);
- готовность к кооперации с коллегами, работе в коллективе (ОК-3);
- использовать основные законы естественнонаучных дисциплин в профессиональной деятельности, применять методы математического анализа и моделирования, теоретического и экспериментального исследования (ОК-10);
В результате изучения дисциплины студент должен:
Знать: основные определения, понятия, теоремы разделов математики предусмотренных программой;
Уметь: решать математические задачи, пользоваться накопленными математическими знаниями при изучении других дисциплин;
Владеть: математическими методами для решения задач производственного характера, методами теории вероятностей и математической статистики при планировании опытов и обработке их результатов.
4. Образовательные технологии
Курсы лекционных и практических занятий организуются по стандартной технологии.
5.1 Содержание учебной дисциплины (модуля). Объем дисциплины и виды учебных занятий
| Вид* учебной работы | Всего часов | Семестры | |
| 1 | 2 | ||
| Аудиторные занятия (всего) | 162 | 90 | 72 |
| В том числе: | - | - | - |
| Лекции | 90 | 54 | 36 |
| Практические занятия (ПЗ) | 72 | 36 | 36 |
| Самостоятельная работа (всего) | 90 | 45 | 45 |
| В том числе: | - | - | - |
| Контрольные работы | 8 | 4 | 4 |
| Другие виды самостоятельной работы | | | |
| Самостоятельное изучение разделов, повторение лекционного материала, подготовка к практическим занятиям | 6 | 3 | 3 |
| Подготовка к текущим и промежуточным контрольным работам | 2 | 1 | 1 |
| Выполнение индивидуальных домашних заданий | 2 | 1 | 1 |
| Подготовка к экзамену | 72 | 36 | 36 |
| Вид промежуточной аттестации (зачет, экзамен) | | экзамен | экзамен |
| Общая трудоемкость час зач. ед. | 252 | 135 | 117 |
| 7 | 3,75 | 3,25 | |
5.2. Содержание разделов учебной дисциплины
| № п/п | Наименование раздела дисциплины | Содержание раздела | Формы текущего контроля успеваемости |
| 1. | Математический анализ | Последовательности: числовая последовательность; предел числовой последовательности; предельный переход в неравенствах; предел монотонной ограниченной последовательности. Число e. Натуральные логарифмы. | ИДЗ 5.1 Опрос |
| Предел функции: предел функции в точке; односторонние пределы; предел функции при x 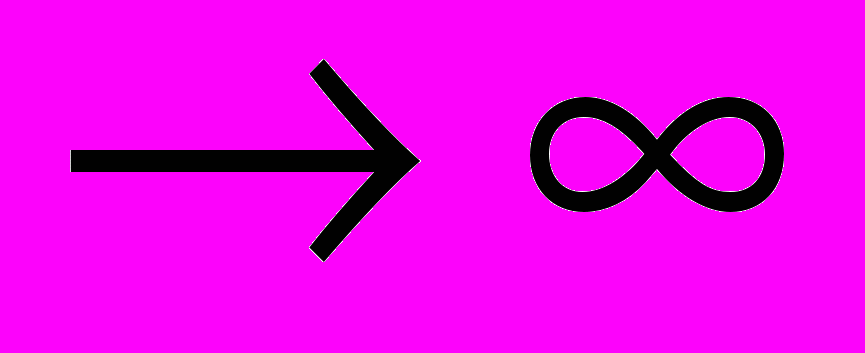 ; бесконечно большие функции (б.б.ф.). Бесконечно малые функции (б.м.ф.): определения и основные теоремы; связь между функцией, её пределом и бесконечно малой функцией; основные теоремы о пределах; признаки существования пределов; первый замечательный предел; второй замечательный предел. ; бесконечно большие функции (б.б.ф.). Бесконечно малые функции (б.м.ф.): определения и основные теоремы; связь между функцией, её пределом и бесконечно малой функцией; основные теоремы о пределах; признаки существования пределов; первый замечательный предел; второй замечательный предел.Эквивалентные бесконечно малые функции: сравнение бесконечно малых функций; эквивалентные бесконечно малые и основные теоремы о них; применение эквивалентных бесконечно малых функций. Непрерывность функций: непрерывность функций в точке; непрерывность функций в интервале и на отрезке; точки разрыва функций и их классификация; основные теоремы о непрерывных функциях. Непрерывность элементарных функций; свойства функций, непрерывных на отрезке. | ИДЗ 5.2 Опрос Контро- льная ра- бота №1 Опрос | ||
| | | Производная функции: задачи, приводящие к понятию производной; определение производной, её механический и геометрический смысл. Уравнение касательной и нормали к кривой; связь между непрерывностью и дифференцируемостью функции; производная суммы, разности; произведения и частного функций; производная сложной и обратной функций; производные основных элементарных функций; гиперболические функции и их производные; таблица производных. Дифференцирование неявных и параметрически заданных функций, логарифмическое дифференцирование. Производные высших порядков: производные высших порядков явно заданной функции; механический смысл производной второго порядка; производные высших порядков неявно заданной функции; производные высших порядков от функций, заданных параметрически. | ИДЗ 6.1 Опрос ИДЗ 6.2 Опрос |
| Дифференциал функции: понятие дифференциала функции; геометри-ческий смысл дифференциала функции; основные теоремы о дифференциалах; таблица дифференциалов; применение дифференциала к приближенным вычислениям; дифференциалы высших порядков. | ИДЗ 6.3 Опрос | ||
| Исследование функций при помощи производных: некоторые теоремы о дифференцируемых функциях; правило Лопиталя; возрастание и убывание функций; максимум и минимум функций; наибольшие и наименьшие значения функции на отрезке; выпуклость графика функции. Точка перегиба; асимптоты графика функции; общая схема исследования функции и построения графика; формула Тейлора для многочлена; формула Тейлора для произвольной функции. | ИДЗ 6.4 Опрос Контро- льная ра- бота №2 | ||
| | | Комплексные числа: понятие и представление комплексных чисел; основные понятия; геометрическое изображение комплексных чисел; формы записи комплексных чисел; действия над комплексными числами; сложение, вычитание, умножение, деление комплексных чисел; возведение комплексных чисел в натуральную степень извлечение корней из комплексных чисел | Опрос |
| Неопределённый интеграл: понятие неопределённого интеграла; свойства неопределенного интеграла; таблица основных неопределённых интегралов. Основные методы интегрирования: метод непосредственного интегрирования; метод интегрирования подстановкой (заменой переменной); метод интегрирования по частям. Интегрирование рациональных функций: понятие о рациональных функциях; интегрирование простейших рациональных дробей; интегрирование рациональных дробей. Интегрирование тригонометрических функций: универсальная тригонометрическая подстановка; интегралы типа 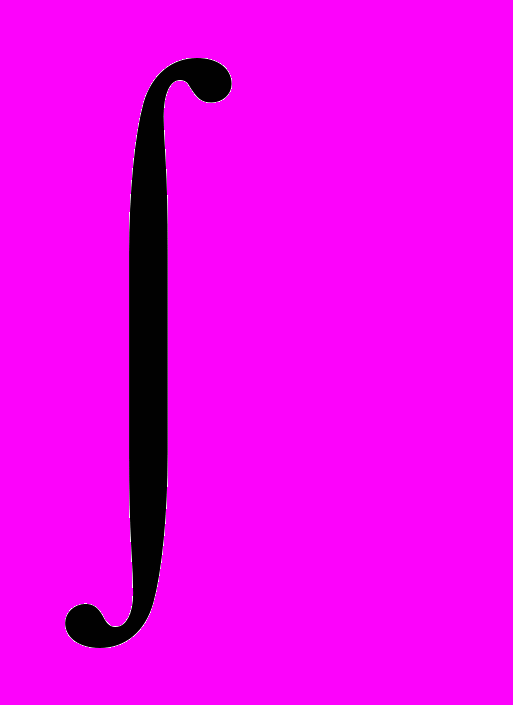 sin sin x cos x cos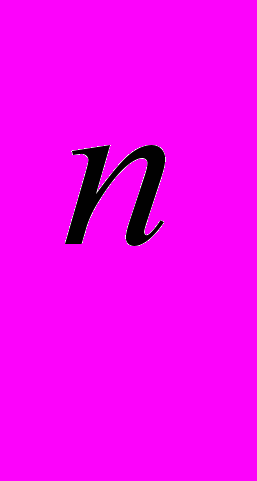 x dx; использование тригонометрических преобразований. x dx; использование тригонометрических преобразований.Интегрирование иррациональных функций: квадратичные иррациональности; дробно– линейная подстановка; тригонометрические подстановки; интегралы типа 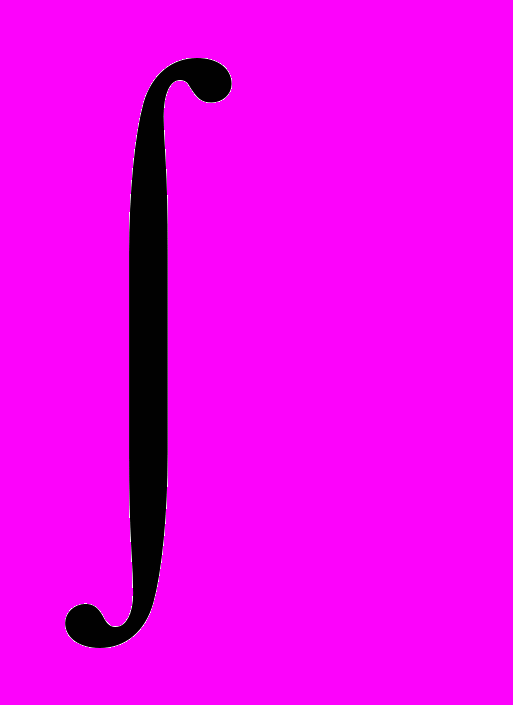 R(x; R(x;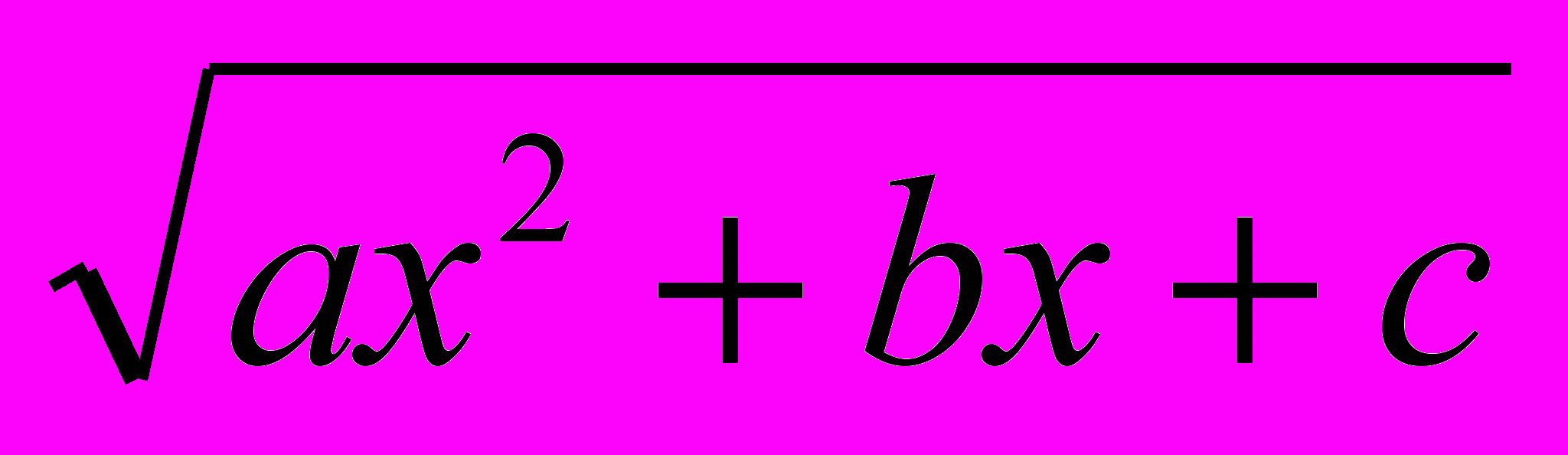 ) dx; интегрирование ) dx; интегрирование дифференциального бинома; «берущиеся» и «неберущиеся» интегралы. | ИДЗ 8.1 | ||
| Вычисления определённого интеграла: формула Ньютона – Лейбница; интегрирование подстановкой (заменой переменной); интегрирование по частям; интегрирование чётных и нечётных функций в симметричных | ИДЗ 8.2 | ||
| | | пределах. Несобственные интегралы: интеграл с бесконечным промежутком интегрирования (несобственный интеграл 1-рода); интеграл от разрывной функции (несобственный интеграл 2-рода). Геометрические и физические приложения определённого интеграла: схемы применения определённого интеграла; вычисление длины дуги плоской кривой; вычисление объёма тела; вычисление площади поверхности вращения; механические приложения определённого интеграла. | ИДЗ 8.3 ИДЗ 8.4 |
| Функции двух: переменных основные понятия; предел функций, непрерывность функции в ограниченной замкнутой области. Производные и дифференциалы функции нескольких переменных: частные производные первого порядка и их геометрическое истолкование; частные производные высших порядков; дифференцируемость и полный дифференциал функции; применение полного дифференциала к приближённым вычислениям; дифференциалы высших порядков; производная сложной функции. Полная производная; инвариантность формы полного дифференциала; дифференцирование неявной функции. Касательная плоскость и нормаль к поверхности. Экстремум функции двух переменных: понятие, необходимые и достаточные условия экстремума; наибольшее и наименьшее значение функции в замкнутой области. | ИДЗ 10.1 Опрос ИДЗ 10.2 Опрос | ||
| Общие сведения о дифференциальных уравнениях: основные понятия; задачи, приводящие к дифференциальным уравнениям. Дифференциальные уравнения первого порядка: основные понятия; уравнения с разделяющимися переменными; однородные дифференциальные уравнения; линейные уравнения; уравнения Я.Бернулли; уравнения в полных дифференциалах. Интегрирующий множитель. Дифференциальные уравнения высших порядков: основные понятия; уравнения с понижением порядка; линейные дифференциальные уравнения высших порядков; линейные однородные дифференциальные уравнения второго порядка; линейные однородные дифференциальные уравнения n-го порядка. Интегрирование линейных однородных уравнений высших порядков с постоянными коэффициентами: интегрирование ЛОДУ второго порядка с постоянными коэффициентами; интегрирование ЛОДУ n-го порядка с постоянными коэффициентами. Линейные неоднородные дифференциальные уравнения (ЛНДУ): структура общего решения ЛНДУ второго порядка; метод вариации произвольных постоянных; интегрирование ЛНДУ второго порядка с постоянными коэффициентами и правой частью специального вида; интегрирование ЛНДУ n-го порядка (n>2) с постоянными коэффициентами и правой частью специального вида. Системы дифференциальных уравнений: основные понятия, интегрирование нормальных систем; системы линейных дифференциальных уравнений с постоянными коэффициентами. | ИДЗ 11.1 Опрос ИДЗ 11.2 Опрос ИДЗ 11.3 Опрос Контрольная Работа №3 ИДЗ 11.4 Опрос | ||
| | | Двойной интеграл: основные понятия и определения; геометрический и физический смысл двойного интеграла; основные свойства двойного интеграла; вычисление двойного интеграла в декартовых координатах, переход к полярным координатам; приложения двойного интеграла. Тройной интеграл: основные понятия и определения; вычисление тройного интеграла в декартовых координатах; замена переменных в тройном интеграле. Вычисление тройного интеграла в цилиндрических и сферических координатах; некоторые приложения тройного интеграла. | ИДЗ 13.1 ИДЗ 13.2 ИДЗ 13.2 ИДЗ 13.3 |
| | | Криволинейный интеграл I рода: основные понятия и определения; вычисление криволинейного интеграла I рода; некоторые приложения криволинейного интеграла I рода. Криволинейный интеграл II рода: основные понятия. Определение криволинейного интеграла II рода. Свойства, вычисление криволинейных интегралов II рода; формула Остроградского-Грина; условие независимости криволинейного интеграла II рода от пути интегрирования; некоторые приложения криволинейного интеграла II рода. | ИДЗ14.1 (2,3) ИДЗ 14.2 (1) |
| Поверхностный интеграл I рода: основные понятия. Определение поверхностного интеграла I рода. Свойства; вычисление поверхностного интеграла I рода; некоторые приложения поверхностного интеграла I рода. Поверхностный интеграл II рода: основные понятия; определение поверхностно го интеграла II рода. Свойства; вычисление поверхностного интеграла II рода; формула Остроградского-Гаусса; формула Стокса; некоторые приложения поверхностного интеграла II рода. | ИДЗ 15.1 ИДЗ 15.2 | ||
| Числовые ряды: основные понятия; ряд геометрической прогрессии; необходимый признак сходимости числового ряда. Гармонический ряд. Достаточные признаки сходимости знакоположительных рядов: признаки сравнения рядов; признак Даламбера; радикальный признак Коши; интегральный признак Коши. Обобщенный гармонический ряд. Знакочередующиеся и знакопеременные ряды. Признак Лейбница; общий достаточный признак сходимости знакопеременных рядов; абсолютная и условная сходимости числовых рядов. Свойства абсолютно сходящихся рядов. Степенные ряды: теорема Н. Абеля; интервал и радиус сходимости степенного ряда; свойства степенных рядов. Разложение функций в степенные ряды: ряды Тейлора и Маклорена; разложение некоторых элементарных функций в ряд Тейлора (Маклорена). Некоторые приложения степенных рядов: приближенное вычисление значений функции; приближенное вычисление определенных интегралов; приближенное решение дифференциальных уравнений. Функциональные ряды: определение функционального ряда. Область сходимости; равномерная сходимость. Ряды Фурье: периодические функции. Периодические процессы: тригонометрический ряд Фурье; вычисление коэффициентов ряда Фурье. Разложение в ряд Фурье 2π - периодических функций; теорема Дирихле; разложение в ряд Фурье четных и не-четных функций; разложение в ряд Фурье функций произвольного периода; представление непериодической функции рядом Фурье; комплексная форма ряда Фурье. | ИДЗ 12.1 ИДЗ 12.2 ИДЗ 12.3 ИДЗ 12.4 Контрольная работа № 4 | ||
| | | Скалярное поле: основные понятия теории поля; поверхности и линии уровня; производная по направлению; градиент скалярного поля и его свойства. Векторное поле: векторные линии поля; поток векторного поля; дивергенция поля. Формула Остроградского-Гаусса; циркуляция поля; ротор поля. Формула Стокса. Оператор Гамильтона: векторные дифференциальные операции II порядка. Некоторые свойства основных классов векторных полей: соленоидальное поле, потенциальное поле, гармоническое поле. | ИДЗ 15.1 ИДЗ 15.2 ИДЗ 15.3 |
| | | Функции комплексного переменного: определение функции комплексного переменного; предел и непрерывность функции комплексного переменного; основные элементарные функции комплексного переменного; дифференцирование функции комплексного переменного. Условия Эйлера-Даламбера, аналитическая функция. Дифференциал; геометрический смысл модуля и аргумента производной. Интегрирование функции комплексного переменного: определение, свойства и правила вычисления интеграла; теорема Коши. Первообразная и неопределённый интеграл. Формула Ньютона-Лейбница; интеграл Коши. Ряды в комплексной области: числовые ряды; степенные ряды; ряд Тейлора; нули аналитической функции; ряд Лорана; классификация особых точек. | Опрос |
| | | Элементы операционного исчисления: преобразование Лапласа: оригиналы и их изображения; свойства преобразования Лапласа. Таблица оригиналов и изображений; обратное преобразование Лапласа: операционный метод решения линейных дифференциальных уравнений и их систем. | Опрос |
5.3 Разделы учебной дисциплины и междисциплинарные связи с обеспечиваемыми (последующими) дисциплинами
| № п/п | Наименование обеспе-чиваемых (последую-щих) дисциплин | № № разделов данной дисциплины, необходимых для изучения обеспечиваемых (последующих) дисциплин |
| 1 | ||
| 1. | Дисциплины профессионального цикла | + |
5.4 Разделы дисциплин и виды занятий
| № п/п | Наименование раздела дисциплины | Лекц. | Практ. зан. | Лаб. зан. | Семин | СРС | Все-го час. |
| 1. | Математический анализ | 90 | 72 | | | 90 | 252 |
6. Лабораторный практикум не предусмотрен.
7. Практические занятия (семинары)
| № п/п | № раздела дисциплины | Тематика практических занятий (семинаров) | Трудо-емкость (час.) |
| 1. | 1 | Числовая последовательность; предел числовой последовательности; предельный переход в неравенствах; предел монотонной ограниченной последовательности. Число e. Натуральные логарифмы. Предел функции: предел функции в точке; односторонние пределы; предел функции при x 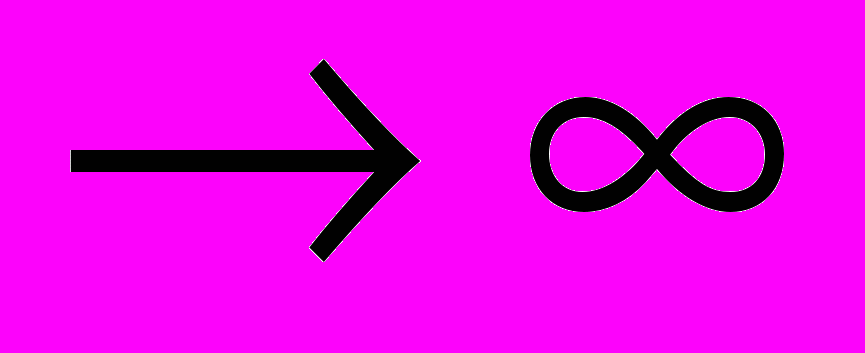 ; бесконечно большие функции (б.б.ф.). Бесконечно малые функции (б.м.ф.). Первый замечательный предел; второй замечательный предел. Эквивалентные бесконечно малые функции; применение эквивалентных бесконечно малых функций при вычислении пределов. ; бесконечно большие функции (б.б.ф.). Бесконечно малые функции (б.м.ф.). Первый замечательный предел; второй замечательный предел. Эквивалентные бесконечно малые функции; применение эквивалентных бесконечно малых функций при вычислении пределов. | 4 |
| 2. | 1 | Непрерывность функций: непрерывность функций в точке; непрерывность функций в интервале и на отрезке; точки разрыва функций и их классификация. Непрерывность элементарных функций; свойства функций, непрерывных на отрезке. Преобразование графиков функций. | 4 |
| 3. | 1 | Вычисление производной по определению, таблица производных основных элементарных функций. Правила дифференцирования. Уравнение касательной и нормали к кривой; связь между непрерывностью и дифференцируемостью функции. Производная сложной и обратной функций. Дифференцирование неявных и параметрически заданных функций, логарифмическое дифференцирование. Производные высших порядков: производные высших порядков явно заданной функции; производные высших порядков неявно заданной функции; производные высших порядков от функций, заданных параметрически. | 8 |
| 4. | 1 | Дифференциал функции. Таблица дифференциалов; применение дифференциала к приближенным вычислениям; дифференциалы высших порядков. | 2 |
| 5. | 1 | Дифференциал функции. Таблица дифференциалов; применение дифференциала к приближенным вычислениям; дифференциалы высших порядков. | 2 |
| 6. | 1 | Исследование функций при помощи производных: возрастание и убывание функций; максимум и минимум функций; наибольшие и наименьшие значения функции на отрезке; выпуклость графика функции. Точка перегиба; асимптоты графика функции; общая схема исследования функции и построения графика; формула Тейлора для произвольной функции. Правила Лопиталя | 4 |
| 7. | 1 | Комплексные числа: геометриическое изображение комплексных чисел; формы записи комплексных чисел; действия над комплексными числами; сложение, вычитание, умножение, деление комплексных чисел; возведение комплексных чисел в натуральную степень извлечение корней из комплексных чисел. Векторные и комплексные функции действительного переменного. | 2 |
| 8. | 1 1 | Таблица основных неопределённых интегралов. Основные методы интегрирования: метод непосредственного интегрирования; метод интегрирования подстановкой (заменой переменной); метод интегрирования по частям. Интегрирование рациональных функций: понятие о рациональных функциях; интегрирование простейших рациональных дробей; интегрирование рациональных дробей. Интегрирование тригонометрических функций: универсальная тригонометрическая подстановка; интегралы типа 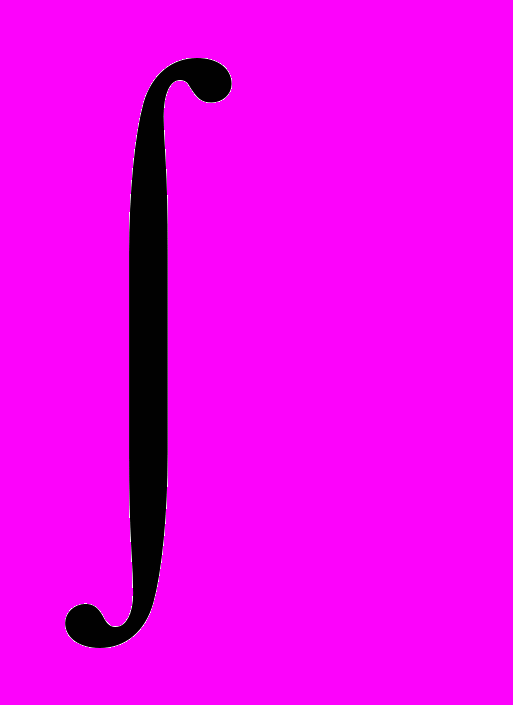 sin sin x cos x cos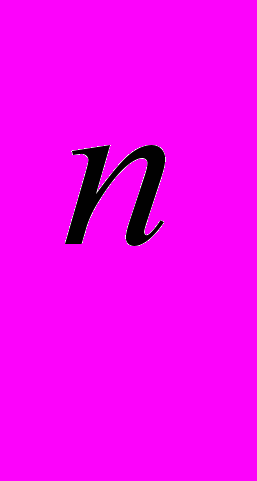 x dx; использование тригонометрических преобразований. Интегрирование иррациональных функций: квадратичные иррациональности; дробно– линейная подстановка; тригонометрические подстановки; интегралы типа x dx; использование тригонометрических преобразований. Интегрирование иррациональных функций: квадратичные иррациональности; дробно– линейная подстановка; тригонометрические подстановки; интегралы типа 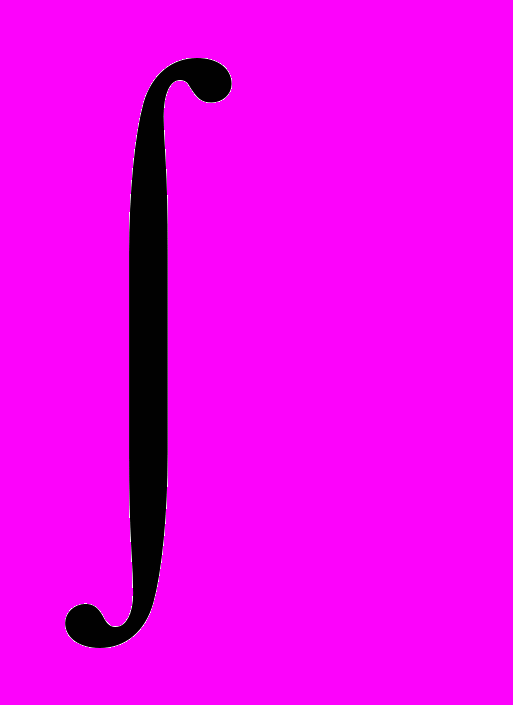 R(x; R(x;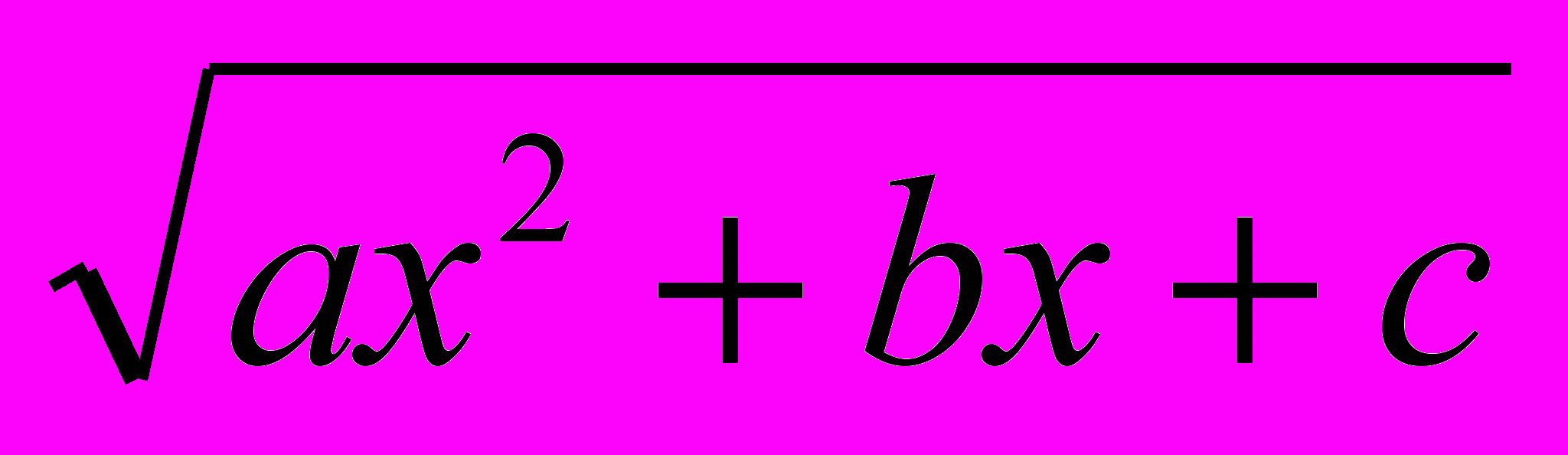 ) dx; интегрирование дифференциального бинома; «берущиеся» и «неберущиеся» интегралы. ) dx; интегрирование дифференциального бинома; «берущиеся» и «неберущиеся» интегралы.Вычисления определённого интеграла: формула Ньютона – Лейбница; интегрирование подстановкой (заменой переменной); интегрирование по частям; интегрирование чётных и нечётных функций в симметричных пределах. Вычисление несобственных интегралов 1-рода и 2-рода. Геометрические и физические приложения определённого интеграла: схемы применения определённого интеграла; вычисление длины дуги плоской кривой; вычисление объёма тела; вычисление площади поверхности вращения; механические приложения определённого интеграла. | 10 6 |
| 9. | |||
| 10. | 1 | Функции двух: переменных, предел функций, непрерывность функции в ограниченной замкнутой области. Частные производные первого порядка и их геометрическое истолкование; частные производные высших порядков; дифференцируемость и полный дифференциал функции; применение полного дифференциала к приближённым вычислениям; дифференциалы высших порядков; производная сложной функции. Полная производная; инвариантность формы полного дифференциала; дифференцирование неявной функции. Нахождение касательной плоскости и нормали к поверхности. Экстремум функции двух переменных; наибольшее и наименьшее значение функции в замкнутой области. | 8 |
| 11. | 1 | Общие сведения о дифференциальных уравнениях: задачи, приводящие к дифференциальным уравнениям. Решение дифференциальных уравнений первого порядка: уравнения с разделяющимися переменными; однородные дифференциальные уравнения; линейные уравнения; уравнения Я.Бернулли; уравнения в полных дифференциалах. Интегрирующий множитель. Дифференциальные уравнения высших порядков: уравнения с понижением порядка; линейные дифференциальные уравнения высших порядков; линейные однородные дифференциальные уравнения второго порядка; линейные однородные дифференциальные уравнения n-го порядка. Интегрирование линейных однородных уравнений высших порядков с постоянными коэффициентами: интегрирование ЛОДУ второго порядка с постоянными коэффициентами; интегрирование ЛОДУ n-го порядка с постоянными коэффициентами. Линейные неоднородные дифференциальные уравнения (ЛНДУ): структура общего решения ЛНДУ второго порядка; метод вариации произвольных постоянных; интегрирование ЛНДУ второго порядка с постоянными коэффициентами и правой частью специального вида; интегрирование ЛНДУ n-го порядка (n>2) с постоянными коэффициентами и правой частью специального вида. Решение системы дифференциальных уравнений. | 12 |
| 12. | 1 | Вычисление двойного интеграла в декартовых координатах, переход к полярным координатам; приложения двойного интеграла. Вычисление тройного интеграла в декартовых координатах; замена переменных в тройном интеграле. Вычисление тройного интеграла в цилиндрических и сферических координатах; некоторые приложения тройного интеграла. | 8 |
| 13. | 1 | Криволинейный интеграл I рода: вычисление криволинейного интеграла I рода; некоторые приложения криволинейного интеграла I рода. Криволинейный интеграл II рода: вычисление криволинейных интегралов II рода; формула Остроградского-Грина; условие независимости криволинейного интеграла II рода от пути интегрирования; некоторые приложения криволинейного интеграла II рода. | 8 |
| 14. | 1 | Поверхностный интеграл I рода: вычисление поверхностного интеграла I рода; некоторые приложения поверхностного интеграла I рода. Поверхностный интеграл II рода: вычисление поверхностного интеграла II рода; формула Остроградского-Гаусса; формула Стокса; некоторые приложения поверхностного интеграла II рода. | 8 |
| 15. | 1 | Числовые ряды: ряд геометрической прогрессии; необходимый признак сходимости числового ряда. Гармонический ряд. Достаточные признаки сходимости знакоположительных рядов: признаки сравнения рядов; признак Даламбера; радикальный признак Коши интегральный признак Коши. Обобщенный гармонический ряд. Знакочередующиеся и знакопеременные ряды. Признак Лейбница; общий достаточный признак сходимости знакопеременных рядов; абсолютная и условная сходимости числовых рядов. Функциональные ряды: область сходимости; равномерная сходимость. Степенные ряды: интервал и радиус сходимости степенного ряда. Разложение функций в степенные ряды. Некоторые приложения степенных рядов: приближенное вычисление значений функции; приближенное вычисление определенных интегралов; приближенное решение дифференциальных уравнений. Ряды Фурье: вычисление коэффициентов ряда Фурье. Разложение в ряд Фурье 2π - периодических функций; разложение в ряд Фурье четных и нечетных функций; разложение в ряд Фурье функций произвольного периода; представление непериодической функции рядом Фурье; комплексная форма ряда Фурье. | 8 |
| 16. | 1 | Теория поля. Скалярное поле: поверхности и линии уровня; производная по направлению; градиент скалярного поля и его свойства. Векторное поле: векторные линии поля; поток векторного поля; дивергенция поля. Формула Остроградского-Гаусса; циркуляция поля; ротор поля. Формула Стокса. Оператор Гамильтона: векторные дифференциальные операции II порядка. Соленоидальное поле, потенциальное поле, гармоническое поле. | 6 |
| 17. | 1 | Предел и непрерывность функции комплексного переменного; основные элементарные функции комплексного переменного; дифференцирование функции комплексного переменного. Условия Эйлера-Даламбера, аналитическая функция. Дифференциал; геометрический смысл модуля и аргумента производной. Комфорные отображения. Интегрирование функции комплексного переменного | 4 |
| 18. | 1 | Оригиналы и их изображения. Таблица оригиналов и изображений; обратное преобразование Лапласа: Теорема разложения; формула Римана-Меллина; операционный метод решения линейных дифференциальных уравнений и их систем. | 4 |
8. Оценочные средства для текущего контроля успеваемости,
промежуточной аттестации по итогам освоения дисциплины и учебно-методическое обеспечение самостоятельной работы студентов.
Экзаменационные вопросы составляются на основе приведенного выше содержания разделов дисциплины (п. 5.2), а экзаменационные задачи – на основе содержания практических занятий (п. 7). Список экзаменационных задач формируется на основе пособий [5], [6] из перечня учебно-методического обеспечения дисциплины (п. 9 ниже). Эти же пособия могут быть использованы на практических занятиях. Индивидуальные домашние задания составляются на основе ИДЗ из пособия [6].
9. Учебно-методическое и информационное обеспечение учебной дисциплины:
а) основная литература
- Конспект лекций по высшей математике. Полный курс Письменный Д.Т., М, Айрис Пресс, 2006 г.
- Пискунов Н.С. Дифференциальное и интегральное исчисление. Т. 1.2.М., Интеграл-Пресс, 2005г.
- Берман Г.Н. Сборник задач и упражнений по математическому анализу, 17-е издание М., профессия, 2006г.
- Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. – М.: Наука, 1987. – 600 с.
- Кузнецов А. Сборник заданий по высшей математике. Типовые расчеты. – М.: Высшая школа, 1983. – 176 с.
- Рябушко А.П., Бархатов В.В., Державец В.В., Юруть И.Б. Сборник индивидуальных заданий по высшей математике: в 3-х частях. – Минск, Высшая школа, 1990-1991.
б) дополнительная литература
1. Ильин В.А., Позняк Э.Г.Основы математического анализа, ч..1, М., Наука, 1980г.
2. Ильин В.А., Позняк Э.Г. Основы математического анализа, ч..2, М., Наука, 1982г.
3. Сборник задач по математике для втузов: Линейная алгебра и основы
математического анализа. Под ред. А.В. Ефимова, Б.П. Демидовича, М., Наука, 1986г.
4. Самохин М.В., Каган М.Л.Математика в инженерном вузе. Алгебра и геометрия, М., Стройиздат. 2003г.
в) программное обеспечение и Интернет-ресурсы
- Википедия [Электронный ресурс] : [свобод. Интернет-энцикл.] – Электрон. дан. и прогр. – Режим доступа: ссылка скрыта, свободный. – Русскояз. часть междунар. проекта «Википедия». – Загл. с экрана. – Дата обращения: 8.01.2011.
10. Материально-техническое обеспечение дисциплины:
Учебная аудитория (наличие доски обязательно), оснащенная оргтехникой.
11. Методические рекомендации по организации изучения дисциплины:
При преподавании курса необходимо ориентироваться на современные образовательные технологии. Аудиторная и самостоятельная работы должны быть направлены на углубление и расширение полученных знаний, на закрепление приобретенных навыков и применение формируемых компетенций. Кроме того, рекомендуется использовать дифференцированное обучение и активные методы проверки знаний при проведении проверочных работ, тестирования. Это достигается, например, путем организации индивидуальной самостоятельной работы студентов.
При проведении промежуточной аттестации (зачета, экзамена), независимо от формы ее проведения (устной или письменной), важно учесть все виды работ, оценить уровень знаний студентов по всем разделам учебной дисциплины.
Примерный перечень экзаменационных вопросов должен доводиться до студентов в начале изучения дисциплины. При необходимости он может быть уточнен не позднее, чем за месяц до начала экзаменационной сессии. На его основе составляются экзаменационные билеты, утверждаемые заведующим кафедрой.
Авторы (разработчики):
| Кафедра математики и теоретической механики | | Зав. кафедрой, доцент | | Борискина И.П. |
| Кафедра математики и теоретической механики | | Старший преподаватель | | Коновалова Н.И. |
| Рецензенты(эксперты) | | | | |
| ____________________ (место работы) | | _______________ (занимаемая должность) | | _________________ (инициалы, фамилия) |
| ____________________ (место работы) | | _______________ (занимаемая должность) | | _________________ (инициалы, фамилия) |
Программа одобрена на заседании
(Наименование уполномоченного органа вуза (УМК, НМС, Ученый совет)
от года, протокол № .
5. Структура учебной дисциплины (модуля)
| № п/п | Раздел учебной дисциплины | Курс | Семестр | Неделя семестра | Виды* учебной работы, в т.ч. СРС и трудоёмкость (в часах) | Формы текущего контроля успеваемости (по неделям семестра) | Форма промежуточной аттестации | |||
| | | | | |||||||
| 1. | Дифференциальное и интегральное исчисление функций одной переменной | | | | | | | | | |
| 2. | Дифференциальное и интегральное исчисление функций многих переменных | | | | | | | | | |
| 3. | Элементы теории поля | | | | | | | | | |
| 4. | Обыкновенные дифференциальные уравнения | | | | | | | | | |
| 5. | Теория рядов и гармонический анализ | | | | | | | | | |
| 6. | Операционное исчисление | | | | | | | | | |
