Программа по математике для специальных (коррекционных) классов VII вида
| Вид материала | Программа |
- Э. Я. Развитие сенсорной сферы детей Программа курса, 298.16kb.
- Программа по информатике для специальных (коррекционных) классов VII вида 5 класс Пояснительная, 1447.84kb.
- Пояснительная записка рабочая программа по чтению и развитию речи для 5 класса составлена, 401.8kb.
- Программа по истории для специальных (коррекционных) классов VII вида 5 класс История, 992.38kb.
- Середова Ольга Назифовна Данная программа, 179.02kb.
- Обеспечение образовательного процесса по программе специальных (коррекционных) образовательных, 218.33kb.
- Протокол №104. 1, 465.25kb.
- Методические рекомендации по обучению и воспитанию детей с задержкой психического развития, 203.26kb.
- Пояснительная записка Учебные программы для V-IX классов специальных (коррек-ционных), 5649.23kb.
- Мотивация деятельности школьников в специальных коррекционных классах VII вида, 251.84kb.
Содержание программы
1. Рациональные дроби (22 ч.) + 5
Рациональная дробь. Основное свойство дроби, сокращение дробей. Сложение, вычитание, умножение и деление дробей. Возведение дроби в степень. Преобразование рациональных выражений. Функция у =
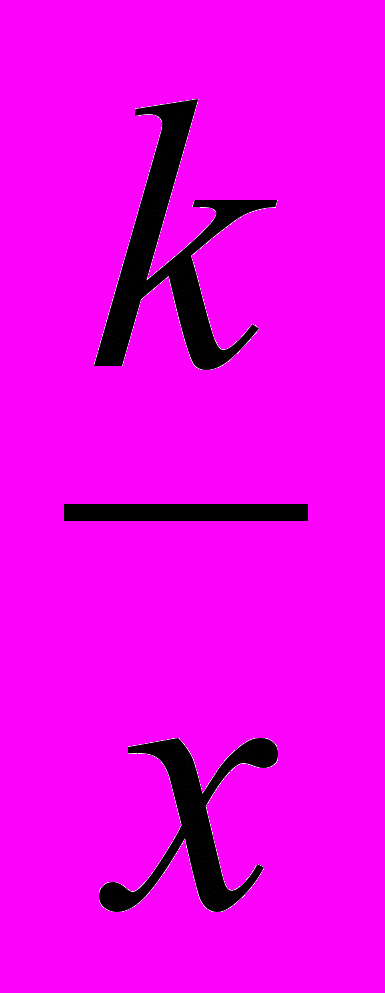и ее график.Основная цель – выработать умение выполнять преобразования рациональных дробей.
Главное место занимают алгоритмы действий с дробями. Задания не должны быть громоздкими. Знаменатели дробей должны раскладываться на множители способом вынесения общего множителя за скобки и (или) по формуле а2 – в2 = (а – в)(а + в).
В комбинированных заданиях на все действия с дробями знаменатели должны быть разложенными на множители. Не рассматривать случаи, когда требуется свернуть знаменатель по формуле квадрат суммы (разности) двух выражений.
Свойства функции у =
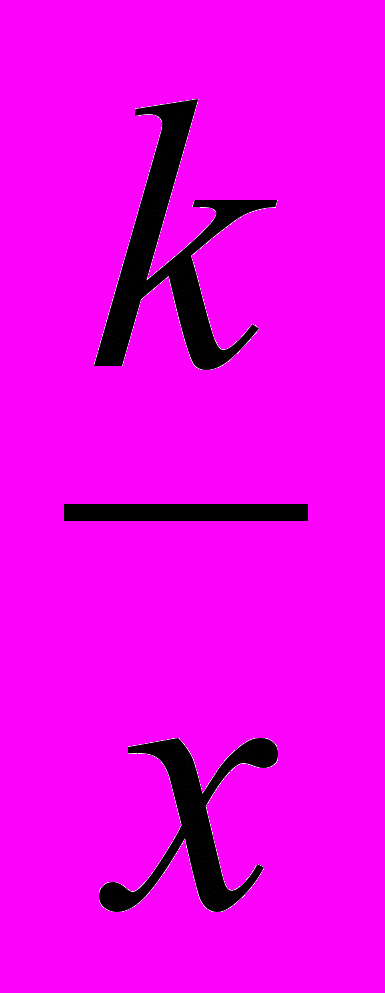рассматривать на конкретных графиках (ознакомительно).В ходе изучения данной темы учащиеся должны усвоить алгоритм выполнения действий с рациональными дробями; должны усвоить выполнять действия с дробями в простых ситуациях, строить график функции у =
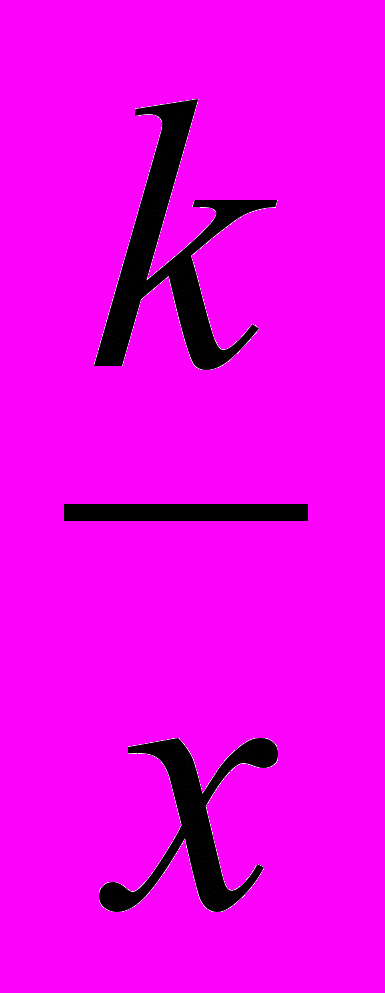.2. Квадратные корни (17 ч.) + 8
Понятие об иррациональном числе (ознакомительно). Общие сведения о действительных числах (ознакомительно). Понятие арифметического квадратного корня. Уравнение х2 = а, свойства квадратных корней. Преобразование выражений, содержащих квадратные корни. Функция у =
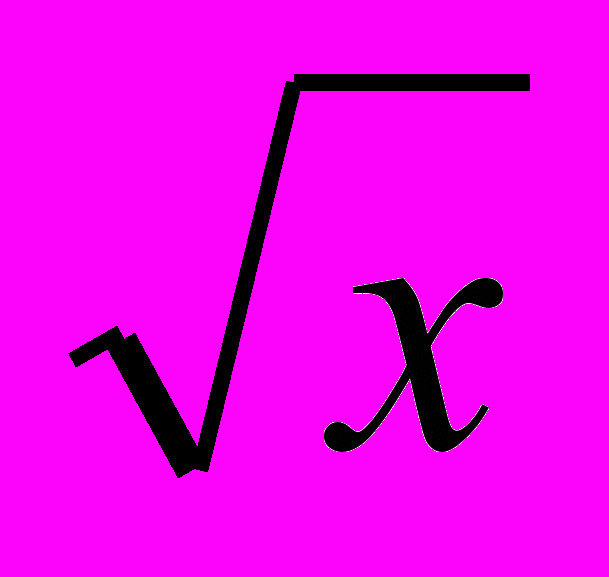, ее график (ознакомительно). Основная цель – выработать умение выполнять простейшие преобразования выражений, содержащих квадратные корни.
В данной теме учащиеся знакомятся с понятием иррационального числа, действительного числа.
Основное внимание следует уделить выработке умений извлекать квадратный корень, выполнять преобразования выражений, содержащих квадратные корни; достаточно ограничиться вынесением числового множителя из-под знака корня и внесением числового множителя под знак корня, а также освобождением от иррациональности в знаменателе в выражениях вида
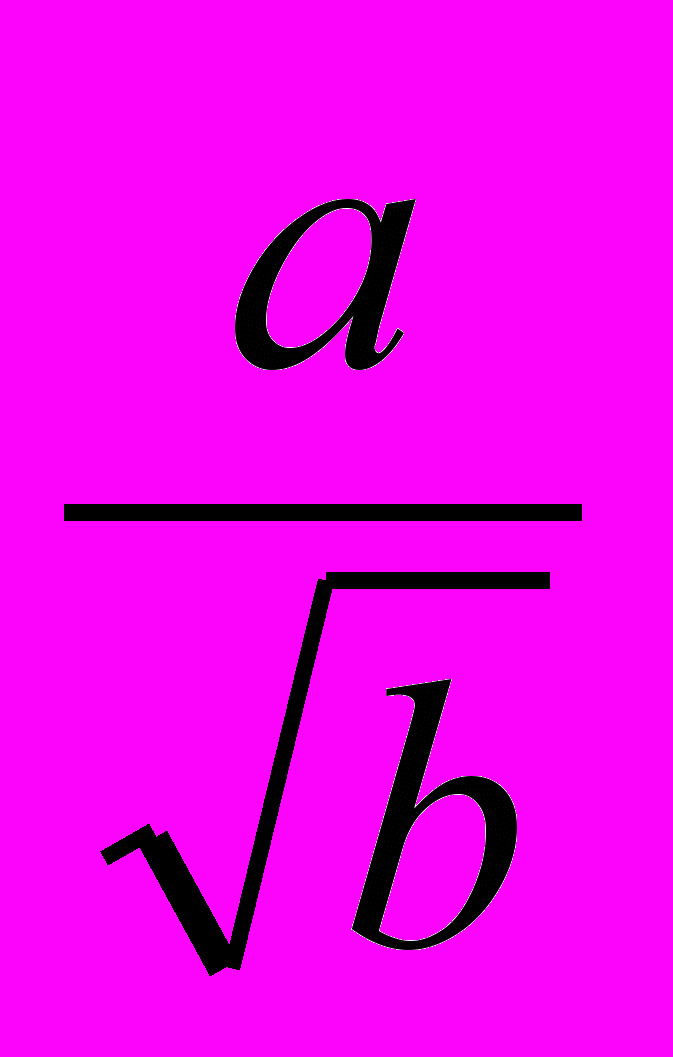.В ходе изучения данной темы учащиеся должны научиться извлекать квадратный корень, использовать свойства арифметического квадратного корня, вносить, множитель под знак корня, выносить множитель из-под знака корня.
3. Квадратные уравнения (20 ч.) + 8
Определение квадратного уравнения. Решение квадратных уравнений по формуле. Решение несложных задач с помощью квадратных уравнений. Решение дробно-рациональных уравнений.
Основная цель – выработать умения решать квадратные уравнения, дробные рациональные уравнения, применять их к решению задач.
Основное внимание следует уделить решению уравнений вида ах2 + bх +с = 0, где а ≠ 0, по формуле корней. Рассмотреть одну (основную) формулу без вывода. Исключить решение квадратных уравнений выделением квадрата двучлена, теорему Виета.
При рассмотрении дробных рациональных уравнений обратить внимание на необходимость дополнительных исследований, позволяющих исключить посторонние корни. При этом не рассматривать такие уравнения, знаменатели которых требуют применения формул квадрата суммы (разности) двух выражений.
При решении тестовых задач решаются задачи, связанные с периметром и площадью прямоугольника. Исключить решение задач составлением дробных рациональных уравнений.
В ходе изучения данной темы учащиеся должны усвоить алгоритм решения квадратного уравнения, уметь решать квадратные уравнения.
4. Неравенства (19 ч.) + 3
Числовые неравенства и их свойства. Почленное сложение и умножение числовых неравенств. Применение свойств неравенств к оценке выражений х + у, ху. Линейное неравенство с одной переменной. Система линейных неравенств с одной переменной.
Основная цель – выработать у учащихся умение решать линейные неравенства с одной переменной и их системы.
Свойства числовых неравенств рассматриваются на конкретных примерах и не доказываются. Дается понятие о числовых промежутках, вводятся соответствующие обозначения. При решении неравенств используются свойства равносильности неравенств, которые разъясняются на конкретных примерах. Особое внимание уделяется отработке умения решать неравенства вида ах > в, ах < в, остановившись специально на случае, когда а < 0.
Умение решать линейные неравенства является основой для решения систем двух линейных неравенств с одной переменной.
В ходе изучения данной темы учащиеся должны решать линейные неравенства с одной переменной и их системы.
5. Степень с целым показателем (10 ч.) + 4
Степень с целым показателем и ее свойства. Стандартный вид числа.
Основная цель – сформировать понятие степени с целым отрицательным показателем; выработать умение выполнять преобразования простейших выражений, содержащих степень с целым показателем, ввести понятие стандартного вида числа.
В теме рассматриваются свойства степеней с целыми показателями (без доказательства). Специальное внимание следует уделить записи чисел в стандартном виде, которая используется в физике, технике.
В ходе изучения темы учащиеся должны усвоить определение степени с отрицательным показателем; уметь выполнять преобразования простейших выражений, содержащих степени с целыми показателями.
6. Элементы комбинаторики и статистики (2 ч.)
Тема рассматривается в ознакомительном порядке.
7. Повторение (12 ч.) + 6
- Рациональные дроби.
- Квадратные корни.
- Квадратные неравенства.
- Степень с целым показателем.
- Неравенства.
Методические рекомендации
Уроки в СКК VII вида необходимо проводить с учетом определенных принципов и требований.
Успешно проходят уроки в нетрадиционной форме - с использованием игровых моментов. Необходимо многократное повторение материала. Формулы, алгоритмы решения должны быть представлены в наглядном виде.
При изучении теоретического материала используется деятельностный подход, т.е. решение задач и выполнение заданий наглядно - практического характера.
В процессе изучения каждый темы проводятся самостоятельные работы обучающего характера. Вначале самостоятельные работы необходимо проводить по образцу, алгоритму, впоследствии постоянно усложняя материал. После изучения темы или раздела организуются контрольные работы.
Геометрия
Пояснительная записка
Преподавание геометрии в 8 классе ведется из расчета 2 часа в неделю (68 часов в год) по учебнику: Геометрия: Учебник для 7-9 кл. общеобразовательных учреждений/ Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. (М.:Просвещение, 1999 и последующие годы).
Некоторые темы рекомендуется давать в ознакомительном плане, сократив количество часов, отводимых на их изучение, исключив доказательства теорем, оставив для заучивания лишь формулировки. К таким темам относятся: «Теорема Фалеса», «Основные тригонометрические тождества», «Пересечение прямой с окружностью».
Следует исключить вопрос о взаимном расположении окружностей.
В теме «Подобие фигур» рекомендуется рассмотреть доказательство одного признака подобия, остальные темы - давать в ознакомительном плане, предложив для заучивания только формулировки теорем.
Ввиду сложности темы «Векторы на плоскости» целесообразно ограничить знакомство с нею понятием вектор, сложением и вычитанием векторов. Остальные разделы темы рекомендуется вынести для более подробного изучения на факультативные занятия.
Освободившиеся часы использовать на решение задач, построения и повторение.
При изучении геометрии в 8 классе следует особое внимание уделять практической направленности курса, исключив и упростив наиболее сложный для восприятия теоретический материал.
Учебно-тематический план
| № п/п | Разделы и темы | Всего | Лаб. работы | Практ. работы | Экскурсии | Контрол. работы | ||||
| 1 | Вводное повторение | 3 | | | | - | ||||
| 1.1 | Повторение по теме «Параллельность прямых» | | | | | | ||||
| 1.2 | Повторение по темам «Признаки равенства треугольников», «Соотношения между сторонами и углами в треугольнике» | | | | | | ||||
| 1.3 | Повторение по темам «Соотношения между сторонами и углами в треугольнике» | | | | | | ||||
| 2 | Четырехугольники | 14 | | | | 1 | ||||
| 2.1 | Понятие многоугольника, выпуклого многоугольника | | | | | | ||||
| 2.2 | Сумма углов выпуклого многоугольника | | | | | | ||||
| 2.3 | Параллелограмм и его свойства | | | | | | ||||
| 2.4 | Признаки параллелограмма | | | | | | ||||
| 2.5 | Трапеция. Равнобедренная трапеция | | | | | | ||||
| 2.6 | Трапеция. Средняя линия трапеции. Теорема Фалеса | | | | | | ||||
| 2.7 | Задачи на построение | | | | | | ||||
| 2.8 | Прямоугольник, его свойства и признаки | | | | | | ||||
| 2.9 | Ромб, его свойства и признаки | | | | | | ||||
| 2.10 | Квадрат, его свойства и признаки | | | | | | ||||
| 2.11 | Осевая и центральная симметрия. Решение задач | | | | | | ||||
| 2.12 | Подготовка к контрольной работе. Решение задач | | | | | | ||||
| 2.13 | Контрольная работа № 1 по теме «Четырехугольники» | | | | | | ||||
| 2.14 | Анализ результатов контрольной работы. Коррекция ЗУН | | | | | | ||||
| 3 | Площади фигур | 14 | | | | 1 | ||||
| 3.1 | Площадь многоугольника. Равносоставленные и равновеликие фигуры | | | | | | ||||
| 3.2 | Площадь прямоугольника | | | | | | ||||
| 3.2 | Площадь параллелограмма | | | | | | ||||
| 3.4 | Площадь треугольника | | | | | | ||||
| 3.5 | Площадь треугольника. Решение задач | | | | | | ||||
| 3.6 | Площадь трапеции | | | | | | ||||
| 3.7 | Решение задач на вычисление площадей фигур | | | | | | ||||
| 3.8 | Решение задач на нахождение площади | | | | | | ||||
| 3.9 | Теорема Пифагора | | | | | | ||||
| 3.10 | Теорема, обратная теореме Пифагора | | | | | | ||||
| 3.11 | Решение задач по теме «Теорема Пифагора» | | | | | | ||||
| 3.12 | Подготовка к контрольной работе. Решение задач | | | | | | ||||
| 3.13 | Контрольная работа № 2 по теме «Площадь» | | | | | | ||||
| 3.14 | Анализ результатов контрольной работы. Коррекция ЗУН | | | | | | ||||
| 4 | Подобные треугольники | 18 | | | | 2 | ||||
| 4.1 | Определение подобных треугольников, коэффициент подобия | | | | | | ||||
| 4.2 | Отношение площадей подобных треугольников | | | | | | ||||
| 4.3 | Первый признак подобия треугольников | | | | | | ||||
| 4.4 | Решение задач на применение первого признака подобия треугольников | | | | | | ||||
| 4.5 | Второй и третий признаки подобия треугольников | | | | | | ||||
| 4.6 | Решение задач на применение признаков подобия треугольников | | | | | | ||||
| 4.7 | Подготовка к контрольной работе. Решение задач | | | | | | ||||
| 4.8 | Контрольная работа № 3 по теме «Признаки подобия треугольников» | | | | | | ||||
| 4.9 | Анализ результатов контрольной работы. Коррекция ЗУН | | | | | | ||||
| 4.10 | Средняя линия треугольника. Свойство медиан треугольника | | | | | | ||||
| 4.11 | Пропорциональные отрезки в прямоугольном треугольнике | | | | | | ||||
| 4.12 | Синус острого угла прямоугольного треугольника. Косинус острого угла прямоугольного треугольника | | | | | | ||||
| 4.13 | Тангенс острого угла прямоугольного треугольника. Котангенс острого угла прямоугольного треугольника | | | | | | ||||
| 4.14 | Значения синуса, косинуса и тангенса для углов от 0º до 180º | | | | | | ||||
| 4.15 | Решение прямоугольных треугольников. Основное тригонометрическое тождество | | | | | | ||||
| 4.16 | Подготовка к контрольной работе. Решение задач | | | | | | ||||
| 4.17 | Контрольная работа № 4 по теме «Соотношения между сторонами и углами прямоугольного треугольника» | | | | | | ||||
| 5 | Вектор. Метод координат | 14 | | | | 2 | ||||
| 5.1 | Понятие вектора. Длина (модуль) вектора | | | | | | ||||
| 5.2 | Координаты вектора | | | | | | ||||
| 5.3 | Метод координат | | | | | | ||||
| 5.4 | Равенство векторов | | | | | | ||||
| 5.5 | Простейшие задачи на координатах | | | | | | ||||
| 5.6 | Решение задач | | | | | | ||||
| 5.7 | Контрольная работа № 5 по теме «Векторы» | | | | | | ||||
| 5.8 | Операции над векторами: умножение на число | | | | | | ||||
| 5.9 | Сложение векторов | | | | | | ||||
| 5.10 | Разложение векторов | | | | | | ||||
| 5.11 | Скалярное произведение векторов | | | | | | ||||
| 5.12 | Угол между векторами | | | | | | ||||
| 5.13 | Решение задач | | | | | | ||||
| 5.14 | Контрольная работа № 6 по теме «Операции над векторами» | | | | | | ||||
| 6 | Итоговое повторение | 5 | | | | 1 | ||||
| 6.1 | Итоговое повторение по темам «Четырехугольники», «Площадь» | | | | | | ||||
| 6.2 | Итоговое повторение по темам «Подобные треугольники», «Вектор. Метод координат»» | | | | | | ||||
| 6.3 | Итоговая контрольная работа № 6 за курс геометрии 8 класса | | | | | | ||||
| 6.4 | Анализ результатов контрольной работы. Коррекция ЗУН | | | | | | ||||
| 6.5 | Итоговое повторение курса геометрии 8 класса | | | | | | ||||
Высвободившееся время используется по усмотрению учителя.